밸브 스프링 서어징 측정을 위한 스트레인 게이지 부착 위치에 관한 연구

1. 서 론

밸브 스프링은 자동차 엔진에서 가장 큰 변동 하중을 받는 부품들 중 하나이다. 엔진이 고속으로 운전 할 경우 스프링에는 서어징 현상이라는 내부 진동이 발생하는데, 이는 밸브 스프링의 피로 수명뿐만 아니라 밸브트레인의 동적 거동에도 큰 영향을 미친다. 그러므로 밸브트레인 설계시 밸브 스프링 서어징 현상을 예측하고 정확히 측정하는 것은 매우 중요한 과정이다.^1,2)

밸브 스프링 서어징의 측정은 일반적으로 스프링 외면에 스트레인 게이지(Strain gauge)를 부착하거나 스프링 하단에 도너츠형 로드 셀(Ring type load cell)을 부착하는 방법이 사용된다. 로드 셀을 부착하는 방식은 실린더 헤드의 스프링 좌면을 로드셀 두께만큼 가공해야하는 문제가 있는데 흡기 포트, 냉각수 수로 등의 간섭으로 인하여 항상 가능한 것은 아니다. 스트레인 게이지를 이용하는 경우에는 게이지의 선정, 부착 위치, 회로 구성, 노이즈 대책, 스프링 회전, 고속 운전시 게이지 선의 보호 방법, 등 다소 성가신 기술적 문제들이 동반된다. 그러나 스프링 선(Spring wire)의 비틀림 응력을 직접적으로 측정할 수 있을 뿐만 아니라 실린더 헤드에 어떤 손상도 입히지 않으므로 보편적으로 사용되는 방식이다.^3-6)

밸브 스프링의 서어징 진폭은 스트레인 게이지의 부착 위치에 크게 영향을 받는데, 최적의 부착 위치가 어디냐 하는 문제는 연구자들 사이에 다소 이견이 존재하는 것이 현실이다. 등피치 원통형 스프링(Constant pitch cylindrical spring)에 대해서는 보편적인 합의점이 존재하지만, 부등피치 벌집형 스프링(Beehive spring)에 대해서는 최근까지도 해소되지 않는 논쟁거리가 존재한다.

본 연구에서는 스트레인 게이지의 부착 위치에 관한 몇 가지 논쟁 사항들을 해소하기 위하여 다양한 실험을 수행하였으며, 게이지를 부착 할 때 고려되어야 할 몇 가지 사항들을 제안하고자 한다.

2. 샘플 제작 및 하중 실험

밸브 스프링 서어징 진폭을 측정하기 위한 최적의 스트레인 게이지 부착 위치를 찾기 위하여 우선 2단 피치 원통형 스프링 1종과 2단 피치 벌집형 스프링 1종을 선정하고, 각각의 스프링에 대하여 2개씩의 샘플을 확보하였다. 샘플 스프링의 설계 사양을 정리하면 Table 1과 같다. 원통형, 벌집형 모두 난형 단면(Oval cross section)을 가지는 스프링 선이 사용되었으며, 하단에 댐핑 코일(Narrow pitch turns)을 가지는 2단 피치 스프링이다.

Table 1

Specifications of cylindrical and beehive springs used in the experiment

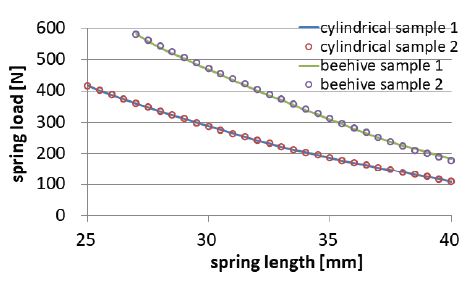
원통형과 벌집형 스프링 각각 2개씩의 동일 사양 샘플에 대하여 스프링 높이에 대한 하중 실험을 수행하였다. Fig. 1은 스프링 하중 측정 장치를 나타낸 것이다. Fig. 2는 원통형 스프링과 벌집형 스프링에 대한 하중 측정 실험 결과를 그래프로 나타낸 것이다. 그림에 보듯이 스프링 높이에 대한 하중들은 그래프로 구별하기 힘들 정도로 샘플별 편차가 적은 것을 확인할 수 있다.

Fig. 1

Valve spring load test equipment (spring height & equivalent load)

Fig. 2

Test result of spring height-load diagram (cylindrical springs & beehive springs)

Table 2는 스프링 장착 높이와 최대 밸브 변위에 해당하는 스프링 높이(최대 작동하중 높이)에 대한 설계 하중과 측정값들을 비교한 것이다. 원통형과 벌집형 모두 스프링 운전 범위에서 설계 값 대비 최대 편차는 2 % 이내라는 것을 확인할 수 있는 데, 이는 밸브 스프링 품질관리 범위를 충분히 만족하는 수준이다.

Table 2

Summary of valve spring load test results

3. 스트레인 게이지 부착위치 선정 및 정하중 실험

밸브 스프링의 서어징 진폭을 측정하는데 있어서 게이지의 부착 위치는 매우 민감한 문제이다. 실제로 부착 위치에 따라서 측정값이 다르게 나타나는 경향이 있다. 본 연구에서는 스프링의 서어징 진폭이 가장 높게 측정되는 지점을 찾는 것이 목적이므로 원통형과 벌집형 각각의 스프링에 대하여 몇 개의 후보 위치를 선정하고 실험을 수행하였다.

3.1 원통형 스프링

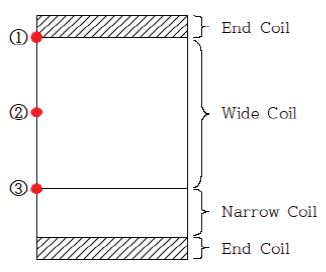
Fig. 3은 본 실험에서 사용된 원통형 스프링의 게이지 부착 위치를 나타낸 것이다. Fig. 3의 ①지점은 스프링 상단의 끝단 코일과 유효코일의 경계지점이며, ③지점은 조권(Wide pitch coil)과 밀권(Narrow pitch coil)의 경계지점이다. ②지점은 ①지점과 ③지점의 중간 지점을 의미한다.

Fig. 3

Strain gauge attachment locations on cylindrical spring

원통형 스프링의 경우 일반적으로 통용되는 부착 위치는 스프링 상단의 끝단과 유효코일의 경계부분(①지점)인데, 지나치게 끝단에 접근하면 스프링 압축 시 게이지 부착 부위가 끝단에 밀착되어 비틀림 응력이 제한되는 현상이 발생한다. 그러므로 끝단을 제외하고 0.5권 정도의 여유를 가지는, 스프링 상단으로부터 1.5권 지점에 게이지를 부착하여 측정하기도 한다. 보다 정밀하게 부착 위치를 선정하기 위해서는 스프링을 작동 범위 최대 하중고(밸브 최대 변위에 해당하는 높이)까지 압축하고 간극 게이지(Gap gauge)를 이용하여 끝단 경계 지점을 찾아서 부착 위치를 선정하는 방법이 널리 사용되고 있다. 이때 간극 게이지는 자동차 업체별로 0.1 mm 혹은 0.05 mm 두께의 게이지를 표준으로 사용하는데, 어느 게이지를 사용하던지 부착 위치에 의미 있는 차이는 없는 것으로 밝혀졌다. Fig. 4는 ①, ②, ③지점에 게이지가 부착된 원통형 스프링을 보여주고 있다.

Fig. 4

Photo of strain gauges attached to the cylindrical spring

3.2 벌집형 스프링

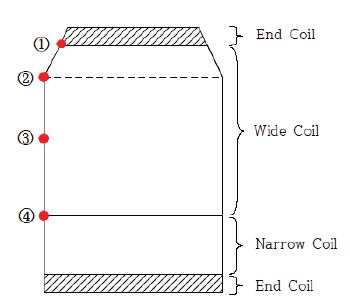
벌집형 스프링은 원통형에 비하여 위치별 응력 분포가 다소 복잡한 양상을 보인다. Fig. 5는 본 실험에서 사용된 벌집형 스프링의 게이지 부착 위치를 나타낸 것이다. Fig. 5의 ①지점은 원통형 스프링에서 설명한 것과 같이 스프링 상단의 끝단 코일과 유효코일의 경계지점이며, ④지점은 조권(Wide pitch coil)과 밀권(Narrow pitch coil)의 경계지점이다. ②지점은 원추부(Conical) 유효코일과 원통부 유효코일의 경계지점이며, ③지점은 ①지점과 ④지점의 중간 지점을 의미한다.

Fig. 5

Strain gauge attachment locations on beehive spring

벌집형 스프링의 경우에도 원통형 스프링과 마찬가지로 1차 진동 모드가 가진 된다면 스프링 상단과 하단의 경계지점(①,④)에서 높은 서어징 진폭이 발생할 가능성이 있다는 것을 쉽게 유추할 수 있다. 만약 2차 진동 모드가 크게 가진된다면 원통형과 마찬가지로 스프링 중앙부위(③)의 변동응력 진폭이 클 것이다. 다만 원추부의 강성과 질량의 분포는 원통 부위와는 달리 균일하지 못하며 스프링 직경이 작아짐에 따라 강성은 증가하고 이동질량(Moving mass)은 감소한다. 따라서 벌집형 스프링의 내부 진동 양상이 원통형과는 크게 다를 것이다. 이러한 점을 고려하여 원추부와 원통부의 경계지점(②)에도 스트레인 게이지를 부착하여 응력변동 사항을 확인하였다. Fig. 6은 ①, ②, ③, ④지점에 게이지가 부착된 벌집형 스프링을 보여주고 있다.

Fig. 6

Photo of strain gauges attached to the beehive spring

3.3 정적 하중에 대한 응력 분포

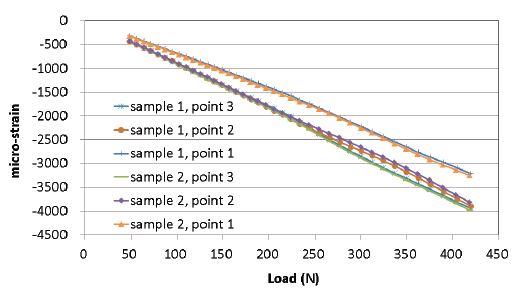
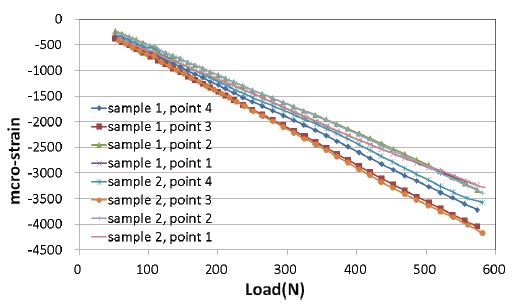
원통형과 벌집형 각각의 스프링에 대하여 정적 하중을 단계적으로 증가시키며 각 지점에서 발생하는 스트레인을 측정하였다. Fig. 7과 Fig. 8은 하중 증가에 따른 스트레인 변화를 그래프로 나타낸 것이다. 원통형 스프링의 시편 1번과 2번의 측정 결과인 Fig. 7을 보면, 시편 차이보다는 부착 위치에 따른 차이가 크고, 일관되게 나타난다. 이는 게이지의 부착 위치가 측정값에 중요한 영향을 미친다는 것을 의미하며, 측정 시편별로 발생할 수 있는 게이지 부착 위치 오차, 부착 각도 오차, 게이지 편차 등의 영향은 상대적으로 미세한 것으로 밝혀졌다. ②번 지점과 ③번 지점에서 상대적으로 높은 스트레인이 측정되었다. ③번 지점의 스트레인은 이상적인 원통형 스프링의 비틀림 응력 계산 값과 비교하여 약 2 % 정도 낮은 값이다. ①번 지점은 ③번 지점에 비하여 약 20 % 정도 낮은 스트레인이 측정되었는데, 이는 스프링 상단의 끝단과 가까운 지점이기 때문에 응력상태가 단순 비틀림과는 다소 차이가 있기 때문으로 판단된다.

Fig. 7

Strain gauge measurement results for static load (cylindrical spring)

Fig. 8

Strain gauge measurement results for static load (beehive spring)

Fig. 8에 나타난 벌집형 스프링의 경우에도 원통형 스프링과 마찬가지로 시편 차이보다는 부착 위치에 따른 차이가 뚜렷한 경향성을 보이고 있다. 스프링 중앙 부위인 ③번 지점에서 가장 높은 스트레인이 측정되었으며, 스프링 상단(①) 지점에서는 원통형 스프링과 마찬가지로 ③번 지점에 비하여 약 20 % 정도 낮은 스트레인 값이 측정되었다.

4. 게이지 부착 위치에 따른 서어징 진폭의 비교

밸브 스프링의 서어징은 게이지가 부착된 스프링을 실린더 헤드에 장착하고, 캠축을 모터로 구동하면서 스프링의 스트레인 파형을 측정하였다. 스프링의 회전을 방지하기 위하여 스프링 하단과 접하는 헤드 면에 미세한 핀을 부착하였다. 또한 고속 운전 시 게이지 선을 보호하기 위하여 스프링 선을 따라 상단에서 하단까지 게이지 코팅제를 이용하여 부착시키는 방법을 사용하였다. 스프링 하단은 상단에 비하여 운동변위가 작기 때문에 고속 운전에도 게이지 선은 안전하게 보호될 수 있다. 본 실험의 목적은 절대 스트레인 값을 측정하는 것이 아니라 정적 스트레인에 대한 동적 스트레인의 진폭비를 측정하는 것이다. 따라서 게이지 부착 방법에 따른 스트레인 값의 차이는 선형성이 유지되는 한 전혀 문제가 되지 않는다.

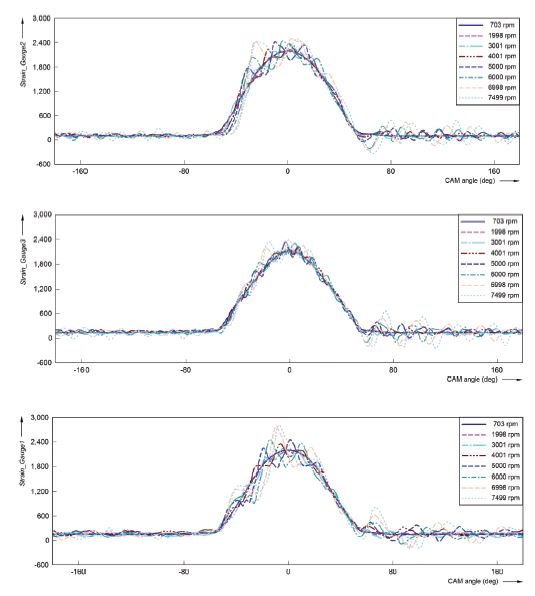
Fig. 9는 원통형 스프링의 ①번, ②번, ③번 지점에서 측정되는 스트레인 파형을 나타낸 것이다. 그래프에서 횡축은 캠축 회전 각도를 의미하며 종축은 Micro-strain을 나타낸다. 각각의 그래프에는 캠축 회전속도를 변화시키며 측정된 서어징 파형이 중첩되어 그려져 있다.

Fig. 9

Surging waveforms at each point of cylindrical spring (points ①, ②, ③ in order from the top)

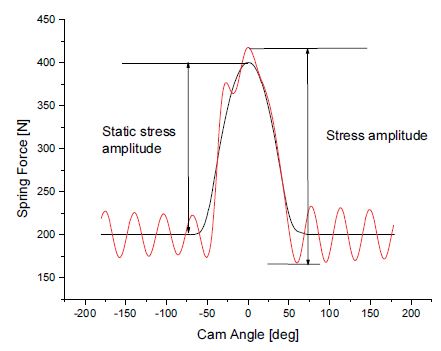
밸브 스프링의 서어징 정도를 파악하기 위하여 식 (1)과 같이 응력 진폭비(Stress amplitude ratio)를 정의하였다. 응력 진폭비는 Fig. 10에 나타난 바와 같이 서어징이 없을 때의 응력 진폭에 대한 실제 응력 진폭의 비율을 의미한다. Fig. 10의 검은 선 파형은 서어징이 없을 때의 정적 응력(Static stress)으로서 스프링 내부의 진동이 없이 기구학적 밸브 변위에 의한 응력의 변화만을 나타낸 것이다. 실제로는 공회전 속도(Idle rpm)와 같은 낮은 속도로 밸브트레인을 구동하고 스트레인 파형을 측정하면 쉽게 얻어질 수 있다.

Fig. 10

Definition of the stress amplitude ratio

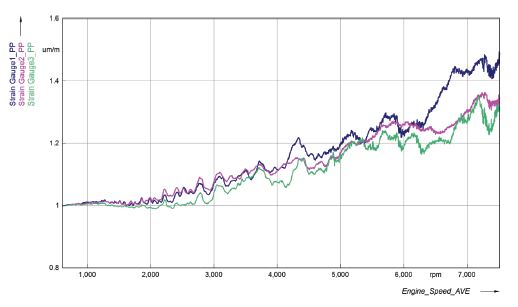
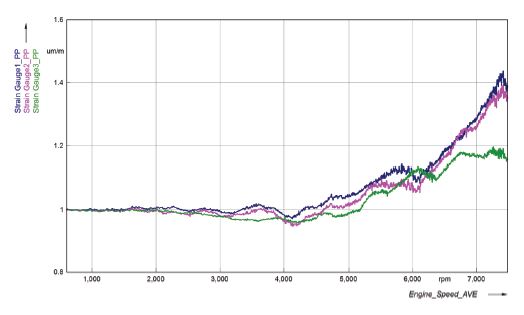
Fig. 11은 원통형 스프링에 대하여 캠축 회전속도에 따른 응력 진폭비의 변화를 나타낸 것이다. 최대 응력 진폭비는 스프링 상단 즉, ①번 지점에서 약 1.5배, 스프링 하단과 스프링 중앙부위에서 약 1.35배로 측정되었다. 이는 스프링 상단이 격심한 서어징이 발생할 때, 변동응력(Alternating stress) 증가로 인한 피로 파괴의 가능성이 높다는 것을 의미한다. 따라서 서어징 실험을 수행할 때 스프링 상단에 스트레인 게이지를 부착하는 기존의 방식은 타당하다고 할 수 있다.

Fig. 11

Comparison of stress amplitude ratio according to gauge attachment location (cylindrical spring)

Fig. 12는 벌집형 스프링에 대하여 캠축 회전속도에 따른 응력 진폭비 변화를 나타낸 것이다. 최대 응력 진폭비는 스프링 상단(①번 지점)에서 약 1.42배, 원추부와 원통부 경계(②번 지점)에서 약 1.41배, 스프링 하단(④번 지점)에서 약 1.2배로 측정되었다. 그래프에 보는 바와 같이 ①번 지점과 ②번 지점은 매우 유사한 응력 진폭비 패턴을 보여주고 있다. 이는 벌집형 스프링이 원통형 스프링에 비하여 최대 응력 진폭비를 가지는 지점이 원추부 전체에 넓게 분포하는 것으로 추정된다.

Fig. 12

Comparison of stress amplitude ratio according to gauge attachment location (beehive spring)

5. 최적의 스트레인 게이지 부착 위치

밸브 스프링 서어징에 관계하는 스프링 내부진동은 스프링 축 방향 진동 모드와 밀접한 관련이 있다. 이론적으로는 다른 방향의 진동(Bending, torsion, 등)도 가능하지만 스프링을 가진시키는 밸브는 스프링 축 방향으로만 운동하기 때문에 축 방향 이외의 진동은 고려할 필요가 없다.

Fig. 9에 나타난 것과 같은 서어징 파형을 분석하면, 축 방향 진동 중에서도 1차 모드와 2차 모드 정도의 주파수 성분이 관찰된다. 2차 모드 진동은 그 진폭이 상대적으로 작기 때문에 문제가 될 정도의 큰 서어징 진폭은 대부분 1차 모드 공진에 관련된다는 것을 알 수 있다.

5.2 벌집형 스프링

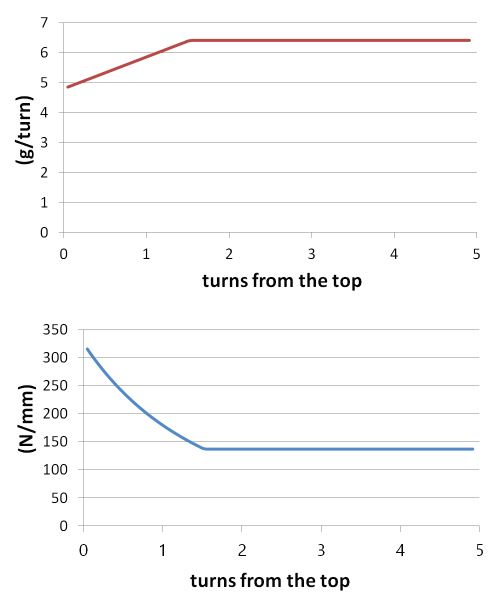
벌집형 스프링은 원통형과는 달리 스프링 축 방향으로 질량 및 강성의 분포가 균일하지 않다. 원추부에서 권당 질량은 감소하고 권당 강성은 증가한다. Fig. 13은 벌집형 스프링의 권당 질량 및 강성을 그래프로 나타낸 것이다.

Fig. 13

Distribution of mass and stiffness per turn of beehive spring

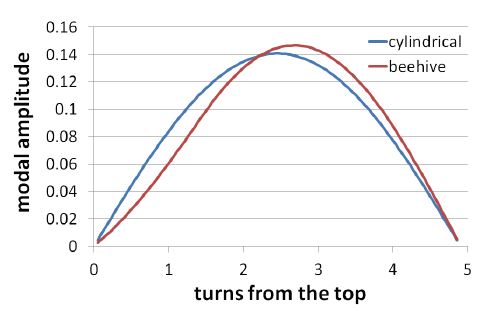
벌집형 스프링의 불균일한 질량 및 강성 분포를 고려하여 축 방향 진동에 대한 1차 진동 모드를 계산하였다. Fig. 14는 벌집형 스프링의 1차 진동 모드를 원통형 스프링의 진동 모드와 비교한 것이다. 원추부는 권당 질량 감소와 강성 증가로 인하여 진동 변위가 제한되며, 그림과 같이 원추부에 해당하는 부위(0∼1.5권)의 모드 변위가 작아지는 것을 확인 할 수 있었다.

Fig. 14

Comparison of vibration modes between cylindrical and beehive springs (1st longitudinal mode)

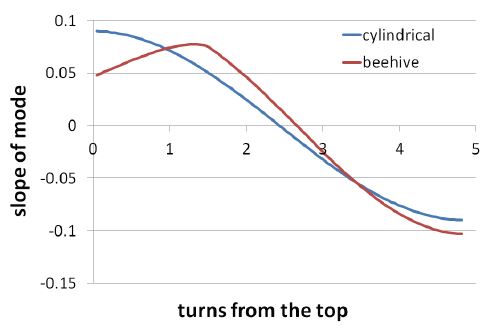
Fig. 15는 Fig. 14에 나타난 진동 모드를 1차 미분한 것으로서 모드 진동에 의한 변형율의 상대적 크기를 나타낸다. 벌집형 스프링의 경우에는 최대 응력 진폭 지점이 반드시 스프링 상단이 아니며 오히려 원추부와 원통부의 경계지점에서 응력이 더 높게 나타날 수도 있다. 원추부의 질량 감소와 강성 증가가 스트레인 증가도 제한한다는 것을 알 수 있다. 이론적으로는 조권부와 밀권부의 경계부위(④번 지점)가 최대응력 지점이지만, 스프링 하단에는 밀권부로 인한 경계조건이 희석되는 효과가 있기 때문에 실제로 어느 지점이 최대응력 지점인지는 판단할 수 없다. 원추부와 원통부의 직경비, 밀권의 권수 등에 영향을 받을 것으로 생각된다. 따라서 벌집형 스프링의 경우에는 스프링 상단(①번 지점), 원추부와 원통부의 경계지점(②번 지점), 조권과 밀권의 경계지점(④번 지점)에 모두 게이지를 부착하고 최대 응력 진폭을 판단하는 것이 바람직할 것이다.

Fig. 15

Slope of the vibration modes for cylindrical and beehive springs (relative strain amplitude)

6. 결 론

자동차 엔진 밸브 스프링의 서어징 진폭을 측정하는데 있어서 최적의 스트레인 게이지 부착 위치를 선정하기 위한 연구를 수행한 결과 다음과 같은 결론을 얻었다.

• 1) 원통형 스프링의 경우 1차 모드 공진에 의한 서어징 스트레인은 양끝단의 경계 조건이 고정(Fixed)된다고 가정할 경우 상단의 유효코일과 끝단의 경계지점, 하단의 조권과 밀권의 경계 지점에서 최대 진폭을 가진다.
• 2) 스프링 하단에서 조권과 밀권의 경계 지점은 비틀림 스트레인이 밀권 쪽으로 침투하여 고정 경계 조건(Fixed boundary condition)이 희석되는 현상이 발생한다. 따라서 이 지점의 서어징 스트레인이 상단보다 낮게 측정되었다.
• 3) 원통형 스프링의 서어징 진폭 측정을 위한 최적의 게이지 부착 위치는 스프링 상단 유효 코일과 끝단의 경계 지점이다. 구체적으로는 밸브 최대 열림 상태(스프링의 작동 범위에서 최대 압축 상태)에서 0.1 mm 두께의 간극 게이지를 이용하여 부착 위치를 결정할 수 있다.
• 4) 벌집형 스프링의 경우에는 1차 모드 공진에 의한 서어징 스트레인은 원추부 상단과 끝단의 경계지점(①번 지점), 스프링 상단 원추부와 원통부의 경계지점(②번 지점), 스프링 하단 조권부와 밀권부의 경계지점(④번 지점) 모두에서 최대 진폭이 나타날 가능성이 있다.
• 5) 벌집형 스프링의 최대 응력 진폭 지점은 원추부의 질량 및 강성 분포에 따라 달라질 수 있기 때문에 앞에서 언급한 세 지점(①,②,④번 지점) 모두 게이지를 부착하고 최대 응력 진폭을 판단하는 것이 바람직할 것이다.

References

• R. S. Prabakar, A. Nagar, M. Patil, N. Umashankar and S. P. Mangalaramanan, “Multi-Body Dynamic Simulation and Experimental Validation of Valve Spring Surge Speed,” SAE 2013-01-2770, 2013. [https://doi.org/10.4271/2013-01-2770]
• H. Liu and D. Kim, “Estimation of Valve Spring Surge Amplitude Using the Variable Natural Frequency and the Damping Ratio,” Int. J. Automotive Technology, Vol.12, No.5, pp.631-638, 2011. [https://doi.org/10.1007/s12239-011-0073-1]
• M. Vandresen, D. C. Lencina, C. P. Fernandes, L. N. Silva, L. D. P. Feliciano and H. R. Cazangi, “Valve Spring Compression Testing System,” SAE 2014-36-0230, 2014. [https://doi.org/10.4271/2014-36-0230]
• R. K. Yanarocak and Y. C. Ozkaptan, “Torsional Stress Measurement on Valve Springs of a Heavy Duty Engine in Collaboration with Valve Lift,” SAE 2016-01-8102, 2016. [https://doi.org/10.4271/2016-01-8102]
• J. Seo, J. Park, T. Park and J. Kim, “Study on Valvetrain Dynamic Characteristics Analysis by Using Vibrometer and High Speed Camera,” KSAE Annual Conference Proceedings, pp.158-159, 2015.
• G. P. Blair, C. McCartan and W. Cahoon, “Measurement and Computation of the Characteristics of Progressive Valve Springs,” SAE 2010-01-1056, 2010. [https://doi.org/10.4271/2010-01-1056]