[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 29, No. 2, pp.157-163

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Feb 2021

Received 28 Aug 2020 Revised 22 Sep 2020 Accepted 05 Oct 2020

DOI: https://doi.org/10.7467/KSAE.2021.29.2.157

랜덤 하중을 받는 보 구조물을 이용한 주파수 영역 Dirlik 피로 평가 방법의 실험적 검증

이은호¹⁾

; 곽시영^*^{, 1)}^{, 2)}

1)과학기술연합대학원대학교 생산기술전공
2)한국생산기술연구원 공정지능연구부문

Experimental Verification of Dirlik Fatigue Evaluation in Frequency Domain Using Beam Structure under Random Vibration

Eunho Lee¹⁾

; Siyoung Kwak^*^{, 1)}^{, 2)}

1)Industrial Technology(Industrial Materials and Smart Manufacturing Engineering), Korea University of Science and Technology(UST), Daejeon 34113, Korea
2)Intelligent Manufacturing R&D Department, Korea Institute of Industrial Technology(KITECH), 113-58 Seohaean-ro, Siheung-si, Gyeonggi 15014, Korea

Correspondence to: ^*E-mail: vlvwlw@kitech.re.kr

Copyright Ⓒ 2021 KSAE / 183-08
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

Most structures(e.g., vehicles, ships, buildings, and airplanes) are subject to random vibration loads. Various methods are used in order to evaluate the fatigue of structures under such random loads. In this paper, Dirlik’s method, a frequency domain random fatigue evaluation method, was compared with a random fatigue test for verification. A hot-rolled steel plate SPFH590 beam model was used for verification, and the random input was referred to ISO 16750-3. Dirlik’s method was used to predict fatigue life from response stress PSD, and calculated by using the frequency response function and Abaqus SW. In addition, two specimens, such as the target model, were used to measure each fatigue life using the vibration testing system and compared with the predicted life by using Dirlik’s method. The fatigue life via Dirlik’s method was similar to the random fatigue tests, and these results can be used as evidence to verify the reliability of Dirlik’s method.

Keywords:

Random fatigue, Power spectral density, Dirlik’s method, Frequency domain, 1 DOF Beam model, SPFH590

키워드:

랜덤 피로, 파워 스펙트럼 밀도, 더릭 방법, 주파수 영역, 1자유도 빔 모델, 자동차용 열간압연 강

1. 서 론

도로주행으로 인한 진동을 받는 자동차, 지진에 의해 흔들리는 건축물, 파도에 의해 흔들리는 선박, 기류와 엔진의 영향을 받는 항공기 등 대부분의 구조물이 받는 하중은 불규칙적인 특성을 갖는다.

자동차 분야에선 규칙적인 하중을 받는 부품과 소재에 대한 피로수명 평가 연구가 활발히 진행되고 있다.^1,2) 하지만 불규칙한 하중의 경우 예측이 어렵고 Photo. 1과 같이 심각한 피해로 연결될 가능성이 높기 때문에 랜덤 피로 분야에서는 정확한 수명 예측을 할 수 있는 방법이 요구된다.

Photo. 1

Fatigue failure of a large ship(left) and aircraft engine turbine(right) under random vibration

불규칙한 하중의 피로 평가에는 시간이력 방법과 주파수 영역 방법이 사용되고 있다. 시간이력 해석 방법은 선형손상합산법³⁾을 활용한 Rainflow counting기법⁴⁾이 주로 사용되고 있으며 전체 시간이력을 계산하기 때문에 데이터 개수가 굉장히 많고 해석시간이 길어지므로 실제 해석에서는 매우 적용하기 어렵다.

주파수 영역에서 손상률을 예측하기 위한 사이클 집계를 위해 사용되는 방법들은 대표적으로 Dirlik,⁵⁾ Benasciutti와 Tovo,⁶⁾ Wirsching과 Shehata,⁷⁾ Zhao와 Baker⁸⁾ 방식 등이 있으며 시간이력해석법에 비해 높은 수치의 값을 예측하므로 보수적이라는 특징을 보이지만 빠르게 피로 손상률을 계산할 수 있다. 장준 등⁹⁾과 Benasciutti와 Tovo¹⁰⁾는 이러한 주파수 영역 피로 평가에 사용되는 다양한 사이클 집계 방법들을 비교하였다.

본 논문에서는 랜덤진동을 받는 보 모델을 구성하여 주파수영역 랜덤 피로 평가 방법 중 하나인 Dirlik’s method의 수명 예측 결과를 랜덤 피로 시험결과와 비교하여 검증하였다. 랜덤 입력 가진은 국제 도로차량 시험 규격인 ISO 16750-3을 참고하였으며 설정한 입력 가진에 대한 보 모델의 응답 응력 PSD를 2가지 방법으로 접근하여 계산하였다. 첫째로 보 구조물의 이론적 주파수 응답 함수를 통해 응답 PSD를 계산하였으며 둘째로 범용 유한요소 해석프로그램 Abaqus를 통해 응답 PSD결과를 구하여 각각 피로 수명 예측에서 적용하였다.

계산된 응력 PSD로 부터 Dirlik 방법을 사용하여 보 구조물에서 일정 응력 범위가 발생할 사이클을 집계하고 시험 대상 보 모델의 재질 SPFH590의 피로물성인 S-N선도에 적용하여 손상률을 계산함으로써 수명을 예측하였다.

결과의 검증을 위해 보 모델 시편을 제작하였으며 랜덤진동 가진기를 통해 시편의 피로 수명을 측정하였고 Dirlik방법으로 예측한 이론 수명과 비교한 결과 평균 13 %의 차이를 보였다.

2. 주파수 영역 피로 평가 방법

2.1 파워 스펙트럼 밀도(PSD, Power Spectral Density)

주파수 영역은 다량의 시간이력 데이터를 각 주파수별 진폭과 위상으로 표현할 수 있기에 다루기 간편하다는 이점이 있지만 랜덤진동의 경우 주기함수가 아니기 때문에 푸리에 변환을 직접적으로 적용할 수 없다. 이러한 이유로 랜덤진동의 주파수 영역 해석을 위해서는 진동수의 특성을 포함하는 자기상관함수를 이용해야 하며 다음 식 (1)과 같이 자기상관함수는 하나의 함수에 대해 어떤 시간 과 τ만큼 떨어진 다른 시간에서 신호와의 상관성을 나타낸다.

R x x τ = E x t 1 x t 1 + τ

(1)

여기서 자기상관함수를 푸리에 변환한 것을 파워 스펙트럼 밀도라고 하며 식 (2)와 같이 자기상관함수와 파워 스펙트럼 밀도의 관계를 위너-킨친(Wiener- Khinchine) 관계라고 한다.

S x x ω = 1 2 π F R x x τ = 1 2 π ∫ - ∞ ∞ R x x τ e - i ω τ d τ R x x τ = 2 π F - 1 S x x ω = ∫ - ∞ ∞ S x x ω e i ω τ d ω

(2)

2.2 Dirlik’s Method

주파수 영역에서 사이클 집계는 랜덤 하중을 받는 구조물의 응답 응력 PSD로부터 진행되며 Dirlik’s Method는 응답 응력 PSD로부터 응력 범위가 발생할 확률 밀도 함수를 구하는 경험 기반 방식이다.

아래 식 (3)과 같이 PSD를 적분함으로써 얻을 수 있는 Spectral moment 값은 랜덤 시간 이력 분포의 통계적인 의미를 갖고 있으며 주로 k=0,1,2,4의를 대입하여 얻은 값을 조합해 사용한다.

m k = ∫ 0 ∞ S x x f ⋅ f k d f

(3)

대표적으로 1초에 발생하는 Peak데이터의 수 E[P]는 식 (3)에서 구한 Spectral moment를 사용하여 아래 식 (4)와 같이 계산된다.

E P = m 4 m 2

(4)

Dirlik⁵⁾은 PSD로부터 얻은 통계적 의미의 변수들을 조합하여 아래 식 (5)와 같이 하나의 확률 밀도 함수 p(S)를 고안하였다. 함수 p(S)의 사용된 변수들은 아래 Table 1에 정리하였으며 p(S)를 특정 응력범위 ΔS에 대해 적분한 값은 랜덤 하중을 받는 구조물에서 응력 ΔS가 발생할 확률로서 평가할 수 있다.

p S = D 1 Q e - Z Q + D 2 Z R 2 e - Z 2 2 R 2 + D 3 Z e - Z 2 2 2 m 0

(5)

Table 1

Dirlik’s constants

시간 T초에 대해 특정 응력범위 발생 횟수 n(S)는 다음 식 (6)으로 계산되며 최종적으로 Miner’s rule로 알려진 선형손상법 식 (7)에 의해 손상률을 계산한다. N(S)은 응력 S에서 피로 수명이며 재료의 피로 물성인 S-N 곡선을 통해 얻을 수 있다. D는 손상률을 의미하며 전체 합이 1이거나 그 이상일 때 피로 파괴가 발생한고 평가한다.

n S = E P T ∫ p S d S

(6)

∑ D = ∑ n S N S ≥ 1

(7)

3. Dirlik’s Method 활용 보 구조물의 피로 평가

3.1 평가 대상 모델

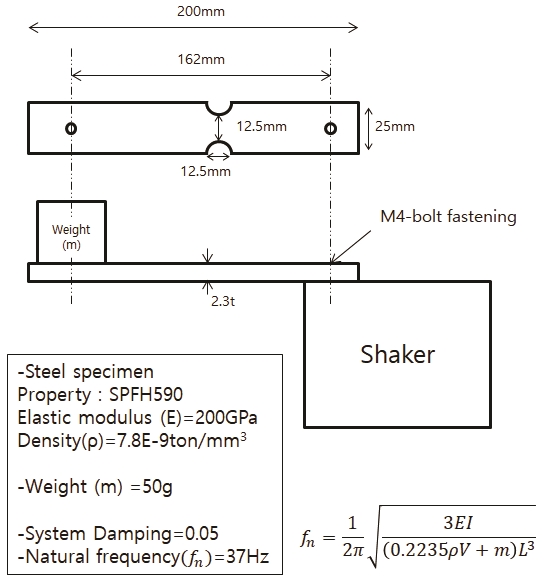
주파수영역방법의 피로 수명 예측 성능을 검증하기 위해 Fig. 1과 같이 랜덤진동을 받는 시험 모델을 구성하였다. 대상 구조물은 노치를 갖는 외팔보 시편으로 끝단에 50 g의 무게 추가 존재하며 구조의 단면은 25 mm x 2.3 mm의 직사각형 형태로 주어졌다. 또한 기저진동을 받는 질량-감쇠-스프링 시스템으로 감쇠비는 0.05이고 구조물의 고유진동수는 37 Hz이며 Fig. 1 하단의 식과 같이 끝단 질량을 갖는 외팔보 구조의 고유진동수 계산식을 활용하였다. 시험 시편의 재질은 자동차분야에서 광범위하게 사용되는 자동차용 열간압연 강판 재질(SPFH590)을 사용하였다.

Fig. 1

Beam specimen for random fatigue test

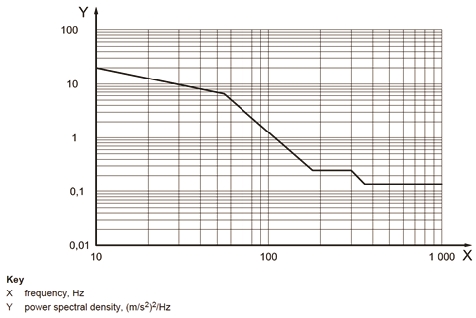
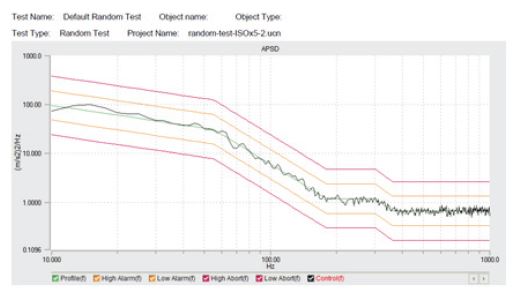
입력 하중은 Fig. 2와 같이 국제 도로차량 시험 규격 PSD(ISO 16750-3)를 참고하였다. 본 연구의 목적은 Dirlik’s method로 예측한 피로 수명과 랜덤 피로 시험결과의 비교 검증으로 실제 피로 시험에서 가혹한 조건으로 피로 파괴를 발생시키기 위해 5배 증폭한 PSD를 사용하였다. 규격 및 증폭된 PSD의 값은 Table 2에 자세히 나타내었다.

Fig. 2

Road vehicles testing standard(ISO 16750-3)

Table 2

Input random PSD

3.2 응답 응력 PSD의 계산(진동 이론 공식)

본 연구의 피로 평가 대상 모델은 기저진동을 받는 진동시스템이며 피로 수명 평가를 위해선 구조물의 응답 응력 PSD를 우선적으로 계산해야 한다. 기저 가속도 진동 y를 받는 1 자유도 시스템의 진동 운동은 다음과 같은 식 (8)로 표현할 수 있다.

m x ¨ + c x ˙ - y ˙ + k x - y = 0

(8)

이러한 기저진동 시스템의 경우 스프링, 질량, 감쇠로 정의되는 시스템의 전달함수 H(ω)는 아래 식 (9)로 표현되며, 이는 주파수 영역으로 표현된 입력에 대한 시스템의 주파수 영역 응답을 결정할 수 있는 함수이다.

H ω = k - c ω j k - m ω 2 + c ω j

(9)

만약 PSD 형태의 입력 가속도가 주어진다면 아래와 같은 식 (10)과 같이 시스템의 응답 가속도 PSD를 구할 수 있다. 여기서 Y는 기저진동에 의해 받는 가속도 PSD를 나타내며 본 예제에서는 ISO규격 PSD가 입력 가진으로 적용되므로 식 (10)을 이용해 응답 가속도 PSD, X를 계산하였다.

X A P S D = H ω 2 Y A P S D = k 2 - c 2 ω 2 k - m ω 2 2 + c 2 ω 2 Y A P S D

(10)

구해진 응답 가속도 PSD로부터 외팔보 이론에 의해서 다음의 식 (11)과 같이 힘, 모멘트, 응력 응답을 쉽게 구할 수 있으며 L은 외팔보의 길이, C는 단면의 중립면까지의 길이, I는 단면모멘트, Kt는 응력집중계수를 나타낸다.

F P S D ω = m X A P S D ω M P S D ω = F P S D ω L σ P S D ω = M P S D ω C I K t

(11)

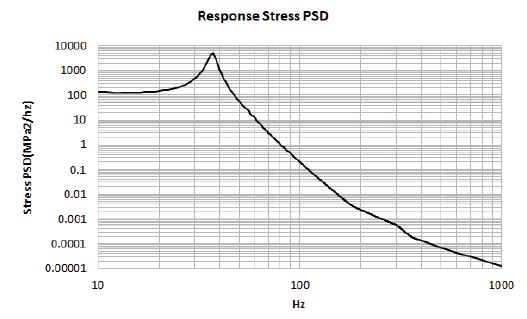
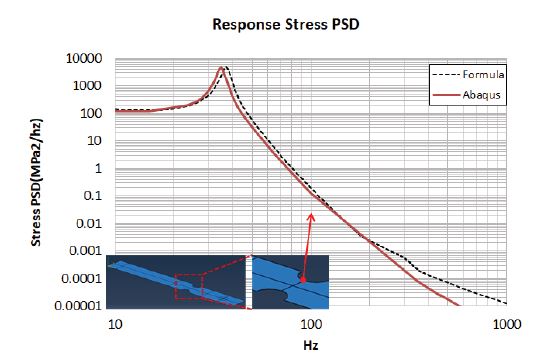
구조물의 응답을 구하기 위한 전체적인 계산과정을 Excel 프로그램을 활용하여 수행하였으며 최종적으로 피로 파괴가 발생할 노치부위의 응답 응력 PSD는 Fig. 3과 같다.

Fig. 3

Response stress PSD of notch in beam specimen

3.3 응답 응력PSD의 계산(Abaqus SW)

1 자유도 보 구조물 같이 간단한 형상에서는 이론식을 이용하여 응답 PSD를 계산할 수 있으나 실제 산업 분야에서 사용되는 복잡한 형상의 제품에 대해서는 상용해석 프로그램을 이용하는 것이 유용하다.

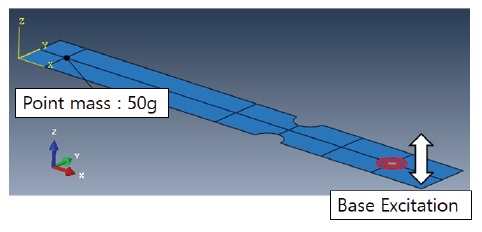
본 연구에서는 범용 유한요소해석 프로그램인 Abaqus 6.14의 Random Response 해석을 이용하여 해당 시스템의 응답 응력 PSD를 계산하였고 이론식으로부터 얻은 결과와 비교하였다. 해석 모델은 Shell 요소S4R(A 4-node reduced integration shell)를 사용하였으며 노치부 메쉬사이즈는 0.9 mm로 설정하여 해석하였다. 해석 대상 모델은 단 자유도의 모델이므로 Fig. 4와 같이 외팔보 시편이 고정되는 끝단의 자유도는 가진 방향으로만 존재하도록 설정하였으며 Point mass를 이용하여 무게 추의 질량을 구현하였다. 또한 Frequency 해석을 통해 하나의 고유진동수를 계산하여 Random response 해석을 진행하였다.

Fig. 4

Beam specimen analysis model in abaqus

Abaqus를 통해 계산된 고유 진동수는 35 Hz이며 3.1절에서 계산된 외팔보 고유진동수 이론치 37 Hz와 약 5 %의 오차를 보였다. 이러한 차이는 해석 시편 형상과 다른 이상적 외팔보 형상의 고유진동수 공식을 활용함에 있어 노치유무, 질량 분포, 유효시편길이 등의 차이로 발생할 수 있다.

보 모델에서 응력이 집중되는 노치부위의 응답 응력 PSD를 아래 Fig. 5에 나타내었으며 이론 공식의 응답 PSD와 비교하였을 때 대체로 유사한 형태를 보였다.

Fig. 5

Comparison of response stress PSD of notch in Abaqus and theoretical formula

3.4 Dirlik’s Method 피로 수명 평가

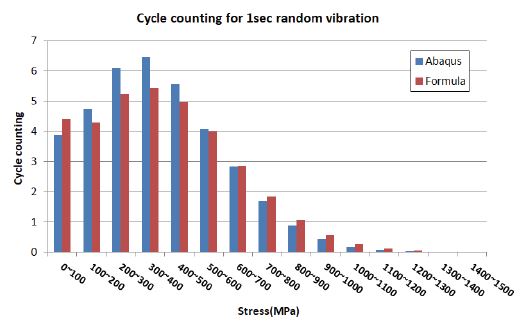
이론식 및 Abaqus에 의해 계산된 각 응답 응력 PSD로부터 2.2절 Dirlik’s method의 과정을 통해 구조물의 피로 평가를 수행하였다. Fig. 6은 1초 동안의 랜덤진동에 의한 시편 노치부위의 응력 발생 횟수를 나타낸다. Abaqus 및 Formula 두 가지 방법으로 얻은 PSD 모두 300∼400 MPa의 응력범위에서 가장 많은 사이클이 발생하였으며 해당 그래프의 모든 사이클을 합하면 식 (4)의 E[P]값 36.96임을 알 수 있다.

Fig. 6

Cycle counting for 1sec random vibration

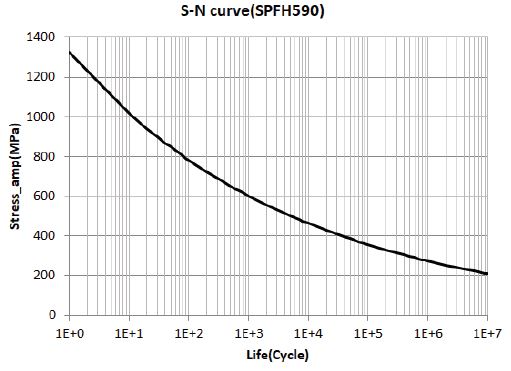
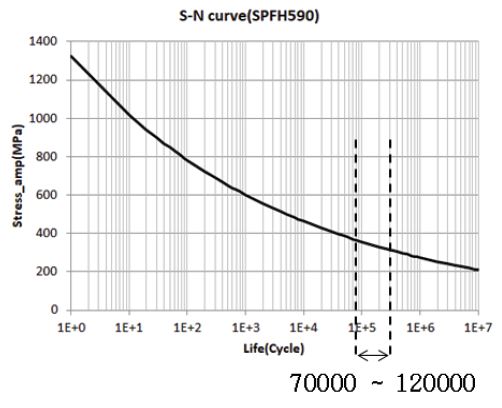
이후 재료의 피로물성인 S-N 곡선과 Miner’s rule 식 (7)을 이용하여 손상률을 계산하였다. 평가 대상 재질인 SPFH590의 S-N 곡선은 강근일과 곽시영¹¹⁾의 피로 시험 데이터를 참고하여 Fig. 7과 같이 정리하였으며 274 MPa의 응력진폭에서 10e6의 수명, 602 MPa의 응력진폭에서 10e3의 수명을 갖는다. 해당 보 구조물의 노치부위에서 1초 동안 발생한 랜덤진동에 대한 피로 손상률은 이론 응답PSD에서 5.334e-4, Abaqus응답 PSD에서 3.158e-4로 계산되었다. 피로 수명은 각 손상률의 역수인 1,874.5초, 3,166초로 평가할 수 있다.

Fig. 7

S-N curve of SPFH590 (강근일과 곽시영11))

4. 보 구조물의 랜덤 피로 수명 측정 시험

4.1 시험 시편 및 시험 방법

Dirlik’s Method의 피로 수명 예측 성능을 검증하기 위해 3.1절에서 구성한 피로 평가 대상 모델과 동일한 2개의 시험 시편을 제작하였다. Fig. 8과 같이 시편 양 끝에 홀 가공을 통해 한쪽에 50 g무게 추를 결합할 수 있고 반대편은 랜덤 피로 시험 장비 지그 부분에 고정될 수 있도록 설계하였다. 랜덤 피로 시험 장비는 SHINKEN사의 Vibration Testing System을 이용하였고 입력 가진은 Fig. 9와 같이 ISO 16750-3규격의 5배 증폭한 값을 사용하였으며 Fig. 10에서 보이는 것처럼 시편이 피로에 의해 파괴될 때까지의 시간을 측정하였다.

Fig. 8

Random fatigue test specimen

Fig. 9

Random fatigue test input acceleration PSD(ISO 16750-3 x5)

Fig. 10

Random fatigue test result

4.2 시험결과 및 비교

주파수 응답 이론 공식을 통한 응답PSD에 Dirlik’s method를 적용한 결과(Formula-Dirlik), Abaqus로 계산된 응답PSD에 Dirlik’s method를 적용한 결과(Abaqus-Dirlik) 그리고 2번의 시험 평가로 측정한 수명을 아래 Table 3에 정리하였다. 피로 시험 수명 측정결과는 2번의 시험에서 각 1,880초, 1,380초이며, Formula-Dirlik의 피로 수명 예측 값 대비 0.3 %, 26.4 %의 오차율을 보였다.

Table 3

Random fatigue test and Dirlik’s method result

Abqus-Dirlik의 예측 수명 값의 경우 Formula-Dirlik 예측값 대비 68.9 %오차율로 다소 높은 값이 발생하였으나 이는 해석에서 노치부 요소 민감도로 인해 낮게 발생된 응력 값 때문에 수명이 높게 평가된 것으로 판단된다. 하지만 Fig. 11에서 보여주는 바와 같이 해당 수명은 약 7e4∼1.2e5의 피로 수명 구간이므로 68.9 %의 차이는 피로측면에서 신뢰도에 크게 벗어나지 않는다.

Fig. 11

Error range of numerical solution in S-N curve

5. 결 론

본 논문에선 주파수 영역 랜덤 피로 평가 방법 중 하나인 Dirlik method를 사용하여 랜덤진동을 받는 보 구조 피로 수명을 평가한 후 실제 시험과 결과를 비교하였다.

주파수 응답 이론 공식을 통한 응답 응력 PSD결과와 범용 해석프로그램 Abaqus를 사용한 응답 응력 PSD로부터 얻은 피로 수명 결과는 다소 차이를 보였으며 이는 유한요소 해석상 노치 응력집중부위의 요소민감도로 인해 발생한 오차로 예상된다.

이론 공식의 응답 PSD로부터 Dirlik’s method의 피로 수명 예측 오차는 실제 랜덤 피로 시험 대비 평균 13.4 %이며 이러한 결과는 Dirlik’s method의 신뢰성을 검증할 수 있는 근거자료로 활용될 수 있다.

Nomenclature


σ_PSD :	stress power spectral density, MPa²/Hz
A_PSD :	acceleration power spectral density, (m/s²)²/Hz
m_k :	k-th spectral moment, Hz^k⋅MPa/Hz
E[P] :	expected number of peaks per second
n(S) :	number of cycles in stress range
D :	fatigue damage
f_n :	natural frequency, Hz

Acknowledgments

본 연구는 산업통상자원부 미래산업선도기술개발사업 “심해유전 개발을 위한 500Mpa급 URF 및 SIL3 manifold 개발과 subsea 시스템 엔지니어링 기술개발”(과제번호 10042430)의 지진해석 기술에서 파생되어 수행되었으며 이에 감사드립니다.

References

R. Walallawita, H. H. Lee, S. Y. Park, T. K. Kim and K. J. Lee, “Shape Design Improvement and Fatigue Life Prediction of Air Compressor Rotor Assembly,” Transactions of KSAE, Vol.27, No.7, pp.577-583, 2019. [https://doi.org/10.7467/KSAE.2019.27.7.577]
M. S. Han and J. U. Cho, “Fatigue Durability Analysis due to the Classes of Automotive Wheels,” Transactions of KSAE, Vol.22, No.6, pp.68-74, 2014. [https://doi.org/10.7467/KSAE.2014.22.6.068]
American Society for Testing and Materials, Annual Book of ASTM Standards, Section 3: Metals Test Methods and Analytical Procedures, ASTM, Philadelphia, 1986.
J. A. Bannantine, J. J. Comer and J. L. Handrock, Fundamentals of Metal Fatigue Analysis, Prentice Hall, Englewood Cliffs, New Jersey, 1990.
T. Dirlik, Application of Computers in Fatigue Analysis, Ph. D. Thesis, University of Warwick, Coventry, 1985.
D. Benasciutti and R. Tovo, “Spectral Methods for Lifetime Prediction Under Wideband Stationary Random Processes,” International Journal of Fatigue, Vol.27, No.8, pp.867-877, 2005. [https://doi.org/10.1016/j.ijfatigue.2004.10.007]
P. H. Wirsching and A. M. Shehata, “Fatigue Under Wide Band Random Stresses Using the Rainflow Method,” ASME Journal of Engineering Materials and Technology, Vol.99, No.3, pp.205-211, 1977. [https://doi.org/10.1115/1.3443520]
W. Zhao and M. J. Baker, “On the Probability Density Function of Rainflow Stress Range for Stationary Gaussian Processes,” International Journal of Fatigue, Vol.14, No.2, pp.121-135, 1992. [https://doi.org/10.1016/0142-1123(92)90088-T]
J. Jang, J. M. Cho, K. H. Lee, W. W. Lee and W. C. Choi, “Comparison of PSD Analysis Methods in Frequency Domain Fatigue Analysis,” Journal of the Korean Society for Precision Engineering, Vol.36, No.8, pp.737-743, 2019. [https://doi.org/10.7736/KSPE.2019.36.8.737]
D. Benasciutti and R. Tovo, “Comparison of Spectral Methods for Fatigue Analysis of Broad-band Gaussian Random Processes,” Probabilistic Engineering Mechanics, Vol.21 No.4, pp.287-299, 2006. [https://doi.org/10.1016/j.probengmech.2005.10.003]
G. I. Kang and S. Y. Kwak, “Study on Predictive Parameter for Fatigue Life Evaluation of Random Notched Specimen Based on Fatigue Test DB,” The Proceeding of 2017 COSEIK Annual Conference, p.102, 2017.

Dirlik’s constants	$D 1 = 2 x m - γ 2 1 + γ 2$
	$D 2 = 1 - γ - D 1 + D 12 1 - R$
	$D 3 = 1 - D 1 - D 2$
	$R = γ - x m - D 12 1 - γ - D 1 + D 12$
	$Q = 1.25 γ - D 3 - D 2 R D 1$
Standardization value	$Z = S 2 m 0$
Irregularity factor	$γ = m 2 m 0 m 4$
Mean frequency	$x m = m 1 m 0 m 2 m 4$

Frequency(Hz)	ISO 16750-3((m/s²)²/Hz)	PSD x 5((m/s²)²/Hz)
10	20	100
55	6.5	32.5
180	0.25	1.25
300	0.25	1.25
360	0.14	0.7
1,000	0.14	0.7

	Numerical solution		Fatigue test result 1	Fatigue test result 2
	Formula-Dirlik	Abaqus-Dirlik	Fatigue test result 1	Fatigue test result 2
Damage(1sec)	5.33E-04	3.16E-04	5.32E-04	7.25E-04
Life	1,874.5sec(31.24min)	3,166sec(52.77min)	1,880sec(31.33min)	1,380sec(23min)
Total cycle(Life x E[P])	69,281.52	117,015.36	69,484.80	51,004.80
Error(Formula)	-	68.90%	0.30%	26.40%