고속 버스 미러 형상 변경에 따른 공력 특성과 평균 항력 계수 산출에 관한 해석적 연구

2.1 격자 볼츠만법

격자 볼츠만법(Lattice Boltzmann method)은 연속체 가정의 방정식을 이산화하는 전통적인 범용 코드와는 달리 유동 입자의 이송 및 충돌에 의한 운동학 이론을 기반으로 한다. 볼츠만 방정식을 이용하여 유체입자의 확률 분포 변화를 통해 유동을 모사하는 수치해석 기법이다. 거시적 및 연속적인 입자의 운동을 얻기 위해 Chanpmann-Enskog 방법을 이용하여 연속적인 유체의 운동방정식을 도출할 수 있으며 식 (1)과 같이 정의된다.⁷⁾

입자 운동은 이동과 충돌로 나눌 수 있으며 식 (1)의 $$ f_i\left(\vec{x}+{\vec{c}}_i\delta t,t+\delta t\right)=f_i\left(\vec{x},t\right)$$는 입자 분포를 이웃하는 격자로 이동시키는 Streaming 과정을 나타낸다. 여기서 f_i는 격자 내에서의 이산화된 속도벡터를 따라 i 방향으로 움직이는 입자 분포 함수(Particle distribution function)이다. δt와 c는 각각 시간 간격과 입자속도를 의미한다. 식 (1) 우변의 $$ {\Omega }_i\left(\vec{x},t\right)$$ 항은 입자간의 충돌(Collision)과정을 나타낸다. Ω_i는 충돌에 의한 입자분포의 변화를 나타내며 충돌시에 질량, 운동량을 보전시켜주는 충돌 연산자이다. 충돌 과정은 복잡한 연산이 요구되나 BGK(Bhatnangar Gross Krook)⁸⁾ 방정식을 활용하여 간략화하면 식 (2)와 같다.

여기서 $$ f_i^{eq}$$는 국소적인 평형상태에서 분포함수이고 τ는 단일 시간 완화 계수를 나타내며 완화시간은 유체의 점성계수에 의해 결정된다. 각 단계마다 경계조건이 적용된 연산이 이루어지면 각 격자점에서 새로운 분포함수 값이 산출되며 이 분포함수 값을 아래의 식 (3)~(5)에 적용하면 유체의 각 물리량을 구할 수 있다.

2.2 해석 모델 및 조건

Fig. 1에는 A필라 및 미러 주위 영역의 볼륨 격자를 도시하였다. 최소격자는 1.25 mm이며 A필라 영역과 측면 곡률부에 적용하였다. 미러 후류 영역 격자 모델링은 횡풍 조건에서 형성되는 유동구조를 먼저 파악한 후 미러 후류가 영향을 미치는 영역까지 충분히 설정하였고 2.5 mm와 5 mm의 크기를 적용하였다. 회전 영역인 휠 영역은 5 mm로 하였고 휠 회전을 고려하기 위하여 격자계를 실제로 회전시키는 LRF sliding mesh 기법을 적용하였다. 차속은 90 kph이고 전체 볼륨 격자는 약 2.2억 개이며 횡풍 조건시 안정화된 결과를 얻기 위하여 150만 번의 반복 계산을 하였다.

Fig. 1

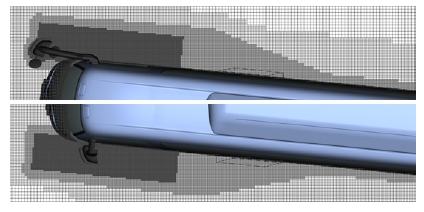
Computational grid resolution around A-pillar and mirror under cross wind condition (top: RH, bottom: LH)

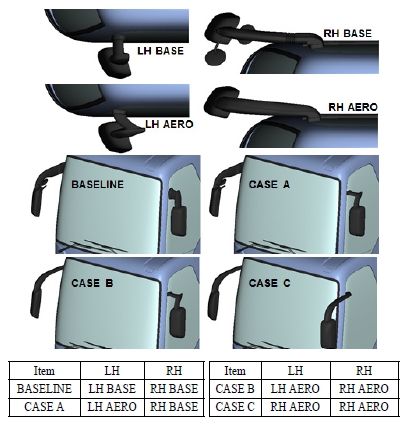
Fig. 2에는 본 연구에서 고려한 미러 형상을 도시하였다. 미러 하우징 형상은 기본 모델과 동일하고 스테이 형상을 변경하였다. A모델은 LH 스테이 단면 축소 및 유선화한 형상이며 모델 C는 LH와 RH 미러를 모두 전방에 배치하고 스테이 단면을 폭 방향이 장축인 단면으로 변경한 모델이다.

Fig. 2

Mirror shape and configuration

3.1 정풍조건 유동특성

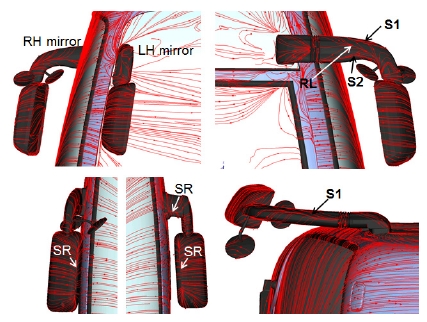
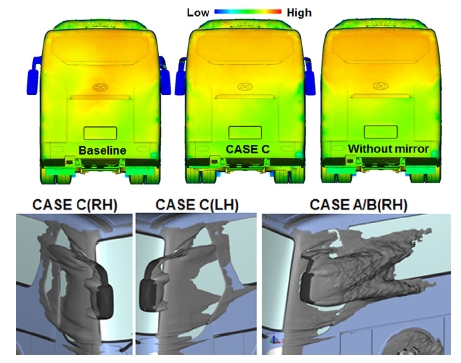
미러 주위의 표면 유선을 Fig. 3에 도시하였다. 미러 하우징 내측면에서 정체영역(Stagnation region, SR)이 형성되고 이 영역을 중심으로 흐름이 분지되고 있으며 표면을 따라 가속이 이루어지고 미러 하우징 끝단에서 떨어져 나감을 유추해 볼 수 있다. LH 스테이 상부 앞면에서 정체영역이 형성되고 스테이 및 미러 하우징 후미에서는 Fig. 4에 도시한 등압력 선도에서 볼 수 있듯이 광범위한 와류를 형성하고 있다. RH 스테이 표면 유선을 보면 내측면을 타고 흐르는 흐름은 스테이 상단과 스테이 외측하단에서 박리(S1, S2)되고 있으며 차량 전방에서 바라볼 때 스테이 외측 상단에서는 반시계 방향, 외측 하단에서는 시계방향의 나선형 와류 흐름이 형성되면서 이 두 와류의 재 부착선(Reattachment line, RL)이 관찰되었다.

Fig. 3

Streamlines around mirrors

Fig. 4

Isosurface of baseline model at a yaw angle of 0° (Cpt = 0 time averaged)

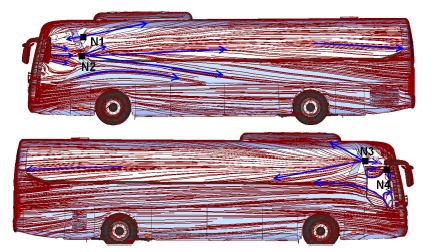
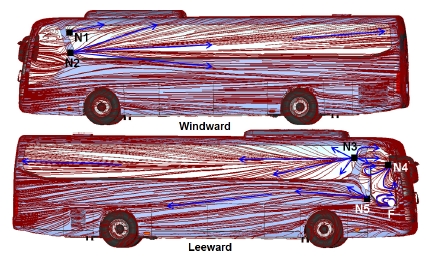
Fig. 5에는 바디에서의 표면 유선을 도시하였다. 요각이 없는 경우 LH의 흐름은 정면에서 불어오던 자유 흐름이 바디 정면 정체점에서 분산되어 흐르다가 미러를 지나면서 큰 와류를 생성하게 된다. A필라와 미러 하우징 내측에서는 고속의 흐름이 형성되며 이 흐름은 스테이 및 미러 하우징 후방에서 생성되는 와류와 만나 재 부착되어 흐르게 된다. 스테이 후방의 재 부착점(N1)을 기준으로 루프를 향하는 상향 흐름과 역류하는 흐름이 형성되고 미러 하우징 후방의 재 부착점(N2)에서는 흐름이 분지되어 상향하는 흐름과 바디 하부를 향하는 하향 흐름이 형성된다.

Fig. 5

Streamlines around body at a yaw angle of 0° (black square: node)

A필라 하단 흐름의 표면 유선은 아래로 휘어지고 있고 하향하는 흐름은 바디 끝단까지 지속되고 있으며 바디 후방의 측면 흐름을 아래로 당겨주는 와류의 존재를 유추해 볼 수 있다. RH 흐름은 스테이 후방의 재 부착점(N3)이 보다 전방에 위치해 있으며 이점을 기준으로 흐름이 분지되어 상향 및 하향하는 흐름이 형성되고 스테이 하단에 또 하나의 재 부착점(N4)을 볼 수 있다. A필라 하단을 타고 흐르는 흐름은 전방으로 역류하는 흐름과 함께 급격하게 상향하여 미러 후류로 유입되고 있다.

3.2 횡풍조건 유동특성

Fig. 6과 같이 요각을 갖으면 바람을 받는 쪽(Windward)에서는 미러 하우징 후방의 재 부착점(N1, N2)을 기준으로 상향하는 흐름 성분이 증대되며 하향하는 흐름은 전반적으로 다소 감소하였다. 바람을 등진 쪽(Leeward)은 스테이 후방 재 부착점(N3)이 보다 후방으로 이동해 있으며 역류하는 흐름이 관찰되었다. A필라에서 추가적인 박리가 발생하면서 스테이 하단에 형성된 재 부착점(N4)을 기준으로 하향하는 흐름과 역류하는 흐름이 발생하였다. A필라 하단에서는 와류 형성의 중심점인 와류 표출점(Focus point, F)과 후방 인접 영역에 또 하나의 재 부착점(N5)이 형성되었고 전반적으로 하향하는 성분이 증대되었다. 이와 같이 요각을 갖는 경우 측면 전방영역에서 광범위한 유동 박리에 의한 와류 발생을 확인할 수 있으며 정풍조건에 비해 매우 복잡한 양상을 보인다.

Fig. 6

Streamlines around body at a yaw angle of 5° (black square: node, white circle: focus point)

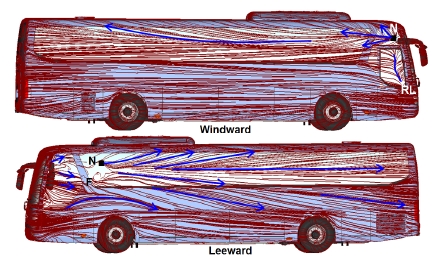
반시계 방향의 요각을 갖는 경우 바람을 받는 RH 쪽에서는 Fig. 7과 같이 재 부착선(RL)이 명확히 형성되었다. A필라에서 박리된 유동이 측면에 재 부착되어 일부는 역류하며 나선형 와류가 형성됨을 유추해 볼 수 있다. 스테이 후방에서 재 부착된 흐름의 표면 유선은 점차 위로 휘어지고 있어 시계 방향의 요각을 갖는 경우에 비해 후방의 측면 흐름을 위로 당겨주는 흐름 성분이 보다 크게 발생함을 알 수 있다. 바람을 등진 LH 쪽의 흐름은 스테이 후방에 재 부착점과 와류 표출점이 존재하며 Fig. 5에 도시한 요각이 없는 경우에 비해 재 부착점을 중심으로 상하 방향으로 분지되는 흐름 성분이 전반적으로 증대되어 있다. 리어바디 표면유선과 압력분포를 Fig. 8에 도시하였다. 복수개의 재 부착점이 형성되고 재 부착점을 중심으로 유동이 분지되는 특징은 요각 조건에 상관없이 동일하나 요각을 갖는 경우 재 부착점이 바람을 받는 쪽과 바디 높이 방향으로 이동해 있음을 볼 수 있다.

Fig. 7

Streamlines around body at a yaw angle of -5° (black square: node, white circle: focus point)

Fig. 8

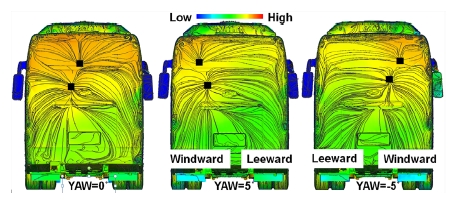
Streamlines and pressure distribution on the rear body surface corresponding to the yaw angle variation

이는 앞서 기술한 상향하는 측면 흐름의 영향으로 판단되며 후류 비대칭성의 증대를 야기한다. 요각을 갖는 경우 리어 바디 표면 압력은 전체적으로 감소하였다. 재 부착점이 바람을 받는 쪽으로 이동하여 바람을 등지는 쪽의 후면 압력회복이 상대적으로 매우 감소하였고 반시계 방향의 요각을 갖는 경우 RH 미러경의 압력이 크게 회복되었다.

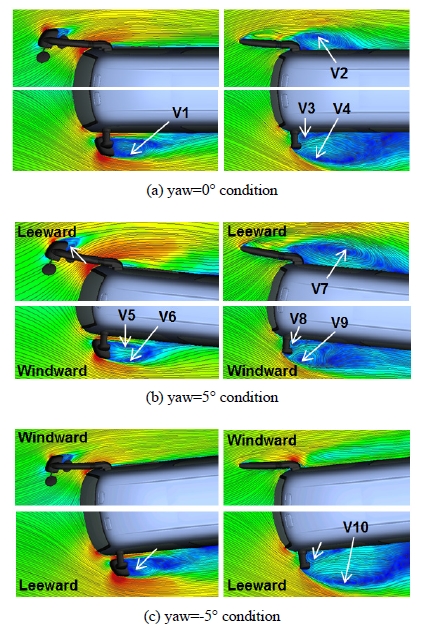
Fig. 9에는 미러 하우징과 스테이단면에서 평균 속도 및 유선 분포를 도시하였다. 요각이 없는 경우 LH 하우징 단면에서 반시계 방형의 와류(V1)가 존재하고 RH 스테이 단면에서는 시계방향의 와류(V2)가 형성되며 LH 스테이 후방에 한쌍의 와류(V3, V4)가 존재한다. LH 쪽이 바람을 맞는 경우 LH 하우징 단면에서 정풍조건에 비해 한쌍의 와류(V5, V6)가 형성되었고 정풍조건시 LH 스테이 단면에서 차량 길이 방향으로 길게 형성되었던 와류(V4)의 크기는 축소되어 있다. 반면 RH 스테이 단면에서는 와류(V7)의 중심점이 후방으로 이동하고 와류의 크기 또한 확장되어 RH 쪽의 속도 결손을 증대시키며 LH쪽의 와류(V8, V9)는 정풍조건에서와 유사한 흐름이다. RH쪽이 바람을 맞는 경우 LH 하우징 단면의 흐름은 정풍조건 흐름과 유사하며 LH 스테이 단면에서는 바깥쪽에 형성되는 와류(V10)는 보다 확장되어 있고 정풍조건에서 RH 스테이 후방에서 형성되는 와류는 소멸되어 있다.

Fig. 9

Velocity and time-averaged streamlines field around baseline mirror (arrow: vortex core)

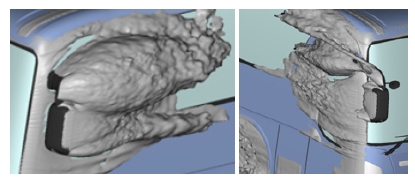
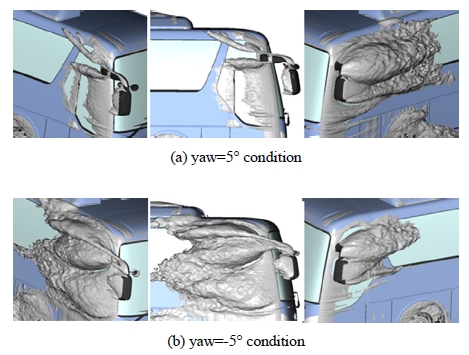
Fig. 10에는 요각 및 시간 변화에 따른 미러 하우징과 스테이 단면에서의 속도분포 및 유선 분포를 도시하였다. 시간 변화에 따라 와류의 생성, 발달, 소멸 과정을 볼 수 있으며 와류의 변화에 따라 바디 재 부착 위치 또한 달라지고 있다. 요각을 갖는 경우 바람을 등지는 스테이 후방의 와류는 확장 되고 축소되는 현상이 반복적으로 발생하고 있다. 횡풍 조건 등압력 표면을 Fig. 11에 도시하였다. 5° 요각을 갖는 경우 바람을 등지는 RH 스테이에서 발생된 와류와 A필라 박리유동이 연동되어 Fig. 4의 요각이 없는 경우 대비 에너지 손실 영역은 크게 확대되었고 LH 쪽은 다소 축소되어 있다. -5° 요각을 갖는 경우 바람을 등지는 LH 쪽의 에너지 손실 영역이 크게 증대된 반면 RH 스테이 영역의 와류가 상대적으로 크게 축소되었다.

Fig. 10

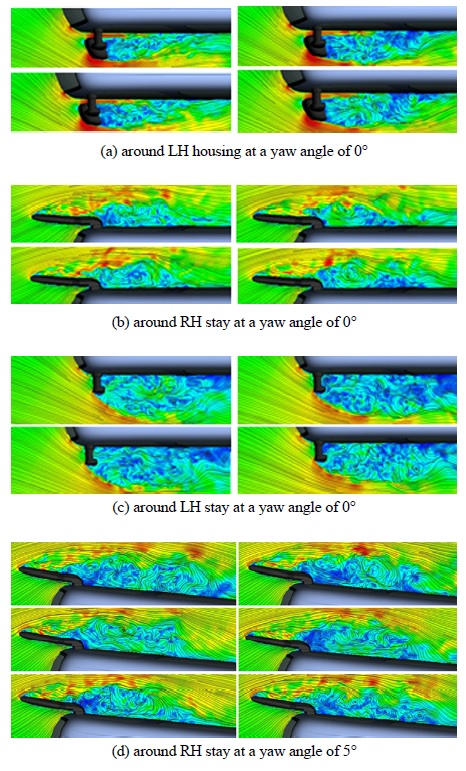
Instantaneous wake structure around baseline mirror: velocity magnitude and streamlines (ΔT=0.14sec)

Fig. 11

Isosurface of baseline model (Cpt=0 time averaged)

이는 Fig. 7과 Fig. 9에 보인 바와 같이 A필라 박리유동이 재 부착되고 스테이와 A필라 와류의 연동하는 흐름 또한 소멸되었기 때문이다.

3.3 미러 형상 변경에 따른 공력 특성

Fig. 12에는 모델 C와 미러가 없는 모델에 대한 리어바디의 압력 분포를 도시하였다. 모델 C 및 미러가 없는 모델의 경우 바디 하단에서 음압이 다소 증가하나 리어바디 상단에서 상대적으로 고압영역이 형성되며 압력회복이 보다 우위에 있음을 볼 수 있다. Fig. 4에 보인 바와 같이 Baseline모델에 비해 모델 C는 미러에 의해 발생하는 에너지 손실 영역이 매우 감소하였고 LH 스테이 형상을 변경한 모델 A와 B는 미러 스테이 후미에서 발생하는 와류 영역은 크게 감소하였지만 미러 하우징 후류는 다소 증대되었다.

Fig. 12

Pressure distribution on the rear body surface and isosurface around modified mirror

미러 형상 변경에 따른 1/4 스케일 모델 풍동시험 및 해석 그리고 실차 해석 결과를 비교하였다. 풍동시험은 독일 Stuttgart에 위치한 FKFS(Forschungsinstitut für Kraftfahrwesen und Fahrzeugmotoren Stuttgart) 실차 풍동에서 수행되었다. Fig. 13에서 도시한 바와 같이 차량의 하부 영역에서 벨트를 이용하여 지면 이동 조건 재현이 가능하며 지면에서 발생하는 경계층이 항력에 미치는 영향을 최소화하기 위해 풍동 입구와 차량 전방부에 흡입영역이 설치되어 있다. 시험이 수행된 실차 풍동의 대략적인 제원과 시험 조건은 Table 1과 같다.

Fig. 13

1/4 scale model in the test section of wind tunnel

Table 1

Specification of wind tunnel and test condition

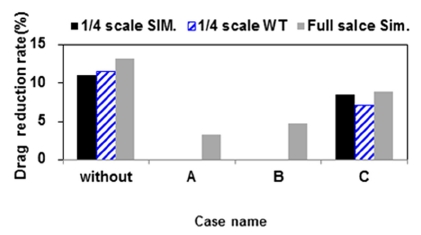
Baseline 모델 대비 미러 형상 변경에 따른 공기저항 감소율을 Fig. 14에 나타내었다. 미러를 제거한 모델과 모델C의 풍동시험 결과와 해석결과는 정성적인 경향이 매우 잘 일치하고 있으며 실차 해석결과는 스케일 모델 풍동시험과 해석결과 대비 항력 개선율이 보다 크게 나타났다. 미러를 제거한 경우 스케일 모델 풍동시험 결과 공기저항은 약 11.5 % 감소하였고 실차 해석결과는 약 13.2 % 감소하였다.

Fig. 14

Drag reduction comparison between measured and predicted value at a yaw angle of 0°

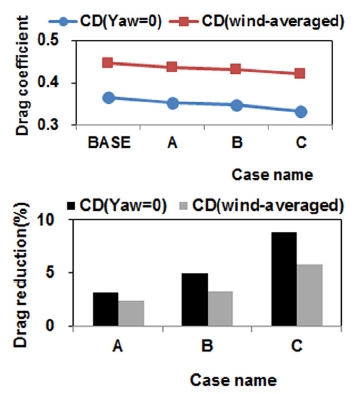
실차 해석결과 A, B, C모델의 항력은 Baseline 모델 대비 각각 3.2 %, 4.7 %, 8.9 % 개선되었다. Fig. 15에 나타낸 요각 변화에 따른 공기저항은 반시계방향 요각 대비 시계방향 요각이 형성될 때 상대적으로 증가하였고 요각 증대시 요각 방향 변경에 따른 공기저항의 편차 또한 증가하였다. Baseline 모델의 공기저항은 -7°대비 7°도인 경우 약 13 % 증가하였다. 스테이 형상이 변경된 A, C 모델은 요각 변화에 따라 공기저항의 편차는 상대적으로 감소하였다. Fig. 16에는 미러 항력과, 형상 항력, 간섭 항력을 도시하였다. 미러 항력과 간섭 항력은 식 (6), (7)과 같이 정의된다.

Fig. 15

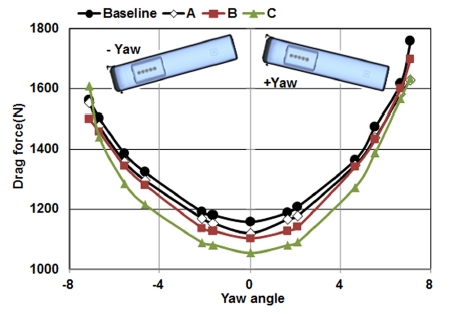
The variation in drag force corresponding to the yaw angle variation for different mirrors (+yaw : clockwise rotation)

Fig. 16

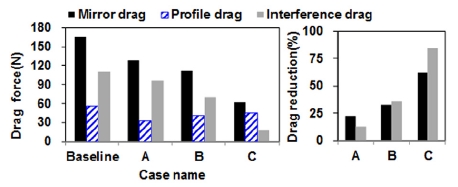
Comparison of mirror, profile and interference drag(left) and drag reduction rate(right) for different mirrors at a yaw angle of 0°

전반적으로 변경모델의 미러 항력과 간섭 항력은 전체적으로 감소하였다. 특히, LH와 RH 미러를 모두 전방에 배치하고 스테이 단면을 폭 방향이 장축인 단면으로 변경한 모델 C의 형상 항력은 Baseline 모델과 큰 차이가 나지 않지만 미러 항력과 간섭 항력은 현저하게 감소되었다. 미러 형상 변경에 따라 미러 항력은 최소 약 23 % 이상 감소하였고 간섭 항력 또한 13 % 이상 감소하였다.

3.4 자연풍을 고려한 Wind-averaged CD 예측

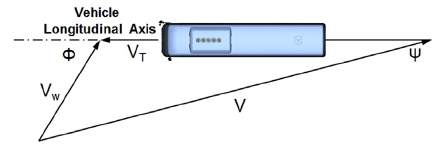
우리나라는 대륙의 동안에 위치하여 대륙과 해양의 사이에서 계절풍의 영향을 크게 받으며 지역별 자연풍의 편차는 있지만 연평균 자연풍의 속도는 약 2 m/sec ~ 4 m/sec수준이다.⁹⁾ Fig. 17에는 자연풍이 존재할 때 차량 주행 방향에 대해 횡풍이 형성되고 이때의 상대적인 속도에 대한 개략도를 도시하였다.

Fig. 17

Relative airspeed vector diagram

자연풍에 의한 요각 정의는 SAE J1252 표준¹⁰⁾을 기준으로 하였으며 식 (11)로부터 자연풍의 방향이 30°간격으로 변화할 때 차량 주행 방향에 대한 상대적인 요각은 식 (13)에 의해 계산되며 요각에 대한 가중치인 식 (10)과 식 (9)로부터 자연풍을 고려한 평균 항력 계수를 얻을 수 있다.

Table 2에는 자연풍을 3 m/sec로 고려했을 때 Baseline 모델에 형성되는 요각과 가중치 그리고 평균 항력 계수 산출과정을 도시하였다. 여기서 CD 값은 정풍조건을 기준으로 환산된 값이다.

Table 2

Wind-averaged drag coefficient computation chart of baseline

Fig. 18에 도시한 실도로 지상풍을 고려한 평균 항력계수는 정풍 조건 항력 계수 대비 전반적으로 약 22 % 이상 증가하였다. Baseline 모델 대비 미러 형상 변경에 따른 항력 개선율은 정풍조건에 비해 약 1 % ~ 3 % 감소하였다. 이는 Fig. 14에서 볼 수 있듯이 요각이 증가함에 따라 공기저항 개선율이 감소하기 때문이다.

Fig. 18

Comparison of drag coefficient and drag reduction rate between Cd at a yaw angle of 0° and wind-averaged Cd for different mirrors