삼차원 유한요소 해석을 이용한 고분자 전해질 연료전지 PEM 변형 연구

1. 서 론

고분자 전해질 연료전지(Polymer Electrolyte Membrane Fuel Cell, PEMFC)는 기존 내연기관 엔진을 대체할 수 있는 청정에너지 기기이다.¹⁾ 연료전지 개발과정에서 고려해야 할 요소는 충분한 파워 밀도(Power density), 제작 비용(Cost), 내구성(Durability) 등이다. 그중 연료전지의 적절한 내구성 유지는 연료전지 기반 자동차의 장기 성능(Long-term performance) 유지에 필수적인 요소이다.

기체확산층(Gas Diffusion Layer, GDL), 양극판(Bipolar plate), 막전극접합체(Membrane Electrode Assembly, MEA)는 고분자 전해질 연료전지의 주요 구성 요소이다. 그중 막전극접합체는 연료전지의 핵심 구성품이며 촉매층(Catalyst layer), 기체확산층, 양성자 교환막(Proton Exchange Membrane, PEM)으로 구성되어있다. 일반적으로 사용되는 PEM의 재료는 DuPont 社의 PFSA(Perfluorosulfonic acid) NAFION^®이다.²⁾ 막전극접합체의 중간에 있는 PEM은 양성자(Proton)를 양극에서 음극으로 지나게 하며 전기 부도체(Electronic insulator)와 가스 분리막으로의 역할을 한다.¹⁾

PEM은 고분자 전해질 연료전지의 성능과 수명에 영향을 끼치는 핵심 구성품이다. 연료전지의 내구성을 유지하기 위해서는 예기치 못한 PEM의 조기 파손을 포함한 연료전지 구성품의 파손 예방 및 파손 메커니즘에 관한 연구가 필요하다. 연료전지 작동 중에 PEM은 수분, 가스의 전달 통로, 전기화학 반응, 그리고 반응에 의한 열의 작용에 노출된다. 화학적 열화(Chemical degradation), 기계적 열화(Mechanical degradation)가 발생한 PEM은 파손 가능성이 증대하여 연료전지 내구성을 감소시킨다.

화학적 열화는 반응 가스의 침투(Permeation), 수산기(Hydroxyl radical), 과수산기(Hydroperoxyl radical) 같은 유리기(Free radical)의 이동(Migration)에 의한 결과로 발생하는 것으로 알려져 있다.³⁾ 기계적 열화는 제조 과정 중 발생할 수 있는 결함, 불균일 접촉 압력, 운전 중에 발생할 수 있는 높은 초기 가스 압력차, 온도/습도에 의한 피로 응력 등에 의하여 발생할 수 있다.¹⁾

실제 운전 중의 PEM은 화학적/기계적 열화가 동시에 발생하여 가속화된다.⁴⁾ 화학적 열화가 PEM의 분해를 가속하여 질량, 두께를 감소시키고 반복하중에 의한 기계적 응력이 이에 작용할 때 크랙 및 핀홀(Pinhole)이 형성되며 이 위치에 가스의 침투 같은 화학적 작용이 심화하여 열화를 가속화 한다.⁵⁾

PEM은 볼트로 체결된 연료전지 셀 내부에 위치하여 반복하는 온/습도 사이클에 의하여 면내(In-plane)와 면외(Out-of-plane) 방향으로 팽창/수축이 나타난다. 팽창 후 수축하는 과정에서 발생할 수 있는 잔류 인장 응력은 PEM에서의 크랙 발생 원인이 될 수 있으며, 잔금(Crazing), 찢어짐(Tearing), PEM과 촉매층 사이의 박리(Delamination) 현상들도 반복되는 기계적인 하중에 의해 생성될 수 있다.^6,7)

PEM의 파손 위치는 연료전지 셀 형상과 작동 조건에 의존하고 박막 타입, 두께에는 무관한 것으로 알려졌다.⁸⁾ 핀 홀이나 크랙이 주로 발견되는 위치는 유동 채널 하부의 저 압축(Low compression)이 발생하는 곳이고 팽창 후 상온 압축과정에서 나타나는 잔류 인장 응력이 나타난다.^9-11) PEM의 크랙 형성은 in-situ 나 ex-situ 환경에서의 온/습도 사이클 반복 시험에서 나타났으며 형성된 크랙은 PEM 단면을 따라 전파되어 결국은 가스 누출이나 교차가 발생한다.

지금까지 수치적인 방법을 사용한 PEM 변형 및 파손에 관한 연구들은 거의 2차원 모델을 사용하여 면내 2방향으로의 변형 형상과 면외 방향의 변형 형상의 상호 영향을 평가하지 못하였으며 셀 내의 구성품 간의 접촉에 의한 상호 작용도 평가하지 못하였다. 본 연구에서는 PEM의 기계적 성능 열화 원인 중에 온/습도 변화에 의한 응력 변동 메커니즘과 그에 따른 파손 위치 및 파손 가능성에 관한 내용을 다룰 것이다. 3차원 모델을 사용하여 2 면내 방향의 변형에 의한 영향과 셀 내의 구성품 간의 접촉 조건에 의한 상호 작용의 영향을 평가하려고 시도하였다. 이러한 연구는 광역모델(Global model) 해석 후 부 모델(Sub-model)을 사용하는 방법을 사용하였고 상세한 국부 변형 거동 해석이 가능하게 하였다.

면내 응력의 크기와 인장/압축의 반복에 의한 소성 변형 발생과 잔류응력 간의 상호 영향에 대한 평가도 진행하였다.

모델링 전처리 프로그램으로는 HYPERMESH, 유한요소해석은 ABAQUS¹²⁾를 사용하여 연구를 진행하였다.

2. PEMFC 모델

2.1 유한요소모델

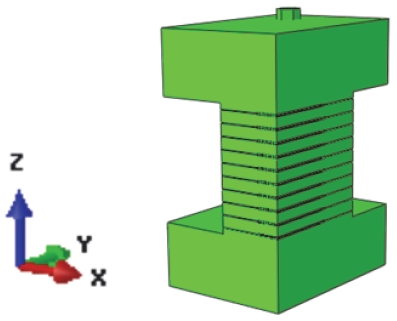
유한요소해석에 사용된 고분자 연료전지 모델은 아래 그림과 같은 3차원 형상이다. 모델은 양극판, 기체확산층, 양성자 교환막으로 구성된 단위 셀을 적층하여 양 끝판(End plate)에 볼트를 체결하여 구성하였으며 효율적인 시뮬레이션을 수행하기 위하여 지난 연구¹³⁾에서의 모델을 수정하여 원 모델 형상의 1/4을 광역모델로 사용하였다(Fig. 1). 지난 연구에서¹³⁾ 사용한 원 모델의 형상 치수는 대부분 Liu 등¹⁴⁾의 모델을 참조하였으며 양극판의 채널형상은 2차원 모델에서 사용한 치수를 적용하였다.¹⁵⁾

Fig. 1

Assembled quarter 3D model of PEMFC stack

시뮬레이션에 적용한 경계조건은 2 절단면에서는 면 수직 방향을 고정하여 대칭면 경계조건을 주었고 바닥 면은 역시 면 수직 방향을 고정하여 강체 운동을 제한하였다. 모델에 적용한 하중은 볼트 체결 하중과 온/습도 하중이고 볼트 체결 하중은 Fig. 1과 같이 실제 볼트를 모형화하여 체결 하중을 가하였다. 온/습도 하중은 ABAQUS의 서브루틴인 UEXPAN을 사용하여 온/습도의 변화에 따른 팽창/수축을 나타내었다.

시뮬레이션 모델은 다음과 같은 가정을 하여 모델링 및 시뮬레이션 과정을 단순화하였다. 먼저, PEM의 팽창/수축은 균일하게 발생한다고 가정하였고 GDL의 재료 모델은 직교이방성을 가정하였고 PEM의 재료 모델은 비선형 탄소성 모델(Nonlinear elastic-plastic)을 선택하였다. 그 밖의 구성품들은(양극판, 끝판, 볼트) 선형 탄성 모델(Linear-elastic)을 가정하였다. 촉매층은 얇은 두께이므로 PEM에 포함된 것으로 가정하였다.

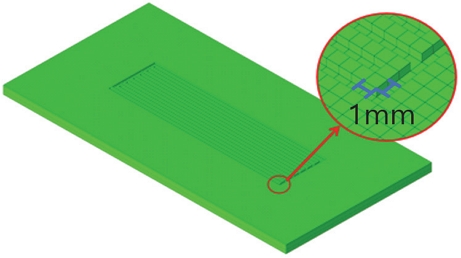
연료전지 스택 모델은 두께가 얇은 구성품으로 이루어져 있으므로 모델 크기가 증가하게 된다.¹⁶⁾ 1/4 스택 전체를 모델링한 3차원 광역모델은 163만 개의 절점과 173만 개의 요소로 구성되어있으며, 반복적인 양극판의 채널, 리브 형상의 폭은 1 mm로 설정하였다(Fig. 2). 사용된 요소는 ABAQUS에서 제공하는 C3D6, C3D8이며 모델의 면외 방향은 z 축, 면내 방향은 x, y 축으로 설정하였다.

Fig. 2

Bipolar plate of global 3D model illustrating width of channel

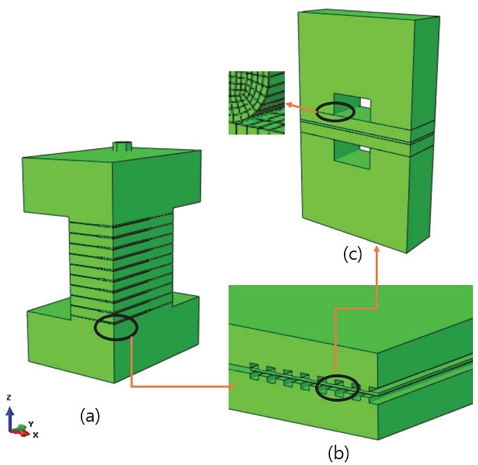
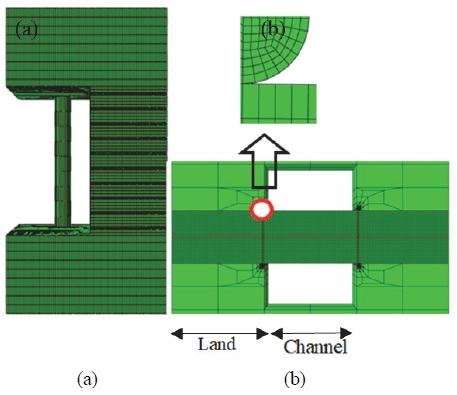
3차원 광역모델의 최 하단 셀(양극판, GDL, PEM으로 구성)의 일부를 절단하여 구성한 3차원 부 모델은 140만 개의 절점과 154만 개의 요소로 구성되어있다(Fig. 3(c)). ABAQUS에서 제공하는 C3D6, C3D8의 요소를 사용하였으며 광역모델과 같이 면외 방향을 z축, 면내 방향은 x, y 축으로 설정하고 부 모델의 절단면에 광역모델의 변위 경계조건을 부여하여 해석을 수행하였다.

Fig. 3

Description of PEMFC model. (a) Global model (b) 1st cell layer of the stack (c) Sub-model

Fig. 3에서는 시뮬레이션에 사용된 광역모델과 부 모델의 형상 및 위치를 표시하였다. (a)는 1/4 광역모델이고 (b)에서는 광역모델의 첫 번째 셀을 확대 표시하였다. 첫 번째 셀의 채널을 포함한 일부분을 사용한 부 모델은 (c)에 나타내었다. 부 모델 분리판의 채널 끝 모서리는 침투에 의한 수치 문제를 완화할 수 있도록 라운드 형상을 모형화하였다(Fig. 3 (c)).

2.2 시뮬레이션 재료 모델과 물성

기체확산층과 PEM의 접촉면은 접촉 조건(Small sliding condition in ABAQUS)을 주어 미끄럼이 가능하며 온/습도 하중에 의한 PEM의 거동은 탄소성(Elastic-plastic) 재료 가동을 가정하였으며 등방성 경화 거동(Isotropic hardening) 모델을 사용하였다. 온/습도 조건을 고려한 PEM의 재료 물성값은 Tables 1, 2에 나타내었다.

Table 1

Elastic modulus of nafion 112 at various temperatures and relative humidities6)

Table 2

Yield stress at various temperatures and humidities for Nafion 11216)

PEM의 온/습도에 의한 팽창은 균일한 변형을 가정하였고 기계적 변형에 다음과 같은 팽창변형 성분을 추가한다.

$\[ {ϵ}_{ij}={ϵ}_{ij}^e+{ϵ}_{ij}^p+{ϵ}_{ij}^{TS} \]$

(1)

여기서, $$ {ϵ}_{ij}^e$$는 탄성 변형률 성분, $$ {ϵ}_{ij}^p$$는 소성 변형률 성분, $$ {ϵ}_{ij}^{TS}$$는 온/습도에 의한 팽창 변형률 성분이다.

온/습도에 의한 변형률은 다음과 같이 수직 성분만 존재하며 온도 구배에 비례해서 증감한다.¹⁵⁾

$\[ {ϵ}_{ij}^{TS}={\alpha }^{\mathrm{\text{'}}}\left(T-T_0\right){\delta }_{ij} \]$

(2)

여기서 α'는 온도와 습도에 의한 팽창계수이며 δ_ij는 Kronecker delta이다.

$\[ {\alpha }^{\mathrm{\text{'}}}\left(T,RH\right)=\frac{\left[1+\alpha \left(T\right)\mathrm{\Delta }T\right]\left[1+\beta \left(RH,T\right)\mathrm{\Delta }RH\left(T\right)\right]-1}{\mathrm{\Delta }T} \]$

(3)

식 (3)에서 습도의 변화는 동등한 온도변화로 변환되어 하나의 팽창계수 α'가 온도와 습도 팽창계수인 α, β를 대체하였다.

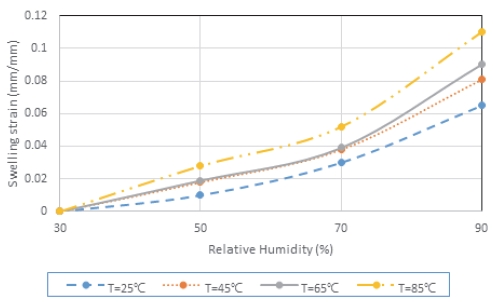
PEM의 팽창변형 모델은 ABAQUS 서브루틴 UEXPAN에 코딩되었고 모델에 적용된 재료 물성값은 온/습도 의존 형태이다. 시뮬레이션에 사용된 열팽창계수와 팽창계수는 참고문헌 실험데이터로부터 수집하였으며 Table 3과 Fig. 4에 정리하였다.

Table 3

Coefficient of thermal expansion and swelling coefficient of each part17)

Fig. 4

Swelling strain as a function of humidity and temperature for Nafion 11218)

탄소섬유의 배열로 인하여 직교 이방성의 성질을 나타내는 기체확산층의 재료 모델은 아래와 같은 모델을 사용하였다.

일반적인 재료의 구성방정식은 아래와 같은 관계로 나타낼 수 있다.

$\[ {\sigma }_{ij}=C_{ijkl}{ϵ}_{kl} \]$

(4)

탄성 텐서 행렬 C_ijkl는 36개의 재료 상수가 필요하지만, 이방성 재료는 21개의 재료 상수의 결정이 필요하다. 직교 이방성을 나타내는 기체확산층의 경우에는 9개의 재료 상수의 결정이 필요하다.¹⁹⁾

일반적인 3차원 상태의 직교 이방성 재료의 구성방정식은 다음과 같다.

$\[ \left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\sigma }_{yz}\\ {\sigma }_{zx}\\ {\sigma }_{xy}\end{array}\right]=\left[\begin{array}{cccccc}\frac{1-v_{yz}{v}_{zy}}{E_y{E}_z\mathrm{\Delta }}& \frac{v_{yx}+v_{zx}{v}_{yz}}{E_y{E}_z\mathrm{\Delta }}& \frac{v_{zx}+v_{yx}{v}_{zy}}{E_y{E}_z\mathrm{\Delta }}& 0& 0& 0\\ \frac{v_{xy}+v_{xz}{v}_{zy}}{E_z{E}_x\mathrm{\Delta }}& \frac{1-v_{zx}{v}_{xz}}{E_z{E}_x\mathrm{\Delta }}& \frac{v_{zy}+v_{zx}{v}_{xy}}{E_z{E}_x\mathrm{\Delta }}& 0& 0& 0\\ \frac{v_{xz}+v_{xy}{v}_{yz}}{E_x{E}_y\mathrm{\Delta }}& \frac{v_{yz}+v_{xz}{v}_{yx}}{E_x{E}_y\mathrm{\Delta }}& \frac{1-v_{xy}{v}_{yx}}{E_x{E}_y\mathrm{\Delta }}& 0& 0& 0\\ 0& 0& 0& 2G_{yz}& 0& 0\\ 0& 0& 0& 0& 2G_{zx}& 0\\ 0& 0& 0& 0& 0& 2G_{xy}\end{array}\right]\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\epsilon }_{yz}\\ {\epsilon }_{zx}\\ {\epsilon }_{xy}\end{array}\right] \]$

(5)

여기서

$\[ \Delta =\frac{1-{\nu }_{xy}{\nu }_{yx}-{\nu }_{yz}{\nu }_{zy}-{\nu }_{zx}{\nu }_{xz}-2{\nu }_{xy}{\nu }_{yz}{\nu }_{zx}}{E_x{E}_y{E}_z} \]$

기체확산층에 사용한 3차원 직교 이방성 모델의 구성방정식의 경우에는 기체확산층의 다공성 구조에 의하여 푸아송비들을 0으로 가정하여 다음과 같이 구성방정식을 간략화할 수 있다.

$\[ \left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\sigma }_{yz}\\ {\sigma }_{zx}\\ {\sigma }_{xy}\end{array}\right\}=\left[\begin{array}{cccccc}{E}_x& 0& 0& 0& 0& 0\\ 0& E_y& 0& 0& 0& 0\\ 0& 0& E_z& 0& 0& 0\\ 0& 0& 0& G_{yz}& 0& 0\\ 0& 0& 0& 0& G_{zx}& 0\\ 0& 0& 0& 0& 0& G_{xy}\end{array}\right]\left\{\begin{array}{c}{ϵ}_{xx}\\ {ϵ}_{yy}\\ {ϵ}_{zz}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right\} \]$

(6)

직교 이방성을 나타내는 기체확산층의 면외 방향의 비선형 탄성계수 함수는 Table 4와 같은 함수를 사용하였다. 소규모의 경화에 의한 초기영역, 대규모의 경화에 의한 마지막 영역, 초기영역과 마지막 영역의 경계 지점인 천이 영역으로 구성되어있다.²⁰⁾

Table 4

Piecewise polynomial fitting model of the out-of-plane direction non-linear behavior of GDL20)

Table 5

Material properties of GDL used for simulation20)

Table 6

Material properties of bipolar plate, end plate & bolt used for simulation14)

면외 방향 (3차원 모델에서 z 방향)의 비선형 변형 거동은 면외 방향의 변형률의 함수로 실험 결과값의 Curve-fitting 함수를 이용하여 나타낸다.

3차원 직교 이방성 모델은 기체확산층의 다공성(Porous)의 특성을 고려하여 푸아송비를 0으로 가정하였다. 면외 방향인 z 방향에서의 변형은 비선형 거동이 관찰되며 z 방향의 탄성계수 E_z는 변형률에 따른 실험 결과값을 커브 피팅한 함수를 사용한다. XY 평면에서의 재료 거동은 등방성이 관찰되어 전단 계수 G_xy는 잘 알려진 다음 식을 사용하여 계산하였다.¹³⁾

$\[ {\left(G_{GDL}\right)}_{xy}=\frac{{\left(E_{GDL}\right)}_x}{2\left(1+{\nu }_{GDL}\right)} \]$

(7)

3. 유한요소해석결과

3.1 모델 검증

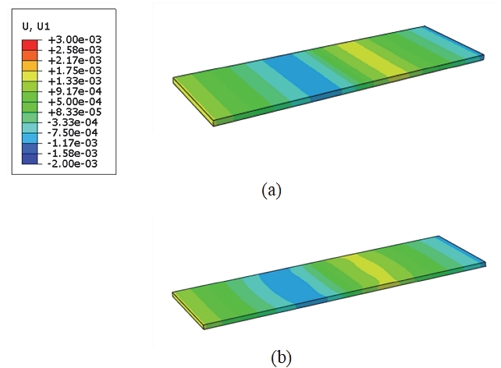
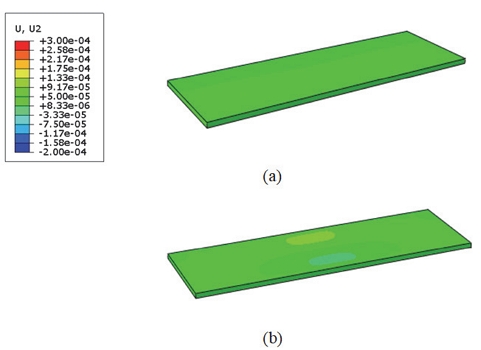
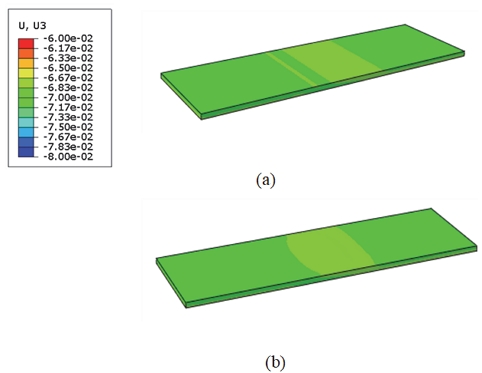
PEM의 상세한 변형 형상을 나타내기 위하여 사용한 부 모델 기법(Sub-modeling method)을 검증하기 위해서는 먼저 광역모델에서의 결과와 광역모델 일부분에 매우 조밀하게 요소 망을 생성한 부 모델에서의 결과가 서로 비교되어야 한다. 광역 모델과 부 모델이 물리적으로 동등함은 부 모델이 파생된 광역모델의 경계 부분과 부 모델의 경계 부분의 변위 성분 등고선도(Contour plot)를 비교하여 확인한다. Figs. 5~7은 같은 위치에서 광역모델과 부 모델의 각각 x, y, z 방향으로의 변위 성분들의 등고선도이며 광역모델과 광역모델에서 파생된 부 모델의 경계 부위의 변위 성분들의 분포가 거의 일치함을 보여준다.

Fig. 5

Comparison of displacement in x-dir (step 3). (a) Global model (b) Sub-model

Fig. 6

Comparison of displacement in y-dir (step 3). (a) Global model (b) Sub-model

Fig. 7

Comparison of displacement in z-dir (Step 3). (a) Global model (b) Sub-model

3.2 시뮬레이션 하중

시뮬레이션에 사용된 유한요소 모델은 Fig. 8과 같다. 부 모델의 PEM 부분은 상세한 해석을 위해 매우 조밀한 유한요소를 사용하였다. 양극판과 접촉하는 GDL, PEM 부분을 랜드(Land)라 하고 채널(Channel) 부분은 접촉하지 않는 부분이다(Fig. 8).

Fig. 8

The FE models used in the simulation. (a) Meshed global model (b) Meshed sub-model (partial)

시뮬레이션 모델의 하중은 볼트 체결 스택 어셈블리 하중과 온/습도에 의한 팽창 하중을 1 사이클(Cycle)로 구성하였다.

• - 볼트 체결 하중 (Step 1): 상온 25 ^oC, 30 % RH에서 볼트 하중을 스택에 적용하여 체결한다.
• - 온/습도 하중 (Step 2): 연료전지 스택의 온도는 25 ^oC에서 85 ^oC, PEM의 상대습도는 30 % RH에서 90 % RH로 높인다.
• - 온/습도 하중 제거 (Step 3): 다시 처음 온도인 25 ^oC, 습도는 30 % RH로 감소시켜 연료전지 스택의 환경을 구현한다.

연료전지 스택의 운전은 이와 같은 하중 사이클이 반복된다고 가정한다.

3.3 PEM 응력

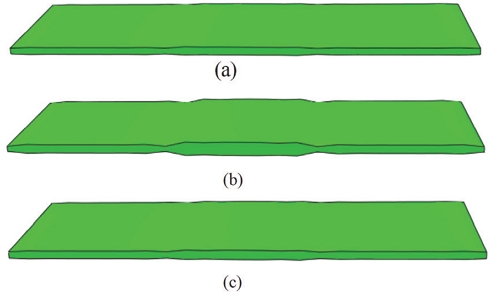
PEM은 복잡한 변형 거동을 나타낸다. 이는 하중의 복합성과 더불어 구성품의 기하학적인 형상 때문에 기인한다. Fig. 9는 단계별 하중 하에서 변형된 PEM의 형상을 나타낸다. 볼트 체결 하중이 적용된 Step 1에서는 랜드 부에서 면외 방향으로의 압축과 채널 부에서의 양극판의 기하학적 형상에 의한 면외 방향의 팽창이 나타난다. 랜드 부와 채널 부의 전환부(Transition region)는 응력 집중에 의한 삼 축 변형이 나타난다.

Fig. 9

Deformed shapes of PEM for 1,400 N bolt load. (a) Step 1 (b) Step 2 (c) Step 3

온/습도 하중에 의한 팽창이 나타나는 Step 2에서는 기하학적인 구속 때문에 더욱 큰 압축 응력이 발생하게 된다. 온/습도 하중이 제거된 Step 3의 형상은 소성 변형 때문에 Step 1과는 다른 형상을 나타낸다.

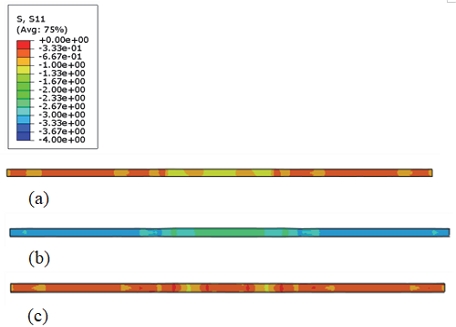
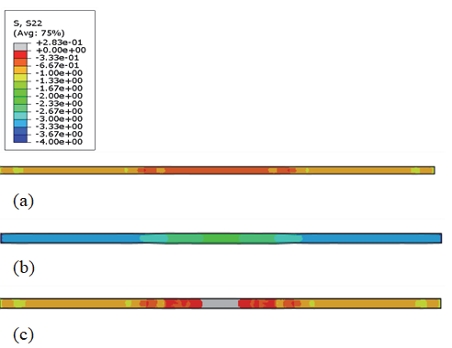
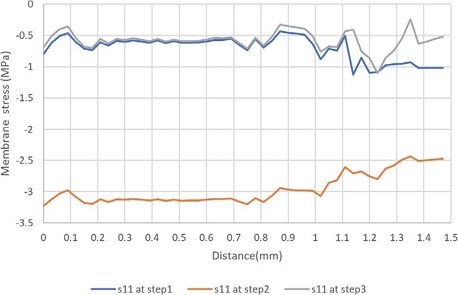
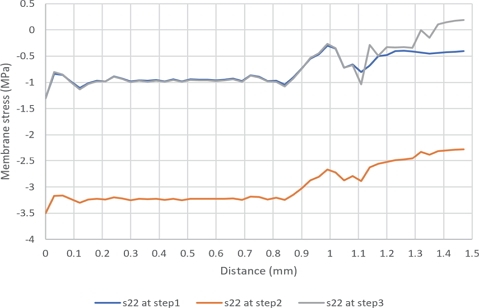
연료전지 단위 셀의 평면 변형만을 고려한 2차원 모델과 달리 3차원 모델에서는 면내 방향의 2 응력의 거동과 면외 방향의 응력 거동을 관찰할 수 있다. Figs. 10~12는 면내 방향 응력인 σ_xx, σ_yy와 면외 방향 응력 σ_zz을 단계별 등고선도로 나타내었다. 면내 응력인 σ_xx는 1 사이클이 반복되는 동안 압축 응력만이 나타났고, 다른 면내 응력인 σ_yy는 Step 3에서 채널의 중심부에서 잔류 인장 응력이 관찰된다(Fig. 11(c)).

Fig. 10

Contour plot of in-plane stress σxx for 1,400 (N) bolt load. (a) Step 1 (b) Step 2 (c) Step 3

Fig. 11

Contour plot of in-plane stress σyy for 1,400 (N) bolt load. (a) Step 1 (b) Step 2 (c) Step 3

Fig. 12

Contour plot of out-of-plane stress σzz for 1,400 (N) bolt load. (a) Step 1 (b) Step 2 (c) Step 3

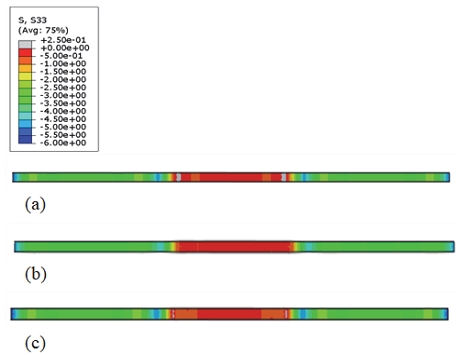
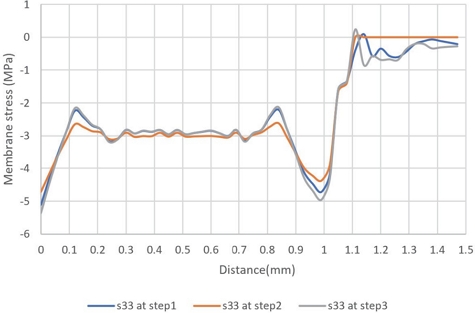
면외 방향의 응력 σ_zz 도 PEM 전 영역에서 주로 압축 응력이 나타났으며 면내 2방향의 응력 값보다 큰 응력 값을 나타내었다. 랜드 부와 채널 부의 전환부에서 기하학적인 구속에 의한 것으로 보이는 인장 응력이 부분적으로 나타났다(Fig. 12(a), (c)).

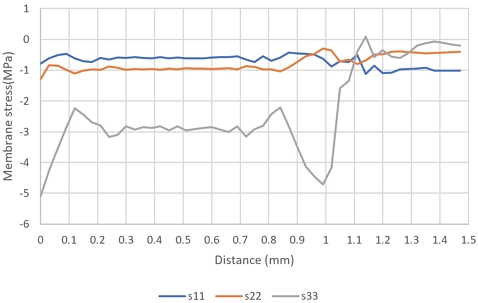
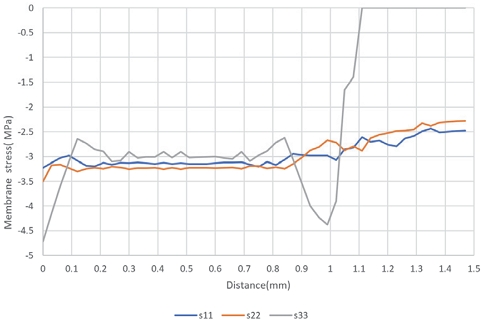
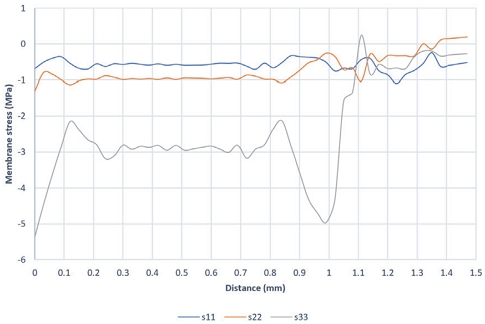
Kusoglu 등¹⁶⁾은 PEM의 평면 변형 기계적 거동 시뮬레이션 결과에서 면외 방향의 응력 (σ_zz) 값보다 면내 응력 (σ_xx)의 값이 더 커서 PEM 변형을 주도한다고 판단하여 면내 응력 σ_xx를 사용한 결과를 바탕으로 연구를 진행하였다. 이 연구 그룹이 고려한 모델은 평면변형모델(Plane strain)이었고 접촉면의 접촉 거동도 고려하지 않았다. 이들의 결과와는 상반되게 본 연구에 사용된 3차원 모델은 대부분 영역에서 면외 방향의 응력 값이 면내 방향보다 큰 압축 응력이 관찰되었다(Figs. 13~15).

Fig. 13

Membrane stress history along a path at the membrane for step 1 (bolt load 1,400 N)

Fig. 14

Membrane stress history along a path at the membrane for step 2 (bolt load 1,400 (N))

Fig. 15

Membrane stress history along a path at the membrane for step 3 (bolt load 1,400 (N))

Figs. 13~15의 가로축은 PEM의 x 축 방향의 거리를 나타내며 PEM의 변형 형상이 대칭이므로 전체 PEM의 좌측 절반에 대하여 응력 값들을 나타내었다. 여기서, 0 ~ 1 mm까지의 영역은 랜드 부이고 1 ~ 1.5 mm 영역은 채널 부이다. 이후 그래프에서도 가로축의 표시는 Figs. 13~15와 동등하다. 그래프의 응력 값들을 기록한 경로는 PEM 앞 단면 중앙 수평선 좌측에서 중앙까지 위치한 절점들이다.

PEM의 변형 거동은 볼트 체결과정인 Step 1에서는 압축 응력 상태, 최대 온/습도 하중이 가해지는 Step 2는 팽창 때문에 더 큰 압축 응력이 나타난다. 그리고 초기 상태인 25 ^oC, 30 % 온/습도 환경인 Step 3에서 항복의 정도에 따라 인장 또는 압축 잔류 응력이 나타나게 된다.

이러한 잔류 응력 중 인장 잔류 응력이 발생하는 위치에서는 반복하중에 의한 피로 파손의 가능성이 커진다. 본 연구의 시뮬레이션 결과에서는 Kusoglu 등⁵⁾의 연구와는 달리 x 방향에서는 인장 잔류 응력이 나타나지 않고 다른 면내 응력(채널 길이 방향)인 y 방향과 면외 방향인 z 방향의 응력 성분에서 인장 잔류 응력이 관찰되었다(Fig. 10(c), Fig. 11(c), Fig. 12(c)). 면내 방향인 y 방향의 인장 잔류 응력은 채널 중앙 부에 광범위한 부분에서 나타났으며 z 방향의 인장 잔류 응력은 국부적인 위치에 나타났다. z 방향의 인장 잔류 응력은 발생 위치가 양극판 끝 라운드가 접촉하는 부분으로 형상적인 원인에 의한 것으로 사료 되며 y 방향의 잔류인장 응력이 실제 압축 후 나타나는 재료의 소성 변형 때문에 발생하는 잔류 응력으로 사료 된다.

3.4 PEM 파손

유리상 폴리머(Glassy polymer)의 파손은 파손 면 앞에 나타나는 얇은 웨지 모양의 간섭밴드(Interference band)형태인 잔금의 발생으로부터 시작된다고 알려져 있다.²¹⁾ 폴리머의 잔금은 금속에서 나타나는 소성 영역(Plastic zone)과 유사하지만, 금속에서의 항복 응력하고는 물리적으로 다른 특징을 보여준다. 금속에서의 항복은 일정 부피를 유지한 상태에서 변형이 나타나는 전단 작용에 의한 것이지만 잔금은 크랙 선단이나 고체 내에서 부피의 증가를 가지고 온다. 그러므로 잔금의 시작과 성장은 인장 정수압(Tensile hydrostatic stress)의 역할이 중요하다.

금속의 응력 기반 항복이론처럼 폴리머도 잔금 형성이론(Crazing formation theory)이 제안되었다. 이론에 사용된 기준들은 보편적으로 사용되지는 않지만, 인장 정수압의 잔금 시작에 대한 역할은 물리적 현상에 의하여 필수적인 것으로 여겨진다.

Ongochin과 Stenstein²²⁾은 잔금 형성에 대한 응력 조건을 제안하였다. 이축응력 조건에서 잔금 생성에 주응력과 정수압 응력이 관여하며 정수압 응력 성분과 주응력 성분이 잔금의 생성과 방향에 경쟁적으로 관여한다.

Argon 등²³⁾은 잔금의 성장 및 전파에 대한 다음과 같은 이론을 제안하였다. 잔금 선단은 반복되는 오목한 공기/폴리머 경계면의 파단에 의해 잔금 다발(Crazing tufts)이 생성되어 전진한다.

잔금은 유리상 폴리머에 나타나는 일반적인 현상이지만 반 결정 열가소성수지(Semi-crystalline thermoplastics)에서도 공동(Void) 생성과 이후 나타나는 잔금이 형성될 수 있다.²⁴⁾

본 연구에서는 온도/습도 하중이 반복되는 연료전지 PEM의 파손 현상을 이해하기 위하여 잔금의 형성 가능성 유무를 판단하고 반복되는 응력에 의한 피로 파손의 가능성을 시뮬레이션으로 알아보고자 한다. Huang 등²⁵⁾은 온도/습도 반복하중을 적용한 PEM의 SEM 사진 관찰을 통하여 크랙의 시작과 진전은 양극과 PEM의 경계면 근처의 잔금 발생 구역에서 나타나는 것을 관찰하였다. 습도가 높은 경우가 그렇지 않은 경우보다 더 많은 잔금 구역이 발생하는 것이 관찰되었으며 이는 원활한 작동을 하기 위하여 수분이 있어야 하는 PEM의 경우 작동 중 잔금이 발생할 수 있으며 성장과 전파에 의한 파손이 발생할 수 있음을 나타낸다.

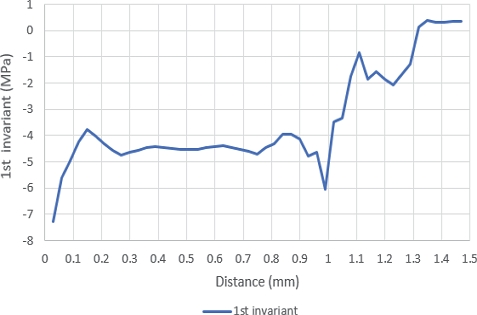
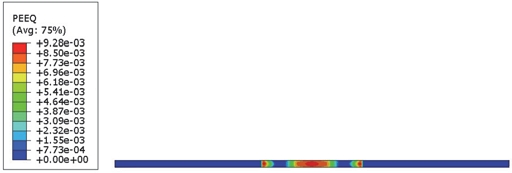
잔금 형성(Crazing formation)의 기준 조건인 인장 정수압 응력의 존재를 시뮬레이션 결과를 통하여 나타내었다. PEM 채널 중심부에서 인장의 1차 불변량이 나타난다(가로축 1.3 ~ 1.5 mm in Fig. 16). 이 부분은 등가 소성변형률(Equivalent plastic strain) 값이 가장 큰 영역이며 인장 잔류 응력이 존재하는 부분이다(Fig. 11, Fig. 17). 그러므로 인장 정수압이 나타나는 채널 중심부에서 잔금 생성이 발생할 수 있으며 높은 압축 응력이 작용하는 랜드 부는 잔금 생성의 가능성이 낮은 부분이다. 실제 실험에서도 PEM의 손상 부위는 랜드부가 아닌 채널부에서 발생함이 관찰되었다.¹¹⁾

Fig. 16

Membrane 1st Invariant history along a path at the membrane for step 3 (bolt load 1,400 (N))

Fig. 17

Contour plot equivalent plastic strain for step 3 (bolt load 1,400 (N))

잔금이 형성된 PEM은 반복적인 온/습도 환경에 의하여 생성된 변동 응력이 충분한 크기의 진폭을 가지고 반복될 때 피로가 발생할 수 있다.

Figs. 18, 19는 각각의 하중 단계에 대하여 면내 응력들인 σ_xx, σ_yy의 변동을 나타낸다. 볼트 체결 후 최대 온/습도 하중이 가해지는 Step 2와 초기 온/습도 조건이 재 부여되는 단계인 Step 3 간의 응력 진폭의 크기가 최대가 된다. 잔금이 발생할 수 있는 채널 중심부와 반복되는 면내 방향 하중 사이클의 조합은 PEM의 기계적 열화에 의한 피로 파손이 발생할 가능성을 높일 수 있다. 반면에 면외 방향의 경우에는 Step 2와 Step 3 하중 단계 간의 응력 진폭의 크기가 최소여서 피로 파손에 대한 면외 방향의 응력 진폭 성분의 영향은 없을 것으로 판단된다(Fig. 20).

Fig. 18

History of membrane stress σxx for each step along a path at the membrane (bolt load 1,400 (N))

Fig. 19

History of membrane stress σyy for each step along a path at the membrane (bolt load 1,400 (N))

Fig. 20

History of membrane stress σzz for each step along a path at the membrane (bolt load 1,400 (N))

4. 결 론

PEM의 온/습도 반복 사이클에 의한 기계적 열화 가능성을 시뮬레이션을 이용하여 연구하였다. PEM의 온/습도 팽창, 수축에 의한 변형 형상 및 응력 변동을 시뮬레이션으로 구현하였으며, 잔금의 생성과 피로 파손 조건을 시뮬레이션으로 확인하였다. 부 모델링 기법을 사용하여 상세한 해석을 진행하였으며 본 연구에서는 다음과 같은 결과를 도출할 수 있었다.

• 1) PEMFC의 3D 광역모델, 부 모델을 연계하여 PEM의 변형 형상, 응력 변동 상세 시뮬레이션을 수행할 수 있었다.
• 2) PEM의 채널 중앙부에서 잔금의 발생 가능성과 피로 파손의 가능성을 확인하였다.
• 3) 채널 중앙부에는 소성 변형에 의한 인장 잔류 응력이 존재하며 동시에 인장 성분의 정수압 응력이 존재한다. 이로부터 사용한 시뮬레이션 조건에서 잔금의 발생 가능성을 확인할 수 있다.
• 4) 피로 파손의 시작 및 진전은 응력 진폭 크기에 의존하며 PEM의 응력 성분 중 면내 응력 성분 들은 상당한 크기의 응력 진폭을 나타내나 면외 방향의 응력 성분의 응력 진폭의 크기는 매우 작아서 PEM의 피로 파손에 영향을 미치는 응력 성분은 면내 방향이라는 것을 확인하였다.

Acknowledgments

이 논문은 안동대학교 기본연구지원사업에 의하여 연구되었음.

References

• Y. Xing, H. Li and G. Avgouropoulos, “Research Progress of Proton Exchange Membrane Failure and Mtigation Strategies,” Materials, Vol.14, No.10, Paper No.2591, 2021. [https://doi.org/10.3390/ma14102591]
• J. Yang and J. Park, “Study for the Deformation and Fatigue Life of a PEMFC,” Journal of The Korean Society for Aeronautical & Space Sciences, Vol.39, No.5, pp.400-407, 2011. [https://doi.org/10.5139/JKSAS.2011.39.5.400]
• D. Seo, I. Jeon, E. Jeong and J. Jho, “Mechanical Properties and Chemical Durability of Nafion/Sulfonated Graphene Oxide/Cerium Oxide Composite Membranes for Fuel-Cell Applications,” Polymers, Vol.12, No.6, Paper No.1375, 2020. [https://doi.org/10.3390/polym12061375]
• M. Crum and W. Liu, “Effective Testing Matrix for Studying Membrane Durability in PEM Fuel Cells: Part 2. Mechanical Durability and Combined Mechanical and Chemical Durability,” ECS Transactions. Vol.3, No.1, Paper No.541, 2006. [https://doi.org/10.1149/1.2356175]
• A. Kusoglu, M. H. Santare, A. M. Karlsson, S. Cleghorn and W. B. Johnson, “Numerical Investigation of Mechanical Durability in Polymer Electrolyte Membrane Fuel Cells,” Journal of Electrochemical Society, Vol.157, No.5, pp.B705-B713, 2010. [https://doi.org/10.1149/1.3328496]
• A. Kusoglu, A. M. Karlsson, M. H. Santare, S. Cleghorn and W. B. Johnson, “Mechanical Response of Fuel Cell Membranes Subjected to a Hygro-Thermal Cycle,” Journal of Power Sources, Vol.161, No.2, pp.987-996, 2006. [https://doi.org/10.1016/j.jpowsour.2006.05.020]
• S. Stucki, G. G. Scherer, S. Schlagowski and E. Fischer, “PEM Water Electrolysers: Evidence for Membrane Failure in 100 Kw Demonstration Plants,” Journal of Applied Electrochemistry, Vol.28, No.10, pp.1041-1049, 1998. [https://doi.org/10.1023/A:1003477305336]
• A. Kusoglu, M. H. Santare and A. M. Karlsson, “Aspects of Fatigue Failure Mechanisms in Polymer Fuel Cell Membranes,” Journal of Polymer Physics Part B, Vol.49, pp.1506-1517, 2011. [https://doi.org/10.1002/polb.22336]
• V. Stanic and M. Hoberecht, “Mechanism of Pinhole Formation in Membrane Electrode Assemblies for PEM Fuel Cells,” Proceedings - Electrochemical Society, IOP Publishing, 2004.
• Y. -H. Lai, K. M. Cortney, S. G. Craig and A. D. David, “Viscoelastic Stress Analysis of Constrained Proton Exchange Membranes Under Humidity Cycling,” Journal of Fuel Cell Science and Technology, Vol.6, No.2, Paper No.021002, 2009. [https://doi.org/10.1115/1.2971045]
• S. Kim and M. M. Mench, “Physical Degradation of Membrane Electrode Assemblies Undergoing Freeze/Thaw Cycling: Micro-Structure Effects,” Journal of Power Sources, Vol.174, No.1, pp.206-220, 2007. [https://doi.org/10.1016/j.jpowsour.2007.08.111]
• ABAQUS User’s Manual, Ver. 6.4, HKS, Providence, RI, 2003.
• D. Kim and C. Yang, “A Study of Modelling Method Comparison on the Deformation of GDL,” Transactions of KSAE, Vol.30, No.12, pp.965-974, 2022. [https://doi.org/10.7467/KSAE.2022.30.12.965]
• B. Liu, L. F. Liu, M. Y. Wei and C. W. Wu “Vibration Mode Analysis of The Proton Exchange Membrane Fuel Cell Stack,” Journal of Power Sources, Vol.331, No.1, pp.229-307, 2016. [https://doi.org/10.1016/j.jpowsour.2016.09.056]
• T. Lee and C. Yang, “A Study on the GDL Deformation and Fatigue Analysis Under Temperature and Humidity Variations,” Transactions of KSAE, Vol.27, No.8, pp.603-609, 2019. [https://doi.org/10.7467/KSAE.2019.27.8.603]
• A. Kusoglu, A. M.Karlsson, M. H. Santare, S. Cleghorn and W. B. Johnson, “Mechanical Behavor of Fuel Cell Membranes under Humidity Cycles and Effect of Swelling Anisotropy on the Fatigue Stress,” Journal of Power Sources, Vol.170, pp.345-358, 2007. [https://doi.org/10.1016/j.jpowsour.2007.03.063]
• Y. Zhou, G. Lin, A. J. Shih and S. J. Hu, “Assembly Pressure and Membrane Swelling in PEM Fuel Cells”, Journal of Power Sources, Vol.192, No.1, pp.544-551, 2009. [https://doi.org/10.1016/j.jpowsour.2009.01.085]
• Y. Tang, A. M. Karlsson, M. H. Santare, M. Gilbert, S. Cleghorn and W. B. Johnson, “An Experimental Investigation of Humidity and Temperature Effects on the Mechanical Properties of Perfluorosulfonic Acid Membrane,” Materials Science and Engineering A, Vol.425, pp.297-304, 2006. [https://doi.org/10.1016/j.msea.2006.03.055]
• J. Kleemann, F. Finsterwalder and W. Tillmetz, “Characterization of Mechanical Behaviour and Coupled Electrical Properties of Polymer Electrolyte Membrane Fuel Cell Gas Diffusion Layers,” Journal of Power Sources, Vol.190, pp.92-102, 2009. [https://doi.org/10.1016/j.jpowsour.2008.09.026]
• P. A. Garcia-Salaberri, M. Vera and R. Zaera, “Nonlinear Orthotropic Model of the Inhomogeneous Assembly Compression of PEM Fuel Cell Gas Diffusion Layer,” International Journal of Hydrogen Energy, Vol.36, No.18, pp.11856-11870, 2011. [https://doi.org/10.1016/j.ijhydene.2011.05.152]
• R. P. Kambour, “Structure and Properties of Crazes in Polycarbonateaned Other Glassy Polymers,” Polymer, Vol.5, pp.143-155, 1964. [https://doi.org/10.1016/0032-3861(64)90128-4]
• L. Ongchin and S. S. Sternstein, “Yield Criteria for Plastic Deformation on Glassy High Polymers in General Stress Fields,” American Chemical Society Fall Meeting, New York, NY, 1969.
• A. S. Argon, J. G. Hannoosh and M. M. Salama, Fracture, Vol.1 Waterloo, Canada, pp.445-470, 1977. [https://doi.org/10.1016/B978-0-08-022136-6.50037-8]
• R. P. Kambour, “A Review of Crazing and Fracture in Thermoplastic,” Journal of Polymer Science: Macromolecular Reviews, Vol.7, pp.1-154, 1973. [https://doi.org/10.1002/pol.1973.230070101]
• X. Huang, R. Solasi, Y. Zou, M. Feshler, K. Refisnider, D. Condit, S. Burlatsky and T. Madden, “Mechanical Endurance of Polymer Electrolyte Membrane and PEM Fuel Cell Durability,” Journal of Polymer Science Part B: Polymer Physics, Vol.44, pp.2346-2357, 2006. [https://doi.org/10.1002/polb.20863]