Q축 스텝 전류지령의 속도응답을 이용한 영구자석 감자율 측정 방법

1. 서 론

최근 여러가지 이점으로 인해 산업계에 전동기 사용이 늘고 있다. 자동차 산업에서도 전기차가 등장함에 따라 전동기 사용이 점차 증가하고 있는데,¹⁾ 그 중에서도 단위 체적당 높은 에너지 효율을 보이는 영구자석 동기전동기(PMSM: Permanent Magnet Synchronous Motor)의 활용이 늘고 있다. 최근에 구동계 모터뿐만 아니라 조향, 제동 제어기에서도 PMSM의 사용이 늘고 있는 추세이다.²⁾

한편 PMSM을 사용하면서 영구자석 감자에 대한 고장진단이 요구되고 있고, 고장 경감 제어를 위해서는 감자율을 정확히 측정하는 것이 필요하다. 현재까지 감자를 진단하는 다양한 방법이 연구되었다.^3-10) 하지만 별도의 장비 설치 없이 간단한 로직으로 감자율을 측정할 수 있는 방법은 제안된 바 없다.

따라서 본 논문에서는 차량용 제어기에 적용 가능하도록 별도의 장비설치 없이 비교적 간단한 로직으로 감자율을 측정하는 새로운 진단 방법을 제안한다. 모터 구동용 인버터를 이용해 Q축 Step 전류지령을 인가하고 특정 시점의 속도를 비교함으로써 감자율을¹¹⁾ 측정하는 방법을 이론적 배경과 실험을 통해 설명한다.

2. 제안하는 고장진단 방법

2.1 영구자석 감자 메커니즘

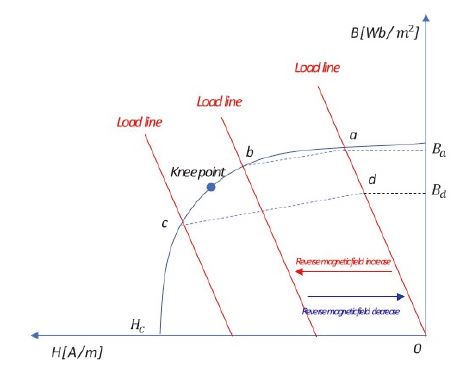
Fig. 1은 영구자석의 감자곡선을 보여준다. 보통 감자곡선은 B-H 특성곡선에서 2사분면을 사용하는데, B는 자속밀도(Magnetic flux density)이고 H는 자계세기(Magnetic field intensity)이다. 부하선(Load line)과 감자곡선이 만나는 점을 동작점이라고 한다. 외부 자계가 없을 때 동작점은 a이고 잔류 자속밀도는 B_a이다. 역방향 자계가 가해질 경우 부하선이 좌측으로 평행이동하여 동작점이 변하게 된다.

Fig. 1

Demagnetization curve

만일 동작점이 Knee point 좌측인 c로 이동하면 감자가 발생하게 되고, 이 상황에서 역방향 자계가 사라져도 본래의 자속을 회복하지 못한다. 이것을 불가역 감자로 부르고 이 때의 잔류 자속밀도는 B_d가 된다.

2.2 부하 토크

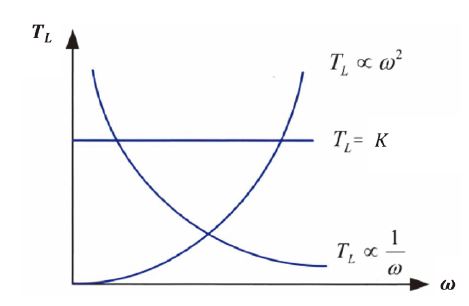
부하 토크란 구동 토크와 반대방향으로 작용하는 토크로 속도 조건에 따라 통상 3가지 종류로 분류한다. Fig. 2는 이러한 부하 토크의 종류를 보여준다.

Fig. 2

Types of load torque

2.2.1 일정 토크 부하 (T_L = constant)

회전속도와 관계없이 일정한 크기의 토크가 발생하는 부하를 의미한다 크레인 또는 엘리베이터 등 권상기 부하가 여기에 해당된다.

2.2.2 일정 출력 부하 (T_L ∝ 1/ω)

회전 속도에 반비례하는 부하로 제지기, 압연기등의 부하가 여기에 해당된다.

2.2.3 속도의 제곱에 비례한 부하 (T_L ∝ ω²)

회전 속도의 제곱에 비례한 부하로, 팬, 펌프, 블로워와 같이 유체를 이동하는데 발생하는 부하가 여기에 해당된다.

부하토크 외에도 회전속도에 따라 증가하는 회전 마찰력 B를 고려하면 최종 토크 방정식은 식 (1)과 같다.

$\[ T_M=\int \frac{d\omega }{dt}+B\omega +T_L \]$

(1)

식 (1)에서 T_M은 모터의 구동 토크, J는 관성모멘트, B는 마찰력, T_L는 부하 토크를 의미한다.

2.3 PMSM 모델링

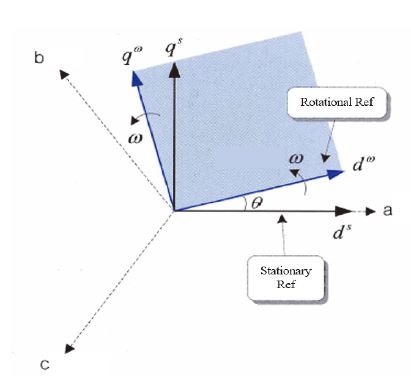
Fig. 3은 d축, q축 변환을 위한 정지 좌표계와 회전 좌표계를 보여준다. 통상적으로 모터 제어를 위해서는 좌표변환을 통해 d, q 축 회전 좌표계를 사용한다. 좌표 변환을 위한 θ는 식 (2)를 통해 얻을 수 있다.

$\[ \theta ={\int }_0^t \omega \left(\tau \right)d\tau \]$

(2)

Fig. 3

Stationary and rotational coordinate system

PMSM의 경우 벡터제어를 위해서 d축을 영구자석의 자속축으로 설정하고, q축을 전류축으로 설정한다.

이렇게 좌표변환을 통한 최종 토크 식은 식 (3)과 같다.

$\[ T_e=\frac{P}{2}\frac{3}{2}\left[{\varphi }_{PM}{i}_{qs}^r+\left(L_{ds}-L_{qs}\right)i_{ds}^r{i}_{qs}^r\right] \]$

(3)

$$ T_{e,},{\varphi }_{PM},i_{qS}^r,P$$는 각각 토크, 영구자석의 자속, 회전자 좌표계의 q축 고정자 전류 그리고 극수를 의미한다. $$ {\varphi }_{PM}{i}_{qs}^r$$의 항은 영구자석에 의한 동기토크(Synchronous Torque)를 의미하고, $$ \left(L_{ds}-L_{qs}\right)i_{ds}^r{i}_{qs}^r$$의 항은 d 축과 q 축의 인덕턴스 차이로 인해 발생하는 릴럭턴스 토크(Reluctance Torque)를 의미한다.

IPMSM, SPMSM 모두 모델링 식은 동일하지만 SPMSM의 경우 L_ds = L_qs 이므로 릴럭턴스 토크 성분이 사라져서 영구자석에 의한 동기토크(Synchronous torque) 토크만 존재한다.

2.4 q축 Step 전류 지령을 이용한 감자율 측정 방법

2.4.1 일정토크 부하, 일정출력 부하

식 (1)을 라플라스($$ \mathcal{L}$$) 변환하여 좌변을 회전자의 속도 (ω)로 전개하면 식 (4)와 같다.

$\[ \omega =\frac{T_M-T_L}{Js+B} \]$

(4)

T_M은 식 (3)에서 전류 제어기를 통해 $$ i_{ds}^r=0,i_{qs}^r=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}ant$$ 지령으로 제어하면 Step 토크를 얻을 수 있다. 일반적으로 전류제어기의 속도가 전동기 시스템보다 훨씬 빠르기 때문에 Step 토크로 가정할 수 있다. 만일 T_M ≫ T_L 이 되도록 충분히 높은 q축 전류를 인가하고 양변에 역 라플라스 변환($$ {\mathcal{L}}^{-1}$$)을 취하면 부하토크가 무시되고 식 (5)가 도출된다.

$\[ \omega \cong \frac{T_M}{B}\mathrm{*}\left(1-e^{-\frac{B}{J}\mathrm{*}t}\right) \]$

(5)

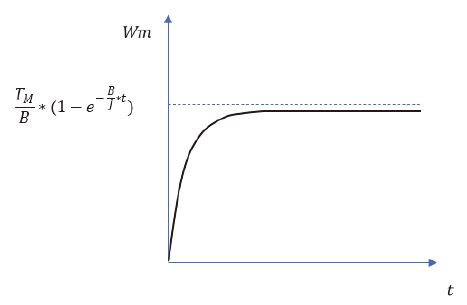
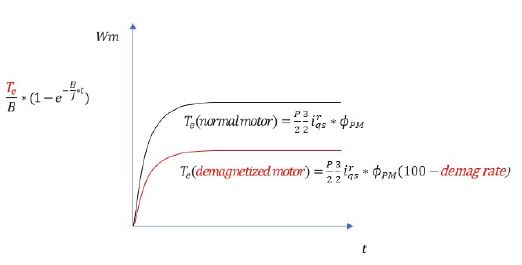
회전자의 속도는 Fig. 4와 같이 최종적으로는 T_M/B 에 수렴하는 1차 Low pass filter 형태의 그래프로 보여진다.

Fig. 4

Rotor speed increase under step torque excitation

만일 감자된 모터에 동일한 q축 전류($$ i_{qs}^r$$)를 인가하게 되면, 감자된 모터는 식 (6)과 같이 ϕ_PM이 감자된 비율만큼 더 낮은 토크를 생성한다.

$\[ \frac{T_{demag }}{T_{normal }}=\frac{\frac{P3}{22}{i}_{qs}^r{\varphi }_{PM- demag} }{\frac{P3}{22}{i}_{qs}^r{\varphi }_{PM- normal }}=\frac{{\varphi }_{PM- demag }}{{\varphi }_{PM- normal }} \]$

(6)

이렇게 감소된 토크는 최종적으로 회전자의 속도를 감소시키고 정상 모터와 감자 된 모터의 속도를 비교함으로써 식 (7)과 같이 감자율을 계산할 수 있다.

$\[ Demag rate =\frac{{\omega }_{demag }}{{\omega }_{normal }}\begin{array}{l}=\frac{\frac{T_{demag }}{B} \mathrm{*}\left(1-e^{-\frac{B}{J}\cdot t_1}\right)}{\frac{T_{normal }}{B} \mathrm{*}\left(1-e^{-\frac{B}{J}\cdot t_1}\right)}\\ =\frac{T_{demag }}{T_{normal }}=\frac{{\varphi }_{PM- demag }}{{\varphi }_{PM- normal }}\end{array} \]$

(7)

Fig. 5는 동일 q축 스텝 전류를 인가했을 때 정상모터와 감자 된 모터의 속도를 보여준다. 어느 시점의 속도를 비교해도 감자 된 비율만큼의 차이가 나타난다.

Fig. 5

Speed comparison of normal motor and demagnetized motor

2.4.2 속도의 제곱에 비례한 부하

유체 부하와 같이 속도의 제곱에 비례한 부하의 경우 속도가 증가할 수록 부하 토크가 증가하기 때문에 T_M ≫ T_L가 성립되지 않아 부하 토크를 무시할 수 없다. T_L = kω² (K = constant)로 가정하면 토크식은 식 (8)과 같다.

$\[ T_e=J\frac{d\omega }{dt}+B\omega +K{\omega }^2 \]$

(8)

속도가 증가하다가, 부하 토크와 구동 토크가 같아지는 시점의 속도(ω=ω₁)는 식 (9)와 같다.

$\[ {\omega }_1=\frac{-B+\sqrt{B^2+4K{T}_e}}{2K} \]$

(9)

q 축 전류를 충분히 높게 설정하여 4KT_e 》B²이고 회전 마찰력이 무시할 정도로 작다고 가정하면 (B≅0)ω₁은 식 (10)이 된다.

$\[ {\omega }_1=\sqrt{\frac{T_e}{K}} \]$

(10)

따라서 감자율은 식 (11)과 같이 최종속도의 제곱의 비로 구할 수 있다.

$\[ \begin{array}{r} Demag rate ={\left(\frac{{\omega }_{demag }}{{\omega }_{normal }}\right)}^2=\frac{T_{demag }}{T_{normal }}\\ =\frac{{\varphi }_{PM- demag }}{{\varphi }_{PM- normal }}\end{array} \]$

(11)

2.5 고장 진단 제약 사항

2.5.1 전압 제한에 의한 최종 속도 제한

이상적으로는 무 부하 조건에서 최종속도가 T_e/B에 수렴해야 한다. 하지만 공급전압의 한계때문에 최종속도에 도달하지 못하고 특정 포화된 속도에 머무르게 된다.

$\[ {v_{qs}^r}^2+{v_{ds}^r}^2={V_{smax}}^2 \]$

(12)

$\[ v_{ds}^r=R{i}_{ds}^r+p{\lambda }_{ds}^r-{\omega }_r\left(L_{qs}^r{i}_{qs}^r\right) \]$

(13)

$\[ v_{qs}^r=R{i}_{qs}^r+p{\lambda }_{qs}^r+{\omega }_r\left(L_{ds}^r{i}_{ds}^r\right)+{\omega }_r{\varphi }_{PM} \]$

(14)

식 (12)에서 V_smax는 공급전압의 한계치이다. 식 (12) ~ (14)에서 $$ i_{ds}^r=0$$이고, $$ i_{qs}^r=constant$$이므로 $$ {\lambda }_{qs}^r\mathrm{와} {\lambda }_{ds}^r$$ 시간에 따라 변하지 않는다. 또한 고속에서는 역기전력에 의한 성분이 매우 크므로 저항에 의한 전압강하 성분을 무시하면 식 (15) ~ (16)이 도출된다.

$\[ {{\omega }_r}^2{\left(L_{qs}^r{i}_{qs}^r\right)}^2+{{\omega }_r}^2{\left({\varphi }_f\right)}^2={V_{smax}}^2 \]$

(15)

$\[ {i_{qs}^r}^2+{\left(\frac{{\varphi }_f}{L_{qs}^r}\right)}^2={\left(\frac{V_{smax}}{L_{qs}^r{\omega }_r}\right)}^2 \]$

(16)

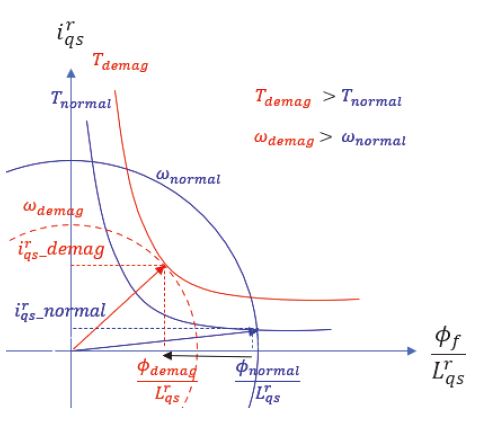
Fig. 6은 X 축을 $$ {\varphi }_f/L_{qs}^r$$로 설정하고 Y 축을 $$ i_{qs}^r$$로 설정한 전압 제한원의 그래프이다. 감자된 모터의 $$ {\varphi }_{demag }/L_{qs}^r$$ 값은 정상모터의 $$ {\varphi }_{normal }/L_{qs}^r$$ 값보다 낮은 값을 갖게 되고, 전압제한원이 더 안쪽으로 이동 할수 있게 되면서, 더 큰 $$ i_{q{s}_{-}demag}^r$$ 값을 인가 할 수 있게 된다. 만일 ϕ_normal/ϕ_demag의 비율보다 $$ i_{q{s}_{-}demag/ }^r{i}_{q{s}_{-}normal}^r$$의 비율이 클 경우 감자된 모터에 정상모터 대비 더 큰 토크가 인가되고, 최종 포화속도 또한 증가하게 된다. 이는 역기전력을 낮추어 더 높은 속도를 얻기 위해 d축에 음의 전류를 인가하는 약자속 제어와 같은 원리이다.

Fig. 6

Change in the speed limit of the demagnetizing motor by voltage limitation

정리하면, 스텝 전류지령을 인가해도 전압제한원의 영향으로 $$ i_{qs}^r$$가 목표치에 도달하지 못하고 회전자의 속도는 포화속도에서 더 증가하지 못한다. 하지만 감자 된 회전자가 더 큰 포화속도 값을 가질 수 있으므로 속도 비교 시점을 포화속도에 도달하기 전 시점으로 설정해야 한다.

2.5.2 모터 동작범위 한계

시스템 특성상 모터의 동작 범위의 한계가 존재할 수 있다. 따라서 이러한 시스템에서는 동작범위의 한계 도달전에 속도를 측정해야 한다.

3. 시뮬레이션 결과

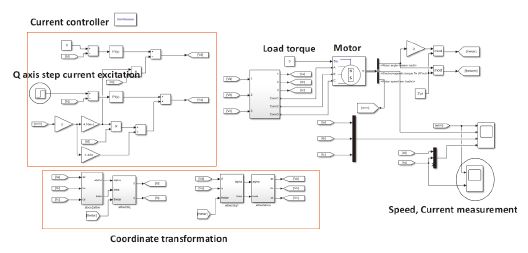
제안한 고장진단 방법의 정합성을 테스트하기 위해 Matlab 社의 Simulink에서 제공하는 모터 모델을 이용하여 테스트를 진행하였다. 모터의 사양은 Table 1과 같다. 전류 제어기 대역폭은 (ω_cc)은 7.5 khz로 설정하였고 비례이득과, 적분이득은 각각 ω_cc⋅L_S, ω_cc⋅R_S로 설정하였다.

Table 1

Simulink motor specification

Simulink 모델은 Fig. 7과 같이 설정하였다. 좌측상단의 전류제어기에서 q축 Target 지령을 Step 지령으로 인가하였고, 모터 모델을 통해 최종 도출된 회전자 속도를 측정하였다.

Fig. 7

Implementation of motor model using simulink

실험은 적은 감자와 큰 감자상황에서 정합성을 확인하기 위해 영구자석의 자속 λ_PM을 각각 30 %, 70 % 감소시켜서 실험하였다. q축 타겟 전류는 2.4.1, 2.5.1에서 설명한 것처럼 측정 시점인 100 ms 시점에서 속도가 포화되지 않는 최대한 높은 전류값인 5 A로 선정하였다.

3.1 무 부하 조건 실험결과 (T_L=0)

무부하 조건에서 실험한 결과는 Table 2와 같다. 예상한 바와 같이 매우 적은 오차율로 감자율을 측정할 수 있었다.

Table 2

Test result under no load torque condition

3.2 일정 토크 부하 조건 실험결과 (T_L=const)

일정 토크 부하 조건에서 실험한 결과 Table 3과 같은 결과를 얻을 수 있었다.

Table 3

Test result under constant load torque condition

일정 토크 부하에서 T_L는 구동 토크의 1/10 수준인 0.63 N.m로 설정하였다. 감자율이 클수록 오차가 더 크게 발생하는데, 그 이유는 감자율이 커질수록 구동 토크가 줄어들게 되고, 이로 인해 부하 토크의 영향성이 증가하게 되기 때문이다.

3.3 속도의 제곱에 비례한 부하 조건 실험결과 (T_L ∝ ω²)

속도의 제곱에 비례한 부하 실험 결과는 Table 4와 같다.

Table 4

Test result under load torque proportional to the square of the speed

부하토크를 T_L = kω²로 생성했고 k값은 2×10^-5로 임의로 설정했다. 또한 T_e ≫ B²를 만족시키기 위해 B값을 0.0001 [N⋅m⋅s]로 조정하였다. 속도의 제곱에 비례한 부하는 식 (11)을 사용하였다.

결과에서 볼 수 있듯이 감자율이 커질수록 구동 토크가 낮아지면서 T_e ≫ B²의 관계가 약해지고, 감자율 계산식에서 B의 영향이 커지면서 오차가 증가하게 된다.

4. IDB 모터 실험 결과

제안된 방법을 만도 社의 전자 브레이크용 모터인 IDB(Integrated Dynamic Brake) 제품에 적용하여 실험을 수행했다.

Fig. 8

SPMSM motor stator (left) rotor (right)

4.1 모터 사양

모터의 사양은 Table 5와 같다.

Table 5

SPMSM IDB motor specification

4.2 실험 구성

영구자석을 감자 시키기 위해 Fig. 9의 온도 챔버와 미니 오븐을 사용하였다.

Fig. 9

Temperature chamber(left) small oven(right)

총 4개의 샘플로 테스트를 수행했으며, 160 ^oC, 200 ^oC, 230 ^oC에서 각각 한 시간씩 고온 감자 시켜 테스트를 수행하였다. 감자시킨 샘플은 Fig. 10의 역기전력 측정 장비로 실제 감자율을 측정하였다. 각 온도 별로 감자 된 비율은 Table 6과 같다.

Fig. 10

Back EMF measuring equipment

Table 6

Bemf data of 4 samples

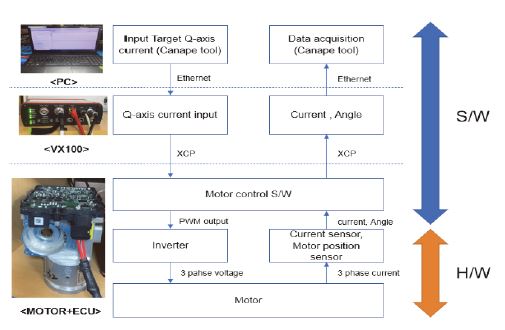
이렇게 감자시킨 샘플을 모터와 ECU(Electronic Control Unit)에 결합시켜 Vector 社의 Canape tool을 이용하여 Target q축 지령을 입력하고 관련 신호를 Fig. 11과 같이 계측하였다.

Fig. 11

Block diagram of signal input and output

ECU는 마이크로 프로세서, 인버터, 전류 센서, 엔코더 등으로 구성되어 모터 제어를 수행할 수 있도록 환경을 제공한다.

4.3 실험 결과

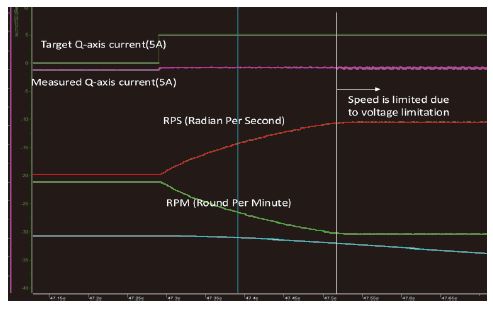
Fig. 12는 무 부하 조건에서 q축 스텝 전류지령 5 A를 인가한 Trace 이다. 특정 시점에서 전압 제한에 의해 속도가 포화되는 것을 확인할 수 있다.

Fig. 12

Trace on canape

실제 실험은 4 A, 5 A를 인가하고 속도 비교 시점은 포화속도에 도달하기 전인 120 ms 시점으로 설정하였다. 각각 5회씩 실험을 수행하고 평균 속도를 측정하였다.

Table 7은 측정 결과를 보여준다. 4 A와 5 A의 Estimated Demag rate의 평균을 취해 최종 예측 감자율(Estimated Demag rate)을 계산하였다. 이를 실제 감자율인 역기전력 측정결과(Actual Demag rate)와 비교한 결과는 Table 8과 같다.

Table 7

Speed response at 120 ms under 4 A, 5 A step current excitation and estimated demagnetization rate

Table 8

Comparison of estimated and actual demagnetization rates

실험 결과 50 %가 넘는 감자가 발생할 경우에도 10 % 이내의 오차로 감자율을 추정하는 것을 확인할 수 있었다. 별도의 장비를 설치하지 않았기 때문에 감자율을 추정할 수 있는 다른 활선진단 방법과 정확도를 직접적으로 비교할 수는 없지만, 모델추정 방식으로 5.2 %의 영구자석 손상 모터를 1 %의 오차로 검출하는 기존 연구결과⁴⁾를 감안했을 때, 큰 감자 상황에서도 비교적 높은 정확도로 감자율을 추정했음을 알 수 있다. 하지만 감자율이 증가할수록 오차가 커지는 경향성을 보여주는데 추정되는 원인은 다음과 같다.

4.3.1 전류제어기 성능 저하

감자가 발생할 경우 영구자석의 자속이 줄어들게 되고 인덕턴스 또한 변하게 된다. 따라서 전향 보상 오차가 발생하고 비례이득, 적분이득이 최적의 성능을 내지 못하게 되면서 정상 모터 대비 전류제어기의 성능이 떨어지게 된다.

4.3.2 부하 토크의 영향

감자가 발생하면 회전자와 고정자의 형상에 따라 발생하는 코깅 토크에 변화가 생기게 되고 이 또한 오차의 원인이 된다. 또한 감자율이 클수록 구동 토크가 낮아지면서 정지 마찰력, 코깅 토크등 부하의 영향성이 커지게 되며 오차를 증가시킨다.

5. 결 론

본 연구에서는 q축 스텝 전류 지령에 의한 속도를 이용하여 새로운 영구자석 감자 진단 방법을 제시하였다. 본 감자 진단 방법은 다른 활선 감자 진단 방식과는 다르게 벡터제어에 필요한 회로 외에 별도의 장비가 필요 없고, 파라미터에 민감하지 않으며, 감자율의 크기를 측정할 수 있다. 본 진단 방법은 오프라인 진단 방법이지만, 타 오프라인 진단 방법과 다르게 전동기 분해가 필요 없고 별도의 장비도 필요하지 않다는 점에서 강점이 있다. 타 활선 진단 방식과 같이 제어 중에 진단을 수행할 수 없지만, 비 제어중에 간단하게 수행할 수 있으며 이는 일정시간 제어기 초기체크를 허용하는 차량용 모터에 충분히 적용될 수 있을 것이다.

여러가지 부하조건 하에서 제안한 감자 진단 방식을 Matlab 시뮬레이션 결과를 통해 정합성을 확인하였고, 무 부하 조건에서 만도 社의 IDB 제품의 SPMSM 모터를 이용한 실험결과를 통해 고장진단 방법을 효과를 검증하였다. 이번 연구를 통해 다음과 같은 결론을 얻었다.

• 1) 진단의 정확도를 높이기 위해서는 부하 토크의 영향성을 최소화하기 위해 구동 토크를 최대한 높여야 하고, 이를 위해 높은 q축 전류를 인가해야 한다.
• 2) 감자율을 측정할 때 속도에 비례한 부하의 경우 속도의 제곱의 비를 사용하고 그 외의 부하조건에서는 속도의 비를 사용한다.
• 3) 전압 제한이 있는 경우, 감자 된 모터가 정상 모터보다 포화속도가 높을 수 있으므로, 포화속도에 도달하기전 속도로 비교해야 한다.
• 4) 감자율이 클수록 오차가 증가하는데 이는 전류제어기의 성능이 떨어지는 요인과, 구동 토크 대비 부하 토크의 영향성이 커지는 요인이 있다.

Acknowledgments

A part of this paper was presented at the KSAE 2022 Spring Conference

References

• S. Hano and M. Hakiai, “New Challenges for Brake and Modulation Systems in Hybrid Electric Vehicles (HEVs) and Electric Vehicles (EVs),” SAE 2011-39-7210, 2011.
• K. Choi, S. Cha, H. Lee and G. Kim, “Development of IDB Simulation Model,” KSAE Fall Conference Proceedings, pp.466-467, 2018.
• S. Rajagopalan, W. le Roux, T. G. Habetler and R. G. Harley, “Dynamic Eccentricity and Demagnetized Rotormagnet Detection in Trapezoidal Flux (brushless DC) Motors Operating Under Different Load Conditions,” IEEE Transactions on Power Electronics, Vol.22, No.5, pp.2061-2069, 2007. [https://doi.org/10.1109/TPEL.2007.904183]
• W. le Roux, R. G. Harley and T. G. Habetler, “Detecting Rotor Faults in Low Power Permanent Magnet Synchronous Machines,” IEEE Transactions on Power Electronics, Vol.22, No.1, pp.322-328, 2007. [https://doi.org/10.1109/TPEL.2006.886620]
• J. C. Urresty, J. R. Riba and L. Romeral, “A Back-emf Based Method to Detect Magnet Failures in PMSMs,” IEEE Transactions on Magnetics, Vol. 49, No.1, pp.591-598, 2012. [https://doi.org/10.1109/TMAG.2012.2207731]
• J. -R. R. Ruiz, J. A. Rosero, A. G. Espinosa and L. Romeral, “Detection of Demagnetization Faults in Permanent-Magnet Synchronous Motors Under Nonstationary Conditions,” IEEE Transactions on Magnetics, Vol.45, No.7, pp.2961-2969, 2009. [https://doi.org/10.1109/TMAG.2009.2015942]
• Y. Da, X. Shi and M. Krishnamurthy, “A New Approach to Fault Diagnostics for Permanent Magnet Synchronous Machines using Electromagnetic Signature Analysis,” IEEE Transactions on Power Electronics, Vol.28, No.8, pp.4104-4112, 2012. [https://doi.org/10.1109/TPEL.2012.2227808]
• J. Hong, D. Hyun, S. B. Lee, J. -Y. Yoo and K. -W. Lee, “Automated Monitoring of Magnet Quality for Permanent-Magnet Synchronous Motors at Standstill,” IEEE Transactions on Industry Applications, Vol.46, No.4, pp.1397-1405, 2010. [https://doi.org/10.1109/TIA.2010.2049811]
• U. Zia and J. Hur, “A Comprehensive Review of Winding Short Circuit Fault and Irreversible Demagnetization Fault Detection in PM Type Machines,” Energies, Vol.11, No.12, Paper No. 3309, 2018. [https://doi.org/10.3390/en11123309]
• B. M. Ebrahimi and J. Faiz, “Demagnetization Fault Diagnosis in Surface Mounted Permanent Magnet Synchronous Motors,” IEEE Transactions on Magnetics, Vol.49, No.3, pp.1185-1192, 2012. [https://doi.org/10.1109/TMAG.2012.2217978]
• K. W. Kim and S. B. Lee, “Diagnosis Method of Demagnetization Rate of Permanent Magnet Using Q-axis Current Command,” KSAE Spring Conference Proceedings, pp.370-371, 2022.