자동차 서스펜션 부시용 고무소재 물성시험 및 평가
Copyright Ⓒ 2019 KSAE / 165-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
As the demand for quality and durability increases for automobiles, it is necessary to develop a technique for improving the characteristics and durability of anti-vibration rubber components in reducing vibration and noise. It is very important to accurately know the mechanical properties of rubber materials. In this study, nonlinear material constants, storage modulus, and loss factor of rubber materials, which are essential for the characterization of rubber components, were obtained through static and dynamic mechanical properties tests. We will contribute to the design and analysis of rubber components by applying it to finite element analysis in order to predict and evaluate the characteristics of rubber components. In addition, the fatigue durability of the rubber materials was evaluated by deriving the fatigue life prediction equations of the rubber material through a method that can predict the fatigue life of rubber components in a fairly accurate manner at the early stage of development. The static, dynamic, and fatigue life properties of rubber materials obtained through this study are expected to contribute to the evaluation of life and reliability of rubber components, which have been difficult to assess.
Keywords:
Rubber material, Mechanical properties, Static test, Dynamic test, Storage modulus, Loss factor, Fatigue test키워드:
고무소재, 기계적 물성, 정적시험, 동적시험, 저장 탄성계수, 손실계수, 피로시험1. 서 론
자동차의 품질 및 내구성 보증에 대한 요구가 높아짐에 따라 진동 및 소음 저감에 중요한 역할을 하는 방진 고무부품의 특성 및 내구성 향상을 위한 기술 개발이 요구되고 있다.1,2) 특히, 방진 고무부품은 차량 수명동안 정숙하고 안락한 승차감을 유지하면서 보증기간을 확보하기 위해서는 높은 내구성이 요구되고 있으나 방진 고무부품의 실차 내구환경 재현 및 내구수명 예측 및 평가기술 능력 부재로 신뢰성 있는 고무부품개발이 어려운 실정이다. 방진 고무부품의 품질 향상을 위해서는 유해물질을 배제하면서 내열성 및 반복 피로 내구성 개선을 위한 최적의 배합설계와 분산성 향상을 통해 균일한 물성을 얻는 것이 무엇보다 중요하다하겠다. 이를 기반으로 형상변형에 따른 유한요소 해석3,4)을 통한 특성과 내구성 평가5,6)가 이루어질 때 최적의 자동차용 고무부품이 만들어지나 아직까지 국내의 기술로는 15년 15만 마일을 보증할 수 있는 고무부품의 평가기술이 미흡한 실정이다. 따라서 본 연구에서는 고무부품의 특성해석에 필수적인 고무소재의 비선형 재료상수와 저장탄성계수 및 손실계수를 정적 및 동적 물성시험을 통해 확보하여 고무부품의 특성을 미리 예측하고 평가하는 전산해석에 활용하여 고무부품의 설계 및 해석기술에 기여하고자 한다. 또한 개발 초기단계에서 비교적 정확하게 고무부품의 피로수명을 예측할 수 있는 방법을 개발하여 고무소재의 피로수명예측 식을 도출하여 자동차 서스펜션 부시에 사용되는 고무소재에 대한 피로 내구성을 평가하였다.
2. 고무소재 물성시험 및 평가
2.1 고무소재 특성
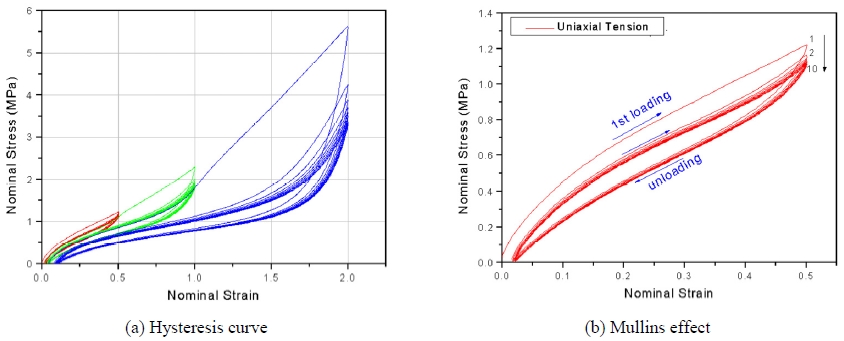
자동차에서 고무부품은 방진, 충격 흡수 및 완충 역할로 많이 사용되고 있어 효과적인 설계를 위해서는 고무소재의 특성을 이해하고 물성을 정확히 파악하여야 한다. 고무소재는 하중과 변형이 비선형 관계이고 대 변형 범위에서도 탄성거동을 나타내는 초 탄성 특성을 지니고 있다. 하중을 가 하였다가 제거하면 하중을 가할 때와 다른 곡선을 나타내는데 이 곡선을 히스테리시스라 하며 이 면적은 고무 내부에 열로 축적된 일의 양으로 발열, 영구 늘음, 피로 등의 원인이 되므로 바람직하지 못한 성질이다. 또한 고무는 하중을 받으면 초기 상태의 분자 구조가 수정 및 재배치로 인해 강성이 낮아지고 댐핑 특성이 변하게 된다. 이러한 응력-변형률 완화현상을 뮬린스(Mullins) 효과라 한다.7) 이러한 특성으로 고무는 부하(Loading)와 제하(Unloading) 시의 응력-변형률 곡선이 다르며 초기 응력-변형률 곡선을 다시 반복하지 않고 동일 변형률 구간에서 대략 5~10회 정도의 반복하중을 받아야 곡선이 안정화된다.
이러한 특성은 수치적으로 고무소재의 거동을 나타내는 변형률에너지함수(Strain energy function, W)의 계수로 표현할 수 있다.8) 고무소재의 거동은 고무 종류에 따라 큰 차이를 나타내기 때문에 시험으로부터 구한 하중-변형 관계를 가장 적절히 표현하는 변형률에너지함수를 구하는 일이 중요한 연구대상이 되고 있다. 고무의 변형을 표현하기 위해서는 재료거동은 탄성이며, 등방성이라는 가정 하에 변형률에너지함수는 연신률 불변량의 함수와 주 연신률의 함수로 식 (1)과 같이 표현할 수 있다.
| (1) |
여기서, λ1, λ2, λ3는 주 연신률이며, 재료가 등방성인 경우 I1, I2, I3는 식 (2)와 같다.
| (2) |
대부분의 고무소재는 비압축성이므로 체적계수(Bulk modulus)는 전단계수(Shear modulus)보다 상당히 크며 재료가 많이 구속되어 있지 않는 경우에는 비압축성의 가정이 타당함이 알려져 있다. 식 (2)에서 재료를 비압축성으로 가정하면 λ1λ2λ3 = 1이므로, I3 = 1이 되며, 의 관계식이 유도되어 식 (1)은 다음과 같이 나타낼 수 있다.
| (3) |
비압축성 고무의 변형 해석에 널리 쓰이는 변형률에너지함수는 식 (4)와 같이 연신률 불변량의 함수로 표시되는 리블린(Rivlin) 형태와 주 연신률의 함수로 표시되는 오그덴(Ogden) 다항식 형태로 나타낼 수 있다.
| (4) |
여기서, cij, μn, αn는 시험결과로부터 결정되는 재료상수로 단순한 변형을 포함하는 단축 인장시험, 등 이축인장시험, 전단시험 등으로 얻어지는 응력과 변형률 관계를 이용하여 정해진다. 또한 고무는 시간에 따라 특성이 변하는 점탄성 성질을 나타내는 등 매우 난해한 거동을 보이기 때문에 고무소재의 정적물성은 변형률에너지함수로 표현되고 동적물성은 저장 탄성계수(Storage modulus)와 손실계수(Loss factor)로 나타내어지는 복소 탄성계수와 포아송 비로 표현되는데 포아송 비는 일반적으로 고무소재가 비 압축성이므로 0.499의 값을 사용한다.9)
고무부품의 기능 및 성능향상을 위해서는 손실계수와 정적 및 동적특성 비로 표현되는 동 배율이 점탄성 재료의 특성을 나타내는 중요한 인자라 할 수 있다. 방진고무의 동특성을 향상시키기 위해서는 동 배율은 낮고 손실계수는 크게 하는 것이 유리하다는 것이 알려져 있다. 손실계수를 높이기 위해서는 충진제 또는 수지, 금속분말 등의 첨가방법이 있으며 동 배율을 낮추기 위해서는 고무분자 끝의 자유 고리의 변성 및 유리섬유 강화 등의 방법 등이 있다.
2.2 고무소재 정적물성
고무부품의 특성을 평가하기 위해서는 유한요소 해석에 필요한 고무소재의 정적, 동적물성을 정확히 파악하는 것이 매우 중요하기 때문에 자동차 서스펜션 부시에 사용되고 있는 일반소재(General material)와 내구성을 향상시킨 장수명 소재(Long material)및 동특성을 개선한 저 동배율 소재(Dynamic material)에 대해 정적 및 동적시험을 수행하여 물성을 평가하였다.
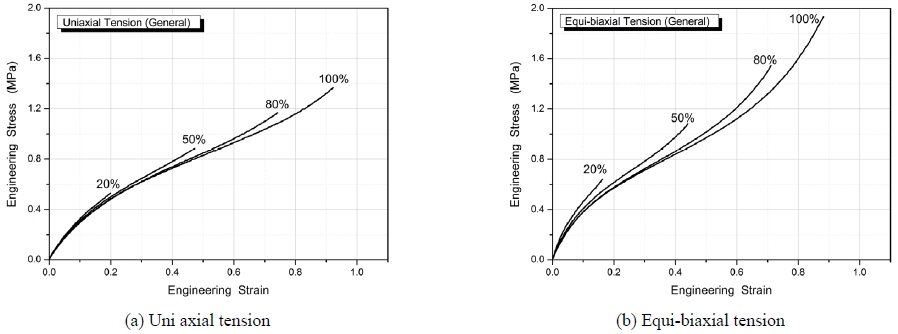
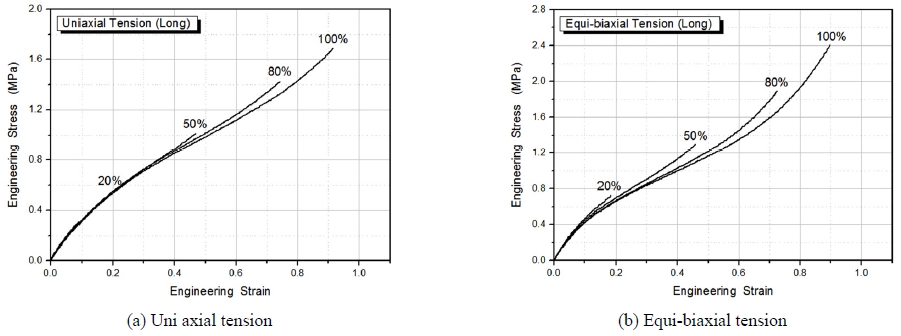
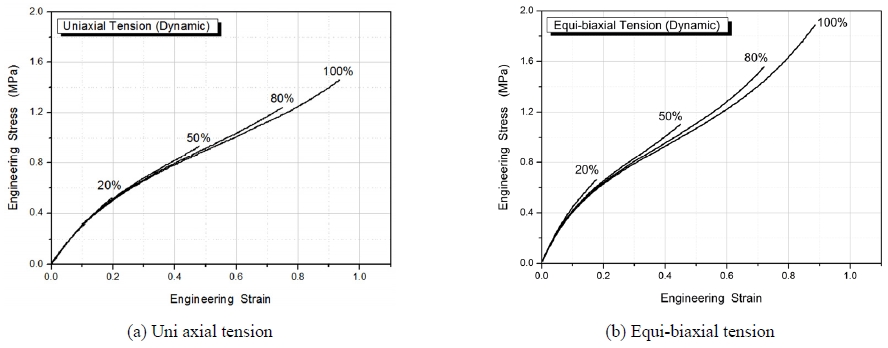
정적 물성시험은 단축인장시편과 원형타입으로 제작된 등 이축인장(Equi-biaxial tension)시편을 방사형으로 신장시켜 이축응력과 이축변형률을 측정할 수 있는 시험 장치를 이용하여 시험 속도 300 mm/min로 변형률 20 %, 50 %, 80 %, 100 % 범위에서 5회 반복 시험을 수행하여 얻어진 응력-변형률 데이터를 각 변형률에서 안정화된 마지막의 응력-변형률 선도를 탄성이론을 통하여 원점으로 이동시킨 결과를 Figs. 3~5에 나타내었다. 그림에서 보는 바와 같이 변형률이 클수록 응력이 완화되는 뮬린스 효과가 나타남을 확인하였으며 응력-변형률 데이터를 변형률에너지함수로 구해진 응력-변형률의 관계식을 이용하여 Table 1~3에서와 같이 변형률 범위에 따른 무니-리블린(Mooney-Rivlin) 2항과 오그덴(Ogden) 3항의 비선형 재료상수를 결정하여 고무부품의 유한요소 해석 물성을 확보하였다.
2.3 고무소재 동적물성
고무의 동특성은 여러 요인에 의해 영향을 받는데 일반적으로 온도, 주파수, 평균 변형률과 변형률 진폭 등의 인자에 따라 변화한다. 이 인자들 중에서 하나의 인자 영향을 검토할 때는 다른 인자를 일정하게 유지하여 실험할 필요가 있다. 이렇게 하여 얻어진 동특성은 변화시킨 독립변수의 이름에 따라 온도특성, 주파수 특성, 진폭의존성 등으로 부르고 있다.
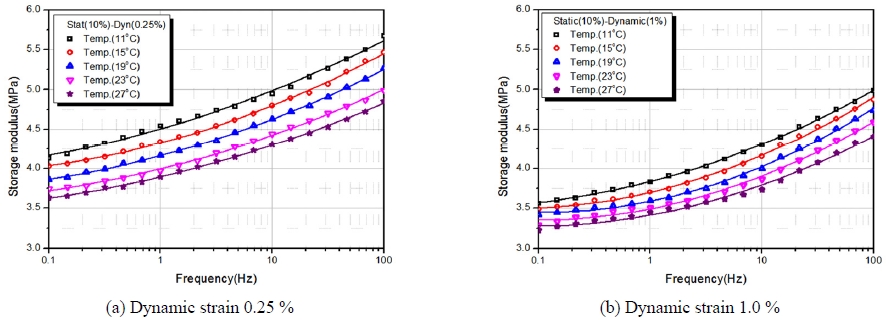
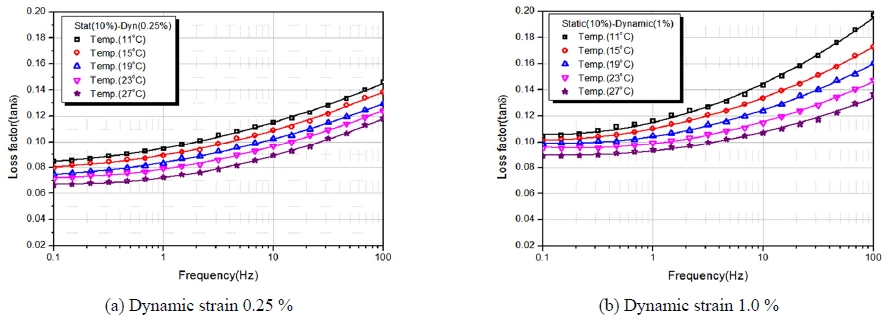
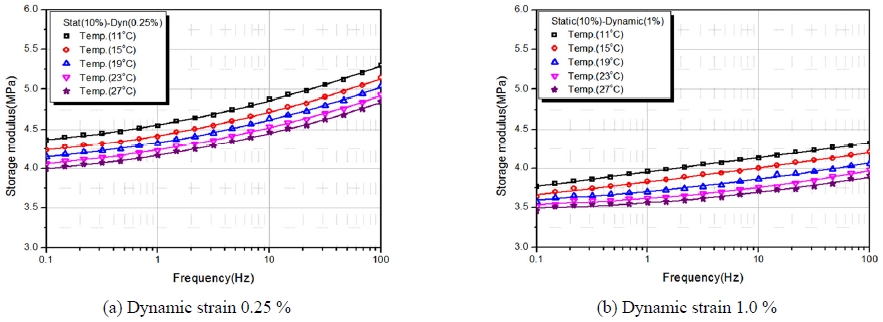
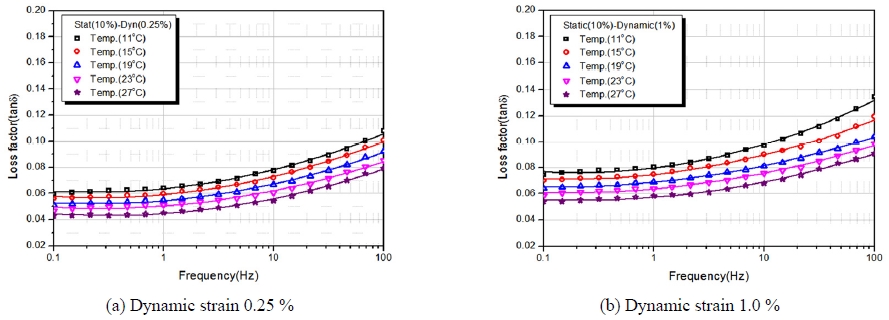
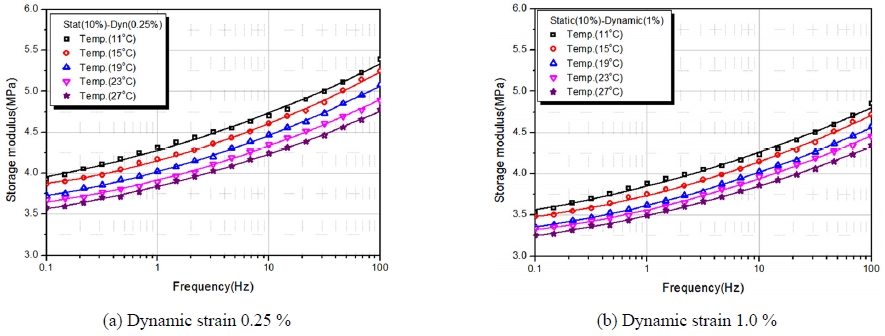
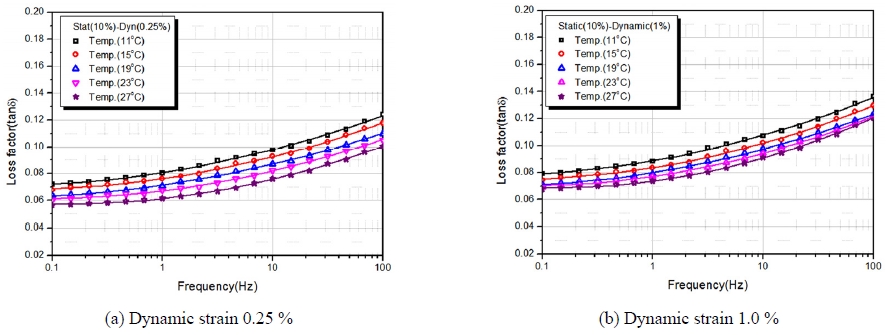
본 연구에서는 Fig. 6에서와 같이 동특성시험기를 이용하여 정적 변형률 10 %에 동적 변형률 0.25 %와 1.0 %에서 주파수 변화(0.1~100 Hz)와 온도변화(11 °C, 15 °C, 23 °C, 27 °C)에 따른 동특성시험을 수행하여 저장 탄성계수와 손실계수의 변화를 파악하였다.
Fig. 7~12에서와 같이 온도가 높아질수록 저장탄성계수와 손실계수는 낮아지고 주파수가 증가할수록 저장계수 및 손실계수는 증가하였으며, 또한 동적 변형률이 클수록 저장탄성계수는 낮아지고 반대로 손실계수는 증가는 경향을 나타내었다. 이는 변형률이 클수록 응력이 완화되는 뮬린스 효과의 영향과 일치함을 알 수 있었다.
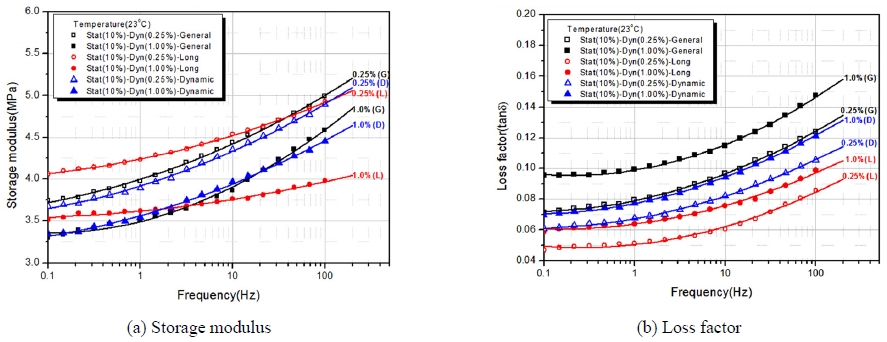
Fig. 13은 일정온도(23 °C)에서 각 소재에 대해 동적물성을 비교한 것으로 저 동배율 소재가 일반 및 장수명 소재보다 저장 탄성계수가 낮게 나타나났으며 손실계수는 일반소재보다는 낮으나 장수명 소재보다는 높아 동특성을 향상시키기 위한 고무소재임을 확인하였다.
2.4 고무소재 피로물성
고무소재에 대한 피로수명 평가기술은 부품의 안전 및 신뢰성을 확보하기 위한 기반 기술로, 국내외 관련 산업계에서는 이의 중요성을 인식하고는 있으나 아직 체계적인 평가방법이 확립되어 있지 못한 실정이다. 이를 위해서는 무엇보다도 피로수명에 영향을 주는 피로손상변수의 규명이 시급하다 하겠다.10-12) 대부분의 방진 고무부품은 반복하중과 노화에 의해 손상을 받기 때문에 고무소재의 피로특성 평가가 반드시 요구된다.
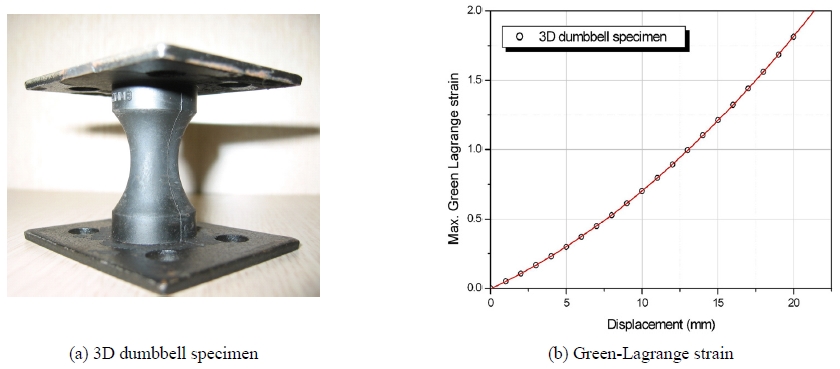
고무소재의 피로수명을 평가하기 위해 단축 인장시험을 위한 덤벨형 시편을 이용할 경우에는 시편과 부품의 피로시험 결과의 상관성 유지가 어렵기 때문에 본 연구에서는 고무부품의 피로하중에 의한 최대 인장변형률을 재현할 수 있는 피로시편을 제작하여 고무소재의 피로수명을 평가하는데 이용하였다.13) 피로시편의 형상은 Fig. 14(a)에서 보는 바와 같이 양단에 금속편을 가황하여 접착시킨 3차원 덤벨형으로 반복하중에 의한 이완이 발생되지 않고 인장과 압축변형이 가능하며 변형에 의한 변형률 분포가 비교적 완만하게 설계되었으며 최대 인장변형률 발생부위가 어떠한 변형에도 일정하게 발생되도록 중심부 형상은 타원형 단면으로 하였다. 피로시편에 발생하는 최대변형률을 구하기 위해 물성시험을 통해 확보한 비선형 재료상수를 이용하여 유한요소 해석을 수행하여 최대변형이 발생하는 부위에서의 그린-라그랑지 변형률(Green-Lagrange strain)을 Fig. 14(b)에서 같이 나타내었으며 이 결과는 고무소재의 피로수명을 평가하는데 활용하였다.
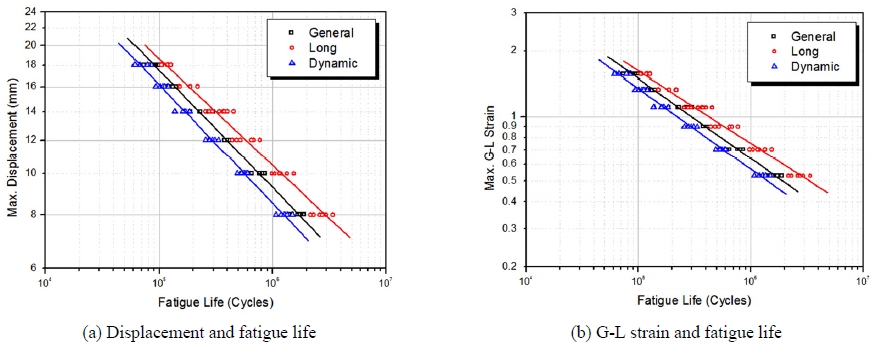
일반소재와 장수명 소재 및 저 동배율 소재에 대한 피로수명을 평가하기 위해 3차원 피로시편을 이용하여 진폭, 최대변위, 평균변위 등을 변화하면서 상온에서 변위제어 피로시험을 수행하였다. 다양한 시험조건에서 얻어진 결과를 이용하여 Fig. 15(a)에서와 같이 최대 인장변위와 피로수명과의 관계선도를 나타내면 진폭과 평균변위에 상관없이 인장변위가 클수록 피로수명은 감소함을 알 수 있었다. 따라서 인장변위를 피로손상변수로 하면 시험조건에 상관없이 피로수명 선도를 잘 표현할 수 있었다. 3차원 덤벨형 피로시편의 유한요소 해석에서 얻어진 인장변위와 그린-라그랑지 변형률과의 관계를 이용하면 Fig. 15(b)와 같이 최대 그린-라그랑지 변형률과 피로수명과의 관계선도로 나타낼 수 있으며 최대 그린-라그랑지의 함수로 고무소재에 대한 피로수명예측 식을 도출하여 Table 4에 나타내었다.
고무소재에 대한 피로수명 평가를 통해 장수명 소재가 일반소재 및 저 동배율 소재보다 피로수명이 길게 나타나 고 내구성 고무소재로 적절함을 알 수 있었다.
본 연구를 통해 확보한 고무소재의 정적 및 동적물성과 피로수명 물성을 고무부품 해석 및 설계에 활용하면 신뢰성 확보에 어려움을 겪어왔던 고무부품의 수명평가 및 신뢰성 향상에 크게 기여할 것으로 사료된다.
3. 결 론
본 연구에서는 자동차 서스펜션 부시용 고무소재로 적용되고 있는 일반소재와 내구수명을 향상을 위한 장수명 소재 및 동특성을 개선한 저 동배율소재에 대해 정적 및 동적시험과 피로시험을 수행하여 소재물성을 평가하여 다음과 같은 결론을 얻었다.
- 1) 고무소재에 대한 정적 물성시험을 통해 고무부품의 유한요소 해석에 필요한 무니-리블린과 오그덴 함수의 비선형 재료상수를 확보하였다.
- 2) 동특성시험기를 이용하여 온도 및 변형률 변화에 따른 동적물성은 온도가 높을수록 저장 탄성계수와 손실계수는 낮아지고 주파수가 증가할수록 저장 탄성계수 및 손실계수는 증가하였다. 또한 동적 변형률이 클수록 저장 탄성계수는 낮아지고 반대로 손실계수는 증가는 경향을 나타내었다.
- 3) 반복 피로하중에 의한 최대 변형률을 재현할 수 있는 3차원 덤벨형 피로시편을 제작하여 다양한 조건에서 피로시험을 수행하여 고무소재의 피로수명은 인장변위와 변형률이 피로손상변수임을 파악하였으며 장수명 소재가 일반 및 저 동배율 소재보다 피로수명이 길게 나타나 고 내구성 고무소재임을 확인할 수 있었다.
- 4) 본 연구를 통해 확보한 고무소재의 정적 및 동적물성과 피로수명 물성을 고무부품 해석 및 설계에 활용하면 신뢰성 확보에 어려움을 겪어왔던 고무부품의 수명평가 및 신뢰성 향상에 크게 기여할 것으로 사료된다.
References
- T. Alshuth, F. Abraham, and S. Jerrams, “Parameter Dependence and Prediction of Fatigue Life of Elastomers Products”, Rubber Chemistry and Technology, 75(4), p635-642, (2002).
- A. Fatemi, and L. Yang, “Cumulative Fatigue Damage and Life Prediction Theories”, International Journal of Fatigue, 20(1), p9-34, (1998).
-
D. Charlton, J. Yang, and K. K. Teh, “A Review of Methods to Characterize Rubber Elastic Behavior for Use in Finite Element Analysis”, Rubber Chemistry and Technology, 67(3), p481-503, (1994).
[https://doi.org/10.5254/1.3538686]

-
J. Zhao, Q. Li, and X. Shen, “Finite Element Analysis and Structure Optimization for Improving the Fatigue Life of Rubber Mounts”, Journal of Macromolecular Science, 45(7), p542-547, (2008).
[https://doi.org/10.1080/10601320802100614]

-
T. Zarrin-ghalami, and A. Fatemi, “Fatigue Life Predictions of Rubber Components : Applications to an Automobile Cradle Mount”, Journal of Automobile Engineering, 227(5), p691-703, (2013).
[https://doi.org/10.1177/0954407012461863]

-
B. Wang, K. Lu, and G. A. Kim, “A Damage Model for the Fatigue Life of Elastomeric Materials”, Mechnics of Materials, 34(8), p475-483, (2002).
[https://doi.org/10.1016/s0167-6636(02)00175-8]

-
L. Mullins, “Effect of Stretching on the Properties of Rubber”, Rubber Chemistry and Technology, 21(2), p281-300, (1948).
[https://doi.org/10.5254/1.3546914]

- R. W. Ogden, Non-linear Elastic Deformation, Dover Publications, INC., Mineola, New York, (1984).
- J. S. Koo, “Study on Effect of Frequency Response Parameters for Vibration Fatigue Analysis”, KSAE Annual Conference Proceedings, p1999-2007, (2011).
-
H. J. Kim, M. W. Song, H. I. Moon, H. Kim, and H. Y. Kim, “Fatigue Life Prediction of Rubber Material Based on Dynamic Crack Growth Considering Shear Effect”, Int. J. Automotive Technology, 15(2), p317-324, (2014).
[https://doi.org/10.1007/s12239-014-0032-8]

- H. L. Oh, “A Fatigue Life Model of Rubber Bushings”, Rubber Chemistry and Technology, 53(5), p1226-1238, (1980).
-
R. K. Luo, W. J. Mortel, and X. P. Wu, “Fatigue Failure Investigation on Anti-vibration Springs”, Engineering Failure Analysis, 16(5), p1366-1378, (2009).
[https://doi.org/10.1016/j.engfailanal.2008.09.005]

-
K. Takeuchi, M. Nakagawa, H. Yamaguchi, and T. Okumoto, “Fatigue Test Technique of Rubber Materials for Vibration Insulators and Their Evaluation”, Nippon Gomu Kyokaishi, 66(4), p247-252, (1993).
[https://doi.org/10.2324/gomu.66.247]