전지형 크레인의 다축조향 알고리즘 설계

1. 서 론

크레인은 동력을 이용하여 하물을 들어 올려 운반하는 기계로서 주행장치의 유무에 따라 고정식 크레인과 이동식 크레인으로 구분할 수 있다. 전지형 크레인은 이동식 크레인의 한 종류로서 다축의 휠에 의하여 조향 및 주행이 가능하다. 따라서 성능면에서는 트럭형 크레인 및 험지형 크레인의 장점을 모두 갖춘 형식이라 할 수 있다. 즉, 크레인 용량도 크고, 좁은 도로 및 험지에서의 주행성능이 우수하며, 주행 속도도 빠르다.

다축 조향차량에 관한 연구로서, Winkler와 Gillespie¹⁾는 3축 차량에 대한 정적 상태에서 핸들링에 대한 수학적 모델을 구성한 바 있고, 허건수 등²⁾은 6개의 휠로 구성된 차량 모델을 구성하여 Yaw rate 및 Lateral acceleration 등을 이용하여 핸들링 성능을 고찰하였다. 안상준 등³⁾은 Sideslip angle과 Yaw rate를 여섯 개 휠의 조향각을 제어하여 선회 시 조작성을 향상시키는 방법을 제시하였다. Qu와 Zu⁴⁾ 그리고 Bayar과 Unlusoy⁵⁾는 3축 차량의 선회 조작성 향상을 위한 이론적 방법들을 제시하였다. 문경호 등⁶⁾은 연결된 차량(Articulated vehicles)에 대한 수식화된 All wheel steeirng mode의 알고리즘을 고려하여 가상축을 이용하는 조향 제어 알고리즘에 대하여 연구하였다. 이러한 다축 조향 차량에 대한 연구논문에서는^1-6) 차량의 조향 성능 검토 및 조향 성능 향상을 위한 제어 이론에 관한 내용으로서 다양한 조향 모드를 갖는 다축 차량의 조향 알고리즘 설계와 관련된 문헌들은 찾아 볼 수 없었다.

본 논문에서는 120톤급 전지형 크레인의 개발의 일부로서 진행된 다축조향차량의 다섯 가지 모드(도로 주행 모드인 Road steering mode, 저속에서 최대로 선회하기 위한 All wheel steering mode, 좁은 공간에서 차량이 평행이동하기 위한 Crab steering mode, 좁은 공간에서 차량이 주변 장애물에 충돌하지 않고 이동하기 위한 Reduced swing out mode, 운전자가 조향각을 임의로 설정하여 주행할 수 있는 Independent steering mode⁷⁾의 조향각 설계과정과 함께 다축 조향 알고리즘 설계기법을 체계적으로 제시하였다. 또한, 설계된 조향각이 각 조향모드의 조향목표를 만족하는지 여부를 차량동역학 해석을 통하여 고찰하였다.

2. 개발차량의 제원 및 성능 목표

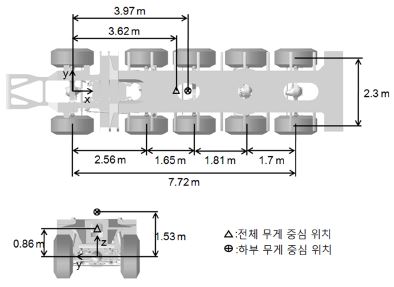
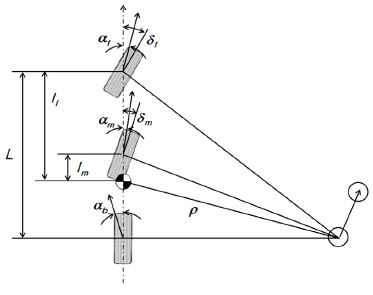
개발대상차량은 전지형 크레인으로서 5개의 축으로 구성되며, 각 축 간 거리, 차량 무게, 차폭, 무게 및 무게 중심에 대한 제원은 Table 1 및 Fig. 1에 제시된 바와 같다.

Table 1

Weight and center of weight of the vehicle

Fig. 1

Weight and center of weight of the vehicle

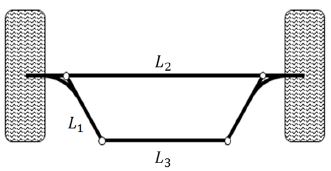
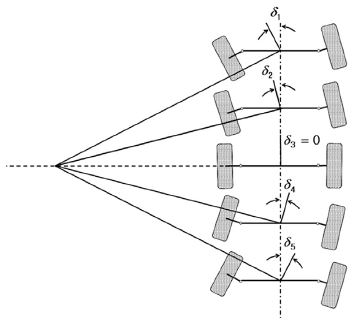
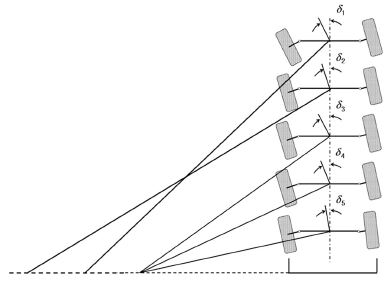
각 차축은 Fig. 2의 Trapezoidal steering과 같은 사다리꼴의 4절 링크 구조로 구성되어 있으며, 이로 인하여 좌측과 우측의 조향각 관계는 비선형적인 상관관계를 가지게 된다. 이러한 조건을 고려하여 각 휠에서의 실제 조향각을 결정하기 위해서는 각 링크의 길이정보가 필요하며, 개발차량에서 이에 대한 정보는 Table 2에 제시된 바와 같다. 각 축의 좌우 조향각이 상이하므로 각 축의 기준 조향각은 축 중앙 조향각(Steering Angle at Center of axle, 이하 “SAC”)으로 정의하였다.

Fig. 2

Trapezoidal steering system

Table 2

Length of steering linkages for each axle

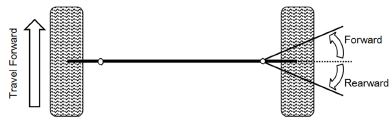
또한 각 축 휠에서의 전후 최대 조향각(Fig. 3 참조)은 Table 3과 같이 제한되어 있다. 이때, SAC의 최대값은 전후 조향각 최대범위를 기준으로 Table 2의 기하학적 상관관계로부터 계산한 후, 작은 값으로 결정된다.

Fig. 3

Definition of maximum steering angle for forward&rearward at an axle

Table 3

Maximum steering angle at each axle of the vehicle

한편, 1축과 2축의 조향 링크는 Fig. 4에서 보는 바와 같이 기계적으로 연결되어 있으므로 2축의 조향각은 1축 조향각에 연동된다.

Fig. 4

Connecting linkages between 1st axle and 2nd axle of the vehicle

개발차량에서 각 조향 모드의 성능목표는 차량주행환경에 관한 경험적 기준 및 동급차량 성능을 기초로 Table 4와 같이 결정되었다.

Table 4

Design criteria for each steering mode of the vehicle

Road steering mode는 선회 안정성을 고려하여 설계하되, 정량적 목표는 설정되지 않았다. 또한 Independent steering mode의 경우, 1, 2축 조향과 3, 4, 5축 조향을 독립적으로 조향하는 모드이지만, 1, 2축은 기구적으로 연결되어 있고 3, 4, 5축은 1, 2 축 조향각과 같은 방향인 경우에는 Crab steering, 반대 방향인 경우에는 All wheel steering mode에서와 동일한 상관관계를 갖도록 설계되므로 별도의 조향각 설계는 불필요하며 조향성능 목표도 설정되지 않는다.

3. 개발 차량에 대한 조향 알고리즘 개발

3축 이상으로 구성된 다축의 차량에 대한 연구들은 주로 3축 차량에 대한 연구이다. 이러한 3축차량에 대한 조향 알고리즘을 개발하기 위하여 Bicycle model을 사용하는 것이 일반적이며, 인휠차량과 같은 좌우의 조향각이 각기 조향 가능하다면 좌우의 휠을 모두 고려하여 조향 알고리즘을 구성한다.

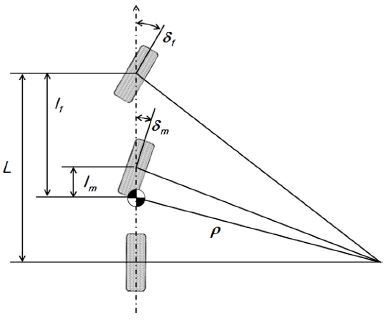
Fig. 5는 저속에서 3축 차량에 대한 Bicycle model이다. 저속인 경우에는 횡력이 발생하지 않으며, 이에 따라 각 휠에 Slip angle이 발생하지 않는다. 이러한 저속 주행 조건에서 각 축의 조향각은 아래의 식과 같이 구성 가능하다.

Fig. 5

Cornering of bicycle model for low speed

Fig. 6은 고속에서 3축에 대한 Bicycle model이다. 고속에서는 횡력이 발생하며, 이로 인하여 각 휠에 Slip angle이 발생하게 된다. 이러한 Slip angle은 코너링 파워에 반비례하며, Slip angle이 크면 코너링 파워가 감소하여 차량의 Slip이 발생하게 된다. 따라서 이러한 Slip angle을 감소시킬 수 있도록 Steering pole의 위치를 변경하여 각 축의 조향각을 결정하여야 한다.

Fig. 6

Cornering of bicycle model for high speed

이러한 3축에 대한 조향 알고리즘을 바탕으로 하여 5축 차량에 대한 조향 알고리즘을 개발하였으며, 그 과정은 다음과 같은 절차에 따라 진행하였다.

(1) SAC 설계 : 각 조향모드의 조향목적에 적합하도록 축중앙조향각을 결정한다. 이때, 1축의 조향각은 운전석의 조향핸들과 선형적으로 비례하고 2축의 조향각은 1축의 조향각과 기구적으로 연동되어 있으므로 조향 알고리즘은 1축의 조향각에 대한 3, 4, 5축의 조향각을 결정하는 과정이라고 할 수 있다.

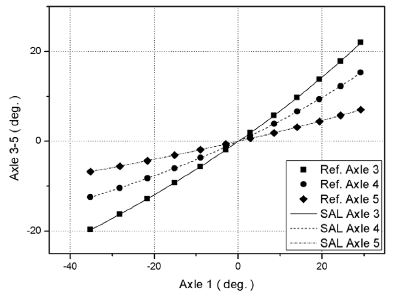
(2) 좌측 휠 조향각 계산 : 축중앙조향각에 대응하는 각 휠에서의 조향각은 Fig. 2 및 Table 2의 기구학적 관계를 이용하여 계산할 수 있다. 한편, 개발대상차량의 조향 제어 시스템은 각 축의 좌측 휠 조향각을 기준으로 제어하도록 구성될 것이므로 좌측 휠에서의 조향각(Steering Angle at Left side wheel, SAL)을 계산한다.

(3) 근사 수식화 : 실차조향제어는 최대 조향각 범위 내에서 연속적으로 변화되어야 하므로 1축의 조향각에 대한 3, 4, 5축의 조향각을 Curve fitting을 이용하여 다항식(Polynomial) 형태의 수식으로 근사하였다. 이와 같이 수학적 모델로 유도함으로써 제어기에 적용 시 폐루프 시스템의 과도 및 정상 상태의 조건을 만족하는 파라미터를 결정하는데 다양한 설계 방식에 적용이 가능하다.

3.1 Road steering mode

Road steering mode에서는 1, 3, 4, 5축의 기준 조향각이 애커만 각(Ackerman angle)을 따르도록 설계하였다. 이때, Steering pole은 3축선상에 위치하도록 설계하였으므로 3축의 조향각은 항상 0이 된다. 한편, 1, 2축의 연결기구 설계는 본 조향 모드의 최대 조향조건에서 모든 축의 축중앙조향각이 애커만 각을 추종할 수 있도록(즉, 선회중심이 일치하도록) 설계된다(Fig. 7 참조).

Fig. 7

Concept of “Road steering mode” with maximum steering angle at zero speed

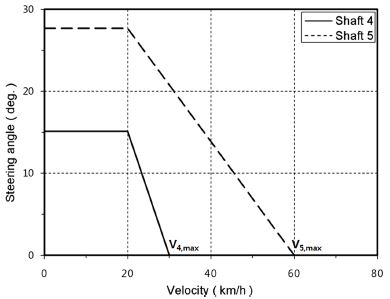
한편, 차량의 속도가 증가할수록 과도 조향(Over-steering)을 유발하게 된다. 이를 완화하기 위하여 4축 및 5축 조향각을 애커만 각보다 속도에 선형적으로 비례하여 감소되도록 하여 선회 반경을 증가시키며, 이를 통하여 Slip angle을 감소시킬 수 있게 하였다. 이에 따라, 4축은 차량속도 30 km/h 이상에서, 5축은 60 km/h 이상에서 조향각이 0°로 고정된다(Fig. 8 참조). 이는 Road steering mode에서도 모든 축의 조향각이 애커만 각을 이루고 조향하지는 않음을 의미한다.

Fig. 8

Steering angle change along with the speed of vehicle change

개발대상차량의 Road steering mode에 대한 차량속도가 0인 조건의 SAC 기준 조향각 설계결과는 Fig. 9에 보인 바와 같다.

Fig. 9

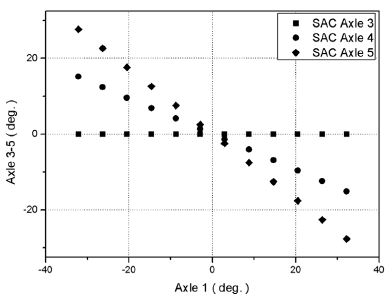
Designed correlation between 1st axle steering angle and 3rd, 4th, 5th axle steering angle with respect to the “SAC” for the “Road steering mode” of the vehicle with zero speed

Road steering mode에 대한 SAL은 식 (2)과 같은 식으로 근사하였다.

when　 0<V<V_i,max,

$\[ {\delta }_i=\left(A_i+B_i{\delta }_1+C_i{\delta }_1^2+D_i{\delta }_1^3\right)\left(1-\frac{V}{V_{i,\text{max}}}\right) \]$

(2)

when 　V≥V_i,max

　δ_i = 0

where

　i=3,4,5

　δ₁ = 1^st axle steerng ∠

　V_i,max = 30km/h for i 3 or 4

　V_i,max = 60km/h for i 5

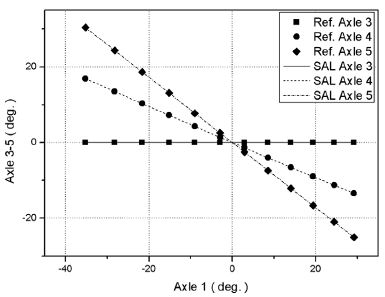
이때, δ는 SAL, V는 차량속도, i는 i번째 축을 표시하며, A, B, C, D는 조향특성 상수이다. 개발대상차량의 Road steering mode의 조향특성상수 계산결과는 Table 5에 나타낸 바와 같고 차량속도가 0인 조건의 SAL 기준 조향각 설계결과는 Fig. 10에 보인 바와 같다.

Table 5

Steering characteristic constants for the “Road steering mode” of the vehicle

Fig. 10

Designed correlation between 1st axle steering angle and 3rd, 4th, 5th axle steering angle with respect to the “SAL” for the “Road steering mode” of the vehicle with zero speed

3.2 All wheel steering mode

All wheel steering mode는 최대 조향각 조건에서 선회반경이 최소가 되도록 조향 알고리즘을 설계하여야 한다. 이를 위하여 Fig. 11에서 보인 바와 같이 All wheel steering mode의 최대 조향각 조건에서는 Road steering mode와 달리 steering pole이 3축선상을 벗어나게 된다. 따라서 상대적으로 2축 조향각은 다른 축들과 동심원을 이루지 못하게 되어, 주행 시각 축 휠간의 상대적인 Slip이 증가하고 그에 따른 타이어 편마모 증가도 불가피하게 된다. 이러한 단점 때문에 All wheel steering mode에서도 특정 조향각(본 차량에서는 1축 SAC 기준으로 최대 조향각보다 5도 작은 값으로 설정함)범위 이내에서는 Road steering mode와 동일한 조향각을 형성하도록 설계하였다.

Fig. 11

Concept of “All wheel steering mode” with maximum steering angle

개발대상차량의 All wheel steering mode에 대한 SAC 기준 조향각 설계결과는 Fig. 12에 보인 바와 같다.

Fig. 12

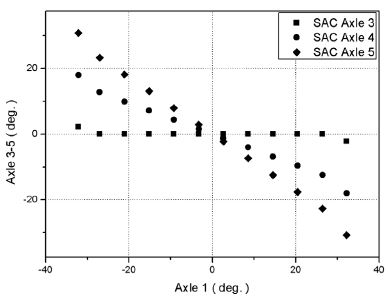
Designed correlation between 1st axle steering angle and 3rd, 4th, 5th axle steering angle with respect to the “SAC” for the “All wheel steering mode” of the vehicle

All wheel steering mode에 대한 SAL은 식 (3)과 같은 식으로 근사할 수 있으며 조향특성상수 계산결과는 Table 6에 나타낸 바와 같고 SAL 기준 조향각 설계결과는 Fig. 13에 보인 바와 같다. 이때, 3축 조향각에 대해서는 구역(Region)에 따라 별도의 조향특성상수를 갖는다.

$\[ {\delta }_i=A_i+B_i{\delta }_1+C_i{\delta }_1^2+D_i{\delta }_1^3,i=\mathrm{3,4},5 \]$

(3)

Table 6

Coefficient of equation for all wheel steering mode

Fig. 13

Designed correlation between 1st axle steering angle and 3rd, 4th, 5th axle steering angle with respect to the “SAL” for the “All wheel steering mode” of the vehicle

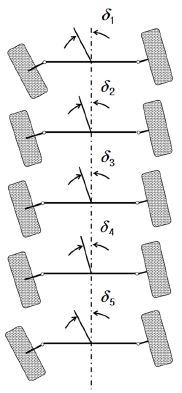
3.3 Crab steering mode의 조향 알고리즘

Fig. 14에서 보인 바와 같이 Crab steering mode는 차량의 평행조향을 위하여 모든 축의 조향각이 같은 값을 갖는 것이 이상적이지만, 1, 2축 조향각 연성 및 3축의 조향각범위가 상대적으로 작은 점을 고려하여 식 (4)과 같은 관계를 따르도록 설계하였다. 최대 조향각 범위가 가장 작은 3축 조향각을 기준으로 이보다 작은 조향각 범위에서는 3, 4, 5축 조향각은 서로 같고 이 값과 1, 2 축 조향각 평균값이 동일하도록 설계함으로써 상대적인 Slip이 최소화되도록 하였다. 한편, 3축 조향각이 최대값에 도달한 이후에는 1, 2축 조향각은 증가하더라도 3, 4, 5축 조향각은 더 이상 증가하지 않도록 설계하였다.

Fig. 14

Concept of “Crab steering mode”

(4)

where
i = 3,4,5
δ₁ = 1^st axle steerng angle
δ₂ = 2^st axle steerng angle

개발대상차량의 Crab steering mode에 대한 SAC 기준 조향각 설계결과는 Fig. 15에 보인 바와 같다.

Fig. 15

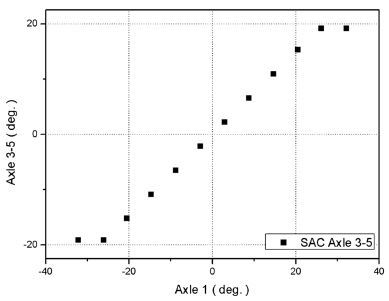
Designed correlation between 1st axle steering angle and 3rd, 4th, 5th axle steering angle with respect to the “SAC” for the “Crab steering mode” of the vehicle

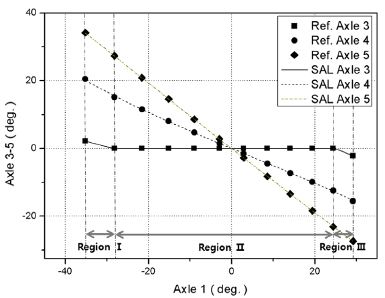
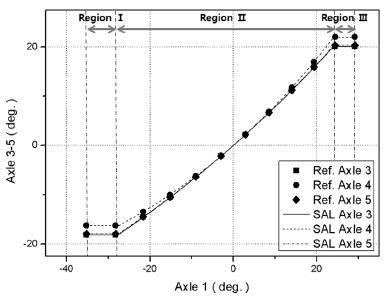
Crab steering mode에 대한 SAL은 식 (4)와 같은 식으로 근사할 수 있으며 조향특성상수 계산결과는 Table 7에 나타낸 바와 같고 SAL 기준 조향각 설계 결과는 Fig. 16에 보인 바와 같다. 이때, 구역(Region) I, II, III에 따라 별도의 조향특성상수를 갖는다. 구역 I은 -35.20°에서 -28.23°까지, 구역 II는 -28.23°에서 24.44°까지, 구역 III은 24.44°에서 29.18°까지이다.

Table 7

Coefficient of equation for crab steering mode

Fig. 16

Designed correlation between 1st axle steering angle and 3rd axle steering angle with respect to the “SAL” for the “Crab wheel steering mode” of the vehicle

3.4 Reduced swing out mode의 조향 알고리즘

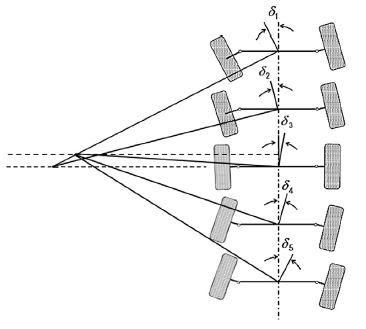
Reduced swing out mode는 선회 시 차량 후미의 횡방향 돌출을 최소화하는 방향으로 조향 알고리즘을 설계한다. 이를 위해 Fig. 17에서 보인 바와 같이 Steering pole의 위치를 차량의 후미에 위치시켜 3-5 축의 조향각을 설계하였다. 최대 조향조건에서 1축 및 2축은 조향한계로 인하여 3, 4, 5축의 Steering pole과 일치할 수 없고 이에 따라 각 휠에서의 상대적인 Slip 발생은 불가피하다.

Fig. 17

Reduced swing out mode

개발대상차량의 Reduced swing out mode에 대한 SAC 기준 조향각 설계결과는 Fig. 18에 보인 바와 같다.

Fig. 18

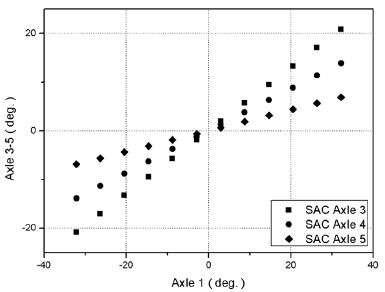
Designed correlation between 1st axle steering angle and 3rd, 4th, 5th axle steering angle with respect to the “SAC” for the “Reduced swing out mode” of the vehicle

Reduced swing out mode에 대한 SAL은 식 (2)와 같은 식으로 근사할 수 있으며 조향특성상수 계산결과는 Table 8에 나타낸 바와 같고 SAL 기준 조향각 설계결과는 Fig. 19에 보인 바와 같다.

Table 8

Coefficient of equation for reduced swing out mode

Fig. 19

Designed correlation between 1st axle steering angle and 3rd, 4h, 5th axle steering angle with respect to the “SAL” for the “Reduced swing out mode” of the vehicle

4. 다물체 동역학 해석을 이용한 조향 알고리즘의 타당성 검토

개발된 조향 알고리즘이 Table 4의 조향목표 만족여부를 검토하기 위해 DAFUL/CAR를 이용한 차량동역학해석을 수행하였다.

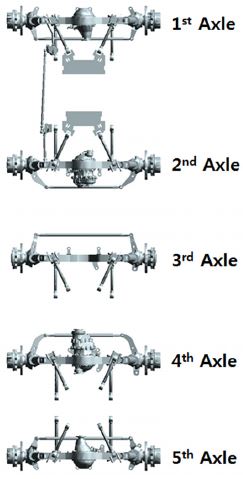
Road steering mode를 제외한 나머지 조향모드에서는 차량의 속도가 낮아 동적 특성이 강하게 나타나지 않을 것으로 판단함에 따라 해석모델링은 다음과 같이 단순하게 구성하였다. Table 2의 중량 조건과 Fig. 20에 보인 바와 같은 각 축의 링크 구조를 반영하되, 타이어 및 유압쇼버를 제외한 모든 구성품은 강체로 구성하였고, 링크간 부싱에 의한 연결은 Ball joint 요소로 단순하게 구성하였다. 각 차축은 차량 프레임과 4개의 링크와 2개의 유압 쇼바를 통하여 연결되어 있으며, 유압 쇼바는 Spring-damper 요소를 이용하여 구성하였다. 타이어는 445/95R25 사양의 PAC2002 모델을 적용하였다. 구성된 해석모델은 Fig. 21에 보인 바와 같다.

Fig. 20

Linkage system of each axle

Fig. 21

Multibody dynamic analysis model of the vehicle

구동축은 2,4,5축이며 트랜스퍼기어에 의해8.27:8.27:8.48 의 토크비를 형성하며 차동기어에 의해 좌우 휠에는 토크가 동일하게 배분된다. 입력 토크를 제어하여 차량의 속도를 10 km/h로 일정하게 유지하는 조건에서 해석을 수행하였다.

최대 조향조건으로 Road steering mode에서 는 선회 반경이 9.104 m, All wheel steering mode에서는 선회 반경이 8.662 m로 나타났다. Crab steering mode에서는 목표조향 19.14°에서 19.98°의 Traveling angle을 형성하여 오차는 4.4 %로 예측되었다. 최대 조향각 조건으로 Reduced swing out mode에서는 측면 돌출 거리는 0 m, 선회반경은 21.86 m로 예측되었다. 이러한 결과로부터 설계조향각이 Table 4의 조향모드별 성능목표를 만족할 것으로 추정할 수 있다.

5. 결 론

120톤급 전지형 크레인의 다섯 가지 조향모드(Road steering mode, All wheel steering mode, Crab steering mode, reduced swing out mode)에 대한 조향각 설계과정을 통하여 다축 조향 알고리즘 설계기법을 체계적으로 제시하였다. 개발차량의 기구학적 제원에 기초하여 각 조향모드에 대한 각 축의 조향각을 설계하고, 이를 1축과 다른 축들의 조향각 관계로 정리하였으며, 이를 조향제어기에 구현하기 위한 근사 수식화 과정을 수행하였다. 또한, 차량동역학 해석모델을 구성하여 설계 조향조건에 대해 해석을 수행한 결과, 설계성능목표를 만족할 것으로 예측되었다.

Acknowledgments

이 논문은 산업통상자원부가 지원한 ‘산업기술혁신사업(과제명: 인공지능 기술이 적용된 120ton급 전지형(All Terrain)크레인 개발, 과제번호: 10044999)’으로 지원을 받아 수행된 연구 결과입니다.

References

• C. B. Winkler, and T. D. Gillespie, “On the Directional Response Characteristics of Heavy Trucks”, Veh. Syst. Dyn, Vol.6(No.2-3), p120-123, (1997). [https://doi.org/10.1080/00423117708968520]
• K. Huh, J. Kim, and J. Hong, “Handling and Driving Characteristics for Six-wheeled Vehicles”, Proceedings of the Institution of Mechanical Engineers, Vol.214(No.2), p159-170, (2000). [https://doi.org/10.1177/095440700021400205]
• S. J. An, K. Yi, G. Jung, K. I. Lee, and Y. W. Kim, “Desired Yaw Rate and Steering Control Method during Cornering for a Six Wheeled Vehicles”, Int. J. Automotive Technology, Vol.9(No.2), p173-181, (2008). [https://doi.org/10.1007/s12239-008-0022-9]
• Q. Qu, and J. W. Zu, “On Steering Control of Commercial Three-axle Vehicle”, ASME J. Dyn. Syst., Meas. Control, Vol.130(Issue 2), p021010-1-10, (2008). [https://doi.org/10.1115/1.2837438]
• K. Bayar, and Y. S. Unlusoy, “Steering Strategies for Multi-axle Vehicles”, Int. J. Heavy Veh. Syst, Vol.15(No.2-4), p208-236, (2008). [https://doi.org/10.1504/ijhvs.2008.022243]
• K. H. Moon, S. H. Lee, S. Chang, J. K. Mok, and T. W. Park, “Method for Control of Steering Angles for Articulated Vehicles Using Virtual Rigid Axles”, Int. J. Automotive Technology, Vol.10(No.4), p441-449, (2009). [https://doi.org/10.1007/s12239-009-0050-0]
• Guide book, MK 88 Mobile Construction Crane, (2014).