측정 데이터의 확률 분포를 이용한 자동차 부품의 시험 데이터 확장
Copyright Ⓒ 2025 KSAE / 234-08
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Automotive components experience performance degradation and fatigue failure due to operational loads and environmental factors. Accelerated durability testing is conducted, but this testing must accurately replicate real-world damage. Existing data extrapolation methods, such as ARMA, Rainflow, and Markov histograms, rely on parameter tuning and expert knowledge, limiting their efficiency and scalability. This study proposes a non-parametric probability-based data extrapolation method of durability testing to overcome said limitations. Using RLDA data from a K151 tactical vehicle, component loads were analyzed with Rainflow Counting and Miner’s rule. The proposed method was validated through repeated measurements on various road conditions. Compared to conventional superposition methods, the probability-based approach reduced extrapolation error by up to 47 %, demonstrating improved accuracy. This research contributes to enhancing reliability assessment in durability testing and can be applied to military vehicles as well as the rail and aerospace industries.
Keywords:
Data extrapolation, RLDA data, Probability distribution, Military vehicle, Fatigue damage키워드:
데이터 확장, 도로 하중 측정 데이터, 확률 분포, 군사 차량, 피로 손상도1. 서 론
자동차 부품은 주행 중에 발생하는 하중과 사용 환경 등에 의해 그의 기능이 저하되거나 파손되어 기능을 상실할 수 있다. 자동차 부품 설계에는 이를 방지하기 위하여 기능을 유지하는 성능인 내구성 확보가 필요하며, 내구 설계 기술뿐만 아니라 내구성을 평가하는 내구 신뢰성시험 평가 기술 등 다양한 기술 개발이 진행되고 있다.
부품의 현실적 성능, 수명, 신뢰성을 보장하기 위한 가장 정확한 방법은 사용 환경과 거의 유사한 시험 평가를 수행하는 것이다. 완성차 업체의 신뢰성 목표는 승용차의 경우 일반적으로 10년 30만km 이상, 상용차의 경우 15년 50만km 이상이다. 따라서 실제 사용 환경에서 시험 평가하는 Fleet 내구시험은 약 1년가량 소요1)되기 때문에 차량 또는 부품 개발 단계에서 수행할 수 없다. 따라서 일반적으로 부품/모듈 개발 단계에서는 시험실 내 가속 내구시험을 시행하고, 차량 개발 단계에서는 Proving ground에서 가속 내구시험을 시행한다.2)
가속 내구시험은 실제 사용 환경에서 발생하는 다양한 파손 인자를 고려하여 짧은 시간 내에 재현하는 시험으로, 필드에서 발생하는 손상도를 최대한 동일하게 인가하여야 한다.3) 가속 내구 시험법은 실제 필드에서 계측한 데이터로부터 손상도를 계산하고, 이를 신뢰성 목표에 해당하는 거리 또는 시간만큼 데이터를 확장한 후, 시험 시간을 최대한 줄이면서도 손상도는 유지되는 방식으로 설계된다.
본 연구는 가속 내구 시험법 개발을 위하여 필드에서 측정한 손상도 데이터를 확장하는 방법에 관한 연구이다. 필드에서 측정한 데이터를 확장하는 방법은 폭넓게 연구된 주제이다. 특히 바람, 해수면, 기후, 지진 등 자연현상에서 정상상태 및 비정상상태 신호의 확장에 대한 모델이 제안되었다.4-7) 이와 같은 모델은 시간 영역, 히스토그램 영역, 주파수 영역, 시간-주파수 영역 및 기타 영역에서 다양하게 제안되었으며 Table 1과 같이 그룹화할 수 있다.
Signal extrapolation models
이러한 모델 중 일부는 커널 추정기와 극단 값 이론 등 신호 극단에 초점을 맞추어 모델 생성이 용이하지만 모델 중 정보의 손실 때문에 발산한다는 단점도 있다. 하지만 시계열 분석에 있어서는 ARMA 모델, 스펙트럼 분석 결과 등이 매우 널리 사용되고 있으며, 자동차 분야에서는 손상도 분석을 위하여 Rainflow, Markov 히스토그램 등을 이용한 다양한 데이터 확장 기법이 사용되고 있다. 그러나 대부분의 확장 모델은 매개변수가 필요하며, 이를 활용하기 위해서는 많은 경험 및 전문 지식이 필요하다. 이에 따라 본 연구에서는 손상도의 확률 분포에 기반하여 데이터를 확장하는 비모수 기법을 제안하고자 한다.
2. 손상도 확률 분포
2.1 실차 데이터
본 연구에는 Fig. 1과 같이 K151 소형 전술차량을 대상으로 창원기동시험장에서 측정한 데이터를 활용하였다. 측정 데이터는 크게 샤시계, 구동계 부품 하중으로 구분될 수 있으며, Table 2와 같이 샤시계 부품 하중으로는 휠 하중과 각종 부품에 작용하는 하중이며, 구동계 부품 하중으로는 변속기 전, 후의 토오크 등 총 82채널을 대상으로 하였다.
Test vehilce (K151 tactical vehicle)
Measurement list
데이터 측정은 창원기동시험장 내 대표적인 내구평가 시험모드인 직선로, 크로스컨트리로, 야지기동로에서 이루어졌으며, 포장로인 직선로에서는 60 kph, 비포장로인 크로스컨트리로와 야지기동로에서는 각각 20 kph, 30 kph 정속주행 조건에서 측정하였다. 데이터 확장의 정확도를 판단하기 위하여 각각 56회, 86회, 107회 반복 측정하였다.
Test track and condition
2.2 손상도 계산
자동차 부품 중 구조부품의 파손 기전은 대부분 반복 하중에 의한 피로 파손이며 응력-수명 식과 Miner 선형손상법칙13)을 이용하여 손상도를 계산한다. Miner의 선형 손상 이론은 피로 파괴가 일어날 때까지의 손상이 누적되는 과정을 선형적으로 설명하며 식 (1)과 같이 표현된다. 응력-수명식은 Log-log 선도에서 선형적인 식 (2)와 같이 표현된다. 두 식에 따라 손상도는 식 (3)과 같이 SN선도 기울기 k값와 재료 물성값인 C값에 의해 영향을 받는데 동일한 부품에서 2개 이상의 상대적인 손상도 계산은 기울기 k값만 영향을 받는다. 본 연구에서는 대표적인 k값으로 k=3(용접부), k=5(일반 강), k=8(알루미늄)을 적용하여 상대 손상도를 계산하였다.
| (1) |
- where
- D : cumulative damage
- ni : total number of cycles in i-th block of constant stress amplitude Sa
- Ni : fatigue life as the number of cycles to failure under Sa
- kn : total number of stress blocks
| (2) |
- where
- k : slope factor of SN curve
- C : material constant
| (3) |
측정 데이터로부터 응력 또는 하중의 진폭 및 반복 횟수 정보를 추출하기 위하여 응력의 폐쇄 히스테리시스를 정의하는 데 사용되는 Rainflow counting 방법을 이용하였다. 손상도 계산은 데이터처리 상용 S/W인 nCode사의 Glypworks를 이용하여 계산하였다.
2.3 손상도 확률 분포
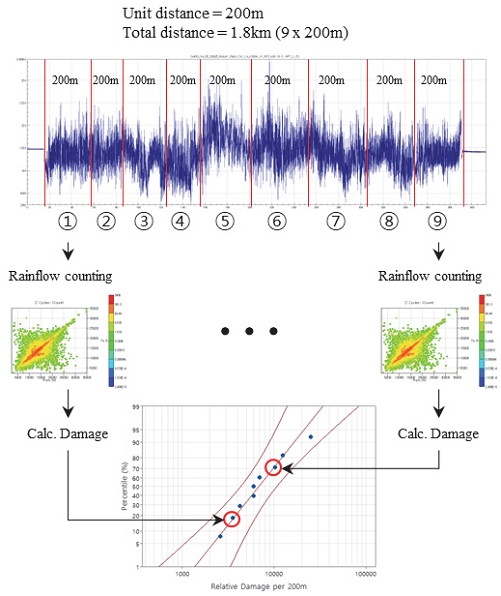
본 연구는 Fig. 2와 같이 필드에서 측정된 데이터를 거리 균등 데이터로 나누고, 나누어진 데이터를 Rainflow counting을 통하여 손상도를 계산하고 이를 이용하여 확률 분포 추정한다. 유사한 도로를 주행할 때 발생하는 손상도가 얻어진 확률 분포를 추종한다고 가정하여 데이터를 확장한다. 손상도 데이터의 확률 분포 추정에 사용되는 분포는 손상도가 하중의 거듭제곱으로 계산되고, 음의 값이 없으므로 아래와 같은 분포로 한정하였다.
- • 대수정규분포
- • 감마분포, 일반화 감마분포
- • 로지스틱 분포
- • Johnson변환 정규분포
- • Boxcox변환 정규분포
- • 와이불 분포
- • 알파 분포
- • 기타 분포(Gumbel, Fisk, Pareto, Burr Chi, Maxwell, Lomax, Mielke)
Scheme to calculate damage probability distribution
3. 데이터 확장
3.1 데이터 확장 방법
일정한 도로 조건에서 일정한 패턴으로 주행하는 경우 균등 거리로 나누어진 시간 이력 데이터로부터 계산된 손상도 데이터가 일정한 확률 분포를 가지고, 유사한 도로 조건에서 같은 운전자가 주행하는 경우 발생하는 손상도가 동일한 확률 분포로 나타낼 수 있다고 가정하면, 얻어진 확률 분포로부터 요구되는 거리에 해당하는 개수의 랜덤한 데이터를 추출할 수 있고 이를 합산하여 확장된 손상도 데이터를 얻을 수 있다.
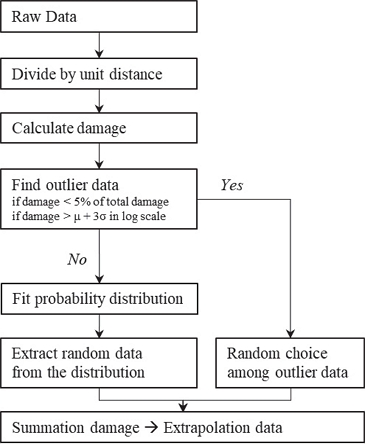
Fig. 3에는 본 연구에서 제안한 데이터 확장 방법을 표현하였다. ① 측정된 데이터는 정해진 균등한 거리대로 구분되어 각각 저장되고, Rainflow counting 방법과 선형 손상 법칙에 따라 손상도를 계산한다. ② 계산된 손상도 데이터 중 전체 손상도에 큰 영향을 주지 않는 5 %미만의 미소 손상도 데이터와 로그 스케일에서 z-score가 3이상인 과대 손상도 데이터는 이상치로 구분한다. ③ 정상 손상 데이터에 대해서 손상도 확률 분포를 식별하고, 이에 대한 매개변수를 추출한다. ④ 추정된 확률 분포를 추종하도록 거리 비(목표 거리/단위 거리)만큼의 개수만큼 무작위 추출을 수행한다. ⑤ 이상치의 경우 거리 비만큼의 개수만큼 무작위 선택을 수행한다.
Data extrapolation procedure
이 과정을 통하여 얻는 ④ 정상 데이터 확률 분포로부터 무작위 추출된 데이터와 ⑤ 이상치 데이터의 무작위 선택 데이터를 합하여 확장된 손상도를 계산한다.
3.2 확률 분포 식별
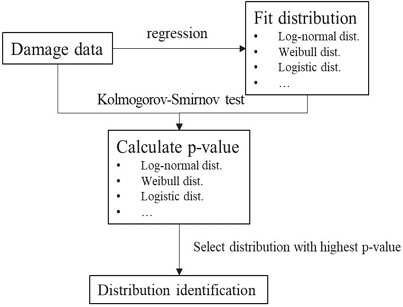
일반적으로 데이터가 분포를 얼마나 가깝게 따르는지를 평가할 때 데이터와 해당 분포에 대하여 적합도 검정을 수행하여 얻어진 p값을 가지고 평가한다. p값은 귀무가설에 반하는 증거를 측정하는 확률이며, p값이 높을수록 데이터와 분포를 따른다는 강력한 증거가 된다. 본 연구에서는 데이터로부터 회귀 분석을 통하여 2.3절에서 언급한 다양한 확률 분포에 대한 매개 변수를 도출하였다. 데이터와 여러 개의 확률 분포 Kolmogorov-Smirnov 검정을 수행하여 각각의 p값을 계산하였으며, 데이터는 이 중 가장 높은 p값을 가지는 확률 분포를 따르는 것으로 하였다.
Scheme to identify probability distribution
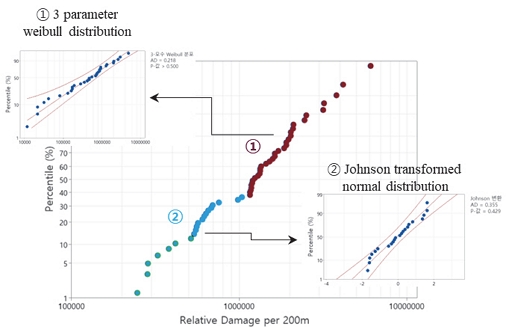
균등 거리 손상도 데이터로부터 계산된 단위 거리 손상도에 대한 확률 분포는 Fig. 5와 같이 2개 이상의 분포가 혼합된 혼합 분포인 경우가 있다. 본 연구에서는 혼합된 분포를 2개로 한정하여 각각의 확률 분포를 식별하였다.
Example of distribution identification on mixture distribution (G1 30 kph, wheel force RL Fz)
균등 거리 손상도 데이터가 최대 2개의 혼합 분포라고 가정하고, 손상도 데이터를 정렬한 후 가장 손상도가 큰 데이터 3개부터 데이터 개수의 2/3까지 확률 분포 식별을 수행하여 가장 높은 p값을 가지는 확률 분포가 하나의 분포로 추출하고, 나머지 데이터로 다른 하나의 분포라고 간주하였다.
3.3 데이터 확장 결과
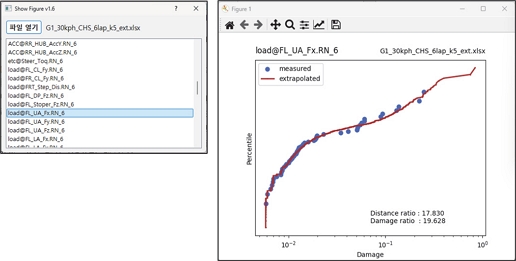
데이터 확장을 위하여 Python 3.2을 사용하였고, Scipy 라이브러리에서 제공하는 확률 통계 함수를 이용하였다. 입력창에 단위 거리와 목표거리를 입력하고, Excel csv파일로 손상도 계산 프로그램인 Glypworks에서 제공되는 손상도 정보에서 채널명 행과 손상도 행을 입력하면 데이터 확장 결과를 Excel xlsx파일로 제공하고 도표 형식으로 표시할 수 있도록 하였다.
Output figure of data extrapolation program
Fig. 7과 같이 데이터 확장 결과 중 측정 손상도와 확장된 손상도의 비율은 측정 거리와 확장된 거리의 비율에 일정 정도 수렴하고 있으며, 손상도 계산을 위한 k값과 신호에 따라 그 비율의 차이가 발생한다. 선형 손상 이론에서 손상도는 응력 - 수명 관계가 누승에 비례하기 때문에 k값이 증가할수록 하중 크기에 민감해진다. 이에 따라 k값이 증가할수록 측정 손상도와 확장된 손상도의 비율이 거리 비율보다 차이가 나지만, 그 차이는 최대 50 % 이내이다.
Damage ratio, extrapolated / measured (G1 30 kph)
4. 데이터 확장법 정합성 검증
4.1 정합성 검증 방법
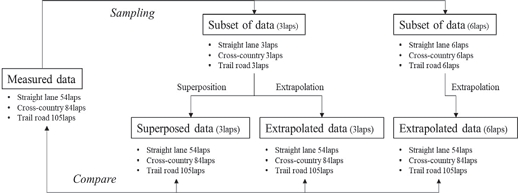
본 연구에서 제안한 데이터 확장 방법의 정합성을 검증하기 위하여, Fig. 8과 같이 직선로, 크로스컨트리로, 야지기동로를 반복 측정하고, 일부 구간으로부터 획득된 손상도 데이터를 확장하여 전체 구간으로부터 계산된 손상도 데이터와 비교하여 연구에서 제시한 데이터 확장 방법의 정합성을 검증하고자 하였다.
Scheme to verify proposed extrapolation method
전체 데이터로부터 3회, 6회 반복 측정된 데이터를 임의로 추출하여 데이터 확장을 수행하고, 이를 전체 측정된 손상도와 비교 분석함으로써 확률 분포에 기반한 데이터 확장법의 정합성을 분석하였고, 손상도를 선형적으로 곱하여 중첩한 결과와 비교하여 연구에서 제시한 방법의 유효성을 살펴보았다.
4.2 정합성 검증 결과
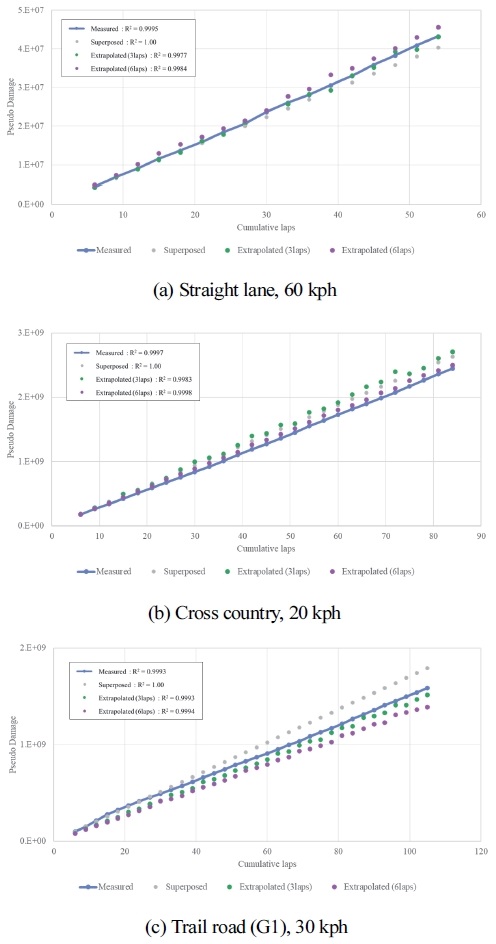
3회, 6회 반복 측정된 데이터 중 임의로 추출된 데이터로부터 데이터 확장한 결과와 전체 측정된 데이터를 누적한 결과 일부를 Fig. 9와 같이 나타내었다. 또한 데이터 확장 방법의 유효성을 살펴보기 위하여 단순히 선형적으로 중첩한 결과도 동시에 표시하였다. 그림과 같이 반복 횟수가 누적되며 거의 선형적으로 증가하는 것으로 보이며, 측정 데이터와 확장된 데이터의 기울기에서 차이가 발생한다.
Result of damage extrapolation (WFT RL Fz, k=5)
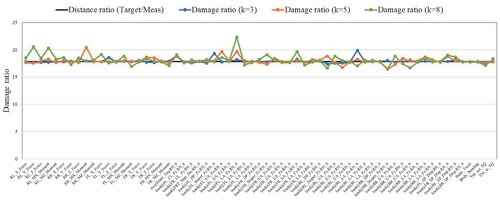
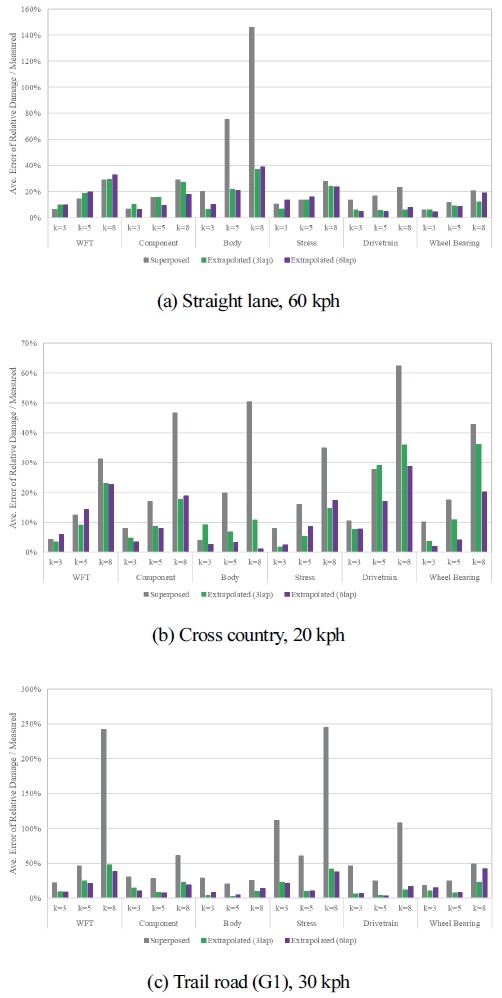
확장된 손상도 데이터와 누적 횟수에 따른 기울기가 측정된 손상도 데이터의 기울기의 오차가 적을수록 확장 방법의 유효성이 증명된다. Fig. 10에 단순 중첩 데이터 확장 방법, 3회 반복 데이터를 이용한 데이터 확장 방법, 6회 반복 데이터를 이용한 데이터 확장 방법에 따라 얻어진 결과로부터 기울기 오차를 계산하여 Table 4와 같이 휠 하중, 부품 하중, 차체 거동, 바디 응력, 구동 토크, 휠 베어링 부분으로 구분하여 평균을 내어 평균 오차율을 표시하였다.
Ave. error of extrapolated damage / measured damage
Description of comparison groups
앞서 언급한 바와 같이 k값이 증가할수록 오차는 크게 발생하며, Table 5와 같이 단순 충접 데이터 확장 방법보다 확률 분포를 이용한 데이터 확장 방법의 오차가 k값에 따라 약 12 ~ 47 % 가량 적게 발생한다.
Average error of ext. damage / meas. damage
5. 결 론
본 논문은 자동차 부품의 가속 내구시험법 개발을 위하여, 측정된 데이터를 신뢰성 목표만큼 데이터를 확장할 수 있는 확률 기반의 데이터 확장 방법을 제안하였다.
현재까지 데이터의 확장 방법으로 시간이력, 히스토그램, 주파수 기반의 데이터 확장 방법이 다양하게 소개되어 있다. 소개된 확장 방법의 대다수는 매개 변수에 종속되어 이에 대한 경험 또는 관련 지식이 필요하다. 본 연구에서는 확률 분포에 기반하여 매개 변수가 필요하지 않은 방법을 소개하였다.
제안된 데이터 확장 방법의 정합성을 확인하기 위하여 직선로, 크로스컨트리로, 야지기동로를 반복 측정하고, 일부 구간으로부터 획득된 손상도 데이터를 확장하여 전체 구간으로부터 계산된 손상도 데이터와 비교하였다. 제안된 방법으로 데이터를 확장한 결과 단순 중첩 확장한 결보다 오차율이 최대 12 ~ 47 %까지 줄어들어 유효성을 확인하였다.
Nomenclature
| D : | cumulative damage |
| ni : | total number of cycles in i-th block of constant stress amplitude Sa |
| Ni : | fatigue life as the number of cycles to failure under Sa |
| kn : | total number of stress blocks |
| k value : | slope of SN fatigue curve |
| C : | material constant of fatigue curve |
Subscripts
| RL, RR, FL, FR : | rear left, rear right, front left, front right |
| Fx, Fy Fz : | longitudinal, lateral, vertical force |
| Mx, Mz : | camber moment, steering moment |
Acknowledgments
이 논문은 2024년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(UI30013UD).
References
- T. H. Lee, B. H. Min and W. W. Jung, “The Study for Domestic Vehicle Field Monitoring,” KSAE Spring Conference Proceedings, pp.1436-1440, 2007.
- G. H. Kim, “Durability Evaluation Technology for Improving Reliability of Automobile Parts,” KSAE Symposium for Materials, pp.22-51, 2003.
- D. S. Kim, E. H. Hong, W. H. Ko and Y. W. Park, “A Study on the Acceleration Durability Test Method Applied to the Rear Axle Integrated E-Transaxle for Commercial Vehicles,” KSAE Spring Conference Proceedings, p.307, 2023.
-
A. Kareem, “Numerical Simulation of Wind Effects: A Probabilistic Perspective,” Journal of Wind Engineering and Industrial Aerodynamics, Vol.96, Nos.10-11, pp.1472-1497, 2008.
[https://doi.org/10.1016/j.jweia.2008.02.048]
-
S. Åberg, K. Podgórski and I. Rychlik, “Fatigue Damage Assessment for a Spectral Model of Non-Gaussian Random Loads,” Probabilistic Engineering Mechanics, Vol.24, No.4, pp.608-617, 2009.
[https://doi.org/10.1016/j.probengmech.2009.04.004]
-
P. M. Della-Marta, H. Mathis, C. Frei, M. A. Liniger, J. Kleinn and C. Appenzeller, “The Return Period of Wind Storms over Europe,” International Journal of Climatology, Vol.29, No.3, pp.437-459, 2009.
[https://doi.org/10.1002/joc.1794]
-
Y. K. Wen and P. Gu, “Description and Simulation of Nonstationary Processes Based on Hilbert Spectra,” Journal of Engineering Mechanics, Vol.130, No.8, pp.942-951, 2004.
[https://doi.org/10.1061/(ASCE)0733-9399(2004)130:8(942)]
-
Y. Ling, C. Shantz, S. Mahadevan and S. Sankararaman, “Stochastic Prediction of Fatigue Loading Using Real-Time Monitoring Data,” International Journal of Fatigue, Vol.33, No.7, pp.868-879, 2011.
[https://doi.org/10.1016/j.ijfatigue.2011.01.015]
-
P. Johannesson, “Extrapolation of Load Histories and Spectra,” Fatigue & Fracture of Engineering Materials & Structures, Vol.29, No.3, pp.209-217, 2006.
[https://doi.org/10.1111/j.1460-2695.2006.00982.x]
-
D. Socie, “Modelling Expected Service Usage from Short-Term Loading Measurements,” International Journal of Materials and Product Technology, Vol.16, Nos.4-5, pp.295-303, 2001.
[https://doi.org/10.1504/IJMPT.2001.001272]
-
I. Rychlik, “Simulation of Load Sequences from Rainflow Matrices: Markov Method,” International Journal of Fatigue, Vol.18, No.7, pp.429-438, 1996.
[https://doi.org/10.1016/0142-1123(96)80001-Z]
-
J. Klemenc and M. Fajdiga, “Prediction of Loading Spectra under Diverse Operating Conditions by a Localised Basis Function Neural Network,” International Journal of Fatigue, Vol.27, No.5, pp.555-568, 2005.
[https://doi.org/10.1016/j.ijfatigue.2004.09.005]
-
M. A. Miner, “Cumulative Damage in Fatigue,” Journal of Applied Mechanics, Vol.12, No.3, pp.A159-A164, 1945.
[https://doi.org/10.1115/1.4009458]