오차 상태 칼만 필터 기반 강건한 고속 라이다 위치 추정 시스템
Copyright Ⓒ 2025 KSAE / 230-08
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Localization is crucial in autonomous driving to estimate the vehicle’s position, which is essential in ensuring safe interaction with obstacles, vehicles, and pedestrians, along with effective decision-making and path planning. Generally, localization relies on cameras and LiDAR, but our method focuses on LiDAR due to its robustness to lighting changes compared to cameras. Traditional LiDAR-based localization involves matching scans with prior maps that were created by using GNSS, IMU, and LiDAR to ensure accurate positioning in diverse environments. However, these methods can experience delays in updating vehicle status due to the low output rate of LiDAR in high-speed driving scenarios. To resolve this, we proposed dynamically updating maps around the vehicle, optimizing CPU thread adjustment, and using IMU with an Error-State Kalman filter to estimate position at high output rates while reducing computation. The effectiveness of the proposed method was verified through experiments at Chungbuk National University’s Ochang C-track, demonstrating its robust and high-precision performance.
Keywords:
Error State Kalman Filter, Localization, LiDAR, IMU, SLAM키워드:
오차 상태 칼만 필터, 위치 추정, 라이다, 관성 측정 장치, 동시적 위치 추정 및 지도 작성1. 서 론
자율주행 기술에서 차량의 위치를 파악하는 로컬라이제이션(이하 측위)는 환경 인식이나 경로나 판단 계획을 수행하는 데 필수적이다.1) 위치 추정의 정확도와 성능을 높이기 위해서는 주행 환경에 대한 사전 지도가 필요하다.2) 일반적인 측위 방법으로는 휠 엔코더(Wheel encoder), 라이다(LiDAR, Light Detection and Ranging), 카메라, GNSS (Global Navigation Satellite System), 관성 측정 장치(IMU, Inertial Measurement Unit) 등의 센서를 사용하여 데드 레커닝(Dead reckoning),3) 삼각 측량, 스캔 매칭(정합), 이미지 매칭 등이 있고, 비교적 정확한 성능을 내기 위해 주행할 환경을 SLAM(Simultaneous Localization and Mapping, 동시적 위치 추정 및 지도 작성) 알고리즘을 이용하여 사전에 지도 작성을 하고, 지도를 기반으로 하는 측위 방법이 많이 사용된다.4) 하지만 어떠한 센서를 이용하는가에 따라서도 위치 추정의 성능이 달라지게 된다. 카메라의 경우 앞서 언급하였던 이미지 매칭 방법을 주로 사용하는데, 이는 영상 데이터로부터 고유한 패턴을 가진 엣지, 코너 등과 같은 특징점을 추출하고 카메라가 이동함에 따라 얻는 여러 시점들의 특징점을 디스크립터(Descriptor)를 이용하여 유사도가 강한 특징점끼리 매칭하여 위치를 추정하는 방법이다. 특징점은 조도 변화에 따라 추출되는 지점이 달라질 수 있기 때문에 일관적인 측위 성능을 보장하기 어렵다는 단점이 있고, 1개의 카메라만 사용하는 경우 연산량은 가벼우나 정확한 거리를 알 수 없어 스케일 추정을 해야 하는 문제가 있다.5) 2개의 카메라를 사용하는 스테레오 카메라의 경우 두 렌즈 간의 기하학적 차이를 이용하여 깊이를 추정하기 때문에 카메라 간 물리적인 거리에 제약이 따르고, 정확한 내부 및 외부 파라미터의 왜곡 보정이 필요하며, 실시간성을 보장하기 위해 스테레오 이미지 처리에 대한 연산량을 최소화시켜야 한다. 이에 반해 라이다의 경우 펄스 레이저의 반사를 이용하여 주변 환경의 거리를 정확하게 알아낼 수 있기 때문에 전처리 과정 없이 물체의 기하학적인 구조를 잘 알아낼 수 있고, 조도 변화에 강건하여 측위 성능이 카메라에 비해 일관적인 경향이 있다.
라이다를 이용한 사전 지도 기반 측위는 과거에 작성한 지도와 차량에 부착되어 있는 센서 간의 정합 방법으로 이루어지게 된다. 정합에는 ICP(Iterative Closest Point),6) NDT(Normal Distribution Transformation)7) 등의 방식이 존재하는데, 일반적으로 지도 작성을 수행할 때는 수행 속도는 느리지만 비교적 정확한 ICP 방법을 사용하고, 측위를 수행할 때는 비교적 덜 정확하지만 수행 속도가 빠른 NDT 방법을 사용한다. 라이다만 사용하는 측위도 문제점이 존재하는데, 첫 번째는 시간에 따른 공간 변화로 인해 지도와 현재 환경이 다른 것이다. 구체적인 사례로 계절 변화로 인한 지형 변화, 공사로 인한 지형 변화 등이 있다. 이는 지도 상에서 동일한 위치에 있다고 하더라도 지도-센서 간 정합이 제대로 이루어지지 않아 측위 성능을 저하시킨다. 두 번째는 라이다의 낮은 출력 주기로 인한 고속 주행 상황에서의 성능 저하이다. 라이다의 일반적인 출력 주기는 10-20 hz이고, 정합 알고리즘도 동일한 주기로 처리되므로 시속 100 km 주행을 가정한다면 10 hz 기준으로 2.78 m, 20 hz 기준으로 1.39 m만큼 이동한 후 업데이트가 가능한 수준이다. 본 논문에서는 측위 알고리즘 출력 주기의 단점을 보완하기 위해 CPU의 스레드를 조절하고, 주행 중인 영역 주변만 잘라 사용하여 효율적이고 동작 속도가 빠른 NDT 측위 알고리즘과 고속의 출력주기를 가지며 차량의 자세 정보를 추정할 수 있는 IMU를 오차 상태 칼만 필터를 활용하여 결합하는 방법을 제안한다. 제안한 방법은 도심주행로, 순환주행로를 포함하여 다양한 환경을 보유한 테스트베드인 C-track8)에서 2.6 km 거리에서 평균 시속 20 km로, 4.2 km 거리에서 평균 시속 58 km로 검증하였다. 기존의 NDT 측위 알고리즘이 동작하는 10 hz 정도에 비해 제안하는 알고리즘의 출력 주기가 모든 구간에서 2000 hz 이상으로 빠르게 출력하면서, 주행 궤적의 안전성 또한 확인하였다.
2. 관련 연구
라이다는 과거 대기 관측, 우주 탐사, 항공 지도 제작 등 여러 방면에서 사용되었다. 2000년대 초반까지 라이다의 초기 모델로 간주되는 2차원 레이저 스캐너인 Laser range finder를 이용하여 로봇의 위치를 추정하거나 객체를 추적하는 등 인지 분야에서 주로 연구되었다.9) 2000년대 중반, 미국의 자율주행 대회인 DARPA grand challenge에서 벨로다인 64채널 3차원 라이다가 차량에 장착된 것을 시작으로 현재까지 기업, 학교, 연구 기관 등 다양한 곳에서 활발하게 연구를 수행하고 있는 중이다.
3차원 라이다 제작 기술이 높은 속도로 발전함에 따라 고해상도의 3차원 포인트 클라우드를 획득할 수 있게 되어 높은 정확도로 주변 환경의 구조를 파악하는 것이 가능하게 되었다. 자율주행 차량이 주변 환경을 파악하는 방법에는 카메라를 이용한 방법(PTAM,10) DTAM,11) ORB-SLAM12-14) 등)과 라이다를 이용한 방법(LOAM,15) FAST-LIO16,17)) 등 2가지 방법이 있다. 카메라를 이용한 방법의 경우 영상의 코너, 엣지 부분 등 시각적인 특징을 띄는 지점을 이용하여 이동한 거리를 추정하기 때문에 빛이나 색상 변화에 취약하다는 단점이 있어 일관된 측위 성능을 보장하기 어렵다. 반면에 라이다를 이용한 방법의 경우, 센서가 거리를 직접적으로 측정하기 때문에 빛이나 색상 변화에 강건하고, 기하적인 특성 또한 획득할 수 있다는 장점이 있다.
일반적으로 3D 라이다를 이용한 자율주행의 측위는 실시간으로 주변 환경을 파악해야 하므로 NDT 정합 방법을 많이 사용한다. 하지만 NDT 정합 만으로 측위를 수행하는 것은 포인트 클라우드 지도의 품질에 따라 위치 추정의 정확도가 결정되기 때문에, IMU, GNSS, 휠 엔코더(Wheel encoder) 등 여러 센서를 이용하여 지도의 품질이 낮더라도 위치 추정 성능을 올리는 방법들에 대한 연구가 활발히 진행되고 있다. Koide 등18)의 경우 라이다의 움직임이 큰 상황에서 정합이 실패하여 측위 성능이 저하되는 문제를 해결하기 위해 IMU와 라이다의 NDT 정합을 무향 칼만 필터(Unscented kalman filter)를 이용하여 결합한 측위를 제안하였고, Jeong 등19)은 움직이는 차량이 많은 영역이나 GNSS의 음영 구역 같은 특수한 상황에서 측위를 잘 수행하기 위해 딥러닝을 이용하여 동적 객체를 제거한 후 NDT 정합을 수행하는 방법을 제안하였다. Rozenberszki와 Majdik20)은 RANSAC 기반의 기하학적 검증으로 온라인 포인트 클라우드와 지도 간의 잘못된 매칭을 줄이고, ICP 정합을 이용하는 방법을 제안하였다. Chen 등21)은 파티클 필터 방식의 측위인 Monte carlo localization를 3D mesh 지도와 거리 이미지에 이용할 수 있는 방법을 제안하였다. Xue 등22)은 확장 칼만 필터를 이용하여 IMU를 라이다 주행거리계 계산하는 과정에 직접적으로 융합하는 방법을 제안하였다. Ahmed 등23)은 NDT 정합에서 사용되는 P2D(Point-to-Distribution) 공식을 Monte carlo localization에 적용하여 실외 환경에서 강건하게 동작하는 측위 방법을 제안하였다. Romero 등24)은 GPS와 휠 엔코더, 2D 라이다를 이용한 파티클 필터를 통해 2차원에서 강건하지 않은 측위의 단점을 개선하는 방법을 제안하였다. Miguel 등25)은 라이다 지도에 특징이 없는 구간에서 GNSS를 이용하여 파티클 필터 측위를 시도하고, GNSS 수신이 양호하지 않은 구간에서는 라이다와 지도를 이용하여 파티클 필터 측위를 수행하는 방법을 제안하였다. 본 연구는 3차원 라이다 기반의 NDT 측위에 대해 2가지의 주요 기여를 제안한다. 첫째, IMU와 라이다 자세 간 오차 상태 칼만 필터를 결합하여 차량의 자세를 안정적인 출력 주기로 획득함으로써 고속 상황에서도 강건한 위치 추정을 가능하게 한다. 둘째, NDT 측위 과정에서 차량 주변의 일부분만 동적으로 지도를 가져오는 서브맵과 NDT-OMP26) 알고리즘을 활용하여 연산량을 효과적으로 줄여 실시간 처리를 더욱 향상시킨다. 이러한 접근법은 기존의 NDT 정합 방법들이 고속 주행 상황의 빠르게 업데이트되는 상황에서 발생할 수 있는 위치 추정 오류를 줄이고, 다양한 주행 환경에서도 일관된 성능을 보장한다는 점에서 차별성이 있다.
3. Methodology
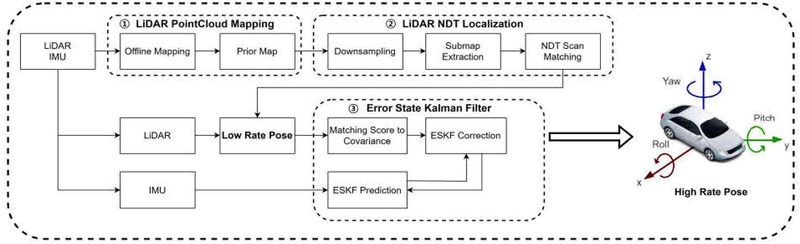
제안하는 알고리즘의 전체 흐름은 Fig. 1의 과정에 따라 처리된다. 먼저 LiDAR PointCloud Mapping(①) 단계에서 먼저 라이다와 IMU를 이용하여 주행할 환경을 사전에 3차원 점군 지도로 작성한다. 작성한 지도는 실외에서 주행하여 주행한 모든 곳의 3차원 점군 데이터를 저장하고 있기 때문에 수백 MB에서 수 GB에 달할 정도로 용량이 매우 크다. 이러한 용량이 큰 지도를 LiDAR NDT Localization(②) 단계에서 포인트 클라우드를 정사각형의 공간으로 묶어 공간 내의 여러 포인트 클라우드들의 중심을 찾아 1개로 바꾸어 용량을 낮추는 다운샘플링 방법을 이용하여 용량을 줄이고, 고속 상황에서 빠르게 움직이는 포인트 클라우드 데이터를 NDT 측위 중 정합 단계에서 빠르고 정확하게 수행하여야 하기 때문에 CPU의 스레드 개수를 조절하여 정합 완료에 필요한 시간을 줄이게 된다. 또한, NDT 측위의 정합할 영역은 Ego-vehicle에서 출력되는 포인트 클라우드와 지도 간 겹치는 일부 영역이기 때문에 이 부분만을 전체 지도에서 추출하여 연산량을 효율적으로 만들고자 서브맵을 추출한다. 이 과정을 거쳐 차량에서 출력되는 최대 10 hz의 낮은 출력 주기를 가진 차량의 자세를 얻고, Error state Kalman filter(③) 단계에서 이를 IMU와 오차 상태 칼만 필터를 통해 융합하여 최종적으로 최대 IMU 출력 주기를 가진 빠른 차량의 자세를 획득한다.
3.1 라이다 지도 작성
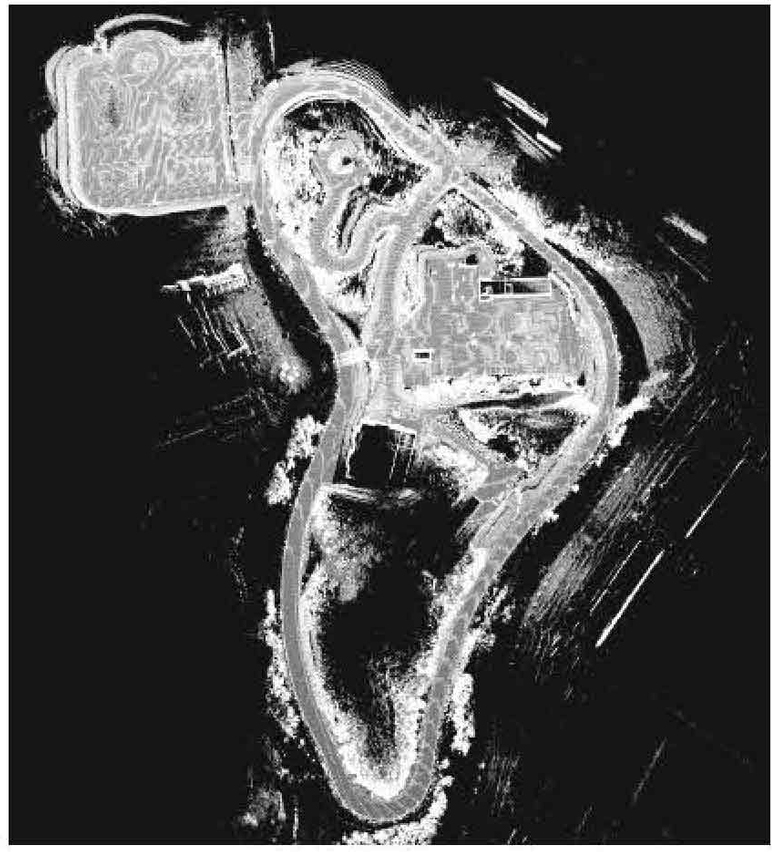
정합 기반의 측위를 수행하기 위해서, 사전에 주행 환경에 대한 지도를 제작하여야 한다. 라이다를 이용하여 지도를 작성하는 방법은 칼만 필터,27) 파티클 필터28) 등을 이용하는 필터 기반의 방법과 노드와 엣지로 구성된 그래프 구조를 사용하는 그래프 기반의 방법이 있다. 필터 기반의 방법은 그래프 기반의 방법에 비해 빠른 속도로 계산할 수 있지만, 로봇의 자세를 추정하는 데 쓰이는 데이터가 한 번 연산이 되고 나면 사용하지 않는 단점이 있다.29) 그래프 기반의 방법은 주행하는 동안 획득한 센서 데이터와 로봇의 자세를 일부 혹은 전체를 저장하여 비선형 최적화 방식을 이용해 처리해야 하기 때문에 필터 기반의 방법보다 계산 속도가 느리지만, 높은 정확도와 일관적인 지도를 작성할 수 있고,30) GNSS, IMU와 같은 부가적인 센서를 쉽게 통합할 수 있다는 장점이 있다. 실외 자율주행에 필요한 지도는 넓은 영역을 높은 정확도로 작성해야 하기 때문에 본 연구에서는 그래프 구조 기반의 SLAM 알고리즘인 hdl-graph-slam18)을 이용하여 Fig. 2와 같이 제작하였다. 이 지도는 충북 오창 C-track에서 IMU, GNSS, LiDAR 센서를 장착한 차량이 모든 구역을 시속 10 km 이하의 속도로 천천히 주행하며 취득한 데이터를 이용하여 생성되었다. Fig. 2는 이러한 과정을 통해 얻어진 2,995,614개의 3차원 점군 데이터를 보여준다. 이 지도를 원본 그대로 사용하게 되면, 용량이 매우 크기 때문에 NDT 정합을 수행하며 위치를 추정하는 과정에서 연산 부하가 생겨 속도가 저하되고, 정확한 위치를 추정하지 못할 수 있다. 따라서, 앞서 언급한 다운샘플링 방법을 이용하여 지도의 용량을 줄였다. 본 연구에서는 반복 실험을 통하여 40 cm 간격으로 다운샘플링을 수행하였다. 다운샘플링이 완료된 지도는 라이다 정합의 기준 점으로 사용된다.
3.2 매칭 점수의 공분산 변환
기존의 NDT 정합은 Point Cloud Library(PCL)31)에서 단일 스레드로 동작하게 설계되어 라이다의 채널 수가 많아질수록, 정합에 사용되는 점군의 개수가 많아질수록 성능과 알고리즘 수행 속도가 현저히 저하되는 문제가 발생한다. 본 연구에서는 이러한 문제를 해결하고, 고속 주행 환경에서도 지연이 없고 최대한 연산이 적은 NDT 정합을 수행하고자 기존 PCL 기반의 정합에 단일 스레드를 이용하는 부분에 NDT 정합에 스레드 개수를 사용자가 지정하여 수행할 수 있게 설계된 NDT-OMP 알고리즘으로 변경하여 사용하였다. 본 연구에서는 실험에 사용된 컴퓨터의 사양을 고려한 반복 실험을 통해 얻은 값인 4개의 스레드를 사용하도록 설정하였다. NDT-OMP를 이용한 지도-차량의 포인트 클라우드 데이터 간 정합의 결과로 매칭 점수가 출력되는데, 이는 정합의 일치하는 정도에 대한 추정 값을 의미하고, 크면 클수록 일치 정도가 높다고 볼 수 있다. 그러나 오차 상태 칼만 필터와 결합하기 위해서는 이러한 점수가 아닌 공분산을 구해야 하므로 매칭 점수를 대략적인 공분산으로 변환하는 과정이 필요하다. 식은 아래와 같다.
| (1) |
| (2) |
| (3) |
식 (1)과 같이 지수 함수를 이용하여 NDT 정합의 결과 값인 매칭 점수가 작을 때는 Scaled matching score 또한 작게 출력하고, 매칭 점수가 클 때는 매우 큰 값으로 출력되게 하였다. 식 (2)에서는 k 값에 Log 함수를 추가하여 수치적으로 원하는 최소 공분산과 Scaled matching score의 비율을 기반으로 계산하였다. 이를 통해 매칭 점수와 공분산의 관계를 반비례적으로 정의할 수 있다. 마지막으로 식 (3)을 통해 k 값과 최소 매칭 점수를 이용하여 매칭 점수가 낮을 때는 NDT 정합의 품질이 낮다고 볼 수 있어 큰 값의 공분산을, 매칭 점수가 높을 때는 매우 낮은 값의 공분산을 획득할 수 있다. 여기서 사용자가 설정할 수 있는 파라미터는 Maximum matching score, Minimum covariance, Minimum matching score이 있고, 반복 실험을 통해 최적의 값을 도출하여 각각 9.2, 0.005, 3.0으로 설정하였다. 이러한 과정을 거쳐 계산된 CovNDT는 최종적으로 오차 상태 칼만 필터의 보정 단계에 사용되어 위치 추정의 정확성을 높이며, 최종적으로 시스템의 출력 결과에 반영된다.
3.3 서브맵 추출
용량이 큰 점군 지도를 원본 상태로 불러오게 되면 불필요한 컴퓨터 자원 소모와 측위 알고리즘의 지연이 발생할 수 있다. 이를 방지하기 위해 PCL의 Cropbox 필터를 이용하여 NDT 측위 알고리즘이 사용해야 할 지도의 크기를 줄임으로써 연산량을 최소화하였다. 제안하는 알고리즘은 처음에 원본 지도를 받아온 후, 차량이 이동하며 측위를 시작할 때 서브맵을 추출하여 업데이트한다. 차량이 일정 거리 이상 움직였을 때 새로운 서브맵을 불러오는 방식으로 지도를 관리하며, 서브맵의 범위는 사용하는 라이다의 특성에 맞게 설정할 수 있다. 본 연구에서는 사용한 라이다의 최대 거리인 120 m와 주변 지형지물을 고려하여 차량 주변 70 m 영역의 지도만 불러오고, 차량이 50 m 이동하였을 때 새로운 서브맵을 불러오게 하였다. 초기 상태에서 차량의 좌표를 알 수 없는 경우에는 임의로 지정해 주었다.
3.4 오차 상태 칼만 필터
오차 상태 칼만 필터32)는 상태의 평균 및 분산을 추정하는 확장 칼만 필터의 방법과 다르게 오차 상태의 평균과 분산을 추정하는 방법이다. 일반 상태 대신 오차 상태를 사용했을 때의 장점은 방향의 오차 상태가 최소한의 파라미터를 사용해서 표현할 수 있어 특이점(Singularity)의 발생을 막을 수 있고, 오차 상태의 값이 작기 때문에 미분 연산을 빠르게 할 수 있다. 이러한 특징으로 인해 자율주행 측위에 적절한 방법으로 평가받고 있다. 일반적으로 오차 상태 칼만필터는 누적 오차가 쌓이는 단점이 있지만 출력 주기가 매우 빠른 IMU를 예측 단계로 사용하고, GNSS, 카메라, 라이다와 같은 센서를 이용하여 보정 단계를 수행한다. 본 연구에서 예측 단계는 IMU를 사용하고, 보정 단계에서 라이다 측위의 출력 값을 사용하는 오차 상태 칼만 필터 시스템을 구성하였다. 또한 전체 시스템은 이산 시간을 따른다고 가정하고, ENU(East, North, Up) 좌표계를 사용하였다.
True 상태는 노이즈가 반영되어 있는 실제 환경의 상태이고, Nominal 상태와 Error 상태의 조합으로 식 (4)와 같이 표현할 수 있다.
| (4) |
여기서 xt는 True state를, x는 Nominal state를, δx는 Error state를 의미한다.
True state의 가속도 at와 wt는 IMU 센서를 측정하여 얻은 가속도 am과 각속도 wm으로부터 구할 수 있고, 식 (5-6)과 같다.
| (5) |
| (6) |
abt와 wbt는 각각 가속도 바이어스, 각속도 바이어스이고, IMU의 센서 측정은 로컬 좌표계를 사용하고 바이어스와 노이즈의 영향을 받는다. 위 식을 이용하여 True 상태 방정식을 다시 정리하면 식 (7-12)와 같다.
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
식 (7-12)는 IMU 측정 값이 추가된 True 상태의 운동 방정식이고, 위치 p, 속도 v, 쿼터니언 q, 가속도 바이어스 ab, 각속도 바이어스 wb, 중력 가속도 q 등 6개의 값을 고려한다. 오차 상태 칼만 필터를 통해 얻고자 하는 값은 오차 상태 방정식이다.
Nominal 상태 방정식은 노이즈나 섭동이 없는 상태를 모델링 한 것으로 각 값을 식으로 나타내면 식 (13-18)과 같다.
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
3.4.5 보정 단계
IMU 센서는 앞서 언급한대로 예측을 수행하는 단계에 사용되고, 보정 단계에서는 LiDAR, Camera, GNSS와 같은 센서의 관측을 통해 IMU의 바이어스 오차를 업데이트 함으로써 현재 오류 상태를 추정할 수 있다. 센서의 관측 방정식은 식 (33)과 같다.
| (33) |
함수 h( )는 True 상태의 비선형 관측 함수이고, v는 평균이 0이고 공분산이 V인 정규분포를 따르는 관측 노이즈이다. 오차 상태를 추정하기 위한 식은 식 (34-36)과 같다.
| (34) |
| (35) |
| (36) |
위 식에서 H는 함수 h( )의 오차 상태에 대한 야코비 행렬을 의미한다.
3.4.6 오차 상태 칼만 필터를 활용한 라이다-관성 측위
본 연구에서 오차 상태는 위치, 속도, 방향, 가속도 바이어스, 각속도 바이어스로 각각 3차원 씩, 총 15차원을 가진다. 중력 가속도는 ENU 좌표계에서 Z축 음의 방향으로 작용하여 상수로 설정하였다.
| (37) |
예측 단계에서는 IMU를 이용하여 노이즈가 없는 상태인 Nominal 상태를 예측하고, Nominal 상태와 True 상태 간의 차이를 나타내는 오차 상태의 공분산을 예측한다. Nominal 상태 방정식은 식 (38-43)과 같다.
| (38) |
| (39) |
| (40) |
| (41) |
| (42) |
| (43) |
IMU의 운동학은 식 (44-45), 회전 오차는 식 (46)과 같다.
| (44) |
| (45) |
| (46) |
여기서 Ri는 IMU 센서의 회전 행렬, wm는 각속도 측정값, bg는 각속도의 바이어스, ng는 각속도의 노이즈를 의미한다. 다음은 오차 상태에 대한 운동학이다.
| (47) |
| (48) |
위 식을 오일러 각과 통합하여 식을 다시 정리하면,
| (49) |
| (50) |
이고, 이를 행렬 형태로 정리하여 Fx와 Fi를 얻었다.
| (51) |
이 과정을 통해 최종적으로 IMU를 통한 오차 공분산의 예측 단계를 수행하고, 예측된 오차 공분산은 보정 단계의 입력 값으로 들어가 라이다로 취득한 자세 값을 활용해 최종적으로 업데이트 된다. 본 연구에서 예측 단계에 필요한 가속도 및 각속도 관측 값의 노이즈는 각각 0.01, 0.0001로 설정하였고, 가속도 및 각속도의 바이어스 노이즈는 0.000001로 설정하였다.
보정 단계에서는 예측된 IMU의 상태와 라이다로 취득한 자세 값을 이용하여 IMU의 오차 상태를 보정한다. 이 단계에서는 NDT 정합을 통해 획득한 라이다의 3차원 x, y, z 좌표와, 매칭 점수의 공분산 변환을 통해 얻은 값을 식 (34-36)의 계산을 이용하여 수행하였다. 만약 라이다 매칭 점수가 높은 경우, COVNDT값을 그대로 사용하고, 낮은 경우는 정합의 품질이 좋지 않다고 판단하여 공분산 값을 매우 큰 값으로 설정하였다. 본 연구에서는 이 값을 100으로 설정하였다.
4. 실험 및 결과
4.1 실험 환경 구성
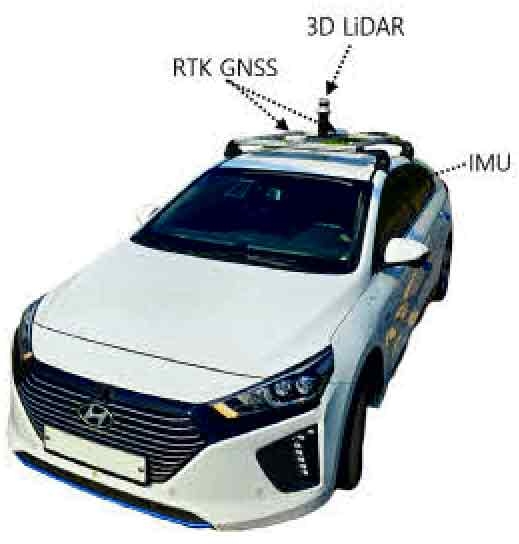
실험에 사용한 차량은 Fig. 3과 같이 아이오닉 PHEV이고, 센서는 Ouster OS-1 32ch 라이다, Microstrain 3DM-GV7-AHRS를 사용하였다. PC는 Intel Xeon E-2176G CPU, RAM 32GB, RTX3080 GPU 제품이 탑재된 Neousys Nuvo-8208GC를 사용하였다. 또한 실험 평가를 위해 Ground Truth를 측정할 수 있는 Novatel Pwrpak 7D RTK GNSS를 사용하였다.
라이다 기반의 측위 성능 실험 평가는 직선도로만 존재하는 단순한 도로보다 직선과 곡선 도로가 모두 있고, 차량이 주행하는 실제 도로 환경과 유사한 다양한 환경에서 실험하는 것이 적절하므로 교차로, 보행자 도로 및 순환 구역 등 실제 도로와 유사하면서, 다양하고 복잡한 환경이 모사된 충북 자율주행 테스트베드인 C-track 내에서 실험하였다. 또한 저속과 고속 환경에서 측위 알고리즘은 모두 강건하게 동작함을 확인하기 위해 평균 시속 20 km로 2.6 km를 주행한 저속 주행 시나리오와, 평균 시속 58 km로 4.2 km를 주행한 고속 주행 시나리오에서 검증을 진행하였다. 저속 주행 시나리오는 Fig. 4와 같이 빨간 원에서 시작하여 반시계 방향으로 주행하여 빨간 원으로 다시 돌아오는 경로로 주행하고, 고속 주행 시나리오는 Fig. 4와 같이 빨간 원에서 시작하여 반시계 방향으로 3바퀴 주행하여 실험하였다.
실험 평가로는 제안하는 알고리즘과 NDT 정합만 이용한 방법(NDT localization), NDT 정합과 무향 칼만 필터(Unscented Kalman Filter)를 결합한 HDL localization18) 방법의 궤적을 RTK GNSS로 측정한 Ground Truth와 비교하고, 알고리즘 동작 주기를 비교하였다. 각 알고리즘 별로 공통 파라미터는 지도 및 포인트 클라우드의 복셀은 0.5 m, 정합 반복 횟수는 35회, NDT voxel 크기는 x, y, z 축으로 각각 3.0 m, 스텝 사이즈 0.1로 지정하였다.
4.2 실험 결과
Fig. 5는 평균 시속 20 kph로 2.6 km를 주행한 결과를 Ground truth와 비교한 것이다. 저속 환경에서는 세 알고리즘 모두 Ground truth의 궤적과 비교했을 때, 이탈하지 않고 잘 추정한 것을 확인할 수 있다. 하지만 NDT localization의 경우 Fig. 6의 (b)와 같이 일부 회전 구간에서 x축으로 최대 2 m, y축으로 최대 4 m가 넘는 큰 오차를 보였다. 또한 (a)와 (b)는 차량 자세가 업데이트 되는 간격이 있고, 제안하는 알고리즘은 빠르게 업데이트 되므로 간격이 없는 것을 확인할 수 있다. Fig. 7은 완만한 회전 구간에서의 궤적을 확대한 그림이다. HDL localization과 제안하는 알고리즘은 Ground truth와 일치한 궤적을 보이며 주행을 하였지만, NDT localization의 경우 일부 지점에서 약 50 cm 이상의 오차가 발생한 것을 확인할 수 있다.
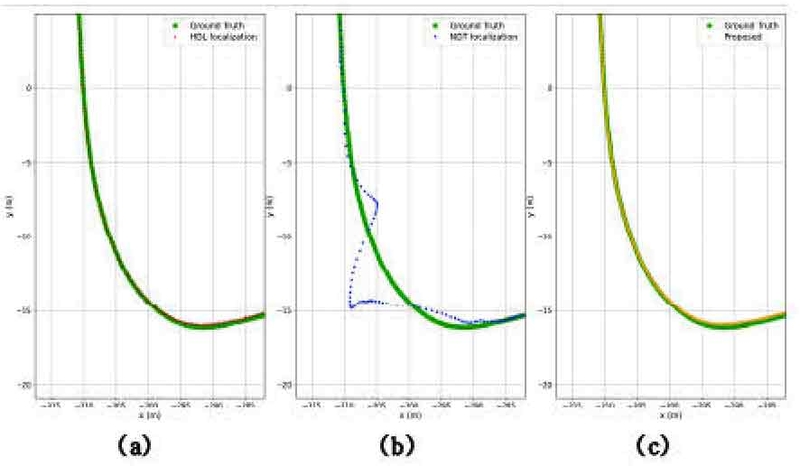
Zoomed-in view of the rotation section from Fig. 6. (a) HDL localization (b) NDT localization (c) Proposed
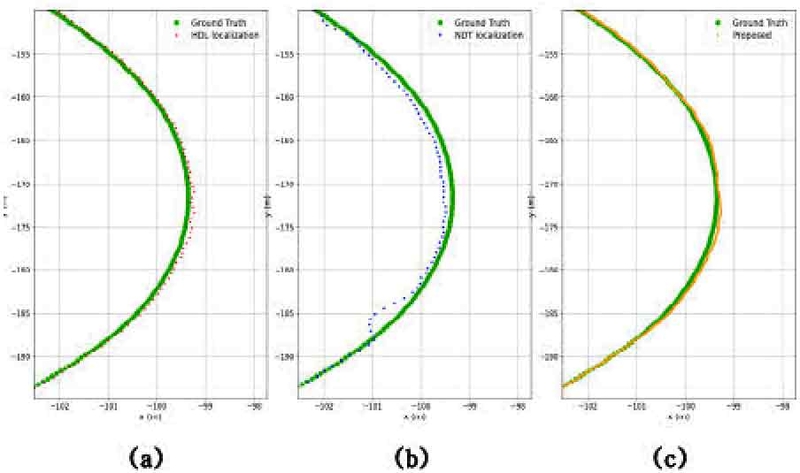
Zoomed-in view of the rotation section from Fig. 5. (a) HDL localization (b) NDT localization (c) Proposed
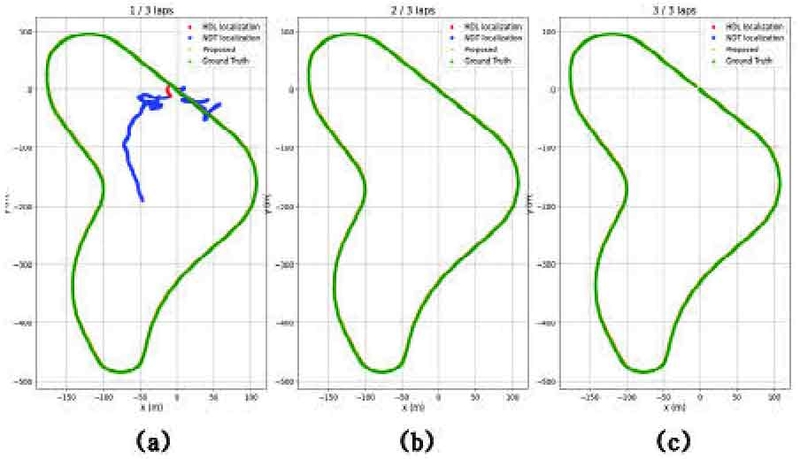
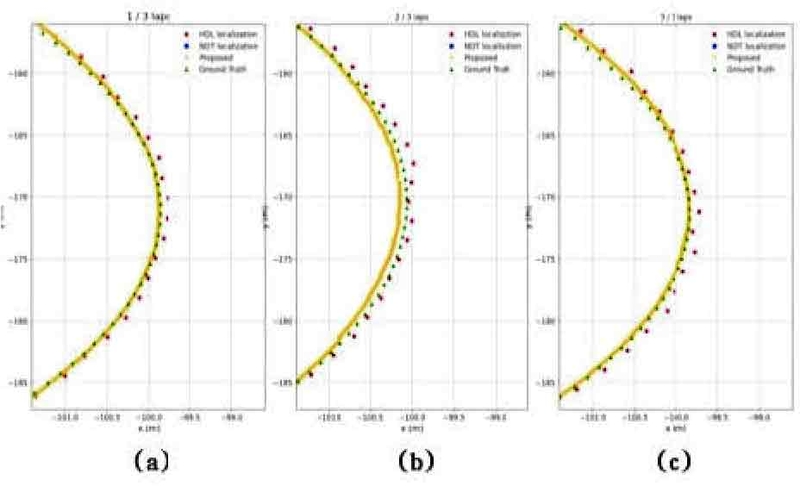
Fig. 8은 평균 시속 58 kph로 동일한 구역을 3바퀴로 총 4.2 km를 주행한 결과를 바퀴 수에 따라 Ground truth와 비교한 것이다. 시작하는 지점에서 NDT localization의 경우 초기 위치를 임의로 주었음에도 불구하고 정합 과정에서 수렴하지 못하여 위치 추정이 실패한 모습과 HDL localization은 초기 위치 정합이 수렴하는 시간이 소요되어 시작 부분에서 Ground truth와 궤적의 차이가 있는 것을 Fig. 8의 (a)를 통해 확인할 수 있다. 또한 2바퀴부터 3바퀴를 주행하는 동안 HDL localization과 제안하는 알고리즘은 모든 구간에서 Ground Truth의 궤적과 유사한 결과를 Fig. 8의 (b), (c)를 통해 보여주었다. Fig. 9는 Fig. 8의 회전 구간 중 일부를 확대한 것이다. HDL localization과 제안하는 알고리즘 모두 회전 구간에서도 Ground truth 궤적과 유사하게 추종하는 모습을 보이지만, 첫 번째 바퀴와 마지막 바퀴를 주행한 결과인 Fig. 9의 (a)와 (c)에서 제안하는 알고리즘이 더 강건하게 추종하는 모습을 확인할 수 있다.
Table 1은 세 알고리즘의 저속 및 고속 주행 시나리오에서의 평균 동작 주기를 나타낸 표이다. 제안하는 알고리즘은 IMU의 각각 1,000 hz로 동작하여 획득한 가속도와 각속도 데이터를 오차 상태 칼만 필터의 예측 단계에서 사용하고, 10 hz로 동작하는 라이다 NDT 정합의 결과를 자세 보정으로 사용함으로써 2,000 hz가 넘는 동작 주기를 확인할 수 있었다.
Table 2는 세 알고리즘의 저속 및 고속 주행 시나리오의 검증을 위한 평가지표로써 ATE(Absolute Trajectory Error)의 RMSE(Root Mean Square Error)를 이용하여 측위 오차의 정도를 나타낸 표이다. 고속 주행 시나리오는 3바퀴의 평균 오차를 나타내었고, ATE의 RMSE 값을 구하는 방법은 식 (52)와 같다.
| (52) |
식 (52)에서 Piest는 세 알고리즘이 각각 추정한 위치, Pigt는 Ground truth의 위치를 의미한다. 이 때 두 위치의 시점은 가장 가까운 시점의 데이터를 사용하였다.
저속 주행 시나리오에서는 제안하는 알고리즘이 다른 두 알고리즘에 비해 오차가 10 cm 정도 낮았고, 고속 주행 시나리오에서 HDL localization의 경우 약 49 cm, NDT localization의 경우 발산하였고, 제안하는 알고리즘은 다른 두 알고리즘에 비해 3바퀴 오차가 약 16 cm 정도로 강건한 모습을 보여주어 저속 및 고속 주행 상황에서도 속도와 안정성을 모두 보장하는 것을 확인하였다.
5. 결 론
본 논문은 기존의 라이다 기반 측위의 낮은 출력 주기로 인한 고속 상황에서 성능이 저하되는 문제를 해결하기 위해 라이다 측위를 개선하고, IMU와 오차 상태 칼만 필터를 활용하는 방법을 제안했다. 라이다 측위의 경우 용량이 큰 3차원 점군 지도를 차량 주변으로 범위를 한정하고, C/C++ 개발 환경에서 공유 메모리 다중 처리 프로그래밍을 지원하는 API인 OpenMP를 활용하여 다중 스레드 접근 방식을 이용하는 NDT-OMP 알고리즘을 이용하였다. 그 결과 기존 NDT 알고리즘과 정확도는 동일하고 속도는 최대 5배 이상 빠른 것을 검증하였고, 또한 IMU와 결합하기 위해 라이다 측위를 수행한 결과로 출력되는 매칭 점수를 공분산으로 변환하여 라이다 기반 측위가 제대로 수행되지 않을 때 IMU의 예측되는 값으로만 측위가 수행되기 때문에 기존 라이다 측위의 단점을 보완하였다.
하지만, 라이다 지도와 실제 주행 환경이 계절 변화, 공사 등의 이유로 차이가 심하게 날 때, IMU에서 출력되는 자세 값을 이용한 이동 추정만으로 측위를 수행 중이지만 적분 오차와 센서 노이즈로 인하여 강건한 측위를 수행할 수 없는 문제가 있다. 이러한 문제를 해결하기 위하여 GNSS, 카메라 등의 센서를 추가하여 라이다 지도와 실제 환경의 변화가 심할 때 더욱 강건하게 측위를 수행할 수 있는 연구를 진행할 계획이다.
Nomenclature
| p : | position, (x, y, z) |
| v : | velocity, m/s |
| Φ : | orientation, (roll, pitch, yaw) |
| am : | measured acceleration, m/s2 |
| wm : | measured gyroscope, rad/s |
| ab : | bias of acceleration, m/s2 |
| wb : | bias of gyroscope, rad/s |
| g : | gravity vector |
| R : | rotation matrix |
Subscripts
| Cov : | Covariance |
| δ : | error state |
| Fx : | Jacobians of error |
| Fi : | Jacobians of perturbation vector |
| Qi : | covariances matrix of perturbation impulses |
| ⊗ : | Kronecker product |
Acknowledgments
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2022R1A5A8026986).
이 연구는 2021년도 산업통상자원부 및 한국산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20014121).
References
-
G. Bresson, Z. Alsayed, L. Yu and S. Glaser, “Simultaneous Localization and Mapping: A Survey of Current Trends in Autonomous Driving,” IEEE Transactions on Intelligent Vehicles, Vol.2, No.3, pp.194-220, 2017.
[https://doi.org/10.1109/TIV.2017.2749181]

-
A. Chalvatzaras, I. Pratikakis and A. Amanatiadis, “A Survey on Map-Based Localization Techniques for Autonomous Vehicles,” IEEE Transactions on Intelligent Vehicles, Vol.8, No.2, pp.1574-1596, 2023.
[https://doi.org/10.1109/TIV.2022.3192102]

-
J. Yee, T. Kim and H. Kim, “Vehicle Position Estimation Using Low-Cost RTK Module, Wheelpulse, and IMU Sensor,” Transactions of KSAE, Vol.26, No.3, pp.407-415, 2018.
[https://doi.org/10.7467/KSAE.2018.26.3.407]

-
A. Charroud, K. El Moutaouakil, V. Palade, A. Yahyaouy, U. Onyekpe and E. U. Eyo, “Localization and Mapping for Self-Driving Vehicles: A Survey,” Machines, Vol.12, No.5, Paper No.118, 2024.
[https://doi.org/10.3390/machines12020118]

-
D. Lim and J. Yoo, “Improved Mono-SLAM Algorithm Using Depth Estimation and Segmentation Based on Deep Learning,” Transactions of KSAE, Vol.31, No.8, pp.619-627, 2023.
[https://doi.org/10.7467/KSAE.2023.31.8.619]

-
P. J. Besl and N. D. McKay, “A Method for Registration of 3-D Shapes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.14, No.2, pp.239-256, 1992.
[https://doi.org/10.1109/34.121791]

- M. Magnusson, The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection, Ph. D. Dissertation, Örebro University, Sweden, 2009.
- Smart Car Research Center, C-track, Retrieved from https://cbnuscrc.org, , 2024.
-
S. Thrun, “Probabilistic Robotics,” Communications of the ACM, Vol.45, No.3, pp.52-57, 2002.
[https://doi.org/10.1145/504729.504754]

-
G. Klein and D. Murray, “Parallel Tracking and Mapping for Small AR Workspaces,” 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, pp.225-234, 2007.
[https://doi.org/10.1109/ISMAR.2007.4538852]

-
R. A. Newcombe, S. J. Lovegrove and A. J. Davison, “DTAM: Dense Tracking and Mapping in Real-Time,” International Conference on Computer Vision (ICCV), pp.2320-2327, 2011.
[https://doi.org/10.1109/ICCV.2011.6126513]

-
R. Mur-Artal, J. M. M. Montiel and J. D. Tardós, “ORB-SLAM: A Versatile and Accurate Monocular SLAM System,” IEEE Transactions on Robotics, Vol.31, No.5, pp.1147-1163, 2015.
[https://doi.org/10.1109/TRO.2015.2463671]

-
R. Mur-Artal and J. D. Tardós, “ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras,” IEEE Transactions on Robotics, Vol.33, No.5, pp.1255-1262, 2017.
[https://doi.org/10.1109/TRO.2017.2705103]

-
C. Campos, R. Elvira, J. J. G. Rodríguez, J. M. M. Montiel and J. D. Tardós, “ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial, and Multimap SLAM,” IEEE Transactions on Robotics, Vol.37, No.6, pp.1874-1890, 2021.
[https://doi.org/10.1109/TRO.2021.3075644]

-
J. Zhang and S. Singh, “LOAM: Lidar Odometry and Mapping in Real-Time,” Robotics: Science and Systems, Vol.2, No.9, pp.1-9, 2014.
[https://doi.org/10.15607/RSS.2014.X.007]

-
W. Xu and F. Zhang, “FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter,” IEEE Robotics and Automation Letters, Vol.6, No.2, pp.3317-3324, 2021.
[https://doi.org/10.1109/LRA.2021.3064227]

-
W. Xu, Y. Cai, D. He, J. Lin and F. Zhang, “FAST-LIO2: Fast Direct LiDAR-Inertial Odometry,” IEEE Transactions on Robotics, Vol.38, No.4, pp.2053-2073, 2022.
[https://doi.org/10.1109/TRO.2022.3141876]

-
K. Koide, J. Miura and E. Menegatti, “A Portable Three-Dimensional LIDAR-Based System for Long-Term and Wide Area People Behavior Measurement,” International Journal of Advanced Robotic Systems, Vol.16, No.2, Paper No.172988 1419841532, 2019.
[https://doi.org/10.1177/1729881419841532]

-
S. Jeong, M. Ko and J. Kim, “LiDAR Localization by Removing Moveable Objects,” Electronics, Vol.12, No.22, Paper No.4659, 2023.
[https://doi.org/10.3390/electronics12224659]

-
D. Rozenberszki and A. L. Majdik, “LOL: Lidar-Only Odometry and Localization in 3D Point Cloud Maps,” IEEE International Conference on Robotics and Automation (ICRA), pp.4379-4385, 2020.
[https://doi.org/10.1109/ICRA40945.2020.9197450]

-
X. Chen, I. Vizzo, T. Läbe, J. Behley and C. Stachniss, “Range Image-Based LiDAR Localization for Autonomous Vehicles,” IEEE International Conference on Robotics and Automation (ICRA), pp.5802-5808, 2021.
[https://doi.org/10.1109/ICRA48506.2021.9561335]

-
H. Xue, H. Fu and B. Dai, “IMU-Aided High-Frequency LiDAR Odometry for Autonomous Driving,” Applied Sciences, Vol.9, No.7, Paper No.1506, 2019.
[https://doi.org/10.3390/app9071506]

-
S. Z. Ahmed, V. B. Saputra, S. Verma, K. Zhang and A. H. Adiwahono, “Sparse-3D Lidar Outdoor Map-Based Autonomous Vehicle Localization,” IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp.1614-1619, 2019.
[https://doi.org/10.1109/IROS40897.2019.8967596]

-
A. Rechy Romero, P. V. K. Borges, A. Pfrunder and A. Elfes, “Map-Aware Particle Filter for Localization,” IEEE International Conference on Robotics and Automation (ICRA), pp.2940-2947, 2018.
[https://doi.org/10.1109/ICRA.2018.8460707]

-
M. Á. de Miguel, F. García and J. M. Armingol, “Improved LiDAR Probabilistic Localization for Autonomous Vehicles Using GNSS,” Sensors, Vol.20, No.11, Paper No.3145, 2020.
[https://doi.org/10.3390/s20113145]

- K. Koide, ndt_omp, Retrieved from https://github.com/koide3/ndt_omp, , 2024.
-
T. Bailey, J. Nieto, J. Guivant, M. Stevens and E. Nebot, “Consistency of the EKF-SLAM Algorithm,” IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp.3562-3568, 2006.
[https://doi.org/10.1109/IROS.2006.281644]

-
G. Grisetti, C. Stachniss and W. Burgard, “Improved Techniques for Grid Mapping with Rao-Blackwellized Particle Filters,” IEEE Transactions on Robotics, Vol.23, No.1, pp.34-46, 2007.
[https://doi.org/10.1109/TRO.2006.889486]

-
T. Takleh Omar Takleh, N. Abu Bakar, S. Abdul Rahman, R. Hamzah and Z. Abd Aziz, “A Brief Survey on SLAM Methods in Autonomous Vehicle,” International Journal of Engineering & Technology, Vol.7, No.4.27, pp.38-43, 2018.
[https://doi.org/10.14419/ijet.v7i4.27.22477]

-
S. Thrun and M. Montemerlo, “The Graph SLAM Algorithm with Applications to Large-Scale Mapping of Urban Structures,” The International Journal of Robotics Research (IJRR), Vol.25, Nos.5-6, pp.403-429, 2006.
[https://doi.org/10.1177/0278364906065387]

-
R. B. Rusu and S. Cousins, “3D Is Here: Point Cloud Library (PCL),” IEEE International Conference on Robotics and Automation (ICRA), pp.1-4, 2011.
[https://doi.org/10.1109/ICRA.2011.5980567]

- J. Solà, “Quaternion Kinematics for the Error-State Kalman Filter,” arXiv preprint arXiv:1711.02508, , 2017.