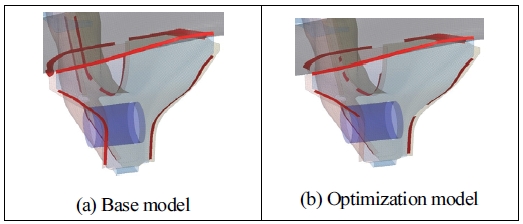
파라미터 최적화를 이용한 차량용 서브프레임 최적 설계

1. 서 론

오늘날 차량 개발 단계에서는 차량의 안정성 확보를 위한 성능 향상뿐만 아니라 차량 중량을 줄이기 위한 경량화 연구가 많이 이루어지고 있다.¹⁾ 그중 차량의 서스펜션 부품은 차량의 안정성 확보에 크게 중요한 부품으로 성능적인 부분뿐만 아니라 차량 경량화 측면에서도 중요하다. 이러한 차량의 서스펜션 부품은 차체에 연결되어 차체의 하중을 지지 및 노면의 타이어에서 들어오는 하중을 흡수하는 중요한 차량 부품임으로 이러한 서스펜션 부품을 평가하기 위하여 롤강성 뿐만 아니라 노면에서 입력된 진동에 대한 동강성 평가도 같이 이루어지고 있다.

그중 서브 프레임의 경우, 이러한 성능 평가를 만족시키기 위하여 용접 공정을 이용하여 제품 간의 파트들을 연결하고 있지만, 이러한 용접 공정이 제품의 강성과는 관련 없이 불필요한 위치까지 이루어짐으로써 제품 제작에 있어서 더 큰 비용을 발생시키게 된다.

본 논문에서는 유한요소모델에 대하여 옵티스트럭트(Optistruct) 및 하이퍼스터디(HyperStudy)를 이용하여 파라미터 최적화를 수행함으로써 초기 모델의 제품 성능을 유지함과 동시에 제품에 불필요한 용접부 구간 및 모델의 중량이 줄어든 개선된 모델을 최적화 해석을 통하여 확인하고자 하였다.

2. 제품 성능 평가

서브 프레임의 성능을 평가하는 항목으로는, 차체 연결 포인트에 특정 하중을 입력하여 평가하는 강도 해석과 고유 진동수 해석, 그리고 서브 프레임의 정강성과 동강성을 확인하기 위한 롤 강성 해석 및 DPDS 해석 등이 대표적이다.^2-4) 본 연구에서는 특히 제품 성능 평가에 중요한 부분을 차지하는 롤 강성 및 DPDS 해석을 기반으로 최적화 작업을 수행하였다.

2.1 롤 강성 해석

롤 강성 해석은 제품에 비틀림 하중이 가해질 때 변형에 대한 저항을 평가하는 방법이다. 이는 자동차나 항공기 등의 구조물에서 안정성을 평가하는 데 필수적이다. 롤 강성은 차량의 핸들링 성능과 승차감에 큰 영향을 미치며, 고속 주행 시 차량의 비틀림 현상을 최소화하는 데 중요하다. 이러한 비틀림에 대한 롤 강성을 평가하기 위하여 선형 정적 해석의 기준식 (1)을 기반으로 하며, 제품의 교차되는 하드 포인트 지점에 특정 하중 또는 변위를 교차 방향으로 입력하여 평가한다.

$\[ K_r=\frac{F}{x} \]$

(1)

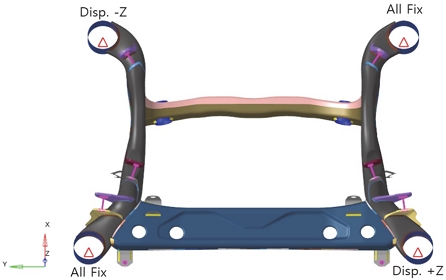
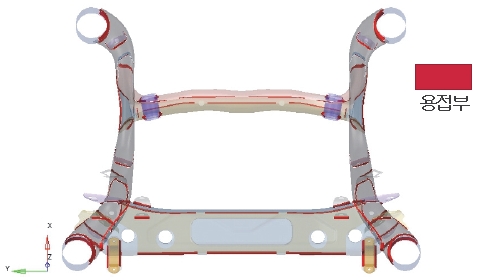
본 연구에서는 서브 프레임의 비틀림에 대한 롤 강성(K_r)을 측정하기 위해, Fig. 1과 같이 서브 프레임의 하드 포인트에 고정(Fix) 조건과 Z 방향 변위(z) 조건을 부여하였다. 이후 해당 방향에 대한 반력(F)을 측정하여 서브 프레임의 비틀림에 대한 강성을 평가하였다.

Fig. 1

Roll stiffness B.C of sub-frame

2.2 DPDS 해석

DPDS 해석은 하드 포인트에서 동하중(Dynamic load)이 특정 주파수 영역 대에서의 가진력으로 작용함에 따른 동특성을 평가하는 방법으로, 이때의 강성을 측정하기 위하여 주파수 응답 해석(Frequency response analysis) 수행 후, 나오는 가속도 커브를 이용하여서 다음의 식 (2)를 바탕으로 구하였다.

$\[ K_d=\frac{4{\pi }^2△f\sum _i{f}_i^2}{A_{DPDS}} \]$

(2)

여기서 K_d는 주어진 주파수 범위 내에서의 동강성을 나타내며, A_DPDS는 DPDS 커브 면적을 의미한다. 이는 주파수 구간(Frequency range)에서의 가진된 방향의 결과 커브를 바탕으로 DPDS 커브의 면적을 측정하여 계산이 이루어진다.

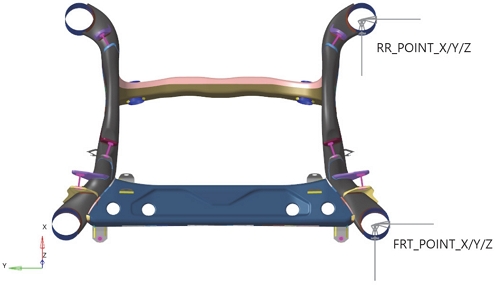
그리하여 본 연구에서 수행하는 서브프레임 모델은 RH와 LH 대칭 모델임으로 Fig. 2처럼 LH 기준으로만 동강성을 평가하였으며, 이때 평가할 주파수 구간은 200 ~ 600 Hz 구간으로 적용하였다. 그리고 Fig. 2에 표현한 FRT와 RR 포인트에 해석 케이스 별로 X/Y/Z 각 방향별로 1 N에 단위하중을 부여하였으며, 하중이 입력되는 하드 포인트 방향을 제외한 나머지 하드 포인트 방향에 고정(Fix) 조건을 적용하고 해석을 수행하였다.

Fig. 2

Dynamic stiffness B.C of sub-frame

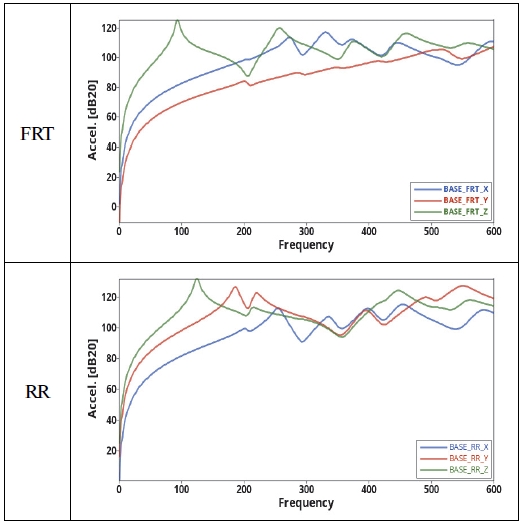
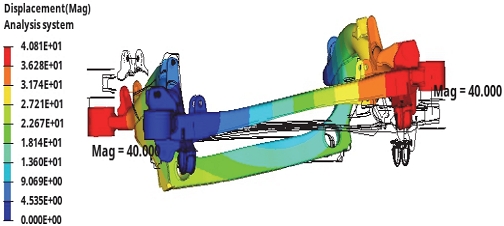
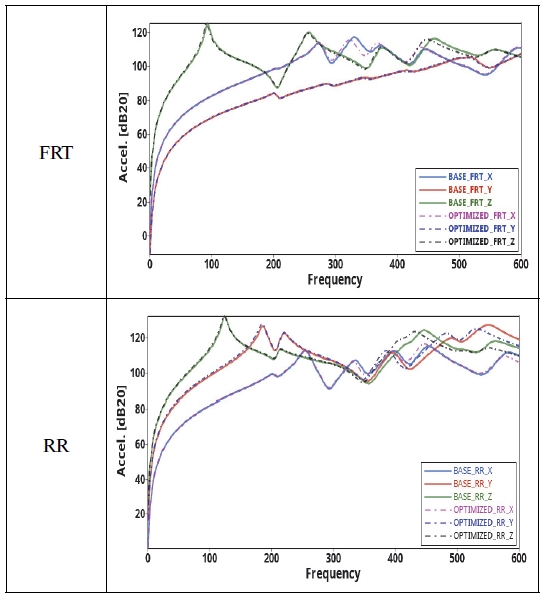
이러한 조건으로 해석을 수행한 기본 모델의 해석 결과는 다음의 Figs. 3, 4에 나타내었다.

Fig. 3

Result curve of dynamic stiffness analysis acceleration

Fig. 4

Result of roll stiffness analysis displacement

동강성은 Fig. 3의 각 방향별로 출력된 커브의 면적을 이용하여 동강성 수치를 측정하였으며, 롤 강성은 Fig. 4에서 하드 포인트에서 측정한 반력과 80 mm의 변위를 이용하여 측정하였으며, 이렇게 측정한 수치는 Table 1에 정리하였다.

Table 1

CAE analysis result of base model

이렇게 해석으로 얻은 서브 프레임의 성능 결과를 기반으로 기존 성능을 유지하면서 모델의 중량을 줄이기 위한 최적화 해석을 수행하였다.

3. 최적화 평가

최적화 해석은 크게 컨셉(Concept) 최적화와 튜닝(Tunning) 최적화로 나눠진다. 컨셉 최적화의 경우 제품 개발 초기 단계에 기존과 달리 제품의 새로운 형상을 확인하고 싶을 때 사용하는 최적화로 위상 최적화(Topology), 비드 최적화(Topography), 프리 사이즈(Free size) 최적화가 이 부분에 해당이 된다. 그리고 튜닝 최적화는 파라미터 최적화(Size), 형상 최적화(Shape)가 이 부분에 해당된다. 본 연구는 기존 제품의 형상을 유지하면서 제품의 중량을 줄이기 위하여 튜닝 최적화 중에 파라미터 최적화 방법으로 진행하였다. 파라미터 최적화 방법은 최적화 변수를 의미하는 CAE 작업에서 입력하게 되는 재료의 성질(Material property), 섹션(Section) 정보 등의 각 항목을 설계 변수(Design variable)로 설정하여 최적화하는 방법이다.⁵⁾ 이러한 파라미터 최적화는 기본 수식인 식 (3)을 바탕으로 수행이 되며, 이때 P는 최적화할 Property를, DV_i인 최적화 설계 변수, DV_i에 대한 가중치를 줄 때의 C_j와 일정한 상수값을 가져갈 때 사용되는 C₀를 정의를 해주면 된다.

3.1 최적화 해석 정의

본 연구에서는 제품의 중량을 줄이기 위하여 서브 프레임 각 파트의 Plate 두께와 용접부를 묘사한 Shell 요소의 각 두께를 설계 변수(Design variable)로 정의하였으며, 이와 관련된 Plate 두께에 대한 설계 변수(Design variable) 항목은 Table 2에 그리고 용접부 구간에 대한 정보는 Fig. 5에 나타내었다.

Table 2

Part Thickness of design variables

Fig. 5

Range of design variable weld

이러한 설계 변수(Design variable)에 대한 제약 조건 범위(Constraints range)는 Table 3에 정의하였으며, 이때 용접부 구간 요소의 경우 최적화 단계에서 정의될 수 있는 기준을 기존 두께와 0에 가까운 0.0001이라는 2가지에 값으로만 정의함으로써 제품에 강성을 유지하는 데 필요한 구간을 찾도록 하였다.

Table 3

Design variable constraints

Table 4는 최적화 수행에 필요한 나머지 최적화 조건을 보여주고 있다.

Table 4

Optimization conditions

이러한 조건을 기반으로 알테어(Altair)의 하이퍼스터디(HyperStudy)를 이용하여 최적화 해석을 수행하였으며, 이때 최적화 방법은 알테어 하이퍼스터디(Altair HyperStudy)에서만 제공하는 GRSM을 사용하였다. 그레이디언트(Gradient)최적화 기법은 초기 설계점 주위에서만 탐색한다는 국소 최적화 한계 및 변수가 많아지면 그레이디언트(Gradient)계산에 부하가 증가한다는 단점을 가지고 있다. 하지만 엑스플로러터리(Exploratory) 기법은 초기 설계점이 아닌 다수의 설계점에서 탐색함으로써 전역 최적화가 가능하며 이에 따른 국소 최적(Local optimum)에 빠질 위험이 없다는 장점이 있다. 하지만, 전역에 대한 설계점을 확인함에 따라 많은 계산이 필요하다는 부분과 설계 변수의 수가 적으면 정밀한 최적화가 어렵다는 단점을 가지고 있다.

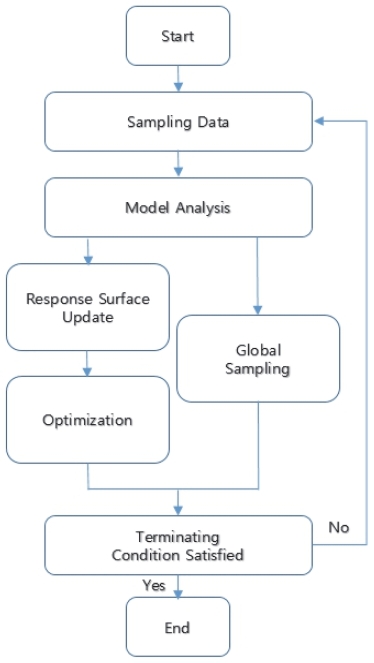
그러나 하이퍼스터디(HyperStudy)에서만 제공하는 엑스플로러터리(Exploratory) 기법의 하나인 Fig. 6의 GRSM은 이러한 단점을 보완한 방법으로 지네틱 알고리듬(Genetic algorithm)과 같은 엑스플로러터리(Exploratory) 기법과는 달리 적은 계산 횟수로도 만족할 만한 최적화 결과를 도출할 수 있다는 장점을 추가로 가지고 있다.^6,7) 따라서 본 연구에서는 이러한 GRSM 방법을 이용하여 1000회에 해석 작업(Solving run)을 실행하였다.

Fig. 6

Process of GRSM

3.2 최적화 해석 수행 결과

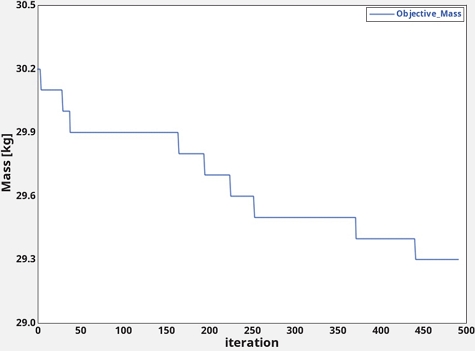
HyperStudy를 이용하여 최적화 해석을 수행한 결과, 초기 샘플링 데이터를 이용하여 생성된 반응 표면을 바탕으로 수행된 최적화 목적 함수인 중량에 대한 Iteration 그래프를 Fig. 7에 나타내었다.

Fig. 7

Optimization iteration of objective

Fig. 7에 그래프와 같이 기존 대비 중량이 Table 5와 같이 약 3 % 감소하였으며, 이렇게 얻은 최적화 모델에 대한 각 파트의 판(Plate) 두께는 Table 6에 나타내었다.

Table 5

Optimization result of total mass

Table 6

Optimization result of plate thickness

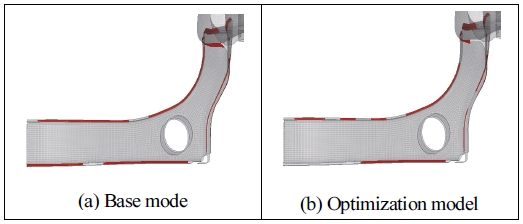
그리고 최적화를 통하여 얻은 용접부 구간에 관한 결과는 Figs. 8, 9와 같다.

Fig. 8

NO2 UPR and LWR connections

Fig. 9

NO2 Reinf and side tube connections

용접부 최적화 구간에 사용된 전체 용접부 요소 개수가 1,616개이며, 최적화 해석 수행 후 용접부 요소 개수가 1,370개로 감소하였다. 서브 프레임 모델의 용접부 요소 1개의 길이가 3 mm라고 가정하였을 때, 4,848 mm에서 4,110 mm로 약 15 % 감소한 결과를 얻을 수 있다.

이렇게 최적화된 모델에 대한 롤 강성 및 동강성 해석 결과, FRT_X 및 FRT_Y에서 약 0.5 % 이내로 강성이 감소하였으나, 나머지 해석 CASE의 경우 동등 또는 성능이 향상된 결과를 얻을 수 있었다. 이를 해석한 결과는 Table 7과 Fig. 10에 나타내었다.

Table 7

Compare CAE Analysis Results

Fig. 10

Compare result curve of dynamic stiffness analysis acceleration

4. 결 론

본 연구에서는 파라미터 최적화를 이용하여 제품 성능을 유지하면서 제품의 중량 및 용접부 구간에 대한 개선이 가능한지 여부를 확인해 보았으며, 이를 통하여 확인한 내용은 다음과 같다.

• 1) 서브 프레임의 중량 감소를 위하여 각 파트의 판재 두께를 설계 변수(Design variable)로 선정하였으며, 또한 제품 성능에 큰 영향을 미치지 않는 용접부 구간을 찾기 위하여 용접부 요소들에 대한 두께도 추가로 설계 변수(Design variable)로 선정하였다. 그리고 이때 용접부 요소의 경우, 기존 두께 및 강성의 영향을 최소화하기 위한 0.001이라는 두 개의 선택 조건을 부여함으로써 최적의 용접부 구간을 확인하였다.
• 2) 최적화 수행 결과, 기존에 서브 프레임의 강성을 유지하면서 중량은 약 3 % 감소하였으며, 용접부 구간 또한 약 15 % 감소한 최적화된 모델을 확인할 수 있었다.
• 3) 본 연구는 CAE만을 이용한 서브 프레임에 대한 검증을 이용하였음으로, 다음에 시험 결과를 동반한 연구 검증이 수행될 필요가 있을 것으로 판단된다.

Acknowledgments

본 논문은 2023년도 인제대학교 학술연구조성비 보조에 의한 것임.

References

• S. G. Kee, J. H. Kim, H. W. Bai and Y. S. Kim, “Load-Path Development Using Topology Optimization for Body Stiffness and Crashworthiness,” Transactions of KSAE, pp.1654-1657, 2012.
• S. Y. Lee, Y. H. Kim and K. S. Lee, “Road Noise Improvement Using Drive Point Dynamic Stiffness (DPDS) Estimation,” Journal of the Korean Society for Noise and Vibration Engineering, pp.612-616, 2007.
• J. H. Park, S. T. Jeon, T. J. Lee, J. D. Kang and M. C. Kang, “Effect on Drive Point Dynamic Stiffness and Lightweight Chassis Component by Using Topology and Topography Optimization,” Journal of the Korean Society of Manufacturing Process Engineers, Vol.17, No.3, pp.141-147, 2018. [https://doi.org/10.14775/ksmpe.2018.17.3.141]
• J. E. Kim, J. H. Kim, C. K. Lee and Y. S. Kim, “A Study of Developing Vehicle Body for Dynamic Stiffness Considering Topology Optimization and Gauge Optimization,” KSAE Spring Conference Proceedings, pp.829-838, 2014.
• H. S. Yun, Research for the Improving Reliability of Pedal Structural Analysis, M. S. Thesis, Inje University, 2020.
• Optimal Design Exploration Using Global Response Surface Method, Altair.
• M. S. Kim, A Study on the Multi-Objective Optimization of Three-Phase Squirrel Cage Induction Motors, Ph.D. Thesis, Hoseo University, 2023.