딥러닝 및 물리 기반 모델을 활용한 차량 경로예측 방법론
Copyright Ⓒ 2024 KSAE / 229-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Various studies have been conducted to develop an autonomous driving system that guarantees the safety of the passengers of an autonomous vehicle. Accurate path prediction is an essential part of improving the autonomous driving system performance to avoid collision and ensure passengers’ safety by determining the risk of collision with nearby vehicles and pedestrians by recognizing various situations. However, it is possible to continue driving with unnecessary and inefficient behaviors due to the inconvenient ride caused by the malfunction of the judgment unit of the autonomous vehicle due to incorrect path prediction and incorrect judgment on the autonomous driving strategy. This study proposes a technique for predicting the path of a vehicle by integrating physical and learning-based models. A deep learning technique using short and long-term memory, a learning-based model that utilizes time series information, predicts the state quantity of the future vehicle based on the past state quantity of the vehicle and calculates the probability for the vehicle’s physical-based model by performing time series classification on CV, CA, CTRV, and CTRA models. The calculated probability for the physical-based model is used as a weight of the trajectory generated by each model later to predict a single path by considering all four physical models.
Keywords:
Autonomous driving system, Trajectory prediction, Deep learning, LSTM, Sequence data, Physics model키워드:
자율주행 시스템, 경로예측, 딥러닝, 장단기 메모리, 시계열 데이터, 물리모델1. 서 론
자율주행 자동차 탑승자의 안전을 보장하는 자율주행 시스템을 개발하기 위하여 다양한 연구들이 진행되고 있다.1,2) 다양한 상황을 인식해 주변 차량 및 보행자와의 충돌 위험도를 판단하여 충돌을 회피하고 탑승자의 안전을 보장하기 위해서 정확한 경로예측은 자율주행 시스템의 성능향상에 필수적으로 고려되어야 할 부분이다. 하지만 잘못된 경로 예측으로 인한 자율주행 차량의 판단부의 오작동으로 인해 불편한 승차감과 자율주행 전략에 대한 잘못된 판단으로 불필요한 거동 및 비효율적인 거동이 발생할 수 있다.
이전부터 차량의 센서 정보를 이용하여 주변 차량의 경로를 예측하는 다양한 방법들이 제시되었고,3-5) 최근에는 딥러닝 네트워크에 HD-Map과 주변차량의 주행데이터를 입력으로 하여 주변차량의 미래 궤적을 예측하는 다양한 연구들이 이뤄지고 있다.6) 하지만, 딥러닝과 같은 영역은 학습 데이터 및 측정 데이터에 대한 의존성이 높기 때문에 학습하지 못한 상황에 대한 예측에 대한 성능은 확보할 수 없으며 차량의 물리적인 특성을 고려하지 않기 때문에 비현실적인 경로로 예측할 가능성이 있다.
차량의 물리적인 특성을 고려하는 대표적인 방법으로는 등속도(Constant Velocity, CV) 모델, 등가속(Constant Acceleration, CA) 모델, 등선회 등속도(Constant Turn Rate Velocity, CTRV) 모델, 등선회 등가속(Constant Turn Rate Acceleration, CTRA) 모델을 사용하여 경로를 예측하는 방법이 있다.7) 차량의 물리모델을 사용할 경우 단기적인 예측에는 예측 정확도가 높지만 장기적인 예측을 진행할 시 차선 변경, 곡선로 및 교차로 진입 등의 예측에 어려움이 존재한다.
최근 경로예측 연구자들은 딥러닝과 물리기반 모델을 함께 사용하여 차량의 물리적인 특성을 고려함과 동시에 기존 딥러닝 모델의 문제점인 비현실적인 경로를 제외함으로 예측성능 확보를 이룰 수 있다.
본 연구에서는 물리기반 모델과 학습기반 모델을 통합하여 차량의 경로를 예측하는 기법을 제안한다. 시계열 정보를 활용하는 학습기반 모델인 장단기 메모리를 통한 딥러닝 기법으로 차량의 과거 상태량을 기반으로 미래의 차량의 상태량을 예측하고 예측된 상태량을 CV 모델, CA 모델, CTRV 모델, CTRA 모델에 대한 시계열 분류를 진행하여 차량의 물리기반 모델에 대한 확률을 산출한다. 이때 산출된 물리기반 모델에 대한 확률은 추후에 각 모델이 생성한 궤적의 가중치로 사용하여 네 가지 물리 모델이 생성한 궤적을 모두 고려해 단일 경로를 예측한다.
2. 관련연구
2.1 경로예측
경로예측은 차량의 센서 정보를 이용하여 복잡한 주변 상황에 대한 미래를 예측하는 기술이다. 정확한 경로 예측은 주변 객체와의 충돌 위험도를 판단하여 충돌을 회피하거나 효율적인 거동을 요구하는 미래의 자율주행 시스템의 성능향상에 필수적으로 고려해야 하는 부분이다. 그렇기에 과거부터 다양한 방법으로 주변 객체의 미래 정보를 예측하는 연구가 이루어져 왔다. 본 절에서는 고전적인 방법인 물리모델을 사용하여 상태방정식을 통해 미래의 궤적을 예측하는 방법부터 딥러닝 네트워크를 사용하여 기존 존재하는 데이터를 기반으로 네트워크를 학습하여 미래 경로를 예측하는 방법, 물리모델과 딥러닝 네트워크 각자를 융합하여 단점을 보완할 수 있는 하이브리드 방법까지 소개한다.
물리 기반 모델은 차량의 물리 상태량을 기반으로 모델링 된다. 차량 경로예측에 대한 모델은 총 4가지로 모델링할 수 있다.
| (1) |
| (2) |
차량의 상태공간벡터 X는 위와 같이 2가지 형태로 나타낼 수 있다. CV모델과 CTRV 모델의 상태공간벡터XCV,CTRV는 차량의 x,y 위치, Heading 방향, 속도 그리고 각속도로 식 (1)과 같이 구성되어 있으며 CA, CTRA 모델의 상태공간 벡터XCA,CTRA는 CV, CTRV 모델의 상태공간백터에서 가속도를 추가하여 식 (2)와 같이 구성한다.
| (3) |
| (4) |
| (5) |
| (6) |
상태공간 방정식을 이용하여 차량의 다음 스텝 상태공간벡터를 계산하려면 천이행렬 F가 필요하게 된다. 식 (3) ~ (6)은 각 모델에 대한 천이행렬이다. 차량의 각속도를 고려하는 선회모델의 경우는 비선형 모델이기에 선형화가 필요하다. CTRV모델과 CTRA 모델은 각각 식 (7), (8)과 식 (9), (10)을 v,a,φ,ω 고려하여 편미분을 진행하는 선형화 작업이 이루어진다.
| (7) |
| (8) |
| (9) |
| (10) |
각 모델을 고려한 예측은 천이행렬과 상태공간벡터의 곱으로 다음 스텝의 상태공간벡터를 구할 수 있다. 하지만, 이렇게 구해진 차량의 미래 궤적은 단일 물리 모델을 사용하기 때문에 복합적인 거동을 예측하는 데에는 한계점이 있다.
최근에는 위와 같은 물리기반 모델의 한계점을 보완하기 위해 딥러닝 네트워크를 이용한 경로예측에 관한 연구들이 진행되고 있다. 김좌헌 등8)과 Ip 등9)은 주변 차량과의 상대거리, 상대속도, Heading 방향 등과 같은 관계정보를 시계열 데이터로 구성하여 주변 차량의 경로를 예측하는 딥러닝 네트워크를 설계하였다. Xin 등10)은 주변차량의 횡방향 상태량을 딥러닝 네트워크를 통해 학습하여 운전자의 의도를 파악하면서 종방향 상태량을 함께 네트워크에 입력하여 주변 차량의 미래 경로를 예측하는 시스템을 제안하였다.
물리 모델의 장기간 예측에 대한 어려움과 학습기반의 딥러닝 모델의 학습 데이터 의존성 및 비현실적 경로 예측 문제점을 보완하기 위하여 물리 모델과 학습 기반 딥러닝 모델의 융합인 하이브리드 모델에 대한 연구 또한 진행되고 있다. Cha 등11)은 차량 경로 예측을 물리 기반 모델과 학습 기반 모델의 장점을 고려하여 칼만 필터 기반 IMM 알고리즘을 이용하여 동역학적 경로를 구성하고, LSTM 기반 딥러닝을 이용하여 미래 경로를 생성 후 시간에 기반한 가중함수를 이용하여 다중 모델 통합 경로 예측 알고리즘을 설계하였다. Bai 등12)은 물리 기반 모델과 차량의 기동을 동적 베이지안 네트워크를 사용하여 추론된 각 기동에 대한 불확실성을 고려하여 예측할 수 있는 모델을 통합하여 다중 모델 궤적 예측(IMMTP) 방법을 제안하였다. Kim 등13)은 이미지를 사용하여 도로 기하학을 고려한 CNN 모델과 물리 모델 및 기동 기반을 불확실성에 따라 결합하여 경로를 예측하는 하이브리드 모델을 제안하였다. 이처럼 물리 모델과 학습 모델의 장점만을 고려하여 주변 차량의 경로를 예측하는 연구가 활발하게 진행되고 있다.
2.2 시계열 데이터 처리 모델
시계열(Time-series data) 데이터는 다른 종류의 데이터들과 다르게 시간 순서에 따라 관측한 데이터를 의미한다. 이러한 데이터는 데이터가 발생한 순서인 과거부터 현재로 이동하는 방향으로 정렬되며 상호 독립적이지 않다. 이러한 데이터를 처리하는 모델에는 여러 가지 종류가 있다.
비학습 모델은 데이터의 내재된 구조를 학습하지 않고 주어진 입력 데이터만을 기반으로 예측을 수행한다. 대표적인 비학습 모델로는 ARIMA(Autoregressive Integrated Moving Average) 나 STL(Seasonal Decomposition of Time Series) 등이 있다.14,15) 이 모델들은 시계열 데이터의 특성을 활용하여 미래 값을 예측하기에 데이터의 내재적인 의미를 고려하지 않아 중요한 정보가 손실되거나 축소될 수 있다. 그렇기에 시계열 데이터의 상관성을 고려하여 내재적인 의미를 학습할 수 있는 구조의 RNN(Recurrent Neural Network), LSTM(Long Short-Term Memory)등이 주목을 받기 시작했다.
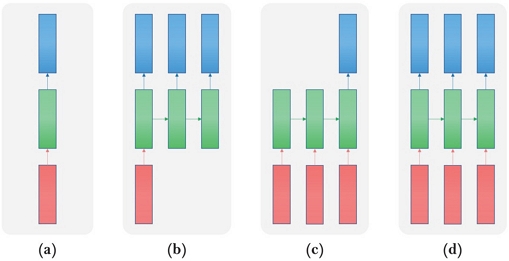
RNN은 순차적인 데이터 처리를 위해 설계된 네트워크이다.16) RNN은 은닉층이 입력층과 이전 타임 스텝의 은닉층으로부터 정보를 받는다. 이렇기에 네트워크는 이전의 정보를 기억할 수 있어 연속적인 시계열 데이터를 처리할 수 있게 된다. RNN의 유형은 Fig. 1과 같다. Fig. 1(a)는 가장 기본적인 모델이며 입력과 출력이 단일인 머신러닝 태스크를 수행한다. Fig. 1(b)는 일대다 모델이며 하나의 이미지를 문장으로 표현하는 태스크 등을 수행한다. Fig. 1(c)는 다대일 모델이며 여러 개의 토큰을 입력받아 하나를 출력하는 텍스트 분류 등의 태스크 등을 수행한다. Fig. 1(d)는 여러 개의 토큰을 입력받아 여러 개의 토큰을 출력하는 예측 태스크를 수행한다.
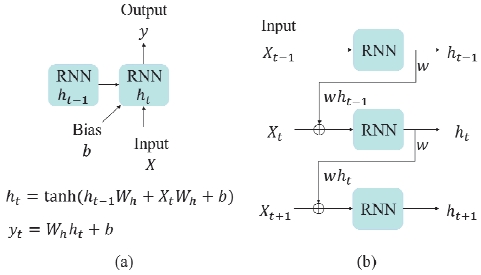
기본적인 RNN 알고리즘의 구조는 Fig. 2(a)와 같다. RNN 알고리즘의 기본 원리로는 과거의 State가 현재의 State에 영향을 미친다는 것이다.
| (11) |
식 (11)을 통하여 RNN 모델의 알고리즘을 설명할 수 있다. ht는 현재의 Hidden state를, Xt는 입력을, Wh와 Wt는 Xt를 ht로 변환하기 위한 가중치이며 b는 편향값이다. 위의 식에서 행렬 곱을 계산하고 그 합을 tanh 함수를 거쳐 이전의 Hidden state가 현재의 Hidden state에 영향을 미치게 된다. Fig. 2(b)는 Fig. 2(a)에서의 기본적인 RNN 모델이 여러 개가 연결되어 있는 모습이며 앞서 설명한 예측 태스크를 수행할 수 있다. 이러한 RNN 모델은 다양한 길이의 입력 시퀀스를 처리할 수 있지만 복잡한 연산으로 인해 기울기 문제가 발생할 수 있으며 시점이 길어질수록 앞의 정보가 뒤로 충분히 전달되지 못하여 비교적 짧은 시퀀스에 대해서만 효과를 보인다. 이러한 문제점을 극복하기 위해 장단기 메모리(LSTM) 모델이 등장했다.
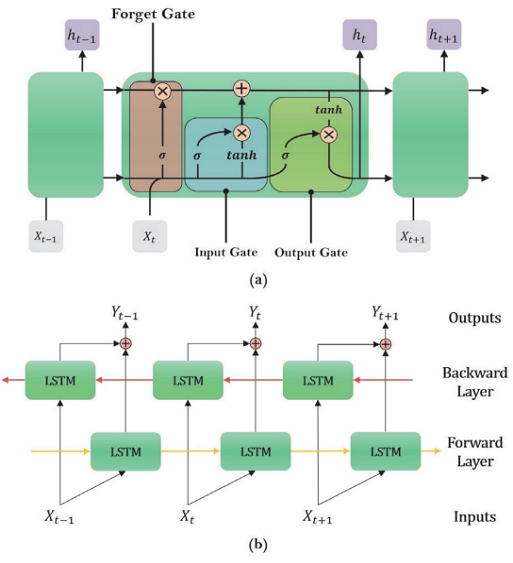
LSTM은 RNN의 긴 의존기간 문제를 피하기 위해 설계되었다.17) LSTM도 RNN과 같은 체인과 같은 구조를 가지고 있지만, 각 반복되는 모듈은 Fig. 3(a)와 같이 RNN과 다른 구조를 가지고 있다.
Gate는 정보가 전달될 수 있는 추가적인 방법으로, Sigmoid와 곱셈으로 이루어져 있다. Sigmoid는 각 요소가 얼마만큼의 정보를 전달해야 하는지에 대한 척도를 0과 1 사이의 숫자로 나타낸다.
LSTM은 3개의 Gate를 가지고 Cell state Ct에 정보 전달을 제어한다. 첫 번째 Gate는 Forget gate로 불리며 ht-1과 Xt-1를 받아 값이 1이면 모든 정보를 보존하며 0이면 정보를 보존하지 않는다. 두 번째 Gate는 Input gate로 불리며 새로운 정보 중 어떤 것을 저장할지를 정한다. Sigmoid가 어떤 값을 업데이트할지 정하고 tanh가 새로운 후보 값들인 을 만들고, Ct-1에 Forget gate의 값과 더하여 업데이트한다. 마지막으로 Sigmoid에 입력 데이터를 넣은 후 tanh에 대입하여 -1과 1 사이의 값을 받은 후 이전에 계산된 Output gate의 결과값과 곱하여 최종 출력 값이 결정된다. 이러한 과정으로 LSTM은 다양한 변형 모델들이 존재하며 시계열 데이터를 처리하는 많은 분야에 사용된다.18-20)
Bi-LSTM(Bidirectional-LSTM)은 기존 LSTM 구조에서 역방향으로 실행되는 LSTM 레이어를 추가한 Fig. 3(b)와 같은 구조를 이루고 있다. Bi-LSTM은 순방향과 역방향 레이어를 통해 양방향으로 문맥의 정보를 추출하여 각 시점에서 이전 시점과 미래 시점의 정보를 가질 수 있게 되어 단방향의 LSTM보다 문장 분류, 감정 분석과 같은 분류 태스크에 더 유연하게 대응할 수 있다는 장점이 있다.21)
3. 제안하는 경로 예측 모델
3.1 전체 아키텍처
본 절에서는 제안하는 경로 예측 모델의 전체적인 구조에 대해서 설명한다. Fig. 4는 경로 예측 모델의 전체 구조를 나타낸다. 예측 모델은 총 3단계로 구성된다. 첫 번째 단계는 차량의 과거 상태량을 입력으로 받아 미래의 상태량들을 예측하는 예측 단계이다. 두 번째 단계는 예측된 상태량들의 연속적인 데이터를 분석하여 각 물리 모델에 대한 확률을 산출하는 분류 단계이다. 마지막 단계는 산출된 확률을 기반으로 각 물리모델이 예측한 궤적을 가중합 하여 단일 예측 경로를 생성해 주는 경로 예측 단계로 구성된다.
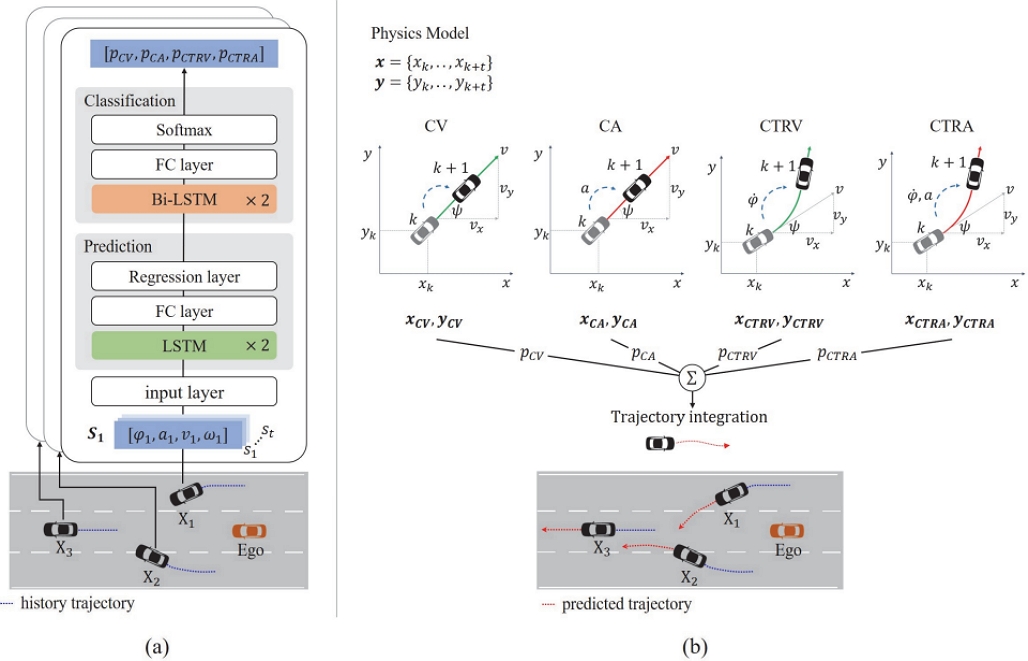
Total architecture of proposed method, (a) State prediction and model classification, (b) Trajectory prediction by physics models
본 논문에서 고려하는 차량의 상태량은 헤딩 각도, 가속도, 속도 그리고 각속도이다. 상태량을 예측하는 모듈은 미래 상태량 예측에 필요하다고 생각되는 최소 정보량인 과거 2초간의 상태량을 입력으로 받아 2초간의 미래 상태량을 예측한다. 네트워크의 경우 얕은 레이어 구성을 통해 낮은 연산량을 확보하고자 Fig. 4(a)의 Prediction 부분과 같이 2개의 LSTM 레이어와 1개의 Fully Connected(FC) 레이어 그리고 Regression 레이어로 구성하였다.
앞서 설명한 차량의 상태량 예측 모듈의 결과값은 과거 2초에 기반한 미래 2초 동안의 상태량이다. 물리 모델 분류 모듈은 예측 모듈의 결과값을 기반으로 앞으로 있을 미래의 2초 상태량들이 어느 물리 모델에 적합한지 분류 및 각 모델에 대한 확률을 산출하는 모듈이다. 네트워크의 구성은 Fig. 4(a)의 Classification 부분과 같으며 미래의 2초 상태량을 입력으로 받아 2개의 Bi-LSTM 레이어와 1개의 FC 레이어를 통과한 후 Softmax 레이어를 마지막으로 예측된 상태량이 각 물리 기반 모델들에 대한 확률로 산출된다. 이때 분류 모듈로 얻어진 확률은 이후 경로 예측 및 통합 모듈에서 각 물리 모델에 대한 가중치로 사용된다.
해당 모듈은 Fig. 4(b)와 같이 구성된다. 먼저 현재 차량의 위치와 상태량을 기반으로 CV 모델, CA 모델, CTRV 모델, CTRA 모델 각 4개의 모델로 2초간의 차량의 미래 궤적을 예측한다. 예측된 각 모델의 궤적들은 앞서 언급했던 각 모델에 대한 확률을 궤적에 대한 가중치로 사용하여 4개의 궤적을 가중합 하여 단일 예측 궤적을 생성한다.
3.2 데이터 셋
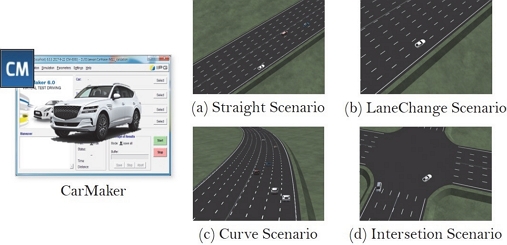
본 절에서는 CarMaker/Simulink 환경에서 예측 모듈을 학습시키기 위한 데이터 셋과 물리 기반 모델 분류 모듈을 학습시키기 위한 데이터 셋을 구축하는 과정에 대해서 소개한다. 예측 모듈과 분류 모듈을 충분히 학습시키기 위하여 CarMaker에서 구성한 도로는 직선로, 일정 곡률이 존재하는 도로 그리고 교차로이다. 데이터 셋을 위한 CarMaker 시나리오는 Fig. 5와 같이 총 4개의 시나리오로 구성하였다.
직선로에서 차량의 거동은 등속, 등가속 그리고 차선 변경으로 구분하였다. 차량이 거동할 때의 속도 범위는 60 km/h부터 140 km/h이며 최대 가속도의 크기는 5 m/s2 미만이 되도록 다양한 차량의 상태량을 얻을 수 있도록 구성하였다. 곡률이 존재하는 도로 또한 차선변경 거동을 제외한 직선로와 같이 거동에 대한 구성을 동일시하였다.
교차로에서의 차량의 거동은 등속, 선회직전 감속 후 등속으로 구분하였으며 속도 범위는 20 km/h부터 50 km/h미만이며 최대 가속도의 크기는 3 m/s2 미만이 되도록 구성하였다.
예측 모듈은 차량의 2초간 과거 상태량을 입력으로 받아 미래 2초 상태량을 예측한다. 학습을 위한 데이터를 구성하기 위해선 현재를 포함한 2초간의 과거 상태량을 X로 2초 미래 상태량을 Y로 구성한다. 시나리오에서 얻은 데이터를 가공하여 데이터를 구성할 때 학습의 발산을 방지하기 위해 데이터의 Normalization 과정을 거쳤다. 총 133개 시나리오에서 얻은 예측 모듈을 학습시킬 수 있는 데이터는 73000개로 네트워크가 충분하게 학습할 수 있도록 구성하였다.
분류 모듈은 예측된 차량의 2초간 상태량을 앞서 언급한 네 가지 물리 모델에 대한 확률 값을 산출한다. 학습을 위한 데이터를 구성하기 위해선 2초간의 상태량 데이터와 각 시계열 데이터에 대한 물리 모델 라벨링 작업이 필요하다. 라벨링 작업 시에는 각 모델의 거동만을 고려한 시나리오 데이터를 라벨링 하여 진행한다. 아래 Table 1은 CarMaker를 통해 얻은 분류 모델의 학습을 위한 데이터 구성 표이다.
각 모델이 포함하는 차량의 거동을 O, X로 표시하였으며 각 모델에 대하여 라벨링 작업을 진행한 결과 각 Class에 포함되는 데이터의 개수는 CV가 9523개, CA가 5760개, CTRV가 7857개, CTRA 가 6960개로 구성되었다. CV 모델의 경우 등속 진진 시나리오 데이터를, CA 모델의 경우 등가감속 시나리오 데이터를, CTRV의 경우 등속선회와 등속 차선변경 시나리오 데이터를 마지막으로 CTRA의 경우 등가속선회와 등가감속 차선변경 시나리오 데이터를 라벨링 한다. 2초간의 시계열 데이터를 X로 라벨링 된 데이터는 Y로 구성하여 총 133개 시나리오에서 얻은 분류 모듈을 학습할 수 있는 데이터는 30300개로 구성하였다.
3.3 실험 환경
본 연구는 Matlab/Simulink와 CarMaker를 사용하여 진행되었다. CarMaker와 Simulink를 연동하여 학습에 필요한 데이터를 수집하였으며 각 모듈에 대한 딥러닝 네트워크 구성 및 학습은 Matlab에서 진행되었다. 예측 및 분류 모듈의 경우 학습 파라미터 및 환경은 아래 Table 2와 같다.
3.4 실험 결과
제안한 경로 예측을 평가할 수 있는 시나리오는 Fig. 6과 같다. 첫 번째 시나리오 Fig. 6(a)는 단일 차량을 예측함으로 평가되며 차량은 65 km/h로 등속도로 주행하다가 70 km/h로 가속하여 속도를 유지한다. 두 번째 시나리오 Fig. 6(b)는 다수 차량을 예측함으로 평가되며 등속 및 등가속 거동이 포함되며 차량들의 속도 분포는 40 km/h부터 90 km/h까지 구성하여 첫 번째 시나리오보다 더욱 다양한 시나리오를 평가하려 하였다.
예측한 궤적과 실제 궤적과의 오차를 정략적으로 평가하기 위해 식 (12), (13)과 같이 평균 변위 오차인 ADE (Average Displacement Error)와 최종 변위 오차인 FDE (Final Displacement Error)를 계산하였다.
ADE는 예측한 궤적과 실제 궤적의 각 예측 시간에서의 평균 거리차이를 의미하며 FDE는 예측한 궤적의 최종 위치에서의 거리차이를 의미한다.
| (12) |
| (13) |
식 (12)에서의 N은 예측 타임 샘플이며 본 논문에서는 20 타임 샘플을 예측하였고 평가를 진행할 때는 ADE와 FDE의 평균값을 사용하였다.
결과 비교를 위한 LSTM 예측 네트워크의 경우 과거 2초 동안의 x,y 위치를 받아 미래 x,y 위치를 예측할 수 있도록 Fig. 4(a)의 Prediction 부분과 같이 구성하여 동일 데이터 셋을 학습 후 동일 시나리오를 통해 평가된다.
결과는 Table 3과 같이 첫 번째 시나리오의 경우 제안하는 방법론이 평균 ADE는 1.2961 m, 평균 FDE는 1.4864 m로 평가되어 LSTM 예측 네트워크 혹은 단일 물리 모델보다 좋은 성능을 확인할 수 있었다.
두 번째 시나리오의 경우 다수의 차량의 예측 궤적을 평가하였으며 평균 ADE가 1.5961 m로 다른 모델보다 좋은 성능을 보이는 것을 확인할 수 있었다.
4. 결 론
본 논문에서는 차량의 경로를 예측할 시 차량의 과거 상태량을 이용하여 미래 차량의 상태량을 예측한 후 미래의 차량 거동에 대한 확률값으로 분류하여 네 가지 물리 모델을 모두 고려해 경로를 예측하는 방법론을 제안한다. 본 연구는 물리 모델 장점과 학습기반의 딥러닝 네트워크의 장점을 융합하여 새로운 하이브리드 방법을 제안한 것에 의의가 있으며 기존 하이브리드 융합 모델들과 달리 네 가지 물리 모델을 모두 고려한 점에 대한 차별점이 있다.
하지만, 주변 차량을 더욱 긴 시간과 높은 정합성을 만족시키기에는 단기적인 예측시간과 급선회 및 급거동을 예측할 수 없음과 주변 객체와의 연관성을 고려하지 못하는 한계점을 가지고 있다고 판단된다. 그렇기에 이후에는 차량이 주행하고 있는 도로 정보 및 주변 객체와의 연관성을 고려할 수 있는 방법으로 연구해 보고자 하며 이러한 방향으로 연구를 해나간다면 경로 예측 분야에 다양한 방법으로 접근할 수 있을 것으로 기대된다.
Nomenclature
| v : | velocity, m/s |
| a : | acceleration, m/s2 |
| φ : | yaw, rad |
| ω : | yaw rate, rad/s |
| F : | transition matrix |
| T : | time gap, s |
| X : | vehicle’s state vector |
Acknowledgments
이 연구는 2023년도 산업통상자원부 및 한국산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(과제번호: 20024814, 과제명: 허브연계형 Lv.4 상용차 자율주행 예측구동제어 및 최적운행 기술 개발).
References
-
Y. Ma, Z. Wang, H. Yang and L. Yang, “Artificial Intelligence Applications in the Development of Autonomous Vehicles: A Survey,” IEEE/CAA Journal of Automatica Sinica, Vol.7, No.2, pp.315- 329, 2020.
[https://doi.org/10.1109/JAS.2020.1003021]

-
W. Schwarting, J. Alonso-Mora and D. Rus, “Planning and Decision-Making for Autonomous Vehicles,” Annual Review of Control, Robotics, and Autonomous Systems, Vol.1, pp.187-210, 2018.
[https://doi.org/10.1146/annurev-control-060117-105157]

-
R. Huang, G. Zhuo, L. Xiong, S. Lu and W. Tian, “A Review of Deep Learning-Based Vehicle Motion Prediction for Autonomous Driving,” Sustainability, Vol.15, No.20, Paper No.14716, 2023.
[https://doi.org/10.3390/su152014716]

-
L. Fang, Q. Jiang, J. Shi and B. Zhou, “TPNet: Trajectory Proposal Network for Motion Prediction,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR), pp.6796-6805, 2020.
[https://doi.org/10.1109/CVPR42600.2020.00683]

-
A. Polychronopoulos, M. Tsogas, A. J. Amditis and L. Andreone, “Sensor Fusion for Predicting Vehicles’ Path for Collision Avoidance Systems,” IEEE Transactions on Intelligent Transportation Systems, Vol.8, No.3, pp.549-562, 2007.
[https://doi.org/10.1109/TITS.2007.903439]

- F. Da and Y. Zhang, “Path-Aware Graph Attention for HD Maps in Motion Prediction,” Proceedings of the IEEE International Conference on Robotics and Automation(ICRA), Philadelphia, PA, USA, pp. 6430-6436, 2022.
- R. Schubert, E. Richter and G. Wanielik, “Comparison and Evaluation of Advanced Motion Models for Vehicle Tracking,” Proceedings of the 11th International Conference on Information Fusion, Cologne, Germany, 2008.
- J. Kim, K. Cho, W. Na, S. Kim and H. Lee, “Development of Surrounding Vehicle Trajectory Prediction Model Using LSTM,” KSAE Annual Conference Proceedings, pp.426-431, 2021.
- A. Ip, L. Irio and R. Oliveira, “Vehicle Trajectory Prediction Based on LSTM Recurrent Neural Networks,” Proceedings of the IEEE 93rd Vehicular Technology Conference(VTC2021-Spring), Helsinki, Finland, pp.1-5, 2021.
-
L. Xin, P. Wang, C. -Y. Chan, J. Chen, S. E. Li and B. Cheng, “Intention-Aware Long Horizon Trajectory Prediction of Surrounding Vehicles Using Dual LSTM Networks,” Proceedings of the IEEE 21st International Conference on Intelligent Transportation Systems(ITSC), Maui, HI, USA, pp.1441-1446, 2018.
[https://doi.org/10.1109/ITSC.2018.8569595]

- J. Cha, G. Kim and K. Huh, “Physics-Maneuver Based Vehicle Trajectory Prediction Algorithm Using Interacting Multiple Models,” KSAE Spring Conference Proceedings, pp.385-388, 2022.
-
W. Bai, H. Li, J. Zhao, Y. Zhou, L. Huang and S. Yang, “IMTP: Intention-Matching Trajectory Prediction for Autonomous Vehicles,” Proceedings of the 29th International Conference on Mechatronics and Machine Vision in Practice(M2VIP), Queenstown, New Zealand, pp.1-6, 2023.
[https://doi.org/10.1109/M2VIP58386.2023.10413410]

-
G. Kim, D. Kim, Y. Ahn and K. Huh, “Hybrid Approach for Vehicle Trajectory Prediction Using Weighted Integration of Multiple Models,” IEEE Access, Vol.9, pp.78715-78723, 2021.
[https://doi.org/10.1109/ACCESS.2021.3083918]

-
V. Ş. Ediger and S. Akar, “ARIMA Forecasting of Primary Energy Demand by Fuel in Turkey,” Energy Policy, Vol.35, No.3, pp.1701-1708, 2006.
[https://doi.org/10.1016/j.enpol.2006.05.009]

- R. B. Cleveland, W. S. Cleveland, J. E. McRae and I. Terpenning, “STL: A Seasonal-Trend Decomposition,” Journal of Official Statistics, Vol.6, No.1, pp.3-73, 1990.
-
D. E. Rumelhart, G. E. Hinton and R. J. Williams, “Learning Representations by Back-Propagating Errors,” Nature, Vol.323, pp.533-536, 1986.
[https://doi.org/10.1038/323533a0]

-
H. Sak, A. W. Senior and F. Beaufays, “Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modeling,” 2014.
[https://doi.org/10.21437/Interspeech.2014-80]

-
F. Karim, S. Majumdar, H. Darabi and S. Chen, “LSTM Fully Convolutional Networks for Time Series Classification,” IEEE Access, Vol.6, pp.1662-1669, 2018.
[https://doi.org/10.1109/ACCESS.2017.2779939]

- M. A. I. Sunny, M. M. S. Maswood and A. G. Alharbi, “Deep Learning-Based Stock Price Prediction Using LSTM and Bi-Directional LSTM Model,” Proceedings of the 2nd Novel Intelligent and Leading Emerging Sciences Conference(NILES), IEEE, 2020.
-
F. Altché and A. de La Fortelle, “An LSTM Network for Highway Trajectory Prediction,” Proceedings of the IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, pp.353-359, 2017.
[https://doi.org/10.1109/ITSC.2017.8317913]

-
B. Jang, M. Kim, G. Harerimana, S. Kang and J. W. Kim, “Bi-LSTM Model to Increase Accuracy in Text Classification: Combining Word2vec CNN and Attention Mechanism,” Applied Sciences, Vol.10, Paper No.5841, 2020.
[https://doi.org/10.3390/app10175841]