3차원 모델 생성 및 진동 가시화 시스템 개발

1. 서 론

자동차를 포함하여 어떤 반복적인 움직임이나 회전이 있는 기계에서는 진동이 발생한다. 그만큼 진동 데이터는 기계에서 얻을 수 있는 기본적인 정보 중 하나이며, 진동을 측정하는 방법이나 진동 데이터를 효과적으로 활용하는 방법 등 이와 관련된 많은 연구가 있다. 특히 진동 데이터를 활용하는 연구는 진동을 이용한 자동차 부품의 내구성 해석¹⁾에서부터 자동차를 이용하는 승객의 승차감에 관한 연구²⁾까지 다양한 분야에 걸쳐 꾸준히 수행되어 왔다.

한편, 컴퓨터 하드웨어의 발전으로 인해 많은 연산량을 필요로 하는 기술이 활발하게 개발되었다. 특히 GPU의 등장으로 3차원 포인트 클라우드, 3차원 모델과 같이 3차원 공간을 활용하거나 대량의 이미지를 활용하는 등 시각적인 정보를 다루는 기술이 크게 발전하였다. 최근에는 컴퓨터 비전 분야의 연구가 활발히 수행되고 있으며, 특히 오픈 소스인 COLMAP³⁾을 통해 여러 시점에서 카메라로 촬영한 이미지로부터 빠르고 쉽게 3차원 물체 복원이 가능하다. 이와 더불어 저가형 3D 스캐너가 등장하면서 3차원 물체 복원에 대한 접근이 용이해지고 있다. 따라서 3차원 물체 복원 기술을 기계 분야에 접목하고자 하였고, 본 연구를 통해 3차원 물체의 진동을 가시화하는 시스템을 개발하였다.

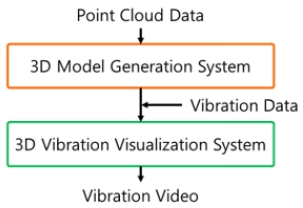
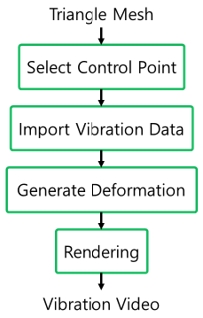
구조 해석, 설계 등 3차원 모델이 필요한 분야에서는 일반적으로 3차원 CAD 프로그램을 이용하여 정확한 크기, 내부, 재료 등의 정보를 가진 모델을 이용한다. 그러나 정확한 3차원 모델이 없고, 내부 구조를 쉽게 알 수 없는 대상에 대한 연구가 필요할 수 있다. 본 연구의 3차원 모델 생성 시스템은 센서로 얻은 3차원 포인트 클라우드로부터 3차원 모델을 생성한다. 이는 정확한 CAD 모델을 얻기 전, 대략적인 외형 정보를 빠르게 획득하여 추후 연구를 계획하는 데에 사용될 수 있다. 또한, 물체의 진동 변화 양상은 물체의 내구성 진단, 수명 예측, 재료 선정 등의 연구에 사용될 수 있다. 따라서 본 연구의 3차원 진동 가시화 시스템을 통해 3차원 모델과 진동 변위 데이터를 이용하여 진동 측정 대상의 진동을 컴퓨터 공간에서 가시화하고자 한다. Fig. 1은 3차원 모델 생성 및 진동 가시화 시스템의 전체 과정을 표현한 그림이다.

Fig. 1

Process of the 3D model generation and vibration visualization system

본 논문은 2장에서 3차원 모델 생성 및 진동 가시화 시스템과 관련된 몇 가지 연구를 소개하고, 3, 4장에서 각각 3차원 모델 생성 시스템과 3차원 진동 가시화 시스템의 구조를 설명한다. 5장에서는 진동 가시화 시스템의 실험 결과를 정리하고, 6장의 결론을 마지막으로 한다.

2. 관련 연구

3. 3차원 모델 생성 시스템

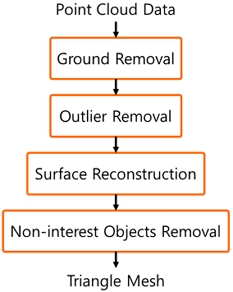
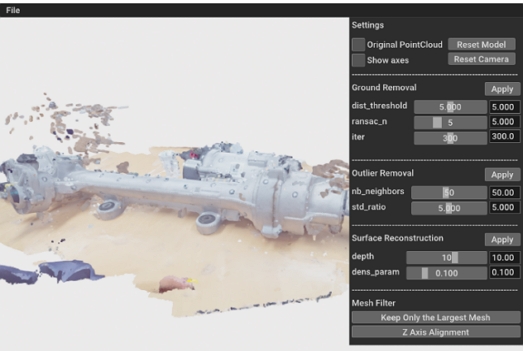
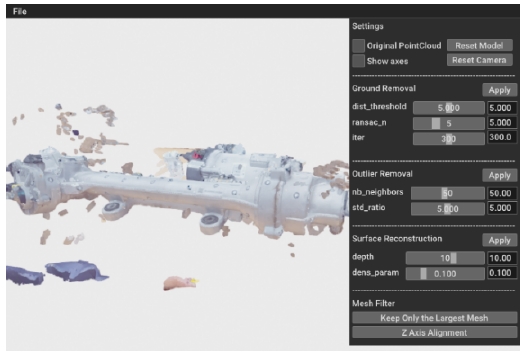
3차원 LiDAR 센서, 3D 스캐너, 카메라를 이용한 3차원 재구성 등의 방법으로 얻은 포인트 클라우드는 센서 노이즈와 관심이 없는 주변 개체 데이터를 포함한다. 따라서 포인트 클라우드에서 메쉬를 만드는 데에 필요한 데이터만 남기는 과정이 필요하다. 본 절에서는 모델의 포인트 클라우드를 필터링하고 표면 재구성 기술로 메쉬를 만들어 3차원 모델을 생성하는 3차원 모델 생성 시스템에 대해 소개한다. 이는 후술할 3차원 진동 가시화 시스템의 모델로 사용 가능하다. Fig. 2는 본 연구에서 개발한 3차원 모델 생성 시스템의 전체적인 순서도이며, Fig. 3은 시스템의 GUI이다. 기능과 GUI는 모두 Open3D 라이브러리¹⁴⁾를 기반으로 구현하였다. 예시의 포인트 클라우드는 자동차의 조향 장치인 R-EPS(Rack Type Electric Power Steering)를 3D 스캐너인 POP3(Revopoint 3D사, 중국)로 촬영하여 획득하였다.

Fig. 2

Process of the 3D model generation system

Fig. 3

3D model generation system GUI

3.1 바닥 제거

RANSAC¹³⁾을 이용하여 물체가 놓인 바닥의 평면 방정식을 찾고, 바닥에 속하는 포인트 클라우드를 제거하여 물체만 남기도록 한다. 이 과정은 Open3D 라이브러리의 Segment_plane 함수로 구현되어 있다.¹⁴⁾ 평면의 방정식은 세 점으로부터 결정되며, 식 (1)과 같이 나타낼 수 있다.

$\[ ax+by+cz+d=0 \]$

(1)

식 (1)의 계수 a,b,c,d에 대해 벡터 n=(a,b,c)는 평면의 법선 벡터이며, d는 원점과의 거리다. n과 d는 다음 식 (2), (3)과 같이 평면 위의 세 점 p₁, p₂, p₃으로 만든 두 벡터의 외적으로 계산할 수 있다.

$\[ n=\frac{\left(p_2-p_1\right)\times \left(p_3-p_1\right)}{\left|\left(p_2-p_1\right)\times \left(p_3-p_1\right)\right|} \]$

(2)

$\[ d=-n\cdot p_1 \]$

(3)

포인트 클라우드에서 임의로 선정한 세 점으로 결정된 평면에 대해 포인트 클라우드를 구성하는 각 점과의 거리를 계산하고, 거리가 임곗값보다 작으면 평면을 지지하는 것으로 간주한다. 포인트 클라우드의 한 점 q와 평면 사이의 거리 l은 다음 식 (4)로 계산된다.

$\[ l=\left|n\cdot q\right| \]$

(4)

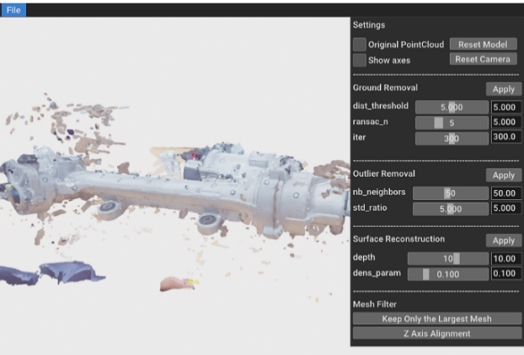
위 과정을 반복하여 생성한 평면 중 가장 많은 점의 지지를 받는 평면을 바닥으로 간주한다. Table 1은 바닥 제거 알고리즘을 표현한 의사코드다. Distance threshold는 점이 그 평면에 속한 것으로 간주되는 최대 거리다. 바닥을 이루는 포인트 클라우드를 제거하는 과정에서도 사용되는 값이므로 물체가 바닥과 맞닿은 부분의 데이터가 손실되지 않도록 적절한 값을 선정해야 한다. Fig. 4는 위 알고리즘을 이용하여 Fig. 3의 포인트 클라우드에서 바닥을 추정하여 제거한 장면이다.

Table 1

Algorithm of ground removal using RANSAC

Fig. 4

Scene with the ground removed where the object is placed

3.2 이상치 제거

포인트 클라우드 획득에 사용한 센서의 노이즈를 통계 기반 이상치 추정을 통해 제거한다. 이 과정은 Open3D 라이브러리의 Statistical_outlier_removal 함수로 구현되어 있다.¹⁴⁾ 포인트 클라우드는 데이터 구조 중 하나인 k-d tree로 나타낼 수 있는데, 이 구조는 k-NN(k-nearest neighbors algorithm)을 빠르게 처리할 수 있다.¹⁸⁾ 포인트 클라우드의 각 점에 대해 가장 가까운 k개의 점을 찾아 거리의 평균 m_total을 계산한다. m_local을 이용하여 계산한 전체 점의 평균 m_global과 표준편차 σ로 이상치가 아닌 것으로 판정되는 임곗값 d_outlier을 구한다. 이는 이상치로 판정하는 정도를 조절하는 파라미터 r_std에 대해 다음 식 (5)로 계산된다.

$\[ d_{outlier}=m_{global}+\sigma r_{std} \]$

(5)

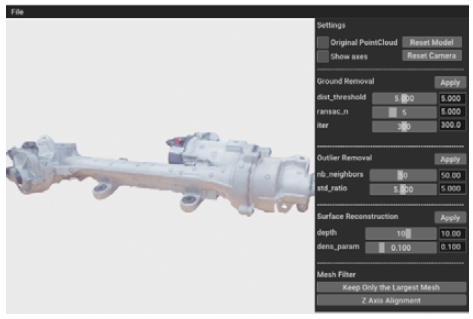
이때, m_total > d_outlier이면 그 점을 이상치로 판단하여 제거한다. 또한, 파라미터 r_std의 값이 작을수록 더 많은 데이터를 이상치로 판단하게 된다. Table 2는 이상치 제거 알고리즘을 표현한 의사코드이다. Fig. 5는 Fig. 4에서 바닥을 제거한 포인트 클라우드 데이터에서 이상치를 제거한 장면이다.

Table 2

Algorithm of outlier removal

Fig. 5

Scene with outliers removed

3.3 메쉬 생성 및 비관심 개체 제거

푸아송 표면 재구성 기술로 포인트 클라우드로부터 삼각형으로 이루어진 메쉬를 생성할 수 있다.¹⁵⁾ 이 과정은 Open3D 라이브러리의 Create_from_point_cloud_poisson 함수로 구현되어 있다.¹⁴⁾ 포인트 클라우드의 점 p와 메쉬의 내부 M에 대해 다음 식 (6)과 같은 지시 함수 X_M을 정의할 수 있다.

$\[ {\chi }_M\left(p\right)=\left\{\begin{array}{cc}1,\hfill & where p\in M\hfill \\ 0,\hfill & where p\notin M\hfill \end{array}\right. \]$

(6)

한편, PCA(Principal Component Analysis)를 이용하면 포인트 클라우드의 각 점에 대해 인접한 점을 고려한 지역적인 평면을 추정할 수 있다.¹⁹⁾ 이 지역 평면의 법선 벡터를 그 점의 방향성으로 하여 포인트 클라우드의 모든 점에 방향성을 부여한다. 방향성이 있는 포인트 클라우드를 $$ \overrightarrow{V}$$라 할 때, 푸아송 표면 재구성은 지시 함수의 기울기, 즉, ∇ X_M가 $$ \overrightarrow{V}$$를 가장 잘 표현할 수 있도록 하는 X_M을 찾는다. 이때, 발산 연산자를 이용하면 X_M과 $$ \overrightarrow{V}$$의 관계를 푸아송 방정식으로 나타낼 수 있다. 이는 식 (7)과 같이 나타낼 수 있다.

$\[ \nabla \cdot \nabla {\chi }_M=\nabla \cdot \overrightarrow{V} \]$

(7)

식 (7)을 수치적으로 풀어 X_M을 추정하고, Marching cube 알고리즘²⁰⁾을 이용하여 메쉬를 생성한다. 위 과정에서 사용되는 팔진 트리(Octree)는 포인트 클라우드와 같은 3차원 공간 데이터에 사용되는 데이터 구조로, 데이터가 조밀한 부분일수록 트리가 깊다.²¹⁾ 팔진 트리로 구조화한 포인트 클라우드로부터 표면을 생성할 때, 깊은 단계에 있는 데이터까지 이용할수록 더욱 정교한 표면이 생성되며, 동시에 데이터의 노이즈에 민감할 수 있다. 따라서 표면 재구성에 사용할 팔진 트리의 깊이를 적절히 선정해야 한다.

푸아송 표면 재구성 과정으로 얻은 메쉬에는 표면을 추정하기 위한 포인트 클라우드 데이터가 부족하여 실제 표면으로 보기 어려운 부분이 존재할 수 있다. 따라서 메쉬를 구성하는 점의 밀도를 계산하고, 표면을 지지하는 점의 밀도가 낮으면 실제 표면으로 간주하지 않고 제거한다. Fig. 6은 점의 밀도가 낮은 부분을 제거하기 전과 후의 그림이다. 마지막으로 이상치 제거 과정에서 제거되지 않은 노이즈와 관심이 없는 주변 개체를 지운다. Fig. 7은 Fig. 5의 포인트 클라우드로부터 메쉬를 생성하고, 가장 큰 메쉬만 남겨 비관심 개체와 이상치 제거 과정에서 지워지지 않은 노이즈를 제거한 장면이다.

Fig. 6

Before and after removing areas with low point density

Fig. 7

Scene with mesh generated from point cloud after removal of non-interest objects

3.4 메쉬 정렬

후술할 3차원 진동 가시화 시스템에서 모델에 x, y, z방향을 가진 진동 데이터를 넣기 위해서는 좌표계를 맞춰야 하다. 따라서 물체가 바닥에 놓여있다는 가정 하에 바닥 제거 과정에서 얻은 법선 벡터 n과 좌표계의 y축이 평행을 이루게 하는 회전행렬을 계산하여 진동 데이터의 z방향과 모델의 방향을 정합하였다. 진동 데이터의 x, y방향 정합 과정은 4.1절에서 서술한다. 회전행렬 계산은 Scipy 라이브러리²²⁾의 Align_vectors 함수를 사용하였다. 벡터 a, b를 정합하는 회전 벡터 r는 다음 식 (8), (9)와 같이 두 벡터의 외적과 회전각 θ로 표현할 수 있다.

$\[ \theta ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\frac{‖a\times b‖}{a\cdot b} \]$

(8)

$\[ r=\frac{\theta }{\sin \theta }\left(a\times b\right) \]$

(9)

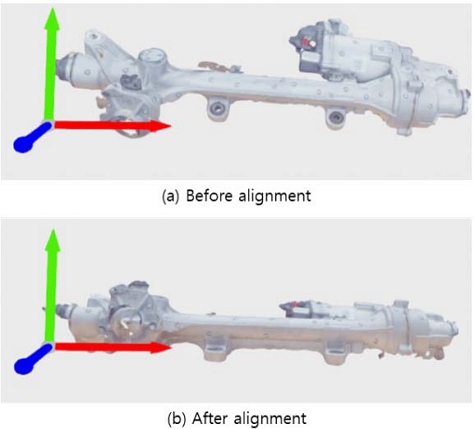
위 수식으로 얻은 회전 벡터는 로드리게스 회전 공식(Rodrigues’ rotation formula)²³⁾을 이용하여 회전 행렬을 얻을 수 있다. Fig. 8은 R-EPS가 놓인 책상의 법선 벡터와 초록색 화살표로 표현된 컴퓨터 그래픽 좌표계의 y축(Fig. 8의 초록색 화살표)을 정합한 결과이다.

Fig. 8

Scene with axes and mesh (a)before alignment and (b)after alignment

4. 3차원 진동 가시화 시스템

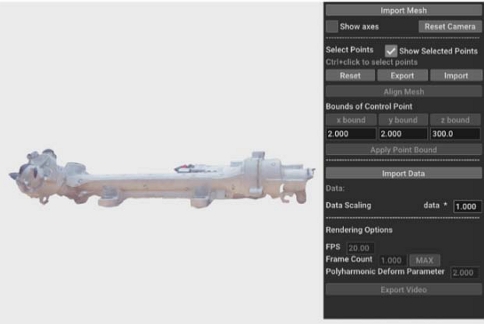
가속도계의 값을 적분하거나 레이저 변위 센서, 카메라를 이용한 변위 측정으로 물체의 한 점의 진동 변위를 측정할 수 있다. 본 절에서는 이러한 방법으로 얻은 진동 변위 데이터를 3차원 재구성 기술 또는 CAD 프로그램으로 만든 모델에 입력하여 변형을 생성하고, 이를 연속적으로 재생하여 모델의 진동을 가시화하는 3차원 진동 가시화 시스템에 대해 소개한다. Fig. 9는 본 연구에서 개발한 3차원 진동 가시화 시스템의 전체적인 순서도이며, Fig. 10은 시스템의 GUI이다. 모델 변형 기술은 Libigl²⁴⁾ 라이브러리, 이외의 기능과 GUI는 Open3D¹⁴⁾ 라이브러리를 기반으로 구현하였다. 예시의 메쉬는 전술한 3차원 모델 생성 시스템으로 얻은 R-EPS의 모델이다.

Fig. 9

Process of the 3D vibration visualization system

Fig. 10

3D vibration visualization system GUI

4.1 진동 측정 지점 선정

제어 지점(Control Points)은 모델 변형 과정에서 진동 변위 데이터가 입력되는 점이다. 따라서 진동 변위를 측정한 지점을 3차원 모델 상에서 선택해야 한다. 2차원 화면에서 마우스로 선택한 지점의 x, y 좌표에 투영된 3차원 모델의 점이 제어 지점으로 선택되도록 한다. Fig. 11은 메쉬를 구성하는 점들 중 세 개의 제어 지점을 선택하여 빨간색 점으로 표시한 것이다. 이때, 제어 지점의 방향 벡터의 평균과 컴퓨터 그래픽 좌표계의 z축(Fig. 11의 파란색 화살표)이 평행을 이루게 하는 회전행렬을 3.4절에서 소개한 방식으로 계산하여 진동 데이터의 x, y방향과 모델의 방향을 정합하였다.

Fig. 11

Control points are selected on the mesh

4.3 변형 생성 및 렌더링 옵션 설정

2.3절에서 소개한 모델 변형 방식 ARAP¹⁶⁾과 다중조화 변형¹⁷⁾은 모두 모델의 변형 정도를 나타내는 에너지 함수를 최적화하여 변형을 생성한다. ARAP에서는 다음 식 (10)과 같이 에너지 함수 E_arap(S')를 최적화하여 변형 전의 모델 S에 대한 변형 결과 S'을 도출한다.

$\[ E_{arap}\left(S^{\text{'}}\right)={\sum }_{t\in T}{a}_t{\sum }_{\left(i,j\right)\in t}{w}_{ij}{‖\left(p_i^{\text{'}}-p_j^{\text{'}}\right)-R_i\left(p_i-p_j\right)‖}^2 \]$

(10)

여기서 T는 모델 S를 구성하는 삼각형의 집합이며, a_t는 t∈T인 t의 면적, p_i, p_j는 삼각형 t의 점, $$ p_i^{\text{'}},p_j^{\text{'}}$$는 변형 이후의 점, w_ij는 가중치, R_i는 회전행렬이다.

다중조화 변형에서는 변형 후의 모델 S를 생성하는 변형 함수 u를 정의한다. 이때, 변형 함수 u는 k차 라플라스 방정식을 만족하는 다중조화 함수이며, 이는 다음 식 (11), (12)와 같이 표현할 수 있다.

$\[ S^{\text{'}}=S+u \]$

(11)

$\[ {\mathrm{\Delta }}^{k}u=0 \]$

(12)

다중조화 변형의 에너지 함수E_poly(u)는 모델 S에 대하여 다음 식 (13)과 같으며, 이를 최적화하는 방식으로 변형을 생성한다.

$\[ E_{poly}\left(u\right)={\int }_S {‖{\mathrm{\Delta }}^{k}u‖}^{2}dA \]$

(13)

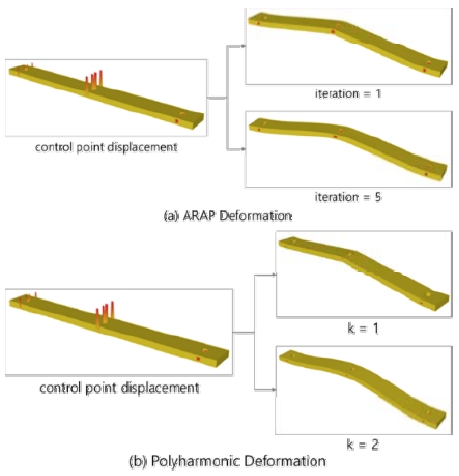
Fig. 12는 캔틸레버의 세 점에 변위를 주어 각각 ARAP과 다중조화 방법으로 변형을 생성한 결과이다. ARAP 변형의 경우, 반복할수록 부드럽게 휘는 변형을 보이며, 다중조화 변형은 경계 조건을 나타내는 파라미터 k=2일 때 더 부드럽게 휘는 변형을 보인다. k>3부터는 수치적 불안정성이 존재하여 경계조건을 만족하는 변형을 생성하지 못하는 경우가 발생한다. 본 연구의 3차원 진동 가시화 시스템에서는 전체적으로 부드러운 변형을 생성하고, 상황에 따라 파라미터를 조절할 수 있는 다중조화 변형¹⁷⁾ 방식을 사용한다.

Fig. 12

The results of applying (a) ARAP deformation and (b) polyharmonic deformation to the cantilever

다중조화 변형 방식은 메쉬 데이터가 커지면 실시간으로 빠르게 변형을 생성하는 데에 한계가 있다. Table 3은 3개의 3차원 모델에 대하여 다중조화 변형을 생성하는 데에 걸리는 시간을 정리한 것이다. Intel Core i3-8145U CPU, 8GB RAM이 장착된 컴퓨터를 사용하였으며, 운영체제는 Windows 10, 파이썬 버전은 3.9.18이다. 3차원 모델로는 Fig. 13과 같은 캔틸레버 CAD 모델, 3D 스캐너로 생성한 캔틸레버 모델과 MDPS 모델을 사용하였다. 다중조화 변형 파라미터 k=1로 각각 100회 변형을 생성하여 최소, 최대, 평균 시간을 계산하였다. 점 개수가 가장 적은 캔틸레버 CAD 모델의 평균 변형 생성 시간은 0.07초로, 14.29 FPS를 가진다. 일반적인 영상이 20~30 FPS인 것과 비교하여 부족한 수치를 보이며, 캔틸레버 CAD보다 점 개수가 많은 3D 스캐너 모델의 평균 변형 생성 시간은 모두 1초를 넘겨 실시간으로 자연스러운 움직임을 생성하기 어렵다. 또한, k값이 커지면 변형을 생성하는 데에 더욱 오랜 시간이 걸리게 된다. 따라서 물체의 변형을 영상으로 렌더링하는 방식을 선택하였으며, 영상의 FPS는 진동 변위 데이터의 샘플링 주파수에 맞춰 설정하였다.

Table 3

Time required to generate deformations when k = 1, along with the number of points and triangles for each 3D model

Fig. 13

Cantilever from CAD(top), cantilever from 3D scanner (middle), MDPS from 3D scanner(bottom)

5. 실 험

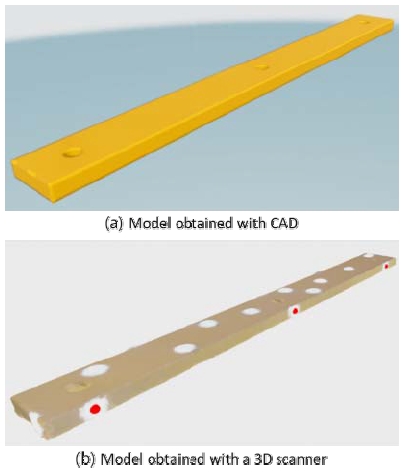
실험에 사용한 진동 변위 데이터는 동역학 해석 소프트웨어인 RecurDyn(Function Bay사, 한국)을 이용하여 취득하였다. 길이 300 mm, 너비 30 mm, 높이 8 mm에 세 개의 직경 8 mm 구멍이 뚫린 알루미늄 캔틸레버의 왼쪽을 위아래로 5 mm씩 0.3초간 흔들었을 때 발생하는 진동 변위 데이터를 사용하였다. 실험은 1, 2, 3차 모드가 발생하는 주파수 각각에 대해 진행하였으며, 주파수와 샘플링 주기는 Table 4와 같다. 실제 속도로 영상을 저장하면 진동을 눈으로 확인하기 어려워 낮은 배속으로 렌더링하였다. 1, 2, 3차 모드 각각에 대한 배속 비율과 샘플링 주파수에 의한 fps는 Table 5와 같이 정리할 수 있다. Fig. 14는 실험에 사용한 캔틸레버의 CAD 모델과 POP3 스캐너로 얻은 모델이며, POP3 스캐너로 얻은 모델의 빨간 점에 진동 데이터를 입력하였다. 이는 캔틸레버에 있는 세 개의 구멍 부근이며, Recurdyn으로부터 진동 변위 데이터를 수집한 위치와 동일하다.

Table 4

Vibration frequencies and sampling rates for the 1st, 2nd, and 3rd modes

Table 5

Video playback speed and fps for the 1st, 2nd, and 3rd modes

Fig. 14

3D Model of a cantilever obtained with (a) CAD and (b) 3D scanner

주파수에 따른 다중조화 변형 파라미터 k의 영향을 확인하기 위해 진동 변위 데이터가 입력되는 세 개의 제어 지점 이외에 4개의 점을 추가로 선정하여 평가하였다. RecurDyn을 이용하여 동일한 방법으로 점 4개의 진동 변위 데이터를 얻고, 이를 다중조화 변형으로 얻은 점 4개의 변위와 비교하였다. 평가 지표로 길이 단위를 유지하고 큰 오차에 민감한 평균 제곱근 오차(Root Mean Square Error, RMSE)를 사용하였다. 각 점의 x, z방향 변위는 값이 크지 않고, 오차도 비교적 작아 y방향(위아래 방향) 변위만을 고려하였다.

5.1 캔틸레버 CAD 파일 진동 가시화

3차원 진동 가시화 시스템을 이용하여 알루미늄 캔틸레버 가공에 사용한 CAD 파일에 RecurDyn 해석으로 얻은 세 점의 진동 데이터를 입력하였다. 변위가 입력되는 지점은 파란색 점으로 표시하고, 렌더링 과정을 통해 진동 가시화 영상을 생성하였다.²⁵⁾ Figs. 15 ~ 17은 각각 진동 모드 1, 2, 3에 대한 RecurDyn 해석 결과와 3차원 진동 가시화 시스템으로 생성한 결과 영상의 프레임 일부이다. k의 값이 클수록 제어 지점에서 부드럽게 변형이 일어나는 것을 확인할 수 있다. 1차, 2차 모드에서는 k≥2일 때 불필요하게 구불거리는 변형이 부자연스러운 반면, 3차 모드에서는 k=2일 때 가장 자연스러운 변형이 생성되었다. Table 6은 1, 2, 3차 모드 각각에 대해 진동 변위 데이터와 k=1, k=2, k=3일 때 다중조화 변형으로 생성한 변위 사이의 RMSE를 정리한 것이다. 전체 RMSE 평균은 0.3314 mm로, 입력 진폭이 5 mm인 것과 비교하여 6.628 %의 오차가 발생하였다. 1, 2차 모드에서는 k=1일 때 가장 작은 오차를 보인다. 3차 모드에서는 k=2일 때 오차가 가장 작으나, Point 4에는 k=1이 가장 적합하다.

Fig. 15

Output frame of the RecurDyn and 3D vibration visualization system for mode 1 (cantilever CAD file)

Fig. 16

Output frame of the RecurDyn and 3D vibration visualization system for mode 2 (cantilever CAD file)

Fig. 17

Output frame of the RecurDyn and 3D vibration visualization system for mode 3 (cantilever CAD file)

Table 6

RMSE between the vibration data and the displacements generated by the polyharmonic deformation with k=1, k=2, k=3 for 1st, 2nd, 3rd modes(cantilever CAD file)

5.2 3D 스캐너로 얻은 캔틸레버 모델 진동 가시화

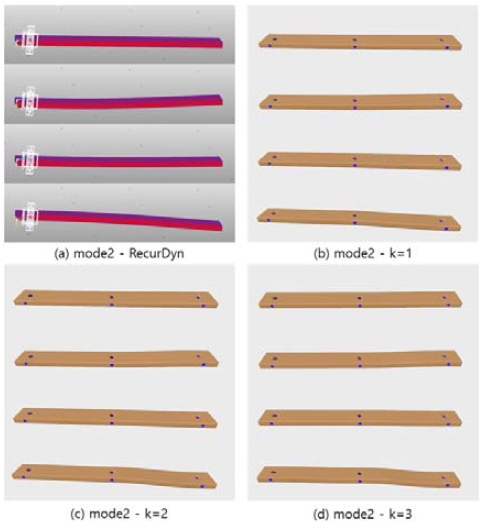
실제 알루미늄 캔틸레버를 POP3로 촬영한 뒤, 3차원 모델 생성 시스템을 이용하여 생성한 모델에 동일한 과정으로 렌더링하여 진동 가시화 영상을 생성하였다.²⁶⁾ Figs. 18 ~ 20은 각각 진동 모드 1, 2, 3에 대한 RecurDyn 해석 결과와 3차원 진동 가시화 시스템으로 생성한 결과 영상의 프레임 일부이다. 변형 양상이 CAD 파일을 이용한 실험과 유사하게 나타나는 것을 확인할 수 있다. Table 7은 1, 2, 3차 모드 각각에 대해 진동 변위 데이터와 k=1, k=2, k=3일 때 다중조화 변형으로 생성한 변위 사이의 RMSE를 정리한 것이다. 전체 RMSE 평균은 0.3363 mm로, 입력 진폭이 5 mm인 것과 비교하여 6.726 %의 오차가 발생하였다. 1, 2차 모드에서는 k=1일 때 가장 작은 오차를 보이며, 3차 모드에서는 k=2일 때 가장 적합하여 캔틸레버 CAD 모델과 비슷한 경향을 보인다.

Fig. 18

Output frame of the RecurDyn and 3D vibration visualization system for mode 1 (cantilever mesh from 3D scanner)

Fig. 19

Output frame of the RecurDyn and 3D vibration visualization system for mode 2 (cantilever mesh from 3D scanner)

Fig. 20

Output frame of the RecurDyn and 3D vibration visualization system for mode 3 (cantilever mesh from 3D scanner)

Table 7

RMSE between the vibration data and the displacements generated by the polyharmonic deformation with k=1, k=2, k=3 for 1st, 2nd, 3rd modes(cantilever mesh from 3D scanner)

CAD 모델과 3D 스캐너로 얻은 모델 모두 전체적으로 실제 값에서 크게 벗어나지는 않으나, 한 점에 대해 가장 적합한 k는 서로 다르다. 또한, Point 1, 3이 Point 2, 4에 비해 오차가 작은 경향을 보인다. Table 8은 CAD 모델과 3D 스캐너로 얻은 모델 각각에 대해 다중조화 변형으로 생성한 변위 사이의 RMSE를 정리한 것이다. 전체 평균은 0.0173 mm로, CAD 모델과 3D 스캐너로 얻은 모델이 비슷한 변형을 생성하는 것을 확인할 수 있다. 또한, k=1일 때 가장 비슷한 변형을 생성함을 알 수 있다.

Table 8

RMSE of displacements generated by the polyharmonic deformation with k=1, k=2, k=3 between cantilever CAD file and mesh from 3D scanner for 1st, 2nd, 3rd modes

6. 결 론

본 연구에서는 3차원 모델 생성 시스템 및 3차원 진동 가시화 시스템을 개발하였다. 3차원 모델 생성 시스템을 통해 센서로 얻은 3차원 포인트 클라우드 데이터의 노이즈 및 비관심 개체를 제거하고, 표면 재구성 기술로 물체의 3차원 모델을 생성할 수 있다. 또한, 3차원 진동 가시화 시스템은 3차원 모델에 특정 점의 진동 변위 데이터를 입력하여 변형을 만들고, 이를 연속적으로 렌더링하여 진동에 의한 물체의 변형을 3차원으로 가시화할 수 있다. 실험을 통해 CAD 프로그램으로 직접 생성한 3차원 모델과 3D 스캐너 및 본 연구에서 제시한 3차원 모델 생성 시스템으로 생성한 3차원 모델 모두 3차원 진동 가시화 시스템에 사용할 수 있음을 확인하였다.

다중조화 변형 방식은 최적화를 이용한 방법이므로 3차원 모델의 데이터 크기가 크면 연산량이 증가하여 실시간으로 변형 결과를 얻기 어렵다. 3D 스캐너로 복원한 캔틸레버의 경우, 형상의 복잡성에 비하여 포인트 클라우드가 많은 경향이 있다. 따라서 메쉬를 생성하기 전에 형태를 유지하는 선에서 포인트 클라우드 다운샘플링 과정을 추가하여 실시간성을 확인할 필요가 있다. 다만 MDPS의 경우, 실제 크기가 비교적 큰 반면에 형상이 복잡한 작은 부품이 포함되어 다운샘플링을 통해 점 개수를 줄이는 데에 한계가 있으며, 메쉬를 구성하는 점과 삼각형의 밀도가 형상 정밀도와 변형 생성 결과에 주는 영향을 검토할 필요가 있다.

다중조화 변형은 많은 연산이 필요한 CPU 집약적 작업이다. 따라서 CPU의 다중 코어를 활용하는 멀티 스레드나 GPU를 이용하여 변형 생성 시간을 단축할 수 있을 것으로 예상한다. 또한, 변형을 빠르게 생성할 수 있는 Mass-Spring Model(MSM)²⁷⁾과 같은 새로운 변형 방식을 사용하여 실시간성을 확보하는 연구가 필요하다.

진동 데이터는 물체의 재료 특성이 반영된 데이터이므로 진동 가시화에 재료 특성이 배제되었다고 볼 수 없으나, 변형을 생성할 때 재료 특성을 고려하지 않아 실제 변형과 차이가 있다. 따라서 MSM과 같은 물체의 재료 특성을 반영한 변형 생성 기술을 통해 보다 사실적으로 진동을 가시화할 수 있을 것이다. 이러한 3차원 모델 생성 및 진동 가시화 연구는 진동 모드 분석을 통한 내부 구조 추정, 기계 수명 예측 등 진동을 기반으로 한 분야에서 사용될 수 있을 것으로 기대한다.

References

• M. Han and J. Cho, “Durability Analysis on Automotive Engine Mount,” Transactions of KSAE, Vol.20, No.2, pp.141-147, 2012. [https://doi.org/10.7467/KSAE.2012.20.2.141]
• S. Kim, J. Nam and D. Ko, “Investigation on Vibration Reduction of Automotive Seat Using Dynamic Dampers Based Design of Experiment,” Transactions of KSAE, Vol.31, No.12, pp.1045-1053, 2023. [https://doi.org/10.7467/KSAE.2023.31.12.1045]
• J. L. Schonberger and J. -M. Frahm, “Structure-from-Motion Revisited,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp.4104-4113, 2016. [https://doi.org/10.1109/CVPR.2016.445]
• R. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, 2003. [https://doi.org/10.1017/CBO9780511811685]
• R. I. Hartley and P. Sturm, “Triangulation,” Computer Vision and Image Understanding, Vol.68, No.2, pp.146-157, 1997. [https://doi.org/10.1006/cviu.1997.0547]
• J. Wang, Y. Zhong, Y. Dai, S. Birchfield, K. Zhang, N. Smolyanskiy and H. Li, “Deep Two-View Structure-from-Motion Revisited,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.8953-8962, 2021. [https://doi.org/10.1109/CVPR46437.2021.00884]
• X. Wei, Y. Zhang, Z. Li, Y. Fu and X. Xue, “DeepSFM: Structure from Motion via Deep Bundle Adjustment,” Computer Vision–ECCV 2020: 16th European Conference, pp.230-247, 2020. [https://doi.org/10.1007/978-3-030-58452-8_14]
• S. Choi, J. Park and W. Yu, “Resolving Scale Ambiguity for Monocular Visual Odometry,” 10th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), pp.604-608, 2013. [https://doi.org/10.1109/URAI.2013.6677403]
• J. Park, Q. -Y. Zhou and V. Koltun, “Colored Point Cloud Registration Revisited,” Proceedings of the IEEE International Conference on Computer Vision, pp.143-152, 2017. [https://doi.org/10.1109/ICCV.2017.25]
• C. Campos, R. Elvira, J. J. G. Rodríguez, J. M. Montiel and J. D. Tardós, “ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial and Multi-Map SLAM,” IEEE Transactions on Robotics, Vol.37, No.6, pp.1874-1890, 2021. [https://doi.org/10.1109/TRO.2021.3075644]
• Z. Mi, C. Di and D. Xu, “Generalized Binary Search Network for Highly-Efficient Multi-View Stereo,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.12991-13000, 2022.
• Y. Na, S. Kim, Y. Kim, J. Park, J. Jeong, K. Jo, S. Lee, S. Cho, M. Sunwoo and J. Oh, “HD Map Usability Verification for Autonomous Car,” Transactions of KSAE, Vol.28, No.11, pp.797-808, 2020. [https://doi.org/10.7467/KSAE.2020.28.11.797]
• M. A. Fischler and R. C. Bolles, “Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography,” Communications of the ACM, Vol.24, No.6, pp.381-395, 1981. [https://doi.org/10.1145/358669.358692]
• Intelligent Systems Lab Org, Open3D, https://github.com/isl-org/Open3D, , 2024.
• M. Kazhdan, M. Bolitho and H. Hoppe, “Poisson Surface Reconstruction,” Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Vol.7, 2006.
• O. Sorkine and M. Alexa, “As-Rigid-As-Possible Surface Modeling,” Symposium on Geometry Processing, Vol.4, pp.109-116, 2007.
• M. Botsch and L. Kobbelt, “An Intuitive Framework for Real-Time Freeform Modeling,” ACM Transactions on Graphics (TOG), Vol.23, No.3, pp.630-634, 2004. [https://doi.org/10.1145/1015706.1015772]
• J. L. Bentley, “Multidimensional Binary Search Trees Used for Associative Searching,” Communications of the ACM, Vol.18, No.9, pp.509-517, 1975. [https://doi.org/10.1145/361002.361007]
• S. P. Mishra, U. Sarkar, S. Taraphder, S. Datta, D. P. Swain, R. Saikhom, S. Panda and M. Laishram, “Principal Component Analysis,” International Journal of Livestock Research, 2017. [https://doi.org/10.5455/ijlr.20170415115235]
• W. E. Lorensen and H. E. Cline, “Marching Cubes: A High Resolution 3D Surface Construction Algorithm,” ACM SIGGRAPH Computer Graphics, Vol.21, No.4, pp.163-169, 1987. [https://doi.org/10.1145/37402.37422]
• D. Meagher, “Geometric Modeling Using Octree Encoding,” Computer Graphics and Image Processing, Vol.19, No.2, pp.129-147, 1982. [https://doi.org/10.1016/0146-664X(82)90104-6]
• SciPy, SciPy, https://github.com/scipy/scipy, , 2024.
• O. Rodrigues, “Des Lois Géométriques Qui Régissent Les Déplacements d'un Système Solide Dans l'Espace, et de la Variation des Coordonnées Provenant de Ces Déplacements Considérés Indépendamment des Causes Qui Peuvent Les Produire,” Journal de Mathématiques Pures et Appliquées, Vol.5, pp.380-440, 1840.
• Libigl dev Team, libigl, https://github.com/libigl/libigl, , 2024.
• https://youtube.com/shorts/hovAnhPIMzY
• https://youtube.com/shorts/mDoA4oPsHi0
• H. Va, M. H. Choi and M. Hong, “Real-Time Surface-Based Volume Constraints on Mass-Spring Model in Unity3D,” IEEE Access, Vol.11, pp.17857-17869, 2023. [https://doi.org/10.1109/ACCESS.2023.3245130]