TMED 댐퍼시스템에 대한 유한요소해석 모델링의 신뢰성 검증
Copyright Ⓒ 2024 KSAE / 224-05
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
The damper system of the hybrid TMED system serves to reduce vibration initiated by the engine, and attenuates the rapid torsional torque applied from the motor with spring rigidity. CAE analysis techniques for these damper systems are currently not clearly presented, and CAE analysis technology development and verification will be necessary in reducing development costs and in suggesting development directions. In this study, a finite element modeling for the damper system was constructed, and the reliability of CAE was secured by comparing it with the test results. Moreover, after conducting structural analysis and fatigue durability analysis based on verified modeling, we attempted to replace the test-oriented research and development method with CAE.
Keywords:
Damper system, Strain gauge, Strain, Torsional test, FEM, Analysis modeling, Fatigue analysis, Fatigue endurance키워드:
댐퍼시스템, 스트레인게이지, 변형률, 비틀림 시험, 유한요소기법, 해석 모델링, 피로내구해석, 피로한도1. 서 론
오늘날 CO2 배출량 저감이라는 시대적 요구를 만족시키기 위한 일환으로 친환경차 및 전기차에 대한 개발 필요성이 높아지고 있다. 그러나 현재 내연기관을 한 번에 순수 전기차로 대체하기에는 산업기반 시설 및 인프라 구축 등 여러 어려움이 있다. 현 시점에서 전동화 시대로 변화하면서 발생하는 과도기적 간극은 하이브리드 HEV(Hybrid Electric Vehicle) 시스템으로 메워줄 수 있으며, 이러한 하이브리드 시스템 개발의 중요성은 매우 높다고 할 수 있다. 하이브리드 시스템의 방식 중 TMED(Transmission Mounted Electric Device) 방식은 구동모터와 엔진 사이에 클러치가 장착되며, 클러치 제어를 통하여 출발 및 저속에서 모터로만 주행한다. 이러한 TMED 방식은 내연기관과 마찬가지로 엔진을 사용하는 시스템이기 때문에 동력성능과 효율에 대한 목표를 모두 만족시켜야 한다.1) 특히 낮은 엔진 속도에서 높은 엔진토크를 사용하는 경우 엔진의 각속도 변동이 크게 발생하기 때문에 관련 부품에 대한 검증이 필요하다.2) 그러나 현재 대부분의 연구개발에서 진행하는 댐퍼시스템 성능 검증방법은 시험 위주로 진행되고 있으며, 이에 따라 시험 실패 비용 및 많은 시간이 소비되고 있다. 이러한 이유로 개선방향성 제시 및 빠른 의사결정 등의 활동에 한계가 있을 수밖에 없다.
본 연구에서는 부품 성능시험보다 물리적 비용과 시간이 비교적 절감될 수 있도록 CAE 수치해석기법을 개발하였다. 검증된 CAE 해석모델링을 구성하고 이를 바탕으로 댐퍼시스템의 구조해석에 대한 신뢰성 검증을 진행하였다. 또한, 피로내구해석을 추가로 진행함으로써, 유한요소기반의 CAE의 성능시험 대체 가능성을 확인하였다.
2. 신뢰성 검증 프로세스
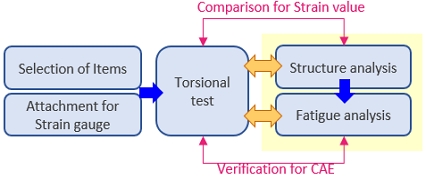
유한요소해석을 통한 탬퍼시스템의 신뢰성 검증을 위하여 Fig. 1과 같은 프로세스로 진행하였다. 좀 더 정확한 신뢰성 검증 및 평가를 위하여 댐퍼조립품 주요부위에 스트레인게이지(Strain gauge)를 부착하여 비틀림 시험을 진행하였으며, 센서를 통해 계측된 변형율(Strain) 값을 CAE 유한요소 해석결과 값과 비교함으로써 해석 결과값에 대한 신뢰성을 높이고자 하였다.
2.1 검증 부품의 선정
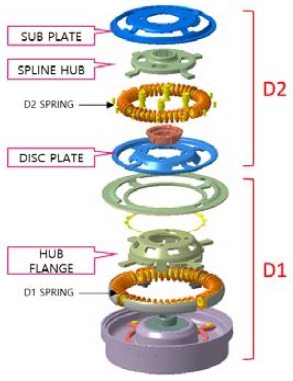
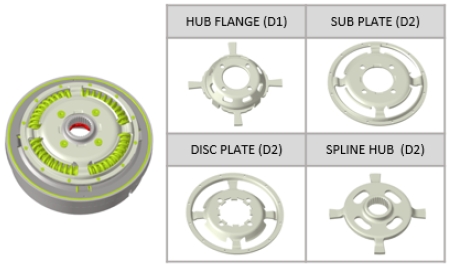
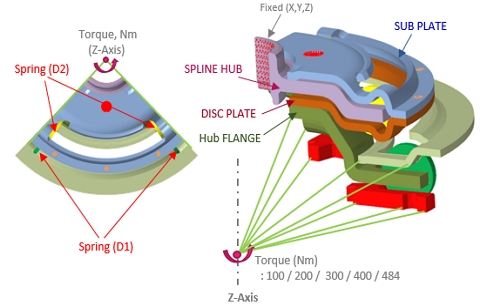
댐퍼시스템의 구성은 Fig. 2에서 보여지는 것과 같다. 댐퍼시스템은 크게 1단(D1) 부품과 2단(D2) 부품들이 스프링에 의해 직렬 연결된 조립품이다. 모터 측에서 발생한 축 방향의 비틀림 하중이 스프링에 의하여 입력되면 비틀림에 의한 충격 및 진동이 저감되며, 일정한 토크로 출력이 유지되는 역할을 한다. 이러한 댐퍼시스템의 검증을 위하여 선정된 부품은 Fig. 3과 같이 D1의 허브플랜지(Hub flange)와 D2의 서브플레이트(Sub plate), 디스크플레이트(Disc plate) 및 스플라인허브(Spline hub) 등 총 4종의 부품에 대하여 검증하였다. 이러한 부품들을 선정하는 가장 큰 이유는 인가된 비틀림 하중에 대하여 가장 취약할 것으로 판단되는 부품들이며, 특히 실제 비틀림 내구시험 중 부품 단면이 줄어드는 목 부에서 쉽게 파손이 일어나고 있는 부품이기 때문이다. 이러한 이유로 파손된 부품의 형상변경이나 물성치 변경 등 여러 개선활동이 필요하다. 댐퍼시스템의 스프링의 경우, 성능스펙이 일정한 범용제품이기 때문에 검증 대상부품으로 선정하지 않았다. 설계 자유도가 높고 조립위치에 따라 총 4종의 부품을 검증대상으로 선정하여 CAE 검증모델을 구성하였다. 이렇게 구성된 부품들의 검증을 통하여 해석 및 설계에 대한 유의미한 개선방향을 제시하고자 하였다.
2.2 스트레인게이지 부착
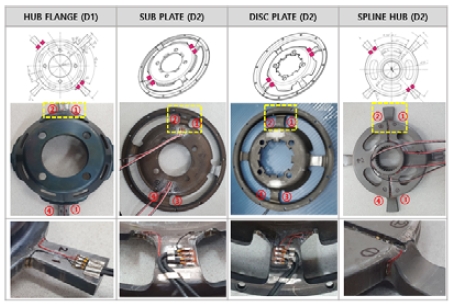
스트레인게이지는 물리적으로 계측된 변형율을 전기신호로 변경하여 피측정물의 변형을 측정하는 저항센서이다. 스트레인게이지의 부착작업은 어떻게 부착했는지에 따라 시험결과에 직접적으로 영향을 줄 수 있는 예민한 작업이기 때문에 스트레인게이지 부착 경험이 많고 숙련된 HMC 전동화구조해석팀의 도움을 받아 센서들을 부착하였다. 스트레인게이지는 Fig. 4 그림처럼 인장 및 압축이 예상되는 부위 각 2개씩, 제품당 각 4개를 사용하여 총 16개의 게이지를 사용하였다. 사용된 스트레인게이지는 내부 스프링에 의해 변형이 급격히 발생하고 응력집중이 예상되는 R부에 부착하였으며, 이를 위해 게이지 길이(Gage length) 가 충분히 작은 1 mm의 스트레인게이지를 선정하였다. 다만, 충분히 작은 게이지 길이임에도 불구하고 서브플레이트 및 디스크플레이트의 경우, R부의 곡률이 R2로 굴곡이 매우 심하기 때문에 부착위치가 협소하고 부착성이 좋지 않은 이유로 R부와 1-2 mm 떨어진 곡면부에 부착하였다.
또한, 각 부품에 부착된 게이지는 부품별로 1 - 4번까지 넘버링 하였다. 제품에 따라 번호별로 인장 및 압축이 발생하는 부위가 상이하지만, 허브플랜지 및 스플라인허브 그리고 서브플레이트 및 디스크플레이트의 인장/압축 경향이 서로 유사하며 이 번호를 기준으로 계측된 변형율 값을 기록하였다.
2.3 비틀림 시험
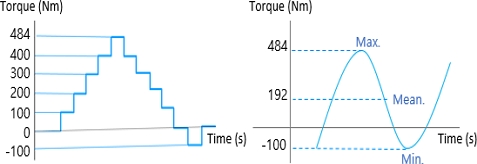
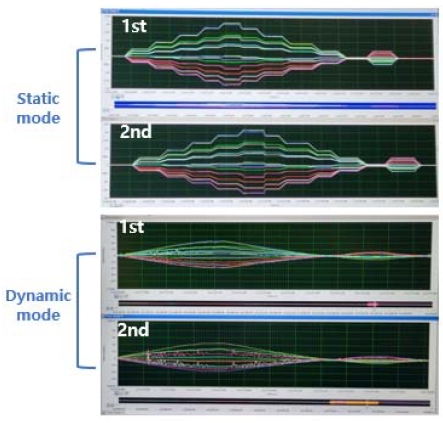
스트레인게이지가 부착된 부품들을 Fig. 6과 같이 조립하였다. 댐퍼시스템은 내구성능을 위해 360도 회전을 통한 동적거동 성능이 만족되어야 한다. 그러나 부착된 게이지 배선들로 인해 회전이 불가하고 거동을 구현하기 힘들기 때문에 당사에서 보유하고 있는 정적 비틀림 시험장비를 활용하여 시험하였다. 시험기에 샘플을 장착하고 구동모터를 통하여 댐핑 작용이 이루어지는 정방향(Drive side, 시계방향)과 역방향(Coast side, 반시계방향)으로 제어하여 비틀림 하중에 따른 변형율을 확인하였다. 비틀림 하중 입력 구간 설정 관련하여 댐퍼시스템 설계 사양인 입력토크의 1.3배(+484 Nm) 수준으로 정방향 토크 값을 선정하였으며, 비틀림 특성상 좌우 대칭인 구조를 지니고 있기 때문에 역방향 토크 값에 대해서는 선형 강성을 유지하는 구간의 최소 단위(-100 Nm)로 선정하였다. 시험 조건 선정에 있어서 Fig. 5와 같이 부착된 변형율 값을 보다 정확하고 안정된 값을 확인할 수 있도록 정적 모드 및 동적 모드 총 2가지 방식에 대하여 진행하였다.
정적 모드에서는 1회의 토크를 100 Nm 간격으로 약 10초동안 유지시키면서 각 부품에 대한 변형율 값을 계측하였다.
또한, 동적 모드의 경우, 실제 비틀림 시험조건 중 토크 가진 속도는 4 Hz로 입력을 하지만 가진 속도에 대한 영향성을 확인하기 위하여 가진 주파수 1 Hz 및 4 Hz 조건상태에서 시험을 진행하였다. 두 가지 모드에 대한 계측 값의 반복성 및 재현성 확보를 위하여 조건 별 2회 반복하여 데이터를 취득하였다.
상기 두 가지 시험모드의 상세 조건에 대해서는 Table 1에 정리하였으며, 시험 샘플 및 비틀림 시험기 구성 사진에 대해서는 Fig. 6 및 Fig. 7에 나타내었다.
2.4 유한요소 해석
댐퍼시스템 조립품을 유한요소 모델링을 통한 수치해석을 진행하기 위하여 검증부품 4종을 유한요소모델로 구성하였다. 또한, 해석시간의 단축 및 해석 효율을 고려하여 1/4 대칭모델 및 해석진행에 필수적인 부품들만 유한요소로 구성하였다. 해석 모델링은 Altair 사의 HyperMesh 프로그램을 활용하여 모든 요소를 탄성모델로 모델링 구성하였다. 요소는 약 12,538 ~ 21,699개, 절점 개수 약 36,279 ~ 57,458개 수준이다. 또한 요소의 크기는 평균 2 mm이며, 타입은 ABAQUS C3D10M 이다. 중심축을 중심으로 일정한 각도로 회전하는 댐퍼시스템의 특성을 고려하여 Fig. 8과 같이 구성하였다. 모터에서 들어오는 비틀림 최대토크 484 Nm는 D1 부 하단에 있는 서브플레이트 및 베이트 스토퍼(Base stopper)에 의하여 회전방향으로 인가되며, D2 스플라인허브 내경부를 강체로 연결하여 회전 및 변위 구속하였다. 각 부품과 스프링의 접촉을 고려하기 위하여 스프링 끝단 부에 스프링시트 모델을 별도로 구성하였으며, 각 부품들과의 접촉부위는 Contact pair 조건으로 마찰계수 0.1으로 설정하였다. 또한, 해석수렴성을 위하여 1/4 대칭모델링을 고려하였으며, 이를 위해 축 방향을 기준으로 ABAQUS Cycle symmetry 명령어를 사용하여 대칭조건을 부여하였다.3) 구조해석의 경우, ABAQUS/Standard solver를 이용하여 해석 진행하였다.
3. 신뢰성 검증 결과
3.1 비틀림 시험 결과
비틀림 시험에서는 모터에 의한 비틀림 하중을 스플라인허브 내경 측에 최대토크 484 Nm을 인가하였다. 앞서 언급한대로 1회의 비틀림 하중이 일정한 시간동안 부여되는 정적내구시험 및 비틀림 토크가 일정한 속도(1 Hz 및 4 Hz)로 반복되는 동적내구시험을 각 2회 반복하여 진행하였고, 이에 대한 시험 결과는 Fig. 9와 같다. 시험 결과를 확인해보면, 게이지를 부착한 모든 부품에 대하여 반복성 및 재현성이 확보된 것처럼 보인다. 실제로 허브플랜지, 디스크플레이트 및 스플라인허브에 대한 반복시험 간 변형율의 오차율은 5 % 내외로 측정되었다. 다만, 서브플레이트의 경우 정적 내구시험에서 최소 7 % ~ 최대 222 % 및 동적 내구시험에서 최소 5 % ~ 최대 292 %의 오차율을 보였다. 이는 스트레인게이지 부착 및 센서응답의 오류로 판단된다. 특히, 1 ~ 4번 게이지 4개의 모든 데이터가 상이하며 인장 및 압축의 경계가 명확히 보이지 않아 해당 부품은 시험/해석 검증대상에서 제외하였다. 또한, 디스크플레이트의 경우, 동적 모드에서 일부 스트레인게이지 센서 데이터 일부 파형이 비정상적으로 튀는 현상이 발생했다. 이는 댐퍼시스템의 협소한 내부구조에 센서 전선이 여러가닥 엉켜있음으로 인해 가진 속도를 이기지 못하고 불안정한 값이 입력된 것으로 판단된다. 결국 두 번째 반복시험 중 해당전선이 끊어져 정확한 데이터를 얻지 못했다. 이러한 이유로 디스크플레이트의 경우 1 Hz 속도에서 최대 20 %, 4 Hz 속도에서 최대 69 % 차이를 보였다. 동적 모드의 시험에서 이와 같은 문제가 발생함에 따라 모든 부품에 대한 동적 모드 전체 데이터를 신뢰할 수 없으므로 본 연구에서는 정적모드 조건의 시험결과만을 이용하여 시험/해석 결과를 검증하였다.
3.2 비틀림 시험/해석 결과비교
앞 절에서 언급한대로 서브플레이트 시험 데이터의 오류로 인해 허브플랜지(D1), 디스크플레이트(D2) 및 스플라인허브(D2) 3종을 대상으로 검증을 진행하였다. 또한, 정적 모드조건에서 토크에 따른 변형율 값의 오차율은 Table 2에 정리하였다. 여기서 오차율은 비틀림 시험 및 구조해석 변형율 값의 차이를 나타낸다. 또한, 부품에 작용하는 압축력과 인장력은 각각 ‘-’부호 및 ‘+’부호로 구분하였으며, 동일한 부위의 압축 및 인장력에 대하여 시험과 해석 결과값을 서로 비교하였다. 시험 계측된 값의 경우, -100 Nm부터 +484 Nm의 하중에 대하여 2회 반복한 후, 그 평균값을 해석결과와 비교하였다.
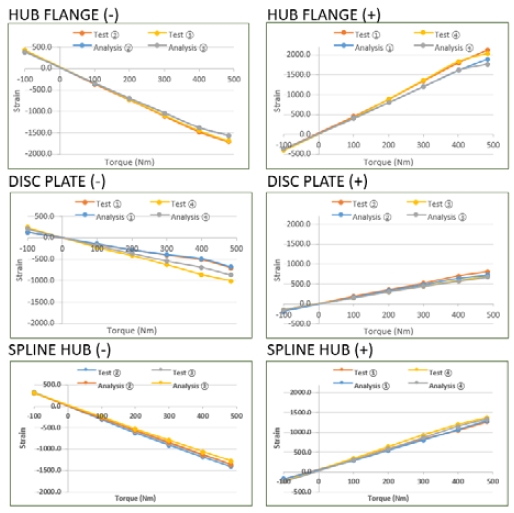
압축력 (-) 및 인장력 (+)에 대한 시험 결과와 해석결과의 비교그림은 Fig. 10과 같다. 3개의 검증부품 모두 해석결과가 시험결과와 유사한 경향으로 도출되는 것을 관찰할 수 있었다.
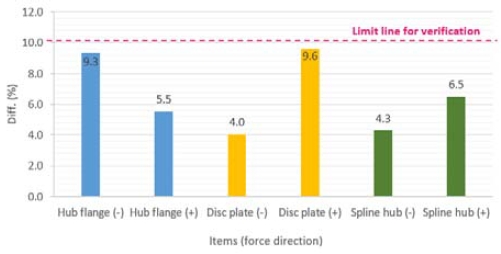
Table 2는 Fig. 10의 각 그래프에서 측정된 시험 및 해석별 2개의 게이지 결과를 각각 평균하였고, 이 값의 차이(시험 및 해석 평균값의 차이, 오차율)를 계산하였다. 대부분의 인장 및 압축 데이터에서는 일반적으로 합리적인 검증 기준인 오차율 10 % 이내의 값을 보이고 있지만, Table 2 및 Fig. 11에서 보는 것과 같이 허브플랜지 압축(토크 300 ~ 484 Nm) 및 디스크플레이트 인장(토크 100 Nm)에 대한 오차율은 10 %를 상회하는 오차율을 보이고 있다. 그러나 부품 3종에서 보여지는 압축력 및 인장력 각각의 오차율의 평균은 10 % 이내의 수준을 보이고 있기 때문에 해석 결과값은 합리적이라고 판단된다. 특히, 디스크플레이트 인장 데이터의 경우, 토크 100 Nm에서 거의 15 %에 육박하는 값이 추출되었다. 정적 모드 조건으로 시험 진행 중 시스템적인 문제로 인하여 불규칙적인 진동이 발생하는 오실레이션(Oscillation) 현상이 생겼으며, 이로 인하여 불안정한 데이터가 추출되었고, 해당 오차율은 일부 타당하다고 판단된다.
이로써, 댐퍼시스템의 구조해석에 대한 신뢰성 검증을 완료하였으며, 이때 구성한 유한요소 모델링을 확인하였다. 이렇게 검증된 모델링을 통해 추출된 변형률은 기계적 물성치 탄성계수를 기반으로 주응력으로 계산되며, 계산된 주응력을 기준으로 피로내 구해석이 진행된다.
4. 피로내구해석 추가 검증
4.1 피로내구 시험 및 해석 진행
댐퍼시스템 성능평가의 일환으로 진행되는 비틀림 시험은 스플라인허브에 비틀림 하중이 특정 횟수만큼 반복되는 피로내구시험이다. 이러한 이유로 CAE 해석을 이용하여 시험 평가를 대체하기 위해서는 궁극적으로 비틀림 피로내구시험 조건에 대한 추가적인 검증이 필요하다. 이에 따라 피로내구해석을 추가로 진행하였으며, 실제 성능평가결과를 피로내구 해석결과와 비교하여 정합성을 확인하였다.
댐퍼시스템은 작동 중 파손이 일어날 경우 심각한 문제를 초래하기 때문에 고객사에서는 일반적인 설계 입력하중보다 약 2.3배 높은 하중에서 13만회의 반복조건으로 성능평가를 요구하고 있다. 때문에 최소 -345 Nm 부터 최대 +654 Nm의 오버토크 하중을 13만회 반복 입력하여 비틀림 시험을 진행하였다. 위 조건에 대한 오버토크 비틀림 시험결과는 Fig. 12와 같다. 시험 결과, 약 10만 7천회에서 서브플레이트 및 디스크플레이트(D2)의 목 부에서 각각 파손이 발생하였다. 해당 부품들은 원가절감을 목적으로 SAPH440 소재를 적용하였다. SAPH440 재질은 구조적인 응력기준 만족에 충분한 항복강도(512 MPa)를 가지고 있지만, 피로성능을 좌우하는 피로한도(Endurance limit) 값이 250 ~ 300 MPa으로 상당히 낮은 수준이었다. 일반적으로 알려져 있는 피로한도 값은 인장강도의 0.5배 수준으로 추정 및 계산할 수 있는데, 적용된 SAPH440 재질도 인장강도 대비 0.5배 정도 낮은 피로한도로 인하여 부품 파손이 일어난 것으로 판단된다.
위 시험 결과를 바탕으로 CAE에 대한 신뢰성 및 정합성을 검증하기 위해 피로내구해석을 추가로 진행하였다. 유한요소 모델링은 앞서 구조해석에서 검증된 해석 모델링 방법을 차용하였으며, 본 시험에 사용된 서브플레이트 및 디스크플레이트 동일사양의 모델링 생성 및 적용하여 구조해석 및 피로내구해석을 진행하였다. 해당 모델에 대한 피로내구해석은 다쏘시스템 개발사의 Fe-safe 툴을 이용하여 진행하였다. 피로물성의 경우, 각 부품의 인장강도를 기준으로 프로그램 알고리즘에 의해 변환되는 내부기능을 이용하여 피로 물성치를 산출하였다. 산출된 피로 물성치는 Table 3과 같다. 피로내구해석은 크게 소성 및 탄성구간에 대하여 계산을 할 수 있지만, 댐퍼시스템의 경우 소성변형이 없는 제품 특성상의 이유로 탄성구간에 대한 피로내구해석을 진행하였다
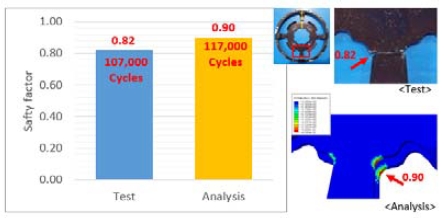
검증된 유한요소 모델링을 통한 댐퍼시스템의 피로내구해석 결과는 Fig. 13과 같다. Fig. 13에서는 피로내구 안전율을 나타내었다. 피로내구 안전율은 하중반복 횟수(13만 회)에 대한 파손발생 횟수의 비로, 값 1.0이 기준이다. 시험 및 해석에 대한 피로내구 안전율은 각각 0.82 및 0.90으로 나왔다. 시험안전율 0.82는 파손횟수 10만 7천회가 13만회 대비 82 % 수준임을 의미한다. 약 0.08 % 정도 해석 결과가 시험 대비 다소 높은 수준으로 계산되었다. 그러나 오버토크 횟수 13만회에 대한 시험 및 해석의 파손횟수를 비교하면 각각 107,000회 및 117,000회로 거의 유사 수준으로 봐도 무방하다.
피로시험결과의 경우, 교번 굽힘하중하에서 피로성능에 결정적인 피로한도에 영향을 주는 변수가 총 6가지 있다. 이러한 변수들에 의하여 결정되는 피로한도(Se)의 계산 수식은 (1)과 같다.4)
| (1) |
- * C1 = size
- * C2 = load,
- * C3 = surface finish,
- * C4 = surface treatment,
- * C5 = temperature
- * C6 = environment
피로시험에서 피로한도(Se’) 값에 의하여 피로내구수명이 결정되지만, 피로내구해석에 사용된 피로한도 값이 식 (1)과 같이 계산되었다고 보기 어렵다. 그러나, 비틀림 피로시험 및 피로내구해석 결과의 약 0.08 %(10,000회) 차이는 부품 물성치 및 공정 산포를 고려할 때, 타당한 결과로 보인다고 판단된다. 특히 피로내구해석에서 나타난 취약부는 비틀림 피로시험의 파손부와 유사한 부위로 확인되었다.
위 결과를 토대로 댐퍼시스템 부품에 대한 피로시험 성능평가를 CAE 피로내구해석으로 대체가 가능하며, 당사의 해석기술개발을 통하여 검증된 FE 모델링이 구성 완료를 최종적으로 확인할 수 있었다.
5. 결 론
본 연구에서는 TMED 시스템 내부에 위치한 댐퍼시스템에 대하여 CAE 해석적 검증을 진행하였으며, 이 과정에서 다음과 같은 결론을 내릴 수 있었다.
- 1) 유한요소 수치해석기법을 활용하여 해석기술개발을 진행하였으며, 댐퍼시스템에 대한 비틀림 시험 및 해석에서 추출된 변형율 값을 비교함으로써, CAE 구조해석에 대한 신뢰성 검증을 완료하였다.
- 2) 검증된 유한요소해석 모델링을 통해 오버토크에 대한 피로내구해석을 진행하였으며, 비틀림 오버토크시험의 파손 수준과 유사함을 확인함으로써, CAE 해석으로 비틀림 내구시험의 예측 가능성을 확인하였다.
- 3) 다만, 당사가 보유하고 있는 시험/해석 검증 이력 횟수가 충분하지 않고, 피로시험은 시험 샘플에 대한 품질수준과 산포에 따라 피로시험 결과가 달라질 수 있는 민감한 사항이므로 지속적으로 시험 및 해석 검증/비교 등의 활동을 통해 DB를 축적하여 관리해야 할 것으로 판단된다.
Subscripts
| HEV : | hybrid electric Vehicle |
| TMED : | transmission mounted electric device |
| CAE : | computer aided engineering |
| FEM : | finite element method |
| FE modeling : | finite element modeling |
References
- T. H. Shin, C. S. Park, S. H. Bark, and H. E. Kang, “Study on Verification Test of Torsional Damper System for P1-P2 Hybrid,” KSAE Spring Conference Proceedings, pp.768-774, 2021.
- T. H. Shin, C. S. Park, D. G. Lim, D. Y. Kim, S. H. Bark, and H. E. Kang, “Study on Durability Method of P1-P2 TMED System for Torsional Vibration,” KSAE Fall Conference Proceedings, pp.935-940, 2021.
- ABAQUS/Standard, User’s Manual, Hibbit, Karlsson & Sorenson Inc, 2005.
- J. A. Bannantine, J. J. Comer, and J. L. Handrock, Basic of Fatigue Analysis, Gyomoon, Korea, pp.10-31, 2001.