인공신경망 대리모델 기반 CFRP 복합재료 부적층판의 강도 역추정에 대한 연구
Copyright Ⓒ 2024 KSAE / 223-06
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Carbon fiber reinforced plastic(CFRP) composites are commonly used in lightening the weight of automobiles to reduce carbon emissions. To apply the material to the automobile, it is important to understand the impact of the material and analyze it using the finite element method. Hence, this study constructed a finite element analysis model of a drop-weight test comprising sub-laminates efficient for the analysis of units of complete vehicles and parts. To obtain the equivalent strengths of the sub-laminates, an artificial neural network surrogate model was developed based on the finite element method, and its reliability was verified. The optimal strengths value was inversely estimated by comparing the error with the result of the drop-weight test, and effectiveness was confirmed under other potential energy conditions.
Keywords:
CFRP, Composite, Finite element method, Drop-weight test, Artificial neural network, Inverse estimation키워드:
탄소 섬유 강화 플라스틱, 복합재료, 유한요소법, 낙하 충격 시험, 인공신경망, 역추정1. 서 론
전 세계적으로 탄소배출 절감과 화석연료의 유한성으로 인해 환경 보호에 대한 규제가 엄격해지고 있다. 따라서 엔진의 효율 향상과 차량 경량화를 통한 배기가스 저감에 대한 연구 개발이 활발히 이루어지고 있다.1,2) 또한 전기에너지를 이용한 친환경 모빌리티 시장이 확장됨에 따라, 배터리나 전기모터 등의 부품의 추가로 인한 경량화를 위한 방안이 필요하다. 그 방안 중 하나로 중량 대비 고강도를 가지는 소재의 적용하는 방법이 있다. 알루미늄 및 티타늄 합금이 경량화를 위한 고강도 소재로 널리 사용되어왔으나, 최근에는 비강도와 비강성이 우수하고, 내부식성, 성형성 측면에서 이점이 있는 탄소 섬유 강화 플라스틱(Carbon Fiber Reinforced Plastic, CFRP) 복합재료가 주목을 받고 있다.3-4) 이 재료는 적층 각도와 패턴에 따라 요구되는 기계적 물성을 맞춤형으로 제작할 수 있다는 장점도 가진다. 따라서 최근 자동차의 범퍼나 프레임 등의 부품에 CFRP 복합재료를 적용하고 있다.5)
이러한 재료의 손상은 곧 차량 구조의 건전성을 저하시켜 모빌리티 탑승자의 안전까지 위해할 가능성이 있다. CFRP 복합재료는 섬유와 기지로 구성된 프리프레그가 적층되어 충격에 취약하고 복합적인 파손 모드가 발생해 육안으로 손상을 분석하기 어렵다. 따라서 충격 시험을 통해 차량의 안전 성능을 평가하고, 짧은 순간에 발생하는 충돌 상황에서 유한요소법(Finite Element Method, FEM)을 활용한 파손 거동의 세부적인 분석이 중요하다.6) 컴퓨터의 연산 처리 속도가 증가하고 머신러닝(Machine learning)에 대한 다양한 기법들이 발전하면서, 실험과의 정합성을 높이면서도 시험 비용을 절감하는 가상 시뮬레이션에 대한 연구가 활발히 이뤄지고 있다.7,8)
본 연구에서는 CFRP 복합재료 적층판의 부적층판(Sub-laminate) 단위로 구성한 유한요소모델의 등가 강도를 예측하기 위해 낙하 충격 시험과 역추정 기법에 대한 연구를 수행하였다. CFRP 복합재료 적층판의 낙하 충격 시험을 수행하고 이에 대한 유한요소모델을 구축하였다. 여러 개의 프리프레그 플라이를 부적층판으로 설정하여 솔리드(Solid) 요소로 구성된 하나의 파트로 생성하여 해석 비용을 감소시키는 모델링 기법을 적용하였다. 강도값을 입력하면 유한요소해석의 에너지 곡선 결과를 출력하는 인공신경망(Artificial Neural Network, ANN) 대리모델(Surrogate model)을 구축하였다. 이에 유전 알고리즘(Genetic Algorithm, GA)을 적용하여 낙하 충격 시험으로부터 도출한 에너지 곡선과의 오차가 최소가 되는 CFRP 부적층판의 강도를 역추정하여 획득하였다. 획득한 강도값을 다른 위치에너지 조건에 대한 유한요소해석에 적용하여 역추정한 강도와 대리모델의 유효성을 확인하였다.
2. 낙하 충격 시험
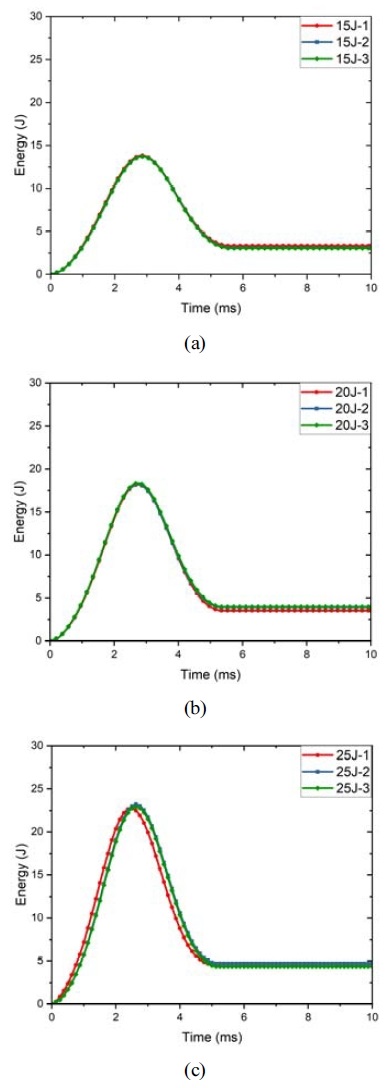
CFRP 복합재료 적층판의 강도에 대한 파라미터를 역추정하기 위하여, 충격에 대한 흡수 에너지 곡선을 이용하였다. 이용한 에너지 곡선은 Fig. 1과 같으며, ASTM D7136/7136M59) 규격에 따른 낙하 충격 시험(Drop-weight test)을 통해 획득하였다. CFRP 복합재료 시편은 Toray사의 T700 s급 탄소섬유와 에폭시로 구성된 일방향 프리프레그를 사용하여 오토클레이브를 사용하여 성형하였다. 시편의 적층 각도는 [45/0/-45/90]3s로 0.11 mm의 프리프레그를 총 24개의 플라이로 적층하여, 150×100 mm 크기의 직사각형 판재로 가공하였다. 프리프레그의 물성은 Table 1과 같다.
본 연구에서 설정한 3가지 위치에너지 조건 중 25 J에서 가장 파손 정도가 심하였다. 따라서 위치에너지가 25 J일 때 획득한 에너지 곡선을 인공신경망 대리모델과 강도 파라미터 역추정 과정에 사용하였다.
3. 복합재료 낙하 충격 시험에 대한 유한요소해석
짧은 시간 동안 발생하는 재료의 충돌 거동에 대하여 유한요소해석이 필수적이고, 해석의 목적에 맞는 유한요소모델을 구축하는 것이 중요하다. 본 연구에서는 해석 비용을 절감하면서도, 복합재료 적층판의 층간분리까지 적절히 모사할 수 있는 모델링기법을 통해 유한요소모델을 구축하였다. 구축한 유한요소모델은 인공신경망 대리모델의 훈련 샘플 생성하는 데 사용하였다.
3.1 복합재료모델
유한요소해석을 통해 복합재료 적층판을 모델링하기 위해서 재료의 방향에 따른 파손 여부 판단 기준 및 다양한 파손 모드를 구현할 수 있는 여러 가지 방법들이 있다. 이는 크게 쉘(Shell) 요소와 솔리드(Solid) 요소를 사용하는 2가지 방법으로 나뉜다. 쉘 요소는 하나의 파트 내에 다수의 적분점(Integration point)을 설정하여, 각 적분점에 대한 적층 정보를 입력할 수 있다. 하지만 솔리드 요소는 하나의 적분점만 가지므로, 하나의 솔리드 파트에 여러 개의 플라이에 대한 정보를 입력할 수 없다. 따라서 Fig. 2의 (a)와 같이 적층판의 플라이 수 만큼의 솔리드 파트를 생성하여 복합재료 적층판을 구성하고 각 플라이의 적층 정보를 입력하여야 한다. 이는 연산 비용이 증가하는 단점이 존재하지만, 두께 방향에 대한 응력을 계산할 수 있고, 충돌 거동에 대하여 실험과 유사하다는 장점이 있어 본 연구에 적용하였다.10)
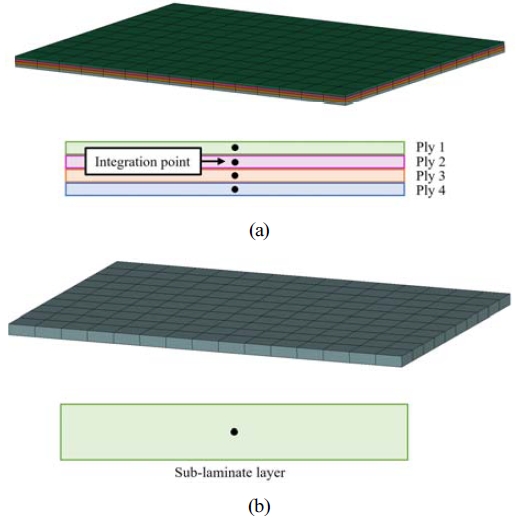
Modeling methods of laminates using solid element (a) Plies consist of solid elements (b) Stacked-solid methods
CFRP 복합재료를 적용한 부품 및 완성차에 대하여 모든 플라이를 솔리드 요소로 구성한 해석 모델을 사용한다면 막대한 연산 자원과 시간이 필요하다. 따라서 본 연구에서는 솔리드 요소의 장점을 갖추면서도 해석 비용을 절감할 수 있는 Stacked-solid 기법을 적용하였다. 프리프레그를 사용한 제품 생산 시 요구되는 기계적 물성을 위한 적층 패턴의 경우의 수는 무한하다. 따라서 제작과 설계의 편리를 위해 여러 개의 플라이와 각도로 구성된 적층 패턴을 반복하여 제작하는 방식을 채택한다. 여기서 다수의 플라이로 구성되어 반복되는 적층 패턴을 부적층판이라 한다. Stacked-solid 기법은 Fig. 2의 (b)와 같이 솔리드 요소로 구성된 하나의 파트를 부적층판으로 가정하여 모델링하는 기법을 의미한다. 본 연구에서는 CFRP 복합재료 시편의 [45/0/-45/90]의 적층 각도가 반복되므로, 4개의 플라이로 구성된 적층 패턴을 부적층판으로 설정하였다. 따라서 총 24개의 플라이를 6개의 솔리드 요소로 구성된 파트로 모델링하였다.
부적층판으로 구성된 파트 간 접착층의 층간분리(Delamination)를 모사하기 위해 LS-DYNA의 Contact automatic oneway surface to surface tiebreak 접촉 조건을 적용하였다. 이 접촉 조건은 접착제의 수직(NFLS) 및 전단(SFLS) 파손 강도와 계면의 응력과 관계된 파손 기준식인 식 (1)에 따라 층간분리를 판단한다. 이후 두 절점 간의 Tie 접촉 조건이 해제되면서 층 간 침투를 방지하는 Surface to surface 접촉 조건으로 변경되어 층간 분리가 구현된다.11)
| (1) |
서로 다른 적층 각도를 가지는 플라이들이 하나의 파트로 구성됨에 따라 그에 상응하는 부적층판의 등가 물성의 입력이 필요하다. 따라서 등가 강성은 고전 적층판 이론을 통해, 등가 강도는 인공신경망 기반 역추정 기법을 통해 획득하는 연구를 수행하였다.
CFRP 복합재료 적층판의 강성은 고전 적층판 이론(Classical Laminate Theory, CLT)를 통해 계산하였다. 고전 적층판 이론은 복합재료 적층판의 등가 물성을 유도하여 그에 대한 거동을 예측하기 위한 이론이다. 직교이방성을 지니는 일방향 프리프레그로 구성된 적층판의 강성 및 포아송비의 계산 과정은 식 (1) ~ (3)과 같다.12)
우선 식 (1)과 프리프레그의 물성을 이용하여 축소 강성 행렬 Qij을 계산한다. 이후 임의의 적층 각도에서 전체 좌표계(x, y, z)로 축변환한 축소 강성 행렬 을 도출한다. 이를 각 플라이에 대한 두께를 고려하여 적층판에 가해지는 힘의 합력을 유도할 수 있고, 그 과정에서 적층판의 면내 강성인 [Aij]를 응력-변형률 관계식에 의해 유도된다. 직교이방성 적층판이 대칭으로 적층된 경우, 전단 커플링의 효과가 상쇄되어 A16=A26=0이 된다. 따라서 적층판의 변형률과 면내력의 관계식은 식 (2)와 같고, 식 (3)을 계산하여 적층판의 강성과 포아송비를 도출한다.
| (2) |
| (3) |
| (4) |
본 연구에서 설정한 부적층판에 대해 계산한 등가 강성 및 포아송비는 Table 2와 같다. 면 내에서 서로 직교하는 방향의 물성의 계산값이 동일하므로 준등방성(Quasi-isotropy)을 띄는 것을 확인하였다. 따라서 본 연구에서는 준등방성 부적층판의 인장, 압축, 전단에 대한 강도를 면내 방향과 두께 방향으로 나누어 총 6가지의 강도(Tp, Tt, Cp, Ct, Sp, St) 역추정을 수행하였다.
복합재료는 금속재료와는 다르게 소성변형이 거의 없이 취성 파괴가 되는 성질이 있다. 복합재료 적층판의 파손 거동은 하나의 층 내에서 섬유와 기지가 손상되거나 섬유와 기지가 분리되는 층내 파괴(Intralaminar failure)와 적층판의 층과 층 사이의 경계면이 분리되는 층간 파괴(Interlaminar failure)로 구분된다. 따라서 유한요소모델 생성 시 다양한 파손 모드에 따른 손상을 판단할 수 있는 적절한 재료 모델을 선정해야 한다. 본 연구에서는 발전된 Hashin의 파손 기준식이 적용된 LS-DYNA의 MAT59 composite failure solid model을 사용하였다.13,14) 이 재료 모델은 3차원 솔리드 요소로 구성된 파트에 적용되어 재료 방향 별 파손 모드에 따른 손상을 판단하고, 점진적인 재료의 물성 저하를 모사할 수 있다. 사용한 복합재료 손상 모델은 강성과 강도에 대한 입력이 필요하다. 따라서 강성은 고전 적층판 이론으로부터 도출한 부적층판의 계산값을 입력하였다. 본 연구에서는 부적층판의 강도를 역추정하는 것이 목적이므로, 인공신경망 대리모델의 샘플데이터 생성을 위해 추출한 임의의 강도값을 입력하여 유한요소해석을 수행하였다.
3.2 낙하 충격 시험의 유한요소모델
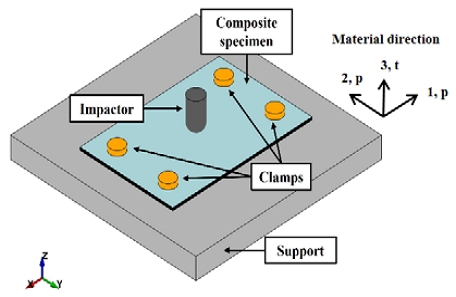
낙하 충격 시험의 유한요소해석을 수행하기 위해 충돌 및 비선형 구조 응답에 대해 특화된 LS-DYNA 프로그램을 사용하였다. 유한요소모델은 Fig. 3과 같이 실험 결과에 영향을 미치는 요소들만 고려하여 시편(Specimen), 충돌체(Impactor), 지지대(Support), 클램프(Clamp)로 구성하였다. 충돌체와 지지대, 클램프는 ASTM D7136/7136M5의 규격에 따른 실험 장비와 동일한 크기로 형상을 생성하고, 강체(Rigid body)로 설정하였다.
충돌체는 실험에서 설정한 질량과 동일하도록 밀도를 부여하고, 시편의 두께 방향으로만 이동하도록 z 방향을 제외한 나머지 자유도를 구속하였다. 실험으로 획득한 에너지 곡선에서 초기 충격에너지를 의미하는 최대점에서의 속도를 충돌체에 초기 속도로 부여하였다. 지지대와 클램프는 모든 자유도를 구속하였다. 모든 파트 간의 접촉 조건은 Contact automatic surface to surface 키워드를 적용하였다.
4. 인공신경망 대리모델 기반 강도 역추정
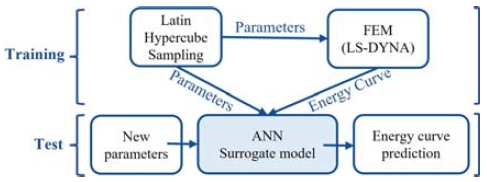
낙하 충격 시험의 유한요소모델과 해석 결과를 바탕으로 인공신경망 대리모델을 구축하였다. 유전 알고리즘을 통한 최적화 과정에 대리모델을 적용하여 복합재료의 준등방성 부적층판의 강도를 역추정하였다. 인공신경망 대리모델의 구축과 파라미터의 역추정 과정을 정리하면 Fig. 4의 플로우차트와 같다.
4.1 인공신경망 대리모델
인공신경망은 머신러닝 기법 중 하나로, 동물 뇌의 뉴런과 시냅스로 이루어진 신경망과 같은 구조로 구성된다. 신경망의 분산적이고 병렬적인 정보처리 능력을 모사하여, 대량의 데이터를 학습하고 결과를 예측한다. 컴퓨터의 연산 처리 속도가 급속히 향상됨에 따라 통계와 수치적 학습 과정으로 빠르게 결과를 예측하는 기법이 발전하고 있으며, 공학, 경제, 생산 공정 등 다양한 분야에서 적용되고 있다.
이러한 인공신경망은 학습을 통해 비선형적인 물리적 현상에 대하여 수학적 모델링 없이 입력에 대한 출력을 예측하는 특징이 있다. 또한 입력 변수들 간 비선형적인 조합이 가능하여, 다수의 입력 파라미터 설정과 결과에 대한 상관관계를 인식할 수 있다는 장점이 있다. 이에 본 연구에서는 복합재료 부적층판의 6 가지 강도에 따른 낙하 충격 시험 에너지 그래프를 예측하기 위하여 인공신경망 기법을 채택하였다.
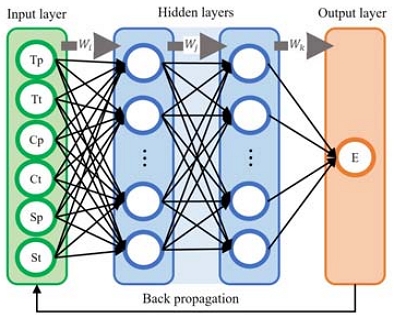
본 연구는 Matlab에서 제공하는 Neural network toolbox를 사용하여 인공신경망 대리모델을 구축하였다. 인공신경망은 일반적으로 Fig. 5와 같은 구조의다수의 층으로 구성되어 반복 학습 후, 새로운 입력값에 대한 출력값을 예측한다. 인공신경망 대리모델은 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)로 구성하였다. 입력층의 입력 데이터는 역추정의 대상인 6가지의 강도 파라미터이다.
훈련 샘플에 대한 입력 데이터는 균일하게 분포된 표본을 추출하는 기법인 라틴 방격 추출법(Latin hypercube sampling)을 통해 획득하였다. 시험 샘플에 대한 입력 데이터는 무작위의 난수를 추출하였고, 훈련과 시험에 대한 입력 데이터 모두 6가지의 파라미터 당 100개 씩 추출하였다. 출력층의 데이터는 추출한 파라미터를 25 J의 위치에너지 조건의 충돌 해석 모델의 해석 결과인 에너지 곡선을 사용하였다.
은닉층은 각각 100개의 노드로 구성된 2개의 층으로 구성하였고, 역전파 알고리즘에 적합한 쌍곡 탄젠트 시그모이드 함수를 활성 함수로 설정하였다.15) 대리모델의 훈련 알고리즘은 가중치와 편향을 업데이트하여 신경망의 일반화가 잘되는 베이지안 정규화 역전파(Bayesian regulation backpropagation) 훈련 알고리즘을 적용하였다.16) 훈련 데이터 중 70 %는 훈련, 15 %는 시험, 그리고 15 %는 검증에 사용되도록 비율을 설정하였다.
인공신경망 대리모델을 생성한 후 새로운 입력값에 대하여 신뢰성있는 결과를 예측할 수 있는지에 대한 검증이 필요하다. 6 가지의 강도에 대하여 무작위로 추출한 시험 데이터를 유한요소해석에 입력하여 도출한 결과와 인공신경망 대리모델에 입력한 예측 결과와 비교하여 신뢰성을 검증하였다.
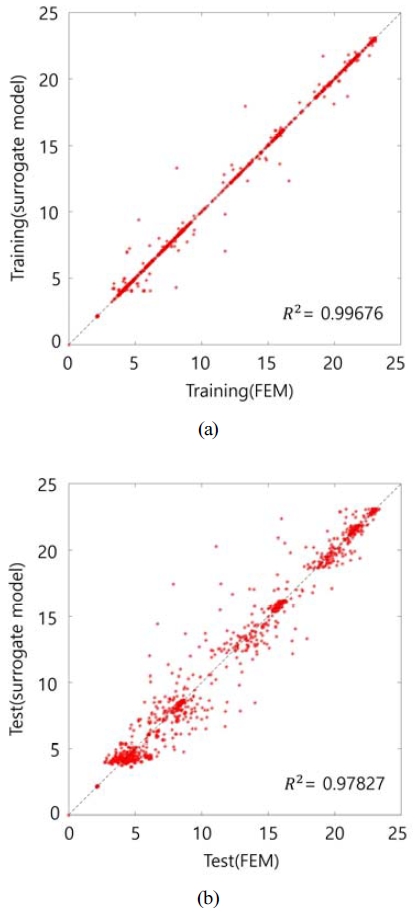
머신러닝에서 대리모델의 적합도에 대한 평가 지표인 결정계수(Coefficient of determination, R2)를 계산하여 신뢰성을 평가하였다.15) 추출한 훈련 및 시험용 샘플데이터를 인공신경망 대리모델에 입력하여 출력한 결과값으로 계산한 결정계수는 Fig. 6과 같다. 일반적으로 결정계수가 0.9이상이며 1에 근접할수록 대리모델의 적합도와 신뢰성이 우수하다고 판단한다.17) 계산한 결정계수는 훈련데이터에서 0.99676, 시험 데이터에서 0.97827의 값을 가지므로, 인공신경망 대리모델이 신뢰성을 갖추었음을 검증하였다.
4.2 CFRP 복합재료의 준등방성 부적층판의 강도 역추정
CFRP 복합재료의 준등방성 부적층판의 강도를 역추정하기 위하여 유전 알고리즘을 적용하였다. 유전 알고리즘은 생물학적 진화에 바탕을 둔 통계적 탐색 알고리즘이다. 자연 선택과 교차(Crossover) 및 변이(Mutation) 연산을 사용하여, 문제에 대한 최적의 해로 진화시킨다.
본 연구에서는 인공신경망 대리모델을 유전 알고리즘에 적용하였다. 먼저 임의의 강도 파라미터를 인공신경망 대리모델에 입력하여 그에 대한 에너지 곡선을 예측한다. 실험 결과와의 평균 절대 오차(Mean absolute error, MAE)를 유전 알고리즘의 목표함수로 설정하였다.18) 평균 절대 오차는 회귀모델의 성능 지표로 널리 활용되며, 0에 근접할수록 신뢰성이 있음을 판단한다.
목표함수의 계산값이 최소가 되는 최적의 강도값을 찾기 위해 이와 같은 과정을 반복한다. 인공신경망 대리모델과 유전 알고리즘을 적용한 역추정 기법으로 획득한 강도값을 Table 3에 나타내었다.
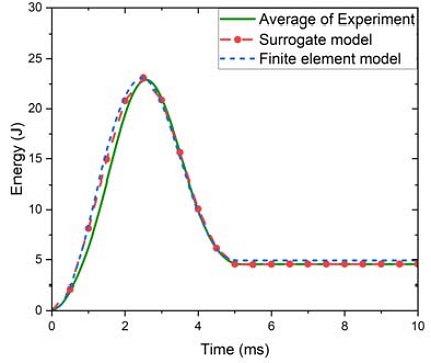
획득한 강도값을 유한 요소 해석과 인공신경망 대리모델에 입력한 결과와 실험 결과를 비교하여 Fig. 7에 나타내었다. 시편이 흡수한 에너지량은 대리모델에서 4.5462 J, 유한요소해석에서 4.927 J로, 실험 결과의 평균인 4.5462 J에 매우 근접한 결과임을 확인하였다. 또한 에너지 곡선의 경향과 최대점이 나타나는 시점도 실험 결과와 유사하다.
획득한 강도의 에너지 곡선 예측에 대한 신뢰성을 판단하기 위해 회귀모델의 성능 지표인 절대 평균 오차와 대칭 절대 평균 백분율 오차(Symmetric mean absolute percentage error, SMAPE)를 계산하였다.18) 대칭 절대 평균 백분율 오차의 계산식은 식 (22)와 같고, 0에 근접할수록 신뢰성이 우수함을 나타낸다.17) 실험과 인공신경망 대리모델 그리고 유한요소모델 간의 결과에 대한 절대 평균 오차와 대칭 절대 평균 백분율 오차를 계산한 결과를 Table 4에 나타내었다. 2가지 오차 계산 결과 모두 0에 근접하므로 획득한 강도값은 신뢰성을 가짐을 확인하였다.
4.3 다른 위치에너지 조건에서 역추정 강도 적용
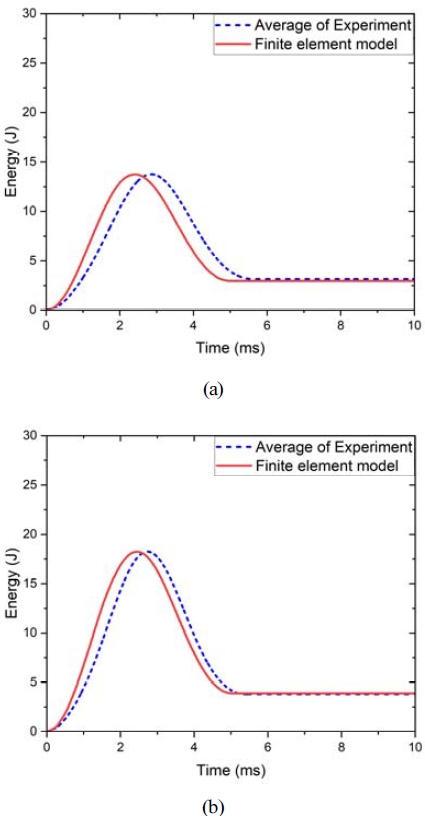
위치에너지가 25 J일 때의 실험 결과와 유한요소모델을 사용하여 CFRP 준등방성 부적층판의 강도를 역추정하였다. 획득한 강도의 유효성을 확인하기 위하여 15 J과 20 J의 위치에너지 조건의 유한요소모델에 적용하여 비교하였다. 실험으로 획득한 에너지 곡선과 유한요소해석의 결과를 Fig. 8에 나타내었다.
실험과 유한요소해석을 통해 도출한 에너지 곡선의 경향성은 서로 유사한 것을 확인하였다. 시편이 흡수한 총 에너지와 오차를 Table 5에 나타내었다. 두 경우 모두 5 % 내외의 오차를 가지므로, 획득한 강도가 총 흡수에너지를 예측하는데 유효성이 있음을 검증하였다. 하지만 Fig. 8에서 볼 수 있듯이 에너지의 최대점은 유한요소해석에서 실험보다 더 일찍 나타난다. 이는 25 J의 위치에너지 조건의 실험 결과를 통해 강도를 역추정하였으므로, 비교적 더 높은 강도의 획득이 그 원인으로 사료된다. 따라서 15 J과 20 J의 위치에너지 조건에서 선택한 복합재료 모델의 점진적 강도 저하에 대한 효과가 적게 나타나고, 충돌체의 반발 속도가 증가하여 최대점에 도달하는 시점이 앞당겨진다.
5. 결 론
본 연구에서는 CFRP 복합재료의 낙하 충격 시험 결과를 수행하고 이에 대한 유한요소모델을 구축하였다. 인공신경망 대리모델과 유전 알고리즘을 적용하여 4개의 플라이로 구성된 부적층판 파트의 준등방성 강도 역추정에 대한 연구를 수행하였다.
- 1) CFRP 일방향 프리프레그를 [45/0/-45/90]의 적층각도를 가지는 부적층판을 대칭 및 반복적으로 적층하여 낙하 충격 시험에 대한 복합재료 시편을 제작하였다. 15 J, 20 J, 25 J의 위치에너지 조건에 대한 낙하 충격 시험을 수행하여 에너지 흡수에 대한 곡선을 도출하였다.
- 2) 25 J의 위치에너지 조건에서의 낙하 충격 시험에 대한 유한요소모델을 구축하였다. 4개의 플라이로 구성된 부적층판을 솔리드 요소로 구성된 하나의 파트로 생성하였고, 고전 적층판 이론을 통해 계산한 부적층판의 강성을 MAT59 복합재료 모델에 적용하였다.
- 3) 인공신경망 대리모델을 생성하기 위해 6가지 방향에 대한 강도의 훈련 및 시험 데이터를 파라미터 당 100개 씩 추출하였다. 구축한 유한요소모델을 바탕으로 추출한 훈련 및 시험 데이터에 대한 에너지 곡선을 출력값으로 획득하였다. 획득한 훈련 샘플을 통해 인공신경망 대리모델을 훈련시키고, 시험 샘플에 대한 결정계수를 계산하여 신뢰성을 검증하였다.
- 4) 구축한 인공신경망 대리모델에 유전 알고리즘을 적용하여, 실험 결과에 대해 목표 함수가 최소가 되는 6가지의 강도값을 역추정하였다. 획득한 강도를 인공신경망 대리모델과 유한요소모델에 적용한 결과, 에너지 곡선의 경향성이 일치하고 성능지표 계산 결과를 통해 신뢰있는 파라미터임을 확인하였다.
- 5) 대리모델을 구축하기 위해 사용한 25 J 외 15 J과 20 J의 위치에너지 조건의 유한요소모델에 획득한 강도를 대입한 결과를 실험 결과와 비교하였다. 유한 요소 해석 결과에서 최대점의 시점이 실험보다 앞당겨지는 경향이 있지만, 에너지 곡선의 전반적인 개형이나 총 에너지 흡수량의 오차가 5 % 내외로 매우 유사하여 획득한 강도의 유효성이 있음을 확인하였다.
본 연구를 통해 해석 비용 측면에서 효율적인 유한요소모델을 구축하기 위한 물성을 인공신경망과 최적화기법을 통해 획득할 수 있음을 확인하였다. 이는 적층 패턴이나 재료의 선정 과정에서 물성 시험을 위한 비용을 대폭 절감할 수 있을 것이라 기대된다. 다양한 에너지 조건이나 파손 모드에 대한 데이터를 인공신경망 대리모델에 추가적으로 훈련시켜 더욱 신뢰성이 있는 물성 역추정 시스템을 구축이 필요하다고 판단된다.
Nomenclature
| σ : | normal stress, MPa |
| NFLS : | tensile failure strength |
| SFLS : | shear failure strength |
| τ : | shear stress, MPa |
| Q : | reduced stiffness matrix |
| ε : | normal strain, mm/mm |
| γ : | shear strain, mm/mm |
| N : | net force of laminate, N |
| tply : | thickness of plies, mm |
| A : | in-plane stiffness matrix |
| E : | elastic modulus, GPa |
| G : | shear modulus, GPa |
| ν : | poisson’s ratio |
| T : | tensile strength, MPa |
| C : | compressive strength, MPa |
| S : | shear strength, MPa |
| R2 : | coefficient of determination |
Subscripts
| n : | normal direction |
| s : | shear direction |
| k : | order of plies |
| p : | in-plane direction |
| t : | thickness direction |
| 1, 2, 3 : | fiber, matrix, thickness direction |
Acknowledgments
이 논문은 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 기본연구지원사업(RS-2023-00253462182065300001)과 교육부 및 한국연구재단의 4단계 두뇌한국21 사업(4단계 BK21 사업)의 지원을 받아 수행된 연구임. 이에 관계자 여러분들께 감사드립니다.
References
- S. Jeong and J. Ha, “Lightweighting Technology Development and Trends in Automotive,” Auto Journal, Vol.40, pp.30-34, 2018.
-
K. Sim, H. Shin, W. Cho, G. Choi, Y. Lee, Y. Son and N. Jeon, “Structure Design of Light Weight Axle Beam for Medium Duty Commercial Vehicle Using Hot Press,” Transactions of KSAE, Vol.23, No.4, pp.371-379, 2015.
[https://doi.org/10.7467/KSAE.2015.23.4.371]

-
Y. Kim and H. Kim, “An Optimal Design of CFRP Prepreg Laminates for Automotive Roof Considering Structural Stiffness and Formability,” Transactions of KSAE, Vol.28, No.10, pp.735-744, 2020.
[https://doi.org/10.7467/KSAE.2020.28.10.735]

-
J. Hong, S. Yoo and S. Chang, “Design and Performance Evaluation of Carbon Fiber/Epoxy Composite-Aluminum Hybrid Wheel for Passenger Cars,” Composite Research, Vol.26, No.6, pp.386-391, 2013.
[https://doi.org/10.7234/composres.2013.26.6.386]

-
J. Kim, K. Kim, S. Kim, D. Shin and D. Kim, “Development of Carbon Continuous-Fiber Composite Frame for Automotive Sun-Roof Assembly,” Transactions of KSAE, Vol.25, No.3, pp.350-359, 2017.
[https://doi.org/10.7467/KSAE.2017.25.3.350]

-
A. Gonzalez-Jimenez, A. Manes, A. Beligni, M. Dziendzikowski, C. Sbarufatti and M. Giglio, “Modeling and Experimental Testing of Thick CFRP Composites Subjected to Low Velocity Impacts,” Procedia Structural Integrity, Vol.24, pp.101-109, 2019.
[https://doi.org/10.1016/j.prostr.2020.02.009]

-
C. Stephen, D. Thekkuden, A. Mourad, B. Shivamurthy, R. Selvam and S. Behara, “Prediction of Impact Performance of Fiber Reinforced Polymer Composites Using Finite Element Analysis and Artificial Neural Network,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol.44, No.9, Paper No.408, 2022.
[https://doi.org/10.1007/s40430-022-03711-8]

-
H. Laaouidi, M. Tarfaoui, M. Nachtane and M. Trihi, “Energy Absorption Characteristics in Hybrid Composite Materials for Marine Applications Under Impact Loading: Case of Tidal Current Turbine,” International Journal of Energy Research, Vol.45, No.4, pp.5894-5911, 2020.
[https://doi.org/10.1002/er.6210]

- ASTM D7136/D7136M, Standard Test Method for Measuring the Damage Resistance of a Fiber-Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event, ASTM International, Pennsylvania, 2015.
-
F. Ahmad, F. Abbassi, M. Kim, J. Jung and J. Hong, “Finite Element Analysis for the Evaluation of the Low-Velocity Impact Response of a Composite Plate,” Advanced Composite Materials, Vol.28, No.3, pp.271-285, 2018.
[https://doi.org/10.1080/09243046.2018.1510589]

-
B. Lawrence Sy, Z. Fawaz and H. Bougherara, “Numerical Simulation Correlating the Low Velocity Impact Behaviour of Flax/Epoxy Laminates,” Composite Part A, Vol.126, Paper No.105582, 2019.
[https://doi.org/10.1016/j.compositesa.2019.105582]

-
C. Cho and M. Kwon, “Prediction of Compressive Behavior of FRP-Confined Concrete Based on the Three-Dimensional Constitutive Law,” Journal of Korea Concrete Institute, Vol.16, No.4, pp.501-509, 2004.
[https://doi.org/10.4334/JKCI.2004.16.4.501]

- W. Cheng and J. Hallquist, “Implementation of Three-Dimensional Composite Failure Model into DYNA3D,” Livermore Software Technology.
- LS-DYNA Theory Manual, Livermore Software Technology Corporation, 2006.
- H. Byun and J. Kim, “Estimating Strain Rate Dependent Parameters of Cowper-Symonds Model Using Electrohydraulic Forming and Artificial Neural Network,” Transactions of Materials Processing, Vol.31, No.2, pp.81-88, 2022.
-
B. Demirbay, D. Kara and Ş. Uğur, “A Bayesian Regularized Feed-Forward Neural Network Model for Conductivity Prediction of PS/MWCNT Nanocomposite Film Coatings,” Applied Soft Computing Journal, Vol.96, Paper No.106632, 2020.
[https://doi.org/10.1016/j.asoc.2020.106632]

-
Y. Kim and K. Lee, “Accuracy Analysis of Machine Learning Methods for Predicting PM Concentration,” Journal of Korean Society for Atmospheric Environment, Vol.39, No.2, pp.149-164, 2023.
[https://doi.org/10.5572/KOSAE.2023.39.2.149]

-
D. Chicco, M. Warrens and G. Jurman, “The Coefficient of Determination R-Squared is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation,” PeerJ Computer Science, Vol.7, Paper No.e623, 2021.
[https://doi.org/10.7717/peerj-cs.623]