다양한 주행환경에서 시뮬레이션 기법을 활용한 전기자동차의 배터리 에너지 손실 분석
Copyright Ⓒ 2024 KSAE / 223-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In winter, the range of electric vehicles significantly decreases due to cabin heating and poor battery performance in low temperatures. As the battery temperature drops, the internal resistance of the battery rises, increasing energy loss. This study developed an electric vehicle simulation model using MATLAB/Simulink, which was used to analyze energy loss caused by battery internal resistance. The MCT mode, commonly employed for the electric vehicle energy efficiency test, was utilized for the drive mode, and various road gradients were applied to investigate the battery characteristics over a broader range of power. The simulation results demonstrated that, at a 0 % road gradient, the energy losses at low temperatures(0 oC) were approximately 4.54 times higher than those at high temperatures(30 oC). Similarly, for 3% and 6 % road gradients, the energy losses were about 7.62 and 7.79 times higher at 0 oC than at 30 oC, respectively.
Keywords:
Electric vehicle simulation, Battery internal resistance, Energy loss, Battery temperature, CC-CV charge키워드:
전기차 시뮬레이션, 배터리 내부저항, 에너지 손실, 배터리 온도, 정전류, 정전압 충전1. 서 론
전기차는 환경 친화적이며 에너지 효율적인 대중 교통 수단으로써 지속 가능한 모빌리티 시스템을 구축하는 데 중요한 역할을 한다. 또한, 기후 변화와 같은 다양한 글로벌 이슈에 대한 대안적인 해결책을 제시하고 있으며, 기술⋅산업적으로 급격한 성장을 이루었다. 이러한 성장은 전기차 시장의 규모를 키웠고, 회사 간의 경쟁을 가속화하였다. 회사의 경쟁력을 판가름하는 요소 중에서도 1회 충전 주행거리는 전기차 기술의 척도이자 전기차의 성능을 결정하는 중요한 요소 중 하나로써, 이를 높이기 위한 연구는 전기차 회사의 기술 경쟁력을 강화하고 전기차 산업의 발전과 보급을 촉진시키는 데 중요한 역할을 하고 있다.
전기차 1회 충전 주행거리는 겨울철이 되면 급감하는 현상이 나타난다.1) 겨울철 전기차 1회 충전 주행거리 급감 현상의 주된 원인으로 지목되는 것은 바로 차량 난방과 배터리 성능인데,2) 배터리 성능은 배터리 내부저항의 영향을 받는다.
배터리는 전기차의 주요 에너지 저장 및 공급 장치로써, 화학 에너지를 전기 에너지로 변환하여 차량의 운행을 가능하게 한다. 배터리 내부저항은 배터리 내부의 전기적인 저항으로, 전기에너지가 열에너지로 변환되는 현상을 포함하고 State of Charge(SOC) 및 배터리 온도 등에 따라 변화한다.
겨울철에는 낮은 외기 온도에 의하여 배터리 온도가 감소함에 따라 배터리 내부저항이 증가하게 된다.3) 이는 배터리 내부에서 더 많은 열이 발생한다는 것을 의미한다. 겨울철 낮은 외기온도에 따라 배터리 온도가 낮아지면 배터리 내부의 화학 반응 속도가 저하되고, 이는 전기화학적 프로세스 효율성에 영향을 미친다. 배터리 온도가 감소함에 따라 상대적으로 높아진 배터리 내부저항에 의하여 열로 손실되는 에너지가 증가하게 되며, 결과적으로 1회 충전 주행거리가 감소하게 된다.
본 연구에서는 겨울철 배터리 온도 감소에 의한 배터리 내부저항의 증가가 전기차 1회 충전 주행거리 감소 현상에 미치는 영향을 규명하고, 향후 전기차의 성능 향상 및 에너지 효율성을 높이기 위한 연구 및 개발에 관한 중요한 인사이트를 제공하기 위하여 시뮬레이션 기법을 통하여 배터리 내부저항에 의한 손실 에너지를 분석하였다.
추가로, 충전 과정에서의 배터리 내부저항에 의한 손실 에너지 또한 포함하여 분석한다.
2. 전기차 파워트레인 모델링
2.1 모델 구성
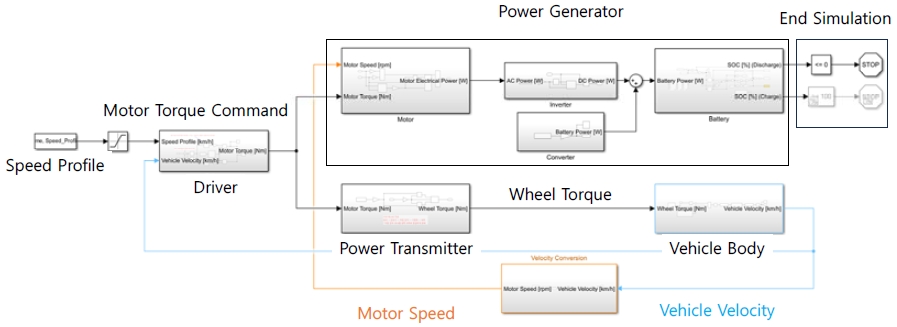
본 연구에서는 Fig. 1과 같이 MATLAB/Simulink를 활용하여 배터리 방전 및 충전 시뮬레이션을 위한 전기차 파워트레인 모델을 구현하였다. 동력전달장치와 동력발생장치로 구성하였고, 동력전달장치는 Forward 방식을 기반으로, 동력발생장치는 Backward 방식을 기반으로 모델링하였다.4)
전기차는 일반적으로 전기에너지를 운동에너지로 변환하여 차량을 구동시킨다. 주행 시 배터리에서 공급되는 직류전원을 인버터가 교류전원으로 변환하고, 모터 토크를 제어하며 모터에 필요한 에너지를 전달한다. 모터가 인버터를 통하여 전달받은 전기에너지를 운동에너지로 변환하여 구동력을 발생시키며, 감속 시 발전기의 역할을 한다. 이와 같은 과정을 역행으로 진행하여 동력발생장치 모델을 구성하였고, 모터를 통하여 전기에너지에서 변환된 운동에너지, 즉 모터의 토크가 동력전달장치를 통하여 바퀴로 전달되는 과정을 순행으로 진행하여 동력전달장치 모델을 구성하였다. 마지막으로, SOC가 0 %에 도달하면 시뮬레이션이 종료되도록 하였다.
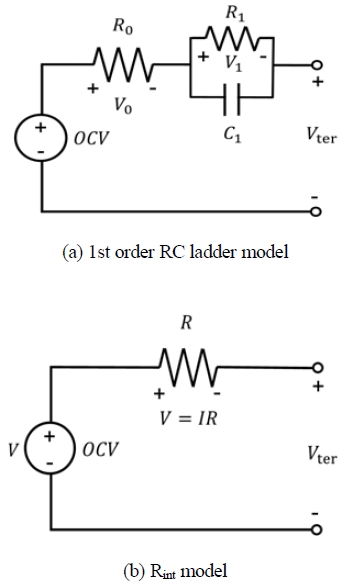
Fig. 2(a)는 일반적인 배터리 등가회로 모델이고,5) Fig. 2(b)는 Fig. 2(a)의 분극 현상을 나타내는 이온화 손실 저항과 커패시턴스를 생략하고 배터리 내부저항만을 고려하여 나타낸 것이다. 본 연구는 전기차 배터리의 실시간 거동을 관찰하는 것이 목적이 아닌, 배터리 내부저항에 의한 에너지 손실에 관심을 두었기 때문에 Fig. 2(b) 회로 모델을 기반으로 배터리 모델링을 진행하였다. Open Circuit Voltage(OCV)는 배터리 양단에 아무것도 연결하지 않고 전압이나 전하의 이동이 없는 상태의 개방회로 전압이다.
Fig. 2(b) 회로 모델로부터 Vter은 다음과 같다. 이때, I는 배터리 전류이고, R은 배터리 내부저항이다.
| (1) |
따라서 전류는 다음의 형태로 나타낼 수 있다. 이때, P는 배터리 출력이다.
| (2) |
| (3) |
| (4) |
| (5) |
배터리 내부저항에 의한 손실 에너지는 다음과 같은 방식으로 계산하였다.
| (6) |
| (7) |
2.2 모델 파라미터
사용된 차량의 제원은 Table 1과 같다. 주행저항 계수 F0, F1, F2는 Driving resistance target value(주행저항 목푯값)로 차량이 주행 중에 받게 되는 구름저항 및 공기저항 등을 정량화한 수치이다.7)
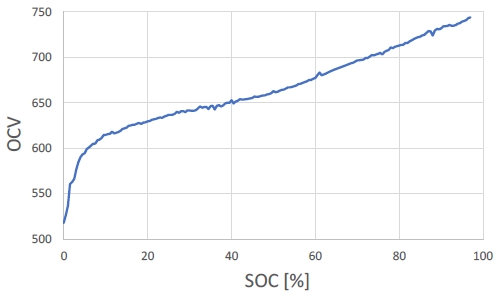
Fig. 4는 SOC의 변화에 따른 개방회로전압을 보여주며, SOC가 10 % 미만 시 급격히 감소하는 경향을 보인다.
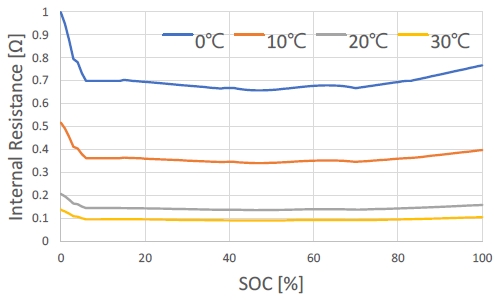
Fig. 5는 SOC의 변화와 배터리 온도에 따른 배터리 내부저항을 보여주며, SOC가 10 % 미만 시 급격히 증가하는 경향을 보인다. 본 연구에서 사용된 시뮬레이션 모델에서는 Fig. 5의 그래프로부터 배터리 온도와 SOC에 따른 배터리 내부저항값을 읽어와 반영함으로써 온도의 영향도를 반영하였다.
3. 시뮬레이션 진행 방법
도로구배, 주행모드, 배터리 온도 조건을 변경하여 10개의 Case를 만들고, 각 Case를 구성하는 시뮬레이션 조건을 Table 2에 나타내었다.
3.1 방전 시뮬레이션
차대동력계 시험은 부하가 낮은 조건에서 진행되는데, 실도로에서는 높은 출력이 요구되는 경우가 많다. 따라서 실도로 주행 상황을 반영하기 위하여 3 %와 6 %의 도로구배 조건을 적용하였다.8) 적용 방법은 아래와 같이 구배저항을 나타내는 아래 식을 구성하는 θ에 도로구배 3 %와 6 %에 대응하는 각도를 대입하였다. 이때, m은 질량이고, g는 중력가속도이다. θ는 경사각이고 단위는 radian이다.
| (8) |
공조장치를 작동하지 않고 MCT(Multi Cycle Test) 모드로 주행하도록 시뮬레이션을 실행하여 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 계산하였다.
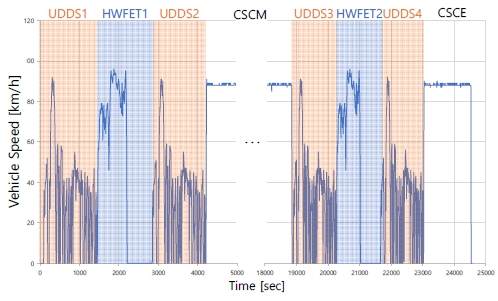
Fig. 6은 MCT의 속도 프로파일을 나타낸 그래프이다. MCT는 도심 주행모드(UDDS(Urban Dynamometer Driving Schedule) 모드) → 고속도로 주행모드(HWFET(Highway Fuel Economy Test) 모드) → 도심 주행모드(UDDS 모드) → 정속 주행모드(CSC(Constant Speed Cycle) 모드) 순서로 조합하여 2회 주행하는 방식이다.9)
UDDS는 City 연비 측정을 위한 Test mode로, Phase 1(초기단계)와 Phase 2(안정단계)로 구성되어 있고, 정지, 가속, 감속 등 실제 도로에서 볼 수 있는 다양한 속도 및 가속도 패턴을 반영한다. SOC가 높은 구간에서 에너지 소모가 많고 배터리 보호를 위하여 회생제동을 상대적으로 적게 하기 때문에 UDDS1과 UDDS2∼4를 구분하여 UDDS1에서는 저온시동특성을 반영하고 UDDS2∼4에서는 고온시동특성을 반영한다. 이때, 최고속도는 91.25 km/h, 평균속도는 31.5 km/h이다.
HWFET는 Highway 연비 측정을 위한 Test mode로 Phase 1으로 구성되어 있고, 상대적으로 빠른 속도에서 정상 속도 주행에 중점을 둔 고속도로주행속도 패턴을 반영한다. 이때, 최고속도는 97 km/h, 평균속도는 77.7 km/h이다.
CSC는 연속적으로 일정한 속도에서 운전하는 정속 주행 구간을 의미하는데, CSC 구간을 주행하는 이유는 전기차 배터리를 방전시키기 위함이다. CSCM(Constant Speed Cycle Middle) 구간이 길어짐에 따라 SOC가 낮은 구간을 정확하게 반영하기 어렵기 때문에 CSCE (Constant Speed Cycle End) 구간은 총 주행거리의 20 % 이내로 주행하도록 CSCM 구간의 주행시간을 설정한다.
MCT 모드 시뮬레이션 다음으로, MCT 모드와 동일하게 공조장치를 작동하지 않고 전기차의 완충 상태에서 완전 방전될 때까지 UDDS 모드로만 반복 주행하도록 시뮬레이션을 실행하고, 동일한 방법으로 주행모드만 변경하여 HWFET 모드 시뮬레이션의 결과와 비교하여 City 주행과 Highway 주행에서의 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 분석하였다.
실험 과정에서 다른 모든 변수에 영향을 미치지 않으며 배터리 온도만을 변경하여 실험을 진행하였다. 배터리 모델을 구성하고 있는 배터리 내부저항 1-D Lookup Table에, Fig. 5에서 확인할 수 있는 각 배터리 온도에 대응하는 배터리 내부저항 데이터를 입력하는 방법으로 배터리 온도를 변경하였다.
3.2 충전 시뮬레이션
50 kW, 100 kW, 200 kW, 350 kW, 400 kW로 급속 충전될 때 발생하는 배터리 내부저항에 의한 손실 에너지를 분석하였다.
3.1.3에서 설명한 방법과 동일한 방법으로 배터리 온도 변경을 진행하였다.
4. 결과 분석
실제 도로에서의 운전에서는 도로구배에 의하여 발생되는, 기존 MCT 모드보다 더 높은 출력 조건을 사용할 수 있다. 따라서 시뮬레이션의 결과를 저부하 조건과 고부하 조건으로 나누어 해석하였다. 저부하 조건은 0 %의 도로구배를 적용한 조건을 의미하고, 고부하 조건은 3 %, 6 %의 도로구배를 적용한 조건을 의미한다.
해석 결과는 아래 식과 같이 Table 1에서 제시한 배터리 전체 에너지(72.6 kWh) 대비 배터리 손실 에너지로써 제시하였다.
| (9) |
4.1 저부하 조건(도로구배 0 %)에서 배터리 에너지 손실
Fig. 7(a)는 MCT 모드로 주행하도록 시뮬레이션을 실행하여 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 계산한 결과이다. 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하는 경향이 관찰되었다. 0 oC에서 2.88 %로 가장 높았고, 30 oC에서 0.384 %로 가장 낮았으며, 약 4.54배의 차이를 보였다.
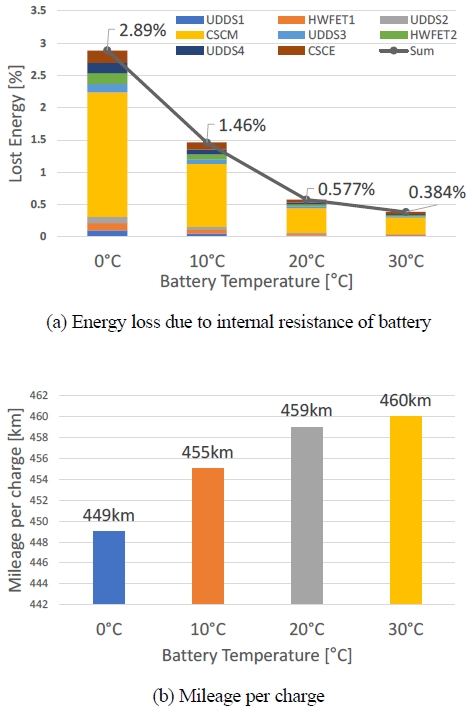
Effect of battery temperature on (a) energy loss and (b) driving range of the MCT mode for the 0 % road gradient condition
이와 같은 결과는 Fig. 7(b)와 같이 1회 충전 주행거리의 감소로 이어진다. 배터리 온도가 30 oC에서 0 oC로 감소함에 따라 1회 충전 주행거리가 460 km에서 448.7 km로 감소하였다. 약 2.61배 감소한 결과이다. 따라서 배터리를 사용할 때 저온에서의 배터리 에너지 손실을 고려하여 배터리 내부 온도를 적절하게 유지하는 것이 중요하다.
Fig. 8(a)는 UDDS1, UDDS2와 UDDS3, UDDS4를 구분하여 나타낸 결과이고, Fig. 8(b)는 HWFET1과 HWFET2를 구분하여 나타낸 결과이다. UDDS1, UDDS2, HWFET1은 SOC가 높은 구간의 배터리 특성을 반영하고, UDDS3, UDDS4, HWFET2은 SOC가 낮은 구간의 배터리 특성을 반영한다. 구간 사이의 배터리 내부저항의 차이는 크지 않지만, UDDS1, UDDS2보다 UDDS3, UDDS4의 결과가 크고(a) HWFET1보다 HWFET2의 결과가 큰 것으로(b) SOC가 높은 구간보다 낮은 구간에서 배터리 내부저항에 의한 에너지 손실이 더 크다는 것을 확인하였다. SOC가 감소함에 따라 전압 또한 감소하기 때문에 동일한 출력을 내기 위하여 더 많은 전류를 필요로 하는 것이 원인이다.
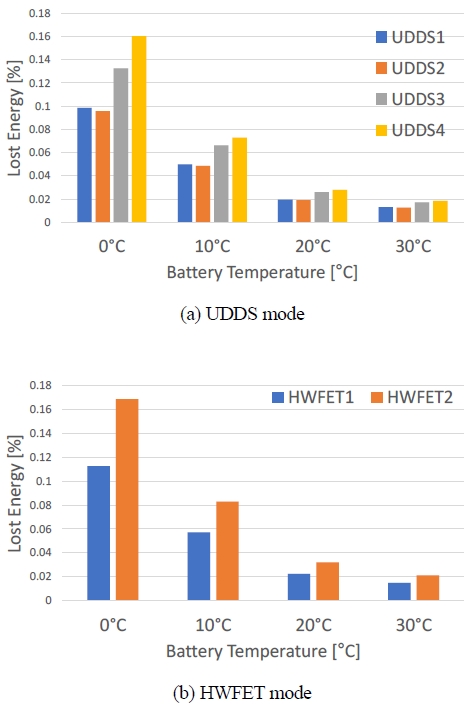
Energy loss of battery for (a) UDDS and (b) HWFET modes of the MCT mode under the various battery temperature and the 0 % road gradient condition
SOC가 높은 구간보다 낮은 구간에서 배터리 온도에 따른 편차 또한 더 높았다. 이는 SOC가 높은 구간보다 낮은 구간에서 배터리 온도가 1회 충전 주행거리에 미치는 영향이 더 크다는 것을 보여준다. 또한, 배터리 온도가 감소함에 따라 SOC에 따른 편차가 증가하였다. 이는 배터리 온도가 감소함에 따라 SOC가 1회 충전 주행거리에 미치는 영향이 증가한다는 것을 보여준다.
Fig. 9는 UDDS 모드와 HWFET 모드를 반복 주행하여 배터리가 완전 방전되도록 시뮬레이션을 실행하여 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 계산한 결과이다. Fig. 9에서 UDDS 모드 및 HWFET 모드에서 모두 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하는 경향이 관찰되었다. UDDS 모드에서는 0 oC에서 5.07 %로 가장 높았고, 30 oC에서 0.698 %로 가장 낮았으며, 약 7.26배의 차이를 보였다. HWFET 모드 또한 UDDS 모드와 동일한 양상을 보였다. 0 oC에서 3.76 %로 가장 높았고, 30 oC에서 0.510 %로 가장 낮았으며, 약 7.37배의 차이를 보였다.
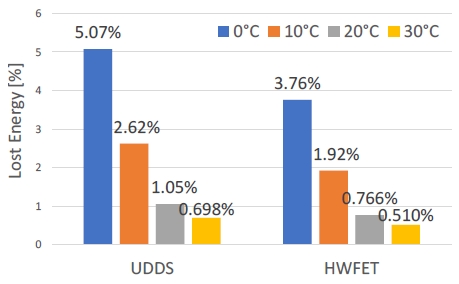
Energy loss due to internal resistance of the battery for the simulation Case 2 (UDDS and HWFET mode, 0 % road gradient, various battery temperatures)
또한, 각 배터리 온도 조건에서 모두 HWFET 모드보다 UDDS 모드에서 배터리 내부저항에 의한 손실 에너지가 더 높았다. 고속 조건인 HWFET 모드에서 에너지 손실이 더 많을 것이라고 예상할 수 있지만, 회생제동으로 에너지가 회수되는 과정에서도 에너지 손실이 발생하기 때문에 다양한 속도 및 가속도 패턴을 반영하는 UDDS 모드에서의 에너지 손실이 HWFET 모드에서의 에너지 손실보다 더 높았다.
편차 또한 더 높았다. 이는 HWFET 모드보다 UDDS 모드에서 배터리 온도가 1회 충전 주행거리에 미치는 영향이 더 크다는 것을 보여준다.
따라서 저부하 조건에서는 고속도로 환경보다 도심 환경에서 배터리 온도가 배터리 성능 및 효율에 미치는 영향을 강조한다.
4.2 고부하 조건(도로구배 3 %, 6 %)에서 배터리 에너지 손실
4.1에서 MCT 모드 시뮬레이션의 결과, 0 oC에서 3 %수준의 배터리 에너지 손실이 발생하였다는 도로구배 0 % 조건의 해석 결과를 제시하였다. 하지만 실제 도로에서의 운전에서는 도로구배에 의하여 기존 MCT 모드보다 더 높은 출력 조건을 사용할 수 있다. 따라서 본 연구에서는 도로구배 3 %, 6 % 조건을 추가적으로 적용하여 해석을 수행하였다.
Fig. 10은 기존 MCT 모드에 도로구배 3 %, 6 % 조건을 추가적으로 적용한 다음, 시뮬레이션을 실행하여 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 계산한 결과이다. 3 %, 6 %의 도로구배 조건을 적용한 MCT 모드에서는 도로구배 0 % 조건과 동일하게 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하는 경향을 보였다. 도로구배 3 % 조건에서는 0 oC에서 5.08 %로 가장 높았고, 30 oC에서 0.667 %로 가장 낮았으며, 약 7.62배의 차이를 보였다. 도로구배 6 % 조건에서는 0 oC에서 7.14 %로 가장 높았고, 30 oC에서 0.917 %로 가장 낮았으며, 약 7.79배의 차이를 보였다.
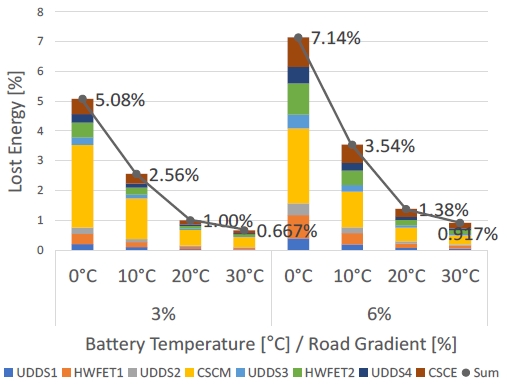
Energy loss due to internal resistance of battery for the MCT mode under the 3 % and 6 % road gradient conditions
Fig. 11은 기존 UDDS 모드 및 HWFET 모드에 도로구배 3 %, 6 % 조건을 추가적으로 적용한 다음, 시뮬레이션을 실행하여 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 계산한 결과이다. Fig. 11(b)는 도로구배 조건별 UDDS 모드에서 회생제동으로 회수된 에너지 및 회생제동으로 에너지가 회수되는 과정에서 발생한 손실이다.
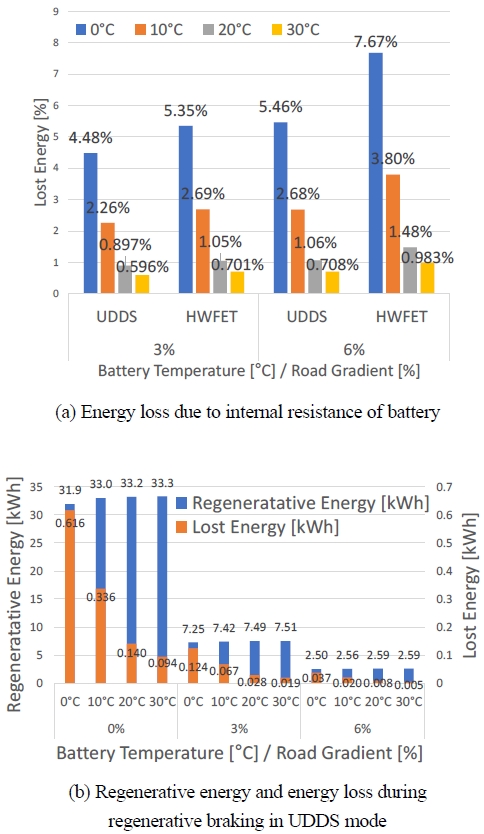
Comparisons of energy loss due to internal resistance of battery for the various road gradient conditions (a) in the UDDS and HWFET modes and (b) during the regenerative braking in the UDDS mode
Fig. 11(a)와 같이 도로구배 3 %, 6 % 조건에서는 도로구배 0 % 조건과 동일하게 UDDS 모드 및 HWFET 모드에서 모두 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하는 경향이 관찰되었다.
하지만, 도로구배 0 % 조건에서는 각 배터리 온도 조건에서 모두 HWFET 모드보다 UDDS 모드에서 배터리 내부저항에 의한 손실 에너지가 높았던 반면, 도로구배 3 %, 6 % 조건에서는 각 배터리 온도 조건에서 모두 UDDS 모드보다 HWFET 모드에서 배터리 내부저항에 의한 손실 에너지가 더 높았다. UDDS 모드에서, 도로구배 0 % 조건에서는 회생제동에 의한 에너지 손실이 높았지만 도로구배가 존재하는 고부하 조건에서는 회생제동보다 마찰식 제동을 사용하여 감속하기 때문에 Fig. 11(b)와 같이 도로구배가 높아짐에 따라 회생제동으로 회수되는 에너지가 감소하고 감소하는 만큼 에너지 손실이 감소한다.10) 따라서 도로구배가 존재하는 고부하 조건에서는 UDDS 모드보다 HWFET 모드에서 에너지 손실이 더 높았다.
마찬가지의 이유로 도로구배 3 % 조건의 UDDS 모드보다 도로구배 0 % 조건의 UDDS 모드에서 에너지 손실이 더 높았다. 도로구배가 높아짐에 따라 회생제동으로 회수되는 에너지가 감소하고, 회생제동으로 에너지가 회수되는 과정에서 발생하는 손실 또한 감소하기 때문이다.
한편, 도로구배 0 % 조건에서는 HWFET 모드보다 UDDS 모드에서 편차가 높았던 반면, 도로구배 3 %, 6 % 조건에서는 UDDS 모드보다 HWFET 모드에서 편차가 더 높았다. 이는 UDDS 모드보다 HWFET 모드에서 배터리 온도가 1회 충전 주행거리에 미치는 영향이 더 크다는 것을 보여준다.
따라서 고부하 조건에서는 도심 환경보다 고속도로 환경에서 배터리 온도가 배터리 성능 및 효율에 미치는 영향을 강조한다.
4.3 충전 시 배터리 에너지 손실
Fig. 12(a)는 충전 모델을 사용하여 충전 시뮬레이션을 실행하고, 50 kW, 100 kW, 200 kW, 350 kW, 400 kW의 전력으로 충전할 때 발생하는 배터리 내부저항에 의한 손실 에너지를 계산한 결과이다. Fig. 12(b)는 충전전력 200 kW 기준 배터리 온도별 SOC에 따른 전압이다.
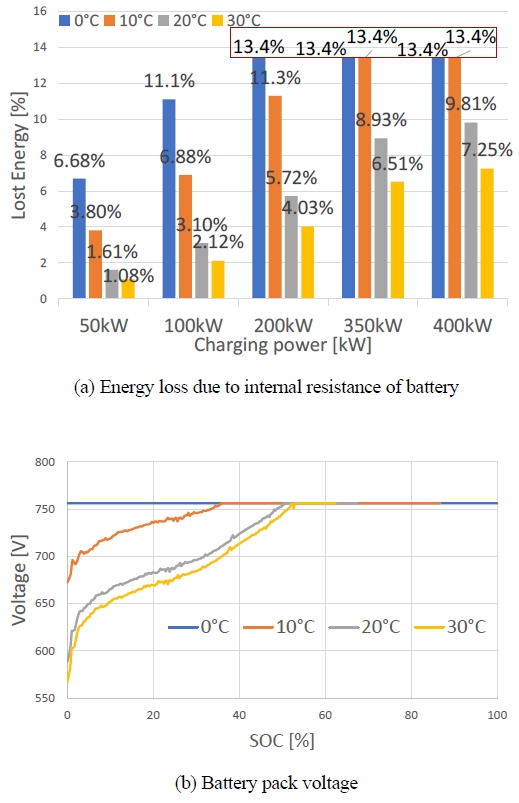
Comparison of (a) energy loss and (b) battery pack voltage for the various battery temperature conditions during battery charging with 200 kW
Fig. 12(a)의 각 충전 조건에서 모두 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하고, 편차 또한 증가하는 경향이 관찰되었다. 이는 배터리 온도가 감소함에 따라 충전 전력이 충전 효율에 미치는 영향이 증가한다는 것을 보여준다. 또한, 각 배터리 온도 조건에서 모두 충전 전력이 증가함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하고, 편차 또한 증가하는 일관된 경향이 관찰되었다.
한편, 예외적으로 200 kW(충전 전력) - 0 oC(배터리 온도) 조건, 350 kW - 0 oC 조건, 350 kW - 10 oC 조건, 400 kW - 0 oC 조건, 400 kW - 10 oC 조건에서는 배터리 온도와 무관하게 13.38 %의 동일한 에너지 손실율이 나타났다. 이는 Fig. 12(b)의 배터리 온도 0 oC 조건과 같이 시뮬레이션 시작부터 배터리 셀 당 전압이 허용 상한 전압인 4.2 V에 도달하였기 때문이다. 배터리 셀 당 전압이 4.2 V의 정전압으로 유지되도록 전류가 제어되는 충전 시뮬레이션 모델을 구현하였기 때문에 상대적으로 높은 충전 전력과 배터리 내부저항에 의하여 목표 충전 전력과 무관하게 모든 조건에서 동일한 충전 전력이 적용되었다.
5. 결 론
본 연구에서는 배터리 온도에 따른 배터리 내부저항에 의한 손실 에너지를 분석하기 위하여 MATLAB/Simulink를 활용하여 전기차 시뮬레이션 모델을 구현하였고, 다양한 시뮬레이션 조건에서 해석을 진행하였다. 본 연구에서 도출한 결과는 다음과 같다.
- - 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하였다. 따라서 저온에서의 배터리 에너지 손실을 고려하여 배터리 내부 온도를 적절하게 유지하는 것이 효율적이다.
- - MCT 모드에서 네 번의 UDDS와 두 번의 HWFET 모드를 비교할 때, SOC가 높은 구간보다 낮은 구간에서 배터리 에너지 손실이 높았다. 이는 내부저항 증가 및 OCV 감소에 의한 것으로, 배터리 효율 측면에서 볼 때 SOC가 높은 구간에서 사용하는 것이 효율적이다.
- - 도로구배 0 % 조건에서는 HWFET 모드보다 UDDS 모드에서 배터리 내부저항에 의한 손실 에너지가 더 높은 반면, 도로구배 3 %, 6 % 조건에서는 UDDS 모드보다 HWFET 모드에서 배터리 내부저항에 의한 손실 에너지보다 더 높았다. 이는 도로구배가 증가할수록 회생제동이 발생하는 비중이 감소하는 것이 원인이라고 분석된다.
- - 충전 조건에서도 배터리 온도가 감소함에 따라 배터리 내부저항에 의한 손실 에너지가 증가하였다. 특히, 200 kW 이상의 충전 조건에서는 충전 시작과 동시에 배터리 전압이 허용 전압 이상으로 상승하였으며, 그에 따라 최대 13.4 %의 에너지 손실을 보였다.
Acknowledgments
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF-2021R1F1A1052133).
References
-
X. Hao, H. Wang, Z. Lin and M. Ouyang, “Seasonal Effects on Electric Vehicle Energy Consumption and Driving Range: A Case Study on Personal, Taxi, and Ridesharing Vehicles,” Journal of Cleaner Production, Vol.249, Paper No.119403, 2020.
[https://doi.org/10.1016/j.jclepro.2019.119403]

-
J. Lindgren and P. D. Lund, “Effect of Extreme Temperatures on Battery Charging and Performance of Electric Vehicles,” Journal of Power Sources, Vol.328, pp.37-45, 2016.
[https://doi.org/10.1016/j.jpowsour.2016.07.038]

- A. H. Mahmud, Z. Daud and Z. Asus, “The Impact of Battery Operating Temperature and State of Charge on the Lithium-Ion Battery Internal Resistance,” Jurnal Mekanikal, Vol.40, No.1, pp.2329-2333, 2010.
-
G. Mohan, F. Assadian and S. Longo, “Comparative Analysis of Forward-Facing Models vs Backward-Facing Models in Powertrain Component Sizing,” IET Hybrid and Electric Vehicles Conference 2013(HEVC 2013), pp.1-6, 2013.
[https://doi.org/10.1049/cp.2013.1920]

-
J. Yeon, D. Park, Y. Lee, H. Sung, Y. Lim, J. Lee and N. Kim, “Prediction of Driving Range of Electric Vehicle Based on Simulation: Focusing on the IONIQ5,” Transaction of the KSAE, Vol.31, No.4, pp.275-282, 2022.
[https://doi.org/10.7467/KSAE.2023.31.4.275]

-
Y. Zhang, Z. Shen, W. Pan, H. Wang, Y. Wu and X. Mao, “Constant Current and Constant Voltage Charging of Wireless Power Transfer System Based on Three-Coil Structure,” IEEE Transactions on Industrial Electronics, Vol.70, No.1, pp.1066-1070, 2023.
[https://doi.org/10.1109/TIE.2022.3150112]

- J. Jung and K. Rho, “A Study of Verification of Observation Station and Onboard Anemometry Driving Resistance Measurement Method on Heavy-Duty Electric Bus,” KSAE Annual Conference Proceedings, pp.896-901, 2021.
-
J. Song, “Altitude Standardization Method to Improve Altitude Data Accuracy in On-Road Driving,” Transaction of the KSAE, Vol.30, No.6, pp.447-456, 2022.
[https://doi.org/10.7467/KSAE.2022.30.6.447]

-
J. Song, J. Cha and M. Choi, “Energy Efficiency Prediction Model of Heavy-Duty Electric Vehicles Using Numerical Simulation,” Int. J. Automotive Technology, Vol.23, No.6, pp.1529-1536, 2022.
[https://doi.org/10.1007/s12239-022-0133-8]

-
J. Bian and B. Qiu, “Effect of Road Gradient on Regenerative Braking Energy in a Pure Electric Vehicle,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.232, No.13, pp.1736-1746, 2018.
[https://doi.org/10.1177/0954407017735020]