자율주행 자동차의 슬라이딩 모드 관측기를 이용하는 외란 재건 기반 되먹임 이득 적응형 경로 추종 제어 알고리즘

1. 서 론

운전자 조작 없이 자동차를 포함하는 다양한 모빌리티가 스스로 주행할 수 있는 자율주행 기술의 연구개발이 활발하다. 경로 추종 제어 기술은 자율주행 모빌리티의 기본이자 가장 중요한 기술 중 하나이다. 계획된 직선 및 곡선 경로 추종 주행을 위해 기본적으로 차량의 자동 조향 제어 기술이 필요하다. 이를 위해 LiDAR, Camera, GPS와 같은 고신뢰성 환경 센서 개발과 관련 환경 정보를 담고 있는 고정밀 지도(HD map)의 구성이 활발히 진행되고 있다. 이러한 기반 기술들을 이용하는 자율주행 자동차의 경로 추종 제어 기술은 근 미래에 데이터의 신뢰성 확보, 제어 방법의 안정성 및 강건성 확보, 효율적 에너지 사용 전략 확보 등을 필요로 한다.

PID(Proportional-Integral-Derivative) 제어법¹⁾은 구조가 간단하고 많은 계산 리소스가 필요 없어 쉽게 구현할 수 있지만, 모든 차량과 환경에 적용 가능한 이득값을 결정하기 힘들고 높은 속도에서 허용 가능한 정확도를 확보하기 어렵다.

경로 추종 제어를 위한 방법론으로 기하학적 모델 기반 제어 방법론이 있으며, 차량의 기하학적 관계식만을 이용해 목표 경로 추종을 위한 제어 입력을 도출한다. 기하학적 제어 알고리즘 중 보편적으로 적용되는 Pure pursuit controller는 목표 경로 위의 전방 주시 거리 끝점과 차체의 사이 각을 이용하여 제어한다. 전방 주시 거리에 따라 Corner cutting, over shooting 현상이 발생하는 문제점이 있기 때문에, 주형진 등은 전방 주시 거리를 종 방향 속도에 비례하게 설계하였다.²⁾ 이홍규 등³⁾은 SISO (Single Input-Single Output)의 간단한 모델에서 발생하는 불안정성 문제를 극복하기 위해 모델 기반의 LQR(Linear Quadratic Regulation) 제어를 복합적으로 사용하는 알고리즘을 제안하였다.

기하학적 제어 알고리즘 중 보편적인 방법으로 Stanley controller⁴⁾ 또한 존재한다. 횡 거리 오차와 요 각도 오차를 모두 고려하므로 고속 주행 상황에서의 비교적 좋은 경로 추종 제어 안정성을 보인다. AbdElmoniem 등⁵⁾은 Stanley controller의 고속 주행 시 큰 곡률의 목표 경로에 대한 단점을 예견 제어를 통해 보완하는 알고리즘을 제안하였다.

모델 기반 제어 알고리즘은 종 방향 속도 혹은 조향에 의한 특성 변화에 대해 시스템의 동특성을 고려한 대응이 가능하고, 제어기 파라미터 조정에 있어 장점이 존재하기에 다양한 연구가 진행되고 있다. 하지만, 제어 알고리즘 설계를 위해 도출한 오차 모델에는 목표 요 각속도와 관련한 항이 존재할 수 있다. 곡선로에 진입하는 과정에서 목표 요 각속도가 0이 아닌 값이 발생하기 때문에 정상상태 오차를 제거하기 위해 Feed forward 관점의 추가 조향각을 계산하여 입력해야 하는 과정이 필요하다. Guo 등⁶⁾은 목표 속도와 목표 요 각속도를 취득하여 적응형 비선형 Fuzzy back stepping 제어 알고리즘을 제안하였다. 하지만 정의된 경로에 따라 목표 요 각속도가 미리 정의되어야 하는 한계점을 확인할 수 있었다. 주어진 경로에 대해 종 방향 속도가 변경되면 목표 요 각속도 또한 변경되어야 한다. 따라서 미리 정의된 요 각속도는 전체 경로 추종 제어에 적합하지 않을 수 있다. 기존 연구들을 살펴보면 목표 요 각속도를 계산하기 위해 제어 주기마다 목표 경로의 곡률을 취득하는 방법론을 주로 사용하고 있었다. Sun 등⁷⁾은 경로 오차를 스위칭하여 차량의 고속 안정성 확보가 가능한 Model Predictive Control(MPC) 알고리즘을 제안하였다. Shangguan 등⁸⁾은 비선형 MPC 기반의 에너지 효율적 경로 추종 알고리즘을 제안했으며, 목표 요 각속도는 슬립각과 경로의 곡률, 속도를 이용하여 계산하였다. Ge 등⁹⁾은 선회 강성 계수의 경계가 적응되는 Adaptive Sliding Mode Control(ASMC) 기법을 통해 강인한 경로 추종 알고리즘을 제안하였으며, 차량의 상태와 주어진 곡률을 통해 목표 요 각속도를 계산하였다.

본 논문에서는 자율주행 자동차의 견고하고 정확한 경로 추종을 위해 슬라이딩 모드 관측기(SMO, Sliding Mode Observer)를 이용하여 목표 요 각속도를 포함하는 모델의 외란 재건 기반 조향 제어 입력을 도출하는 알고리즘을 제안한다. 목표 경로 오차 동역학에 기반한 경로 추종 조향 제어는 목표 요 각속도의 항을 포함한다. SMO를 이용하여 모델링 되지 않은 불확실성으로 인한 외란과 함께 목표 요 각속도를 재건하여 강건한 경로 추종을 목표하였다. SMO는 모델링되지 않은 불확실성이 있는 상태에서 플랜트의 상태를 견고하게 관찰할 수 있으며 등가 주입항을 통해 불확실성 또는 외란을 재건할 수 있어 이에 대한 연구들이 진행되고 있다. 임채윤 등¹⁰⁾은 쿼드로터 시스템의 외란을 관측하고 보상하는 적분 슬라이딩 모드 관측기를 제안하였다.

본 논문의 2장에서는 외란 재건 경로 추종 제어 알고리즘에 대해 기술한다. 제안하는 알고리즘은 오차 모델의 목표 요 각속도 항을 제어 입력에 포함하여 모델의 추종 제어 안전성을 확보하였다. 제어에 필요한 목표 요 각속도는 외란을 포함하여 SMO에서 실시간으로 재건되도록 설계하였다. 3장에서는 Matlab/Simulink 및 CarMaker 시뮬레이션 소프트웨어 기반 도출한 성능 평가 결과들을 보여준다. 마지막 4장에서는 결론 및 한계점 분석 그리고 향후 계획에 대해 기술한다.

2. 외란 재건 기반 경로 추종 제어

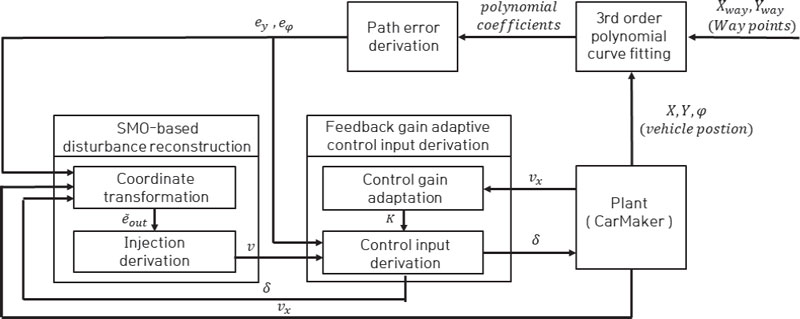
본 장에서는 차량과 추종 경로 간의 횡 거리 및 요 각도 오차를 이용하는 되먹임 제어기에 대해 기술한다. 목표 경로 도출을 위해 차량 질량 중심 기준 반경 20 m 내의 Way-points를 실시간으로 획득하고, 차량 좌표계에 대하여 3차 다항함수 기반 커브 피팅하는 과정이 설계되었다. 목표 경로를 실시간으로 갱신하는 과정을 통하여 차량의 목표 경로에 대한 횡 방향 거리 오차 e_y, 요 각도 오차 e_ψ를 도출한다. 조향 제어 입력 δ에 목표 요 각속도 $$ {\dot{\psi }}_{des }$$와 관련한 항을 포함하여 설계하고, 오차 동역학 모델 기반 극점배치 기법을 적용함으로써 되먹임 오차를 0으로 수렴할 수 있도록 설계하였다. 제어 입력 계산에 사용된 목표 요 각속도는 설계된 슬라이딩 모드 관측기의 등가 주입항을 이용하여 재건되었다. 아래의 Fig. 1은 제안하는 경로 추종 제어 알고리즘의 전반적 블록선도를 보여준다.

Fig. 1

Overall block diagram of path tracking algorithm

2.1 경로 추종을 위한 오차 동역학 모델

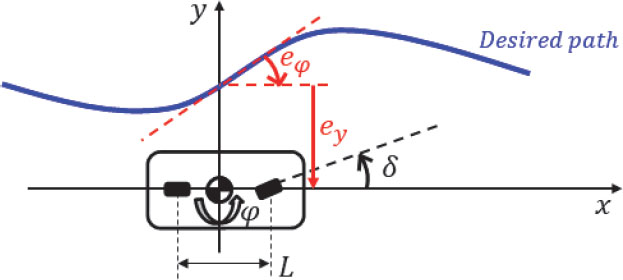
경로 추종 제어 입력 도출을 위해 횡 방향 거리 오차 e_y, 요 각도 오차 e_ψ를 이용하는 오차 동역학 모델을 설계하였다. 아래의 Fig. 2는 목표 경로 기준 두 가지 오차의 기하학적 관계를 보여준다.

Fig. 2

Geometry explanation of vehicle bicycle model

목표 경로 기준 오차 동역학 모델 도출을 위하여 e_y와 e_ψ의 시간에 대한 미분방정식을 식 (1), (2)와 같이 정의할 수 있다.

$\[ \frac{d}{dt}{e}_y=v_x{e}_{\psi } \]$

(1)

$\[ \frac{d}{dt}{e}_{\psi }=\dot{\psi }-{\dot{\psi }}_{des } \]$

(2)

차량이 애커먼 스티어 상태로 선회한다고 가정하면 식 (2)의 차량 요 각속도 $$ \dot{\psi }$$를 다음과 같이 차량의 축거와 종 방향 속도의 관계식으로 정의할 수 있다.

$\[ \dot{\psi }=\frac{v_x}{L}\delta \]$

(3)

식 (1) ~ (3)을 통해 최종적으로 식 (4) ~ (6)과 같은 목표 경로 관점 오차 동역학 모델을 도출할 수 있다. 본 연구에서는 모델 불확실성을 고려하기 위해 식 (5)와 같이 집중화된 불확실성 d와 행렬 F를 이용해 모델 불확실성 W를 정의하였다.

$\[ \dot{e}=Ae+B\delta +F{\dot{\psi }}_{des }+W,y=Ce \]$

(4)

$\[ W=Fd \]$

(5)

$\[ e=\left[\begin{array}{c}{e}_y\\ e_{\psi }\end{array}\right],A=\left[\begin{array}{cc}0& v_x\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ \frac{v_x}{L}\end{array}\right],F=\left[\begin{array}{c}0\\ -1\end{array}\right],C=\left[\begin{array}{c}\begin{array}{cc}1& 1\end{array}\end{array}\right] \]$

(6)

2.3 SMO 기반 목표 외란 재건

설계된 제어 입력은 목표 요 각속도 $$ {\dot{\psi }}_{des }$$와 모델 불확실성을 필요로 한다. 계측된 데이터를 이용해 목표 요 각속도를 계산하더라도 모델링 되지 않은 요소들의 불확실성에 의하여 자율주행 경로 추종 제어 성능이 저하될 수 있다. 따라서 목표 요 각속도 $$ {\dot{\psi }}_{des }$$와 모델 불확실성이 포함된 항을 재건할 수 있도록 관측기 모델을 설계하고 SMO를 통해 차량의 상태를 관측한다. 이때 등가 주입항을 이용하여 목표 요 각속도와 모델 불확실성을 재건한다.

슬라이딩 모드 관측기는 실제 모델의 출력과 관측기 모델의 출력 간 오차를 0에 수렴시킬 수 있도록 주입항 v의 설계가 필요하다. 그러므로 먼저 선형 변환한 관측기의 수학적 모델을 식 (13) ~ (15)와 같이 정의한다.

$\[ \dot{\widehat{e_t}}=A_t\widehat{e_t}+B_t\delta +G_{n}v \]$

(13)

$\[ \widehat{y}=C_t{e}_t \]$

(14)

$\[ e_t=T_{C}e,A_t=T_{C}A{T}_C{}^{-1},B_t=T_{C}B,C_t=C{T}_C{}^{-1} \]$

(15)

A_t와 B_t는 선형 변환된 행렬이며, 이때 선형 변환 행렬T_C를 아래 식 (16)과 같이 정의하여 기존 상태 변수 e_t를 상태량과 출력으로 분리할 수 있다. 식 (17)에서 선형 변환된 상태변수 e_t가 상태량 e_t,1와 출력 e_out으로 정의되었음을 확인할 수 있다. 여기서 N_C는 출력 행렬 C의 영 공간이다.

$\[ T_C={\left[\begin{array}{c}\begin{array}{cc}{N}_C^T& C\end{array}\end{array}\right]}^T \]$

(16)

$\[ e_t={\left[\begin{array}{c}\begin{array}{cc}{N}_C^T& C\end{array}\end{array}\right]}^{T}e={\left[\begin{array}{cc}{e}_{t,1}& e_{out}\end{array}\right]}^T \]$

(17)

목표 요 각속도와 모델 불확실성을 외란으로 취급하는 목표 경로 오차 동역학 모델과 식 (13)의 관측기 모델 간의 오차에 대한 수학적 모델을 정의하기 위해, 상태변수의 오차인 상태변수 오차 $$ \widetilde{e_t}$$와 출력의 오차인 출력 오차 $$ {\tilde{e}}_{out}$$를 식 (18)과 (19)과 같이 정의한다. 이를 기반으로 관측기 오차에 대한 수학적 모델을 정의된 식 (20)과 같이 정의할 수 있다.

$\[ \widetilde{e_t}=\widehat{e_t}-e_t \]$

(18)

$\[ {\tilde{e}}_{out}=\widehat{y}-y \]$

(19)

$\[ \dot{\widetilde{e_t}}=A_t\widetilde{e_t}+G_{n}v \]$

(20)

G_n은 L_s와 단위행렬 I를 이용하여 G_n= [L_s-I]^T로 정의하였다. 주입항 v의 경우 식 (21)과 같이, 출력 오차 $$ {\tilde{e}}_{out}$$의 부호와 Magnitude of injection term ρ를 이용하여 정의했다.¹¹⁾

$\[ v=\rho sign\left({\tilde{e}}_{out}\right) \]$

(21)

선형 변환된 상태변수 e_t는 식 (17)에서 상태량 오차와 출력 오차로 정의되었기에 관측기 오차의 수학적 모델은 다음 식들과 같이 분리될 수 있다.

$\[ {\dot{\tilde{e}}}_{t,1}=A_{t11}{\tilde{e}}_{t,1}+A_{t12}{\tilde{e}}_{out}+L_{s}v \]$

(22)

$\[ {\dot{\tilde{e}}}_{out}=A_{t21}{\tilde{e}}_{t,1}+A_{t22}{\tilde{e}}_{out}-v \]$

(23)

출력 오차 $$ {\tilde{e}}_{out}$$가 유한 시간 내 0으로 수렴하게 하기 위해 리아프노프 함수(Lyapunov candidate function)를 식 (24)와 같이 정의하고 리아프노프 안정성(Lyapunov stability) 조건을 식 (25)와 식 (26)과 같이 적용한다. 리아프노프 함수 V가 Positive definite을 만족하고, 시간에 대한 변화율 $$ \dot{V}$$이 Negative definite을 만족해야 한다.

$\[ V=\frac{1}{2}{\tilde{e}}_{out}{}^2 \]$

(24)

$\[ Condition-1: \underset{{\tilde{e}}_{out\to \infty }}{lim} V=\infty \]$

(25)

(26)

양수 α를 이용하여 조건식 (26)을 아래의 식 (27)로 정의할 수 있으며, 이 식을 수렴 유한시간 t_r로 적분 구간 정의 및 분리 적분하면 식 (28)으로 조건을 정리할 수 있다.

$\[ \dot{V}\le -\alpha V^{\frac{1}{2}},(\alpha >0) \]$

(27)

$\[ 2V^{\frac{1}{2}}\left(t_r\right)-2V^{\frac{1}{2}}\left(0\right)\le -\alpha t_r \]$

(28)

유한 시간 t_r 내 리아프노프 함수 V가 0으로 수렴한다고 가정하면 식 (28)은 최종적으로 수렴 시간 t_r이 유한 시간임을 증명하는 다음 식 (29)로 표현할 수 있다.

$\[ t_r\le \frac{2V^{\frac{1}{2}}\left(0\right)}{\alpha } \]$

(29)

리아프노프 함수의 시간 변화율 $$ \dot{V}$$에 대한 조건식 (26)을 통해 출력 오차를 유한 시간 내 0으로 수렴시키는 ρ의 크기 조건을 도출할 수 있다. 식 (23)과 (24)의 정의에 따라 함수 V의 시간 변화율을 다음과 같이 정리할 수 있다.

$\[ \begin{array}{c}\dot{V}={\tilde{e}}_{out}{\dot{\tilde{e}}}_{out}={\tilde{e}}_{out}\left(A_{t21}{\tilde{e}}_{t,1}+A_{t22}{\tilde{e}}_{out}-v\right)\\ ={\tilde{e}}_{out}\left(A_{t21}{\tilde{e}}_{t,1}+A_{t22}{\tilde{e}}_{out}\right)-{\tilde{e}}_{out}v\end{array} \]$

(30)

(A_t21$$ {\tilde{e}}_{t,1}$$+A_t22$$ {\tilde{e}}_{out}$$)에 대한 경계값을 식 (31)과 같이 L_e를 통해 정의하면, 위의 식 (30)을 식 (32)와 같이 정리할 수 있다.

$\[ \left|A_{t21}{\tilde{e}}_{t,1}+A_{t22}{\tilde{e}}_{out }\right|\le L_e \]$

(31)

$\[ \dot{V}={\tilde{e}}_{out}{\dot{\tilde{e}}}_{out}\le -\left|{\tilde{e}}_{out}\right|\left(\rho -L_e\right) \]$

(32)

위와 같이 ρ와 경계값 조건 L_e에 대해 정리된 시간 변화율 $$ \dot{V}$$과 식 (27)에서 재정의한 유한 시간 수렴 조건식 간의 수렴 조건을 만족하기 위한 관계식은 다음과 같다.

$\[ -\alpha V^{\frac{1}{2}}\ge -\left|{\tilde{e}}_{out}\right|\left(\rho -L_e\right) \]$

(33)

식 (24)에서 정의한 리아프노프 함수 V에 의해 위의 식은 아래의 식 (34)로 정리할 수 있다. 이를 통하여 최종적으로 출력 오차 $$ {\tilde{e}}_{out}$$이 유한 시간 내 0으로 수렴하게 하기 위한 ρ의 조건 부등식을 식 (35)와 같이 도출할 수 있다.

$\[ -\alpha \frac{\left|{\tilde{e}}_{out}\right|}{\sqrt{2}}\ge -\left|{\tilde{e}}_{out}\right|\left(\rho -L_e\right) \]$

(34)

$\[ \rho \ge \frac{\alpha }{\sqrt{2}}+L_e \]$

(35)

출력 오차가 0으로 수렴하면 관측기 오차 관점의 수학적 모델 중, 식 (23)은 등가 주입항 v_eq에 대해 다음 식과 같이 정리하여 도출할 수 있다.

$\[ v_{eq}=A_{t21}{\tilde{e}}_{t,1} \]$

(36)

이렇게 도출된 등가 주입항 v_eq를 관측기 오차 모델 중, 상태량 오차 $$ {\tilde{e}}_{t,1}$$에 대한 식 (22)에 대입하면 다음과 같이 정리할 수 있다.

$\[ \begin{array}{c}{\dot{\tilde{e}}}_{t,1}=A_{t11}{\tilde{e}}_{t,1}+L_s\left(A_{t21}{\tilde{e}}_{t,1}\right)\\ =\left(A_{t11}+L_s{A}_{t21}\right){\tilde{e}}_{t,1}\end{array} \]$

(37)

따라서 상태량 오차 $$ {\tilde{e}}_{t,1}$$가 0으로 수렴하기 위한 조건은 식 (37)의 고유값이 음수인 조건이며, 다음과 같이 L_s에 대한 조건식으로 도출할 수 있다.

$\[ L_s\le -\frac{A_{t11}}{A_{t21}} \]$

(38)

모델 불확실성을 포함하는 외란은 상태량 오차 및 출력 오차 모두 0으로 수렴한 관측기 오차 모델을 통해 재건할 수 있다. 정의된 외란과 출력 오차에 대한 식 (23)은 다음과 같이 정리할 수 있다.

$\[ 0=F_2\left({\dot{\psi }}_{des }+d\right)-v_{eq} \]$

(39)

최종적으로 등가 주입항으로 외란을 재건하기 위한 식 (40)을 다음과 같이 도출할 수 있다.

$\[ v\approx {\dot{\psi }}_{des }+d \]$

(40)

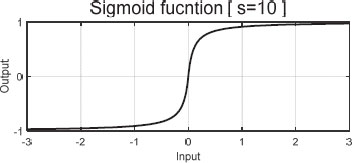
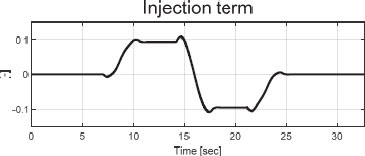
본 논문에서 제안하는 알고리즘은 SMO의 채터링 현상을 완화하기 위하여 식 (21)의 주입항을 다음 식과 같이 시그모이드 함수(Sigmoid function)로 설정하여 성능 평가를 진행하였다. s는 10을 적용하였다. 개형은 Fig. 3에서 확인할 수 있다.

Fig. 3.

Shape of sigmoid function

$\[ v=\rho sign\left({\tilde{e}}_{out}\right)\Rightarrow v=\rho \frac{s{\tilde{e}}_{out}}{1+s\left|{\tilde{e}}_{out}\right|} \]$

(41)

3. 성능 평가

본 논문에서 제안하는 경로 추종 제어 알고리즘은 상용 소프트웨어 Matlab/Simulink와 CarMaker를 연동하여 성능이 평가되었다. Table 1은 성능 평가에 이용된 차량의 대표적 물성치들을 보여준다.

Table 1

Vehicle parameters used for performance evaluation

성능 평가는 반경 100 m, 중심각 45 deg의 원호와 시점, 종점이 직선으로 구성된 S 형상 주로에서 수행되었다. 저속 주행 상황 [40 km/h]과 고속 주행 상황 [70 km/h] 두 가지 속도 시나리오를 설정하였으며, 종 방향 속도는 CarMaker 소프트웨어의 운전자 모델을 이용하여 목표 속도를 최대한 유지하도록 설정하였다. 재건된 외란을 이용한 조향 제어 입력이 경로 추종 성능에 미치는 영향을 비교 분석하였다. 이를 위해 각각의 시나리오에서, 목표 요 각속도를 포함하는 외란을 재건하여 제어하는 경우 (w/ reconstruction)와 외란을 재건하지 않는 경우 (w/o reconstruction)로 구분되어 평가가 수행되었다. Table 2는 성능 평가를 위해 설계된 피드백 제어기의 극점과 슬라이딩 모드 관측기 설계에 적용된 파라미터들을 보여준다.

Table 2

Used parameters for controller and observer

3.1 Case 1) 상대적 저속 주행 (40 km/h)

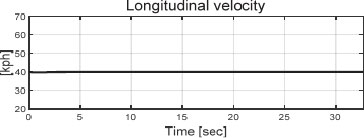
Case 1은 40 km/h 속도로 S 형상 주로를 주행하는 시나리오에서 수행된 평가이다. Fig. 4 ~ Fig. 9는 차량의 거동 결과와 제어 오차들을 보여준다. 차량의 종 방향 속도는 Fig. 4에서 확인할 수 있다.

Fig. 4

Longitudinal velocity

Fig. 5

Trajectory of vehicle

Fig. 6

Trajectory of vehicle (zoom in)

Fig. 7

Lateral error comparison

Fig. 8

Yaw angle error comparison

Fig. 9

Injection term of SMO

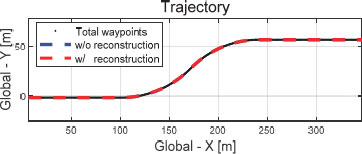
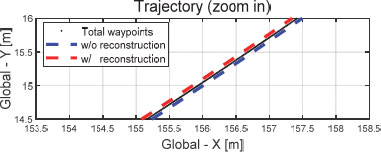
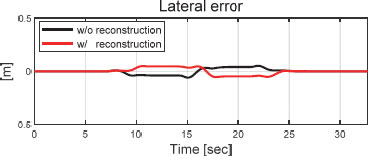
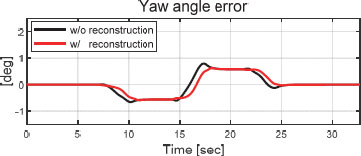
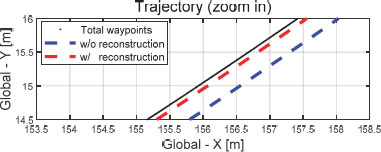
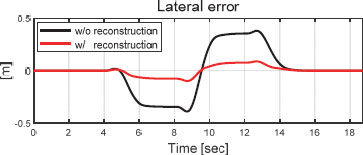
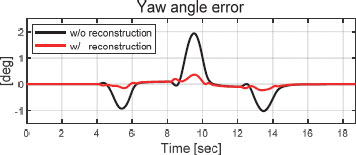
Fig. 5는 목표 경로와 재건된 외란의 적용 유무에 대한 주행 궤적을 보여준다. 제어 입력에 재건된 외란을 반영한 결과와 그렇지 않은 결과를 비교했을 때, 비교적 저속 상황에서는 두 경우 모두 합리적 경로 추종 결과를 확인할 수 있었다. Fig. 6은 선회 궤적 중 일부분 (지면 좌표계 상 X축 153.5 m ~ 158.5 m)를 확대한 그림으로, 두 경우의 주행 궤적과 Way-points와의 횡 거리 오차는 미미하고 부호의 차이만 발생하는 점을 확인할 수 있다. 이는 Fig. 7의 횡 거리 오차 그래프에서 또한 확인할 수 있다. 외란을 재건하는 경우 약 0.05 m의 최대 횡 거리 오차를 보여준다. 최대 횡거리 오차 관점에서 비 재건 차량 최대 횡 거리 오차 약 0.06 m 대비 약 0.01 m의 추종 성능 향상을 확인할 수 있다. Fig. 8에서도 외란을 재건하여 제어 입력에 적용할 경우 요 각도 오차가 감소하는 것을 확인할 수 있다. 재건된 외란을 제어에 사용할 경우 경우 최대 요 각도 오차는 약 0.62 deg로, 그렇지 않은 차량의 약 0.79 deg 보다 약 0.17 deg 만큼 최대 요 각도 오차 감소를 확인할 수 있다.

Fig. 9 ~ Fig. 14에서는 오차 모델 상태 추정 및, 외란을 재건하는 슬라이딩 모드 관측기의 결과 그래프들과 제어 입력을 확인할 수 있다.

Fig. 10

Reconstructed disturbance with SMO

Fig. 11

Output estimation value of SMO

Fig. 12

Front wheel angle comparison

Fig. 13

Lateral error estimation of SMO

Fig. 14

Yaw angle error estimation of SMO

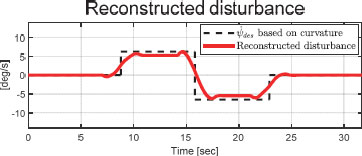
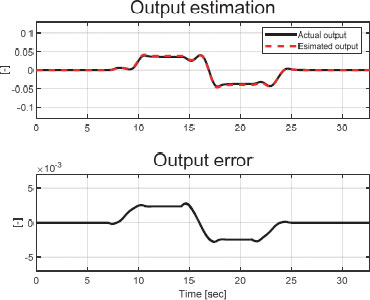
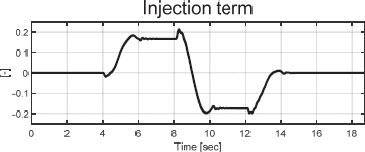
위의 Fig. 9는 주입항 v를 보여준다. 부호 함수 대신 시그모이드 함수를 적용하여 SMO의 한계점인 채터링 현상이 감소 된 모습을 확인할 수 있다. Fig. 10에서는 곡률을 이용하여 계산한 목표 요 각속도 ($$ {\dot{\psi }}_{des }$$ based on curvature)와 등가 주입항 v_eq로 재건된 외란 (Reconstruction)를 비교할 수 있다. Fig. 11에서 경로 오차 모델의 출력 y와 SMO의 출력 추정값 $$ \widehat{y}$$간의 비교를 확인할 수 있다. 출력 오차 $$ {\tilde{e}}_{out}$$를 약 ±2.81×10^-3 범위 내로 유지하는 SMO의 실제 출력 추정 성능을 확인할 수 있다.

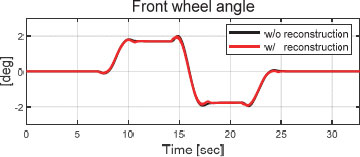
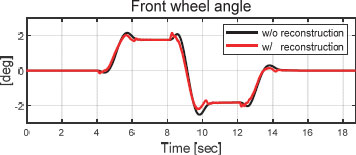
위의 Fig. 12에서는 제어 입력인 전륜 조향 각도를 확인할 수 있다.

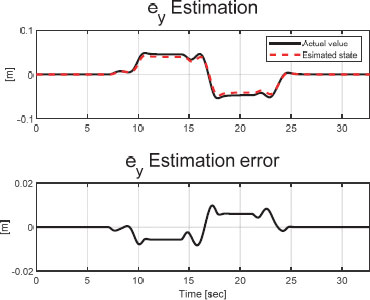
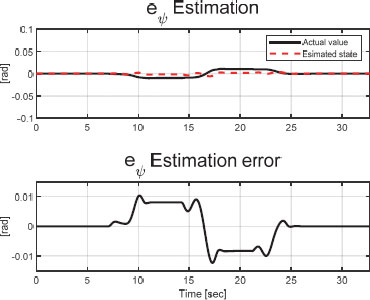
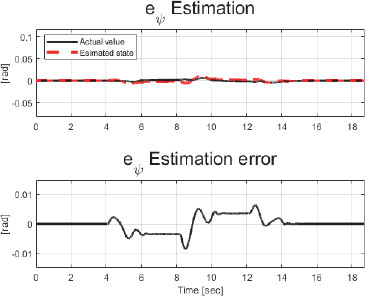
Fig. 13과 Fig. 14는 각각 슬라이딩 모드 관측기의 횡 거리 오차와 요 각도 오차의 추정 성능을 보여준다. 관측기의 횡 방향 거리 최대 상태량 오차 크기는 약 0.010 m 내로, 요 각도 최대 상태량 오차 크기는 약 0.012 rad 내로 유지되며 오차 모델의 상태 변수가 추정되었음을 확인할 수 있다.

3.2 Case 2) 상대적 고속 주행 (70 km/h)

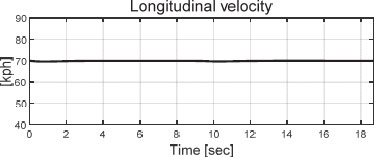
Case 2는 동일한 S 형태의 주로에서 비교적 고속인 70 km/h로 주행하는 시나리오에서 수행된 평가이다. Fig. 15 ~ Fig. 20은 차량의 제어 결과와 제어 오차를 보여준다. 차량의 종 방향 속도는 Fig. 15에서 확인할 수 있다.

Fig. 15

Longitudinal velocity

Fig. 16

Trajectory of vehicle

Fig. 17

Trajectory of vehicle (zoom in)

Fig. 18

Lateral error comparison

Fig. 19

Yaw angle error comparison

Fig. 20

Front wheel angle comparison

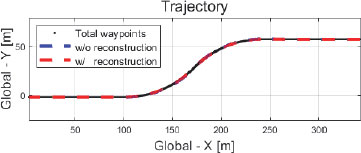
Fig. 16은 검정색 점선으로 표시된 Way-points및 자율주행 차량의 주행 궤적을 재건된 외란의 적용 유무에 따라 구분하여 보여준다. Fig. 17은 주행 궤적 그래프를 Case 1) 저속 주행의 Fig. 6과 동일한 일부분을 확대한 그래프이다. 저속 주행 시나리오와 비교하면, 외란을 재건하여 제어 입력에 적용하는 경우의 추종 성능 우수성이 고속 상황에서 비교적 뚜렷하게 관찰된다. 이는 Fig. 18의 횡 거리 오차 그래프에서 또한 확인할 수 있다. 고속 주행 시나리오에서 외란을 재건하는 차량의 최대 횡 거리 오차는 약 0.01 m로, 비 재건 차량의 약 0.39 m 대비 약 0.38 m 만큼 적은 최대 횡 거리 오차를 보인다. 고속 주행 시나리오에서도 외란을 재건하여 제어에 적용할 경우 횡 거리 오차 관점에서 비교적 정확한 경로 추종 성능을 보이는 것을 확인할 수 있다. 또한, 외란을 재건하지 않은 차량의 횡 거리 최대 오차량이 저속일 때 0.06 m에서 고속일 때 0.39 m로 증가한 반면, 외란을 재건하여 제어하는 경우, 0.05 m에서 0.01 m로 감소한 것을 확인할 수 있다.

Fig. 19에서는 목표 경로와 차량의 요 각도 오차를 확인할 수 있다. 외란을 재건하여 제어 입력에 적용할 경우 최대 요 각도 오차량은 약 0.36 deg로 그렇지 않은 차량의 최대 요 각도 오차량 약 1.93 deg 보다 1.57 deg 정도 적은 최대 오차량을 보이며 오차가 적게 나타나는 것을 확인할 수 있다. 또한 시나리오간 비교를 하면, 외란 재건 차량의 요 각도 최대 오차량은 저속일 때 약 0.79 deg에서 약 1.93 deg로 1.14 deg 만큼 증가를 보인 반면, 외란을 재건하여 제어하는 경우, 약 0.62 deg에서 약 0.36 deg로 0.28 deg 만큼 감소하는 최대 오차량을 확인할 수 있다.

Fig. 20에서 저속 주행 시나리오와 마찬가지로 외란 재건 알고리즘 적용 차량은 비교적 앞서 제어하는 점을 확인할 수 있다.

Fig. 21 ~ Fig. 26은 오차 모델 상태량을 추정하고, 외란을 재건하는 슬라이딩 모드 관측기의 결과 그래프들을 보여준다. Fig. 21에서는 주입항 v를 확인할 수 있다.

Fig. 21

Injection term of SMO

Fig. 22

Reconstructed disturbance with SMO

Fig. 23

Output estimation value of SMO

Fig. 24

Lateral error estimation of SMO

Fig. 25

Yaw angle error estimation of SMO

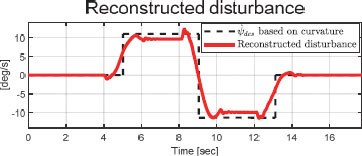
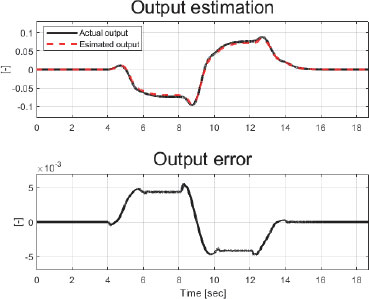
Fig. 22에서는 등가 주입항 v_eq로 재건한 외란 (Reconstructed disturbance)를 곡률 기반 계산한 목표 요 각속도 ($$ {\dot{\psi }}_{des }$$ based on curvature)와 비교할 수 있다. Fig. 23에서 출력 오차 $$ {\tilde{e}}_{out}$$를 약 ±5.62×10^-3 범위 내로 유지하는 SMO의 추정 성능을 확인할 수 있다.

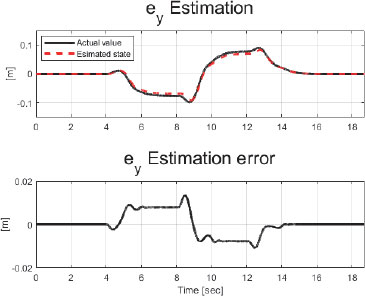
Fig. 24와 Fig. 25는 각각 SMO의 횡 거리 오차와 요 각도 오차의 추정 성능을 보여준다. 관측기의 횡 방향 거리 상태량 추정 최대 오차 크기는 약 0.001 m 내에서, 요 각도 상태량 추정 최대 오차 크기는 약 0.012 rad 내에서 유지되며 오차 모델의 상태 변수가 추정되었음을 확인할 수 있다.

전반적인 평가 결과를 통해 본 논문에서 제안하는 알고리즘이 저속, 고속 상황에서도 외란을 합리적으로 재건함을 보여준다. 이를 경로 추종 제어에 적용하여 비교평가를 진행한 결과, 도로의 곡률 정보 없이 경로 추종 제어가 가능함을 보여준다. 하지만 본 연구의 성능 평가는 종 방향 등속 운동 시나리오에서만 진행되었다. 또한, 시뮬레이션 기반의 이상적인 가상환경에서 진행되었다는 한계점이 존재한다. 그러므로 가속 상황 등에서도 안정성 확보를 위해, 전방 주시 거리 기반 알고리즘 고도화 및 실차 기반 성능평가를 계획하고 있다. 다음 장에서는 결론 및 한계점 분석 그리고 향후 계획에 대해 기술한다.

4. 결 론

본 논문에서는 제어 입력 설계로 소거한 목표 요 각속도와 모델의 불확실성이 통합된 외란을 SMO로 재건하여 제어 입력에 이용하는 알고리즘을 제안하였다. 목표 경로에 대하여 차량의 횡 거리 오차와 요 각도 오차를 모두 고려하는 목표 경로 오차 동역학 모델은 요 각속도 항을 포함하고 있다. 제어 입력에 목표 요 각속도항을 포함 설계하고, 극점 배치 기법을 통해 경로 오차 모델의 상태 변수들을 0으로 수렴시켰다. 제어 입력에 필요한 목표 요 각속도는 외란으로 취급하고 SMO로 이를 모델 불확실성과 함께 재건하였다. 제안하는 SMO의 추정 성능 평가 및 알고리즘의 경로 추종 성능 평가를 위하여 CarMaker 소프트웨어를 사용하여 고속과 저속 두 가지 시나리오에서 재건된 외란을 제어입력에 적용하는 차량과 적용하지 않는 차량을 비교하였다. 성능 평가 결과 제안하는 알고리즘의 우수한 추종 성능을 통해 두 가지 상황에서 모두 합리적으로 외란을 재건했음을 확인하였다. 하지만 본 논문의 성능 평가는 종 방향 속도를 등속 유지 상황으로 설정하였기에 변화하는 속도에서의 성능을 평가할 수 없었다. 또한, 이상적인 시뮬레이션 기반 성능 평가 아래에서 실제 자율주행 차량의 GPS 오차 등 더욱 많은 불확실성에 대한 알고리즘의 안정성을 평가할 수 없었다. 그러므로, 종 방향 속도 변화 및 GPS 드리프트 등 비교적 불안정한 상황을 보완하기 위해 전방 주시 거리를 고려하는 알고리즘 고도화 및 다양한 곡률을 포함하는 도로에서 수행하는 실 차량 기반 성능 평가를 향후 연구로 계획하고 있다.

Acknowledgments

본 연구는 2022년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원(NRF-2022R1F1A1075167)을 받아 수행되었음.

References

• T. Le-Anh and M. B. M. De Koster, “A Review of Design and Control of Automated Guided Vehicle Systems,” European Journal of Operational Research, Vol.171, No.1, pp.1-23, 2006. [https://doi.org/10.1016/j.ejor.2005.01.036]
• H. Joo and K. Lee, “Changes in Path Tracking Performance of Autonomous Vehicle According to Design Feedback Gain and Look-Ahead Distance of Pure-Pursuit Algorithm,” Transaction of the KSAE, Vol.29, No.9, pp.839-846, 2021. [https://doi.org/10.7467/KSAE.2021.29.9.839]
• H. Lee, T. Kim, D. Yu and S. Hwang, “Path-Following Correction Control Algorithm Using Vehicle State Errors,” Transaction of the KSAE, Vol.30, No.2, pp.123-131, 2022. [https://doi.org/10.7467/KSAE.2022.30.2.123]
• G. Hoffmann, C. Tomlin, M. Montemerlo and S. Thrun, “Autonomous Automobile Trajectory Tracking for Off-Road Driving: Controller Design, Experimental Validation and Racing,” 2007 American Control Conference, pp.2296-2301, 2007. [https://doi.org/10.1109/ACC.2007.4282788]
• A. AbdElmoniem, A. Osama, M. Abdelaziz and S. A. Maged, “A Path-Tracking Algorithm Using Predictive Stanley Lateral Controller,” International Journal of Advanced Robotic Systems, Vol.17, No.6, Paper No.1729881420974852, 2020. [https://doi.org/10.1177/1729881420974852]
• J. Guo, Y. Luo and K. Li, “Adaptive Non-Linear Trajectory Tracking Control for Lane Change of Autonomous Four-Wheel Independently Drive Electric Vehicles,” IET Intelligent Transport Systems, Vol.12, No.7, pp.712-720, 2018. [https://doi.org/10.1049/iet-its.2017.0278]
• C. Sun, X. Zhang, Q. Zhou and Y. Tian, “A Model Predictive Controller With Switched Tracking Error for Autonomous Vehicle Path Tracking,” IEEE Access, Vol.7, pp.53103-53114, 2019. [https://doi.org/10.1109/ACCESS.2019.2912094]
• J. Shangguan, M. Yue, H. Qi and C. Fang, “Coordinated Control of Path Tracking and Energy Optimization for In-Wheel Motor Drive Electric Buses with Velocity Estimation,” European Journal of Control, Vol.65, Paper No.100641, 2022. [https://doi.org/10.1016/j.ejcon.2022.100641]
• Z. Ge, Z. Man, Z. Wang, X. Bai, X. Wang, F. Xiong and D. Li, “Robust Adaptive Sliding Mode Control for Path Tracking of Unmanned Agricultural Vehicles,” Computers and Electrical Engineering, Vol.108, Paper No.108693, 2023. [https://doi.org/10.1016/j.compeleceng.2023.108693]
• C. Lim, J. Heo and D. Chwa, “Integral Sliding Mode Based Disturbance Observer and Control for Robust Tracking Control of Quadrotor Systems,” The Transactions of The Korean Institute of Electrical Engineers, Vol.71, No.1, pp.157-163, 2022. [https://doi.org/10.5370/KIEE.2022.71.1.157]
• Y. Shtessel, C. Edwards, L. Fridman and A. Levant, Sliding Mode Control and Observation, Springer, New York, 2014. [https://doi.org/10.1007/978-0-8176-4893-0]