[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 32, No. 1, pp.95-107

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jan 2024

Received 12 Sep 2023 Revised 01 Oct 2023 Accepted 27 Oct 2023

DOI: https://doi.org/10.7467/KSAE.2024.32.1.95

경로 추종 제어를 위한 다양한 구동기 조합의 비교 연구

김진우 ; 임성진^*

서울과학기술대학교 기계자동차공학과

Comparative Study on Effects of Multiple Actuator Combinations on Path Tracking Control

Jinwoo Kim ; Seongjin Yim^*

Department of Mechanical and Automotive Engineering, Seoul National University of Science and Technology, Seoul 01811, Korea

Correspondence to: ^*E-mail: acebtif@seoultech.ac.kr

Copyright Ⓒ 2024 KSAE / 218-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

This paper presents a comparative study on the effects of multiple actuator combinations on path tracking control. First, the state-space model with a lookahead distance is derived from a 2-DOF bicycle model and a target path. There are several actuators for path tracking: front-wheel steering(FWS), rear-wheel steering(RWS), 4-wheel steering(4WS), and 4-wheel independent steering/driving/braking(4WIS/4WID/4WIB). A control input is composed through front-wheel steering, 4-wheel steering, and the control yaw moment. Then, the control yaw moment is converted into tire forces generated by FWS, RWS, RWIS, 4WS, 4WIS, 4WID, and 4WIB. The controller is designed based on the model predictive control(MPC). To check the effects of these actuators on path tracking, a simulation is done on a vehicle simulation package. Simulation results show that additional actuators, except for FWS and 4WS, have little impact on path tracking performance.

Keywords:

Path tracking control, Lookahead distance, Model predictive control, 4-wheel steering, 4-wheel independent steering/driving/braking

키워드:

경로 추종 제어, 예견 거리, 모델 예측 제어, 4륜 조향, 4륜 독립조향/구동/제동

1. 서 론

차량동역학 및 제어 분야에서 경로 추종 제어에 관한 연구는 지난 50여년 동안 다양하게 진행되어져 왔다.^1,2) 이 분야는 1970년대부터 1990년대까지 활발하게 연구되어져 왔지만 2000년대 이후 연구가 거의 진행되지 않다가 2010년대 자율주행의 유행에 힘입어 다시 현재까지 활발하게 연구되고 있다.^3-5) 현재까지 경로 추종 제어에 관한 연구는 대부분 전륜 조향(Front-Wheel Steering, FWS) 차량에 대해 수행되었다. 하지만 2010년대 중반부터 FWS를 제외한 다양한 장치들을 장착한 차량에 대한 경로 추종 제어 관련 논문들이 다수 발표되고 있다.⁴⁾

1995년 제동 기반의 자세 제어 장치(Electronic Stability Control, ESC)가 제안된 이후로 다양한 구동기들이 차량 안정성 제어(Vehicle Stability Control, VSC)를 위해 제안되었고 이들을 통합하기 위한 섀시 통합 제어(Integrated Chassis Control, ICC)에 관한 연구도 활발하게 진행되었다.⁶⁾ VSC를 위한 대표적인 구동기들로는 능동 전륜조향(Active Front Steering, AFS), 후륜 조향(Rear Wheel Steering, RWS), 4륜 조향(4-Wheel Steering, 4WS)이 있다.⁷⁾ 최근 인휠모터 또는 e-Corner 모듈의 발달로 인해 후륜 독립 조향(Rear Wheel Independent Steering, RWS)과 4륜 독립조향/구동/제동(4-Wheel Independent Steering/Driving/Braking, 4WIS/4WID/4WIB) 등이 VSC를 위한 새로운 구동기로 각광받고 있다.^7,8) VSC의 목적이 운전자의 의지, 즉 기준 요율을 추종하는 것이므로 이들 구동기들은 주로 기준 요율 추종을 위해 사용되었다.^7,8)

최근 10년 동안 VSC를 위해 개발된 다양한 구동기들은 자율주행의 유행으로 인해 경로 추종 제어에 적용되기 시작했다.^10-12) 이는 두 가지 이유가 있는데 하나는 최근 시판되는 차량들에 RWS가 장착되기 시작했다는 점이고 다른 하나는 인휠모터 장착 차량들이 속속 개발되면서 4WIS, 4WID, 4WIB 기능을 장착하고 있기 때문이다.^8-12)

지난 10여년간 다양한 구동기들 또는 이들의 조합을 경로 추종 제어에 적용하는 방법에 관한 많은 수의 논문들이 발표되었지만 실제 이들 구동기가 경로 추종 제어 성능을 얼마만큼 향상시키는지에 대한 연구는 극히 드문 실정이다. 최근의 연구로는 2023년에 LQR 제어기를 적용하고 조향, 제동, 구동을 위한 다양한 구동기들의 조합이 경로 추종 제어에 미치는 영향을 연구한 논문이 발표되었다.¹³⁾ 이 논문의 결론은 FWS를 제외하고 다른 구동기들을 경로 추종 제어에 적용한다고 해도 별다른 성능 향상이 없다는 점이다. 본 연구에서도 이 논문의 논지를 따라 조향, 제동, 구동을 위한 구동기들의 조합이 경로 추종 제어 성능에 미치는 영향에 대해 살펴 본다.

본 논문에서는 제어기 설계를 위해 2-자유도 자전거 모델과 목표 경로에서 상태-공간 모델을 유도한다. 제어 입력은 전륜 조향각 δ_f, 후륜 조향각δ_r, 그리고 제어 요 모멘트 ∆M_Z로 구성되며 이들을 조합하면 5개의 제어 입력 구성(Input configuration)이 만들어진다.¹³⁾ 제어기는 모델 예측 제어(Model Predictive Control, MPC)를 이용하여 설계한다. 제어 요 모멘트는 4개 차륜의 타이어 힘으로 변환되어야 하는 데 이를 위해 제어 할당 (Control Allocation) 방법을 적용한다. 제어 요 모멘트를 만들어 내는 타이어 힘들은 FWS, RWS, RWIS, 4WIS, 4WID, 4WIB가 만들어 낸다. 본 논문에서 제어할당을 위해 가중최소제곱법(Weighted Least Square, WLS)을 이용한다. 경로 추종 제어의 성능을 비교하기 위해서는 단일한 기준에 의한 성능지표가 필요하다. 이를 위해 2중 차선변경과 충돌회피를 결합하는 목표 경로를 이용하며 이 경로에서 성능지표를 유도한다. 단일 구동기 또는 여러 가지 구동기의 조합이 경로 추종 제어에 미치는 영향을 파악하기 위해 차량 시뮬레이션 패키지에서 시뮬레이션을 수행한다.

본 논문의 구성은 다음과 같다. 먼저 2장에서는 상태-공간 모델을 유도하고 제어 입력을 정의하며 이를 이용하여 MPC를 적용하는 방법에 대해 설명한다. MPC에서 구해진 제어 요 모멘트를 타이어 힘으로 분배하는 제어할당 방법에 대해서도 설명한다. 3장에서는 목표 경로를 정의하고 성능지표를 유도한다. 4장에서는 시뮬레이션을 수행하고 결과에 대해 논의한 후 5장에서는 결론을 맺는다.

2. 경로 추종 제어기 설계

본 장에서는 제어기 설계를 위한 상태-공간 모델을 유도하고 이를 이용하여 MPC 제어기를 설계하는 방법을 설명한다. MPC에서 구해진 제어 요 모멘트를 개별 구동기의 힘으로 할당하는 제어할당방법에 대해서 설명한다.

2.1 경로 추종을 위한 상태-공간 모델

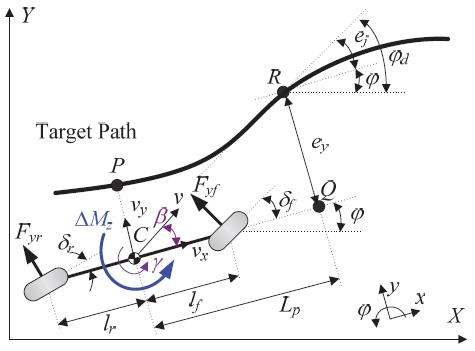
Fig. 1은 2-자유도 자전거 모델과 목표 경로를 보여 준다. Fig. 1에서 보듯이 예견 거리 L_p를 가지는 예견 기능을 도입한다. L_p의 정의는 식 (1)과 같다. 식 (1)에서 k_v는 속도 게인이며 v_x는 종방향 속도이다. 2-자유도 자전거 모델의 운동방정식은 식 (2)와 같이 유도된다.^2,14,15) 식 (3)과 같이 전륜과 후륜의 슬립각을 정의하고 선형 타이어 모델을 가정하면 식 (4)가 얻어진다. 횡슬립각 β와 요율 γ를 상태 변수로 정의한 후 식 (3)과 (4)를 식 (2)에 대입하면 식 (5)가 얻어진다. Fig. 1에서 제어 입력은 전륜 조향각 δ_f, 후륜 조향각 δ_r, 그리고 제어 요 모멘트 ∆M_z이다.

L p = k v ⋅ v x

(1)

m v x β ˙ + γ = F y f + F y r I z γ ˙ = l f F y f - l r F y r + Δ M z

(2)

α f = δ f - β - l f γ v x, α r = δ r - β + l r γ v x

(3)

F y f = 2 C f α f, F y r = 2 C r α r

(4)

β ˙ = ζ 1 m v x β + ζ 2 m v x 2 - 1 γ + C f m v x δ f + C r m v x δ r γ ˙ = ζ 2 I z β + ζ 3 I z v x γ + l f C f I z δ f - l r C r I z δ r + Δ M z I z ζ 1 = - C f - C r, ζ 2 = - C f l f + C r l r, ζ 3 = - l f 2 C f - l r 2 C r

(5)

Fig. 1

2-DOF bicycle model and a target path

Fig. 1에서 차량의 무게 중심에서 예견 거리 L_p만큼 떨어진 점이 Q이고 Q에 대해 횡방향 오차 e_y와 방위각 오차 e_φ가 정의된다. e_y와 e_φ의 시간 미분은 식 (6)과 같이 유도된다.^14,15) 식 (6)에서 χ는 점 R에서의 곡률이다.

e ˙ y = v x s i n ⁡ e φ - v x β - L p γ ≈ v x e φ - v x β - L p γ e ˙ φ = φ ˙ d - φ ˙ = v x χ - γ

(6)

식 (7)과 같이 e_y, e_φ, β, γ를 상태 변수로 정의하고 χ를 외란, δ_f, δ_r, ∆M_z를 제어 입력으로 정의하면 식 (8)과 같은 상태-공간 방정식이 얻어진다. 식 (8)에서 행렬 A, B₁, B₂는 식 (9)와 같이 구해진다.

x = e y e φ β γ T, w = χ, u = δ f δ r Δ M z

(7)

x ˙ = A x + B 1 w + B 2 u

(8)

A = 0 v x - v x - L p 000 - 1 00 ζ 1 m v x ζ 2 m v x 2 - 1 00 ζ 2 I z ζ 3 I z v x, B 1 = 0 v x 00, B 2 = 000000 C f m v x C r m v x 0 l f C f I z - l r C r I z 1 I z

(9)

본 논문에서 경로 추종 제어기에 대한 구동기의 영향을 파악하기 위해서 Table 1과 같이 5개의 입력 구성(Input Configuration, IC)을 사용한다.¹¹⁾ Table 1에서 보듯이 5개의 IC는 제어 입력 δ_f, δ_r, ∆M_z의 조합이며 각 IC에 따라 입력 행렬 B_2i가 정의된다. Table 1에서 B₂(i)는 식 (9)의 B₂에서 i번째 열이다. 또한 Table 1에서는 개별 IC마다 사용할 수 있는 구동기의 목록이 제시되어 있다. 예를 들어 IC#3의 경우 FWS, RWS, RWIS, 4WID, 4WIB를 사용할 수 있는 데 FWS는 δ_f에 해당하고 나머지 구동기는 모두 ∆M_z를 만드는 데 사용된다.

Table 1

Input configurations for path tracking control

MPC는 LQ 목적함수를 사용한다. 본 논문에서는 개별 IC에 대해 식 (10)과 같은 목적함수를 사용한다. 식 (10)에서 ρ_i는 각 항의 가중치로서 Bryson rule (11)을 이용하여 결정하는 데 v_i는 각 항의 최대 허용치이다. 식 (10)을 벡터-행렬 형태로 바꾸면 식 (12)와 같다.

J 0 = ∫ 0 ∞ ρ 1 e y 2 + ρ 2 e φ 2 + ρ 3 β 2 + ρ 4 γ 2 d t J 1 = J 0 + ∫ 0 ∞ ρ 5 δ f 2 d t for IC#1 J 2 = J 0 + ∫ 0 ∞ ρ 5 δ f 2 + ρ 6 δ r 2 d t for IC#2 J 3 = J 0 + ∫ 0 ∞ ρ 5 δ f 2 + ρ 7 Δ M z 2 d t for IC#3 J 4 = J 0 + ∫ 0 ∞ ρ 5 δ f 2 + ρ 6 δ r 2 + ρ 7 Δ M z 2 d t for IC#4 J 5 = J 0 + ∫ 0 ∞ ρ 7 Δ M z 2 d t for IC#5

(10)

ρ i = 1 v i 2

(11)

J i = ∫ 0 ∞ x u i T Q 0 0 R i x u i d t Q = d i a g ρ 1, ρ 2, ρ 3, ρ 4 R 1 = ρ 5 for IC#1 R 2 = d i a g (ρ 5, ρ 6) for IC#2 R 3 = d i a g (ρ 5, ρ 7) for IC#3 R 4 = d i a g (ρ 5, ρ 6, ρ 7) for IC#4 R 5 = ρ 7 for IC#5

(12)

2.2 MPC 설계

MPC를 설계하기 위해서는 샘플링주기 T_s에 대해 상태-공간 방정식 (8)을 이산화해야 한다. 식 (8)을 T_s에 대해 이산화하면 식 (13)과 같고 LQ 목적함수 (12)를 T_s에 대해 이산화하면 식 (14)와 같다. 이산시간 상태-공간에서 임의의 시점 k에서 상태 벡터는 식 (15)와 같이 구해진다. 식 (16)과 같이 현재시점 0에서 시점 k까지 상태 변수에 대해 각각 벡터와 행렬을 정의하고 이를 이용하여 식 (15)와 (14)를 정리하면 각각 식 (17)과 (18)이 얻어진다. 식 (17)을 (18)에대입하고 최적화 변수 U에 대해 정리하면 식 (19)와 같이 2차계획법 문제가 유도된다.^16,17) 제어 입력에 대한 제한조건은 식 (20)과 같이 IC#1의 경우 전륜 조향각의 최대값으로 설정된다. 식 (19)와 (20)의 2차계획법 문제는 MATLAB의 quadprog()를 이용하여 해를 구한다. 이렇게 구한 최적해의 벡터 U에서 가장 위에 있는 값이 현재 시점 k의 제어 입력이 된다.

x k + 1 = Γ x k + Ω w k + Φ u k Γ = I + A ⋅ T s, Ω = B 1 ⋅ T s, Φ = B 2 ⋅ T s

(13)

J M P C = ∑ k = 0 N - 1 x k T Q x k + u k T R u k

(14)

x k + 1 = Γ k x 0 + ∑ i = 0 k - 1 Γ i - 1 Φ u k - i - 1

(15)

X = x 1 x 2 x 3 ⋮ x N, Γ ¯ = Γ Γ 2 Γ 3 ⋮ Γ N, U = u 0 u 1 u 2 ⋮ u N - 1, Φ ¯ = Φ 0000 Γ Φ Φ 000 Γ 2 Φ Γ Φ Φ 00 ⋮ ⋮ ⋮ ⋱ 0 Γ N - 1 Φ Γ N - 2 Φ Γ N - 3 Φ ⋯ Φ, Q ¯ = d i a g Q, ⋯, Q R ¯ = d i a g R, ⋯, R

(16)

X = Γ ¯ x 0 + Φ ¯ U

(17)

J M P C = x 0 T Q x 0 + X T Q ¯ X + U T R ¯ U

(18)

J M P C = U T Φ ¯ T Q ¯ Φ ¯ + R ¯ U + 2 x 0 T Γ ¯ T Q ¯ Φ ¯ U

(19)

- δ max ≤ U ≤ δ max

(20)

2.3 WLS를 이용한 제어 할당

Table 1에서 보듯이 IC#3, IC#4, IC#5는 제어 요 모멘트 ∆M_z를 이용한다. MPC에서 얻어지는 ∆M_z는 모든 구동기에서 만들어 내는 제어 타이어 힘(Control tire force)으로 변환될 수 있다. 이 과정을 제어 할당이라고 하며 이를 위해서 본 논문에서는 가중최소제곱법 (WLS)을 이용한다.^13,14)

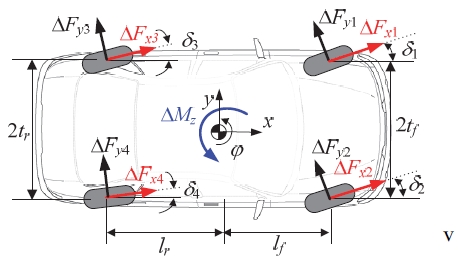
Fig. 2는 제어 요 모멘트 ∆M_z와 ∆M_z를 만들어 내기 위해 필요한 각 차륜의 제어 타이어 힘 사이의 관계를 보여 준다. Fig. 2에서 차륜의 번호는 전륜 좌측과 우측, 후륜 좌측과 우측이 각각 1, 2, 3, 4이다. 종방향 제어 타이어 힘 ∆F_x₁, ∆F_x₂, ∆F_x₃, ∆F_x₄는 4WID의 구동력 또는 4WIB의 제동력으로 변환되며 횡방향 제어 타이어 힘 ∆F_y₁, ∆F_y₂, ∆F_y₃, ∆F_y₄는 FWS, RWS, RWIS, 4WS, 4WIS의 조향각으로 변환된다. Fig. 2에 있는 ∆M_z와 제어 타이어 힘들 사이의 평형방정식은 식 (21)과 같이 얻어진다. 식 (21)에서 벡터 p의 요소는 식 (22)와 같다. Fig. 2와 식 (22)에서 알 수 있듯이 4륜의 조향각은 서로 독립적으로 자유롭게 움직일 수 있다. 하지만 RWS는 후륜 조향각이 서로 동일해야 하며 4WS의 경우 전륜과 후륜의 조향각은 각각 서로 동일해야 한다. 이를 강제하기 위해 식 (23)과 같은 등식 제한조건을 추가한다.^11,13)

p 1 p 2 p 3 p 4 p 5 p 6 p 7 p 8 ⏟ p Δ F y 1 Δ F y 2 Δ F y 3 Δ F y 4 Δ F x 1 Δ F x 2 Δ F x 3 Δ F x 4 ⏟ q = Δ M z

(21)

p 1 = - l f c o s ⁡ δ 1 - t f s i n ⁡ δ 1, p 2 = - l f c o s ⁡ δ 2 + t f s i n ⁡ δ 2, p 3 = l r c o s ⁡ δ 3 - t r s i n ⁡ δ 3, p 4 = l r c o s ⁡ δ 4 + t r s i n ⁡ δ 4, p 5 = - l f s i n ⁡ δ 1 + t f c o s ⁡ δ 1, p 6 = - l f s i n ⁡ δ 2 - t f c o s ⁡ δ 2, p 7 = l r s i n ⁡ δ 3 + t r c o s ⁡ δ 3, p 8 = l r s i n ⁡ δ 4 - t r c o s ⁡ δ 4

(22)

RWS: 001 - 1 0000 ⏟ G q = 0 ⏟ 0 4WS: 1 - 1 000000 001 - 1 0000 ⏟ G q = 00 ⏟ 0

(23)

Fig. 2

Control yaw moment and control tire forces generated by actuators

식 (23)은 ∆M_z를 만들어 내기 위해 반드시 만족되어야 하지만 이 식 하나만으로는 제어 타이어 힘을 결정할 수 없다. 따라서 식 (24)와 같이 제어 타이어 힘으로 구성된 2차 목적함수 J_A를 정의한다. 식 (24)에서 ξ는 가변가중치 ξ_i의 벡터로서 각 항의 크기를 조절하는 역할을 한다. 등식 제한조건 (21)을 식 (25)과 같이 J_B로 변형하여 식 (26)과 같이 식 (24)의 목적함수에 더해서 J_C_를 구함으로써 제한 최적화 문제를 비제한 최적화 문제로 변환한다. 식 (26)에서 η는 등식 제한조건 (25)에 대한 가중치로서 식 (21)의 등식 제한조건을 어느 정도 만족시킬 것인지 결정하는 상수이다. 식 (26)의 최적해를 구하면 식 (27)과 같이 구해진다.¹²⁾ 만약 RWS 또는 4WS가 적용된다면 식 (23)의 등식 제한조건을 고려해야 한다. 식 (26)을 전개해서 정리하면 식 (28)이 얻어진다. 식 (28)의 목적함수와 식 (23)의 등식 제한조건을 가지는 2차계획법의 최적해는 식 (29)와 같이 해석적으로 구해진다.¹³⁾

J A = κ 1 Δ F y 1 2 + κ 5 Δ F x 1 2 μ F z 1 2 + κ 2 Δ F y 2 2 + κ 6 Δ F x 2 2 μ F z 2 2 + κ 3 Δ F y 3 2 + κ 7 Δ F x 3 2 μ F z 3 2 + κ 4 Δ F y 4 2 + κ 8 Δ F x 4 2 μ F z 4 2 = q T W q X = diag 1 μ F z 1 2, 1 μ F z 2 2, 1 μ F z 3 2, 1 μ F z 4 2 W = diag X, X ξ ξ = d i a g ξ 1 ξ 2 ξ 3 ξ 4 ξ 5 ξ 6 ξ 7 ξ 8

(24)

J B = p q - Δ M z T p q - Δ M z

(25)

J C = J A + J B = q T W q + η p q - Δ M z T p q - Δ M z

(26)

q o p t = η W + η p T p - 1 p T Δ M z

(27)

J C = q T W + η p T p q - 2 η Δ M c p q + η Δ M c 2 = q T M q + c T q + η Δ M c 2 M ≜ W + η p T p, c ≜ - 2 η Δ M z p T

(28)

q o p t = - M - 1 c - G T G M - 1 G T - 1 G M - 1 c T

(29)

식 (24)에서 벡터 ξ의 요소인 가변가중치 ξ_i는 식 (21)의 벡터 q의 요소인 제어 타이어 힘에 대응한다. ξ₁, ξ₂, ξ₃, ξ₄는 각각 ∆F_y₁, ∆F_y₂, ∆F_y₃, ∆F_y₄에 대응하고 ξ₅, ξ₆, ξ₇, ξ₈은 각각 ∆F_x₁, ∆F_x₂, ∆F_x₃, ∆F_x₄에 대응한다. 가변가중치 ξ_i는 대응하는 제어 타이어 힘의 크기를 조절한다.^11,13) 예를 들어 가변가중치 ξ_i가 모두 동일한 값을 가진다고 했을 때 ξ₂의 값만 증가한다면 그에 대응하는 ∆F_y₂의 값은 감소한다. 이러한 원리를 이용하여 각 조향장치에 대응하는 벡터 ξ를 설정하면 식 (30)과 같다. 식 (30)에서 ϵ_i의 값은 모두 1e-4이다. 4WIB의 제동을 사용하는 경우 ∆M_z가 양(+)인 경우 ∆F_x₁, ∆F_x₃만 사용하고 음(-)인 경우 ∆F_x₂, ∆F_x₄만 사용하게 된다. 이를 표현한 것이 식 (31)이다. 4WID의 구동을 사용하는 경우 이와는 반대로서 이를 표현한 것이 식 (32)이다. 제동과 구동을 모두 사용하는 경우 식 (33)과 같이 표현된다. 이와 같은 방식으로 벡터 ξ의 요소를 조절함으로써 벡터 q의 제어 타이어 힘의 크기를 조절하여 구동기의 조합을 표현할 수 있다.^11,13)

FWS: ξ=diag RWS/RWIS: ξ=diag 11 ε 3 ε 4 ∙ ∙ ∙ 4WS/4WIS: ξ=diag ε 1 ε 2 ε 3 ε 4 ∙ ∙ ∙

(30)

4WIB: ξ = d i a g * * * * ε 5 1 ε 7 1 if Δ M z > 0 ξ = d i a g * * * * 1 ε 6 1 ε 7 if Δ M z < 0

(31)

4WID: ξ = d i a g * * * * 1 ε 6 1 ε 8 if Δ M z > 0 ξ = d i a g * * * * ε 5 1 ε 7 1 if Δ M z < 0

(32)

4WID+4WIB: ξ = d i a g * * * * ε 5 ε 6 ε 7 ε 8

(33)

Table 1에서 IC#3은 이미 전륜 조향각 δ_f를 포함하고 있다. 따라서 IC#3를 사용하는 경우 ∆M_z를 분배할 때 조향에 있어서는 전륜 조향각을 만들어 낼 필요는 없으며 RWS만을 이용한다. 따라서 식 (30)에서 두번째 항, 즉 RWS/RWIS만을 이용해야 한다. 동일한 이유로 IC#4를 이용하는 경우 전륜과 후륜의 조향각은 이미 결정되었으므로 ∆M_z를 분배할 때 4WID와 4WIB의 구동력과 제동력만 만들어 낸다. 이와는 반대로 IC#5에서는 그 어떤 구동기의 입력도 결정되지 않았으므로 ∆M_z를 분배할 때 모든 종류의 구동기 조합을 만들어 낼 수 있다. 이것을 나타내는 것이 식 (30)의 마지막 행과 식 (33)의 조합이다.

2.4 개별 구동기의 출력 결정

앞절에서 보았듯이 제어할당 과정을 거치면 최적해로서 식 (21)의 벡터 q가 얻어진다. 이후 벡터 q의 요소인 제어 타이어 힘들은 각각 조향 장치(FWS, RWS, 4WS, RWIS, 4WIS)의 조향각, 4WID의 구동력, 4WIB의 제동력으로 변환되어야 한다.

벡터 q의 ∆F_x₁, ∆F_x₂, ∆F_x₃, ∆F_x₄로부터 4WIB와 4WID가 만들어 내야 하는 제동력과 구동력은 각각 식 (34)와 (35)로 계산된다.^11,13) 이들 식에서 r_wi, ω_i, ζ_i는 각각 차륜의 반지름, 차륜의 회전 각속도와 모터 감쇠비를 나타내며 h(•)는 모터의 성능 곡선을 의미한다.

T B i = h r w i Δ F x i ζ i, ω i if Δ F x i < 0 0 if Δ F x i ≥ 0

(34)

T D i = h r w i Δ F x i ζ i, ω i if Δ F x i > 0 0 if Δ F x i ≤ 0

(35)

다음으로 벡터 q의 ∆F_y₁, ∆F_y₂, ∆F_y₃, ∆F_y₄로부터 각 차륜의 조향각을 결정해야 한다. 이때 주의해야할 점은 4WS와 4WIS의 경우 각각 다른 식을 사용해야 한다는 점이다. 4WS의 경우 자전거 모델에서와 같이 전방 차륜의 조향각이 서로 동일하고 후방 차륜의 조향각도 서로 동일하다. ∆F_y가 주어지면 자전거 모델에서 횡방향 타이어 힘의 정의 (4)로부터 식 (36)을 얻을 수 있는데 이 식은 슬립각의 정의와 동일하다. 식 (36)에서 σ는 슬립률과 동일한 역할을 한다. 식 (3)과 (36)을 결합해서 조향각으로 정리하면 4WS의 조향각으로서 식 (37)이 얻어진다. 식 (3)과 이를 이용한 식 (37)은 4WIS에 대해서는 적용할 수 없으므로 각 차륜에 대해 슬립각의 정의를 식 (38)과 같이 새롭게 유도한다. 식 (36)과 (38)을 결합하면 4WIS의 조향각은 식 (39)와 같이 구해진다.^11,13)

ϕ i = - Δ F y i σ C i, i = 1,2, 3,4

(36)

δ i = - α i + β + l f γ v x = - ϕ i + β + l f γ v x, i = 1,2 δ i = - α i + β - l r γ v x = - ϕ i + β - l r γ v x, i = 3,4

(37)

α i = δ i - v y + l f γ v x + - 1 i t f γ, i = 1,2 α i = δ i - v y - l r γ v x + - 1 i t r γ, i = 3,4

(38)

δ i = - ϕ i + v y + l f γ v x + - 1 i t f γ i = 1,2 δ i = - ϕ i + v y - l r γ v x + - 1 i t r γ, i = 3,4

(39)

3. 시뮬레이션 및 해석

본 장에서는 주어진 목표 경로에 대해 성능 지표를 정의하고 개별 IC에 대해 시뮬레이션을 수행하여 특정 구동기 또는 구동기의 조합이 경로 추종에 미치는 영향을 분석한다.

3.1 경로 추종 성능 지표

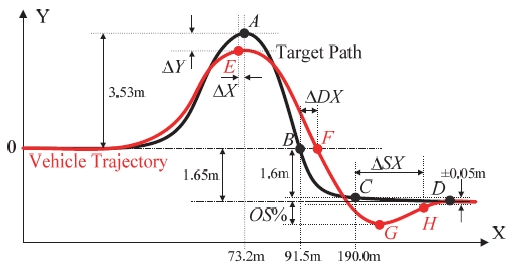
Fig. 3은 본 논문에서 사용하는 목표 경로를 보여 준다. 이 목표 경로는 장애물 회피와 2중 차선변경조향을 모두 포함하는 경로이다. Fig. 3에서 빨간색 실선은 차량의 궤적으로 이 궤적과 목표 경로 사이에서 5개의 성능 지표, 즉 ∆X, ∆Y, OS %, ∆DX, ∆SX가 식 (40)과 같이 정의된다.^13,17) ∆X는 제어공학에서 상승시간에 해당하는 개념으로 목표까지 도달하는 데에 필요한 거리를 나타낸다. ∆Y는 목표까지 도달했는지 여부를 나타내며 OS %는 제어공학에서 오버슈트와 동일하다. ∆DX는 X축 기준으로 차량의 궤적이 목표 경로에서 밀린 정도를 정의한다. ∆SX는 제어공학의 수렴시간에 대응하는 개념으로 차량의 궤적이 점 C에서 목표 경로의 점 D에 도달하는 데에 필요한 거리를 나타낸다. 이들 5개의 성능 지표는 작을수록 좋다. 다만, ∆Y의 경우 크기가 0.05 m보다 작다면 만족한 것으로 간주한다. LQ 목적함수의 가중치를 튜닝할 때에도 이 기준을 먼저 만족하도록 튜닝하고 이후 다른 성능 지표를 줄이도록 튜닝한다. 경로 추종에서 다루어야 할 또 다른 지표는 횡슬립각이다. 횡슬립각이 3º 이상 커지는 경우 운전자 또는 탑승자는 불편함을 느끼게 되므로 가급적이면 이 값을 작게 유지하도록 튜닝한다. 본 논문에서는 횡슬립각이 2º 이하로 유지하도록 튜닝하였다.

Δ X = X E - X A = X E - 73.20 Δ Y = Y E - Y A = Y E - 3.53 Δ D X = X F - X B = X F - 91.50 Δ S X = X H - X C = X H - 190.00 O S % = Y G - 1.65 1.65 + 3.53 × 100

(40)

Fig. 3

Definitions of performance measures for path tracking

차량의 선회에서 가장 중요한 요인은 횡방향 타이어 힘이며 이 힘의 크기는 식 (41)과 같이 마찰원의 크기에 따라 좌우된다. 마찰원의 개념을 이용하면 현재 타이어 힘들이 주어진 상황에서 각 타이어 힘이 얼마만큼 더 생성될 수 있는지를 알 수 있으며 본 논문에서는 이를 타이어 힘 마진(Tire Force Margin, TFM)이라고 하고 식 (41)과 같이 계산한다.¹³⁾

μ F z 2 ≥ F x 2 + F y 2 ⇒ T F M = μ F z - F x 2 + F y 2

(41)

3.2 시뮬레이션 환경과 조건

주어진 목표 경로에서 e_y와 e_φ를 구하는 과정과 MPC는 MATLAB/Simulink 환경에서 구현하였다. MPC에서 T_s는 0.01초, 예측 단계는 30으로 설정하였다. 제어 입력의 크기 제한을 나타내는 식 (20)에서 전륜과 후륜의 조향각의 최대값은 각각 30º와 1º로 설정하였고 IC#3, IC#4, IC#5에서 ∆M_z의 최대값은 각각 1,000, 1,000, 18,000으로 설정하였다. 시뮬레이션은 MATLAB/Simulink와 연동된 CarSim에서 수행하였다.^{6,7,11,13,17)} CarSim에서 차량 모델은 F-class 세단 모델로 선정하였다. 노면 마찰 계수가 0.6 이상인 경우 대부분의 경로 추종 제어기 또는 운전자 모델은 우수한 성능을 보이므로 경로 추종이 어려운 저마찰 노면으로 가정하여 0.4로 설정하였다.¹⁷⁾ 차량의 속도는 60 km/h로 설정하였고 CarSim에서 제공하는 속도 제어기를 이용하여 일정한 속도를 유지하도록 제어하였다. 모든 구동기는 10 Hz의 대역폭을 가지는 1차 시스템으로 모델링하였다.

Table 1에 제시된 5개의 IC에 대해 시뮬레이션을 수행하였다. 각 IC마다 가장 좋은 성능을 제공하도록 LQ 목적함수의 가중치와 속도 게인 k_v를 튜닝하였다. 또한 개별 IC에 대해 가능한 모든 구동기를 적용하여 IC와 구동기별로 성능을 점검하였다.

3.3 시뮬레이션 결과 및 해석

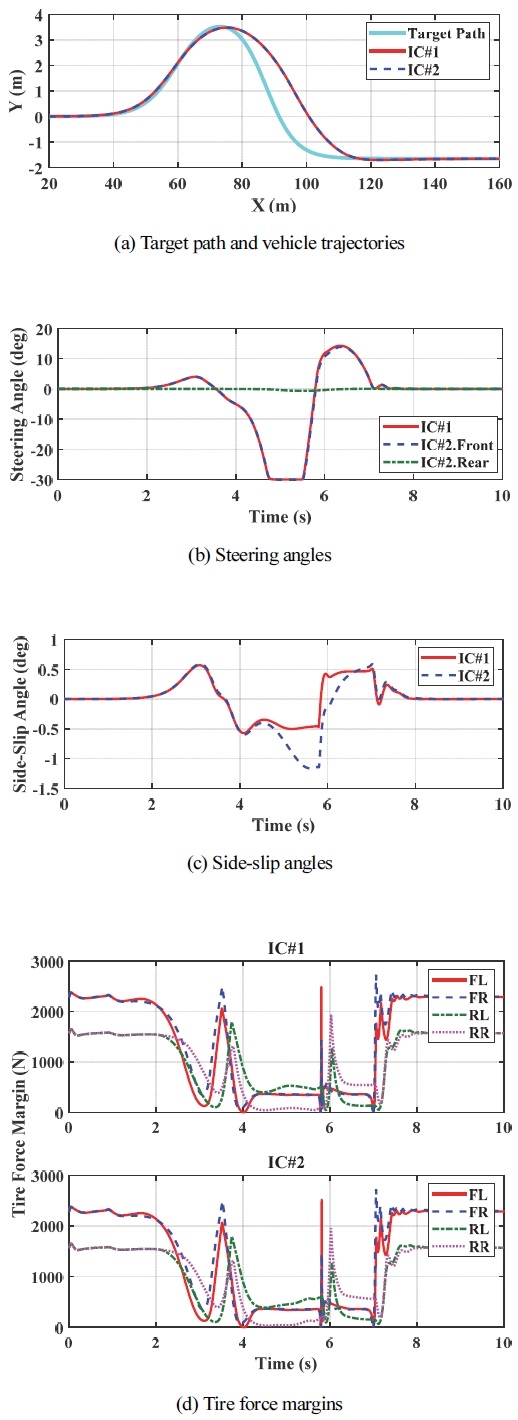
가장 먼저 IC#1과 IC#2에 대한 시뮬레이션을 수행하였다. Fig. 4는 IC#1과 IC#2의 시뮬레이션 결과를 보여 준다. Fig. 4의 (a)와 (b)에서 보듯이 IC#1와 IC#2는 서로 거의 동일한 결과를 보여 준다. Fig. 4의 (c)와 같이 횡슬립각만 차이를 보여줄 뿐이다. Fig. 4의 (d)는 TFM을 보여 주는 데 그림에서 보듯이 선회 과정에서 TFM은 저마찰 노면이기 때문에 매우 작은 값을 보여 주며 심지어 0이 되는 순간도 있다. 이 경우 다른 구동기를 이용하여 물리적으로 횡방향 타이어 힘을 만들어 낼 수 있는 여지가 없게 된다. 상황이 이러하므로 IC#2, IC#3, IC#4, IC#5의 결과에서도 보듯이 주어진 구동기 이외에 별도의 구동기를 추가한다고 해도 성능 향상의 여지가 거의 없게 된다.

Fig. 4

Simulation results for IC#1 and IC#2

Table 2는 IC#1과 IC#2의 시뮬레이션 결과에 대한 요약을 보여 주는 데 Table 2에서 보듯이 FWS를 이용하는 IC#1과 4WS를 이용하는 IC#2는 서로 동일한 성능을 보여 준다. FWS에 RWS를 더한 것이 4WS이므로 이 결과는 FWS에 RWS를 추가한다고 해도 별다른 성능 향상이 없음을 의미한다. Table 2에서 최대횡슬립각(Maximum Absolute Side-Slip Angle, MASSA)을 보면 IC#1에 비해 IC#2의 경우 RWS로 인해 횡슬립각이 증가하는 것을 알 수 있다. 일반적으로 VSC에서 RWS를 사용하는 경우 횡슬립각이 현저하게 감소하지만 경로 추종 제어에서는 반대의 결과가 나타남을 알 수 있다.^7,8) 이는 목표 경로와 차량 궤적 사이의 횡방향 오차 e_y를 줄이기 위해 FWS의 조향각과 같은 방향으로 RWS가 과도하게 사용되어 차량의 방위각이 거의 변하지 않게 되고 그 결과 차량은 회전을 하지 않고 횡으로만 움직이게 되어 횡슬립각이 심각하게 커지게 된다. 따라서 이를 방지하기 위해서는 RWS를 사용하게 되면 MPC에서 후륜 조향각을 1º 이내로 제한해야 한다.¹¹⁾

Table 2

Summary of the simulation results for IC#1 and IC#2

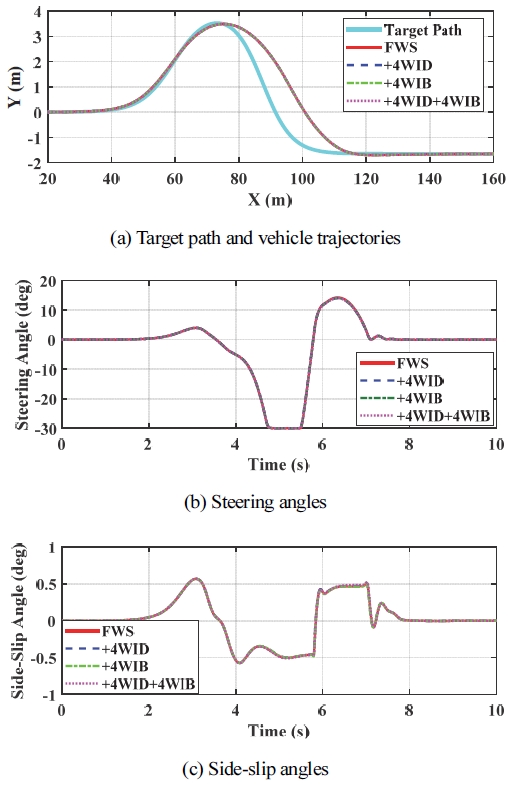
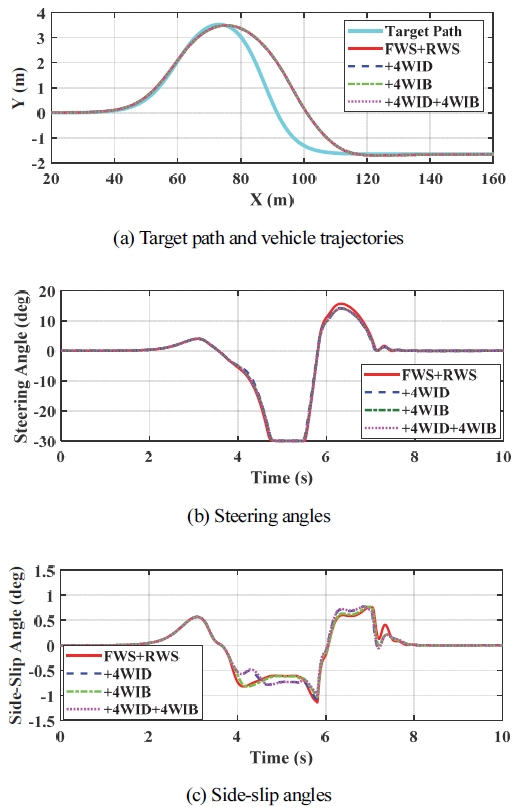
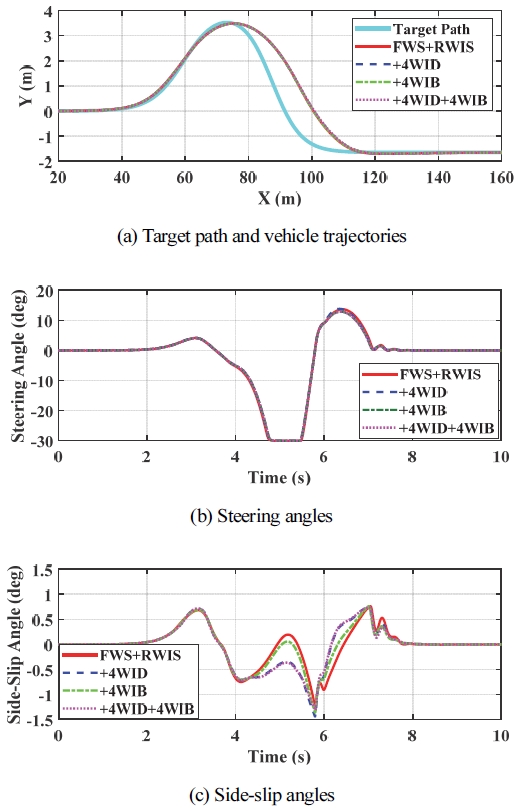
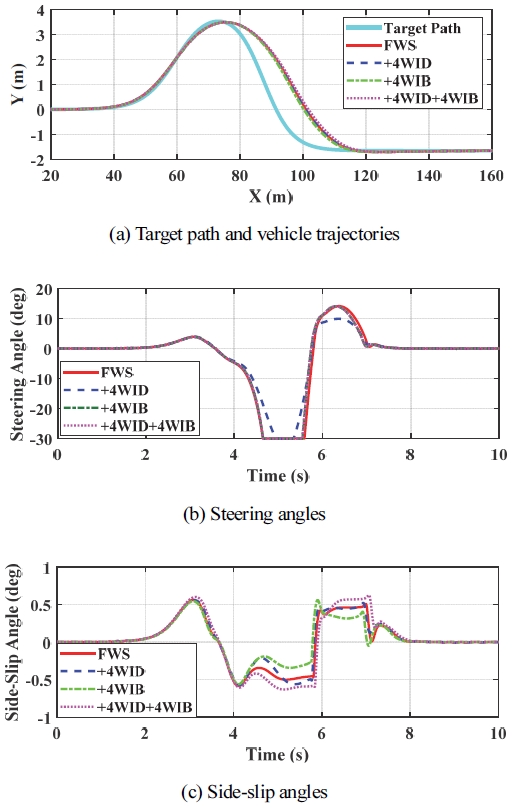
다음으로 IC#3에 대한 시뮬레이션을 수행하였다. Table 3은 IC#3에 대한 시뮬레이션 결과에 대한 요약을 보여 준다. Table 1에서 보듯이 IC#3는 ∆M_z를 만들어 내기 위해 RWS, RWIS, 4WID, 4WIB를 사용할 수 있다. Table 3에서 보듯이 FWS 이외에 다른 구동기를 추가한다고 해도 성능상의 차이가 없음을 알 수 있다. 성능상의 차이가 있다면 FWS에 RWS를 함께 사용함으로써 횡슬립각이 증가되었고 RWIS를 함께 사용한 경우 횡슬립각이 더욱 증가되었다는 점인데 이것은 Table 2에서 IC#1과 IC#2의 경우와 동일하다. Figs. 5 ~ 7은Table 3에서와 같이 각각 FWS, FWS+RWS, FWS+RWIS에 대해 4WID와 4WID를 결합한 경우에 대한 시뮬레이션 결과를 보여 준다. 그림에서 보듯이 각 구동기 조합에 대해 조향각과 궤적은 거의 동일하며 횡슬립각은 어느 정도 차이를 보인다. 하지만 최대 횡슬립각은 Table 3에서 보듯이 RWS, RWIS의 사용여부에 따라 차이를 보이지만 4WID와 4WIB에 대해서는 별다른 차이를 보이지 않는다는 것을 알 수 있다.

Table 3

Summary of the simulation results for IC#3

Fig. 5

Simulation results with FWS for IC#3

Fig. 6

Simulation results with FWS+RWS for IC#3

Fig. 7

Simulation results with FWS+RWIS for IC#3

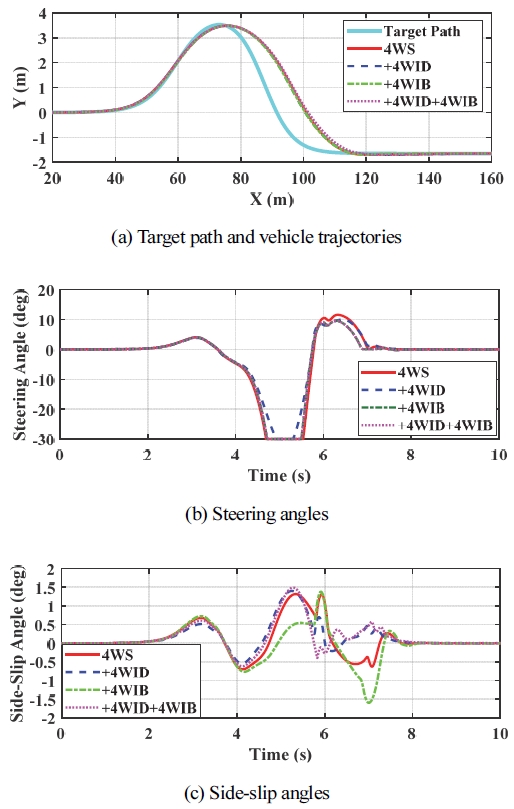
다음으로 IC#4에 대한 시뮬레이션을 수행하였다. Table 4는 IC#4에 대한 시뮬레이션 결과에 대한 요약을 보여 준다. Table 4에서 IC#4는 이미 4WS, 즉 FWS와 RWS를 사용하고 있으므로 조향 구동기는 더 사용할 수 없고 ∆M_z를 만들어 내기 위해 4WID와 4WIB만 추가해서 사용할 수 있다. Table 4에서 보듯이 4WS에 4WID와 4WIB를 추가한다고 해도 별다른 성능상의 차이점이 없음을 알 수 있다. 앞서 IC#2, IC#3와 같이 4WS에 4WID와 4WIB를 추가하는 경우 4WS에 비해 횡슬립각이 더욱 증가하였다. Fig. 8은 Table 4에서 제시한 결과에 대한 시뮬레이션 결과를 보여 준다. Fig. 8에서 보듯이 구동기 조합에 따라 궤적 상에서는 차이가 없으며 4WS를 사용하는 경우 FWS에 비해 횡슬립각이 증가하는 것을 알 수 있다. 다만 4WS에 비해 4WID와 4WIB를 사용하는 경우 조향각이 더 증가하는 것을 알 수 있다.

Table 4

Summary of the simulation results for IC#4

Fig. 8

Simulation results for IC#4

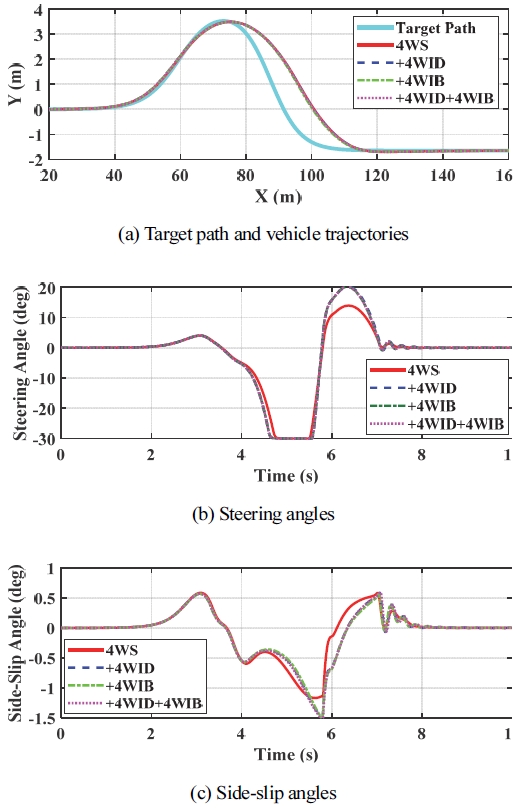
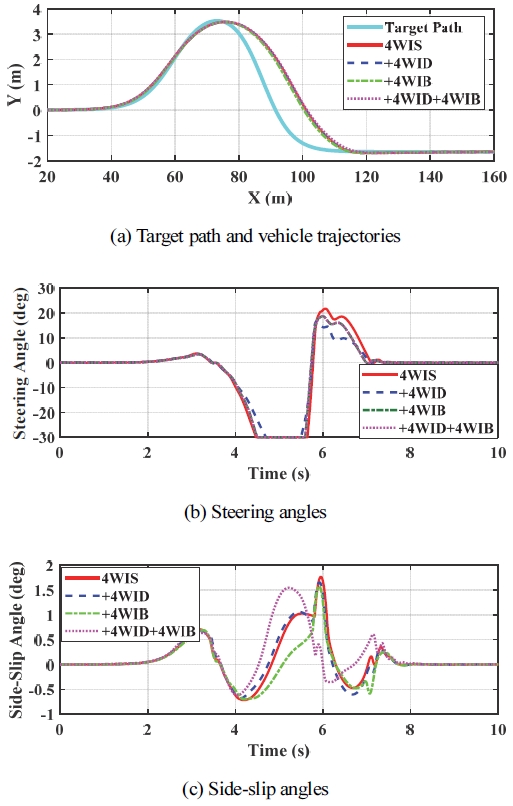
다음으로 IC#5에 대한 시뮬레이션을 수행하였다. Table 5는 IC#5에 대한 시뮬레이션 결과에 대한 요약을 보여 준다. IC#5에서 제어 입력은 ∆M_z뿐이므로 ∆M_z를 만들어 내기 위해 모든 구동기들의 조합이 가능하다. Table 5에서 보듯이 기존의 결과들과 큰 차이가 없다. Table 2의 결과와 비교하면 ∆M_z를 만들어 내기 위해 FWS와 4WS를 사용하는 경우를 보면 오히려 IC#1과 IC#2보다 ∆X가 증가하며 FWS와 4WS만을 사용하는 경우보다 성능이 더 저하되었다. 앞선 결과들에서 FWS에 RWS 또는 RWIS를 함께 사용함으로써 횡슬립각이 증가되었는 데 Table 5의 결과에서도 동일한 사실을 확인할 수 있다. Figs. 9 ~ 11은 Table 5에서와 같이 각각 FWS, 4WS, 4WIS에 대해 4WID와 4WID를 결합한 경우에 대한 시뮬레이션 결과를 보여 준다. 그림에서 보듯이 각 구동기 조합에 대해 궤적은 거의 동일하며 4WID를 제외한 조향각도 거의 동일함을 알 수 있다. 횡슬립각은 FWS에 비해서 RWS와 RWIS의 사용에 따라 증가하지만 4WID와 4WIB에 대해서는 별다른 차이를 보이지 않음을 확인할 수 있다.

Table 5

Summary of the simulation results for IC#5

Fig. 9

Simulation results with FWS for IC#5

Fig. 10

Simulation results with 4WS for IC#5

Fig. 11

Simulation results with 4WIS for IC#5

4. 결 론

1) 본 논문에서는 경로 추종 제어의 성능을 향상시키기 위해 예견 거리를 포함하는 상태-공간 모델을 유도하였으며 이 모델에 MPC를 적용하였다. 3개의 제어 입력으로 구성되는 5개의 입력 구성을 설정하였고 MPC에서 구해지는 제어 입력에 대해 제어할당방법 WLS를 적용하여 FWS, RWS, RWIS, 4WS, 4WIS, 4WID와 4WIB의 출력을 유도하였다. 이 과정을 MATLAB/Simulink에서 구현하고 시뮬레이션을 통해 각각의 구동기들이 경로 추종 제어에 미치는 영향을 점검하였다.
2) 시뮬레이션을 통해 경로 추종 제어에 다양한 구동기를 적용한 결과 기존에 널리 사용되어져 오던 FWS 차량에 대한 경로 추종 제어기에 비해 4WS 또는 RWIS, 4WIS, 4WID, 4WIB를 추가한 제어기들은 성능상의 향상을 보이지 않았다. 따라서 결론적으로 FWS 이외에 별도의 구동기를 추가한다고 해도 경로 추종 성능상의 이점은 없다는 것을 확인하였다.
3) FWS 장착 차량에 대해 RWS 또는 RWIS를 적용하거나 4WIS를 적용하는 경우 경로 추종 제어 성능의 향상 없이 횡슬립각이 증가하는 것을 확인하였다. 일반적으로 횡슬립각이 증가하는 것은 차량에 탑승한 사람의 불편함을 유발하므로 권장되지 않는다. 따라서 FWS 이외에 다른 조향 장치를 추가하는 것은 승차감의 측면에서 부정적인 영향을 미친다는 것을 확인하였다.

Nomenclature


C_f, C_r :	cornering stiffness of front and rear wheels (N/rad)
e_y :	lateral offset error with respect to a target path (m)
e_φ :	heading error with respect to a target path (rad)
I_z :	yaw moment of inertia at vehicle C.G. (kg⋅m²)
F_x, F_y, F_z :	longitudinal, lateral and vertical tire forces (N)
F_yf, F_yr :	lateral tire forces of front and rear wheels (N)
l_f, l_r :	distances from C.G. to front and rear axles (m)
m :	vehicle total mass (kg)
T_s :	sampling time (s)
T_Bi, T_Di :	traction and braking torques at wheel i (N⋅m)
t_f, t_r :	half of track widths of front and rear axles (m)
v_x, v_y :	longitudinal and lateral velocities at vehicle C.G. (m/s)
α_f, α_r :	slip angles of front and rear wheels (rad)
β :	side-slip angle (rad)
χ :	curvature of a target path at a target point (1/m)
δ_f,δ_r :	steering angles of front and rear wheels (rad)
δ_i :	steering angle of wheel i (rad)
*ΔF_x,ΔF_y* :**	longitudinal and lateral control tire forces (N)
*ΔM_Z* :**	control yaw moment (N⋅m)
ξ_i :	variable weight on a particular tire force
ϕ_i :	pseudo-slip angles of wheel i (rad)
*φ, φ_d* :**	target and real heading angles (rad)
γ :	yaw rate (rad/s)
μ :	tire-road friction coefficient

Acknowledgments

이 논문은 2023년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. NRF-2019R1A6A1A03032119).

References

T. Gillespie. Fundamentals of Vehicle Dynamics, Society of Automotive Engineers, 1992. [https://doi.org/10.4271/R-114]
R. Rajamani, Vehicle Dynamics and Control, Springer Science & Business Media, 2011. [https://doi.org/10.1007/978-1-4614-1433-9_2]
Q. Yao, Y. Tian, Q. Wang and S. Wang, “Control Strategies on Path Tracking for Autonomous Vehicle: State of the Art and Future Challenges,” IEEE Access, Vol.8, pp.161211-161222, 2020. [https://doi.org/10.1109/ACCESS.2020.3020075]
M. Rokonuzzaman, N. Mohajer, S. Nahavandi and S. Mohamed, “Review and Performance Evaluation of Path Tracking Controllers of Autonomous Vehicles,” IET Intelligent Transport Systems, Vol.15, No.5, pp.646-670, 2021. [https://doi.org/10.1049/itr2.12051]
P. Stano, U. Montanaro, D. Tavernini, M. Tufo, G. Fiengo, L. Novella and A. Sorniotti, “Model Predictive Path Tracking Control for Automated Road Vehicles: A Review,” Annual Reviews Control, Vol.55, pp.194-236, 2022. [https://doi.org/10.1016/j.arcontrol.2022.11.001]
I. E. Mousavinejad, Y. Zhu and L. Vlacic, “Control Strategies for Improving Ground Vehicle Stability: State-of-the-Art Review,” 2015 10th Asian Control Conference(ASCC), June 2015. [https://doi.org/10.1109/ASCC.2015.7244795]
S. Yim, “Comparison among Active Front, Front Independent, 4-Wheel and 4-Wheel Independent Steering Systems for Vehicle Stability Control,” Electronics, Vol.9, No.5, Paper No.798, 2020. [https://doi.org/10.3390/electronics9050798]
J. Nah and S. Yim, “Vehicle Stability Control with Four-wheel Independent Braking, Drive and Steering on In-Wheel Motor-Driven Electric Vehicles,” Electronics, Vol.9, No.11, Paper No.1934, 2020. [https://doi.org/10.3390/electronics9111934]
E. Katsuyama, M. Yamakado and M. Abe, “A State-of-the Art Review: Toward a Novel Vehicle Dynamics Control Concept Taking the Driveline of Electric Vehicles Into Account as Promising Control Actuators,” Vehicle System Dynamics, Vol.59, No.7, pp.976-1025, 2021. [https://doi.org/10.1080/00423114.2021.1916048]
S. Oh, M. Kim, B. Lee and K. Oh, “Integral Action Based Model Predictive Fault-Tolerant Control for Yaw Rate Tracking of 4-Wheel Independent Steering Vehicle with Multiple Constraints,” Transactions of KSAE, Vol.29, No.6, pp.493-505, 2021. [https://doi.org/10.7467/KSAE.2021.29.6.493]
Y. Jeong and S. Yim, “Path Tracking Control with Four-wheel Independent Steering, Driving and Braking Systems for Autonomous Electric Vehicles,” IEEE Access, Vol.10, pp.74733-74746, 2022. [https://doi.org/10.1109/ACCESS.2022.3190955]
T. Kim, H. Lee, K. Kim and S-H. Hwang, “Path-Following Strategies for 4-Wheel Independent Steering EVs Using PPO Reinforcement Learning and Turning Radius Gain,” Transactions of KSAE, Vol.31, No.8, pp.575-584, 2023. [https://doi.org/10.7467/KSAE.2023.31.8.575]
M. Park and S. Yim, “Comparative Study on Effects of Input Configurations of Linear Quadratic Controller on Path Tracking Performance under Low Friction Condition,” Actuators, Vol.12, No.4, 153, 2023. [https://doi.org/10.3390/act12040153]
J. Guo, Y. Luo and K. Li, “An Adaptive Hierarchical Trajectory Following Control Approach of Autonomous Four-wheel Independent Drive Electric Vehicles,” IEEE Transactions on Intelligent Transportation Systems, Vol.19, No.8, pp.2482-2492, 2018. [https://doi.org/10.1109/TITS.2017.2749416]
J. Guo, Y. Luo, K. Li and Y. Dai, “Coordinated Path-following and Direct Yaw-moment Control of Autonomous Electric Vehicles with Sideslip Angle Estimation,” Mechanical Systems and Signal Processing, Vol.105, pp.183-199, 2018. [https://doi.org/10.1016/j.ymssp.2017.12.018]
G. Bai, Y. Meng, L. Liu, W. Luo, Q. Gu and L. Liu, “Review and Comparison of Path Tracking Based on Model Predictive Control,” Electronics, Vol.8, Paper No.1077, 2019. [https://doi.org/10.3390/electronics8101077]
J. Lee and S. Yim, “Comparative Study of Path Tracking Controllers on Low Friction Roads for Autonomous Vehicles,” Machines, Vol.11, No.3, Paper No.403, 2023. [https://doi.org/10.3390/machines11030403]

IC	Control inputs	Input matrix and available actuators
IC#1	u₁ = δ_f	B₂₁ = B₂(1) FWS
IC#2	u₂ = [δ_f δ_r]^T	B₂₂ = [B₂(1) B₂(2)] 4WS
IC#3	u₃ = [δ_f ΔM_z]^T	B₂₃ = [B₂(1) B₂(3)] FWS, RWS, RWIS, 4WID, 4WIB
IC#4	u₄ = [δ_f δ_r ΔM_z]^T	B₂₄ = [B₂(1) B₂(2) B₂(3)] 4WS, 4WID, 4WIB
IC#5	u₅ = ΔM_z	B₂₅ = B₂(3) FWS, 4WS, 4WIS, 4WID, 4WIB

Actuators	∆X (m)	∆Y (m)	OS%	∆DX (m)	∆SX (m)	MASSA (deg)
IC#1 (FWS)	2.10	-0.037	0.96	9.23	5.58	0.57
IC#2 (4WS)	2.15	-0.036	0.96	9.23	5.70	1.17

Actuators	∆X (m)	∆Y (m)	OS%	∆DX (m)	∆SX (m)	MASSA (deg)
FWS (IC#1)	2.10	-0.037	0.96	9.23	5.58	0.57
+4WID	2.10	-0.036	0.88	9.21	5.77	0.57
+4WIB	2.10	-0.036	0.90	9.22	5.68	0.57
+4WID+4WIB	2.12	-0.035	0.96	9.28	5.68	0.57
FWS+RWS	2.28	-0.038	0.96	9.36	5.68	1.14
+4WID	2.09	-0.037	0.95	9.35	6.23	1.09
+4WIB	2.35	-0.033	0.94	9.44	6.20	1.03
+4WID+4WIB	2.07	-0.035	0.96	9.41	6.23	0.99
FWS+RWIS	2.25	-0.040	0.95	8.98	5.14	1.25
+4WID	2.21	-0.041	0.94	9.14	5.81	1.43
+4WIB	2.24	-0.042	0.81	9.03	5.95	1.35
+4WID+4WIB	2.22	-0.041	0.96	9.26	6.02	1.31

Actuators	∆X (m)	∆Y (m)	OS%	∆DX (m)	∆SX (m)	MASSA (deg)
4WS (IC#2)	2.15	-0.036	0.96	9.23	5.70	1.17
+4WID	2.05	-0.035	0.83	9.05	5.66	1.50
+4WIB	2.01	-0.037	0.82	8.81	5.25	1.52
+4WID+4WIB	2.05	-0.035	0.96	9.13	5.53	1.53

Actuators	∆X (m)	∆Y (m)	OS%	∆DX (m)	∆SX (m)	MASSA (deg)
FWS	2.30	-0.040	0.95	9.46	6.21	0.58
+4WID	2.38	-0.038	0.96	9.32	6.32	0.58
+4WIB	2.27	-0.040	0.96	8.71	5.44	0.56
+4WID+4WIB	2.39	-0.045	0.96	10.21	7.57	0.63
4WS	2.50	-0.042	0.96	9.34	5.22	1.31
+4WID	2.48	-0.040	0.95	9.04	5.93	1.41
+4WIB	2.50	-0.040	0.89	9.04	5.42	1.58
+4WID+4WIB	2.65	-0.043	0.94	9.98	7.32	1.49
4WIS	2.56	-0.045	0.94	9.55	5.00	1.76
+4WID	2.53	-0.043	0.94	9.34	4.90	1.65
+4WIB	2.39	-0.045	0.92	8.84	4.66	1.57
+4WID+4WIB	2.72	-0.043	0.93	9.79	6.59	1.54