K겹 교차검증 및 심층신경망을 활용한 자동차 시트의 BSR 소음 지표 예측 연구

1. 서 론

자동차에서 발생되는 진동 소음은 접촉한 두 물체의 상대 운동의 결과로 발생된다. 최근 미래형 자동차는 모터를 동력원으로 사용하기 때문에 기존의 내연기관에서 발생되는 1차 소음원이 사라졌다. 따라서, 소음 마스킹 효과가 사라져 탑승자가 느끼는 차량 내부 소음에 대한 민감도가 높아지고 있다. 자동차 내부에서 발생되는 진동 소음은 BSR(Buzz, Squeak, Rattle) 소음이 대표적이며, 주로 자동차의 패널, 시트 및 도어에서 전체 BSR 이슈 중 50 % 가 넘는 비율로 발생되고 있다. BSR 소음은 차량에서 발생되는 이음으로 감성품질 문제와 시스템의 구조적인 안정성 문제와 결합되어 나타난다.

여러 연구자들은 BSR 소음을 저감시키는 방안에 대해 많은 연구를 수행하였다.^1-3) 특히, 마찰 소음은 브레이크 시스템에 대한 연구를 통해 선형 이론을 기반으로 동적 불안정성의 메커니즘에 대한 연구가 주로 수행되었다. Kang 등⁴⁾은 브레이크 스퀼에서 발생될 수 있는 종합적인 메커니즘에 대해 수학적으로 전개하여 브레이크 스퀼에 대한 연구를 수행하였다. 남재현과 강재영⁵⁾은 단순 마찰 시스템으로 마찰 소음에 대한 메커니즘을 분석하고, 실험적으로 검증하였다.

시트 BSR 소음 중 Rattle 소음에 대한 연구는 주로 실험적인 방법을 통해 수행되었다. 최호일 등⁶⁾은 차량 시트의 가진 및 작동 내구성 시험을 수행한 후 BSR 시험법에 대한 연구를 수행하여 주요 소음원을 추적하였다. 또한 저자의 다른 연구에서는 시트 쿠션 프레임의 내구 전후 BSR 진동 특성을 분석하여 프레임의 강성 변화에 따른 소음 특성을 분석하였다.⁷⁾

시뮬레이션 기반의 BSR 소음 연구는 최근 하드웨어와 소프트웨어가 발전됨에 따라 많은 연구가 수행되고 있다. 신영철 등⁸⁾은 하중 전달 매개체인 BIW(Body In White) 바디 시스템과 이에 장착되는 시스템 별 모듈의 강건성 확보를 위해 BSR 관점에서 개발된 동강성 해석 기법, 열화 BSR 해석 기법, 직접 버추얼 방법에 대해 소개하였다. Lee 등⁹⁾은 BSR 소음을 예측하는 일반적인 방법인 E-Line Method의 단점을 보완하고자 산포로 표현되는 파트간 공차와 동적 변형량을 통계적인 방법을 활용한 개선된 사례를 소개하였다. 김소울 등¹⁰⁾은 자율 주행 시트의 Rattle 소음에 대한 직접적인 거동을 표현하고자 정현파 실험 기준으로 해석 모델을 보정하고, 외연적 해석을 통해 충격성 소음이 발생되는 위치 및 특성에 대해 기술하였다.

전체 시스템에 대한 BSR 소음 해석은 많은 비용과 시간이 소요된다. 따라서 실험적 측정방법이 주로 수행되지만, BSR 소음 실험은 관련 규정과 계산 방법이 복잡하여 숙련된 전문성 요구된다. 또한, BSR 소음 실험은 복잡한 시스템 및 고가의 장비가 구축되어 있어야한다.

최근 딥러닝은 비약적인 발전을 통해 특정 분야에서 복잡한 계산에 대한 인간의 사고를 대체하고 있으며, 알고리즘이 비선형성을 기반으로 구축되었기 때문에 비선형적인 데이터에 대한 예측 정확성이 높아지고 있다. Nam과 Kang¹¹⁾은 동역학계에서 가장 복잡한 카오스 현상을 이미지 기반의 데이터를 사용하여 CNN(Convolution Neural Network)을 통해 분류할 수 있음을 보였다. Wiercioch와 Kirchmair¹²⁾는 분자의 특성을 예측하기 위한 새로운 DNN(Deep Neural Network) 기반 모델을 제안하여 화학적 특성에 대한 정확한 예측 성능을 보여주었다. Yu 등¹³⁾은 MD-DNN(Multi-channel Decoupled Deep Neural Network) 모델을 제안하여 공유 파트와 분리 파트를 통해 출력 변수 간 상관관계를 절충하는 전략을 제안하였다. 위와 같이 DNN은 다양한 분야에서 시스템의 특성을 예측하기 위해 널리 활용되고 있다.

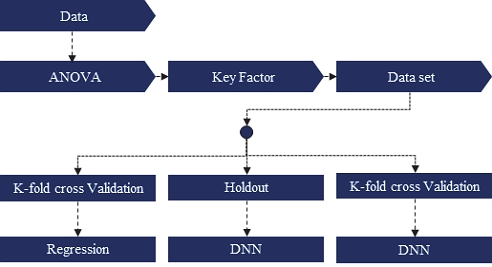
본 논문에서는 BSR 소음을 결정하는 정량적 지표인 Loudness N10을 다양한 음향 및 음질 물리량을 통해 예측하였다. BSR의 정량적인 분석 지표인 Loudness N10을 계산하는 방법은 고가의 장비 및 특정 소프트웨어가 요구되며, 부품의 개발 및 설계 단계에서 검증이 매우 어렵다. 따라서, 본 연구에서는 고가의 장비나 특정 소프트웨어 없이 데이터셋 관점에서 상대적으로 적은 측정 결과를 통해 정량적 지표를 예측할 수 있는 방안에 대해 연구하였다. Loudness N10 예측을 위한 유의미한 물리량은 시트 소음 측정 데이터의 상관분석을 통해 도출되었다. 도출된 물리량은 K겹 교차검증 방법과 머신러닝의 DNN방법을 통해 Loudness N10을 예측하는데 활용되었다. 데이터 기반 정량적 BSR 예측 절차는 Fig. 1에서 나타냈다.

Fig. 1

Flow diagram of prediction method for Loudness N10

Fig. 1과 같이 본 논문에서는 Loudness N10을 예측하기 위해 측정된 데이터를 기반으로 분산 분석을 수행하여 유의미한 변수를 정의하였다. 데이터 셋은 BSR을 예측하기 위한 유의미한 변수로 구성되었고 K겹 교차검증을 통한 회귀분석, 홀드아웃 기반의 DNN과 K겹 교차검증을 적용한 DNN으로 Loudness N10을 예측하였다.

2. 본 론

2.1 BSR 데이터베이스 구축

BSR 소음에 대한 정량적 평가는 Zwicker Loudness를 기반으로 계산되었다. 데이터는 총 136개의 서로 다른 단일 시트 모델에 대해 9개의 위치(P1 ~ P9)에서 마이크로폰을 이용하여 계측하였다. 따라서 총 1224개의 데이터셋을 확보하였다.

본 연구에서는 실험을 통해 Loudness N10의 정량적 예측을 위한 다양한 음질 및 음향 데이터를 확보하였다. 실험은 모두 BSR에 대한 정량적 지표 도출을 위해 동일 방법으로 수행되었다. 무소음 가진기는 30 dB(A)이하의 소음이 발생되며, 최대 Payload 350 kg, 주파수 범위는 1-200 Hz까지 측정 가능하고, 최대 변위는 25 mm이다. 필터는 300 Hz high pass 필터를 사용하였다. 물리량은 총 10가지 방법을 통해 계산되었으며 모두 상위 10 % 위치에서 최하위 레벨(N10)을 기준으로 하였다.

음질 및 음향 물리량은 Loudness(M1), 3rd octave(M2), Sound pressure level(M3), Fluctuation strength(M4), Roughness(M5), Sharpness(M6), Tonality(M7), Harmonic distortion(M8), Speech intelligibility index(M9), Articulation index(M10)로 총 10가지이다.

통계 분석 이전에 데이터 간의 직관적인 분석을 위해 각 데이터는 최소-최대 정규화가 수행되었다. 데이터 분석은 모든 데이터를 반영하여 분석되지만, 논문의 가시성을 위해 표는 첫 번째 샘플에 대해 나타내었다. 정규화된 첫 번째 샘플은 Table 1에 나타냈다.

Table 1

Normalized value of #s1

Fig. 2

Experimental setup

2.2 데이터 상관 분석

유의미한 변수를 선정하는 것은 데이터 분석의 오류를 줄일 수 있는 효과적인 방법이다. 본 연구에서는 상관분석을 통해 Loudness 예측에 사용될 유의미한 변수를 선정하였다. 상관 분석은 변수간 선형관계의 존재 여부를 결정하여 선형성의 강도에 대한 통계적 분석의 결과를 제시한다. 상관분석의 진행 절차는 먼저 공분산 분석을 수행하여 변수간 연관성을 정의하고, 측정 단위에 관계없이 각 변수의 레벨에 따른 관계의 정도를 정의하게 된다.

공분산은 두 변수가 독립이 아닌 경우 변수들 간 연관성이 있음을 가정하여 연관성의 정도를 파악하게 된다. 연관성은 한 변수의 값이 증가되고 다른 변수 값이 증가되면 양의 연관성이 있고, 반대의 경우는 음의 연관성이 있음을 나타낸다. 또한 공분산이 0이면, 두 변수는 서로 독립된 변수임을 보여준다. 각 물리량에 대한 분산분석 결과는 Table 2에 나타냈다.

Table 2

Analysis of variance

공분산 분석결과에 나타난 것과 같이 각 물리량은 독립적인 변수는 아님을 나타내고 있다. 공분산 분석은 앞서 언급했듯이 변수의 측정 단위 범위에 의존적이다. 따라서, 분산분석의 결과는 정규화된 물리량을 기반으로 표현되었다.

공분산 분석 결과는 정규화된 데이터 분석결과와 유사하게 레벨 기반의 물리량인 M2, M3와 변조 기반의 물리량인 M4가 0.07 이상의 연관성이 나타났다. 또한 BSR 소음은 음성관점에서 불명확한 신호이기 때문에 음성에 관한 지수와 부의 연관성이 높게 나타나는 것을 볼 수 있다. 공분산은 두 변수의 레벨에 따른 관계의 정도를 결과에 포함하지 않기 때문에 상관분석을 통해 두 변수에 대한 관계를 분석하였다. 다만, 앞선 공분산 분석의 결과는 레벨의 편차에 대한 오차를 최소화하기 위해 정규화를 기반으로 수행되었다. 따라서 상관분석의 결과는 정규화된 공분산 분석 결과와 유사한 특성을 나타냄을 알 수 있다. 결과는 Table 3에 나타냈다.

Table 3

Correlation analysis

상관계수의 분석은 총 10개의 물리량에 대해 다중상관 분석을 통해 수행되었으며, 표본 상관계수의 의미는 변수간 선형 상관성을 나타낸다. 각 물리량에 대한 상관관계 분석의 결과는 음압 레벨과 관련된 물리량(M2:0.94, M3:0.96)이 가장 높은 선형 상관성을 나타내고 있으며, 변동강도(M4:0.79)가 3번째로 높은 선형 상관성을 나타내고 있다. 따라서, Loudness 추정은 음압레벨을 대표하는 Sound pressure level(M3)과 주파수의 특성을 일부 반영할 수 있는 Fluctuation strength(M4)로 선정하여 수행하였다.

2.3 K겹 교차검증(K-fold Cross Validation)

회귀 모델은 모형이 복잡해질수록 학습 데이터를 상세하게 묘사할 수 있지만 학습에 사용하지 않은 새로운 데이터에 대한 정확한 예측이 어려워지는 과적합 문제가 발생할 수 있다. 회귀 모델은 전체 모집단에서 추출된 표본집단을 활용하여 모델링된다. 따라서, 회귀 모델은 전체 모집단의 모든 특성을 완벽하게 표현할 수 없으며, 경우에 따라 편향된 특성만을 반영하는 모델이 만들어질 수 있다. 이러한 문제는 K겹 교차검증 방법을 사용하여 표본집단의 데이터베이스를 학습데이터와 평가데이터로 적절하게 구분하여 회귀 모델을 구축하고 평가함으로서 모델의 예측 정확성을 높일 수 있다.

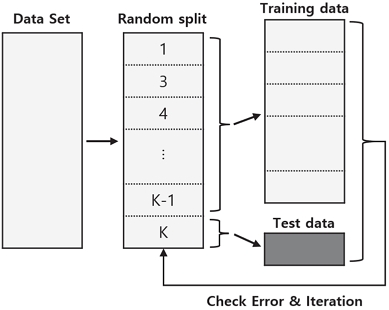
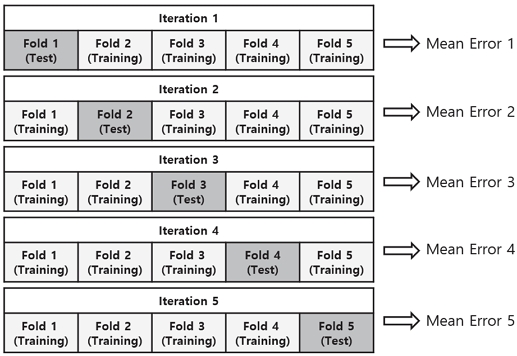
K겹 교차검증 방법은 Fig. 3에 도식화 하였고, 평가방법은 Fig. 4에 나타냈다. 진행절차는 다음과 같다.

• ① 표본집단을 K개의 부분집단으로 무작위 분할
• ② i=1, ..., K 일 때, 각 I에 대해 i번째 그룹을 제외한 나머지 k-1개 그룹의 자료를 바탕으로 회귀식 도출
• ③ i번째 그룹을 이용하여 ②번에서 도출된 회귀식의 예측오차 도출
• ④ 각 i에 대하여 ②, ③번 과정을 반복 수행
• ⑤ K개의 절대오차의 평균을 기준으로 모형 평가

Fig. 3

K-fold cross validation method

Fig. 4

Evaluation of 5-fold cross validation data set

K의 개수는 회귀 모델의 편향(Bias) 및 분산(Variance) 오차의 균형(Trade off)을 위해 통상적으로 5 또는 10을 사용한다.¹⁴⁾

회귀 모델의 모형이 비선형적인 경향을 가지면 선형 모델의 예측력이 제한될 수 있다. 이러한 경우에는 비선형 모델을 사용하면 더 정확한 예측을 할 수 있는 경우가 있다. 그러나 비선형 모델이 항상 선형 모델보다 우수한 것은 아니며 데이터의 형태에 따라 달라질 수 있어 선형과 비선형 모델의 비교를 통해 최적 모델을 선택하는 것이 중요하다. 본 연구에서는 다중 선형 회귀 방법과 다중 비선형 회귀 방법의 비교를 통해 최종 모델을 선택하였다.

2.3.1 다중 선형 회귀 모델

다중 선형 회귀는 종속 변수와 둘 이상의 독립 변수 간의 선형 관계를 모델링하는 회귀분석 기법이다. 다중 선형 회귀 모델은 식 (1)과 같은 형태의 선형 방정식으로 표현된다. y는 독립변수, x_i는 독립변수이고, β_i는 회귀계수이며 각 독립 변수의 영향력을 나타낸다.

$\[ y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_n{x}_n \]$

(1)

선형회귀분석에서는 회귀계수의 추정량을 구하기 위해서 잔차의 제곱합을 최소로 하는 최소자승법을 사용한다. 그러나 독립변수의 수가 증가하면 변수들 사이의 상관관계로 다중공산성이 존재할 수 있다. 이에 따라 최소제곱 회귀계수 추정량의 분산이 커져, 회귀식의 예측정확도에 대한 안정성이 낮아지는 문제가 있다.¹⁵⁾

2.3.2 다중 비선형 회귀 모델

본 연구에서는 로그 변환을 통해 식 (2)와 같이 지수함수 형태로 가정된 비선형 회귀 모델 구축하였다. y는 독립변수, x_i는 독립변수이고, β_i는 회귀계수이며 각 독립 변수의 영향력을 나타낸다.

$\[ y={\beta }_0{x}_1^{{\beta }_1}{x}_2^{{\beta }_2}\cdots x_n^{{\beta }_n} \]$

(2)

독립변수와 종속 변수 사이에 비선형 관계가 있는 경우, 시스템은 로그 변환을 통해 비선형성을 제거하고 선형 관계로 모델링 할 수 있다. 이 방법은 지수함수 형태의 비선형 모델은 선형 모델에서만 적용할 수 있는 최소 자승법을 적용하여 회귀계수를 도출 할 수 있게 된다. 로그 변환은 식 (3)과 같이 자연로그를 사용하여 변수들을 선형 형태로 변환 가능하다.

$\[ \mathrm{l}\mathrm{n}y=\mathrm{l}\mathrm{n}{\beta }_0+{\beta }_1\mathrm{l}\mathrm{n}{x}_1+{\beta }_2\mathrm{l}\mathrm{n}{x}_2+\cdots +{\beta }_n\mathrm{l}\mathrm{n}{x}_n \]$

(3)

여기서, 회귀모델은 행렬변환을 통해 i개의 데이터 집합에 대해 식 (4)와 같이 표현될 수 있다.

$\[ \left[\begin{array}{c}\mathrm{l}\mathrm{n}{y}_1\\ \mathrm{l}\mathrm{n}{y}_2\\ ⋮\\ \mathrm{l}\mathrm{n}{y}_3\end{array}\right]=\left[\begin{array}{ccccc}1& \mathrm{l}\mathrm{n}{x}_{1_1}& \mathrm{l}\mathrm{n}{x}_{2_1}& \dots & \mathrm{l}\mathrm{n}{x}_{n_1}\\ 1& \mathrm{l}\mathrm{n}{x}_{1_2}& \mathrm{l}\mathrm{n}{x}_{2_2}& \dots & \mathrm{l}\mathrm{n}{x}_{n_2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& \mathrm{l}\mathrm{n}{x}_{1_i}& \mathrm{l}\mathrm{n}{x}_{2_i}& \dots & \mathrm{l}\mathrm{n}{x}_{n_j}\end{array}\right]\left[\begin{array}{c}\mathrm{l}\mathrm{n}{\beta }_0\\ {\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_n\end{array}\right] \]$

(4)

식 (4)를 Y=Xβ로 치환하여 표현하면, 최소제곱추정량은 (X′X)^-1이 존재할 때 식 (5)와 같이 간단히 나타낼 수 있다.¹⁶⁾ 회귀계수는 식 (5)를 통해 결정된다. 식 (5)를 식 (3)에 대입하면, 역으로 지수변환을 수행하여 최종적으로 식 (2)와 같은 다중 비선형 회귀식을 도출 할 수 있다.

$\[ \underset{\_}{\beta }=\left[\begin{array}{c}\mathrm{l}\mathrm{n}{\beta }_0\\ {\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_n\end{array}\right]={\left(X^{\mathrm{\text{'}}}X\right)}^{-1}{X}^{\mathrm{\text{'}}}Y \]$

(5)

2.4 머신러닝 모델

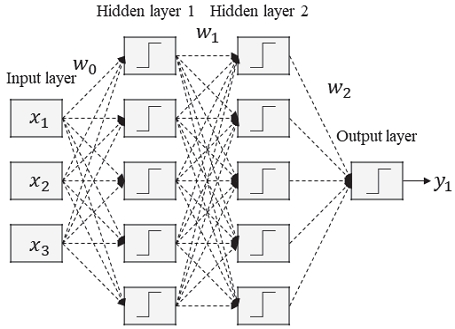
머신러닝은 데이터 기반으로 수행되기 때문에 정확성 향상을 위해서는 많은 양의 데이터 확보는 필연적이다. 정확성을 향상시키는 일반적인 방안은 네트워크의 깊이며, 정교한 하이퍼 파라미터의 튜닝을 통해 최적화된 모델이 구성될 수 있다. 순방향 신경망 또는 다중 퍼셉트론으로 알려진 심층신경망(DNN)은 2개 이상의 히든 레이어를 포함하는 신경망이다.^16-19) Fig. 5와 같이 심층 신경망은 입력차원이 3개이며, 히든 레이어의 뉴런은 5개로 표현되었다. 히든 레이어 출력은 식 (6)과 같이 표현된다.

$\[ z_i^1=\sigma \left(w_{i,1}^0{x}_1+w_{i,2}^0{x}_2+w_{i,3}^0{x}_3+w_{i,4}^0{x}_4+b_i^0\right) \]$

(6)

Fig. 5

Structure of the traditional DNN model

여기서, $$ z_i^1$$ 히든 레이어1의 i번째 뉴런의 출력이다. σ는 활성화 함수이며, 일반적으로 ReLU 가 사용된다.^20,21) $$ w_{i,j}^0$$는 j번째 입력에 대한 히든 레이어 1의 i번째 뉴런 사이의 연결된 가중치이다. 또한 $$ b_i^0$$는 히든 레이어 1의 i번째 뉴런의 바이어스이다. k-1 레이어에 n개의 뉴런이 있다고 가정하였을 때, 레이어 k의 i번째 뉴런의 출력은 식 (7)과 같이 계산된다.

$\[ z_i^k=\sigma \left(\sum _{j=1}^n{w}_{i,j}^{k-1}{z}_1^{k-1}+b_i^{k-1}\right),\left(k=\mathrm{1,2},\dots ,K\right) \]$

(7)

신경망의 순방향 신경망은 입력 레이어에서 시작하여 출력 레이어의 결과까지 이전 레이어의 출력을 사용하여 계산한다. 신경망은 손실함수를 사용하여 모델의 예측 값과 실제 값의 편차를 측정하고, 모델의 예측값이 점차 실제 값에 가까워지도록 경사하강법을 사용하여 각 레이어의 가중치와 바이어스를 업데이트한다. K 번째 레이어에 대한 회귀의 손실함수는 식 (8)과 같이 계산된다.

$\[ \begin{array}{c}L\left(\mathit{w},\mathit{b},\mathit{x},y\right)=\frac{1}{2}{‖{\mathit{z}}^K-y‖}_2^2\hfill \\ =\frac{1}{2}{‖\sigma \left({\mathit{w}}^{K-1}{\mathit{z}}^{K-1}+{\mathit{b}}^{K-1}\right)-y‖}_2^2\hfill \end{array} \]$

(8)

여기서, z^K는 심층 신경망 모델의 예측값이고 y는 실제 값이다. 손실함수의 기울기는 식 (9), (10)과 같이 계산될 수 있다. 여기서, ⊙는 Hadamard 곱을 의미한다.

$\[ \begin{array}{c}\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{w}}^{K-1}}=\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{z}}^K}\frac{\partial {\mathit{z}}^K}{\partial {\mathit{w}}^{K-1}}\hfill \\ =\left({\mathit{z}}^K-\mathit{y}\right)\odot {\sigma }^{\mathrm{\text{'}}}\left({\mathit{w}}^{K-1}{\mathit{z}}^{K-1}+{\mathit{b}}^{K-1}\right){\left({\mathit{z}}^{K-1}\right)}^{\mathit{T}}\hfill \end{array} \]$

(9)

$\[ \begin{array}{c}\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{b}}^{K-1}}=\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{z}}^K}\frac{\partial {\mathit{z}}^K}{\partial {\mathit{b}}^{K-1}}\hfill \\ =\left({\mathit{z}}^K-\mathit{y}\right)\odot {\sigma }^{\mathrm{\text{'}}}\left({\mathit{w}}^{K-1}{\mathit{z}}^{K-1}+{\mathit{b}}^{K-1}\right)\hfill \end{array} \]$

(10)

Inactive 출력을 식 (11)로 가정하면, K번째 레이어 출력 z^K의 Inactive 출력은 식 (12)와 같이 전개할 수 있다.

$\[ \begin{array}{c}{\mathit{\delta }}^k=\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)/\partial {\mathit{z}}^k\hfill \\ =\left({\mathit{z}}^K-\mathit{y}\right)\odot {\sigma }^{\mathrm{\text{'}}}\left({\mathit{w}}^{K-1}{\mathit{z}}^{K-1}+{\mathit{b}}^{K-1}\right)\hfill \end{array} \]$

(11)

$\[ \begin{array}{c}{\mathit{\delta }}^k=\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{w}}^k}\hfill \\ =\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{z}}^K}\frac{\partial {\mathit{z}}^K}{\partial {\mathit{z}}^{K-1}}\frac{\partial {\mathit{z}}^{K-1}}{\partial {\mathit{z}}^{K-2}}\dots \frac{\partial {\mathit{z}}^{K+1}}{\partial {\mathit{z}}^K}\hfill \end{array} \]$

(12)

이후 손실 함수의 기울기는 식 (13), (14)와 같이 변환될 수 있다.

$\[ \begin{array}{c}\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{w}}^{k-1}}=\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{z}}^k}\frac{\partial {\mathit{z}}^k}{\partial {\mathit{w}}^{k-1}}\hfill \\ ={\mathit{\delta }}^k{\left({\mathit{z}}^{k-1}\right)}^T\hfill \end{array} \]$

(13)

$\[ \frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{b}}^{k-1}}=\frac{\partial L\left(\mathit{w},\mathit{b},\mathit{x},\mathit{y}\right)}{\partial {\mathit{z}}^k}\frac{\partial {\mathit{z}}^k}{\partial {\mathit{b}}^{k-1}}={\mathit{\delta }}^k \]$

(14)

여기에서, δ^k과 δ^k+1의 관계는 식 (15)와 같이 얻을 수 있다.

$\[ {\mathit{\delta }}^k={\mathit{\delta }}^{k+1}\frac{\partial {\mathit{z}}^k}{\partial {\mathit{z}}^k}={\left({\mathit{w}}^k\right)}^T{\mathit{\delta }}^{k+1}\odot {\sigma }^{\mathrm{\text{'}}}\left({\mathit{z}}^k\right) \]$

(15)

k번째 레이어의 가중치와 바이어스 변화는 경사하강법에 의해 식 (16), (17)과 같이 정의할 수 있다.

$\[ {\mathit{w}}^k⟵{\mathit{w}}^k-\alpha \sum _{j=1}^n{\delta }_j^k{\left(z_j^{k-1}\right)}^T \]$

(16)

$\[ {\mathit{b}}^k⟵{\mathit{b}}^k-\alpha \sum _{j=1}^n{\delta }_j^k \]$

(17)

여기서, α는 스텝 사이즈를 의미하고, 경사하강법을 이용한 최적화함수는 SGD, RMSprop, Adam 등이 있다.^22-24) 본 연구는 파라미터에 대한 최적화 연구가 아니기 때문에 아키텍처를 비교적 단순하게 구성하였고, 사용된 최적화 함수는 Adam을 사용하였다. Loudness 예측모델은 Table 4에 나타냈다.

Table 4

Architecture of DNN

활성화 함수는 ReLu 함수를 사용하였고, 최적화 함수는 Adam 최적화로 정의하였다. 최적화 함수의 학습률은 0.001로 설정하였다. 초기 가중치는 수렴성 문제 및 지역 최적화 문제를 발생을 최소화 할 수 있는 Xavier initialization, He initialization 등 다양한 방법이 개발되었다.^25,26) 그러나 현재 고려하는 문제는 머신러닝 관점에서 상대적으로 단순한 예측 문제이기 때문에 초기화 문제에 대해 고려하지 않았다.

데이터 셋 분할은 일반적으로 학습 데이터 셋, 검증 데이터 셋, 테스트 데이터 셋으로 총 3개의 파트로 분할된다. 학습에 사용된 데이터셋은 Table 5에 나타냈다. 학습은 데이터의 순서도 영향을 크게 미치기 때문에 데이터 셔플을 수행하여 순차적 데이터에 대한 과적합 문제를 방지하였다. 입력 데이터는 각 데이터의 크기로 인한 오류를 없애기 위해 표준화가 수행되었다. 총 학습은 1,000회 수행하였으며, 학습 종료는 20번 학습 시 오차에 대한 개선이 없으면 실행을 종료시키는 Early stopping을 적용하였다.

Table 5

Data set split ratio

3. 결 과

3.1 다중 선형 및 비선형 회귀 결과

회귀 모델은 2.3절에서 언급한 것과 같이 5겹 교차검증을 통해 평균 절대오차(Mean absolute error)가 가장 낮은 모델로 선택되었다. 독립변수는 음압레벨(Sound pressure level)과 변동 강도(Fluctuation strength)이며, 최종 선택된 회귀식의 결과는 다음과 같다.

최종 선택된 선형 회귀식의 계수는 식 (18)에 나타냈으며, y는 라우드니스(Loudness), x₁은 음압레벨(Sound pressure level), x₂는 변동 강도(Fluctuation strength)이다.

$\[ y=-25.02+0.63x_1+1.92x_2 \]$

(18)

F 통계량은 회귀모델의 유의성을 판단하는 지표이며 유의수준의 기준은 0.05이하의 값을 사용한다. 결정계수(R²)는 회귀모델의 설명력을 나타내며 1에 가까운 값일수록 높은 설명력을 갖는다. 식 (18)의 F 통계량은 0.05이하의 값으로 나타났으며, 결정계수는 0.8로 나타나 회귀식의 유의성 및 적합성을 확인하였다. P-값 검정의 유의수준은 두 가지 변수 모두 0.05 이하의 값을 나타내어 회귀 계수의 유의성을 확인하였다. 검증 데이터에 대한 식 (18)의 평균 상대오차는 41.5 %로 확인되었다.

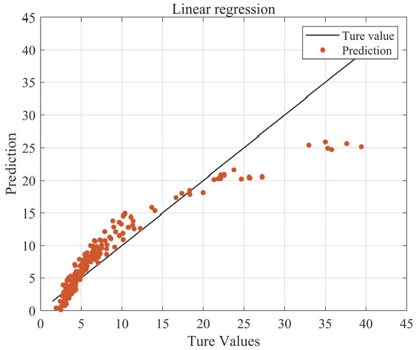
Fig. 6과 같이 다중 선형 모델의 결과는 실제 Loudness N10 값인 솔리드 라인의 결과와 비교하여 Loudness N10 예측 값인 포인트는 상대적으로 오차가 매우 크게 나타났다. 따라서 다중 선형 모델은 Loudness 추정에서 적합하지 않은 모델로 고찰되며, 비선형 모델을 통한 회귀식을 다음과 같이 도출하였다. 비선형 모델의 회귀식 계수는 식 (19)에 나타내었다.

$\[ y=6.92\times {10}^{-7}{x}_1^{3.99}{x}_2^{-0.11} \]$

(19)

Fig. 6

Prediction error by linear regression ; Ture value : solid line(-), Prediction : dot (⋅)

F 통계량의 유의수준은 0.05 이하의 값으로 나타났으며, 또한 결정계수(R²)는 0.96로 나타나 회귀식의 유의성을 확인하였다. P-값 검정의 유의수준은 두 가지 변수 모두 0.05 이하의 값을 나타내어 회귀 계수의 유의성을 확인하였다. 검증 데이터에 대한 식 (19)의 평균 상대오차는 9.1 %로 확인되었다.

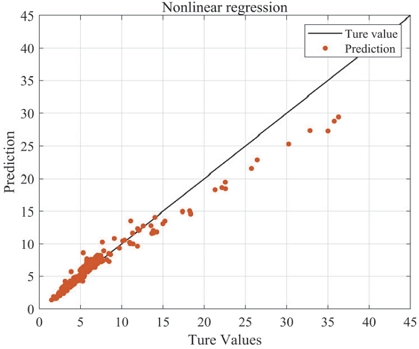
비선형 회귀식 기반의 결과는 Fig. 7에 나타냈으며, 선형 회귀식으로 추정한 예측결과 보다 상대적으로 높은 정확성을 나타낸다. 그러나 BSR의 정량적 평가 방법은 1 sone 범위 내에서 Fail/Pass가 결정되기 때문에 높은 정확성이 요구된다. 따라서 예측 모델은 더 정밀한 결과가 필요하기 때문에 심층신경망을 이용한 예측 모델을 구성하였다.

Fig. 7

Prediction error by nonlinear regression ; Ture value : solid line(-), Prediction : dot (⋅)

3.2 머신러닝 기반의 Loudness 예측결과

Loudness 예측 결과는 K겹 교차검증과 동일한 데이터 기반으로 머신러닝을 이용하여 수행되었다. 두 결과 모두 오차는 Loudness 레벨이 높은 결과에서 상대적으로 큰 오차가 발생된다. 이 결과는 일반적으로 자동차 시트의 BSR 소음은 주로 10 sone 이하에서 발생되기 때문에 데이터가 Loundness가 낮은 영역에 군집되어 있는 것을 볼 수 있다. 다시 말해서 25 이상의 결과는 통계적 관점에서 이상치로 정의될 수 있다. 또한 제품 개발 규격 상 높은 레벨의 Loudness는 Fail로 분류되기 때문에 실질적으로 5 sone 근방의 데이터만 정확성이 요구된다.

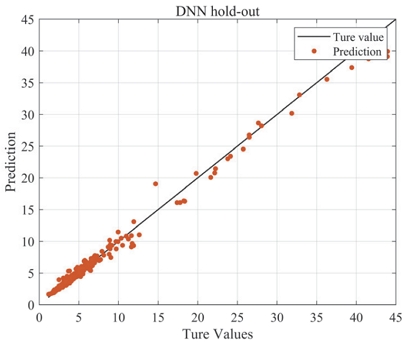
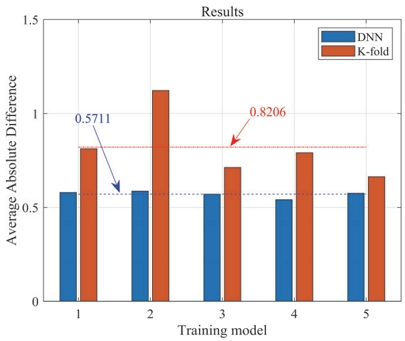
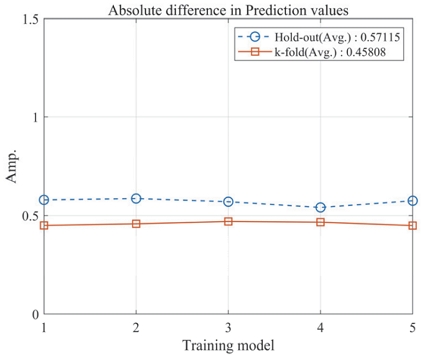
홀드 아웃을 이용한 DNN 결과는 Fig. 8에 나타냈다. 비선형 회귀식으로 추정한 예측결과 보다 상대적으로 높은 정확도로 예측하고 있으며, 두 결과에 대한 절대 오차는 Fig. 9에서 나타냈다. 도출된 유의미한 인자로부터 Loudness N10을 예측하기 위해 본 연구에서는 Root mean squared error(RMSE)를 사용하였다. Fig. 9와 같이 절대 오차의 크기는 5번의 학습 평균 결과 상대적으로 K겹 교차검증 기반 비선형 회귀 방법은 0.82 수준의 오차가 나타냈다. 또한 평균 예측 오차의 산포도 상대적으로 크게 나타났다. 반면에 DNN 모델은 절대 오차의 차이가 평균 0.57 수준에서 나타났으며, 통계 기반의 K겹 교차검증에 비해 머신러닝 기반의 DNN은 약 30 % 수준의 높은 성능을 보였다.

Fig. 8

Prediction error by DNN using hold out method ; Ture value : solid line(-), Prediction : dot (⋅)

Fig. 9

Comparing performance of nonlineaer regression using K-fold cross validation and DNN using hold out

머신러닝은 일반적으로 과적합 문제 및 과소적합 문제만 발생하지 않는다면, 데이터의 개수가 모델의 성능에 크게 기여한다. BSR 실험은 개발의 최종 단계에서 실시되며, 모든 제품에 대한 결과를 확인할 수 없기 때문에 일부 제품에 대한 결과만 분석된다. 따라서 실제 실험 결과는 많은 수의 데이터를 확보하는 것은 매우 어렵다. 본 연구에서는 적은 데이터 수 기반의 강건한 예측 모델 설계를 위해 DNN 모델에 K겹 교차검증을 적용하여 성능을 분석하였다.

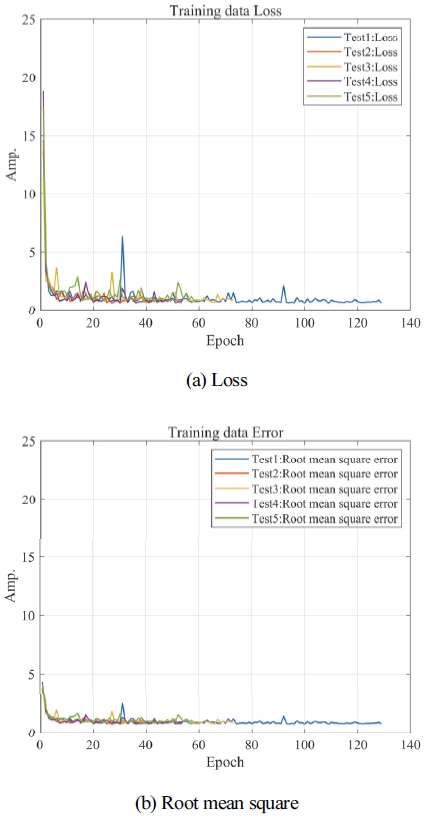
머신러닝은 앞선 결과에서 보듯이 일반적으로 홀드아웃 방법을 이용하여 데이터 셋을 분할한다. 그러나 홀드아웃 방법은 검증 데이터 셋으로 인해 상대적으로 적은 학습 데이터 셋이 구성된다. 다시 말해서 검증용 데이터는 학습에 사용할 수 없는 큰 단점을 갖는다. 적은 수의 데이터는 모델의 과적합 문제 및 과소적합 문제를 야기하기 때문에 데이터 증강이 필연적으로 요구된다. 따라서 제안된 모델은 K겹 교차검증을 DNN 모델에 적용하여 데이터 수에 대한 문제를 해결하고, 모든 데이터 추세를 포함하여 Loudness를 예측하고자 하였다. 사용된 모델의 K는 5로 정의하였다. 학습의 과정은 Fig. 10에서 보여준다.

Fig. 10

Result of the experiment

학습 진행에 대한 결과는 대부분의 머신러닝 모델과 유사하게 Fig. 10의 (a), (b)에서 보듯이 초기에는 큰 Loss가 나타지만, 학습이 진행될수록 매우 빠르게 수렴하고 모델의 정확도가 상대적으로 높은 것을 볼 수 있다. K겹 교차검증을 적용을 적용한 DNN의 예측 결과는 Fig. 11에서 나타냈다. 예측 결과는 K겹 교차검증이 적용된 DNN 모델이 평균 0.113수준의 상대적으로 높은 정확도로 Loudness를 예측하였다. 또한 결과는 총 다섯 번의 실험 결과에서 모두 우수한 성능이 나타났다.

Fig. 11

Comparing performance of hold out and k-fold

4. 결 론

본 연구에서는 자동차 시트의 음향 및 음질 물리량을 기반으로 계산하기 복잡하고, 까다로운 BSR 정량적 지표인 Loudness N10을 예측하였다. 다양한 물리량 중 유의미한 인자는 분산 분석의 결과로 음압 레벨과 변동 강도로 도출하였고, 전통적인 방법인 K겹 교차 검증을 통해 선형 및 비선형 회귀식을 도출하였다. 그러나 예측의 정확성은 다섯 번의 평균 절대 오차 0.8206 수준의 오차가 나타났다. 반면에 심층신경망을 이용한 예측은 0.5711 수준의 오차가 발생하여 상대적으로 Loudness 값을 정확하게 추정하였다. 실제 실험에서는 많은 양과 다양한 종류의 데이터를 얻는 것은 매우 어렵다. K겹 교차검증은 개발 목적 및 방법론에서 설명되듯이 한정적인 데이터 셋 내에서 최대의 효율을 발휘한다. 따라서 제안된 방법은 한정된 데이터에서 Loudness 예측을 위해 K겹 교차검증 방법을 심층신경망에 적용하였다. 결과는 0.45 수준의 오차가 나타났으며, 비선형 회귀 방법과 홀드 아웃을 적용한 심층신경망 보다 좋은 예측 성능의 모델을 얻을 수 있었다. 결론적으로 일반적인 제한된 환경에서 많은 데이터를 확보할 수 없기 때문에 제안된 방법으로 구성된 심층신경망은 상대적으로 높은 정확도의 모델을 만들어 낼 수 있음을 예측할 수 있다.

Acknowledgments

이 연구는 2022년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의해 수행되었고 이에 감사를 표합니다(‘20018493’).

References

• S. S. Gosavi, “Automotive Buzz, Squeak and Rattle (BSR) Detection and Prevention,” SAE 2005-26-056, 2005. [https://doi.org/10.4271/2005-26-056]
• R. Sohmshetty, R. Kappagantu, B. Naganarayana and S. Shankar, “Automotive Body Structure Enhancement for Buzz, Squeak and Rattle,” SAE 2004-01-0388, 2004. [https://doi.org/10.4271/2004-01-0388]
• S. H. Shin and C. Cheong, “Experimental Characterization of Instrument Panel Buzz, Squeak, and Rattle (BSR) in a Vehicle,” Applied Acoustics, Vol.71, No.12, pp.1162-1168, 2010. [https://doi.org/10.1016/j.apacoust.2010.07.006]
• J. Kang, C. M. Krousgrill and F. Sadeghi, “Comprehensive Stability Analysis of Disc Brake Vibrations Including Gyroscopic, Negative Friction Slope and Mode-coupling Mechanisms,” Journal of Sound and Vibration, Vol.324, Nos.1-2, pp.387-407, 2009. [https://doi.org/10.1016/j.jsv.2009.01.050]
• J. Nam and J. Kang, “Friction-induced Vibration by Dust,” The Korean Society for Noise and Vibration Engineering, Vol.30, No.2, pp.201-210, 2020. [https://doi.org/10.5050/KSNVE.2020.30.2.201]
• H. Choi, J. Kang and J. Park, “BSR Test Method for Vehicle Seat Using Excitation and Operating Durability Test,” Journal of the KAIS, Vol.16, No.4, pp.2436-2441, 2015. [https://doi.org/10.5762/KAIS.2015.16.4.2436]
• H. Choi, J. Nam, J. Kang and J. Park, “Investigation of the BSR Noise Characteristics in Seat Cushion-Frame with Pespect to Vibration Durability Test Using Multi-Simulator,” Vol.15, No.8, pp.4776-4783, 2014. [https://doi.org/10.5762/KAIS.2014.15.8.4776]
• Y. Shin, H. Lee, J, Kim and S. Choi, “A Study on CAE Technology for Establishing the Vehicle BSR Virtual Development System,” KSME22CA-Th03C01, pp.149-150, 2022.
• H. Lee, E, Kong, C. Hong and Y. Kim, “Study on Rattle Noise Analysis of In-vehicle in Infotainment System Considering Tolerance,” 20SKSAE_E018, p.670, 2020.
• S. Kim, D. Ko, H. Lee, J. Nam and J. Lee, “A Study on Design Method for BSR Noise Reduction Based on Simulation of Vehicle Seat,” Transactions of KSAE, Vol.31, No.3, pp.199-208, 2023. [https://doi.org/10.7467/KSAE.2023.31.3.199]
• J. Nam and J. Kang, “Classification of Chaotic Squeak and Rattle Vibrations by CNN Using Recurrence Pattern,” Sensors, Vo1.21, No.23, Paper No.8054, 2021. [https://doi.org/10.3390/s21238054]
• M. Wiercioch and J. Kirchmair, “DNN-PP: A Novel Deep Neural Network Approach and its Applicability in Drug-related Property Prediction,” Expert Systems with Applications, Vol.213, Paper No.119055, 2023. [https://doi.org/10.1016/j.eswa.2022.119055]
• H. Yu, C. Qin, J. Tao, C. Liu and Q, Liu, “A Multi-channel Decoupled Deep Neural Network for Tunnel Boring Machine Torque and Thrust Prediction,” Tunnelling and Underground Space Technology, Vol.133, Paper No.104949, 2023. [https://doi.org/10.1016/j.tust.2022.104949]
• T. Hastie, R. Tibshirani, J. H. Friedman and J. H. Friedman, The Elements of Statistical Learning: Data mining, Inference, and Prediction, Springer, New York, 2009. [https://doi.org/10.1007/978-0-387-84858-7]
• D. Kim and K. Seo, “Comparison of Linear and Nonlinear Regressions and Elements Analysis for Wind Speed Prediction,” Journal of Korean Institute of Intelligent Systems, Vol.25, No.5, pp.477-482, 2015. [https://doi.org/10.5391/JKIIS.2015.25.5.477]
• W. R. Lee, Regression Analysis, 2nd Edn., Tamjin, Seoul, 2012.
• K. Zhang, H. M. Lyu, S. L. Shen, A. Zhou and Z. Y. Yin, “Evolutionary Hybrid Neural Network Approach to Predict Shield Tunneling-induced Ground Settlements,” Tunnelling and Underground Space Technology, Vol.106, Paper No.103594, 2020. [https://doi.org/10.1016/j.tust.2020.103594]
• Q. Lü, C. L. Chan and B. K. Low, “Probabilistic Evaluation of Ground-support Interaction for Deep Rock Excavation using Artificial Neural Network and Uniform Design,” Tunnelling and Underground Space Technology, Vol.32, pp.1-18, 2012. [https://doi.org/10.1016/j.tust.2012.04.014]
• M. Koopialipoor, A. Fahimifar, E. N. Ghaleini, M. Momenzadeh and D. J. Armaghani, “Development of a New Hybrid ANN for Solving a Geotechnical Problem Related to Tunnel Boring Machine Performance,” Engineering with Computers, Vol.36, pp.345-357, 2020. [https://doi.org/10.1007/s00366-019-00701-8]
• K. Eckle and J. Schmidt-Hieber, “A Comparison of Deep Networks with ReLU Activation Function and Linear Spline-type Methods,” Neural Networks, Vol.110, pp.232-242, 2019. [https://doi.org/10.1016/j.neunet.2018.11.005]
• J. Schmidt-Hieber, “Nonparametric Regression Using Deep Neural Networks with ReLU Activation Function,” Ann. Statist, Vol.48, No.4, pp.1875-1897, 2020. [https://doi.org/10.1214/19-AOS1875]
• E. Yazan and M. F. Talu, “Comparison of the Stochastic Gradient Descent Based Optimization Techniques,” International Artificial Intelligence and Data Processing Symposium (IDAP), pp.1-5, 2017. [https://doi.org/10.1109/IDAP.2017.8090299]
• D. P. Kingma and J. Ba, “Adam: A Method for Stochastic Optimization,” arXiv preprint arXiv:1412.6980, , 2014.
• R. Zaheer and H. Shaziya, “A Study of the Optimization Algorithms in Deep Learning,” Third International Conference on Inventive Systems and Control(ICISC), pp.536-539, 2019. [https://doi.org/10.1109/ICISC44355.2019.9036442]
• X. Glorot and Y. Bengio, “Understanding the Difficulty of Training Deep Feedforward Neural Networks,” Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp.249-256, 2010.
• S. Koturwar and S. Merchant, “Weight Initialization of Deep Neural Networks(DNNs) Using Data Statistics,” arXiv preprint arXiv:1710.10570, , 2017.