회귀최소자승법을 활용한 도로 노면 마찰계수 추정 및 실차 검증

2.1 차량 모델 선정

2.1.1 TruckSim 모델

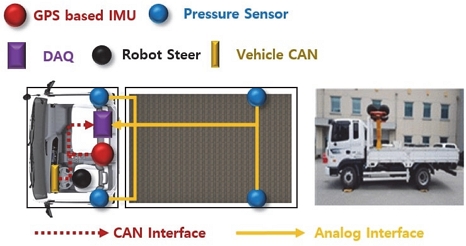
차량 동역학 해석 소프트웨어인 TruckSim은 실제 차량에서 얻을 수 있는 센서 정보를 적용하여 상용 트럭과 유사한 모델을 설계할 수 있다. 또한, 운전자 모델을 통해 차량의 속도제어, 제동제어, 조향제어, 변속제어, 노면의 상태 및 주행 도로 환경 설정이 가능하다. 이러한 기능을 활용하여 시뮬레이션을 진행하였으며, 도로 노면 마찰계수 추정 알고리즘 성능분석을 위해 활용하게 되었다. Fig. 1은 대상 차량 모델과 가장 유사한 LCF VAN 5.5T/8.5T(4X2) 모델을 선정하였고, TrcukSim 모델의 상세한 제원은 Table 1과 같다.

Fig. 1

TruckSim(LCF VAN 5.5T/8.5T) model

Table 1

TruckSim(LCF VAN 5.5T/8.5T) model specification

2.1.2 실험 대상 차량

본 논문에서는 실험 대상 차량 모델을 상용 트럭인 국내 H사의 Mega Truck으로 선정하였다. 실험 대상 차량 모델은 5톤 급으로 중형 트럭에 해당하며, 차량의 동특성 신호를 측정하기 위해 Oxford 사의 RT3100 장비를 활용하였다. 실험 대상 차량의 센서 네트워크와 차량 사진은 Fig. 2와 같다.

Fig. 2

H-mega truck(5 Ton)

2.2 차륜 동역학 모델

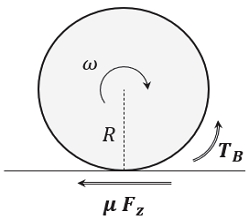
Fig. 3을 보게 되면 노면을 주행 중인 차륜에 대한 동역학적 표현을 묘사한다. 노면을 주행 중인 피동 차륜에 대한 모멘트 평형 식을 구하면 식 (1)과 같이 나타낼 수 있다. 구동 차륜은 식 (1) 우변에 구동 토크(T_F)가 더해진다. 여기에 타이어와 노면 사이의 마찰력 방향이 바뀌기 때문에 음의 부호로 표현하면 식 (2)와 같이 나타낼 수 있다.⁹⁾

Fig. 3

Wheel dynamics

식 (1)과 (2)를 도로 노면 마찰계수 추정을 위해 μ 항으로 정리하면 식 (3)과 (4)와 같이 표현된다.

이때 후륜의 도로 노면 마찰계수 식 (4)에서 구동 토크(T_F) 항을 제거하여 전⋅후륜의 도로 노면 마찰계수를 추정하게 된다. 식 (1)과 식 (2)에서 제동 토크(T_B)는 제동 챔버 압력과 실제 차량 시험으로 구한 Gain 값을 곱하여 얻게 된다. 또한, 차륜의 회전반경, 속도와 차륜 Inertia는 차량 시험을 통하여 측정하였다. 도로 노면 마찰계수 추정 조건은 다음과 같은 가정들을 통해 추정하였다.

• 1) 평지(Flat and straight) 직선 주행
• 2) 초기속도 40 km/h, 60 km/h, 80 km/h에서 차량 감속
• 3) 차량이 감속할 때, 후륜에 작용하는 구동 토크 무시
• 4) Pitch에 따른 차량의 종 방향 하중 이동 고려

2.3 타이어와 노면간의 수직방향 타이어 힘

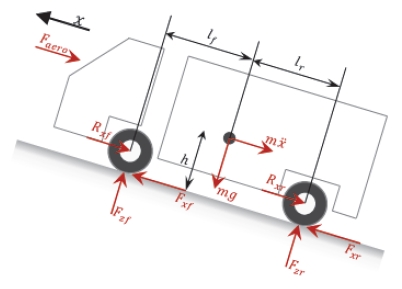
Fig. 4는 차량 주행 시 감속될 때의 종 방향 요소들을 묘사하고 있다. 이 조건에서의 전륜 및 후륜에 작용하는 수직 방향 타이어 힘은 정적상태와 동적 상태의 수직 방향 힘으로 식 (5)와 같이 표현할 수 있다. 이때 노면 상태가 평지이고 공기저항을 무시할 경우 차량의 전륜 및 후륜에 대한 수직 방향 타이어 힘을 구하면 식 (6)과 식 (7)로 나타낼 수 있다.^9-11)

Fig. 4

Longitudinal dynamics

2.4 제동 토크 계산

차륜 동역학 식 (1)과 식 (2)에 필요한 제동 토크 값은 제동 챔버 압력(P_B)과 실차시험 데이터를 통해 구한 제동 Gain(G_B)을 곱하여 사용하게 된다. 실험으로 얻게 된 전⋅후륜의 제동 Gain은 Table 2와 같고 제동 토크는 식 (8)과 같이 구하게 된다.⁹⁾

Table 2

Braking gain used in simulation

Table 2를 보면 전륜 및 후륜의 제동 Gain 값이 서로 다르게 설정된 것을 볼 수 있다. 차량이 주행 중 제동 시 차량의 무게 중심이 이동되어 후륜보다 전륜에서 큰 제동압력이 요구되기 때문으로 해석할 수 있다.

3.1 회귀최소자승법 알고리즘

회귀최소자승법 알고리즘은 관측된 입력 신호와 선형 최소 제곱 비용함수를 최소화하는 계수를 재귀적으로 찾아 계산된 데이터 간의 차이에 대한 제곱의 합을 최소화하여 값을 예측하는 방법이다. 이 방법은 추정하고자 하는 파라미터를 정확하게 측정할 수 없는 경우에 흔히 사용된다. 또한, 추정 결과에 대해 직관적으로 설계자에게 제공하게 되어 시간과 계산 비용이 줄어든다. 회귀최소자승법 알고리즘은 매개 변수 추정을 위하여 회귀 처리의 형태인 식 (9)와 같이 표현된다. 이에 따라 이 식을 망각인자(Forgetting factor)를 갖는 회귀최소자승법 알고리즘을 나타내면 식 (10)과 같이 나타낼 수 있다.^12,13)

위 식에서 y_k와 Ψ_k는 이미 측정한 데이터 값이며, θ_k는 추정하고자 하는 예측 값을 나타낸다. 또한, $$ V\left({\hat{\theta }}_k\right)$$는 비용함수를 나타내며, $$ y\left(i\right)-\Psi \left(i\right){\hat{\theta }}_k$$가 0이 되면 비용함수는 최소화된다. 이 비용함수를 실시간 매개 변수 추정을 위하여 회귀 처리 형태로 변환하면 식 (11)과 같은 추정 해($$ {\hat{\theta }}_k$$)를 얻을 수 있다. 이때 L_k와 P_k는 식 (12)와 식 (13)과 같이 표현된다.

식 (12)에서 이득 벡터(L_k)는 반복 계산 과정에서 이득 값이 도출된다. 또한, 식 (13)에서 공분산 행렬(P_k)값은 실제 값과 예측 값의 데이터 분포 형태를 나타내고, 과거 측정값의 비중이 커지는 것을 방지하기 위해서 망각인자를 적용한다. 망각인자 λ값이 작아질수록 새로운 측정 데이터의 비중이 더 크게 되며, λ값이 커질수록 시스템 변화에 둔감해진다. 일반적으로 망각인자 λ는 0.95 ~ 0.99 사이의 값을 가진다.¹³⁾ 본 논문에서는 도로 노면 상태 추정 성능 연구를 위해 망각인자가 포함된 회귀최소자승법 알고리즘을 구성하였다.

도로노면 마찰계수 추정을 위하여 식 (3)을 통해 각 변수를 다음과 같이 정의한다.

3.2 도로 노면 마찰계수 추정 알고리즘 구성도

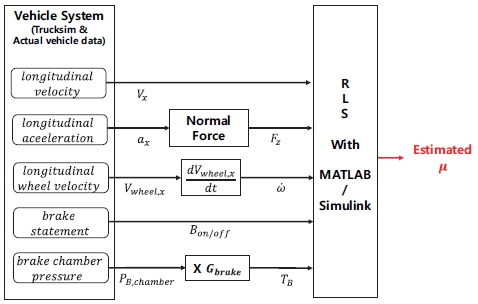
Fig. 5는 도로 노면 마찰계수 추정 알고리즘의 흐름을 나타낸다. Fig. 5를 보면 마찰계수 추정을 위해서 보편적으로 활용되는 센서 정보인 종 방향 속도(V_x), 종 방향 가속도(a_x), 종 방향 차륜 속도(V_wheel,x), 제동 작동 신호(B_on/off)와 제동 챔버 압력 센서의 정보들이 입력 정보로 사용된 것을 볼 수 있다. 여기서 타이어에 작용하는 수직항력 힘(F_Z)은 종 방향 가속도 센서 정보를 통해 계산하였고, 제동 챔버 압력 센서 정보에 실험적으로 구한 제동 게인(G_B)을 곱하여 제동 토크(T_B)를 산출하였다. 그뿐만 아니라 차량의 차륜 각가속도($$ \dot{\omega }$$)는 종 방향 차륜 속도를 시간에 대하여 미분한 값을 통해 구하였다. 이러한 센서 정보를 휠 다이나믹스 모델 식에 적용하였으며, 최소회귀자승법 알고리즘은 차량의 센서 정보 5개만을 사용하여 도로 노면을 추정하게 된다. 본 논문에서는 TruckSim 데이터와 실제 차량 데이터를 이용하여 MATLAB /Simulink를 통해 도로 노면 마찰계수 추정 알고리즘 로직을 검증하였다.

Fig. 5

Schematic of road surface friction coefficient estimation

3.3 실험 차량 주행 시나리오

도로 노면 마찰계수 추정을 위한 주행 시나리오는 공차 상태인 실제 차량이 직진 주행 시, 도로 노면 상태가 중 마찰로(Wet asphalt, 0.5 ~ 0.6)와 고 마찰로(Dry asphalt, 0.8)인 노면에서 차량을 완전히 정지하는 시나리오로 선정하였다. 그리고 차량의 주행 초기 속도가 40 km/h, 60 km/h, 80 km/h일 때 차량을 감속시킨 상황에서 3.2절에서 언급한 5개의 센서 정보를 계측하였다.

Table 3은 실제 차량에 대한 주행 시나리오를 보여주며, TruckSim 주행 시나리오는 실제 차량 주행 시나리오와 동일한 노면 조건과 주행 속도로 선정하였다. TruckSim과 실제 차량의 시뮬레이션 횟수는 주행 속도 변화에 따른 중 마찰로에서 6회, 고 마찰로에서 9회 진행하여 각각 총 15회씩 진행하였다.

Table 3

Driving scenario

TruckSim 시뮬레이션의 제동조건은 실제 차량에서 얻은 제동 챔버 압력을 입력조건으로 설정하여 시뮬레이션을 진행하게 된다. 이에 따라 실제 차량과 같은 주행상황을 구현하였다.

도로 노면 마찰계수 추정 알고리즘의 추정 범위 설정은 아래의 세 가지 조건으로 설정하였다.

• 1) 차량이 직진 주행 중 제동 시점, B_on = 1
• 2) 제동 작동 시점에서의 속도, V₀
• 3) 추정 범위 V_x > 0.4V₀, V_x < 0.8V₀

위 세 가지 조건을 만족시킬 때 회귀최소자승법 알고리즘에서 도로 노면 마찰계수를 추정하게 된다.

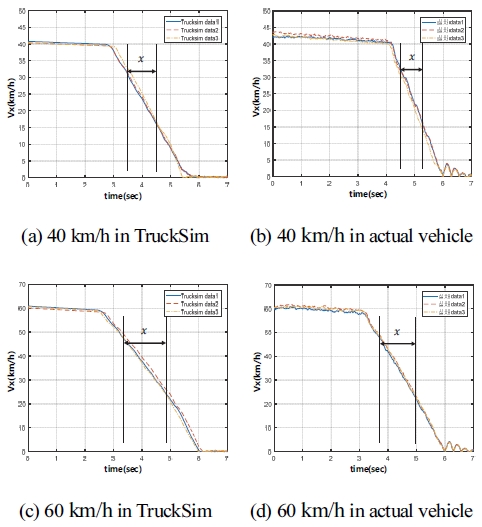
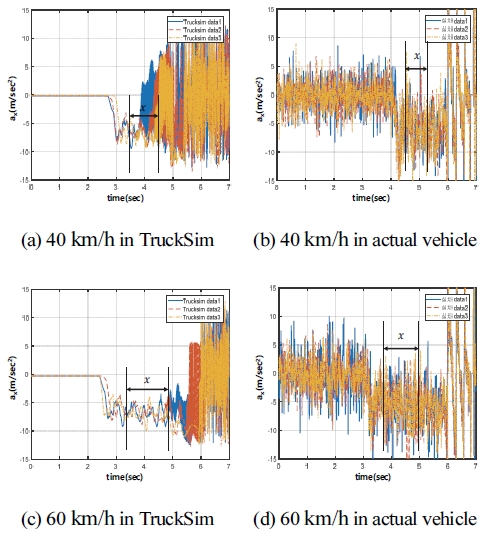
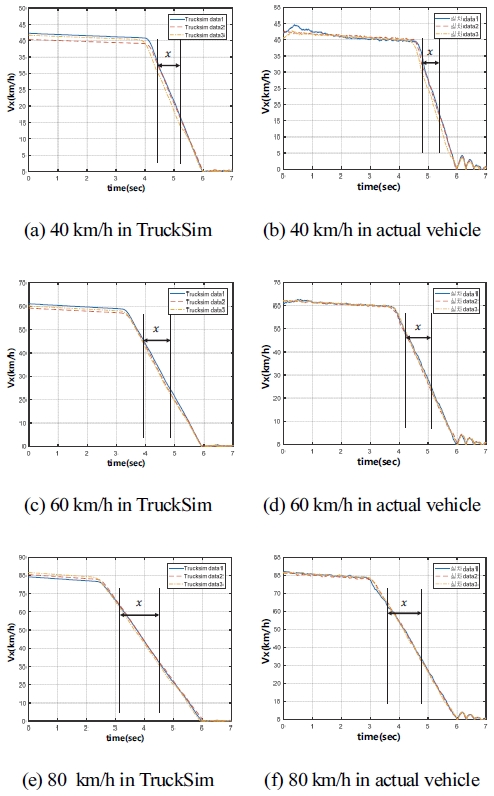
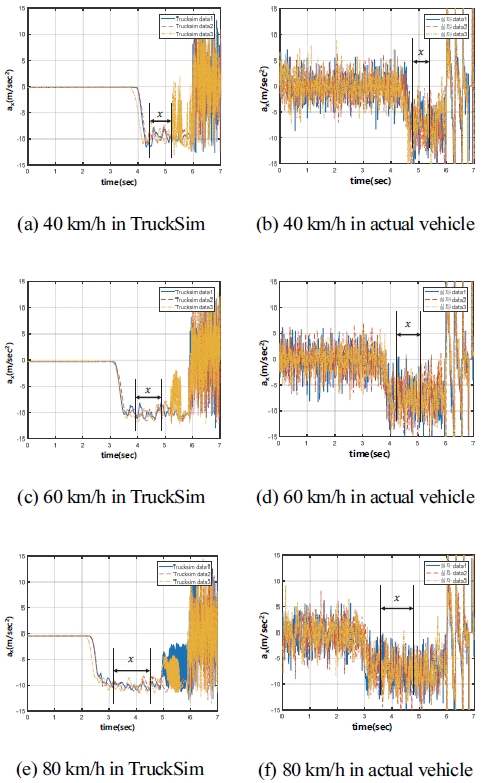
주행 시나리오 중 대표적으로 중⋅고 마찰로 주행시나리오에 대한 TruckSim과 실제 차량의 종 방향 주행 속도(V_x)와 종 방향 가속도(a_x) 그래프를 Figs. 6 ~ 9에 도시하였다. Figs. 6 ~ 9의 그래프에서 x는 추정 조건 중 세 번째 V_x>0.4V₀, V_x<0.8V₀에 해당한다. 종 방향 속도 종 방향 가속도 그래프에서 x인 추정 범위를 설정하여 시뮬레이션과 실제 차량 시험 주행 시나리오가 같은 조건으로 추정될 수 있도록 조건을 설정하게 되었다.

Fig. 6

Longitudinal velocity in wet asphalt

Fig. 7

Longitudinal acceleration in wet asphalt

Fig. 8

Longitudinal velocity in dry asphalt

Fig. 9

Longitudinal acceleration in dry asphalt

3.4 실제 차량의 타이어 미끄럼 율

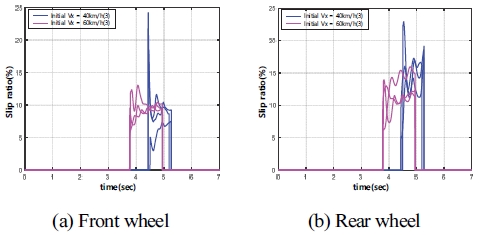
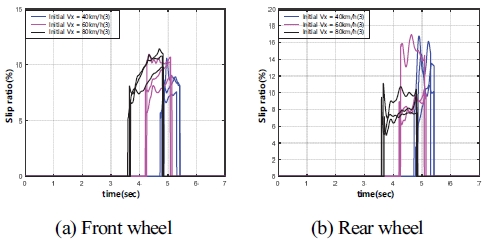
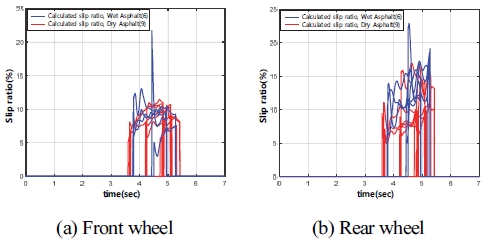
다음은 실제 차량이 주행 중 감속할 때, 차량의 주행 속도와 도로 노면 상태 변화에 따른 시간에 대한 전⋅후륜의 타이어 미끄럼 율(Slip ratio, %)을 Fig.10과 Fig.11에 도시하였다. 타이어 미끄럼 율은 차량과 타이어의 종 방향 속도 관계를 통해 타이어 미끄럼 율을 계산할 수 있다. 이때 타이어 미끄럼 율은 도로 노면 마찰계수 추정 범위와 같은 조건에서 구해진 결과이다. Fig. 10과 Fig. 11을 보면 중 마찰로 조건에서 전⋅후륜의 작용하는 타이어 미끄럼 율은 각각 평균 8 ~ 13 %와 10 ~ 15 %를 보여준다. 또한, 고 마찰로에서 전⋅후륜에 작용하는 타이어 미끄럼 율은 각각 평균 8 ~ 10 %와 10 ~ 15 %를 보여준다. Fig. 12는 Fig. 10과 Fig. 11의 결과들을 도로 노면의 상태에 따른 타이어의 미끄럼 율을 도시하였다. Fig. 12에서 전륜과 후륜의 타이어 미끄럼 율은 주행 속도 변화에도 유사한 값을 가지는 것을 볼 수 있다. 즉, 실제 차량에서 각 차륜에 정확한 타이어의 미끄럼 제어가 되는 것을 확인할 수 있다.

Fig. 10

Longitudinal acceleration in dry asphalt

Fig. 11

Longitudinal acceleration in dry asphalt

Fig. 12

Longitudinal acceleration in dry asphalt

4.1 TruckSim 데이터를 이용한 시뮬레이션

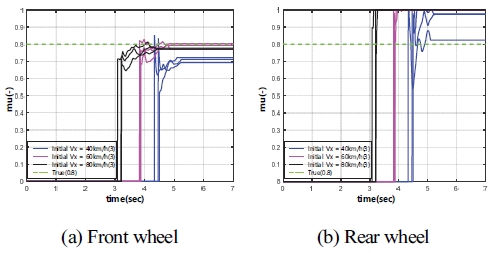
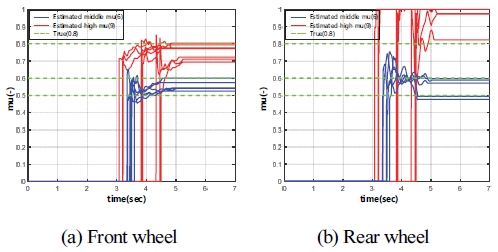
본 절에서는 TuckSim 모델의 차량이 주행 중 감속할 때, 차량의 주행속도와 도로 노면 상태 변화에 따른 도로 노면 마찰계수 추정 결과를 Figs. 13 ~ 15에 나타내었다. Fig. 13을 보면 중 마찰로에서 전⋅후륜의 경우 주행 속도가 변화하여도 오차율 2 % 이내로 추정됨을 확인할 수 있다. 또한, Fig. 14를 보면 고 마찰로에서 전륜의 경우 주행 속도가 40 km/h일 때를 제외하고 적은 오차율을 가진 추정 결과를 보여준다. 하지만 후륜의 경우 주행 속도 40 km/h일 때, 1개의 경우를 제외하고 최대 오차율 20 %의 결과가 발생하였다. 종합적인 결과인 Fig. 15를 보면 중 마찰로에서 전⋅후륜 모두 추정 오차율은 2 % 이내 결과를 보여준다. 또한, 고 마찰로에서 전륜의 경우 주행 속도 40 km/h의 결과를 제외하면 주행 속도에 따라 오차율 5 % 이내 결과를 볼 수 있다. 그리고 후륜의 경우 추정 성능은 전륜보다 어느 정도 떨어지지만, 후륜에 작용하는 구동 토크를 무시했음에도 불구하고 중 마찰로와 고 마찰로의 차이를 확인할 수 있다.

Fig. 13

Road friction coefficient estimation(μ=0.5 ~ 0.6)

Fig. 14

Road friction coefficient estimation(μ=0.8)

Fig. 15

Overall road friction coefficient estimation(μ=0.5 ~ 0.6, 0.8)

4.2 실험 차량 데이터를 이용한 시뮬레이션

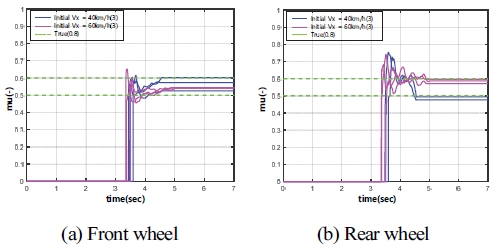
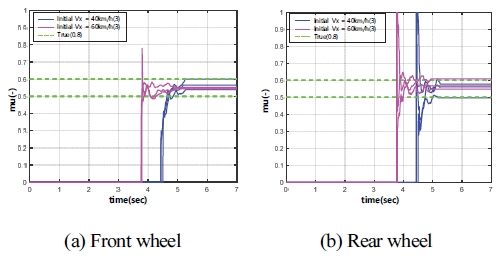
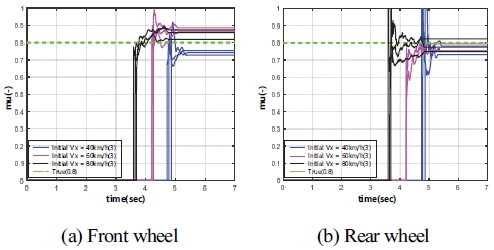
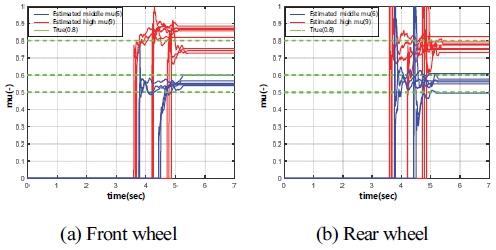
본 절은 실험 차량 데이터를 이용하여 회귀최소자승법 알고리즘 기반 도로 노면 마찰계수 추정 시뮬레이션을 진행한 결과를 보여준다. 실제 차량 데이터 시뮬레이션 시 사용된 전⋅후륜의 제동 게인 값은 Table 2와 동일하다. Fig. 16과 Fig. 17은 차량의 주행속도 변화에 따른 중 마찰로와 고 마찰로의 도로 노면 마찰계수 추정 결과를 나타낸다. 또한, 도로 노면 상태 변화에 따른 전⋅후륜의 도로 노면 마찰계수 결과를 Fig. 18에 도시하였다.

Fig. 16

Road friction coefficient estimation(μ=0.5 ~ 0.6)

Fig. 17

Road friction coefficient estimation(μ=0.8)

Fig. 18

Overall road friction coefficient estimation(μ=0.5 ~ 0.6, 0.8)

Fig. 16에서 전⋅후륜은 주행속도가 변화하여도 도로 노면 마찰계수 추정 성능이 뛰어난 것을 볼 수 있다. 반면에 Fig. 17의 그래프를 보면 고 마찰로에서 전⋅후륜 추정 성능은 추정 오차율 10 % 이내로 추정된 결과를 보여준다. 이에 따라 Fig. 18 그래프 결과를 보면 주행 속도가 변화하여도 도로 노면 마찰계수를 안정적으로 추정된다.

실험 차량 데이터 기반 시뮬레이션 결과를 통해 도로 노면 마찰계수 2등급(Wet asphalt, Dry asphalt) 추정이 가능하고, 오차율은 10 % 이내 결과를 확인하였다. 실제 차량 데이터 기반 시뮬레이션은 TruckSim의 추정 결과보다 더 안정적인 성능을 보여준다. TruckSim 모델의 추정 결과를 향상하기 위해서는 실제 차량과 동일하게 전⋅후륜에 작용하는 타이어 미끄럼율을 정확하게 적용해야 한다. 그리고 모델의 정확성을 향상한다면 실제 차량과 동일한 성능이 나올 것으로 예상한다.