MF(Magic Formula) 타이어 모델 활용 기술 개발

1. 서 론

타이어는 차량이 노면과 상호작용하기 위한 유일한 수단으로 R&H 성능뿐만 아니라 NVH, 구/제동, 연비, 내구 등 차량의 전반적인 성능에 영향을 미치는 매우 중요한 요소이다. R&H 및 차량 동역학적 관점에서만 보더라도 차량의 주요 제원(중량, 관성 제원, 휠 베이스, 휠 트레드, 무게 중심 등)의 범위가 주어진 상황에서의 타이어 특성 영향은 타 시스템 대비 차량 레벨의 거동에 지배적인 영향을 미친다.¹⁾ 물론 K&C 특성으로 대표되는 현가, 조향 시스템의 특성으로 확보할 수 있는 성능은 타이어의 특성으로 확보할 수 있는 성능과는 차별화되는 부분도 있기 때문에 어느 하나의 시스템도 간과할 수는 없다. 하지만 세부적인 상황들을 차치하고서라도 타이어로 인한 기본 성능 확보는 차량 R&H 성능의 최대 확보 가능 범위를 좌우한다. 그렇기 때문에 초기 개발 단계에서 목표 차량 성능에 근거한 타이어 특성 목표 설정과 사전 검증은 매우 중요하다. 특성에 대한 현실적이고 명확한 목표가 확보되어야 이를 토대로 실제적인 설계인자들의 목표를 설정할 수 있으며, 이러한 과정이 현재 개발프로세스의 기본적이고 대표적인 형태라고 할 수 있다.²⁾ 보다 효과적이고 효율적인 타이어 특성에 대한 목표 설정과 차량 레벨에서의 성능 예측, 검증 과정은 차량을 구성하는 타 기본 시스템과 마찬가지로 과거부터 시뮬레이션에 기반하여 지속적으로 구축되었으며 적용되고 있다.

차량 동역학 시뮬레이션에서 중요한 측면 중 하나는 차량의 움직임이 타이어에 가해지는 힘과 모멘트에 따라 달라지기 때문에 타이어와 노면간의 상호작용력을 정확하게 모델링하는 것이다. 타이어에 가해지는 하중, 주행 중 발생하는 슬립각, 캠버각, 노면 마찰 특성 등의 다양한 조건에 대해 비선형적이고 복잡한 거동을 보이는 타이어 특성을 표현하기 위하여 Pacejka는 Magic Formula(MF)를 사용하여 이를 모사하는 방법을 제안하였다.^3-5) 모델이 표현할 수 있는 특성 또한 연구 초기에는 차량 핸들링 성능과 주로 연관된 특성들이었으나, 이후에는 벨트(Belt)의 강체 운동을 고려하여 100 Hz 미만의 진동 특성과 저속에서 돌기물과의 상호작용과 연관된 인벨로핑(Enveloping) 특성이 표현되는 MF-Swift 모델로 발전하였다.⁶⁾ 최근에는 한계 특성과 연관된 온도 모델, 저마찰 노면에서의 특성을 표현하기 위한 모델, 극저속에서의 턴 슬립 모델 등으로 세분화하여 발전하고 있다.^7-9) 이러한 MF 타이어 모델은 현재 ADAMS, CarMaker 등 대부분의 상용 차량 동역학 해석 툴에 적용되어 활용되고 있다.

타이어 모델과 연관된 연구가 앞서 제시한 것과 같은 모델링 이론과 방법론, 검증 그리고 이와 연관되어 정밀한 타이어 모델을 생성하기 위한 시험 방법¹⁰⁾에 대한 것들만 존재하는 것은 아니다. 실제 차량 성능 개발 단계에서 검증된 모델을 생성하고 모델을 활용하여 차량의 성능을 예측할 뿐 아니라 더 나아가 목표 수준을 만족하는 타이어의 특성을 제안하는 수준까지 확대되는 것이 요구된다. 이중에는 타이어 모델이 주어졌을 때 모델로부터 코너링 강성, 최대 횡력, 지연 길이, 캠버 강성 등의 대표적인 타이어 특성을 파악하는 것이 포함되어 있다. 이들 특성은 타이어 모델을 특정 조건에서 시뮬레이션하여 얻은 데이터를 기반으로 추가적인 계산 절차를 거쳐 얻어내야 한다. 대표 특성을 활용하여 타이어 간의 특성을 비교하고 차량 성능 인자와의 상관성을 파악한다. 그렇다면 생성된 혹은 실제 존재하는 타이어 모델이 아닌 가상의 목표 타이어 특성에 대한 차량 성능을 사전에 평가하고자 한다면 어떻게 타이어 모델을 활용할 수 있을까? 이 경우에는 흔히 타이어 모델의 파라미터를 반복적으로 변경하여 임의의 특성을 갖도록 모델을 변경하여 사용한다. 이를 위하여 타이어 모델에는 Magic formula 수식의 계수에 해당하는 파라미터 뿐만 아니라 주요 특성에 대한 스케일링 계수(Scaling coefficient)도 포함되어 있어 이와 같은 목적에 대하여 활용할 수 있다. 하지만 스케일링 계수의 형태로 제공되는 파라미터와 대표 단품 특성은 다소 상이한 부분이 있어 특정 특성을 변경하기 위해서 어떤 파라미터를 변경 해야하는지 혼동이되거나 하나의 스케일링 계수가 다수의 특성 변화에 영향을 미쳐 각 인자를 독립적으로 제어할 수 없어 그로 인한 결과의 부정확성을 내포한다는 단점을 가지고 있다. 또한 파라미터를 찾는 과정이 주로 시행착오 과정을 거쳐 도출되기 때문에 실제로 활용 단계에서 이와 같은 행위를 반복적으로 수행하는 것은 상당한 비효율성을 수반한다. 본 연구에서는 이와 같은 비효율성에 대한 해결책을 제시하고자 성능 개발 단계에서 상시적으로 활용 가능한 타이어 모델 활용 기술과 분석 프로그램을 개발하였다.

2. 타이어 모델 활용 기술 개발 내용

2.1 전체 개요

Fig. 1은 본 연구에서 수행한 MF 타이어 모델 활용 기술의 개요를 보여주는 그림이다. 전체 구성은 크게 순방향과 역방향 두가지 모듈로 구성된다. 먼저 그 중 첫 번째 모듈은 타이어 모델로부터 단품의 특성을 대표하는 지수들을 추출(Extraction)하는, 순방향(Forward) 분석에 해당하는 모듈이다. 모듈의 입력인자는 타이어 모델의 파라미터(수식, 스케일링 계수)이며, 해당 모듈을 통해 코너링 강성, 최대 횡력, 지연 길이 등 도면, 성적서 등에 적용되는 대표적인 타이어 단품 특성을 계산한다. 단, 입력에 해당하는 인자들은 타이어 폭, 편평비, 휠 인치 등 타이어 설계 시 직접적으로 활용하는 인자와는 별개의 인자이다. 두 번째 모듈은 역방향(Backward)에 해당하는 절차로 임의의 타이어 모델로부터 특정 특성 지수들에 대한 목표값을 설정하면 최적화 기법을 통해 이를 만족하는 타이어 모델 파라미터 조합을 찾아주는 모듈이다. 최적화 모듈은 일반적인 최적화 절차에 기반하였으나 타이어 모델에 맞춤화된 절차를 개발하여 적용하였다. 양 방향 절차에 대한 모듈을 통해 보유한 타이어 모델로부터 특성 수준을 파악하고 비교할 수 있으며, 반대로 목표 타이어 특성에 대한 차량 성능 변화 영향을 파악하고자하는 경우 해당 특성을 갖는 타이어 모델을 상시적으로 생성하여 차량 모델에 적용하고 성능 수준을 예측할 수 있다. 각 모듈은 서로 다른 세부 목적을 가지고 있지만, 프로그램 개발 관점에서는 솔버와 주요 라이브러리를 공유하는 형태로 구성되어 있다. 아래 절 부터는 각 모듈에 대한 상세 내용을 기술한다.

Fig. 1

Overview of development of MF(Magic Formula) tire model application technique

2.2 타이어 단품 특성 추출 모듈

타이어 모델로부터 단품 특성을 추출하는 순방향(Forward) 모듈은 2가지 서브 모듈로 구성된다. 첫 번째 서브 모듈에서는 다양한 버전과 형태의 타이어 모델 파일을 읽어들여 내부에 포함된 파라미터들을 선별/분석하고 이들과 다양한 단품 시험 조건을 MF 솔버(TNO 사에서 제공하는 라이브러리)에 입력하여 타이어의 힘과 모멘트 등의 상태량을 얻어내는 모듈이다.¹¹⁾ 단품 시험 조건이란 인가하중(Fz), 종방향 슬립율(Kappa), 횡방향 슬립각(Alpha), 캠버 각(Camber), 주행 속도(Vx) 등이 있으며, 목적에 따라 이들인자를 조절하여 가상 단품 시험을 수행한다. 예를 들어 표준조건의 코너링 강성을 얻기 위해서는 횡방향 슬립각 외에 타 인자를 제어하여 가상 시험을 수행하고, 힘과 모멘트 등을 산출하여 다음 서브 모듈로 전달한다. 마찬가지로 캠버 강성의 경우에는 위 조건에서 캠버각을 추가적으로 변경하여 타이어의 캠버각 변화와 타이어 슬립각 변화에 따른 힘과 모멘트 특성을 얻어낸다. 이와 같이 각 특성 지수의 계산에 필요한 Raw data들을 사전에 정의된 다양한 시험 조건에 대한 가상 시험 수행하는 절차가 첫 번째 서브 모듈의 역할이다. 기존에는 이러한 과정을 이론식에 근거하여 별도의 솔버를 개발하여 적용하거나 ADAMS/Car와 같은 상용 동역학 해석 SW에 연계하여 해석한 후 얻어내었지만 본 연구에서는 제공되는 라이러리를 사용하여 효율적으로 구현하였다.

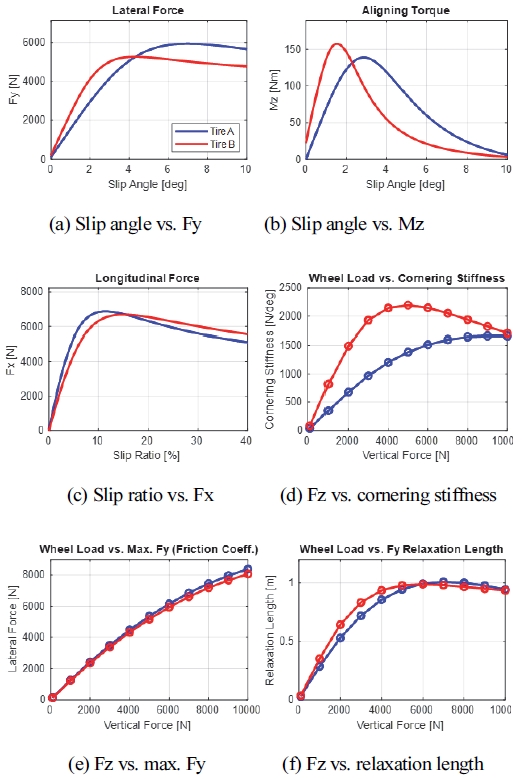
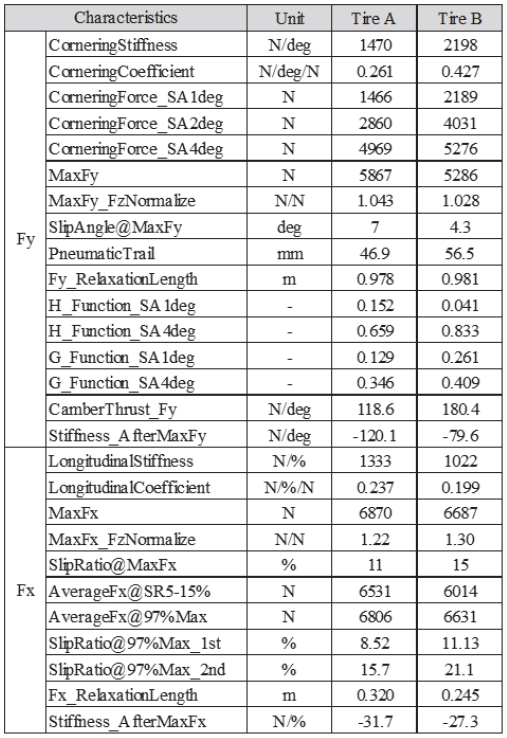
두 번째 서브 모듈에서는 첫 번째 서브 모듈에서 출력된 Raw data로 부터 성능 개발 단계에서 유의미하다고 판단되는 다양한 단품 특성 지수들을 일관된 산출 근거에 기반하여 계산한다. Table 1에서는 횡력(Fy)과 구제동력(Fx)과 관련된 주요 특성지수 리스트와 임의의 두 종류의 타이어 모델에 대한 계산 결과를 보여준다. 특성 지수 중에는 잘 알려진 코너링 강성, 코너링 계수, 최대 횡력, 지연길이, 캠버 강성 등과 같은 지수들을 기본으로 다양한 특성지수가 포함되어 있다.¹²⁾ 이 중 H-Function은 Load sensitivity를 의미하는 인자로 값이 클수록 수직력 변화에 의한 횡력 변화폭이 큰 크며, G-Function은 Load transfer sensitivity를 표현하는 인자로 값이 클수록 하중이동에 의한 횡력 손실량이 큰 것을 의미한다.¹³⁾ 제시된 대표 특성지수 외에도 의미있는 인자를 발굴하여 얼마든지 추가할 수 있다. 뿐만 아니라 Fig. 2와 같이 주요 특성 그래프도 제공하여 타이어 모델 간 주요 특성을 효과적으로 비교, 분석할 수 있다. 해당 모듈을 이용하여 타이어 모델 파일만으로 추가적인 시뮬레이션 없이 즉시 유효한 특성들을 파악할 수 있다. 본 논문에서 제시하는 모델의 특성은 기본적으로 실제 타이어 모델과의 정합성이 확인된 모델임을 언급한다.

Table 1

List of tire characteristics and example value

Fig. 2

Graph of major tire characteristic(Tire A, Tire B)

2.3 타이어 모델 파라미터 최적화 모듈

다음은 역방향(Backward) 모듈이다. 역방향 모듈은 생성하고자 하는 타이어 특성 지수 목표에 기반하여 해당 목표를 만족하는 타이어 모델 파라미터를 최적화 기법을 통해 찾아주는 모듈이다. 최적화의 개념이 적용되기 때문에 특성지수들 중에서 목적함수(Objective function)와 구속조건(Constraint)을 설정할 수 있으며, 변경하고자 하는 파라미터들에 대해서는 설계 변수(Design variable)로 지정하고 경계조건(Boundary condition)을 설정하여 원하는 형태의 최적화를 수행할 수 있다. 하지만 일반적인 최적화 절차의 개념을 적용하기에는 타이어 모델 파라미터가 매우 많으며, 개별 사용자들이 그 의미를 모두 이해하거나 주요 특성 지수들과의 상관관계를 고려하여 활용하기에는 어려움이 존재한다. 이러한 특수한 상황이 일반적인 최적화 절차를 그대로 적용하거나 상용 최적화 SW를 연계하는 대신 별도의 최적화 모듈을 개발하게 된 이유이다. 본 최적화 모듈은 단순히 하나의 문제를 정의하고 해결하기 위한 것만은 아니며, 실제로 사용자가 이 행위를 수행하기 위한 모든 효율적 과정을 포함하고 있다. 상세 내용은 다음 절에서 설명한다.

2.3.1 최적화 절차 정의

앞서 언급한 수행 과정에서의 현실적인 어려움을 최소화하고 활용성을 극대화하고자 타이어 모델 파라미터 최적화를 위한 맞춤 절차를 Fig. 3과 같이 정의하였다. 먼저 ‘Read/Analyze Tire Model’에서는 최적화를 수행할 초기 타이어 모델을 불러오면 파일내에 저장된 텍스트를 분석하여 알고리즘 상에서 처리 가능한 파라미터와 값 형태로 변수화하고 각 변수로부터 앞 절에서 언급한 타이어 특성 지수를 추출한다. 추출된 특성 지수들은 최적화 전 특성이 된다. 다음 절차로 ‘Define Optimization Problem(CI)’에서는 특성 지수(CI, Characteristic Index) 별 역할을 정의한다. 역할이란 목적함수, 구속조건 또는 이 두가지에 해당하지 않는 자유 조건(Free)을 의미한다. 먼저 목적함수는 최적화를 통해 특성치를 만족시키고자 하는 인자를 의미하며, 구속 조건은 목적 함수는 아니지만 특정 범위(Lower/Upper Constraint)를 벗어나지 않도록 최적화를 수행해야한다는 조건을 의미한다. 자유 조건은 최적화 후에 값이 어떻게 변하더라도 관계없는 인자임을 의미한다. 추가적으로 구속조건의 경우 인자마다 상/하한치를 개별적으로 입력대는 대신 일괄 비율을 적용할 수 있도록 하였으며, 목적함수와 구속조건에는 가중치(Weighting factor)를 적용하여 다중 목적 함수 최적화 시 인자가 중요도를 차별화하거나 값의 스케일을 상충하도록 문제를 정의할 수 있다.

Fig. 3

Flow of tire model parameter optimization process

다음으로 ‘Define Optimization Problem(DV)’에서는 타이어 모델 파라미터에 해당하는 설계 변수(DV, Design Variable)를 선택하고 경계 조건을 정의한다. 타이어 모델 파라미터의 종류는 앞서 언급하였듯이 크게 스케일링 팩터와 수식을 구성하는 계수가 존재하는데, 이들 중 대부분은 중복되는 역할을 가지고 있어 연관 인자들을 동시에 설계변수로 설정할 시 최적화 솔루션의 개수가 무한대가 될 수 있다. 각 인자 종류의 장단점을 언급하자면, 스케일링 팩터의 경우 그 의미가 상대적으로 직관적이지만, 특성 지수를 독립적으로 제어하는 데에 한계가 있으며, 수식의 계수는 정확한 의미를 파악하기 어렵고 개수가 많으나, 특성 지수를 보다 독립적으로 제어할 수 있다. 각각의 장점을 취하는 것이 목적함수를 만족하는 파라미터 조합을 찾는 데에 보다 유리하다고 판단되어 복수 조합이 가능하도록 구현하였다. 설계변수 별 경계조건의 경우에는 타이어 특성 시험 데이터부터 모델 파라미터를 피팅하는 MF-Tool에 정의된 모델 파라미터 범위를 적용하였다. 사실 경계조건의 경우 본 모델 파라미터 최적화에서는 설정된 범위를 적용한다면 크게 중요하지 않다. 설계 변수가 실제 제품의 규격을 결정하거나 제작 시 적용되는 인자인 경우 현실적인 경계조건이 반드시 적용되어야 하지만 타이어 모델 파라미터의 경우에는 단순 수식 계수로서 그러한 대상이 아니기 때문이다. 설계 변수까지 적용하였다면 마지막으로 최적화 알고리즘 선택할 수 있으며, 본 논문에서는 타이어의 비선형 특성 최적화 문제에 대한 다양한 솔버 선택 옵션을 제공하고자 MATLAB에서 제공하는 Fmincon, Global search, Pattern search, Particle swarm, Genetic algorithm과 같은 지역, 전역 최적화 솔버를 적용할 수 있도록 구현하였다.¹⁴⁾ 여기까지의 절차로 하나의 최적화 문제에 대한 정의가 완료되며, 이를 하나의 Task로 정의하고자 한다.

실제로 개발 기술을 활용하는 단계에서는 다양한 타이어 모델과 목적함수에 대하여 최적화를 상시적으로 수행하고 활용할 필요가 있다. 이 경우 그 때마다 최적화 문제를 정의하고 문제를 풀고 결과물을 적용하는 방식으로 활용할 수 있으나 최적해 도출에는 시간이 소요되는 만큼 이 과정에서도 비효율성이 발생한다. 이러한 문제를 최소화하고 개발 프로세스 활용성을 극대화하고자 Task manager의 개념을 도입하였다. 앞서 언급한 하나의 Task를 정의하면 실제 최적화를 수행하기에 앞서 새로운 복수개의 Task를 추가하거나 기존에 정의한 Task를 복사하여 추가 변경하여 정의할 수 있다. 목적 함수의 값을 변경하거나 설계 변수의 개수를 증감하거나 같은 문제에서 솔버만 다른 것을 적용하여 수행하고자 하는 경우 매우 손쉽게 다중 Task 를 생성할 수 있다. 모든 Task가 정의되어 실제로 최적화를 수행하면 이들이 순차적으로 수행되고 최적화 전/후의 특성 지수, 설계 변수, 그래프 등 관련된 모든 정보가 해당 Task에 저장된다. 서로 다른 최적화 문제에 대한 결과들은 단순히 해당 Task를 활성화 함으로서 효율적으로 확인할 수 있다.

2.3.2 모델 파라미터와 특성 지수간 상관성 분석

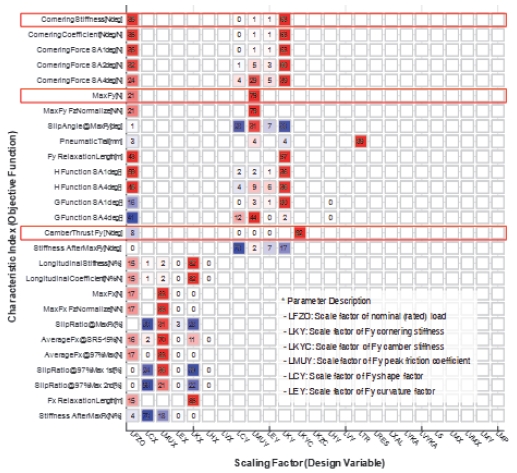
앞 절에서 언급하였듯이 타이어 모델 파라미터를 최적화하는 과정에서 특정 목적 함수를 지정했을 때 설계 변수로 어떠한 파라미터를 선택해야할 지 직관적으로 파악하기 어렵다. 스케일링 계수의 경우 각 계수마다 정의가 명시되어 있지만, 하나의 인자가 다양한 특성 지수에 영향을 미치기도 하며, 수식 계수의 경우에는 의미도 직관적이지 않을뿐더러 파라미터 개수 또한 특성 별로 매우 많다. 이러한 점이 사용자가 최적화를 수행하는 데에 방해요소로 작용한다. 이러한 점을 개선하고자 본 연구에서는 타이어 파라미터와 특성 지수간 상관성 분석을 통해 목적 함수로 특정 특성 지수를 선택할 시 이와 연관된 파라미터를 추천하여 손쉽게 선택할 수 있는 절차를 포함하였다.

Fig. 4는 Table 1에서 제시한 횡력, 구제동력 관련 대표 특성 지수와 타이어 모델 파라미터 중 스케일링 팩터와의 상관성 분석 결과이다. 상관성 분석은 각각의 스케일링 팩터를 ±30 % 증감하며, 특성 지수 값의 변화를 비교하는 방법으로 수행하였다. 그래프에서 붉은색 상관성의 의미는 스케일링 팩터를 증가시켰을 때 특성 지수 값도 양의 방향으로 증가한다는 것을 의미하며, 파란색은 반대를 의미한다. 또한 값으로 제시된 상관성은 하나의 특성 지수에 대하여 각 인자가 얼마만큼의 상관성을 갖는지의 비율을 수치화한 지수이다. 즉 각 행의 상관성 지수의 합은 100이다. Fig. 4에서 첫 번째 특성 지수인 코너링 강성의 경우 스케일링 팩터 LKY(Scale factor of Fy cornering stiffness)와 LFZO(Scale factor of nominal load)의 민감도가 절대적이며, 최대 횡력의 경우에는 LMUY(Scale factor of Fy peak friction coefficient)와 LFZO, 캠버 강성의 경우에는 LKYC(Scale factor of Fy camber stiffness)의 영향도가 큰 것을 확인할 수 있다. 본 예시는 스케일링 팩터의 정의와 직관적으로 연결이 되지만 이를 통해 추가적인 인자들의 복합 영향 여부도 파악할 수 있다. 전체 수식 계수에 대해서도 이와 동일한 방법으로 상관성을 분석하였으며, 이들의 관계를 최적화 절차 내에 모두 포함하였다. 다시 말해, 목적함수로 코너링 강성을 선택하면 LKY, LFZO가 상관지수 제시와 함께 자동으로 추천이 된다. 이를 통해 최적화 과정에서 사용자는 추가적인 고민없이 손쉽 손쉽게 설계 변수를 지정하고 빠르게 최적화를 수행할 수 있다.

Fig. 4

Relationship between tire model parameter and characteristic index(scaling factor)

2.3.3 최적화 프로세스 검증

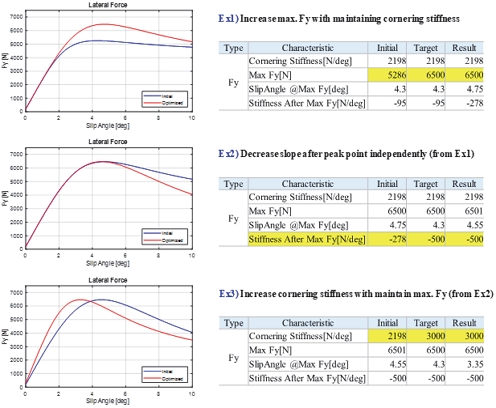
개발된 최적화 프로세스를 검증하기 위하여 Fig. 5와 같이 대표 특성에 대한 임의의 최적화 문제를 정의하고 설정한 목표 단품 특성을 만족하는 모델 파라미터를 도출해보았다. 코너링 강성, 최대 횡력, 최대 횡력 이후 횡력 감소량 총 3개의 특성 지수 중 하나씩을 목표 특성으로 선정하여 초기 타이어 특성으로부터 변경하였다. 첫번째로는 코너링 강성을 초기 특성 수준으로 유지하는 상황에서 최대 횡력을 감소(MaxFy[N]: 5,286 → 6,500)한 모델을 얻어냈으며, 두 번째로는 첫 번째 최적화 결과에서 최대 횡력 이후 고 슬립각 영역에서의 횡력 감소 경향만 독립적으로 감소(Stiffness AfterMaxFy[N/deg]: -278 → -500)한 모델을 최적화를 통해 얻어냈다. 마지막으로 세번째 검증 예시는 최대 횡력을 유지하면서 코너링 강성만 독립적으로 증가(Cornering Stiffness[N/deg]: 2,198 → 3,000)하는 특성을 갖는 타이어 모델 파라미터를 도출하였다. 본 예제를 수행하는 과정에서 각 문제의 최적화에 소요되는 시간은 30초 전후이며, 문제의 난이도와 솔버 선택에 따라서 시간은 다소 증가할 수 있으나 매우 빠른 시간내에 결과를 얻을 수 있다. 이와 같은 문제에 대하여 실제 시행착오를 거쳐 얻어낼 경우 수행 시간이 과다하게 소요될뿐만 아니라 일부 특성이 종속적으로 변경되어 원하는 결과를 얻기 어렵다. 이처럼 직관적인 예제이지만 이를 통해 개발 최적화 프로세스의 효용성을 검증할 수 있으며 타이어 특성의 Shape design과 정교한 목표 설정이 가능함을 확인하였다.

Fig. 5

Verification of developed process through optimization problem

2.4 MF 타이어 모델 활용 기술 SW 개발

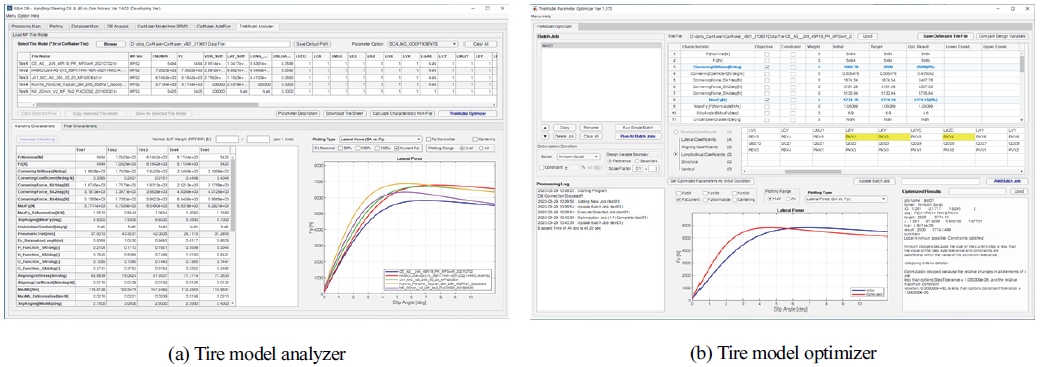
이러한 개념을 기반으로 Fig. 6(a), (b)와 같이 누구나 개발 기술을 활용할 수 있는 Matlab 기반 어플리케이션(Application)을 개발하였다. Fig. 6(a)는 Tire model analyzer이며, 타이어 모델 파일로부터 특성 지수를 추출하는 순방향 분석을 주목적으로 하는 어플리케이션이며, Fig. 6(b)는 Tire model optimizer로서 목표 타이어 단품 특성을 만족하는 MF 모델 파라미터 최적화를 할 수 있는 어플리케이션이다. 두 어플리케이션은 동일한 솔버와 라이브러리를 사용하여 상호간에 연계되어 있다. 각 어플리케이션에 대하여 보다 구체적으로 설명하자면 Tire model analyzer에서는 복수의 타이어 모델을 일괄적으로 비교/분석할 수 있으며 모델 파라미터 뿐만 아니라 수직 하중, 캠퍼각과 같은 외부 인가 조건을 변경하며 즉시 특성 변화 정도를 확인할 수 있다. 또한 사전에 파라미터 셋에 대한 실험계획(DOE, Design of Experiment)을 정의하고 이를 적용하여 특성들을 일괄적으로 계산할 수 있다. Tire model optimizer에서는 앞서 언급하였듯이, 대표 타이어 특성 지수 연계, 목적 함수와 연관된 설계변수 자동 추천, 구속 조건 일괄 설정, 설계 변수의 경계조건 일괄 자동 설정과 같이 MF 타이어 모델 최적화를 위한 맞춤 절차들이 포함되어 있다. 또한 복수개의 최적화 문제를 사전에 정의하고 일괄적으로 최적화를 수행할 수 있으며, 각 Task들을 Export하여 사용자간에 전체 결과를 교환, 공유할 수 있다. 그 밖에도 최적화 전후 설계 변수 비교와 최적화 후 파라미터를 적용한 타이어 모델 생성 등의 기능도 포함되어 있다. 이를 통해 개발 기술을 차량 성능 개발 단계에서 누구나 효율적으로 활용할 수 있다.

Fig. 6

MF tire model application SW

3. 타이어 변경에 따른 차량 성능 변화 기여도 분석

3.1 분석 시나리오 및 방법

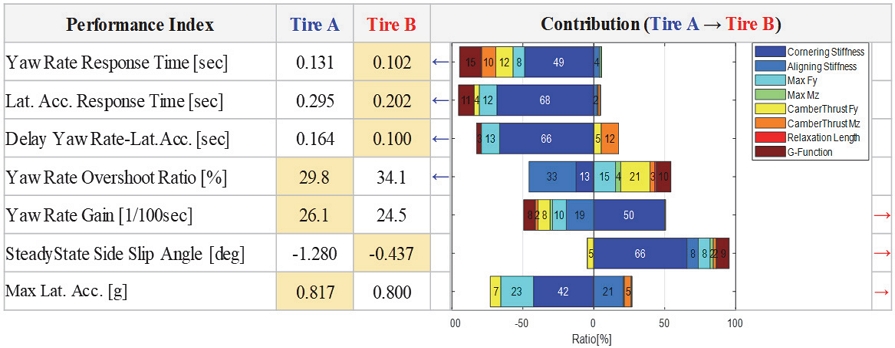
본 장에서는 본 연구를 통해 개발된 기술을 활용하여 차량 핸들링 성능에 대한 타이어 특성의 기여도를 성능 인자 기준으로 분석하고자 한다. 시나리오는 다음과 같다. 동일 차량에 타이어를 교체하였을 때 타이어 특성 차이로 인한 차량 레벨 성능 차이가 발생하는데, 이를 대표 타이어 특성 별로 분리 분석을 하고 그 원인을 수치적으로 설명하고자 한다. 일반적으로는 타이어 교체에 대한 성능 차이 설명 시, 타이어 특성 지수 차이와 이론적 상관관계를 토대로 간접적으로 설명한다. 하지만 본 연구에서는 각 특성 지수에 대한 기여도를 수치적으로 명확하게 설명하는 방법을 제시하고자 한다. 먼저 Fig. 7은 임의의 동일 차량 모델에 앞서 Table 1에서 언급한 두 타이어를 적용하였을 때의 핸들링 거동을 비교한 결과이다. Fig. 7(a) ~ (c)는 100 kph, 목표 정상상태 횡 가속도 0.4 g 조건에서의 스텝 스티어 시험 모드 해석 결과인데, 이를 통하여 과도 상태 반응성, 오버슛과 정상상태 게인 등을 파악할 수 있다.¹⁵⁾ Fig. 7(d)는 100 kph 스텝 시리즈 시험 모드 해석 결과로, 언더스티어 구배 및 한계 레벨을 파악할 수 있다. 그림을 통해 알 수 있듯이 Tire A 대비 Tire B 적용 시, 요 레이트, 횡 가속도 반응 시간이 빠르고 사이드 슬립각이 작아 안정성이 향상된다. 반면 오버슛은 미소 증가하며 한계 성능도 열세해진다.

Fig. 7

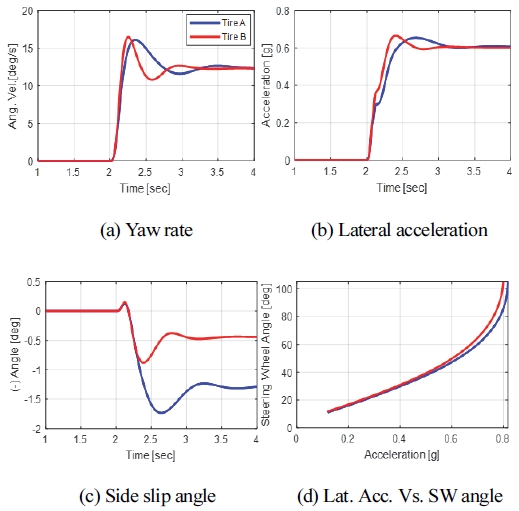
Comparison of handling characteristics by tire (a, b, c: step steer 100 kph / d: step series 100 kph)

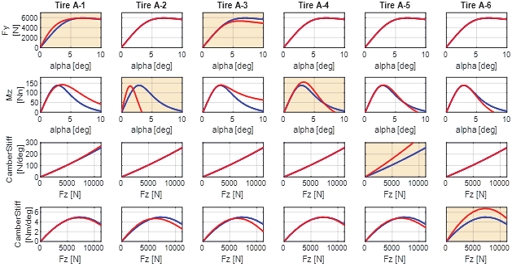
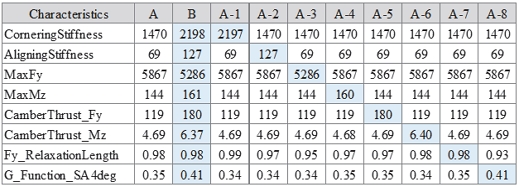
차량 레벨에서 위와 같은 거동 변화가 발생하는 원인을 파악하기 위하여 핸들링 성능 관련하여 주요한 8개의 특성 인자들에 대하여 타이어 A의 특성을 기반으로 B의 특성이 각각 적용된 타이어 모델을 생성하였다. Table 2는 최적화를 통해 생성한 타이어 모델에서 추출한 특성이다. 예를들어 타이어 A-1은 타이어 A에서 코너링 강성만 타이어 B의 특성을 갖도록 파라미터가 최적화된 모델이며, 타이어 A-3는 최대 횡력만 조절된 타이어이다. Fig. 8은 A-1 ~ 6모델에 대하여 슬립각에 대한 횡력, 정렬 모멘트와 수직 하중에 대한 횡력 캠버 스러스트, 정렬 모멘트 캠버 스러스트 특성 그래프를 보여준다. 각 타이어 모델이 목적한 특성 관련된 부분(그래프 중 음영 처리된 부분)만 변경되고 그 외의 특성은 대체적으로 유지되는 것을 확인할 수 있다. 정렬 모멘트 같은 경우에는 피크 이후 특성이 다소 상이해지긴 하나 타이어 슬립각이 적은 일반 영역에서의 특성은 유지하고 있으며, 또한 정렬 모멘트의 영향이 횡력 대비 작은 것을 고려했을 때 감안할 수 있는 수준으로 간주하였다. 지연길이와 G-Function의 경우는 그래프로 도시하는 것이 적절하지 않아 제외하였다. 일반적으로 이와 같이 다수의 특성들이 연성이 되어 있는 타이어 모델에서 목적한 특성만 변경하여 그 영향을 파악하기는 매우 어렵다. 즉, 하나의 특성을 변경시키기 위해 스케일링 팩터를 조절하면 다른 특성도 동시에 변화하기 때문에 분석 결과들에는 연성으로 인한 효과가 동시에 반영된다. 개별 특성만이 적용된 타이어 모델들을 이용하여 기여도 분석을 수행한다.

Table 2

Tire model variation for contribution analysis

Fig. 8

Comparison of major tire characteristics for each tire variation (A-1 ~ 6)

3.2 기여도 분석 결과

Fig. 9는 앞 절에서 언급한 시나리오와 타이어 모델 Variation을 이용하여 해석을 수행하고 각각의 결과를 통해 타이어 A와 B로 인한 차량 성능 차이 이유를 설명한 기여도 분석 결과이다.¹⁶⁾ 기여도 분석은 개별 특성 변경 시 차량 레벨 성능 변화가 그 특성의 영향도라고 가정하여 수행한다. 각 특성 변화의 선형 조합이 전체 특성 변화와 정확히 일치하지는 않을 수 있으나 그 기여도를 파악하기에는 충분하다. 동일 차량에 타이어 A를 적용했을 때(전/후륜 동일 타이어 적용) 대비 타이어 B를 적용했을 때, 요 레이트 반응 시간이 0.131초에서 0.102초로 감소하는데, 타이어 단품 특성 상에서 그 이유는 코너링 강성 차이가 약 49 % 기여하며, 하중이동 민감도인 G-Function이 약 15 %의 영향을 미치고 나머지 인자들도 동일 영향을 미치는 것을 확인할 수 있다. 요 레이트 게인의 경우에는 타이어 B 적용 시 26.1 → 24.5로 감소하는데 코너링 강성은 요 레이트 게인이 증가하는 방향의 특성을 갖지만 나머지 특성들이 게인을 감소시키는 방향으로 설정되어 있다. 마지막으로 최대 횡 가속도의 경우에는 코너링 강성과 최대 횡력 모두 타이어 A가 유리한 영향을 미치는 방향의 특성을 갖는 것을 알 수 있다. 타이어가 전/후륜에 장착되고 차량 거동에 대한 기여도가 상충이 되느 방향으로 영향을 미치기 때문에 전/후륜 특성에 대한 추가적인 원리 분석의 여지는 존재하나, 기여도 분석을 통해 타이어로 인한 차량 성능 차이 원인을 각 성능지수 별로 분리하여 수치적으로 설명할 수 있다.

Fig. 9

Contribution analysis result by changing tire model

4. 결 론

본 연구에서는 R&H 성능 개발 단계에서 MF 타이어 모델을 효율적으로 활용하기 위한 기술과 공유를 위한 어플리케이션을 개발하고 활용 방안을 제시하였다. 세부 내용을 요약하자면 아래와 같다.

• 1) MF 타이어 모델로부터 코너링 강성, 최대 횡력, 지연길이 등 횡/종 방향 대표 단품 특성을 손쉽게 추출할 수 있는 분석 프로세스(Tire model analyzer)를 개발하였다. 해당 모듈은 특성 지수를 추출하기 위하여 내부적으로 다양한 조건에 대한 타이어의 힘과 모멘트를 계산하며 유효한 지수 추출을 위한 전 과정이 자동화되어 있다. 이를 이용하여 보유한 타이어 모델의 특성 지수와 그래프 등을 신속, 정확하게 비교/분석 할 수 있다.
• 2) 주어진 타이어 모델의 특성을 추출하는 것뿐만 아니라 반대로 목표 타이어 특성을 정의하면 그 것을 만족하는 모델 파라미터를 도출해주는 최적화 프로세스(Tire model optimizer)를 개발하였다. 목적함수, 구속조건, 설계변수 등 최적화 기법의 개념이 반영되어 사용자가 원하는 가상의 타이어를 생성할 수 있으며, 그 과정에서 목적함수와 연관된 설계변수 자동 추천 기능 등 타이어 모델 최적화를 위한 맞춤형 절차를 개발하고 적용하였다.
• 3) 최적화 문제 정의를 통해 개발 최적화 프로세스를 검증하였다. 다양한 시나리오에 대한 검증을 통해 특성지수를 독립적으로 제어하면서 신규 타이어 특성을 도출할 수 있으며, 특성 Shape design의 가능성을 확인하였다. 이를 이용하면 보다 세부적인 목표 단품 특성을 제시할 수 있다.
• 4) 개발 기술을 상시적으로 활용하고 공유하기 위한 Application을 개발하였다. User friendly한 GUI 개발을 통해 엔지니어링을 하고자 하는 누구나 손쉽게 해당 기술을 통해 타이어 모델 관련 결과물을 얻을 수 있다.
• 5) 개발 기술을 활용하여 타이어 변경에 따른 차량 핸들링 성능 변화 기여도 분석 방법을 제시하였다. 개별 특성만 변경된 타이어 모델 생성과 적용을 통해 특정 차량 성능 지표가 변화되는 원인이 타이어의 어떤 특성의 차이로 인하여 발생하는지 정량적으로 설명할 수 있다.

본 연구의 결과물을 통해 성능 개발 단계에서 MF 타이어 모델을 활용하는 과정에서 다양한 활용 효과를 얻을 수 있다. 본 논문의 결과물들은 지속적인 추가 개발을 통해 설계, 시험, 해석, 아키텍쳐 등 다양한 연관 분야에서 보다 활발하게 활용될 수 있도록 할 것이며, 이를 통해 R&H 부분에서 타이어 모델을 이용한 효율적인 분석과 개발 목표 설정에 활용 되길 기대한다.

Acknowledgments

본 논문의 최적화 모듈은 ㈜파낙스시스템과의 협업을 통해 개발되었으며 지원에 감사드립니다.

References

• H. Cho, B. Lee, S. Chang, Y. Park, M. Kim and S. Hwang, “Design Sensitivity Analysis and Tolerance Design to Improve,” Transactions of KSAE, Vol.26, No.6, pp.717-727, 2018. [https://doi.org/10.7467/KSAE.2018.26.6.717]
• H. Cho, B. Lee, S. Chang, Y. Park, M. Kim and S. Hwang, “Suspension Design to Achieve Vehicle Handling Performance Targets by Target Cascading Methodology,” Transactions of KSAE, Vol.29, No.9, pp.879-727, 2021. [https://doi.org/10.7467/KSAE.2021.29.9.879]
• H. B. Pacejka and E. Bakker, “The Magic Formula Tyre Model,” Vehicle System Dynamics, Vol.21, pp.1-18, 1992. [https://doi.org/10.1080/00423119208969994]
• H. B. Pacejka and I. J. M. Besselink, “Magic Formula Tyre Model with Transient Properties,” Vehicle System Dynamics, Vol.27, pp.234-249, 1997. [https://doi.org/10.1080/00423119608969658]
• E. Bakker, L. Nyborg and H. B. Pacejka, “Tyre Modelling for Use in Vehicle Dynamics Studies,” SAE 870421, 1987. [https://doi.org/10.4271/870421]
• I. J. M. Besselink, H. B. Pacejka, A. J. C. Schmeitz and S. T. H. Jansen, “The SWIFT Tyre Model: Overview and Applications,” AVEC ‘04 : 7th International Symposium on Advanced Vehicle Control, pp.525-530, 2004.
• A. Sorniotti, “Tire Thermal Model for Enhanced Vehicle Dynamics Simulation,” Tire and Wheel Technology and Vehicle Dynamics and Simulation, 2009-01-0441, 2009. [https://doi.org/10.4271/2009-01-0441]
• A. Ružinskas and H. Sivilevičius, “Magic Formula Tyre Model Application for a Tyre-Ice Interaction,” 10th International Scientific Conference Transbaltica, Vol.187, pp.335-341, 2017. [https://doi.org/10.1016/j.proeng.2017.04.383]
• A. J. C. Schmeitz, I. J. M. Besselink, J. Hoogh and H. Nijmeijer, “Extending the Magic Formula and SWIFT Tyre Models for Inflation Pressure Changes,” Reifen-Fahrwerk-Fahrbahn, pp.201-225, 2005.
• C. Kim, C. Ludwig, S. Park and C. Im, “Improvement of Tire Development Process Through Study of Tire Test Procedure and Vehicle Correlation,” SAE 2018-01-1337, 2018. [https://doi.org/10.4271/2018-01-1337]
• MF-Tyre/MF-Swift 6.2.0.4 Help Manual, TNO Automotive, 2010.
• T. D. Gillespie, Fundamentals of Vehicle Dynamics, SAE International, 1992. [https://doi.org/10.4271/R-114]
• Y. Nakajima, Advanced Tire Mechanics, SprinerLink, 2019. [https://doi.org/10.1007/978-981-13-5799-2]
• Optimization Toolbox: User’s Guide(R2022b), MathWorks Inc., 2022.
• ISO 7401, Road Vehicles – Lateral Transient Response Test Methods – Open-loop Test Methods, The International Organization for Standardization, 2011.
• J. H. Lee, B. L. Choi and C. S. Kim, “Proposal of CAT Model Based Benchmarking and System Characteristic Optimization Method for Developing Vehicle Handling Performance,” APAC21, APAC-21-114, 2021.