특장용 하이브리드 동력인출장치 시스템의 영구자석 동기모터 내부의 3차원 오일 냉각 성능 해석

2.1 모터의 내부 발열

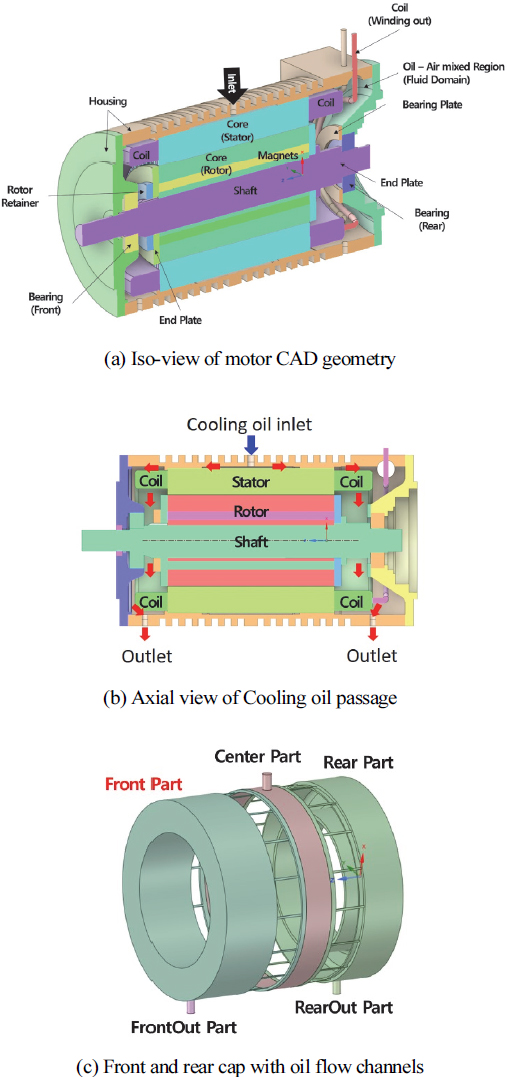
모터의 발열은 전기에너지가 열에너지로 변환된 주울열(Joul heat)로 인한 동손실과 자계에 의한 철손실(Iron loss)이 발생하여 온도상승의 주요 원인이 된다. 이 온도상승을 억제하기 위하여 본 연구에서는 고정자 외곽에 유로를 따라 중앙부를 냉각시키고 이와 동시에 전자코일 끝단부와 베어링부룰 냉각시키기 위하여 오일을 드리핑시키는 직접냉각방식을 동시에 채택하였다. Fig. 1(a)는 본 연구에서 사용된 모터의 주요 부품의 위치 및 형상을 나타내었으며 Fig. 1(b)는 중앙단면에서의 주요부품의 배열과 냉각유로 및 오일의 냉각흐름을 도식적으로 나타내었다. Fig. 1(c)에 냉각유가 흐르는 주요부위를 나타내었다. 그림에서 볼 수 있듯이 고정자 외곽에 환형방향 등 간격으로 총 16개의 채널이 위치해 있다.

Fig. 1

Iso and axial schematic views of the motor, from CAD

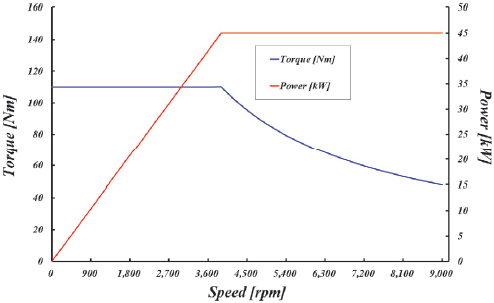
한편 열유동해석을 위하여 모터의 운전점에서 각각의 발열원의 발열량 계산이 필요한데 본 연구에서 사용된 모터의 두 운전점의 회전수는 각각 3,800 rpm과 9,000 rpm이다. 3,800 rpm인 지점에서 정격부하 성능이 45 kW로 가장 최적화된 속도이며 9,000 rpm인 지점에서 최대속도와 정격출력 45 kW의 작동점으로 동작한다. Fig. 2에 본 해석대상 모터의 토크 및 출력 선도를 속도에 대하여 나타내었다.

Fig. 2

Curves of power and torque of the motor

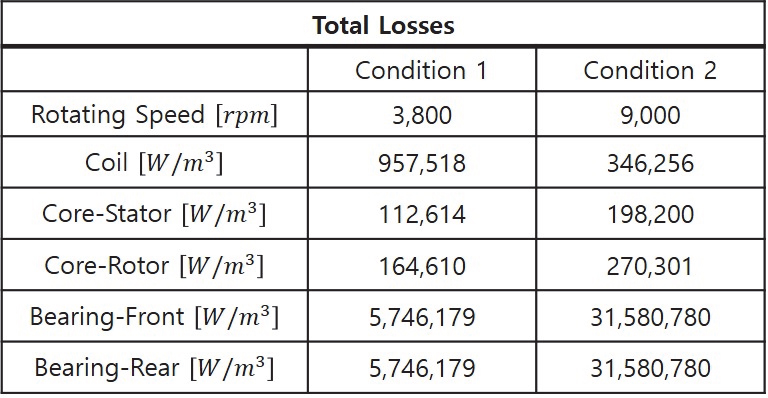
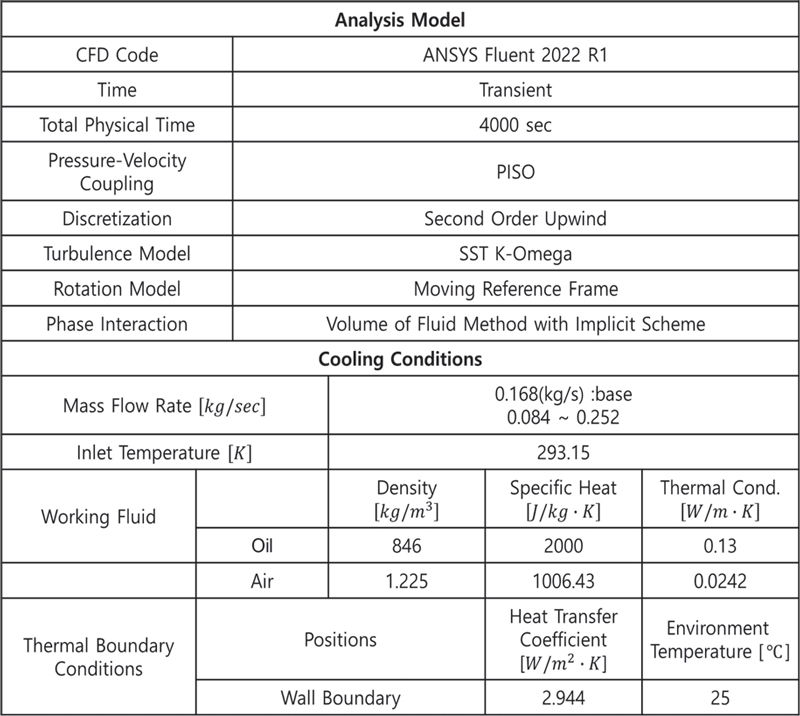
두 운전점에 대한 전자기장 해석을 통해 모터 내부의 발열원의 발열량을 계산할 수 있다. 전자기장 해석은 상용 소프트웨어인 Ansys Maxwell™을 사용하여 2-D로 수행하였으며 여기서 나온 손실값을 3차원 상용 CFD코드인 Ansys Fluent¹⁰⁾의 에너지방정식의 단위체적당 열생성항으로 처리하였다. 실제로는 회전자의 작동에 따라 손실량의 분포는 위치별로 상이하고 회전자와 고정자 사이의 상대각도에 따라 변하지만 본 연구에서는 전자기장 해석결과로 산출된 각 파트의 손실량이 해당 파트의 체적에 균일하게 분포하는 것으로 가정하였다. Table 1에 전자기장 해석으로부터 계산된 전체 손실값을 발열량으로 계산하여 2개의 운전조건에 대하여 나타내었다. 본 연구에서 고려된 손실은 발생위치에 따라 동손, 철손, 기계손, 표유부하손실이다.

Table 1

Heat sources at the two operating points

2.2 공기간극(Air-Gap)에서의 열전달

회전자와 고정자 사이의 공기간극은 모터의 냉각해석에서 가장 어렵고 중요한 영역이다. 공기간극에서의 열전달 방향은 고정자와 회전자 간의 상대온도에 따라 달라지게 된다. 그러나 공기간극에서의 정확한 해석은 매우 어려운데, 그 이유는 기하학적 형상, 공기의 물성치, 회전자의 회전속도등에 영향을 받기 때문이다. 따라서 많은 연구들이 공기간극 내의 유동을 축방향 유동의 존재 유무에 따라 Taylor-Coutte유동 또는 Taylor-Couette-Poiseuille 유동으로 고려한 여러가지 실험식을 적용하여 열전달계수를 계산하였다.⁹⁾

그러나 본 연구의 경우와 같이 액상과 기상이 존재하는 작동유체를 고려해야 하는 경우는 액상과 기체의 체적분율에 따라 열전달 특성이 달라지게 되고, 모터의 공기 간극은 완전발달된 Taylor유동으로 보기 어려우므로 이러한 오차를 극복하기 위하여 본 연구에서는 MRF (Multiple Reference Frame)기법⁹⁾을 이용하여 로터의 회전효과를 3차원적으로 직접 고려하였다. MRF의 적용을 위해 계산영역의 격자를 회전영역과 고정영역으로 나누었다. 고정영역은 하우징, 코일, 고정자 코어이며 회전영역은 회전자, 영구자석, 샤프트이다.

2.3 공기와 오일의 경계면 해석

본 연구에서와 같이 오일을 채널유동 및 드리핑 직접냉각방법을 통하여 계산하기 위해서는 액체와 공기의 경계면을 추적해야 한다. 본 연구에서는 액상과 기상의 경계면에서의 증발과 응축을 해석하기 위하여, 유체체적법(VOF: Volume of Fluid)¹¹⁾을 사용하였다. 이 모델은 격자 크기에 비해 큰 입자들을 가지고 있는 비혼합유체의 액상과 기상의 경계면을 추적하는 수치기법이다. 이 수치기법은 액상과 기상 역역이 모두 같은 운동량 및 에너지 방정식을 사용할 수 있다. 즉 각 상에서 같은 압력, 온도, 속도장을 공유할 수 있어 매우 경제적이며, 많은 연구자들이 사용하여, 해석 정확도가 입증된 바 있다.^6,7) 본 연구에서는 모터 내부의 액상과 기상의 연속상을 계산하기 위해 동일한 지배방정식들이 액상과 기상의 체적분율을 계산하는데 사용되며, 이는 밀도와 점성에 적용되어 각 상을 연계시킨다. 기상과 액상 경계면의 추적은 각 상의 체적분율(α)에 대한 아래의 연속방정식을 사용하여 수행된다.

즉, 계산셀이 전부 증기로 채워져 있으면, α = 1이고 반대의 경우는 영이다. 상 경계면에서는 0≤α≤1의 값을 가지게 된다. 위의 식 (1)의 우측항에 포함되어 있는 $$ {\dot{S}}_v$$와 $$ {\dot{S}}_c$$는 액체 표면에서의 증발율과 응축률이다. 각 계산셀에서의 액상과 기상의 혼합 밀도 및 동점성계수는 아래의 방정식으로 표현될 수 있다.

VOF 모델에서는 에너지방정식에 포함되어 있는 에너지, 온도는 아래와 같이 질량평균을 하여 각 셀에서 사용한다.

여기서, E = c_PT 이다.

오일이 베어링이나 전자코일 끝단부분을 드리핑에 의해 직접 냉각하는 경계면 처리는 로터의 강한 회전으로 인하여 Weber수가 50,000 이상이 되므로 폭발수준의 분열을 경험한다.¹¹⁾ 따라서 별도의 계면추적방법은 적용하지 않고 식 (1)에 의한 체적분율 계산으로 진행하였다.

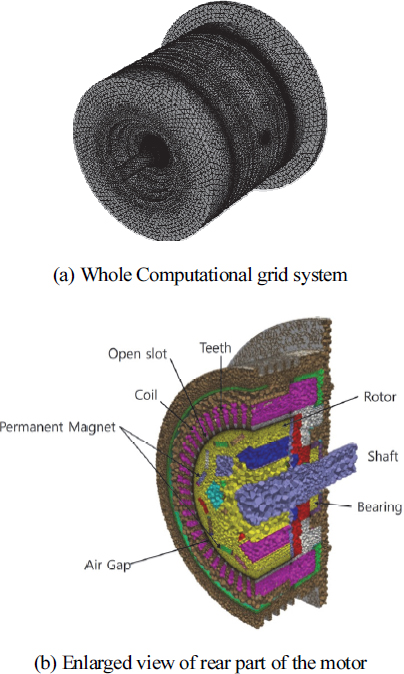
Fig. 3에 본 연구에서 사용된 계산격자를 나타내었다. 총 36,245,590개의 다면체격자를 사용하였으며 Fig. 3(b)은 중앙단면 이후의 모터의 후방 부분의 격자구성을 나타낸 것이다. 그림에서 볼 수 있듯이, 화전자, 고정자, 영구자석, 샤프트, 내부공기, 오일, 외부하우징, 공기간극, 슬롯, 코일 등을 매우 상세히 격자로 표현하였다.

Fig. 3

Computational grid system

2.4 해석 및 경계조건

본 연구의 경계조건은 Fig. 1에서 볼 수 있듯이, 1개의 입구를 통하여 0.168 kg/s(12 liter/min)으로 20 ^oC 온도의 오일이 일정한 유량으로 유입되고 있으며 오일의 부피비(α)는 0.33으로 설정하였다. 2개의 출구는 대기압으로 설정하였다. 모터의 외기온도는 26.85 ^oC이며 하우징표면과 대기온도와의 열전달을 계산하기 위한 대류열전달 수는 모터를 원통으로 고려하여 아래의 수평 원통 형상에 대한 Nusselt수 관계식¹²⁾을 이용하였다. 초기조건으로는 전체 모터가 26.85 ^oC 완전 균열상태로 가정하였다. 또한 영구자석들은 회전자에 완전히 압착되었다고 가정하여 접촉열저항은 고려하지 않았다.

본 연구에서는 오일의 유동을 비정상 3차원 비압축성 난류유동으로 고려하였으며 각 지배방정식의 대류항차분은 2차정도를 지닌 상류차분법을 적용하였다. 난류의 영향을 고려하기 위하여 SST K-ω모델을 사용하였다. 본 연구에서는 고체영역과 유체영역을 공역열전달(Conjugate heat transfer)로 고려하여 동시에 계산하였다.

또한 해석에 사용된 주요 수치제어 및 입력조건들은 Table 2에 정리되어있다.

Table 2

Summary of numerical controls

본 연구에서는 Intel Xeon E5-2690@2.6 GHz에서 120 코어를 사용하여 계산하였으며 경우당 254시간의 계산시간이 소요되었다.

3.1 운전조건에 따른 모터 내부 냉각특성

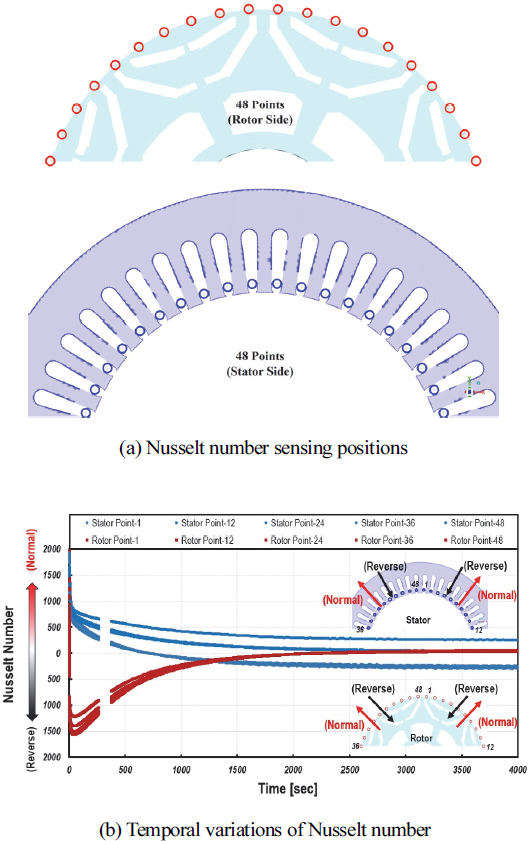
본 연구에서는 2가지 회전속도에 대하여 대상모터의 오일냉각 성능을 상세히 고찰하였다. 비정상상태의 계산이므로 시간경과에 따른 모터 대표 열전달 특성을 분석하기 위하여 Fig. 4(a)와 같이 회전자의 축방향 중앙부위의 개방 슬롯(파란색) 및 회전자 표면(빨간색) 위치에서 횡방향으로 각각 48곳의 Nusselt number를 시간에 대하여 나타내었다. 이때 모터의 회전속도는 3,800 RPM이다. 그림에서 볼 수 있듯이, 회전자의 회전에 따라 열발생량이 점차 증가하여 영구자석 및 회전자의 온도가 점차 상승하기 시작하며 계산 시작 후 2,000초에 들어서 냉각에 의하여 온도상승이 감소하기 시작하는 열전달특성을 알 수 있다. 즉, 초기 로터의 온도는 주변온도 보다 낮기 때문에 로터로 열이 흡수되고, 이후 로터의 온도가 상승한 이후에는 로터의 열이 공기간극으로 전달되고 있으며 개방슬롯의 경우는 이와 반대되는 경향을 보이고 있다. 그러나 4,000초 이후에는 Nu수의 시간에 따른 변화가 거의 없이 정상상태에 도달하는 것을 알 수 있다. 이는 부하에 의한 발열과 오일 유입에 의한 냉각효과가 포화가 이르는 시간을 의미하므로 이후의 모든 경우의 비교는 4,000초의 결과를 이용하였다.

Fig. 4

Transient heat transfer in motor

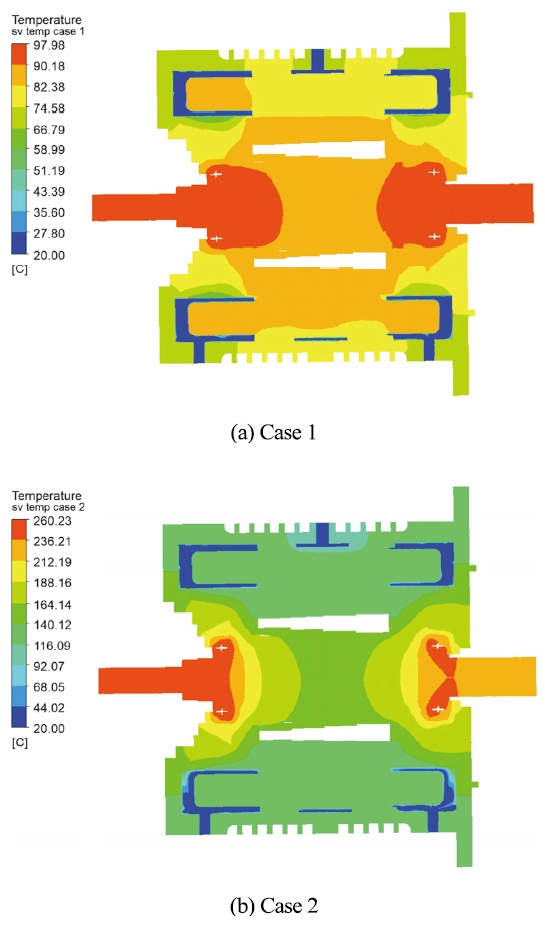
아래 Fig. 5는 2가지 회전속도에 따른 모터 내부의 온도분포를 중앙단면에서 나타낸 것이다. Case 1에서의 온도 산출결과, 최대온도는 베어링부에서 나타났으며 97.89 ^oC였다. Case 2 역시 베어링부에서 최대온도분포가 형성되었으며 이때 온도는 260.23 ^oC였다. 2개의 냉각유의 유출구에서의 온도는 Case 1, 2에서의 앞쪽 유출구에서 각각 22.5 ^oC, 32.2 ^oC였다. 뒤쪽 유출구에서는 각각 22.7 ^oC, 35.3 ^oC였다.

Fig. 5

Temperature distribution at mid-section

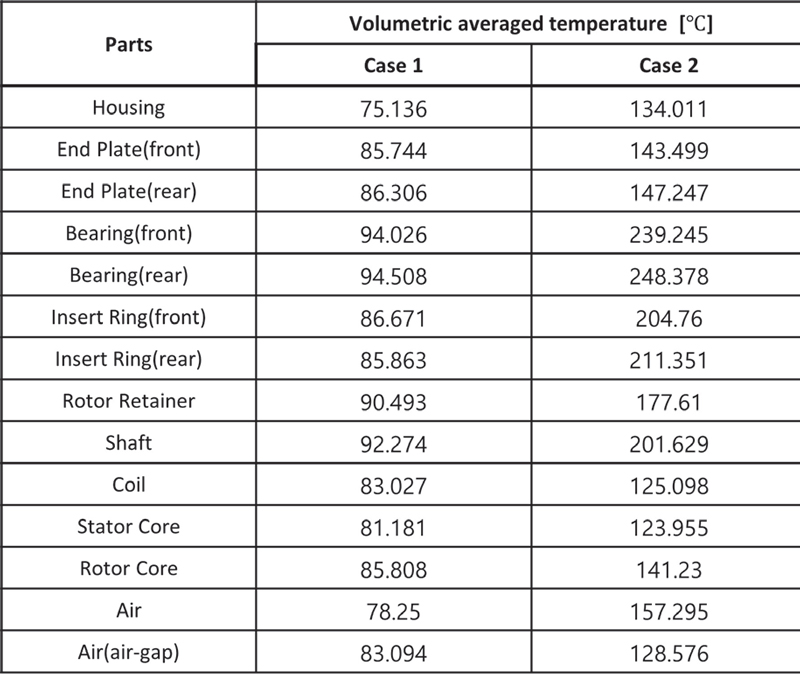
Table 3에 모터 내 주요부품들에 대한 체적 평균된 온도를 나타내었다. 그 결과, Case 1에서는 최대 온도는 94.5 ^oC이며 베어링에서 발생했다. Case 2에서도 역시 베어링이었으며 약 248.5 ^oC로 산출되었다. 최적화된 정격속도인 경우보다 최대 속도점에서는 베어링의 온도는 약 2.6개 증가함을 알 수 있다. 모터 성능에 큰 영향을 미치는 코일의 온도는 Case 1에서 약 83 ^oC, Case 2에서는 약 125 ^oC로 계산되었다.

Table 3

Volumetric ave. temperature at each parts

Table 4

Volumetric Averaged temperature at each magnets

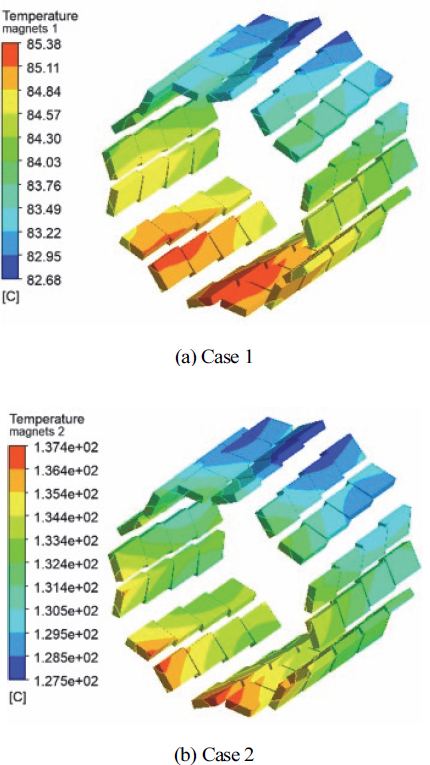
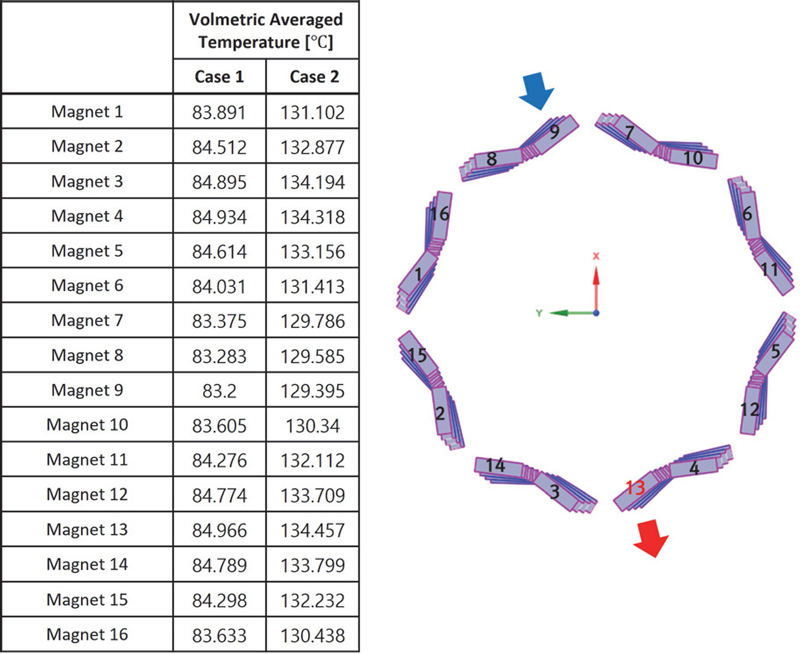
운전 중 온도상승에 의하여 모터의 효율이 저하하는 주요원인은 회전자 내에 삽입되어있는 영구자석의 온도상승에 따른 감자이다.^13,14) 따라서 아래 Table 3에 회전자에 삽입되어있는 영구자석을 숫자로 표시하여 체적 평균된 온도를 정리하여 나타냈다. 오른쪽의 그림에 각 영구자석의 조각들에 번호를 부여하여 나타내었다. 영구자석들에 대한 체적평균온도 산출결과, Case 1에 비해 Case 2는 약 1.6배 상승된 온도가 분포함을 알 수 있다. 또한 최대 온도는 Case 1, 2 동일하게 13번 영구자석에서 발생하고 있으며, 각각 84.97 ^oC, 134.46 ^oC으로 나타났다. 이유는 13번 영구자석은 냉각 오일의 출구부분에 자리잡고 있기 때문에 유입된 냉각 오일이 출구부까지 충분히 냉각시키지 못하는 것으로 판단된다.

Fig. 6에 영구자석들의 온도분포를 2가지 운전조건에 대하여 나타냈다. 2가지 경우 모두 눈에 띄는 특이점은 출구근처에서 냉각효과가 두드러지게 떨어진다는 점이다. 이는 1개의 유입부로부터 중력에 의해 아래쪽으로 유량배분이 되는데 이때 아래쪽은 냉각유의 유량이 작아지기 때문으로 생각되어진다. 따라서 향후 유로면적을 위치에 따라 가변적으로 변화시켜서 균일한 유량배분을 유도해야 할 것으로 생각되어진다.

Fig. 6

Temperature distribution within permanent magnets

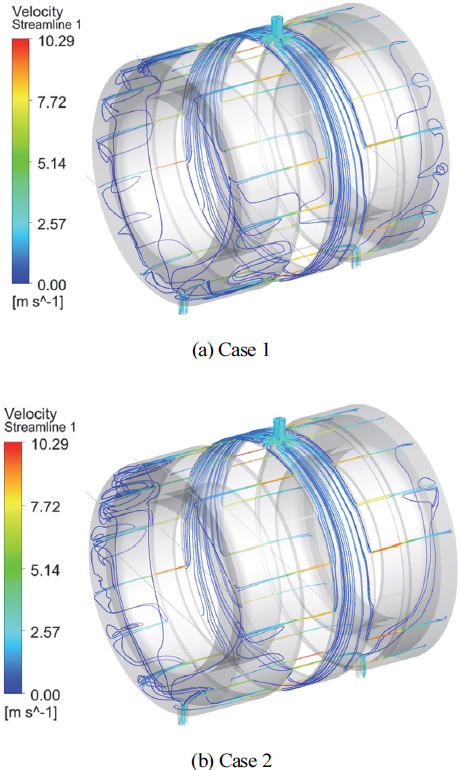
Fig. 7에 Case 1의 경우의 유입부로 들어오는 오일입자의 유적선을 속도와 함께 나타내었다. 유입부로 들어온 오일은 중앙부 유로를 타고 아래쪽으로 흐르면서 전후 끝단으로 16개의 미세유로를 통하여 냉각유를 전달한다. 미세유로 내 오일의 속도는 환형 및 축방향 위치에 따라 다름을 알 수 있고, 최대속도인 Case 2의 경우는 유로가 있는 고정자의 온도가 Case 1보다 약 1.5배 높아 점도가 낮아져 보다 높은 미세유로 내 속도분포를 확인할 수 있다.

Fig. 7

Particle streaklines for two different speed

3.2 공기 간극에서의 열유동 특성

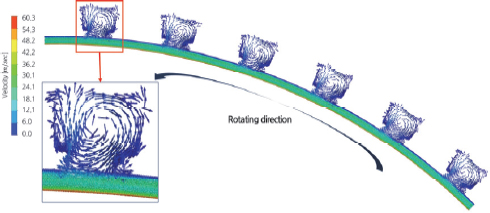
회전자와 고정자 사이의 공기간극 특성을 정확하게 분석하는 것은 매우 어려운 작업이다. 본 연구에서는 그동안 시도해왔던 실험적이고 경험적인 등가모델을 쓰지않고 직접 격자를 회전시키는 MRF방법을 사용하였다. Fig. 8에 Case 1에서의 로터가 회전함에 따라 공기간극과 고정자의 개방슬롯에서의 유동패턴을 나타내었다.

Fig. 8

Recirculating flows in open slots

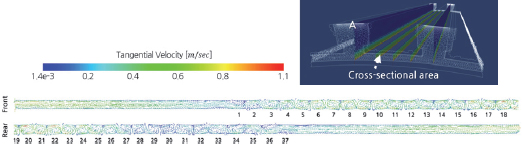
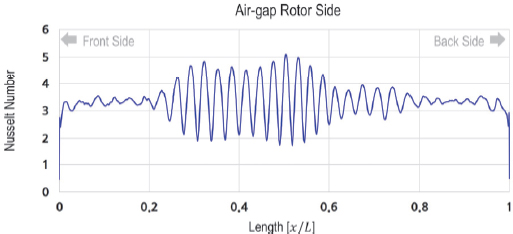
그림에서 볼 수 있듯이, 회전자의 빠른 회전에 의하여 고정자 개방슬롯에서 한 개의 강한 재순환영역이 존재함을 확인할 수 있다. 이러한 유동은 코일과 슬롯에서의 열전달을 촉진할 수 있는 긍정적인 효과로 생각되어진다. Fig. 9에는 슬롯의 치(Teeth)와 치 사이의 중앙 종단면에서의 공기간극 내의 유동특성을 나타내었다. 냉각유유입구를 기준으로 상류와 하류로 나누어 나타내었다. 그림에서 볼 수 있듯이, 공기간극으로 유체의 유입되면서 점성과 환형표면의 회전에 의한 불안정성으로 인하여 일정한 발달영역을 지나면서 중간부위부터 테일러 와류들이 확인된다. 와류들의 회전방향은 서로반대이며 총 37개의 테일러 와류들을 확인할 수 있다. 이러한 와류들은 회전자 표면에서의 열전달을 증가시켜 냉각효율을 향상시킨다. 회전자의 회전에 의한 열전달촉진을 확인하기 위해서 같은 단면위치에서 회전자측의 표면에서의 Nu수 분포를 Fig. 10에 나타내었다. 그림으로부터 확인할 수 있듯이, 점성력과 회전력에 의한 테일러 와류의 발생은 유입부로부터 20 %, 출구로부터 20 % 위치를 제외한 영역에서 발생함을 알 수 있다. 테일러 와류가 존재하는 영역에서는 매우 불규칙하고 높은 Nu수가 확인할 수 있다. 와류가 존재하지 않는 영역에 비해 약 1.5배 높은 Nu수가 확인된다. 이러한 테일러와류는 회전속도와 공기간극과 회전자와의 크기에 따라 변화하므로 최대한 발달영역을 줄이고 강한 와류가 형성할 수 있도록 향후 많은 연구가 필요할 것으로 생각된다.

Fig. 9

Taylor vortices at air-gap between stator and rotor

Fig. 10

Axial distribution of Nusselt number on the surface of rotor

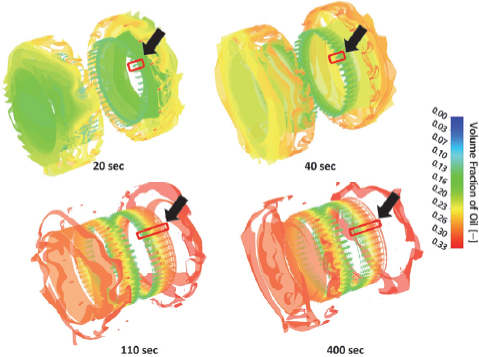
Fig. 11에 냉각오일의 체적분율 분포를 등고선으로 시간에 따라 나타내었다. 끝단부에서 오일의 분포들이 로터의 회전에 강하게 영향을 받고 있음을 볼 수 있다. 시간이 경과함에 따라 미세유로를 지나 전자코일 끝단부분으로 드리핑되는 오일량이 증가하고 있음을 볼 수 있으며 이 중 일부가 20초 이후부터 점차 공기간극으로 유입되기 시작하고 있으며 400초까지 공기간극 내 오일의 침투유량이 증가하고 있음을 볼 수 있다. 오일 침투가 발생하는 영역을 검정색 화살표로 나타내었다. 이러한 공기간극으로 오일의 유입은 냉각 성능을 떨어뜨릴 수 있으므로 향후 이에 대한 집중적인 수치적 연구가 필요할 것으로 사료된다.

Fig. 11

Temporal variation of iso-contours of oil phase volume fraction

3.3 냉각유량의 변화에 따른 냉각특성

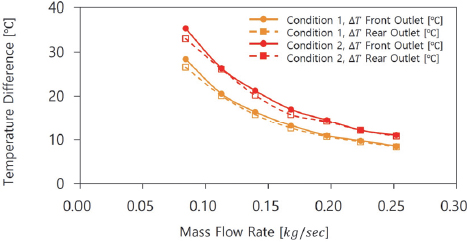
냉각오일 유량의 변화에 따른 2가지 운전조건(Condition 1=3,800 rpm, Condition 2=9,000 rpm)에서의 냉각특성을 알아보기 위하여 유입유량을 0.084 ~ 0.252 kg/s로 변화시켜가며 2가지 운전조건에 대하여 냉각특성을 분석하였다. Fig. 12에서는 작동 조건별 공급 유량 변화에 따른 출구와 입구에서의 온도차이를 나타내었다. 출구에서의 최대온도상승은 공급유량이 0.084 kg/s일 때 약 27.15 ^oC로 계산되었으며 유량 증가에 따라 출구에서의 온도 상승값은 비선형적으로 감소하였다. 유입유량이 0.2 kg/s 이상되면 유량증가에 따른 출구 온도하강 폭이 급격하게 떨어짐을 볼 수 있다.

Fig. 12

Difference of oil temperature between inlet and oulet

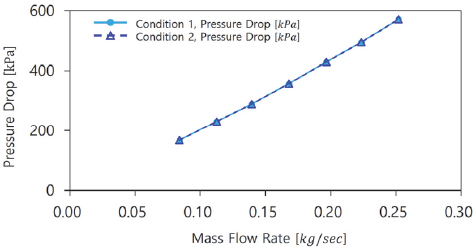
Fig. 13에 작동조건별, 공급 냉각유량 변화에 따른 입구와 출구에서의 감력강하를 나타내었다. 유량이 증가함에 따라 압력강하는 선형적으로 증가하고 있음을 볼 수 있다. 또한 압력강하는 운전조건에 무관하게 나타나고 있는데 이는 본 연구에서 작동유체의 물성치를 온도에 종속적으로 고려하지 않고 상수로 적용하였기 때문으로 생각되어진다.

Fig. 13

Pressure drop between inlet and outlet for various oil mass flow rate

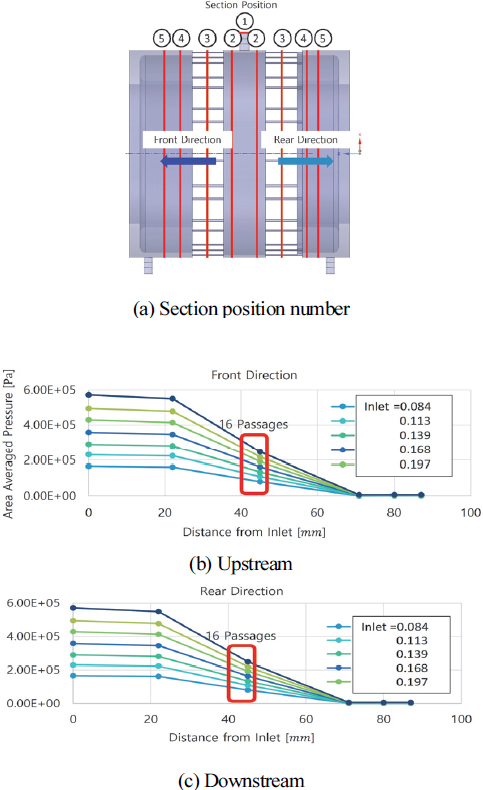
Fig. 14에는 3,800 rpm의 운전조건에서 냉각유의 흐름방향에 대하여 전면 및 후면부로의 길이방향 유로단면 5곳에서의 압력을 나타내었다.

Fig. 14

Cross-area averaged pressure in axial direction

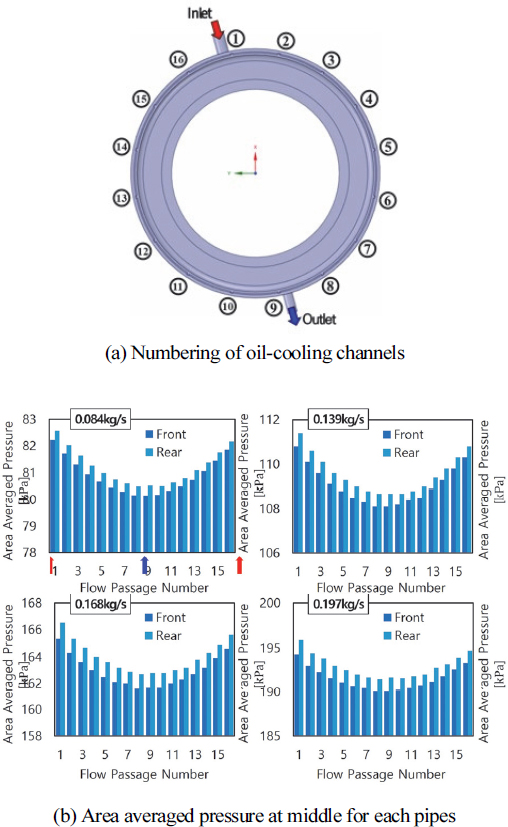
결과로부터 알 수 있듯이, 대부분의 압력강하는 16개의 미세유로를 통과하면서 발생하고 유입유량이 증가할수록 압력강하 폭은 증가함을 알 수 있다. 상류와 하류로의 유동방향에 따라 축방향 압력강하 형상은 동일함을 알 수 있다. 가장 압력강하가 큰 미세유로 내에서의 압력분포를 보다 상세히 알아보기 위하여 16개의 미세유로 전체 각각의 중앙단면에서 평균압력을 오일유량의 변화에 대하여 Fig. 15에 나타내었다.

Fig. 15

Comparison of pressure inside micro channels for various oil mass flow rates

계산결과로부터 알 수 있듯이, 공급유량에 관계없이 유입구 근처인 미세유로(1,16번)의 관내 내부압력이 가장 높게 계산되었으며 또한 출구 근처의 미세유로관(8,9)의 관내 압력이 가장 낮게 분포하고 있음을 확인할 수 있다. 이는 유입구 근처의 미세유로관 일수록 많은 유입유량이 흐르고, 출구근처의 관으로의 유량이 작기 때문이다. 따라서 이러한 미세유로의 유량감소는 Fig. 6의 결과와 같이 영구자석의 온도를 국부적으로 상승시킬 수 있으므로 안정적인 성능확보를 위하여 향후 각 미세유로로의 균일한 유량배분을 위한 유로의 개수와 형상 최적화를 연구할 계획이다. 그리고 오일 유량이 증가할수록 상류 대비 하류의 압력이 점차 높게 형성되어 있음을 알 수 있는데, 이는 유입부에서 하강하는 오일의 유동이 관벽과 부딪히며 비대칭적 재순환유동이 형성되기 때문이며 유입유량이 증가할수록 넓고 비대칭이 심화된 재순환 영역이 형성되기 때문이다.