초안전 주행플랫폼을 위한 해석적 중복 기반 가상센서 설계

1. 서 론

최근 자동차 제조사 및 IT 기업들이 자율주행 자동차 상용화에 박차를 가하면서 전체적인 자율주행 자동차 시장 규모가 점차 확대되고 있다. 이에 따라 자율주행에 대한 기대감 또한 더욱 커지고 있지만 자율주행 시스템 고장 및 오작동에 의한 사고가 종종 발생하여 안전성에 대한 의심 또한 지속되고 있다.

현재 레벨 3 자율주행 시스템은 시스템 고장에 의한 위험한 상황이 발생했을 때 운전자에게 수동 운전 모드로 전환하도록 요청한다. 만약 운전자가 제어권을 이양받지 않는다면 자율주행 자동차는 위험 최소화 운행 및 비상 운행을 수행해야 한다. 따라서 자율주행 시스템의 신뢰성을 보다 개선하기 위해서는 자율주행에 활용되는 중요 센서 및 액추에이터들의 고장 상황에서도 다른 도메인의 정상적인 센서 혹은 액추에이터들로 폐루프 제어 시스템을 재설계하여 최소한 안전한 상태까지 자율주행을 지속할 수 있는 초안전 주행플랫폼 개발이 요구된다.¹⁾

본 연구에서는 요레이트 센서, 횡가속도 센서, 전륜 조향각 센서, 총 3가지 센서 고장을 대비하여 타 샤시 도메인의 다른 센서 신호들, 센서 신호 간 Kinematics, 그리고 차량 횡 동역학모델을 활용하여 해당 고장 센서의 대체 신호를 출력하는 가상센서를 개발하였다.

일반적으로 센서의 고장 진단 및 고장 대응 방법으로는 크게 하드웨어 중복(Hardware redundancy)과 해석적 중복(Analytical redundancy)^2-6)으로 나뉜다.

하드웨어적 중복은 동일한 센서를 추가 설치하는 방법으로 직접적인 해결책을 제시하지만, 차량의 원가 상승 및 패키지 상의 문제를 초래하는 단점이 있다. 다른 방법인 해석적 중복은 대체 대상이 되는 센서와 가용할 수 있는 다른 센서들 사이의 기구학적 관계, 혹은 동역학 관계를 이용하여 해당 센서 신호를 대체할 수 있는 추정 모델을 만드는 방법이다. 추가적인 센서를 설치할 필요가 없기 때문에 원가를 상승시키지 않으면서 어느 정도의 예측 성능 목표를 달성할 수 있다.

이러한 측면 때문에 차량 제어 관련된 기존의 많은 연구에서 요레이트, 횡가속도, 전륜 조향각 등 센서의 해석적 중복 모델을 이용하여 해당 센서들의 고장을 진단하였다.^3-6) 해석적 중복 모델들은 특정 주행 조건에서는 원 센서 신호와 일치도가 높은 경향을 보이지만, 결국 근사 신호이기 때문에 오차가 발생하는 주행 조건이 존재한다. 만약, 특정 추정 모델에서 고려하지 않은 여러 요인이 극단적으로 커져 모델에 영향을 끼치게 된다면 해석적 중복 모델은 목표 신호와 전혀 다른 값을 출력하게 될 수도 있다. 따라서, 본 연구에서는 다양한 도메인의 센서들을 활용한 복수의 해석적 중복 모델들을 도출하고 이들의 주행 상황 별 적절한 조합을 통해 상호 보완하도록 하여 가상센서의 정확도를 개선하고자 한다.

본 연구에서는 차량 거동 제어 관점에서 차량의 거동을 측정하는 대표 센서인 요레이트, 횡가속도 센서와 차량 선회에 있어 가장 중요한 입력인 전륜 조향각 센서, 총 3개의 가상센서를 설계하였으며, 각각 두 가지 설계 방법론으로 개발하였다. 첫 번째 방식은 전문가의 샤시 도메인 지식을 기반으로 중복 모델의 오차 요인을 분석하여 주행 상황에 따른 모델 별 신뢰도를 결정한다. 이 신뢰도를 바탕으로 상황에 따른 모델 별 가중치를 적용하고 해석적 중복 모델을 조합하여 가상센서 모델을 구성한다. 두 번째 방법은 주행 데이터를 기반으로 기계 학습을 통해 해석적 중복 모델과 실제 신호 사이의 관계를 학습시키는 방법이다. 이러한 두 가지 방법을 통해 센서가 고장 난 상황에서도 제안된 가상센서를 통해 효과적인 센서 신호 대체가 가능하도록 하였다.

본 논문의 구조는 2장에서 요레이트, 횡가속도, 전륜 조향각에 대한 해석적 중복 모델들의 도출 과정을 기술하고, 3장에서는 제안된 해석적 중복 모델을 기반으로 차량 도메인 지식과 머신 러닝을 각각 적용한 가상센서 설계에 대해 다룬다. 4장에서는 CARSIM SW를 활용하여 제안된 가상센서에 의한 고장 대체 신호들의 예측 정확도를 검증하고 5장에서 결론을 맺는다.

2. 해석적 중복 모델

2.1 요레이트 중복 모델

본 논문에서는 요레이트 가상센서 개발을 위해 네 가지 해석적 중복 모델을 구성하였다. 각 해석적 중복 모델은 Table 1에 정리하여 나타냈다. 각 모델은 요레이트 신호를 활용하지 않고 타 센서 신호 및 그들 간의 기구학/동역학 관계들을 활용해서 생성된 요레이트 중복 모델들이다.

Table 1

Yaw rate analytic redundant models

첫 번째 중복 모델(γ_M1)은 차량 전륜의 좌/우 휠속 차이를 이용하여 요레이트를 추정한다. 선행 문헌들에 제안된 모델에서는 양륜의 조향각이 평행하다는 가정하에 식을 전개하지만, 실제 차의 전륜은 직진 안정성을 위해 부여된 토우 각(δ_f,toe)에 의해 좌/우 서로 다른 각도로 배치되어 있다.⁷⁾ 이에 따라 기존 방법에 의해 추정되는 요레이트와 실제 요레이트 사이에 오차가 발생한다. 모든 주행 상황을 고려해서 정확도 개선을 위해 이 좌/우 토우 각을 보상하기 위해선 초기 설정 토각 뿐 만 아니라 횡속도도 필요하다. 한편 횡속도를 추정하기 위해서는 요레이트와 횡가속도 신호가 필요하지만, 본 연구는 특정 센서들을 대체하는 것이 목적이므로 특정 센서를 다시 사용해서 별도의 추정기를 사용하는 것에 제약이 있다. 그렇기에 조향각 입력에 의한 Bicycle model에서 출력되는 횡슬립각을 이용한 횡 속도를 추정한다.

$\[ \begin{array}{c}{V}_{wheel.fl }=\left(V_x-\frac{T_f}{2}\gamma \right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\delta }_{fl}\right)+\left(V_y+l_f\gamma \right)\mathrm{s}\mathrm{i}\mathrm{n}\left({\delta }_{fl}\right)\hfill \\ V_{wheel.fr }=\left(V_x+\frac{T_f}{2}\gamma \right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\delta }_{fr}\right)+\left(V_y+l_f\gamma \right)\mathrm{s}\mathrm{i}\mathrm{n}\left({\delta }_{fr}\right)\hfill \end{array} \]$

(1)

$\[ \begin{array}{c}{V}_{wheel.rl }=\left(V_x-\frac{T_r}{2}\gamma \right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\delta }_{rl}\right)+\left(V_y-l_r\gamma \right)\mathrm{s}\mathrm{i}\mathrm{n}\left({\delta }_{rl}\right)\hfill \\ V_{wheel.rr }=\left(V_x+\frac{T_r}{2}\gamma \right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\delta }_{rr}\right)+\left(V_y-l_r\gamma \right)\mathrm{s}\mathrm{i}\mathrm{n}\left({\delta }_{rr}\right)\hfill \end{array} \]$

(2)

$\[ \begin{array}{cc}{\delta }_{fl}={\delta }_f-{\delta }_{f, toe }\hfill & {\delta }_{fr}={\delta }_f+{\delta }_{f, toe }\hfill \\ {\delta }_{rl}={\delta }_r-{\delta }_{r, toe }\hfill & {\delta }_{rr}={\delta }_r+{\delta }_{r, toe }\hfill \end{array} \]$

(3)

$\[ V_{x,i}=\left\{\begin{array}{c}{V}_{wheel ,i}\left(1-{\kappa }_i\right) for driving \hfill \\ V_{wheel ,i}/\left(1-{\kappa }_i\right) for braking \hfill \end{array}, i=fl,fr,rl,rr\right. \]$

(4)

$\[ \begin{array}{c}\left[\begin{array}{c}\dot{\beta }\\ \dot{\gamma }\end{array}\right]=A\left[\begin{array}{c}\beta \\ \gamma \end{array}\right]+B\left[\begin{array}{c}{\delta }_f\\ {\delta }_r\end{array}\right]\hfill \\ A=\left[\begin{array}{ccc}-\frac{C_f+C_r}{m{V}_x}& & -\frac{l_f{C}_f-l_r{C}_r}{m{V}_x^2}-1\\ -\frac{l_f{C}_f-l_r{C}_r}{I_z}& & -\frac{C_f{l}_f^2+C_r{l}_r^2}{I_z{V}_x}\end{array}\right]B=\left[\begin{array}{cc}\frac{{\mathrm{C}}_{\mathrm{f}}}{m{V}_x}& \frac{{\mathrm{C}}_{\mathrm{r}}}{m{V}_x}\\ \frac{{\mathrm{C}}_{\mathrm{f}}{l}_f}{I_Z}& -\frac{{\mathrm{C}}_{\mathrm{r}}{l}_r}{I_Z}\end{array}\right]\hfill \end{array} \]$

(5)

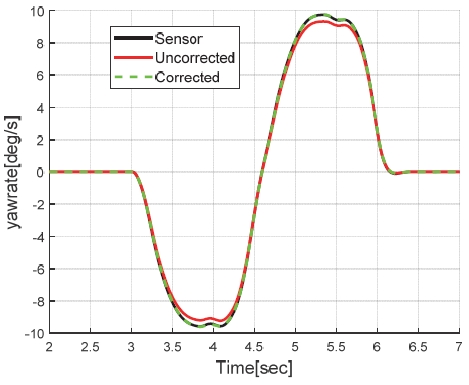
식 (1)에서와 같이 전륜의 좌/우 휠속을 정의한 다음 그 관계를 이용하여 첫 번째 요레이트 추정 모델(γ_M1)을 도출한다. 후륜을 이용하는 두 번째 중복 모델(γ_M2)에서도 토우 각의 영향은 동일하게 나타난다. 차속과 휠속의 관계식 (2)을 이용하여 두 번째 요레이트 추정 모델을 도출한다. 토우 각이 고려된 전 후륜 조향각은 식 (3)과 같다. Fig. 1에 토우 각의 영향을 보정해준 결과를 나타냈다. 후륜 휠속을 이용한 요레이트 추정 결과로, 적용된 초기 토우 각은 0.3 deg이다.

Fig. 1

Yaw rate redundant model2 w/ and w/o considering toe angle

차량에 설치된 휠속 센서는 차륜의 회전속도를 측정한다. 하지만 노면의 상태와 샤프트 토크, 수직 하중 등 여러 요인에 의해 휠 미끄러짐이 발생하고 차륜의 회전 속도로 도출된 휠속과 실제 차륜 중심의 종속도는 일치하지 않는다. 이 차이로 인하여 슬립이 큰 경우 중복 모델에서 추정한 요레이트와 실제 요레이트 사이에 오차 발생이 가능하다.

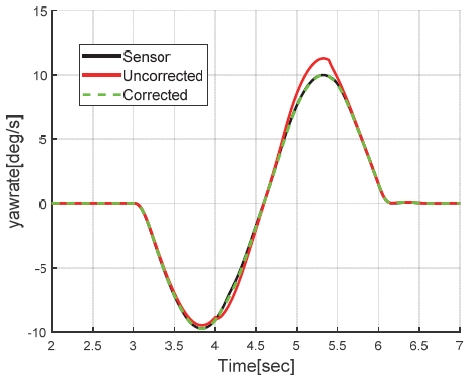
본 연구에서는 고 마찰 노면에서 종 슬립율(κ:Slip ratio)과 종방향 힘 F_x, 수직방향 힘 F_z 사이의 관계를 포함하는 타이어 특성맵을 사전에 잘 알고 있고, 현재의 F_x와 F_z는 충분히 정확히 추정할 수 있다고 가정하여 기지의 타이어 특성맵, F_x, F_z 정보를 기반으로 종슬립율을 추정한 후 식 (4)에서 나타난 관계를 이용하여 휠 슬립을 보상한다.^8,9) 또한 차량이 구동할 때와 제동할 때의 슬립율의 정의가 다르기 때문에 구별하여 적용하였다. Fig. 2에는 후륜 휠속을 이용한 요레이트 추정 모델에 슬립율을 보정해준 결과를 나타냈다. 검증에 사용된 시나리오는 SLC(Single Lane Change) 중 감속하는 상황이다.

Fig. 2

Yaw rate redundant model2 considering slip ratio

세 번째 중복 모델(γ_M3)은 물리적 차량 횡방향 모델인 식 (5)의 Bicycle model을 활용한다. 선형 타이어 횡력 모델을 기반으로 한 Bicycle model은 전륜 및 후륜 조향각과 차속을 입력으로 받아 요레이트와 횡슬립각을 출력하며 모델에서 출력되는 요레이트를 사용한다.

본 연구에서 고려된 초안전 주행 플랫폼은 전륜 조향 시스템 고장을 고려하여 후륜 조향 시스템도 장착이 되어있어 후륜 조향각도 입력 신호로 고려하였다. Bicycle 모델의 정확도는 모델에 사용되는 각종 차량 파라미터 정확도에 의존하며 특히 주행 중 변화 가능한 코너링 강성의 정확도에 크게 의존한다. 제안 연구에서는 실제 타이어의 비선형성을 고려하기 위해 코너링 강성을 횡가속도에 대한 룩업 테이블로 가변화 하여 적용하여 모델 오차를 최소화하였다.

네 번째 중복 모델(γ_M4)은 정상상태 선회 시의 요레이트, 차속, 횡가속도 관계식을 활용하여 설계하였다. 횡가속도 $$ a_y={\dot{v}}_y+\gamma V_x$$는 기구학적으로 횡속도 미분치를 무시하였을 때, 요레이트와 차속의 곱으로 구할 수 있다. 이 정상상태 선회 관계를 이용하여 횡가속도 센서의 값을 차속으로 나누는 방식으로 요레이트를 추정한다. 이 모델의 정확도는 전체 횡가속도에서 횡속도 미분치의 비율에 의존하며 정상상태 선회일수록 그 비율이 낮아져 정확도가 높아진다.

2.2 횡가속도 중복 모델

횡가속도는 2.1절 네 번째 모델에서 언급하였듯, 횡슬립 각속도를 무시한다면 요레이트와 차속의 곱으로 표현할 수 있다. 이를 이용하여 횡가속도 센서 신호에 대한 각 중복 모델은 Table 2에 정리하여 나타냈다.

Table 2

Analytic redundant models for lateral acceleration

횡가속도를 추정하는 첫 번째(a_y.M1)와 두 번째 모델(a_y.M2)은 앞서 제안된 γ_M1, γ_M2에 차속을 곱하여 횡가속도를 추정한다. 이들 모델의 정확도는 2.1절에서 제시된 γ_M1, γ_M2 모델의 정확도와 선회 중 발생하는 횡가속도에서 횡슬립 각속도의 비율에 의존한다.

세 번째 모델(a_y.M3)은 Bicycle model에서 출력되는 횡슬립 각속도와 요레이트를 이용한다. 횡가속도는 Bicycle model에서 출력된 요레이트와 횡슬립 각속도를 더한 값에 차속을 곱하여 추정한다. 따라서 세 번째 모델의 정확도도 일종의 물리적 모델인 Bicycle model의 정확도에 의존한다.

네 번째 모델(a_y.M4)은 요레이트 센서값을 이용하여 횡가속도를 추정한다. 횡슬립 각속도를 무시하였을 때, 요레이트 센서값에 차속을 곱하여 횡가속도를 추정한다.

2.3 전륜 조향각 중복 모델

전륜 조향각은 동역학 측면에서 보면 현재 나타나는 차량 거동의 원인이 되는 과거의 입력 물리량이기 때문에 실시간 추정이 어려운 측면이 있다. 하지만 정상상태 Bicycle model을 활용하여 과도 상태를 무시한다면, 요레이트를 이용하여 전륜 조향각을 특정하는 것이 가능하다. 하지만 실제 차량은 조향각이 입력되면 이후에 요레이트가 반응하는 시스템이고, 이런 근본적인 문제로 인하여 추정되는 신호는 실제 전륜 조향각보다 위상이 다소 지연된 상태로 출력된다. 이러한 위상 지연으로 앞서 제시된 요레이트, 횡가속도 신호 대비 급 조타 상황에서는 가상센서의 예측 정확도가 다소 저하될 수 있으며 이는 고장 허용 제어(Fault tolerant control) 부분에서 고려가 필요하다.

$\[ {\delta }_r=K\left(V_x\right){\delta }_f \]$

(6)

$\[ {\gamma }_{ss}=f\left({\delta }_f\right)=\frac{V_x\left(1-K\left(V_x\right)\right)}{L+\frac{C_r{l}_r-C_f{l}_f}{C_f{C}_{r}L}m{V}_x^2}{\delta }_f \]$

(7)

$\[ {\delta }_f=f^{-1}\left({\gamma }_{ss}\right) \]$

(8)

식 (6)의 K(V_x)는 본 초안전 주행 플랫폼의 후륜 조향 시스템에서 후륜 조향각을 결정하는 전륜 조향각에 대한 차속 별 게인이다. 식 (7)에서는 정상상태 Bicycle model을 이용하여 전륜 조향각을 산출 가능하다는 것을 나타낸다.

본 연구에서는 정상상태 횡동역학 모델과 후륜 조향각 정보를 이용하여 4가지 방식의 전륜 조향각 추정 모델을 구성하고 각 중복 모델은 Table 3에 정리하여 나타낸다.

Table 3

Analytic redundant models for front steer angle

전륜 조향각 추정의 첫 번째(δ_f.M1)와 두 번째 중복 모델(δ_f.M2)은, 전/후륜의 휠속을 이용하여 요레이트를 추정한 다음 식 (8)에 대입하여 전륜 조향각을 추정한다. 전륜 조향 센서를 대체하기 위한 모델이기 때문에 식 (1), 식 (2)를 이용한 요레이트 추정 방식은 제약이 있기에 단순한 추정 모델을 이용한다.

세 번째 모델(δ_f.M3)은 요레이트 센서로부터 직접 요레이트 신호를 받은 다음 관계식에 적용하여 전륜 조향각을 추정한다.

네 번째 모델(δ_f.M4)은 γ_M4를 이용해 요레이트를 추정하고 이를 관계식에 대입해 전륜 조향각을 추정한다.

3. 가상센서 모델 개발

2장에서 제안된 해석적 중복 모델들은 각자 다른 원리에 의해 도출되었기 때문에 각각의 모델들의 정확도는 주행 상황에 따라 달라지게 된다. 따라서, 해석적 중복 모델들을 주행 상황 별 신뢰도를 고려하여 하나의 가상센서 모델의 최종 출력으로 결정이 필요하다. 본 연구에서는 이러한 중복 모델들의 가중치를 크게 두 가지 방식으로 제안한다. 하나는 도메인 전문가의 튜닝에 의해 룩업 테이블 형식으로 경험적으로 결정하는 방식이고, 다른 하나는 데이터 기반으로 머신 러닝 방법론을 적용하여 결합 가중치를 설계하였다.

3.1 도메인 지식 기반 가중치 적용 가상센서 모델

3.1.1 요레이트 가상센서 모델 개발

2장에서 설명한 바와 같이 요레이트 모델 γ_M1과 γ_M2는 각각 전륜, 후륜에서 좌/우륜의 휠속 차이를 이용하여 요레이트를 유도한다. 그러나, 좌/우 한 쪽 휠에 구동력 혹은 제동력이 발생하면 휠슬립으로 인해 요레이트 예측 모델에 필연적으로 오차가 발생한다. 따라서, 이를 보상하기 위해 F_x,F_z,κ로 구성되는 타이어 맵을 이용해 종 슬립율 κ를 보상해준다.

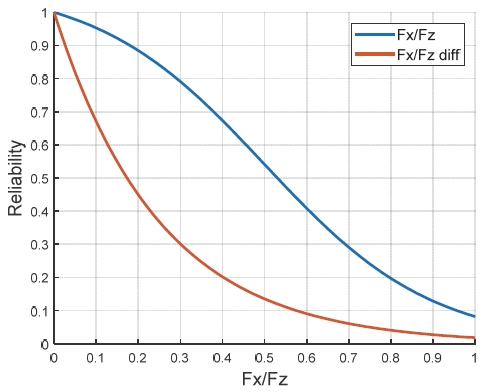
상기와 같이 슬립율을 보상하더라도, 여전히 신뢰도 측면에서 한계가 존재하며 이를 해석 모델 간 결합 시 가중치로 고려하기 위해 좌/우 특정 휠에서의 종방향 힘의 수직방향 힘 대비 비율 (F_x/F_z)을 γ_M1과 γ_M2의 신뢰도 척도로 사용한다. 좌/우 중 어느 하나가 F_x비율이 커지는 상황과 좌/우륜의 비율 차이인 $$ \left|\frac{F_{x,r}}{F_{z,r}}-\frac{F_{x,l}}{F_{z,l}}\right|$$가 커지는 상황은 독립적이므로, 산출되는 신뢰도를 서로 곱해 사용하였다. 최종 신뢰도(σ)는 식 (9)과 식 (10)에 의해 경험적으로 결정되고 적용된 신뢰도 특성맵 f_M1,f_M2과 f_M1,diff,f_M2,diff는 Fig. 3에 나타냈다. 모델 γ_M1과 γ_M2는 동일한 신뢰도 특성맵을 사용하였다.

$\[ \begin{array}{c}{\sigma }_{\gamma .model1}\hfill \\ =Min\left(f_{M1}\left(\frac{F_{x,fl}}{F_{z,fl}}\right),f_{M1}\left(\frac{F_{x,fr}}{F_{z,fr}}\right)\right)\times f_{M1,diff}\left(\frac{F_{x,fl}}{F_{z,fl}}-\frac{F_{x,fr}}{F_{z,fr}}\right)\hfill \end{array} \]$

(9)

$\[ \begin{array}{c}{\sigma }_{\gamma . model 2}\hfill \\ =Min\left(f_{M2}\left(\frac{F_{x,fl}}{F_{z,fl}}\right),f_{M2}\left(\frac{F_{x.fr}}{F_{z,fr}}\right)\right)\times f_{M2, diff }\left(\frac{F_{x.fl}}{F_{z,fl}}-\frac{F_{x,fr}}{F_{z,fr}}\right)\hfill \end{array} \]$

(10)

Fig. 3

Reliability map for yawrate model1 and model2

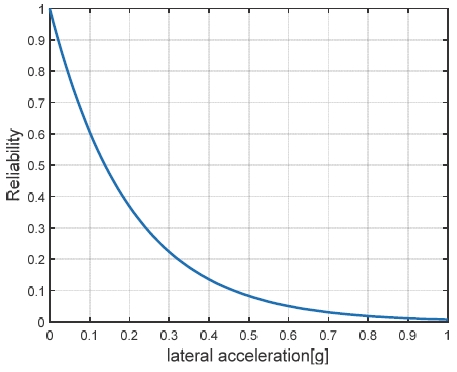
요레이트 중복 모델 γ_M3은 Bicycle model에서 출력되는 요레이트다. γ_M3의 오차는 주로 Bicycle model에 사용된 파라미터와 실제 차량 파라미터의 차이에서 야기된다. Bicycle model은 선형 타이어 모델을 가정하고 단순화한 모델이기에 마찰 한계영역에서 주행할 때 오차가 커진다. 따라서, γ_M3의 신뢰도는 횡가속도 센서 계측값과, Bicycle model에서 출력된 요레이트와 횡슬립 각속도로부터 구한 횡가속도의 차이와 관련이 있다. 그러므로 γ_M3의 신뢰도는 |a_y,sensor - a_y,model|의 크기가 커질수록 낮게 산출되도록 설계한다. 신뢰도는 식 (11)로 산출되고 결정된 신뢰도 특성맵은 Fig. 4에 나타냈다.

$\[ {\sigma }_{\gamma , model 3}=f_{\gamma .M3}\left(a_{y, sensor }-a_{y, model }\right) \]$

(11)

Fig. 4

Reliability map for yawrate model3

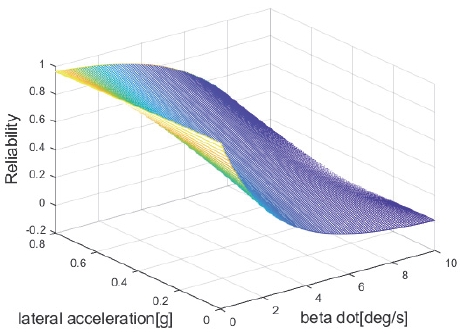
γ_M4는 횡가속도 센서를 이용하여 요레이트를 추정한 모델이다. 즉, $$ a_y={\dot{v}}_y+\gamma V_x$$ 에서 횡속도 변화량을 무시하고 산출한 모델이기 때문에 횡속도 변화량의 크기, 비율에 따라서 그 정확도가 변화한다. 따라서, γ_M4의 신뢰도는 횡슬립 각속도의 절댓값이 커질수록 낮게 산출되도록 설계하였다. 당연히 횡슬립 각속도가 오차 요인으로 작용하지만, 횡가속도와 횡슬립 각속도의 상대적 크기 또한 모델의 신뢰도에 영향을 끼친다. 이를 고려하기 위해 신뢰도 맵을 3차원으로 만들어 비율을 반영하였다. 신뢰도는 식 (12)로 산출되었고 적용된 신뢰도 특성맵은 Fig. 5에 나타냈다.

$\[ {\sigma }_{\gamma , model }=f_{\gamma .M4}\left({\dot{\beta }}_{model },a_{y, sensor }\right) \]$

(12)

Fig. 5

Reliability map for yawrate model4

3.1.2 횡가속도 가상센서 모델 개발

횡가속도 중복 모델 중 a_y.M3를 제외한 나머지 모델들은 단순히 앞서 제시된 요레이트 중복 모델에 종속도를 곱해서 구하기 때문에 횡슬립 각속도가 사용되지 않는다. 그러므로 a_y.M3를 제외한 모델들은 횡슬립 각속도가 모델의 정확도에 끼치는 영향을 추가적으로 고려하여야 한다.

a_y.M1과 a_y.M2는 양륜의 휠 속 차이를 이용해 구한 요레이트에, 종속도를 곱해서 구하기 때문에 요레이트 추정 모델과 오차의 원인 및 신뢰도 추정 방식이 동일하다.

횡가속도의 a_y.M3은 Bicycle model에서 출력되는 값을 이용하기 때문에 |γ_sensor - γ_model| 차이를 이용하여 신뢰도를 산출한다. 형태는 앞서 모델 오차로 산출한 Fig. 5와 동일하며 단지 3.1.1에서는 요레이트 대체 신호라 요레이트 신호를 사용하지 않고 신뢰도를 산출했고, 여기서는 횡가속도 대체 신호 측면에서 횡가속도 신호를 사용하지 않고 대신 요레이트 신호를 사용하는 것이 다른 점이다.

a_y.M4는 요레이트 센서를 이용하여 횡가속도를 추정한 모델이며, 오차 요인과 신뢰도 특성은 γ_M4와 동일하다.

3.1.3 전륜 조향각 가상센서 모델 개발

δ_f.M1과 δ_f.M2는 양륜의 휠 속 차이를 이용해 구한 요레이트를 횡동역학 역모델에 해당하는 식 (8)에 대입하여 구하기 때문에, 요레이트 추정 모델과 오차의 원인 및 신뢰도 추정 방식이 동일하다. 신뢰도는 식 (9), (10)로 산출되고 신뢰도 특성맵은 Fig. 3과 같다.

δ_f.M3예측에는 요레이트 센서 값을 이용한다. 전륜 조향각 추정 모델에서의 주된 오차 요인은 정상 상태 가정과 코너링 강성의 오차이다. 하지만 이는 전륜 조향각을 구하는 모든 추정 모델에 동일하게 적용되는 오차 요인이기에, δ_f.M3의 신뢰도 판별에 사용하기에는 부적절하다. 타 중복 모델 대비 δ_f.M3에 추가되는 오차 요인이 없기 때문에 δ_f.M3의 신뢰도는 식 (13)과 같이 항상 1로 주어진다.

$\[ {\sigma }_{{\delta }_f, model 3}=1 \]$

(13)

δ_f.M4는 횡가속도 센서를 이용하여 예측된 요레이트를 사용한다. 오차 요인과 신뢰도 추정 방식이 요레이트 추정 모델 γ_M4와 동일하다. 그러나 전륜 조향각 센서 대체를 위해 전륜 조향각 신호를 입력으로 활용할 수 없기 때문에 Bicycle model에서 출력되는 횡슬립 각속도를 사용할 수 없다. 이를 해결하기 위해 요레이트와 횡가속도의 Kinematic 관계를 이용하여 횡슬립 각속도를 도출하였다.

$\[ {\sigma }_{{\delta }_f, model4 }=f_{{\delta }_f.M4}\left({\dot{\beta }}_{kinematic },a_{y, sensor }\right) \]$

(14)

각 해석적 중복 모델들의 신뢰도가 정해지면, Soft-max 함수를 적용하여 해석적 중복 모델의 최종 가중치(W_i)를 구한다. 식 (15)와 같은 방법으로 가중치를 각 모델에 적용시켜 가상센서를 설계하였다. 횡가속도와 전륜 조향각 가상센서 모두 요레이트 가상센서와 같은 방식으로 설계되었다.

$\[ \begin{array}{c}{w}_{i=\mathrm{1,2},\mathrm{3,4}}=\frac{e^{{\sigma }_i}}{\sum _{i=1}^4{e}^{{\sigma }_i}}\hfill \\ {\gamma }_{weight }=w_1{\gamma }_{M1}+w_2{\gamma }_{M2}+w_3{\gamma }_{M3}+w_4{\gamma }_{M4}\hfill \end{array} \]$

(15)

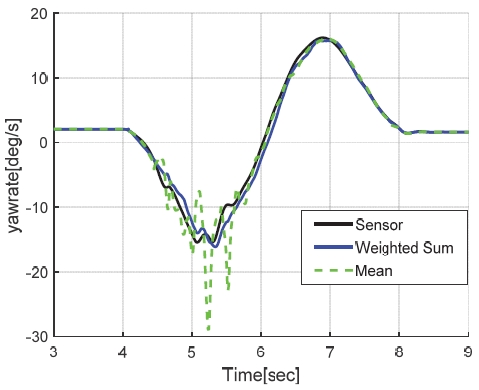
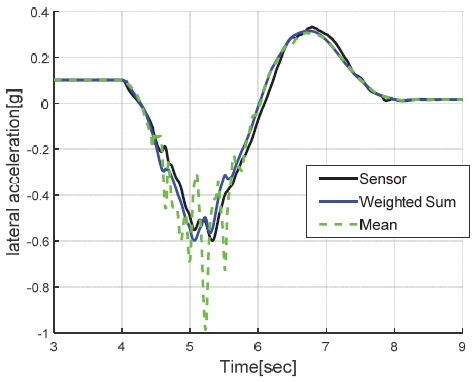
한편, 제안된 중복 모델들의 신뢰도에 근거한 결합방식이 효과적인지 파악하기 위해 단순 평균으로 결합한 방식과 가상센서 예측 정확도를 Figs. 7∼9에 비교하였다. 모두 경우에서 주행 상황 별 모델 신뢰도를 고려해서 가중치 합을 설계한 방식이 예측 정확도가 더 우수한 것을 확인할 수 있다.

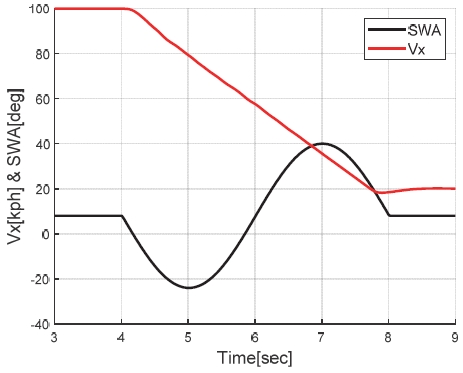
한편, 검증 시나리오는 차속 100 kph에서 20 kph로 급감속하며 선회 중 SLC를 진행하는 시나리오로 차속과 조향각을 Fig. 6에 나타냈다. 해당 시나리오는 직진 시 차선 변경보다 악의주행이며 실제 자율주행 중 고장 발생시 필요한 위험최소화운행(MRM: Minimum Risk Maneuver)에 해당하는 선회 중 갓길 이동과 같은 상황이다.

Fig. 6

Longitudinal speed and steer wheel angle for driving scenarios

해당 시나리오에서 차량이 종가속도 0.6 g 감속을 하므로, 타이어 휠 속을 이용하는 모델1, 모델2의 추정 성능은 크게 발생된 종슬립률의 영향에 의해 저하된다. 또한 요레이트와 횡가속도 추정에 종방향 힘을 고려하지 않은 Bicycle model을 사용하기 있기 때문에, 시뮬레이션 차량과의 코너링 강성 오차가 발생하여 모델3의 추정 성능이 저하되었다. 모델4는 횡슬립 각속도에 의해서 오차가 발생하지만, 다른 모델에 비해 상대적으로 정확한 추정 성능을 유지하여 최종 출력되는 Weighted sum 신호에서 가장 높은 가중치를 갖고 있다. 또한 Fig. 10에는 감속 이후 모델3의 추정 성능이 회복됨에 따라 Weighted sum 신호가 단순히 모델4를 따라가는 것이 아니라, 다른 모델의 가중치를 높여 단일 모델 추정보다 개선된 결과를 보임을 나타냈다.

Fig. 7

Prediction result of proposed yaw rate weighted sum model

Fig. 8

Prediction result of proposed lateral acceleration weighted sum model

Fig. 9

Prediction result of proposed front wheel angle weighted sum model

Fig. 10

Comparison of Model4 and weighted sum

한편 전륜 조향각 추정에는 코너링 강성의 정확성이 가장 중요한데, 본 연구에서는 횡 가속도에 대한 코너링 강성 변화만을 고려하였기 때문에 감/가속 상황에서 시뮬레이션 차량과 Bicycle model의 코너링 강성 오차가 커졌다. 이는 전륜 조향각을 추정하는 4가지 해석적 중복 모델의 정확도를 낮추었고 전륜 조향각 추정 성능에 다소 악영향을 끼쳤다고 볼 수 있다.

3.2 머신 러닝을 활용한 가상센서 모델 개발

앞서 설계된 가상센서 모델은 도메인 전문가의 경험에 의해 룩업 테이블 형식의 신뢰도 결합 방식으로 결정하는 모델이었고, 본 절에서는 순수 데이터 기반 방법으로 머신 러닝 방법론을 적용하여 획득된 해석적 중복 모델간 결합 가중치가 포함된 예측모델을 제안한다.

본 연구에서 개발하는 가상센서 예측 모델은 시계열 데이터를 기반으로 하기 때문에 이와 관련된 대표적인 신경망인 RNN(Recurrent Neural Network)을 활용하였다. RNN은 각 Hidden layer 사이의 순환 구조를 가지는 신경망으, 데이터의 시간 순서에 영향을 고려하는 신경망이다.^10,11)

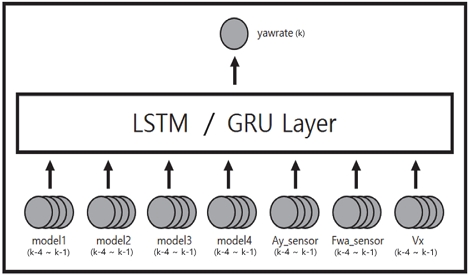
가상센서 예측 모델 학습을 위해 10초마다 주행 시나리오가 달라지는 총 40분 분량의 해석 데이터가 사용되었다. Sampling time을 10 ms로 설정하여 입력 신호당 총 240,000개의 데이터를 활용한다. 모델은 이전 4개의 시간 간격, 즉 과거 40 ms동안의 데이터로 다음 시간 간격인 10 ms 지점의 값을 추정한다. 예측 모델의 입력 신호는 앞서 제안된 해석적 중복 모델 4개의 출력신호와 대체 목표 센서신호를 제외한 다른 센서의 출력을 사용하여 총 7개의 입력신호로 이루어진다. 요레이트 예측 모델을 예로 들면 요레이트 해석적 중복 모델 4개, 횡가속도 센서, 전륜 조향각 센서, 추가로 차량의 종방향 속도 센서의 값을 입력으로 받는다(요레이트 센서 신호 제외). 구체적으로 검토된 신경망모델은 널리 알려진 RNN계열의 신경망인 LSTM(Long Short-Term Memory)과 GRU(Gated Recurrent Unit)이며, 두가지 방식의 예측모델을 비교하여 연산 비용 대비 높은 예측 성능이 나오는 신경망을 채택하였다. 구성된 순환신경망의 구조는 Fig. 11에 나타냈다.

Fig. 11

Prediction model structure for yaw rate virtual sensor

가상센서 모델의 예측 정확도 최적화 및 성능 향상을 위하여 모델의 하이퍼 파라미터의 튜닝을 진행하였다. 성능 지표는 MSE(Mean Square Error)와 추론 시간(Inference time)으로 정하였다. MSE는 테스트를 위해 학습 데이터와 별도로 준비된 100초 분량, 즉 10,000개의 데이터를 이용하여 비교하고, 추론 시간은 양이 많은 학습용 데이터 중 1,000초 분량으로 측정하여 예측에 몇 초가 소요되는지를 비교한다. 물론, 여기서 예측 시간은 PC(CPU : Intel i7-8,700)에서의 예측 연산 시간을 의미하며 신경망의 입력이 되는 해석적 중복 모델들의 연산 시간도 포함하고, 그 결과는 Table 4에 나타냈다.¹²⁾

Table 4

MSE and inference time of case

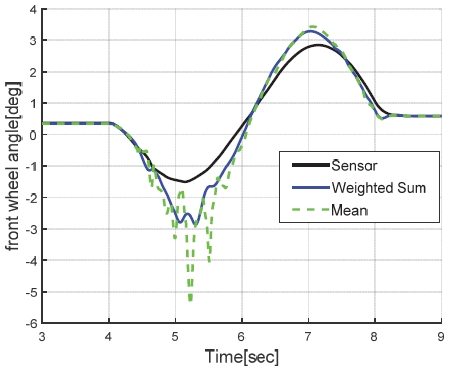
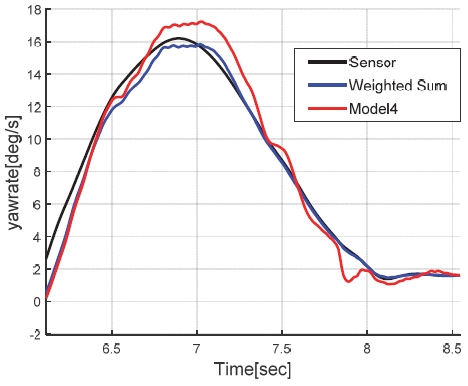
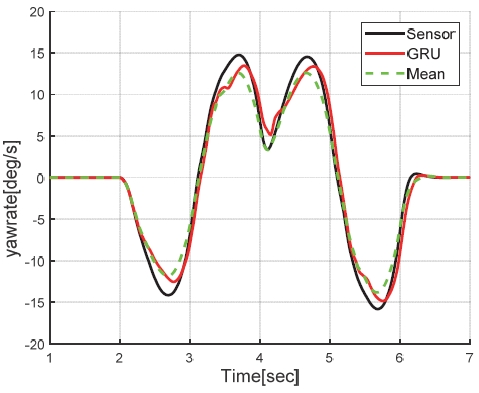
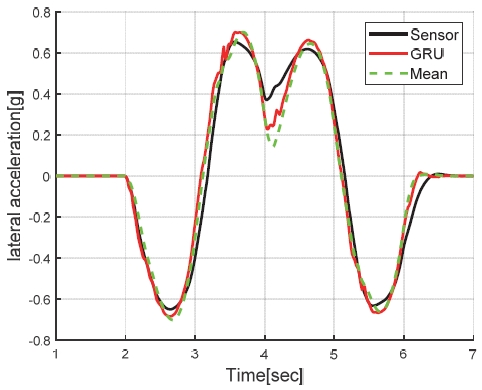
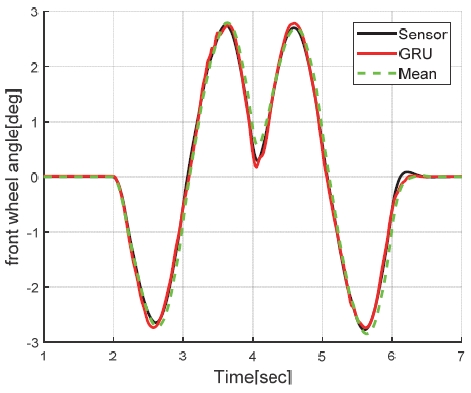
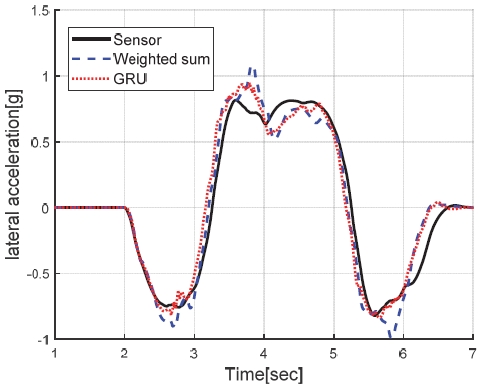
충분한 정확도에 해당하는 MSE가 0.3 이내면서 추론 시간가 가장 적은 모델인 Case 5 의 GRU 신경망을 채택했다. 이 모델의 예측 성능을 Fig. 12와 같이 차속 120 kph에서 80 kph로 감속하면서 동시에 ± 45도 범위의 DLC(Double Lane Change) 조향을 동시에 수행하는 시나리오에서 기존 해석적 중복 모델의 단순 평균(예컨대 γ_M1,2,3,4의 동일 가중 평균)과 비교하여 Figs. 13∼15에 나타냈다. 제안된 모델이 특정 주행 상황에서 상대적으로 정확도가 높은 해석적 중복 모델로 가중치를 적절히 부여하여 모델 단순 평균 예측 대비 예측 정확도가 향상된 결과를 나타내고 있다. 3장에서 제안된 두가지 방식의 가상센서 모델 간의 비교는 4장에서 설명하였다.

Fig. 12

Vx and SWA for driving scenarios

Fig. 13

Prediction result of proposed yaw rate GRU model

Fig. 14

Prediction result of proposed Ay GRU model

Fig. 15

Prediction result of proposed front wheel steer angle GRU model

4. 시뮬레이션 검증

본 연구를 통해 개발된 가상센서의 성능을 CARSIM SW와 MATLAB/SIMULINK로 구현된 가상센서 알고리즘의 통합 해석 환경을 통해 검증하였다. 사용된 차량 모델은 국내 제조사의 대형 세단 전기차 모델을 사용하였고 간략한 제원은 Table 5와 같다.

Table 5

Vehicle parameter for simulation analysis

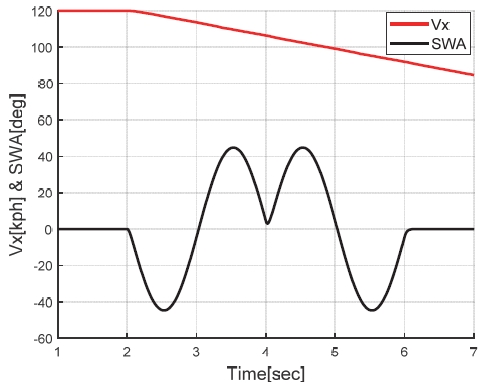
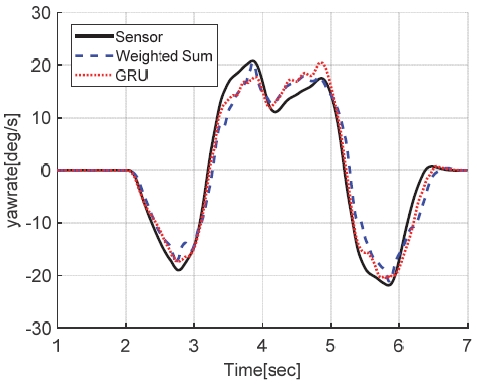
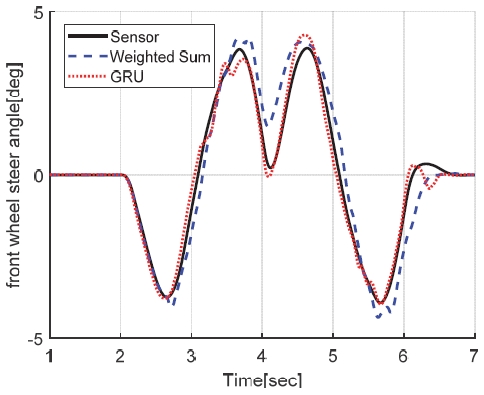
검증 시나리오는 다소 악의 조건에 해당하는 상황으로, 차속 120 kph에서 80 kph로 감속하면서 동시에 DLC(Double lane change) 조향을 진행하는 시나리오로 설정하였다. 해당 시나리오에서의 차속과 조향각을 Fig. 16에 나타내었으며, 해당 주행 상황에서의 도메인 지식 기반 가중치 적용 방식(Weighted sum), 기계 학습 방식(GRU)으로 각각 구현된 차량 요레이트, 횡가속도 및 전륜조향각에 대한 가상센서들의 성능 차이를 비교하였다.

Fig. 16

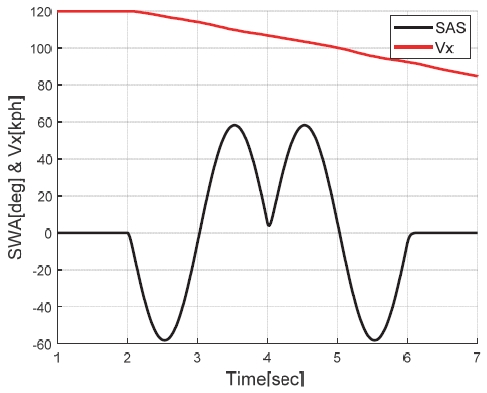
The longitudinal vehicle speed and steering wheel angle in driving scenario for simulation validation

시뮬레이션 검증에 사용된 노면 최대마찰계수는 0.85인데, 검증 시나리오에서의 차량의 최대 횡가속도는 0.8 g, 최대 종가속도는 0.2 g로 마찰한계 영역 주행에 해당한다. 이러한 마찰한계 영역에서 해석적 중복 모델들의 추정 성능이 전반적으로 저하되는데, 제안된 가상센서들은 이러한 성능 저하 상황에서도 주행 상황에 적합한 모델 가중치를 부여하여 결과적으로 우수한 추정 성능을 유지하는 것을 Figs. 17∼19에서 확인할 수 있다.

Fig. 17

Prediction result of proposed yaw rate virtual sensors

Fig. 18

Prediction result proposed lateral acceleration virtual sensors

Fig. 19

Prediction result proposed front wheel steer angle virtual sensors

한편, 전륜 조향각 추정 시, 차량 횡방향 모델의 파라미터 정확성이 매우 중요하지만, Fig. 19에서 4초 영역 에서와 같이 마찰한계 영역에서 과도 조향 시 도메인 지식 기반 가중치 방식의 경우 다소 적절한 가중치가 부여되지 않아 예측 오차가 커지는 결과를 보였다. 하지만 머신러닝 예측 모델에서는 해당 주행 상황에 적합한 가중치가 고려됐기 때문에 추정 결과가 개선됨을 확인하였다. 전반적인 두 모델의 정량적 예측 정확도를 Table 6에 정리하였다.

Table 6

Mean square error of virtual sensors

5. 결 론

본 연구에서는 신뢰성 높은 자율주행을 위한 초안전 주행 플랫폼에서 중요한 센서들의 고장 시 해당 신호를 다른 건강한 센서 신호의 조합으로 대체할 수 있는 가상센서를 개발하였다.

제어 관점에서 중요도가 높은 요레이트, 횡가속도, 전륜 조향각에 대한 각 센서 신호에 대해 4가지의 해석적 중복 모델을 도출하였다. 실제로 정확한 예측 성능을 갖는 가상센서는 이 4가지 독립적인 해석적 중복 모델들에 적절한 가중치가 부여되어야 하며, 본 연구에서는 도메인 지식 기반 방법, 데이터 기반 머신 러닝 기반 방법으로 각각 설계된 가상센서 모델을 개발하였다.

제안된 요레이트, 횡가속도, 전륜 조향각 가상센서들은 CARSIM SW와 Matlab Simulink를 활용하여 대형 승용 전기차 해석 모델을 통해 검증하였고, 이를 통해 다양한 주행 상황에서 4가지 해석적 중복 모델들에 상황에 적합한 가중치를 부여하여 결과적으로 대체하고자 하는 차량 신호를 강건하게 예측할 수 있음을 확인하였다.

한편, 대상 차종 변경 시 차량 파라미터의 영향을 받는 요레이트, 횡가속도, 조향각 가상센서의 4가지 해석적 중복 모델들은 차량 질량, 무게 중심 위치, 타이어 특성 등의 해당 차량 파라미터를 반영하여 재설계되어야 하나, 3장에서 설계된 각 해석적 모델들의 가중치들은 차량 파라미터 자체 보다는 특정 주행 상황에 의해 영향도가 결정되기 때문에 별도의 추가적인 가중치 설계 필요 가능성은 낮을 것으로 예상된다.

본 연구에서 제안된 가상센서 모델은 자율주행 차량의 센서 고장 상황 시, 기존 센서를 효과적으로 대체하여 더욱 안전한 자율주행 제어를 실현할 수 있기를 기대한다.

Acknowledgments

이 연구는 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(‘20015831’). 이 논문은 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2022R1A2C1004405, No.2021R1F1A1050200).

References

• A. N. Lee, J. H. Jung, B. G. Koo and H. B. Cha, “Vehicle Stability Enhancement by The Integration System with EPS and ESC,” Proceedings of the KSAE Conference, pp.728-731, 2008.
• E. Chow and A. Willsky, “Analytical Redundancy and the Design of Robust Failure Detection Systems,” IEEE Transactions on Automatic Control, Vol.29, No.7, pp.603-614, 1984. [https://doi.org/10.1109/TAC.1984.1103593]
• K. C. Min, J. T. Kim, G. B. Lee and K. S. Lee, “Model-Based Fault Detection and Failsafe Logic Development,” Proceedings of the KSME Conference, pp.774-779, 2004.
• K. S. Oh and K. S. Yi, “Model based Fault Detection and Robust Steering Control Algorithm for Autonomous Vehicle Using Sliding Mode Observer,” Transactions of KSAE, Vol.25, No.6, pp.732-741, 2017. [https://doi.org/10.7467/KSAE.2017.25.6.732]
• S. H. Chung, “A Study on Multi-Sensor Fault Detection and Compensation Control for Autonomous Vehicles,” Transactions of KSAE, Vol.30, No.4, pp.265-271, 2022. [https://doi.org/10.7467/KSAE.2022.30.4.265]
• H. Fennel and E.L. Ding, “A Model-Based Failsafe System for the Continental TEVES Electronic-Stability-Program (ESP),” SAE 2000-01-1635, 2000. [https://doi.org/10.4271/2000-01-1635]
• Y. W. Jeong, K. J. Lee, H. J. Chong, B. C. Ko and K. S. Yi, “Virtual Sensor based Vehicle Sensor Fault Tolerant Algorithm,” Proceedings of the KSME Conference, pp.1761-1766, 2015.
• E. Bakker, H. Pacejka and L. Lidner, “A New Tire Model with an Application in Vehicle Dynamics Studies,” SAE Trans. J. Passenger Cars, Vol.98, pp.101-113, 1989. [https://doi.org/10.4271/890087]
• H. B. Pacejka and E. Bakker, “The Magic Formula Tyre Model,” Vehicle System Dynamics, Vol.21, pp.1-18, 1992. [https://doi.org/10.1080/00423119208969994]
• G. H. Lee, Y. D. Lee and I. S. Koo, “An RNN-based Fault Detection Scheme for Digital Sensor,” The Journal of the Institute of Internet, Broadcasting and Communication, Vol.19, No.1, pp.29-35, 2019.
• M. Y. Mikheev, Y. S. Gusynina and T. A. Shornikova, “Building Neural Network for Pattern Recognition,” International Russian Automation Conference, pp.357-361, 2020. [https://doi.org/10.1109/RusAutoCon49822.2020.9208207]
• K. D. Kim, H. S. Lee and S. H. You, “Estimation of Vehicle Sideslip Angle Using Machine Learning,” KSFC Fall Conference, pp.161-163, 2019.