4륜 독립 조향 및 구동 차량의 슬라이딩 모드 관측기 기반 고장 탐지 및 적응형 고장 허용 적분 제어 알고리즘 개발

1. 서 론

차량의 전기, 전자, 통신 분야가 발전하고 있고 전기 차량 시장이 확대됨에 따라, 기계요소들이 ECU(Electronic Control Unit)를 이용하는 전기적 시스템으로 대체되고 있다. 이에 따라 XBW(X-By-Wire) 시스템 기반의 4륜 독립 조향, 구동, 제동 차량 등의 개발 및 상용화가 가속화되고 있다. XBW 시스템은 차량의 제어 자유도와 공간 효율성을 증대시킬 수 있으며, 독립 조향 및 구동 기능을 통해 선회 반경 감소, 핸들링 성능 확보 등의 주행 편의성을 운전자에게 제공할 수 있다. 하지만 많은 구동기와 센서를 이용함으로써 구조가 복잡해지고 시스템의 비선형성이 높아짐에 따라 고장 발생 확률과 경우의 수가 높고, 고장에 대한 합리적 대응이 이루어지지 않으면 치명적 사고로 이어질 수 있다. 따라서 위험 상황 발생 시 안전 및 일반 주행 성능 확보를 위해 고장-안전 시스템 개발의 필요성이 요구되고 있으며, 이에 따라 유수 연구 기관들이 고장 탐지 및 고장 허용 제어와 관련된 다양한 연구들을 진행하고 있다.

Dhari 등¹⁾은 H_∞ 슬라이딩 모드 관측기(Sliding Mode Observer, SMO)를 이용하여 요 각속도 센서 고장 신호를 재건하였다. Im 등²⁾은 SMO를 이용하여 조향각 센서와 코너링 강성 고장 신호를 재건하였다. Chan 등³⁾은 미지 입력 관측기를 이용하여 전륜 조향각의 고장 탐지 알고리즘을 제안하였다. Cho 등⁴⁾은 인공 신경망을 이용하여 차량 상태량 추정 알고리즘을 개발하였고, 실제 값과 추정 값 사이의 잔차를 기반으로 고장 탐지를 수행하였다. Lan 등⁵⁾은 SBW(Steer-By-Wire) 시스템의 Bond Graph 모델을 이용하여 고장을 탐지하고 Finite state machine을 이용하여 고장을 분리하였다. Judalet 등⁶⁾은 칼만 필터를 이용하는 상호작용 다중 모델을 설계하여 구동기 또는 센서의 고장을 탐지하였다. Mellah 등⁷⁾은 확장형 칼만 필터를 이용하여 실제 값과 추정 값 사이의 잔차를 기반으로 고장을 탐지하는 알고리즘을 제안하였다. 수학적 모델 기반 관측기 또는 필터링 기법을 이용하여 고장 신호를 재건할 경우 강건한 고장 재건이 가능하지만 차량의 상태량 또는 시스템 파라미터의 정확한 값을 알아야 한다. 실제 시스템에서 정확한 시스템 파라미터를 아는 것은 쉽지 않기 때문에 수학적 모델의 불확실성을 고려하는 관측기 또는 필터링 기법의 개발이 필요하다.

Huang 등⁸⁾은 모델 예측 제어 기반 SBW 시스템의 구동기 고장 허용 제어를 수행하였다. Huang 등⁹⁾은 모델 불확실성을 극복하기 위해 슬라이딩 모드 예측 제어기를 설계하였고, 이를 통해 SBW 시스템의 구동부 고장 허용 제어를 수행하였다. Lu 등¹⁰⁾은 인휠 모터 고장 허용 제어를 위해 적응형 Fuzzy-PID 기반 목표 요 모멘트 출력 및 슬라이딩 모드 제어를 이용하여 차량의 모션 제어를 수행하였다. Guo 등¹¹⁾은 4륜 독립 구동 차량의 구동기 고장 허용 제어를 위해 적응형 고속 터미널 슬라이딩 모드 제어기를 설계하였다. Zhang 등¹²⁾은 고장 발생 이후 모션 제어를 수행하기 위해 차량의 타이어 힘을 포함하는 비용 함수 설계를 통해 최적 제어 분배를 수행하였다. Geng 등¹³⁾은 자율주행 차량의 경로 추종을 위한 모델 예측 제어 기반 고장 허용 조향 알고리즘을 개발하였다. Shi 등¹⁴⁾은 모델 예측 제어-LQR 융합을 통해 고장의 영향을 완화하는 고장 허용 제어 알고리즘을 제안하였다. Hang 등¹⁵⁾은 모바일 로봇의 고장 허용 제어를 위해 비선형 모델 예측 제어 기반 제동 토크 분배 알고리즘을 설계하였다. 기존 연구를 통해 고장 신호를 포함하는 수학적 모델을 설계하고 이를 기반으로 허용 제어를 수행하는 다수의 연구가 진행되고 있음을 확인할 수 있었다. 하지만 고장 시스템의 수학적 모델을 이용할 경우 실제 시스템과의 불확실성이 존재하기 때문에 합리적 제어 입력 도출이 어려울 수 있다. 하지만, 이를 고려하는 모델 독립 적응형 고장 허용 제어 연구는 미비하게 진행된 것을 확인할 수 있었다. 타이어 힘 추정을 통해 여유 구동력을 분석하고 이를 기반으로 제어 입력 분배를 수행하는 연구가 진행되었으며, 대표적으로 다음과 같다. Liu 등¹⁶⁾은 종/횡방향 타이어 힘의 구동 가능 영역을 분석하고 LQR 기반 구동기 고장 허용 제어를 수행하였다. Chen 등¹⁷⁾은 종/횡방향 타이어 힘을 추정하였고, 이를 기반으로 슬라이딩 모드 기반 고장 허용 제어기의 제어 입력 분배를 수행하였다.

본 논문은 4륜 독립 조향 및 구동 차량의 SMO를 이용한 구동부 고장 탐지 및 경사 하강법 기반 적응형 적분 고장 허용 제어 알고리즘을 제안한다. 휠 동역학 모델을 이용하여 SMO를 설계하고, 시스템의 불확실성을 포함하는 외란을 주입항을 통해 추정하였다. 각 휠마다 추정된 외란의 상대 오차를 계산하여 임계값 기반 구동부 고장 탐지를 수행하였다. 다중 망각 인자를 포함하는 재귀 최소 자승법과 경사 하강법을 이용하여 모델 독립 적응형 이론을 설계하였고, 이를 이용하여 적분 제어기의 이득값을 실시간으로 갱신하였다. 또한 계산된 각 휠의 수직 힘을 기반으로 적응 이득을 분배함으로써 여유 구동력을 고려하는 제어 이득 분배를 수행하였다. 계산된 적분 제어 입력은 차량의 개별 구동 토크로 인가하여 고장 허용 제어를 수행하였다. 본 논문은 다음과 같이 구성되었다.

2장은 구동부 고장 탐지 및 고장 허용 제어 알고리즘의 설계 과정을 기술하고, 3장에서는 Matlab/Simulink와 CarMaker 소프트웨어를 이용하는 직진 및 선회 주행 시나리오 기반 성능 평가 결과를 보여준다. 4장에서는 결론 및 한계점 분석 그리고 향후 계획에 대해 기술한다.

2. 구동부 고장 탐지 및 허용 제어 알고리즘

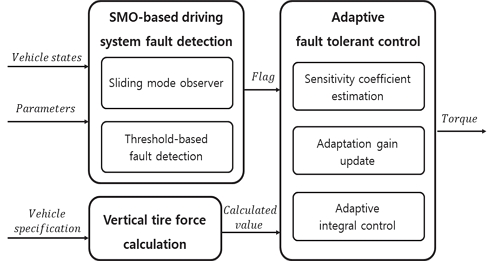
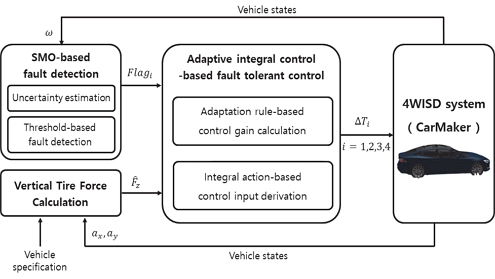
본 논문은 4륜 독립 조향 및 구동 차량의 SMO를 이용하는 구동부 고장 탐지 및 경사 하강법 기반 모델 독립 적응형 적분 제어 기반 고장 허용 제어를 수행 하는 고장-안전 알고리즘을 제안한다. SMO를 설계하여 구동부의 불확실성을 추정하고, 추정값의 상대 오차가 임계값 계산을 통해 고장을 판단한다. 이후 경사 하강법을 기반으로 설계된 적응형 규칙을 이용하여 적분 이득을 실시간으로 갱신함으로써 적분 제어 기반 구동부 고장 허용 제어를 수행한다. Fig. 1은 제안하는 고장-안전 알고리즘의 모델 개략도이다.

Fig. 1

Overall block diagram

2.1 슬라이딩 모드 관측기 기반 구동부 고장 탐지

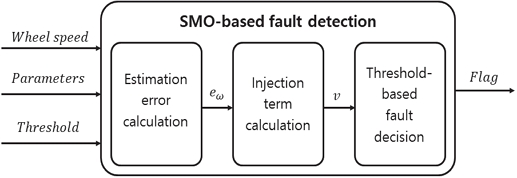
본 연구에서는 SMO를 이용하여 시스템의 외란을 관측하고 이를 기반으로 구동부의 고장을 탐지하는 방법론을 제안한다. 관측 시스템에 고장이 발생하였을 때 시스템의 불확실성 또는 외란이 변화하며, 이를 고장으로 인한 물리적 특성 변화로 간주하였다. 해당 변화를 SMO의 주입항으로 설정하여 추정하고, 추정값의 상대 오차가 임계값 이상일 경우 고장 탐지 신호를 출력하도록 알고리즘을 구성하였다. Fig. 2는 설계된 SMO 기반 구동부 고장 탐지 알고리즘의 모델 개략도이다. 식 (1)의 휠 동역학 모델을 이용하여 SMO를 설계하였으며, 실 시스템에서 계측이 쉽지 않은 종/횡방향 타이어 힘, 모터 토크 등의 값은 시스템의 외란을 포함하여 D_eq로 정의하였다. 식 (2)와 (3)은 각각 SMO 설계를 위해 정리된 휠 동역학 모델과 추정 상태량을 이용하는 관측기 모델을 보여준다. 구동부의 관성 모멘트와 댐핑 계수는 성능 평가에 이용된 차량의 제원을 이용하여 계산하였다.

$\[ I_{\omega }\dot{\omega }=-b\omega +T-F_{z}a-F_{x}r+\Delta w \]$

(1)

$\[ \dot{\omega }=-\frac{b}{I_{\omega }}\omega +D_{eq} \]$

(2)

• where, $$ D_{eq}=\frac{1}{I_{\omega }}\left(T-F_{z}a-F_{x}r+\Delta w\right)$$

$\[ \dot{\widehat{\omega }}=-\frac{b}{I_{\omega }}\widehat{\omega }+v \]$

(3)

Fig. 2

Model schematic for SMO-based fault detection

휠 속도 추정값과 계측값의 차이를 추정 오차(e_ω)로 정의하였으며, 식 (5)와 같이 설계된 리아푸노프 함수를 기반으로 비용 함수를 정의하였다.

$\[ e_{\omega }=\widehat{\omega }-\omega \]$

(4)

$\[ V=\frac{1}{2}{e}_{\omega }^2 \]$

(5)

정의된 비용 함수의 시간에 대한 미분은 식 (6)과 같이 전개될 수 있으며, 식 (3)에서 정의된 주입항은 식 (7)과 같이 설계하였다.

$\[ \dot{V}=e_{\omega }{\dot{e}}_{\omega }=e\left(-\frac{b}{I_{\omega }}{e}_{\omega }+v-D_{eq}\right) \]$

(6)

$\[ v=-\rho sign\left(e_{\omega }\right) \]$

(7)

이때, 유한 시간 수렴 조건을 통해 비용 함수를 식 (8)과 같이 설정할 수 있으며, 외란 경계 영역(L_b)을 정의함으로써 주입항의 크기를 식 (9)와 같이 도출할 수 있다.

$\[ \begin{array}{cc}\dot{V}\le -\alpha V^{\frac{1}{2}}\hfill & where, \alpha >0\hfill \end{array} \]$

(8)

$\[ \rho =L_b+\frac{\alpha }{\sqrt{2}} \]$

(9)

• where, $$ \left|-\frac{b}{I_{\omega }}-D_{eq}\right|\le L_b$$

SMO의 부호 함수로 인한 채터링 현상은 고장 탐지 성능에 영향을 미칠 수 있으므로, 이를 완화하기 위해 포화 함수를 적용하였다. 적용된 포화 함수는 식 (10)과 같으며, 오차 임계값(e_ω,th)의 경우 평가 과정을 기반으로 결정되었다.

$\[ sat\left(e_{\omega }\right)=\left\{\begin{array}{ccc}sign\left(e_{\omega }\right)\hfill & \hfill & \text{if }\left|e_{\omega }\right|>e_{\omega ,th}\hfill \\ \frac{e_{\omega }}{e_{\omega ,th}}\hfill & \hfill & \text{if }\left|e_{\omega }\right|\le e_{\omega ,th}\hfill \end{array}\right. \]$

(10)

개별 휠의 고장 탐지를 위해 주입항의 상대 오차를 계산하였으며, 이는 고장을 탐지하고자 하는 개별 휠과 나머지 휠의 주입항 오차로 정의하였다. 예를 들어 전륜 좌측 휠의 고장 탐지를 수행할 경우, 전륜 좌측 휠과 나머지 세 개 휠의 주입항 크기의 차이를 각각 계산한다. 이후 각 휠마다 계산된 상대 오차의 크기가 모두 정해진 임계값(e_v,th) 이상일 경우 해당 휠에 고장이 발생한 것으로 판단하였으며, 고장 탐지 신호 (flag_FL,FR,RL,RR)를 이용하여 고장을 탐지하였다. 고장 탐지 신호는 정상 상태일 때 0, 고장이 탐지되었을 때 1 로 정의하였다. Table 1은 설계된 고장 탐지 알고리즘의 상대 오차 계산 방법과 고장 탐지 조건을 보여준다.

Table 1

Fault detection flag condition of each wheels

제안하는 고장 탐지 방법론은 고장으로 인해 발생하는 시스템의 물리적 특성 변화를 SMO의 주입항을 이용하여 추정하고, 추정된 주입항의 상대 오차를 계산하여 단일 임계값 기반의 고장 탐지를 수행한다. 현 단계에서는 한 개 휠 고장 상황만을 고려하였으며, Table 1에서 설명하는 고장 탐지 조건 외의 경우는 모두 정상 상태로 간주하였다. 본 알고리즘에서 적용한 단일 임계값을 이용하여 고장 탐지를 수행할 경우 다양한 고장 상황에서 주입항의 상대 오차가 각 휠마다 다르게 계산되어 합리적 고장 탐지가 어려울 수 있다. 따라서 추후 다양한 고장 상황에서의 합리적 고장 탐지를 위해 상대 오차 학습을 통한 인공 신경망을 이용하는 방법론을 적용함으로써 알고리즘의 고도화가 진행될 예정이다.

2.2 적응형 적분 제어 기반 구동부 고장 허용 제어

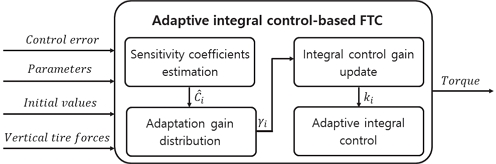
과구동 시스템은 다양한 구동기와 센서가 사용되기 때문에 수학적 모델을 기반으로 제어를 수행할 경우 모델 불확실성과 최적 제어 분배에 한계가 발생할 수 있으며, 고장 발생 시 이를 허용할 수 있는 제어 입력의 합리적 도출이 어려울 수 있다. 따라서 본 논문에서는 구동부 고장 허용 제어를 위한 모델 독립 적응형 제어 알고리즘을 설계하였다. 도출된 제어 입력은 운전자의 조향 입력 기반 요구 물리량을 추종하기 위한 각 휠의 개별 토크 입력으로 차량에 인가되었다. Fig. 3은 제안하는 적응형 적분 제어 알고리즘의 모델 개략도이다.

Fig. 3

Model schematics for adaptive integral control

목표 물리량은 중립 조향(Neutral steering) 기반 목표 요 각속도를 도출하여 설정하였으며, 제어 오차는 도출된 목표 요 각속도와 현재 요 각속도의 차이로 정의하였다. 식 (11)과 (12)를 통해 가상 중심 휠을 기반으로 목표 요 각속도 도출 과정을 확인할 수 있으며, 식 (13)은 목표 요 각속도와 현재 요 각속도를 기반으로 정의된 제어 오차를 나타낸다.

$\[ {\dot{\psi }}_{des }=\frac{v_x}{L}{\delta }_c \]$

(11)

$\[ {\delta }_c=\left({\delta }_{FL}+{\delta }_{FR}\right)/2 \]$

(12)

$\[ e_{\dot{\psi }}={\dot{\psi }}_{des}-{\dot{\psi }}_{cur} \]$

(13)

모델 독립 적응형 규칙을 설계하는 과정은 다음과 같다. 각 휠의 민감도 계수를 포함하는 가상 관계 함수를 식 (14)와 같이 설계하였고 다중 망각 인자를 포함하는 재귀 최소 자승법을 이용하여 민감도 계수를 추정하였다. 식 (15)을 통해 시스템의 입력과 출력값을 나타냈으며, 출력은 요 각속도 오차의 미분항으로 정의하였다. 식 (16)과 (17)은 식 (15)에서 정의한 선형 시스템의 추정값과 입력값을 의미한다.

$\[ {\dot{e}}_{\psi }=C_{FL}{\dot{k}}_{FL}+C_{FR}{\dot{k}}_{FR}+C_{RL}{\dot{k}}_{RL}+C_{RR}{\dot{k}}_{RR} \]$

(14)

$\[ y={\varphi }^T\widehat{\theta } \]$

(15)

$\[ \theta =\left[C_{FL}{C}_{FR}{C}_{RL}{C}_{RR}\right] \]$

(16)

$\[ \varphi =\left[{\dot{k}}_{FL}{\dot{k}}_{FR}{\dot{k}}_{RL}{\dot{k}}_{RR}\right] \]$

(17)

식 (18)을 통해 이산 시간에서 실시간으로 갱신되는 추정값을 나타내었으며, 식 (19)와 (20)은 각각 추정값 갱신을 위한 다중 망각 인자를 포함하는 추정 이득과 공분산 행렬이다.

$\[ {\widehat{\theta }}_{i,k}={\widehat{\theta }}_{i,k-1}+L_{i,k}\left(y_k-\sum _{i=1}^4\left({\varphi }_{i,k}{\widehat{\theta }}_{i,k-1}\right)\right) \]$

(18)

$\[ L_{i,k}=P_{i,k-1}{\varphi }_{i,k}{\left({\lambda }_i+{\varphi }_{i,k}^T{P}_{i,k-1}{\varphi }_{i,k}\right)}^{-1} \]$

(19)

$\[ P_{i,k}=\left(I-L_{i,k}{\varphi }_{i,k}^T\right)P_{i,k-1}\frac{1}{{\lambda }_i} \]$

(20)

• where, i = FL,FR,RL,RR

앞서 설계한 고장 탐지 알고리즘에 의해 구동부에 고장이 탐지되었을 경우 해당 항은 민감도 계수가 갱신되지 않고 일정한 값을 유지되도록 설계하였다. 또한 효과적인 고장 허용 제어 수행을 위해 재귀 최소 자승법의 초기값을 크기는 같지만 반대의 부호를 가지도록 적용함으로써 제어 오차의 부호에 따라 좌/우 휠의 구동 토크 부호가 다르게 인가되도록 설계하였다. 추후 재귀 최소 자승법의 Wind-up 현상과 같은 한계점을 극복하기 위해 가변 망각 인자를 적용하는 알고리즘 고도화를 계획하고 있다.¹⁸⁾

적분 이득은 경사 하강법을 이용하여 실시간으로 갱신되며, 식 (21)과 같이 리아푸노프 함수 기반 비용 함수 설계를 통해 제어 오차가 감소할 수 있는 적분 이득을 도출하였다. 식 (22)는 앞서 추정된 민감도 계수를 이용하여 적분 이득이 계산되는 과정이다.

$\[ J=\frac{1}{2}{e}_{\dot{\psi }}^2 \]$

(21)

$\[ \frac{d{k}_i}{dt}=-{\gamma }_i\frac{\partial J}{\partial k_i}=-{\gamma }_i{e}_{\dot{\psi }}{C}_i \]$

(22)

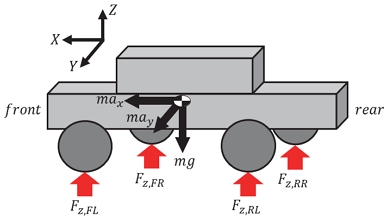
이때 여유 구동력을 고려하여 제어 입력 분배를 수행하기 위해 각 휠 수직 힘의 상대적 크기 비율을 이용하는 적응 이득 분배 법칙을 설계하였다. 각 휠의 수직 힘은 센서를 통해 계측 가능한 차량의 종/횡방향 가속도 값 기반 운동 역학적으로 계산되었으며, 계산된 수직 힘의 상대적 크기 비율을 이용하여 적응 이득을 분배하였다. 수직 힘 계산을 위해 Fig. 4와 같이 자유물체도를 나타내었고, 각 휠의 수직 힘은 식 (23)∼(25)의 과정을 통해 계산할 수 있다. 전륜과 후륜의 수직 힘은 아래와 같이 도출할 수 있으며,

$\[ F_{z, front/rear }=\pm \frac{m{a}_x}{L}h+\frac{l_r}{L}mg \]$

(23)

Fig. 4

Free-body diagram of vehicle

좌측 휠과 우측 휠의 수직 힘은 각각 식 (24)와 식 (25)와 같이 계산될 수 있다.

$\[ F_{z,j}=\frac{1}{2}{F}_{z, front }\mp \frac{h{a}_y}{t_{w}g}{F}_{z, front } \]$

(24)

• where, j =FL,RL

$\[ F_{z,l}=\frac{1}{2}{F}_{z,rear }\mp \frac{h{a}_y}{t_{w}g}{F}_{z,rear } \]$

(25)

• where, l =FR,RR

계산된 각 휠의 수직 힘의 상대적 크기 비율을 기반으로 분배되는 적응 이득은 식 (26)과 같다.

$\[ {\gamma }_i=\frac{F_{z,i}}{\sum _{i=1}^4{F}_{z,i}}\gamma \]$

(26)

제어 입력은 아래 식 (27)과 같이 적분 제어를 통해 도출되었으며, 이는 성능 확보를 위한 보조 구동 입력으로 차량에 인가되었다.

$\[ \Delta T_i=k_i{\int }_0^t{e}_{\dot{\psi }}dt \]$

(27)

최종적으로 차량의 구동부에 인가되는 각 휠의 토크 입력은 식 (28)과 같다.

$\[ T_i=T_{wheel }+\Delta T_i \]$

(28)

3. 성능 평가

제안하는 알고리즘의 성능 평가는 Matlab/Simulink 및 CarMaker 상용 소프트웨어를 연동하여 진행하였다. SMO를 이용하여 주행 중 구동부에 발생한 고장을 탐지하고, 적응형 적분 제어를 통해 운전자 조향 입력을 기반으로 도출되는 요구 요 각속도를 추종하는 각 휠의 토크 입력을 도출하였다. 성능 평가는 직진 주행, 선회 주행 시나리오로 적용하였으며, 구동부의 전기적, 기계적 고장으로 인한 고착 결함을 가정하여 고장을 정의하였다. 성능 평가를 위해 구성된 가상 환경 내 고장 상황은 전륜 좌측 휠에 음의 방향의 토크를 인가하여 재현하였다. Fig. 5는 성능 평가를 위해 구성된 알고리즘의 모델 개략도이며, 성능 평가에 이용된 차량의 제원과 적용된 제어 파라미터는 아래 Tables 2와 3을 통해 확인할 수 있다.

Fig. 5

Overall block diagram for performance evaluation

Table 2

Vehicle specification for performance evaluation

Table 3

Parameters for performance evaluation

3.1 Case 1) 직진 주행

Case 1은 30 km/h 의 등속 직진 주행 중 전륜 좌측 휠에 고장이 발생한 시나리오를 기반으로 성능 평가를 진행하였다. SMO를 이용하여 구동부 외란을 추정하여 고장을 탐지하였으며, 고장이 탐지되지 않은 나머지 휠을 이용하여 적응형 적분 제어를 통해 고장 허용 제어를 수행하였다. 아래의 Figs. 6∼20은 이에 대한 성능 평가 결과를 보여준다.

Fig. 6

Driver steering input

Fig. 7

Longitudinal velocity

Fig. 8

Lateral velocity

Fig. 9

Yaw rate

Fig. 10

Load torque – FL (faulty wheel)

Fig. 11

Estimated and actual wheel speed

Fig. 12

Estimated uncertainty (zoom in)

Fig. 13

Relative errors of each wheel

Fig. 14

Fault detection flag

Fig. 15

Sensitivity coefficient (zoom in)

Fig. 16

Estimated and actual vertical tire force (zoom in)

Fig. 17

Adaptation gain

Fig. 18

Integral gain

Fig. 19

Integral control input

Fig. 20

Total torque input

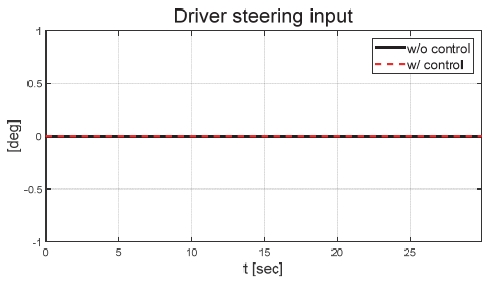
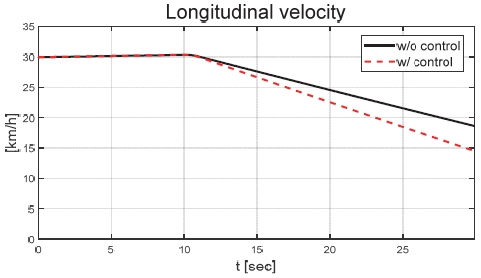
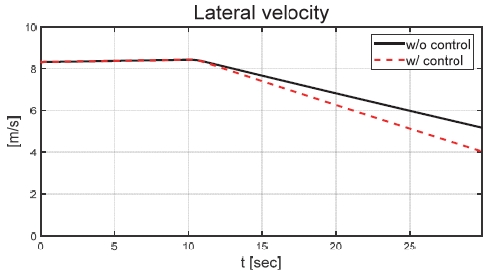
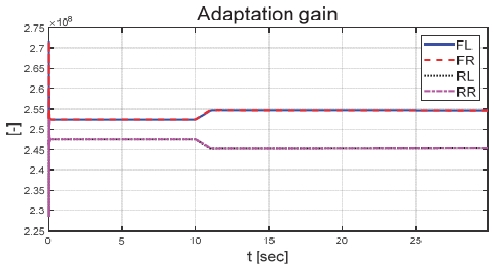
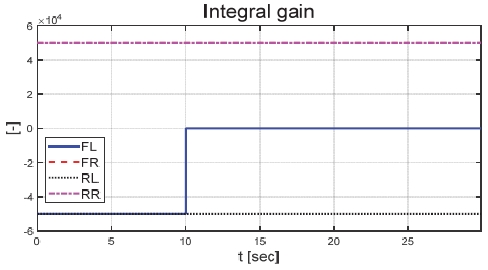
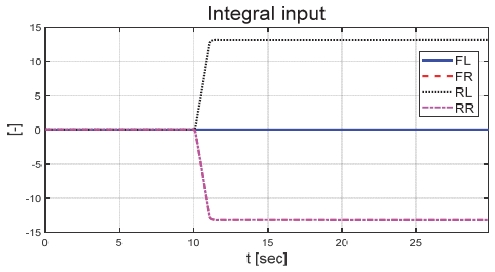
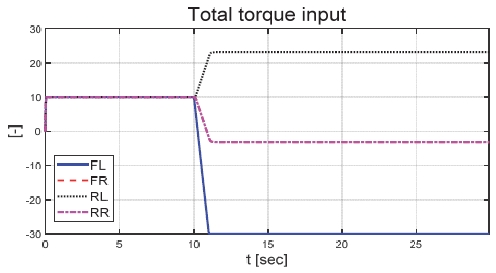
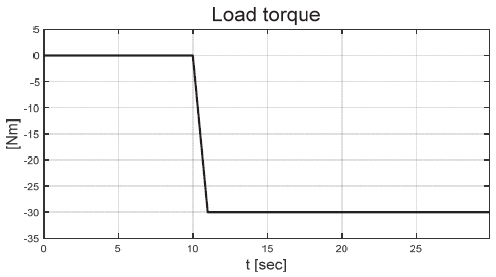
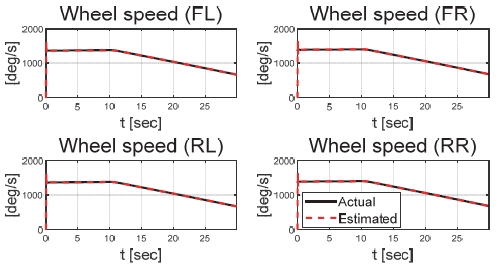
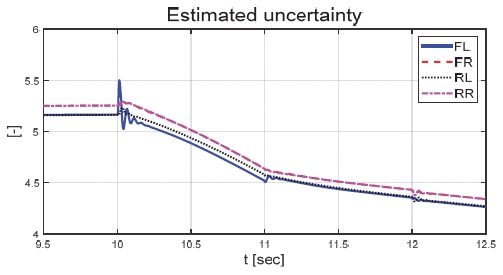
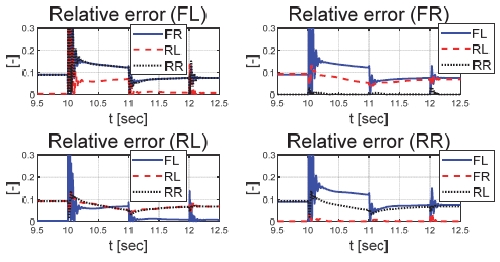
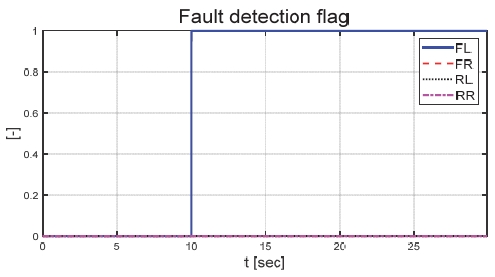
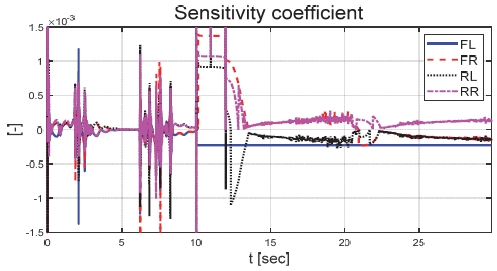
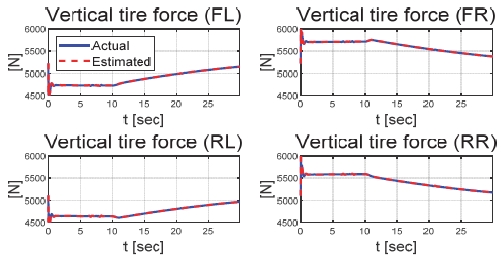
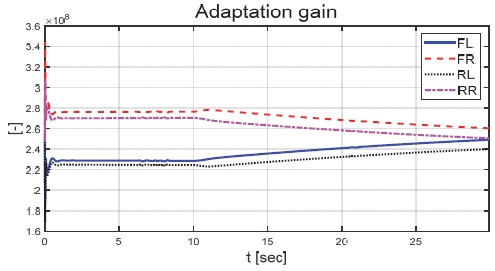
Fig. 6은 운전자 조향 입력을 나타낸 그래프로, 운전자는 직진 주행을 수행하기 위해 0 deg의 일정한 조향 입력을 인가하였다. Figs. 7과 8은 각각 차량의 종/횡방향 속도 그래프이며 10 초에 차량의 구동부에 고장이 발생하여 감소하였다. Fig. 9를 통해 고장 허용 제어가 개입할 경우 차량의 요 각속도의 최대값이 약 0.15 deg/s에서 약 0.015 deg/s 로 감소하는 것을 확인할 수 있다. 고장으로 차량의 전륜 좌측 휠에 인가된 부하 토크는 Fig. 10을 통해 확인할 수 있다. Fig. 11은 SMO를 이용하여 추정한 각 휠의 속도로 합리적인 추정 결과를 보였다. Fig. 12는 SMO의 주입항을 통해 추정한 구동 시스템의 외란을 나타낸 그래프이며, 고장이 발생한 이후 전륜 좌측 휠의 외란이 상대적으로 크게 변화하는 것을 확인할 수 있다. Fig. 13은 계산된 주입항의 상대 오차를 나타낸 그래프이고, Fig. 14를 통해 전륜 좌측 휠의 flag가 1 로 변화하면서 고장이 탐지된 것을 확인할 수 있다. Fig. 15는 재귀 최소 자승법을 통해 추정된 민감도 계수이다. Figs. 16과 17은 계산된 각 휠의 수직 타이어 힘과 이를 기반으로 분배된 적응 이득을 나타낸 그래프이다. Fig. 18은 최종적으로 계산된 적분 이득이며, Fig. 19를 통해 계산된 적분 제어 입력을 확인할 수 있다. 요 각속도 오차의 부호에 따라 좌/우 휠에 부호가 다른 토크 입력을 인가하기 위해 민감도 계수와 적분 이득의 초기 부호 값을 다르게 적용하였다. 민감도 계수와 적분 이득은 설정해준 초기치 값을 기반으로 갱신되었으며, 이에 따라 좌/우 휠에 부호가 다른 적분 제어 입력이 계산되었다. 전륜 좌측 휠에 고장이 탐지된 이후 민감도 계수가 일정한 값으로 유지되고 적분 이득은 0의 값을 갖도록 알고리즘을 설계하였다. 고장이 발생하지 않은 나머지 휠의 적분 이득은 설계된 적응형 규칙에 따라 갱신되었으며, 고장 허용 제어를 수행하기 위한 적분 제어 입력을 도출하였다. 하지만 재귀 최소 자승법의 Wind-up 현상으로 인해 민감도 계수가 불안정한 값으로 계산되었으며, 이를 해결하기 위해 가변 망각 인가를 적용하여 알고리즘 고도화를 진행할 예정이다. Fig. 20은 최종적으로 차량에 인가된 개별 휠의 토크 입력을 나타낸다. 전륜 좌측 휠에 30 Nm 크기를 가지는 음의 방향의 토크 입력을 인가함으로써 고장 상황을 재현하였으며, 고장 탐지 이후 좌/우 휠에 고장 허용 제어를 위한 부호가 다른 토크 입력이 인가된 것을 확인할 수 있다. Table 4를 통해 제어 오차 분석 결과를 나타내었다. 고장 허용 제어가 개입되었을 시 요 각속도 최대 오차는 0.0152 deg/s이며, 오차의 표준 편차와 제곱 평균 제곱근은 각각 0.0055 deg/s와 0.0062 deg/s로 제어 오차가 0에 가깝게 수렴했음을 알 수 있다.

Table 4

Yaw rate error analysis

3.2 Case 2) 선회 주행

Case 2 는 선회 주행 중 전륜 좌측 휠의 구동부에 고장이 발생한 시나리오를 적용하여 성능 평가를 진행하였다. 운전자는 30 km/h의 등속도로 30 deg의 일정한 조향 입력을 인가하였다. SMO를 이용하여 구동부 외란을 추정함으로써 고장 탐지를 수행하였으며, 고장이 탐지되지 않은 휠을 이용하여 적응형 적분 제어 기반 고장 허용 제어를 수행하였다. 아래의 Figs. 21∼35는 이에 대한 성능 평가 결과를 보여준다.

Fig. 21

Driver steering input

Fig. 22

Longitudinal velocity

Fig. 23

Lateral velocity

Fig. 24

Yaw rate

Fig. 25

Load torque – FL (faulty wheel)

Fig. 26

Estimated and actual wheel speed

Fig. 27

Estimated uncertainty (zoom in)

Fig. 28

Relative errors of each wheel (zoom in)

Fig. 29

Fault detection flag

Fig. 30

Sensitivity coefficient (zoom in)

Fig. 31

Estimated and actual vertical tire force (zoom in)

Fig. 32

Adaptation gain

Fig. 33

Integral gain

Fig. 34

Integral control input

Fig. 35

Total torque input

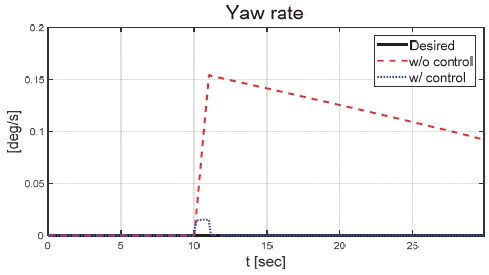
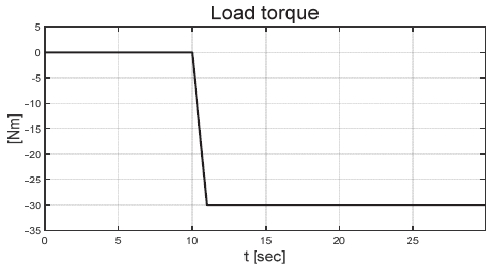
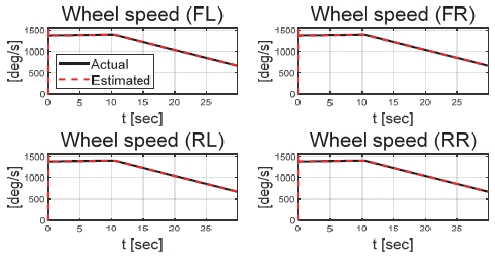
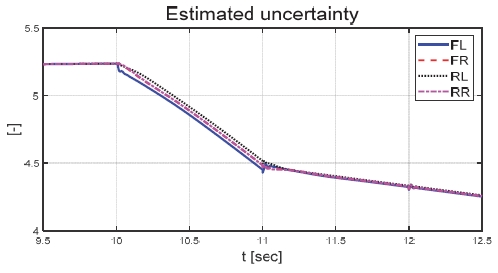
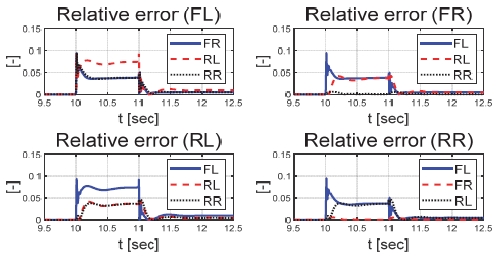
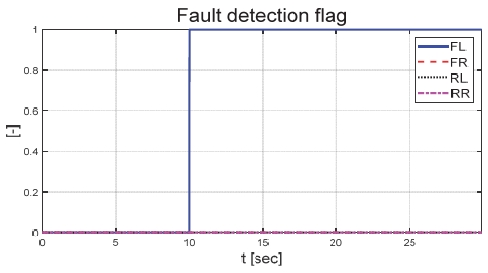
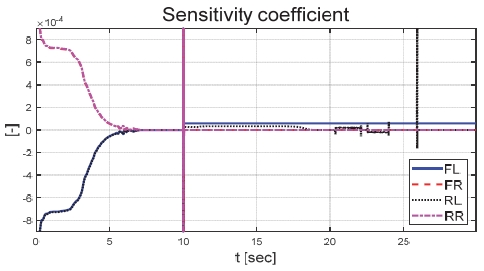
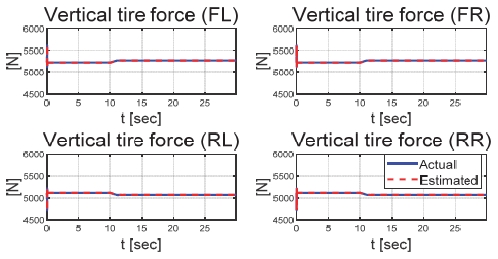
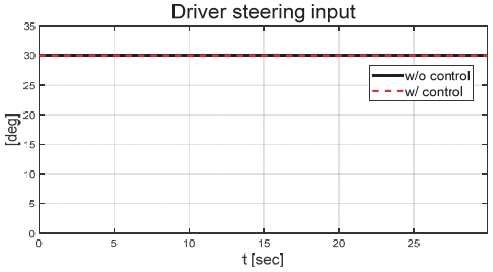
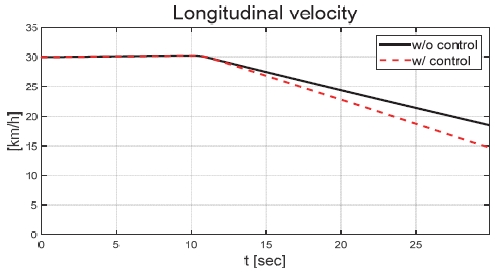
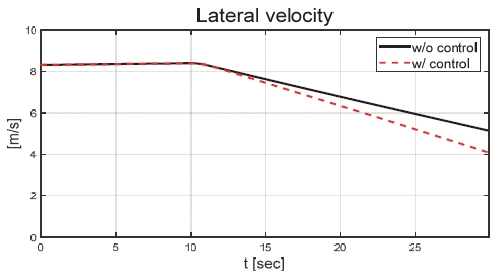
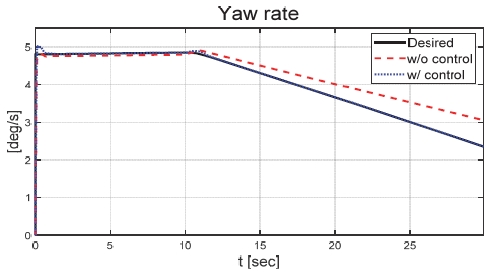
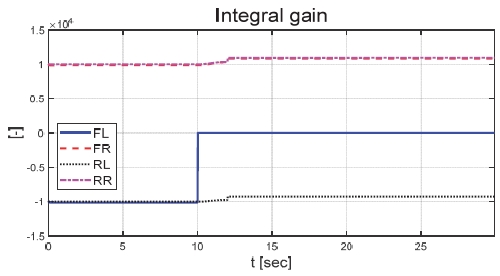
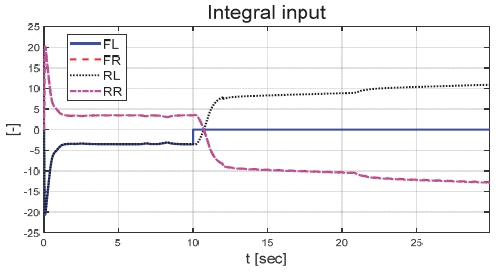
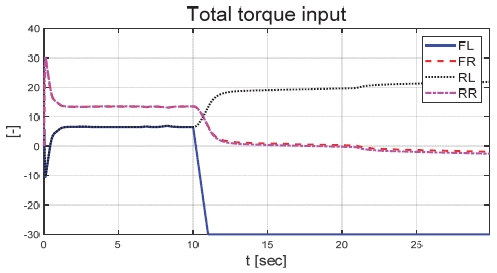
Fig. 21은 운전자 조향 입력을 나타낸 그래프로, 일정한 30 deg의 조향 입력을 인가하며 좌선회 주행 중인 것을 확인할 수 있다. Figs. 22와 23은 각각 차량의 종방향과 횡방향 속도 그래프이며 10 초에 차량의 구동부에 고장이 발생함에 따라 속도가 감소하였다. Fig. 24는 차량의 요 각속도를 나타낸 그래프로 10 초에 고장 발생하여 이전 값 대비 최대 약 0.1 deg/s 증가하였으며, 고장 허용 제어가 개입하였을 때 이전 값 대비 최대 약 0.05 deg/s 증가하였다. Fig. 25를 통해 차량의 전륜 좌측 휠에 인가된 부하 토크를 나타내었다. Fig. 26은 SMO를 이용하여 추정한 각 휠의 속도를 나타낸 그래프로 합리적인 추정 성능을 보였다. Fig. 27은 SMO의 주입항을 통해 추정한 각 구동 시스템의 외란을 나타낸 그래프이며, 전륜 좌측 휠에 고장이 발생한 10 초 이후 외란이 상대적으로 크게 변화하는 것을 확인할 수 있다. Fig. 28은 계산된 주입항의 상대 오차를 나타낸 그래프이고, 전륜 좌측 휠의 flag가 0에서 1로 변화함으로써 고장이 탐지된 것을 Fig. 29를 통해 확인할 수 있다. Fig. 30은 재귀 최소 자승법을 통해 추정된 민감도 계수이다. Figs. 31과 32는 계산된 각 휠의 수직 힘과 이를 기반으로 분배된 적응 이득을 나타낸 그래프이다. Fig. 33은 최종적으로 계산된 적분 이득이며, Fig. 34를 통해 계산된 적분 제어 입력을 확인할 수 있다. 요 각속도 오차의 부호에 따라 좌/우 휠에 부호가 다른 토크 입력을 인가하기 위해 민감도 계수와 적분 이득 초기값의 부호를 다르게 적용하였으며, 10초에 발생한 고장으로 인해 요 각속도 오차가 변화함에 따라 민감도 계수와 제어 이득이 변화하는 것을 확인할 수 있다. 또한 전륜 좌측 휠에 고장이 탐지됨에 따라 민감도 계수가 일정한 값으로 유지되고 적분 이득이 0으로 유지되었다. Fig. 35는 차량에 인가된 각 휠의 토크 입력을 나타낸다. 10 초에 전륜 좌측 휠에 30 Nm 크기의 음의 방향의 토크를 인가하여 고장 상황을 재현하였으며, 고장이 탐지된 이후 좌/우 휠에 부호가 다른 토크 입력을 인가함으로써 고장 허용 제어를 수행하였다. Table 5는 제어 오차 분석 결과로 제어 오차의 최대값, 표준 편차, 제곱 평균 제곱근을 분석하였으며, 각각 0.0632 deg/s, 0.0192 deg/s, 0.0242 deg/s의 값을 가짐으로써 제어 오차가 0에 가까운 값을 가지는 것을 확인할 수 있다.

Table 5

Yaw rate error analysis

4. 결 론

본 논문은 4륜 독립 조향 및 구동 차량의 고장-안전 시스템 구축을 위해 SMO를 이용하여 구동부의 고장을 탐지하고 경사 하강법 기반 적응형 규칙 설계를 통해 적분 제어를 이용하는 고장 허용 제어 알고리즘을 제안한다. 고장 발생으로 인해 관측 시스템의 물리적 특성이 변화하는 상황을 SMO의 주입항을 이용하여 추정하였으며, 주입항의 상대 오차를 이용하여 임계값 기반 고장 탐지를 수행하였다. 고장이 발생한 과구동 시스템의 불확실성을 최소화하기 위해 경사 하강법을 이용하는 모델 독립 적응형 규칙을 설계하였다. 설계된 적응형 규칙을 통해 적분 이득을 실시간으로 갱신하였으며, 이를 기반으로 계산된 적분 제어 입력을 보조 구동력으로 인가함으로써 고장 허용 제어를 수행하였다. Matlab/Simulink 및 CarMaker 소프트웨어를 연동하여 직진 및 선회 주행 시나리오를 기반으로 성능 평가를 수행하였으며, 전기적, 기계적 고장으로 인한 고착 결함을 가정하여 고장 상황을 재현하였다. 성능 평가 결과 구동부 고장이 발생하였을 때 추정된 주입항이 상대적으로 크게 변화하였으며, 이를 통해 합리적 고장 탐지를 수행하는 것을 확인할 수 있었다. 고장 허용 제어 결과는 제어 오차의 최대값, 표준 편차, 제곱 평균 제곱근 분석을 진행하였으며, 고장 허용 제어가 적용되었을 때 그렇지 않은 경우 대비 제어 오차가 감소하는 것을 확인할 수 있었다.

상대 오차를 기반으로 고장 탐지를 수행할 때 하나의 임계값을 이용할 경우 다양한 고장 상황에서 합리적인 고장 탐지에 어려움이 있을 수 있다. 따라서 추정된 시스템 외란의 상대 오차를 학습시켜 인공 지능 기반 고장 탐지 알고리즘의 고도화를 계획하고 있다. 또한 가변 망각 인자를 이용하여 민감도 계수를 추정함으로써 불안정한 적분 제어 이득의 계산 과정을 보완할 수 있을 것으로 기대한다. 본 연구에서 제안한 고장 탐지 및 고장 허용 제어 알고리즘은 시스템의 정확한 모델 파라미터를 요구하지 않고, 고장 탐지 및 모델 독립 적응형 제어를 수행함으로써 불확실성이 큰 실 시스템의 고장-안전 시스템으로 적용 가능할 것으로 기대한다.

Acknowledgments

본 연구는 2022 현대자동차 산학 협동 연구과제의 지원을 받아 수행된 연구임.

References

• S. Dhahri, A. Sellami and F. Hmida, “Robust Sensor Fault Detection and Isolation for a Steer-by-Wire System Based on Sliding Mode Observer,” 2012 16th IEEE Mediterranean Electrotechnical Conference, pp.450-454, 2012. [https://doi.org/10.1109/MELCON.2012.6196470]
• J. Im, F. Ozaki, T. Yeu and S. Kawaji, “Model-based Fault Detection and Isolation in Steer-by-wire Vehicle using Sliding Mode Observer,” Journal of Mechanical Science and Technology, Vol.23, pp.1991-1999, 2009. [https://doi.org/10.1007/s12206-009-0357-9]
• T. Chan, Y. Cai, L. Chen, X. Xu and X. Sun, “Trajectory Tracking Control of Steer-by-wire Autonomous Ground Vehicle Considering the Complete Failure of Vehicle Steering Motor,” Simulation Modeling Practice and Theory, Vol.109, Paper No.102235, 2021. [https://doi.org/10.1016/j.simpat.2020.102235]
• C. Cho, J. Hong and H. Kim, “Neural Network Based Adaptive Actuator Fault Detection Algorithm for Robot Manipulators,” Journal of Intelligent & Robotic System, Vol.95, pp.137-147, 2019. [https://doi.org/10.1007/s10846-018-0781-0]
• D. Lan, M. Yu, Y. Huang, Z. Ping and J. Zhang, “Fault Diagnosis and Prognosis of Steer-by-wire System based on Finite State Machine and Extreme Learning Machine,” Neural Computing and Applications, Vol.34, No.7, pp.5081-5095, 2022. [https://doi.org/10.1007/s00521-021-06028-0]
• V. Judalet, S. Glaser, D. Gruyer and S. Mammar, “Fault Detection and Isolation via the Interaction Multiple Model Approach Applied to Drive-By-Wire Vehicles,” Sensors, Vol.18, No.7, p.2332, 2018. [https://doi.org/10.3390/s18072332]
• S. Mellah, G. Graton, E. Adel, M. Ouladsine and A. Planchais, “On Fault Detection and Isolation Applied on Unicycle Mobile Robot Sensors and Actuators,” 2018 7th International Conference on Systems and Control, pp.148-153, 2018. [https://doi.org/10.1109/ICoSC.2018.8587845]
• C. Huang, H. Huang, F. Naghdy, H. Du and D. Ma, “Actuator Fault Tolerant Control for Steer-by-wire Systems,” International Journal of Control, Vol.94, No.11, pp.3123-3134, 2021. [https://doi.org/10.1080/00207179.2020.1752399]
• C. Huang, F. Naghdy and H. Du, “Fault Tolerant Sliding Mode Predictive Control for Uncertain Steer-by-Wire System,” IEEE Transactions on Cybernetics, Vol.49, No.1, pp.261-272, 2019. [https://doi.org/10.1109/TCYB.2017.2771497]
• S. Lu, S. Cen and Y. Zhang, “Driver Model-Based Fault-Tolerant Control of Independent Driving Electric Vehicles Suffering Steering Failure,” Autonomotive Innovation, Vol.1, pp.85-94, 2018. [https://doi.org/10.1007/s42154-018-0013-0]
• B. Guo and Y. Chen, “Robust Adaptive Fault Tolerant Control of Four-wheel Independently Actuated Electric Vehicles,” IEEE Transactions on Industrial Informations, Vol.16, No.5, pp.2882-2894, 2020. [https://doi.org/10.1109/TII.2018.2889292]
• Y. Zhang, H. Zheng, J. Zhang and C. Cheng, “A Fault-Tolerant Control Method for 4WIS/4WID Electric Vehicles Based on Reconfigurable Control Allocation,” SAE 2018-01-0560, 2018. [https://doi.org/10.4271/2018-01-0560]
• K. Geng, N. A. Chulin and Z. Wang, “Fault-Tolerant Model Predictive Control Algorithm for Path Tracking of Autonomous Vehicle,” Sensors, Vol.20, No.15, 2020. [https://doi.org/10.3390/s20154245]
• K. Shi and X. Yuan, “MPC-based Fault Tolerant Control System for Yaw Stability of Distributed Drive Electric Vehicle,” 2019 3rd Conference on Vehicle Control and Intelligence, pp.1-16, 2019. [https://doi.org/10.1109/CVCI47823.2019.8951719]
• P. Hang, B. Lou and C. Lv, “Nonlinear Predictive Motion Control for Autonomous Mobile Robots Considering Active Fault-Tolerant Control and Regenerative Braking,” Sensors, Vol.22, No.10, 2022. [https://doi.org/10.3390/s22103939]
• Y. Liu, C. Zong, D. Zhang, H. Zheng, X. Han and M. Sun, “Fault-tolerant Control Approach based on Constraint Control Allocation for 4WIS/4WID Vehicles,” Proceedings of Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.235, No.8, pp.2281-2295, 2021. [https://doi.org/10.1177/0954407020982838]
• T. Chen, L. Chen, X. Xu, Y. Cai, H. Jiang and X. Sun, “Passive Fault-tolerant Path Following Control of Autonomous Distributed Drive Electric Vehicle Considering Steering System Fault,” Mechanical Systems and Signal Processing, Vol.123, pp.298-315, 2019. [https://doi.org/10.1016/j.ymssp.2019.01.019]
• L. Cao and H. Schwartz, “A Directional Forgetting Algorithm Based on the Decomposition of the Information Matrix,” Automatica, Vol.36, No.11, pp.1725-1731, 2000. [https://doi.org/10.1016/S0005-1098(00)00093-5]