자율주행을 위한 정적 장면 컨텍스트 변조 기반 차량 궤적 예측 네트워크
Copyright Ⓒ 2023 KSAE / 213-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In this paper, we are proposing a vehicle trajectory forecasting network based on static scene context modulation. First, in modeling the distribution over future trajectories efficiently via variational auto-encoder frameworks, we suggest using a transformer-based trajectory encoder that models the interaction between neighboring vehicles. The proposed encoder is trained to remove interaction between irrelevant vehicles, and model key interaction more efficiently. Moreover, to increase the diversity of generated trajectories, we propose using latent variables during the trajectory generation process in modulating static scene context. Then, we can use large-scale, real-world datasets like nuScenes in evaluating performance. Experimental results showed that the proposed model generates plausible and diverse future trajectories with the techniques proposed in this paper. Furthermore, it outperformed the baseline models in terms of prediction accuracy.
Keywords:
Autonomous driving, Deep learning, Trajectory forecasting, Planning, Context modulation키워드:
자율주행, 딥러닝, 궤적 예측, 판단, 컨텍스트 변조1. 서 론
최근 10년 사이 자율주행기술은 센서 및 인공지능 분야의 혁신과 더불어 비약적인 발전을 이루었다. 일부 자동차 제조 회사들은 낮은 수준의 자율주행 기능이 탑재 된 차량을 판매하고 있으며 일부 IT 기업들은 개발된 완전 자율주행차량을 이용하여 제한된 지역 내에서 택시 서비스를 제공하고 있다.
대부분의 자율주행시스템은 인지(Perception), 판단(Planning), 제어(Control) 세 단계의 연속으로 이루어진 프레임워크를 따르고 있다. 인지 단계에서는 시스템이 자율주행차의 현재 위치 및 자세를 추정함과 동시에 자율차 주변의 동적, 정적 객체를 인식한다. 이러한 인식 결과를 바탕으로 판단 단계에서는 자율차의 이동 경로를 결정하고 제어 단계에서는 이동 경로를 따라 차량을 이동시키기 위한 제어 신호를 계산한다.
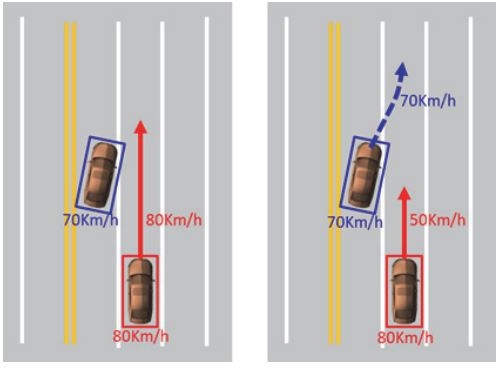
판단 단계에서 자율차의 이동 경로를 결정 시 주변 이동 객체들의 미래 움직임을 고려하는 것은 안전을 위해 매우 중요하다. Fig. 1은 그 예를 보여주고 있다. 그림에서 붉은색 사각형은 자율주행차량을 파란색 사각형은 주변 차량을 의미한다. 사각형 아래의 속도는 각 차량의 현재 속도이다. 붉은색 화살표는 판단 과정에서 결정된 이동 경로 및 속도이며 파란색 점선 화살표는 주변 차량의 미래 이동 경로이다. Fig. 1의 왼쪽 그림과 같이 주변 차량의 미래 움직임을 알 수 없는 경우 자율차의 판단 시스템은 현재 속도를 유지하도록 이동경로를 설정하며 이는 충돌을 야기한다. 그러나 오른쪽 그림과 같이 주변 차량이 자율차가 주행하는 차선으로 이동할 것을 미리 예측할 수 있다면 자율차의 속도를 줄이도록 이동경로를 설정할 수 있고 그 결과 충돌을 미리 방지할 수 있다.
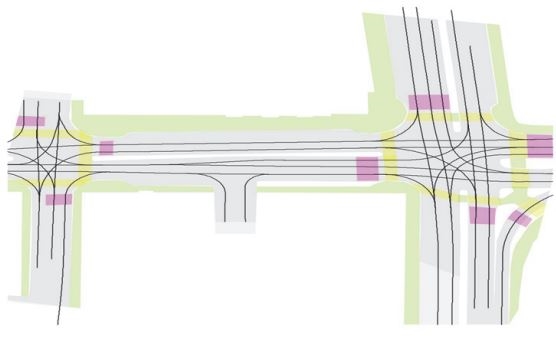
고정밀 지도(High definition map)는 자율주행을 위해 센티미터(cm) 수준의 정밀도를 갖도록 제작한 3D 입체 지도이다. 도로 중심선, 경계선 등 차선 단위의 정보는 물론 신호등, 표지판, 연석, 노면마크, 각종 구조물 등의 정보가 3차원 위치정보 데이터로 담겨있다. 고정밀 지도는 인지 단계에서 자율차의 자기위치인식 뿐만이 아니라 판단 단계에서 이동 경로의 계획 및 생성에도 활용된다. Fig. 2는 nuScenes1) 데이터셋이 제공하는 고정밀 지도를 가시화한 결과를 보여준다. 그림에서 검은 실선은 차로 중앙선, 회색 영역은 주행 가능 영역, 노란색 영역은 횡단보도, 초록색 영역은 인도를 나타낸다.
일반 도로 위 차량의 움직임은 도로 구조 및 차선의 형태에 많은 제약을 받는다. 따라서 자율차 주변 차량의 미래 움직임 예측에 있어 고정밀 지도의 활용은 정확한 움직임 예측을 위해 매우 중요하다. 그 결과 자율차 주변 차량의 미래 움직임을 예측하기 위해 고정밀 지도를 활용하는 다양한 방법들이 제안되었다. 고정밀 지도를 활용하는 방법은 크게 두 가지로 나뉘는데 첫 번째는 고정밀 지도 내 차선 등의 정보를 2D 이미지로 그리는 방식이며 두 번째는 차선 등의 정보를 2차원 좌표값들의 연속인 벡터로 표현하는 것이다. 전자의 경우 횡단보도, 주행가능영역 등과 같은 영역 정보를 표현하기에 유리하며 후자의 경우 차선과 같은 선 정보를 보다 세밀하게 표현 가능하다는 장점이 있다.
본 논문에서는 고정밀 지도가 그려진 2D 이미지를 활용하여 차량의 미래 움직임을 예측하는 딥 뉴럴 네트워크(Deep neural network, DNN)을 제안한다. 제안하는 DNN의 특징은 다음과 같다. 1) 차량 사이의 상호작용을 그래프로 정의하고 Transformer2)를 통해 효율적으로 모델링한다. 이를 통해 차량의 과거 움직임 이력 및 고정밀 지도 정보로부터 차량의 미래 궤적을 보다 정확히 예측할 수 있게 된다. 2) 미래 궤적의 확률 분포로부터 궤적을 샘플링(Sampling) 하는 과정에서 은닉 변수(Latent variable)를 이용하여 고정밀 지도 정보와 관련된 정적 장면 컨텍스트 피쳐(Static scene context feature)를 변조한다. 이를 통해 샘플링 된 궤적들의 다양성(Diversity)이 증가 된다.
2. 관련 연구
2.1 미래 궤적 예측 기법
이동 객체의 미래 궤적 예측은 컴퓨터 비젼(Computer vision) 분야에서 오랫동안 관심을 받아왔으며 많은 연구자들이 관련 연구를 공개하고 있다. 초창기 미래 궤적 예측은 주로 보행자에 초점이 맞추어져 있으며 정확한 예측을 위해 보행자 사이의 상호작용을 모델링 하는 것이 가장 큰 관심사였다. 그 이유는 보행자의 움직임은 보행자가 가고자 하는 목적지뿐 아니라 주변 보행자의 움직임에 의해 크게 영향을 받기 때문이다. Social force,3) Gaussian process4) 등은 보행자 사이의 상호작용을 모델링 하는 가장 대표적인 수학적 모델이다.
딥러닝(Deep learning)의 발전과 더불어 시계열 데이터의 학습에 용이한 Recurrent neural network(RNN)이 소개됨에 따라 RNN를 이용해 보행자 사이의 상호작용을 학습하고자 하는 시도가 이루어졌다. Alahi 등5)은 RNN의 은닉 상태(Hidden state)를 이용하여 보행자 사이의 상호작용을 학습하는 방식인 Social pooling을 처음으로 제안하였으며 이는 기존의 수학적 모델 기반 방식들 보다 월등한 성능을 보였다. 이후 많은 연구자들이 Social pooling 방식에 영감을 받아 보행자 또는 차량 사이의 상호작용을 모델링하는 다양한 방식을 제안했다. Gupta 등6)은 Max-pooling 기법을 통해 멀리 있는 보행자 사이의 상호작용 또한 고려하는 방식을 제안하였으며 Sadeghian 등7)은 Attention 방식을 도입하여 관련성이 높은 보행자 사이의 상호작용이 전체 상호작용에서 높은 비중을 갖도록 하는 방식을 제안하였다.
이동 객체와 이동 객체 사이의 상호작용을 각각 그래프의 노드(Node)와 엣지(Edge)로 모델링 하고 Graph neural network(GNN)를 통해 상호작용을 모델링 하고자 하는 시도도 많이 이루어져 왔다. Kosaraju 등8)은 Graph attention network(GAT)을 통해 동일 시점에 존재하는 객체 사이의 상호작용을 모델링 하는 방식을 제안하였다. 상호작용 학습 시 동일 시점뿐 아니라 서로 다른 시점의 객체도 고려하기 위해 Huang 등9)은 Spatio-temporal GAT을 제안하였다.
Transformer2)는 Self-attention을 기반으로 하는 자연어 처리를 위해 고안된 DNN이다. Transformer가 자연어 처리와 관련된 작업에서 매우 우수한 성능을 보여줌이 확인된 이후로 많은 분야에서 Transformer를 사용해 왔으며 미래 궤적 예측도 그중 한 분야이다. Transformer를 이용하여 객체 사이의 상호작용을 모델링하는 여러 방식이 제안되었으며 그 중 AgentFormer10)는 차량 사이의 상호작용을 모델링하기 위해 Transformer를 도입하였다. 본 논문에서도 차량 사이의 상호작용을 Transformer를 통해 모델링 한다. 그러나 보다 효과적인 모델링을 위해 목표 차량과 연관성이 낮은 주변 차량과의 상호작용을 완전히 무시하는 새로운 Self-attention 방식을 제안한다.
2.2 미래 궤적 예측을 위한 고정밀 지도 사용
미래 궤적 예측에 고정밀 지도를 활용하는 방법은 크게 두 가지로 나뉜다. 첫 번째는 고정밀 지도 내 차선 등의 정보를 2D 이미지로 그리는 방식이며11-13) 두 번째는 차선 등의 정보를 2차원 좌표값들의 연속인 벡터로 표현하는 것이다.14-16) 첫 번째 방식은 횡단보도, 주행가능영역 등과 같은 영역 정보를 표현하기에 유리하나 2D 이미지의 크기를 무한정 키울 수 없어 차선 등의 정보를 세밀하게 표현하는데 한계가 있다. 이에 반해 두 번째 방식은 차선 등의 정보를 보다 세밀하게 표현 가능하다는 장점이 있으나 영역 정보를 표현하는데 한계가 있다. 본 논문에서는 고정밀 지도 내 정보를 2D 이미지에 그려서 사용하는 방식을 따른다. Fig. 2는 고정밀 지도 정보를 2D 이미지에 그린 예를 보여주고 있다. 보다 구체적으로는 Rotated region of interest(RROI) pooling17) 기법을 이용하여 전역 지도 정보로부터 목표 차량 주변 영역의 지도 정보를 추출한 후 목표 차량을 위한 지역 지도 정보로 사용한다.
2.3 미래 궤적 확률 분포 학습을 위한 생성 모델
이동 객체의 미래 위치를 예측하는 것은 매우 어려운 일이다. 그 이유는 목적지와 같은 객체의 의도는 관찰자가 알 수 없기 때문이다. 이러한 이유로 많은 연구자들이 이동 객체의 미래 궤적 확률분포 학습을 제안해 왔다. 예측된 미래 궤적 분포로부터 다양한 궤적을 샘플링 하여 객체가 이동할 수 있는 여러 경우를 고려할 수 있기 때문이다.
은닉 변수(Latent variable)를 통해 데이터의 확률분포를 학습하는 방식 중 Variational auto-encoder(VAE)18)와 Generative adversarial networks(GAN)19)이 가장 널리 사용된다. 이 중 VAE는 이론적으로 잘 정립되어 있고 학습이 쉬우며, 훌륭한 다양체 표현(Manifold representation)을 가지고 있다. 이러한 이유로 VAE를 활용하여 미래 궤적의 확률분포를 학습하는 다양한 방식이 제안되었다. 그러나 VAE는 학습과정에서 은닉 변수가 무시 되어 예측된 확률분포로부터 동일한 궤적이 샘플링되는 사후 붕괴(Posterior collapse)20) 문제가 자주 발생한다.
VAE의 사후 붕괴를 막기 위해 다양한 방식이 제안되었으며 이는 주로 이미지 생성 및 합성 분야에 많이 활용되어 왔다.20-22) 미래 궤적 예측에서는 Casas 등12)이 사후 붕괴를 최소화하기 위해 Cyclic annealing22) 기법을 사용하였다. 본 논문에서는 VAE의 사후 붕괴를 완화하기 위해 은닉 변수를 이용하여 고정밀 지도로부터 획득한 정적 장면 컨텍스트 벡터를 변조하는 방식을 제안한다. 미래 궤적의 확률분포 특성을 포함하는 은닉 변수가 정적 장면 컨텍스트 벡터를 직접 변조함으로써 정적 장면 컨텍스트와 은닉 변수로부터 미래 궤적을 샘플링 하는 과정에서 은닉 변수가 무시되는 문제가 완화된다.
3. 제안하는 네트워크
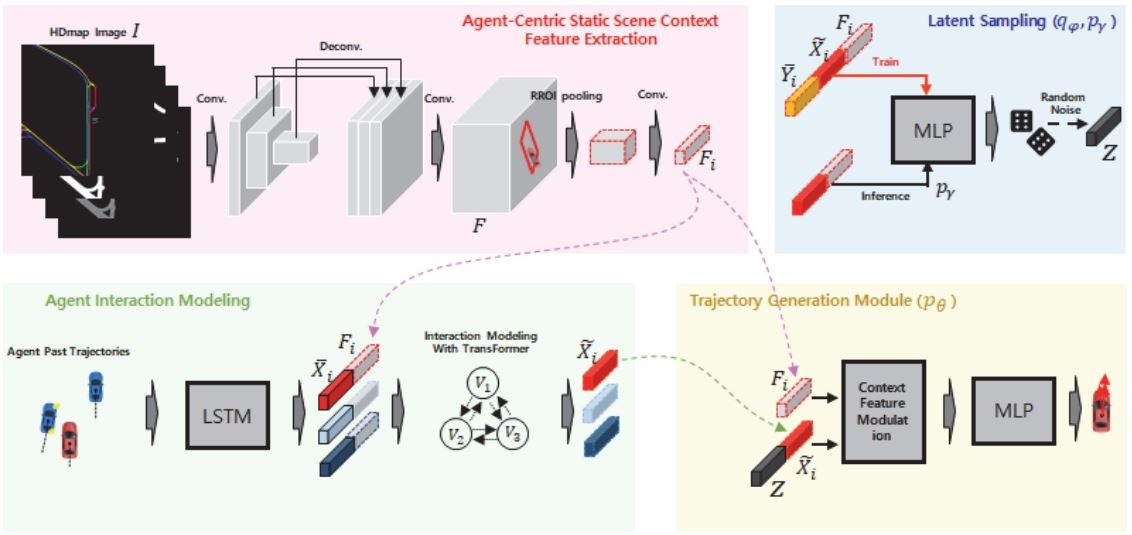
Fig. 3은 제안하는 네트워크의 구조를 보여준다. 먼저 Agent-centric static scene context feature extraction module은 고정밀 지도 이미지로부터 차량 중심의 정적 장면 컨텍스트 피쳐(Agent-centic static scene context feature, ASSCF)를 추출한다. Agent interaction modeling module은 차량의 과거 궤적을 인코딩 한 후 주변 차량과의 상호작용을 반영하여 인코딩을 갱신한다. 이때 갱신은 제안하는 Transformer 구조의 Neural network(NN)를 이용하여 이루어진다. Latent sampling module은 미래 궤적 분포를 모델링하는 가우시안(Gaussian) 분포로부터 은닉 변수를 샘플링 한다. 마지막으로 Trajectory generation module은 ASSCF, 상호작용이 반영된 과거 궤적 인코딩, 그리고 은닉 변수를 이용하여 미래 궤적 분포로부터 미래 궤적을 생성한다.
3.1 문제의 정의
현재 시간 t의 시점에 자율차를 포함하여 총 N개의 차량 이 있다고 가정하자. 우리의 목표는 확률 분포 Pθ(Y|X,C)를 모델링 하는 것이다. 여기서 는 Vi의 과거 H time-step 동안의 상태 정보, 그리고 는 Vi의 미래 T time-step 동안의 상태 정보이다. 본 논문에서는 를 다음과 같이 정의하였다.
| (1) |
여기서 는 Vi의 시간 t에서의 전역 위치 좌표이며 는 를 Vi 중심의 위치 좌표계로 변환한 결과이다. C는 고정밀 지도로부터 얻을 수 있는 정적 장면 정보이며 마지막으로 θ는 NN의 파라메터이다. 따라서 우리는 Pθ(Y|X,C)를 최대화 하는 θ를 다음과 같이 찾아야 한다.
| (2) |
그러나 N이 커질수록 최대화 문제는 매우 복잡해지므로 I.I.D 가정을 통해 다음과 같이 최대화 문제의 복잡도를 줄일 수 있다.
| (3) |
이제 최대화 문제는 -logPθ(Yi∣Xi,C)의 최소화 문제로 바뀔 수 있으며 이는 은닉 변수 z의 도입과 함께 Evidence lower bound(ELBO)의 최소화로 해결할 수 있다18):
| (4) |
여기서 β는 임의의 상수, qϕ는 근사화된 사후 확률분포, pγ는 사전 확률분포, KL은 Kullback-leibler divergence이다.
3.2 Agent-centic Static Scene Context Feature Extraction
이 과정은 고정밀 지도로부터 목표 차량 중심의 정적 장면 컨텍스트 피쳐(Agent-centic static scene context feature, ASSCF)를 추출한다. Fig. 3의 좌상단 영역의 이미지가 그 과정을 보여주고 있다. 먼저 자율차를 중심으로 특정 범위 내 모든 고정밀 지도 정보를 2D 이미지로 그린다. 본 논문에서는12)를 따라서 차로 중심선, 주행가능영역, 횡단보도 등의 정보를 2D 이미지의 각 채널에 그려 넣었다. 고정밀 지도 이미지는 먼저 ResNet5023)를 거쳐 복수의 피쳐맵으로 변환된다. 서로 다른 크기의 피쳐맵들은 보간 과정을 거쳐 동일 크기로 변환되며 채널(Channel) 방향으로 이어붙여 진 후 별도의 Convolution layer를 거쳐 최종적으로 하나의 피쳐맵이 된다. 고정밀 지도 이미지와 피쳐맵을 각각 와 라 하자. 일반적으로 을 만족하여 s는 1보다 큰 상수이다.
피쳐맵으로부터 를 추출하기 위해 Rotated region of interest(RROI) pooling17) 기법을 사용한다. 먼저 Fig. 3의 그림처럼 목표 차량의 현재 위치와 헤딩(Heading) 방향을 고려하여 차량 주변 영역에 해당하는 F 안의 일부 영역을 추출한다. 추출된 피쳐맵은 다시 Convolutional layer를 거쳐 Fi로 변환된다.
앞서 언급한 바와 같이 NN의 입력으로 사용되는 고정밀 지도 이미지는 자율차를 중심으로 특정 범위 내 존재하는 모든 지도 정보를 포함한다. 그러나 자율차 주변 목표 차량의 미래 궤적 예측에는 목표 차량 주변의 지도 정보만 사용하는 것이 효과적이다. 따라서 본 논문에서는 목표 차량의 미래 궤적 예측 시 F 전체를 사용하는 대신 목표 차량 주변의 지도 정보에 해당하는 Fi를 F로부터 추출하여 사용하도록 설계하였다.
3.3 Agent Interaction Modeling
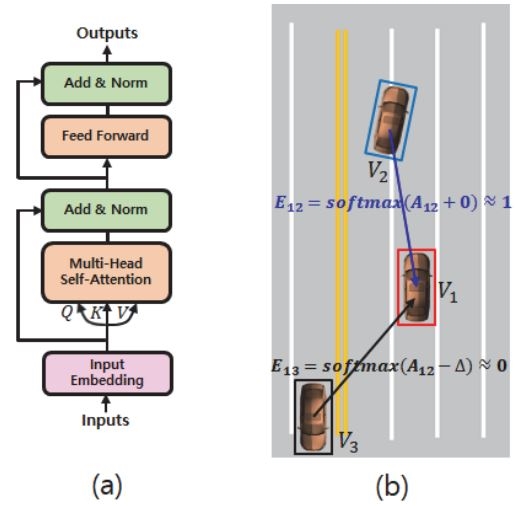
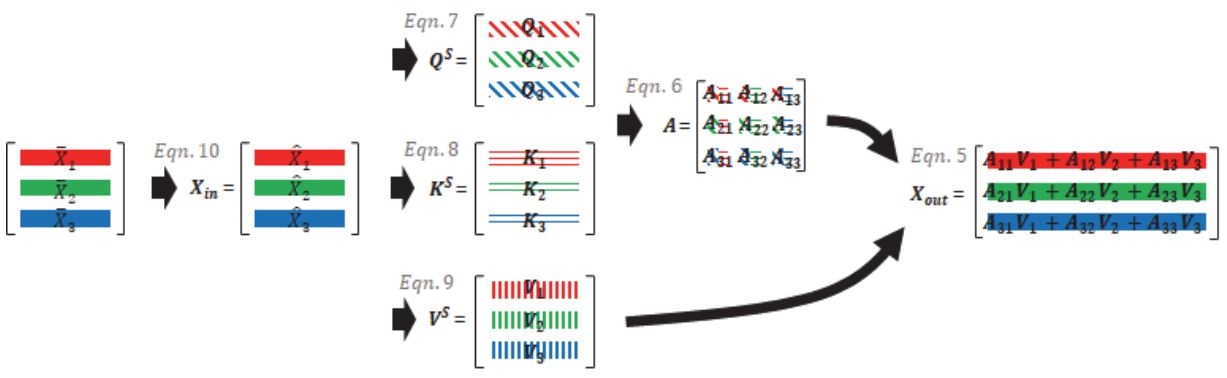
자율차 주변 차량의 과거 궤적 Xi를 Long short-term memory(LSTM)을 통해 인코딩한 결과를 라 하자. 는 주변 차량 사이의 상호작용 모델을 통해 로 갱신되며 그 방법은 다음과 같다. 주변 차량 사이의 상호작용을 모델링하기 위해서 먼저 그래프 G(V,E)를 정의한다. 여기서 는 노드(Node)들의 집합이며 는 노드들 사이의 상호작용을 나타내는 엣지(Edge)이다. 따라서 Vi는 자율차 주변 i번째 차량에 해당하며 Ei,j는 자율차 주변 i번째 차량과 j번째 차량 사이의 상호작용이다. 본 논문에서는 G(V,E)를 정의하기 위한 NN로 Transformer2)를 사용한다. Fig. 4의 (a)는 Transformer의 구조를 보여주고 있다. Transformer는 아래의 식과 같이 Self-attention을 이용하여 노드들 사이의 상호작용을 계산하고 노드들의 피쳐를 갱신한다.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
여기서 과 은 입력 및 출력 피쳐 행렬로 i번째 행은 노드 Vi의 피쳐에 대응된다. 은 NN의 학습 가능한 파라메터이다. QS, KS, VS는 각각 Query, Key, Value로 Self-attention의 입력으로 사용되며 식 (7) ~ (9)의 정의에서 알 수 있듯이 WQ,WK,WV를 이용하여 Xin을 사영시킨 결과물이다. 본 논문에서는 Xin의 i번째 행, 즉 노드 Vi의 피쳐를 다음과 같이 계산한다.
| (10) |
여기서 [a;b]은 a와 b 두 벡터의 이어 붙임 연산을 말하며 MLP()는 Multi-layer perceptron(MLP)을 의미한다. 식 (10)의 정의에서 알 수 있듯이 Vi의 피쳐는 i번째 차량의 과거 움직임 정보뿐만이 아니라 차량 주변의 지도 정보를 포함하고 있다. 따라서 노드 사이의 상호작용 계산 시 차량의 움직임을 보다 명확히 반영할 수 있게 된다. 마지막으로 AS의 i번째 행 j번째 열의 요소 Aij는 Vi와 Vj사이의 상호작용을 의미하며 식 (6)과 같이 스케일링 된 내적으로 계산된다.
식 (5)의 Attetion 과정은 모든 노드 사이의 상호작용을 반영하여 노드의 피쳐를 갱신한다. 그림 5는 그 과정을 그림을 통해 설명하고 있다. 그러나 아주 멀리 떨어진 차량 사이의 상호작용은 완전히 무시되는 것이 상호작용 계산에 유리하다. 그 이유는 사람은 운전 속도 및 도로 상황에 따라 고려할 주변 대상을 다르게 정하기 때문이다. 본 논문에서는 이를 Self-attention에 반영하기 위해 Learnable masking 기법을 제안한다. 먼저 다음의 추가적인 Self-attention을 통해 마스크 을 계산한다.
| (11) |
| (12) |
| (13) |
| (14) |
여기서 a는 임의의 상수로 sigmoid함수의 기울기를 결정한다. 본 논문에서는 a의 값으로 100을 설정하였다. δ는 학습이 가능한 변수이다. 식 (11)에서 알 수 있듯이 AM의 요소들은 sigmoid함수에 의해 0 또는 1의 값으로 변환되어 M의 요소가 되며 이는 학습 가능한 δ에 의해 결정된다. 다음으로 식 (6)을 다음과 같이 변형한다.
| (15) |
여기서 ∆는 임의의 매우 큰 양수이며 본 논문에서는 1010으로 정하였다. 식 (15)의 오른쪽 마지막 항에서 계산되는 노드 사이의 상호작용 값은 오른쪽 첫 번째 항의 M에 의해 원래의 값을 유지하거나 혹은 매우 작은 음의 값이 된다. 따라서 AS가 식 (5)의 softmax함수를 거치게 될 경우 매우 작은 음의 값이 된 상호작용 값은 0에 수렴하게 되며 그 결과 노드 피쳐의 갱신 과정에서 완전히 무시 된다. Fig. 4의 (b)는 그 예를 보여주고 있다. 4장의 실험 결과는 제안하는 Learnable mask의 도입으로 제안하는 NN의 미래 궤적 예측 성능이 향상됨을 보여준다.
3.4 Latent Sampling Module
식 (4)에서 보듯 미래 궤적의 확률분포는 은닉 변수 z에 의해 모델링되며 z는 근사화 된 사후 확률분포 를 따른다. 본 논문에서는 qϕ를 다음의 NN로 정의한다.
| (16) |
여기서 는 미래 궤적 Yi를 LSTM을 통해 인코딩한 결과이며 는 Transformer를 통해 갱신된 차량의 과거 궤적 인코딩이다. 마지막으로 μq와 σq는 사후 확률분포의 평균과 분산 벡터이다. qϕ로부터 z의 샘플링은 Re-parameterization18) 기법을 통해 다음과 같이 이루어진다.
| (17) |
여기서 ϵ은 정규분포를 따르는 랜덤 벡터이다. 식 (4)의 사전 분포 pγ는 다음과 같이 NN로 정의한다.
| (18) |
식 (4)의 ELBO의 정의에서 알 수 있듯이 qϕ는 학습 과정에서만 사용할 수 있다. 그 이유는 는 테스트 과정에서 사용할 수 없기 때문이다. 따라서 EBLO의 KL divergence를 통해 pγ가 qϕ를 따르도록 학습하고 테스트 시에 pγ를 통해 z를 샘플링 한다.
3.5 Trajectory Generation Module
샘플링 된 은닉 변수 z로부터 미래 궤적을 생성할 때 일반적으로 다음과 같이 이어 붙임 연산을 이용한다.
| (19) |
그러나 VAE의 사후 붕괴 문제로 인해 미래 궤적을 생성하는 과정에서 z가 종종 무시되며 결국 샘플링된 다수의 z로부터 식 (19)를 통해 생성된 미래 궤적들이 매우 유사한 모습을 띄게 된다. 본 논문에서는 이러한 사후 붕괴 현상을 완화하기 위해 Latent modulation 기법을 제한한다:
| (20) |
| (21) |
여기서 ⊙는 요소별 곱하기 연산이다. 정적 컨텍스트 정보 Fi는 Vi 주변의 차로 중심선, 주행 가능영역 등의 정보를 압축하여 포함하고 있다. 식 (21)은 z를 이용하여 Fi를 직접적 변조함으로써 미래 궤적 생성 시 정적 컨텍스트 정보를 보다 다양하게 활용하도록 고안되었다. 4장의 실험 결과에서 보듯 단순 이어 붙임 연산을 통해 z를 사용하는 것보다 제안하는 변조 방식을 통해 z를 이용하는 것이 다양한 궤적 생성에 더 효과적임을 할 수 있다.
3.6 학습 방법
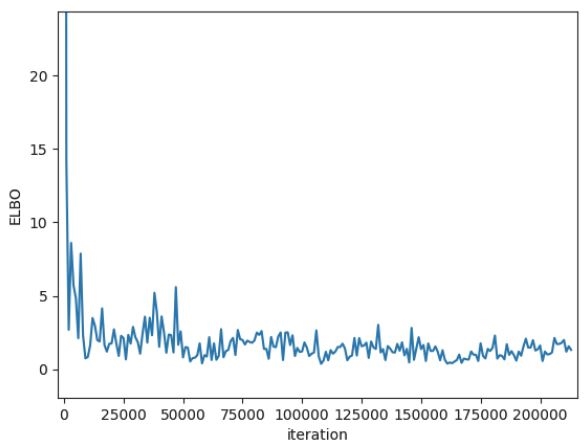
제안하는 NN모델은 식 (4)의 ELBO를 최소화 하도록 학습되었다. 식 (4)의 β는 0.5로 고정하였으며 이는 실험을 통해 정하였다. 최소화를 위해 Adam optimizer24)를 사용하였으며 Batch size는 8, Initial learning rate은 0.001로 정하고 50 epoch 동안 학습하였다. 그림 6은 학습 횟수에 따른 식 (4)의 LELBO 변화를 보여주고 있다. 학습과정 초반 동안 LELBO은 매우 빠르게 감소하다가 그 이후로 안정되는 모습을 볼 수 있다. NN의 학습 및 테스트를 위한 PC의 사양은 다음과 같다: Intel i7 CPU, 32 GB RAM, NVIDIA RTX 2080Ti GPU.
4. 실험 결과
4.1 데이터 셋
본 논문에서는 제안하는 모델 및 비교 평가를 위한 모델의 학습 및 테스트를 위해 nuScenes1) 데이터 셋을 사용하였다. 이 데이터 셋은 Boston과 Singapore에서 수집한 20초 길이의 1000개의 시퀀스로 이루어져 있다. 또한 각 시퀀스에 포함된 도로 위 객체의 3D bounding box와 각 객체의 Tracking ID 및 고정밀 지도를 제공한다.
본 논문에서는 자율차 주변 차량에 대하여 2초의 과거 궤적으로부터 4초의 미래 궤적을 예측하도록 모델을 학습하였다. 이를 위해 6초 길이의 연속되는 로깅 데이터로부터 주변 차량의 Tracking ID 및 3D Bounding box를 획득하고 Box의 중심점을 계산하여 학습에 필요한 궤적을 획득하였다. 또한 고정밀 지도 이미지를 획득하기 위해 2초 시점에서의 자율차의 위치 정보를 획득하고 해당 위치로부터 90미터 이내의 모든 지도 정보를 900×900 Pixels 크기의 이미지 위에 그렸다. 고정밀 지도 이미지는 3.2절에서 설명한 바와 같이 Convolution 과정을 거쳐 피쳐 맵 F로 변환된다.
4.2 평가 지표
모델의 객관적 평가를 위해 기존 연구에서 사용하는 두 가지 지표 Average displacement error(ADE)와 Final displacement error(FDE)를 사용하였으며 이 둘은 다음과 같이 정의 된다.
| (22) |
| (23) |
여기서 , Y와 는 각각 정답 미래 궤적과 예측된 미래 궤적을 의미한다. 본 논문에서는 ADEK와 FDEK를 각각 생성된 K개의 미래 궤적 중 ADE와 FDE의 최소값으로 정의하겠다. Choi 등16)에 따르면 ADE1과 FDE1은 모델에 의해 생성된 궤적의 평균 퀄리티를 ADEK≥15와 FDEK≥15 모델에 의해 생성된 궤적의 최고 퀄리티를 의미한다.
4.3 비교 대상 모델
● CoverNet11): 고정밀 지도 이미지와 자율차의 현재 상태를 입력으로 받아 다이내믹하게 갱신되는 미래 궤적 후보들로부터 최적의 미래 궤적들은 선택하는 모델.
● ILVM12): 고정밀 지도 이미지 및 연속되는 라이다 포인트 클라우드(Lidar point cloud)로부터 객체를 검출하고 검출된 객체 주변의 맵 피쳐로부터 객체의 미래 궤적을 예측하는 모델.
본 논문에서는 공정한 비교를 위해 각 모델이 사용하는 고정밀 지도 이미지를 일치시켰다. 단, CoverNet의 경우 고정밀 지도 이미지 외에 주변 객체의 과거 움직임 이미지가 별도로 필요하기 때문에 고정밀 지도 이미지와 과거 움직임 이미지를 채널 방향으로 이어붙임을 하여 사용하였다. 또한 ILVM을 학습 시 라이다 포인트 클라우드 대신 주변 객체의 과거 궤적을 LSTM을 통해 인코딩하여 사용하는 방식을 별도로 테스트하였으며 이 모델을 ILVM(Trajectory)라고 표현하였다.
4.4 객관적 평가
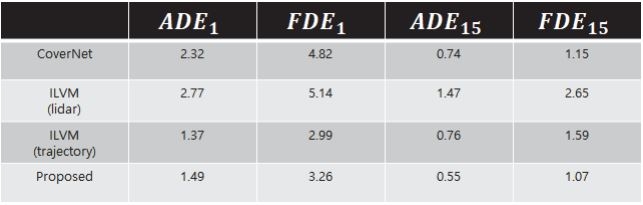
Table 1은 각 모델의 객관적 평가 결과를 보여준다. 앞에서 언급한 바와 같이 ADE1과 FDE1은 모델에 의해 생성된 궤적의 평균 퀄리티를 ADEK≥15와 FDEK≥15은 모델에 의해 생성된 궤적의 최고 퀄리티를 의미한다. 표에서 알 수 있듯이 제안하는 모델에 의해 생성된 궤적의 평균 및 최고 퀄리티가 매우 우수함을 알 수 있다. 특히 최고 퀄리티의 경우 나머지 모델에 비해 최대 2배 이상 개선됨을 알 수 있다. 평균 퀄리티의 경우 ILVM(Trajectory)가 가장 좋음을 알 수 있다. 그러나 ILVM(Trajectory)의 경우 생성된 궤적들의 다양성이 매우 부족하여 최고 퀄리티가 매우 나쁨을 알 수 있다. 마지막으로, 객체의 과거 궤적 대신 연속 된 라이다의 포인트 클라우드를 사용하는 ILVM이 가장 나쁜 성능을 보임을 알 수 있다. nuScenes 데이터 셋이 제공하는 라이다 포인트 클라우드의 경우 채널 수가 32로 매우 낮은 편에 속한다. 따라서 연속되는 포인트 클라우드로부터 자율차로부터 멀리 있는 객체의 과거 움직임 이력을 계산함에 있어 NN가 많음 어려움을 겪었을 것으로 예상한다.
4.5 제안하는 모델의 특성 분석
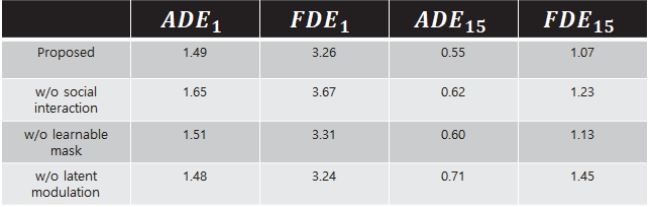
Table 2는 본 논문에서 제안하는 여러 기법들이 제안하는 모델의 성능 개선에 얼마나 도움을 주는지를 보여주고 있다. 표의 Proposed는 제안하는 모델의 학습 결과이다. w/o social interaction은 제안하는 모델에서 과거 궤적을 LSTM으로 인코딩 후 Transformer를 적용시키지 않았을 때의 결과이다. w/o learnable mask는 Transformer 적용 시 식 (15)의 Masking을 적용하지 않았을 때의 결과이다. 마지막으로 w/o latent modulation은 제안하는 모델에서 식 (21)의 Latent modulation을 적용하지 않았을 때의 결과이다. 표에서 알 수 있듯이 주변 객체 간의 상호작용을 고려하는 것이 모델의 성능 개선에 매우 중요함을 알 수 있다(Proposed v.s. w/o social interaction). 또한 제안하는 Learnable masking은 주변 객체 간의 상호작용을 보다 잘 모델링하는 데에 도움을 주는 것을 알 수 있다(Proposed v.s. w/o learnable mask). 마지막으로 제안하는 Latent modulation기법을 통해 생성된 궤적들의 다양성이 매우 높아지는 것을 알 수 있다(Proposed v.s. w/o latent modulation).
4.6 주관적 평가
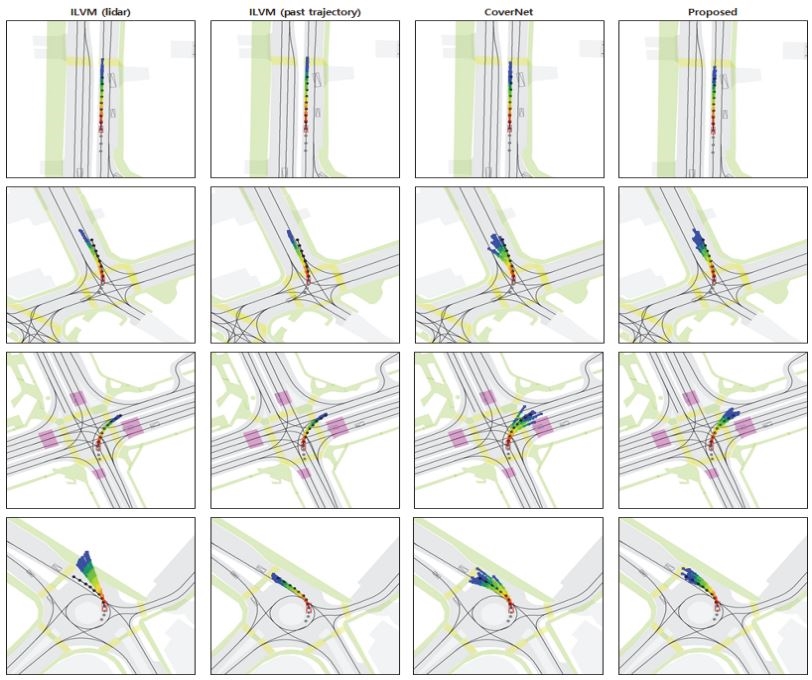
Fig. 7은 각 모델을 이용하여 객체의 미래 궤적을 예측한 결과이다. 그림에서 붉은색 사각형과 회색 사각형은 각각 목표 객체 및 주변 객체이다. 회색 동그라미는 과거 움직임 이력이며 검은색 동그라미는 객체의 실제 미래 움직임이다. 마지막으로 무지개색 실선은 생성된 15개의 미래 궤적이다. 그림에서 각 열은 서로 다른 모델에 의해 생성된 결과를 보여준다. 그림에서 알 수 있듯이 제안하는 모델은 실제 움직임과 매우 유사하면서도 다양하고 상황에 어울리는 미래 궤적을 생성함을 알 수 있다. 그러나 ILVM의 경우 실제 움직임과는 유사하지만 다양성이 매우 낮음을 알 수 있다. 마지막으로 CoverNet의 경우 상황에 어울리지 않는 궤적이 상당히 많이 생성됨을 알 수 있다.
5. 결 론
본 논문에서는 고정밀 지도 기반 미래 궤적 예측 네트워크를 제안하였다. VAE를 이용한 미래 궤적의 확률분포의 모델링을 보다 효과적으로 수행하기 위해 먼저 Transformer 기반의 차량 궤적 인코더를 제안하였다. 제안하는 인코더는 Learnable mask를 통해 관련성이 적은 차량 사이의 상호작용을 제거하도록 학습되며 따라서 과거 궤적 인코딩 시 차량 사이의 상호작용을 보다 효과적으로 반영할 수 있다. 또한 제안하는 모델에 의해 생성되는 궤적들의 다양성을 높이기 위해 은닉 변수를 이용하여 정적 장면 컨텍스트 정보를 변조하는 방식을 제안하였다. 대규모 실제 데이터를 통한 학습 및 테스트 결과는 제안하는 모델이 주행 상황에 어울리는 매우 다양한 미래 궤적을 생성함을 보여주었다.
Acknowledgments
이 논문은 2021년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(No.2021-0-00891, (총괄/1세부) 자율주행 AI 서비스 통합 프레임워크 개발).
References
-
H. Caesar, V. Bankiti, A. H. Lang, S. Vora, V. E. Liong, Q. Xu, A. Krishnan, Y. Pan, G. Baldan and O. Beijbom, “nuscenes: A Multimodal Dataset for Autonomous Driving,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.11621-11631, 2020.
[https://doi.org/10.1109/CVPR42600.2020.01164]

- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, “Attention is All You Need,” Advances in Neural Information Processing Systems, 2017.
-
D. Helbing and P. Molnar, “Social Force Model for Pedestrian Dynamics,” Physical Review E, Vol.51, No.5, Paper No.4282, 1995.
[https://doi.org/10.1103/PhysRevE.51.4282]

- M. K. C. Tay and C. Laugier, “Modeling Smooth Paths Using Gaussian Process,” Field and Service Robotics, 2008.
-
A. Alahi, K. Goel, V. Ramanathan, A. Robicquet, L. Fei-Fei and S. Savarese, “Social LSTM: Human Trajectory Prediction in Crowded Spaces,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp.961-971, 2016.
[https://doi.org/10.1109/CVPR.2016.110]

-
A. Gupta, J. Johnson, L. Fei-Fei, S. Savarese and A. Alahi, “Social GAN: Socially Acceptable Trajectories with Generative Adversarial Networks,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp.2255-2264, 2018.
[https://doi.org/10.1109/CVPR.2018.00240]

-
A. Sadeghian, V. Kosaraju, A. Sadeghian, N. Hirose, S. H. Rezatofighi and S. Savarese, “SoPhie: An Attentive GAN for Predicting Paths Compliant to Social and Physical Constraints,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.1349-1358, 2019.
[https://doi.org/10.1109/CVPR.2019.00144]

- V. Kosaraju, A. Sadeghian, R. M. Martin, I. Reid, S. H. Rezatofighi and S. Savarese, “Social-BiGAT: Multimodal Trajectory Forecasting Using Bicycle-GAN and Graph Attention Networks,” Advances in Neural Information Processing Systems, 2019.
-
Y. Huang, H. Bi, Z. Li, T. Mao and Z. Wang, “STGAT: Modeling Spatial-temporal Interactions for Human Trajectory Prediction,” Proceedings of the IEEE/CVF International Conference on Computer Vision, pp.6272-6281, 2019.
[https://doi.org/10.1109/ICCV.2019.00637]

-
Y. Yuan, X. Weng, Y. Ou and K. Kitani, “AgentFormer: Agent-aware Transformers for Socio-stemporal Multi-Agent Forecasting,” Proceedings of the IEEE/CVF International Conference on Computer Vision, pp.9813-9823, 2021.
[https://doi.org/10.1109/ICCV48922.2021.00967]

-
T. Phan-Minh, E. C. Grigore, F. A. Boulton, O. Beijbom and E. M. Wolff, “CoverNet: Multimodal Behavior Prediction Using Trajectory Sets,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 14074-14083, 2020.
[https://doi.org/10.1109/CVPR42600.2020.01408]

-
S. Casas, C. Gulino, S. Suo, K. Luo, R. Liao and R. Urtasun, “Implicit Latent Variable Model for Scene-consistent Motion Forecasting,” Computer Vision–ECCV 2020: 16th European Conference, pp.624-641, 2020.
[https://doi.org/10.1007/978-3-030-58592-1_37]

-
H. Cui, V. Radosavljevic, F. -C. Chou, T. -H. Lin, T. Nguyen, T. -K. Huang, J. Schneider and N. Djuric, “Multimodal Trajectory Predictions for Autonomous Driving Using Deep Convolutional Networks,” International Conference on Robotics and Automation (ICRA), pp.2090-2096, 2019.
[https://doi.org/10.1109/ICRA.2019.8793868]

-
M. Liang, B. Yang, R. Hu, Y. Chen, R. Lao, S. Feng and R. Urtasun, “Learning Lane Graph Representations for Motion Forecasting,” Computer Vision–ECCV 2020: 16th European Conference, pp.541-556, 2020.
[https://doi.org/10.1007/978-3-030-58536-5_32]

-
B. Kim, S. Park, S. Lee, E. Khoshimjonov, D. Kum, J. Kim, J. Kim and J. Choi, “LaPred: Lane-aware Prediction of Multimodal Future Trajectories of Dynamic Agents,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.14636-14645, 2021.
[https://doi.org/10.1109/CVPR46437.2021.01440]

-
D. Choi and K. W. Min, “Hierarchcial Latent Structure for Multi-modal Vehicle Trajectory Forecasting,” European Conference on Computer Vision, pp.129-145, 2022.
[https://doi.org/10.1007/978-3-031-20047-2_8]

-
J. Ma, W. Shao, H. Ye, L. Wang, H. Wang, Y. Zheng and X. Xue, “Arbitrary-oriented Scene Text Detection Via Rotation Proposals,” IEEE Transactions on Multimedia, Vol.20, No.11, pp.3111-3122, 2018.
[https://doi.org/10.1109/TMM.2018.2818020]

- D. P. Kingma and M. Welling, “Auto-encoding Variational Bayes,” arXiv preprint arXiv:1312.6114, , 2013.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courvill and Y. Bengio, “Generative Adversarial Nets,” Advances in Neural Information Processing Systems, 2014.
- H. Higgins, L. Matthey, A. Pal, C. Burgress, X. Glorot, M. Botvinick, S. Mohamed and A. Lerchner, “Beta-vae: Learning Basic Visual Concepts with a Constrained Variational Framework,” International Conference on Learning Representations, 2017.
- H. Huang, Z. Li, R. He, Z. Sun and T. Tan, “Introvae: Introspective Variational Autoencoders for Photographic Image Synthesis,” Advances in Neural Information Processing Systems, 2018.
- H. Fu, C. Li, X. Liu, J. Gao, A. Celikyilmaz and L. Carin, “Cyclical Anealing Schedule: A Simple Approach to Mitigating Kl Vanishing,” arXiv pre-print arXiv:1903.10145, , 2019.
- K. He, X. Zhang, S. Ren and J. Sun, “Deep Residual Learning for Image Recognition,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.770-778, 2016.
- D. P. Kingma and J. Ba, “Adam: A Method for Stochastic Optimization,” International Conference on Learning Representations, 2015.