차량용 램프 내열 온도 예측을 위한 CFD 해석 및 알고리즘 개발

1. 서 론

고객의 자동차 구매에 있어서 자동차의 가격, 성능, 크기뿐만 아니라 자동차의 심미성 또한 매우 중요한 요소이다. 자동차 외관 디자인에서 차량용 전방 및 후방 램프의 디자인이 심미성에 미치는 영향이 매우 크고, 이로 인해 다양한 디자인의 램프 설계 및 생산으로 이어졌다.^1,2) 하지만 설계된 램프는 자동차 조립에 앞서, 사전 내열 테스트를 필요로 한다. 조명 기술의 발전에 따라 램프에 입력되는 전력의 세기가 증가하였고, 이는 램프의 내열 문제로 이어졌다.³⁾ 램프의 광원에서 발생하는 열은 전도와 대류, 복사의 열전달 메커니즘에 따라 램프의 리플렉터(REF) 및 렌즈(Lens)로 전달되고, 전달된 열이 리플렉터 혹은 렌즈의 제작에 사용된 재료의 내열 한계를 넘어설 경우 Fig. 1과 같이 재료의 변형을 가져오는 문제가 발생하기 때문이다.

Fig. 1

Deformation of automobile lamp material

따라서 내열 측면에서 램프의 변형을 막기 위해 많은 연구가 진행되어 왔고, 램프를 냉각시키기 위하여 다양한 방법이 사용되고 있으나, 이는 램프 제작 비용이 상승하는 문제를 동반하고 있다.^4-7) 설계된 램프의 시제품이 내열 테스트를 통과하기까지는 디자인을 개선하고, 시제품을 재생산하며, 내열 테스트를 반복하는 등의 번거로움이 있으며, 이러한 과정을 줄여 제품 생산의 효율을 증대시키기 위해서는 첫 번째 설계 단계에서 램프의 온도를 예측해 주는 프로그램 개발이 필요하다.⁸⁾ 장영기 등⁹⁾은 램프 내 내열 성능 예측을 위한 내열인자와 주요 인자를 설정하여 램프의 최소 내열 거리를 예측하였다. 또한, 최봉근 등¹⁰⁾은 램프의 점등으로 인해 발생하는 열적인 물리현상을 효과적으로 모사할 수 있는 다수의 해석 기법을 제안하기도 하였다.

전산유체역학(Computational fluid dynamics, CFD)은 온도 예측 정확도가 높고, 다양한 설계 사양에 대한 검토가 가능하다는 장점이 있지만, 해석 소요 시간이 길고 설계 모델이 완성된 후에 해석 진행이 가능하다는 단점이 있다. 따라서 본 연구에서는 빠르고 정확도 높게 온도를 예측해주는 프로그램의 개발을 위해, CFD 해석 데이터를 기반으로 기능별 램프의 온도 특성을 파악하고 이를 기반으로 램프 온도 예측 알고리즘을 개발하였다.

2. CFD 해석 및 결과

본 연구에서는 CFD 해석을 통해 여러 설계 조건에서의 온도 데이터를 생산하였다. CFD 해석은 상용 전산유체역학 Solver인 Fluent 20.1을 사용하였다. 램프 내 열전달 특성을 반영하기 위해 3차원 유한 체적법을 사용하였다. 복사 열전달 모델은 공간을 Discrete Solid Angle로 유한하게 나누어 Radiative Transfer Equation(RTE)을 계산하는 복사 계산 방법인 DO(Discrete Ordinates)모델을 사용하였다.

램프의 온도에 영향을 미치는 주요 인자를 열전달 메커니즘인 전도, 대류, 복사에 따라 설정하였다. 전도 열전달에서는 재료의 열전도율과 두께가 주요 인자이고, 복사 열전달에서는 반사율, 투과율, 열원까지의 거리이다. 본 CFD 해석에 사용된 재료는 Polybutylene Terephthalate(PBT)와 Polycarbonate(PC)이며, 물성치는 Table 1과 같다.

Table 1

Properties of the lamp material11)

대류 열전달에 주로 영향을 미치는 주요 인자는 전구 온도와 주변 온도, 전구와 재료 사이의 거리 등이다. 전구 온도는 전구의 종류와 전력의 크기에 영향을 크게 받으며, 전구와 재료 사이의 거리는 박스의 크기를 의미한다. 실제 램프 제작 시, 상대적으로 작은 전력 및 부피의 램프에는 P계열 혹은 W계열 전구를 주로 사용하고, 상대적으로 큰 전력 및 부피의 램프에서는 H 계열 전구를 사용한다. 램프는 전구(열원)의 숫자에 따라 단일기능(Single Function)과 복합기능(Multi-Function)으로 구분하였다. 단일기능이란 하나의 전구를 포함한 램프를 의미하며, 복합기능은 여러 개의 전구를 포함한 램프를 지칭한다.

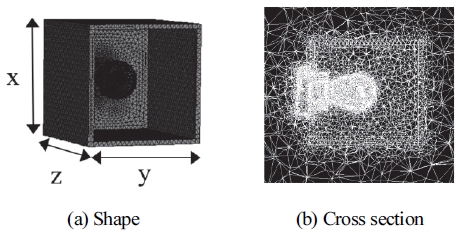
본 연구에서는 복잡한 디자인의 램프의 열전달 현상을 분석하기 위한 연구의 첫 단계로 직육면체 형태의 모델로 형상을 단순화하여 기초 연구를 수행하였다. 추후 실제 램프의 디자인을 반영하여 온도를 예측할 수 있도록 램프의 형상 인자를 도출하여 해석 모델링을 수행할 계획이다. 본 논문에서 단일기능의 CFD를 수행한 Case를 Table 2에 정리하였다.

Table 2

Single function analysis case

램프 내 부품은 기능에 관계없이 전구, REF, Lens 및 유동장을 포함하고 있으므로, 각 기능별로 부품에 대한 격자를 각각 형성하였다. 기초 연구에 사용된 CFD 해석은 Fig. 2와 같다. 이 때, 램프 내부의 유체는 공기로 가정하였고, 전구의 열이 외부로 완전히 전달된다고 보고 정상상태 조건으로 가정하였다. 전구의 해석조건으로, 내부를 채운 아르곤 가스와 전구의 유리를 구성하는 석영의 열전도율을 활용하였다. 램프 내부는 자연 대류 상태를 층류로 가정하여 해석을 진행하였다.

Fig. 2

CFD grid model

계산에 사용된 최소 볼륨 모델의 3차원 격자(Mesh) 수렴성을 검토한 결과, Fig. 3과 같이 최소 격자 개수가 330,000 이상부터 온도가 수렴함을 확인할 수 있었으며, 이에 따라 최소 셀(Cell)의 격자 개수를 330,000으로 설정하고 계산을 수행하였다. Table 3은 Table 2에서 정리한 Case 별 격자 수를 나타낸 것이다.

Fig. 3

Grid convergence review for 70 × 70 × 74

Table 3

Mesh of CFD cases

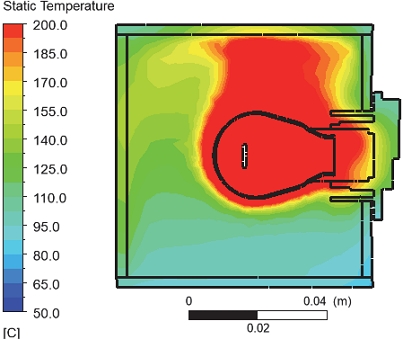
설정한 CFD 격자 모델에서 Fig. 4와 같은 CFD 해석 결과를 얻었다. 여기서 획득된 램프의 REF 표면과 Lens 표면의 온도 분포 데이터를 통해 램프의 각 표면의 온도에 영향을 미치는 주요 인자를 확인할 수 있었다.

Fig. 4

CFD analysis of single function

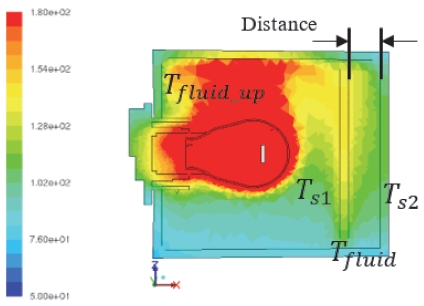
일반적으로 내부렌즈(Inner Lens)는 차량용 램프 규제상 램프의 색상을 맞추기 위해 사용되며, 전구에서 나온 빛이 내부렌즈를 통과하며 색상을 바뀌게 된다. 램프 내에 내부렌즈가 포함되는 경우, 내부렌즈와 바깥렌즈 사이의 거리에 따라 바깥 렌즈의 온도가 변한다. 이에 따라 에스엘㈜에서 생산되는 내부렌즈를 포함한 램프의 규격을 고려하여 내부렌즈-바깥렌즈 사이의 거리를 선정하여, Table 4와 같이 총 96 Case를 선정하였다. 그리고 Fig. 5는 내부 렌즈가 포함된 단일기능 램프의 CFD 해석을 진행한 것이다.

Table 4

Inner lens analysis case

Fig. 5

CFD analysis of single function with inner lens

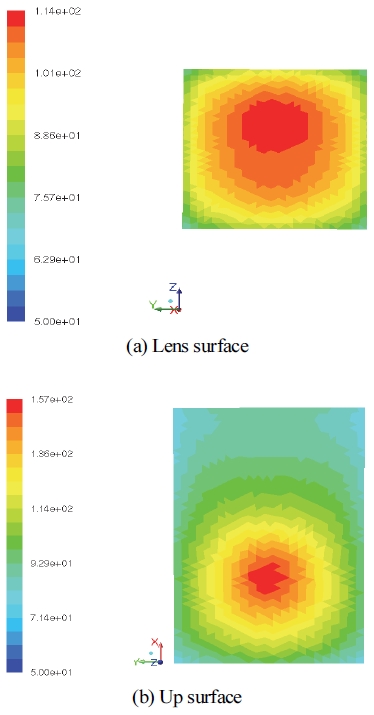
단일기능의 CFD 결과를 분석한 결과, 앞서 Fig. 4에서 확인할 수 있듯이, 램프의 상단면과 렌즈면에서 각각 PBT와 PC 재료의 최고 온도가 나타났다. 전구의 중심과 램프 각 면의 거리가 가까워질수록 면의 온도는 상승하였으며, 전구 입력 전력이 증가할 때도 온도가 상승하였다. 또한, 주변 온도가 상승하는 경우에도 온도가 상승함을 확인할 수 있었다. Fig. 6은 CFD 해석을 통해 램프의 상단면과 렌즈면의 온도 분포를 구한 결과이다. 상단면에서는 전구의 중심이 위치한 곳에서 표면의 최고 온도가 나타났고, 렌즈면에서는 전구의 중심보다 약간 위쪽에서 표면의 최고 온도가 나타났다.

Fig. 6

Temperature distribution of CFD

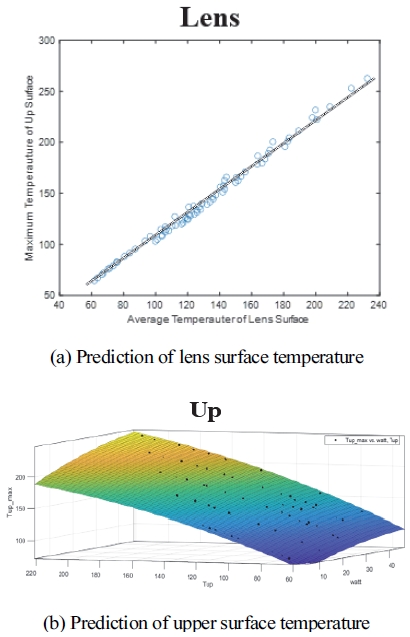
CFD 데이터를 기반으로 Curve fitting을 활용하여, 각 면의 평균 온도와 최고 온도 사이의 선형 회귀식을 찾았다. Fig. 7에서 확인할 수 있듯이 렌즈면은 아래 식 (1)의 직선식으로 평균온도와 최고온도 사이의 상관관계가 표현되었다.

Fig. 7

Multi variable prediction of surface temperature

반면, 상단면은 단순한 직선식으로는 온도 예측 정확도가 떨어졌기 때문에, 식 (2)와 같이 평균 온도와 전구의 입력 전력 값을 활용한 다변수 다항식으로 이루어진 최고 온도 상관식을 개발하였다.

3. 알고리즘 설계

3.1 단일기능 알고리즘 설계

램프 온도 예측 프로그램을 구성하는데 사용된 알고리즘은 초기 조건과 경계 조건을 입력으로 받아 정상상태 조건에서 입력 전구 열량과 리플렉터와 렌즈 표면을 통한 출력 열량이 모두 수렴할 때까지 열전달 계산을 반복적으로 수행한다. 이 때 알고리즘은 CFD와 같이 유한체적 해석 방법이 아니라 면적 단위의 열전달 계산이며, 각 면의 평균 열량과 평균 온도를 계산하고 평균온도와 최고온도 사이의 계산식을 도출하여 최고온도를 예측하는 방식이다.

알고리즘에 사용되는 열전달 메커니즘 이론식은 전도, 대류, 복사 세 가지가 있다.¹²⁾ 본 논문에서는 일어나는 열전달 현상을 1차원(One-dimension)으로 단순 해석하였다.

$\[ Q_{conduction }=k·\text{Δ}T/\text{Δ}x \]$

(3)

위 전도 식에서 k는 재료의 정해진 열 전도율이며, 온도차인 ∆T 와 열이 이동하는 물체의 길이 ∆x가 있다.

$\[ Q_{convection }=\stackrel{-}{h}·A·\left(T_1-T_2\right) \]$

(4)

대류 열전달 식은 평균 대류 열전달 계수 $$ \stackrel{-}{h}$$를 구하는 것이 매우 중요하다. 대류 열전달 계수는 아래의 식 (5)과 같이 평균 너셀 수$$ \overline{Nu}$$, 열 전도율k, 표면의 길이 L_ch로 구성되어 있다.

$\[ \stackrel{-}{h}=\overline{Nu}·k/L_{ch} \]$

(5)

대류 열전달 계수를 구성하는 식에서 열전도율 k와 특성 길이 L_ch은 고정되어 있지만, 너셀 수는 대류와 전도의 비로 구성된 무차원수다. 너셀 수는 열 전달 조건마다 다르기 때문에 상황에 맞는 수식을 적용했다. 알고리즘에 사용되는 너셀 수는 자연대류 기준에서 수직 평판과 수평 평판에 관한 두 가지 식을 사용하였다. 또한 너셀 수를 구성하는 무차원수인 레일리(Rayleigh) 수와 프란틀(Prandtl) 수에서, 레일리 수는 부력에 의해 유도된 흐름과 관련된 무차원 수이다.

레일리 수는 다음과 같이 열팽창 계수β, 동점성 계수v, 열확산 계수α, 특성길이L, 표면 온도 T_s와 유체의 온도 T_fluid로 이루어져 있다.

$\[ Ra=g·\beta ·\left(T_s-T_{fluid}\right)·L^3/v\alpha \]$

(6)

프란틀 수는 운동 점성도와 열 전도율의 비로 나타내는 무차원 수다. 프란틀 수는 공기를 비롯한 많은 기체에서는 0.7로 가정하며, 본 연구에서 개발한 알고리즘에서 또한 프란틀 수는 0.7로 사용되었다.

$\[ Pr=\frac{v}{\alpha }=0.7 \]$

(7)

사각 램프 모델에서 수직 평판(The Vertical Plate)은 Left, Right, Base, Lens 면 4개이며 너셀 수는 아래와 같다.

$\[ \overline{Nu}=0.68+0.670R{a}^{\frac{1}{4}}/{\left[1+{\left(\frac{0.492}{Pr}\right)}^{\frac{9}{16}}\right]}^{\frac{4}{9}} \]$

(8)

또한, 사각 램프 모델에서 수평 평판(Horizontal Plate)는 Up, Down면 2개이며, 각 Case 마다 식 (9), (10)과 같이 너셀 수가 다르게 사용된다.

$\[ \overline{Nu}=0.54R{a}^{\frac{1}{4}}\left(\text{Up Surface}\right) \]$

(9)

$\[ \overline{Nu}=0.52R{a}^{\frac{1}{5}}\left(\text{Down Surface}\right) \]$

(10)

여기서 각 면의 온도 예측은 식 (11), (12)와 같이 내부 공기의 온도를 정의해주고 전도와 대류를 통해 각 면의 온도를 계산하도록 되어있다.

$\[ T_{bulk\left(up\right) }=f\left(T_{bulb }, Volume\right) \]$

(11)

$\[ T_{bulk\left(lens\right) }=f\left(T_{bulb },T_{surface },T_{bulk\left(lens\right)}\right) \]$

(12)

마지막으로, 복사 열전달에 영향을 미치는 인자는 열이 이동하는 물체들의 온도, 재료의 방사율, 면적, 형상계수(View factor)가 있다. 이때 형상계수는 열이 전달되는 두 표면의 기하학적 형상과 헤드램프 치수와 관련이 있다. 복사 열전달 식은 열원과 주변의 배치에 따라 두 가지 경우로 나눌 수 있다.

첫 번째 경우는 램프 외부와 바깥과 같이 열원과 주변이 멀리 떨어져 있을 때로, 식은 다음과 같이 구성된다.

$\[ Q_{rad}=\sigma ·A·\left({\overline{T_1}}^4-{\overline{T_2}}^4\right) \]$

(13)

두 번째 경우는 램프 내부와 같이 열원과 주변이 가까울 때이며, 식 (14)와 같이 구성된다.

$\[ Q_{rad}=\sigma ·\frac{{\overline{T_1}}^4-{\overline{T_2}}^4}{\frac{1-{ϵ}_1}{{ϵ}_1{A}_1}+\frac{1}{A_1{F}_{1-2}}+\frac{1-{ϵ}_2}{{ϵ}_2{A}_2}} \]$

(14)

형상 계수는 아래와 같이 표현된다. 아래에서 D는 전구의 지름, L은 전구에서 렌즈 표면까지의 거리를 의미한다.

$\[ F_{1-2}=\frac{D^2}{D^2+4L^2} \]$

(15)

이와 같이 자연대류, 복사 열전달 식을 조합해서 헤드램프 각 면의 에너지 평형식을 구성할 수 있으며, 이에 따른 램프 상단 면(Up면)과 렌즈면(Lens면)의 에너지 평형식은 다음 식 (16), (17)와 같다. 이 때, ϵ_Al은 표면에 증착된 리플렉터의 재료 알루미늄의 방사율이다.

$\[ \begin{array}{c}{\stackrel{-}{h}}_{up,in}{A}_{up}\left({\stackrel{-}{T}}_{fluid }-{\stackrel{-}{T}}_{up}\right)\hfill \\ +\sigma ·\frac{{\stackrel{-}{T}}_{bulb}^4-{\stackrel{-}{T}}_{up}^4}{\frac{1-{ϵ}_{bulb}}{{ϵ}_{bulb}{A}_{bulb}}+\frac{1}{A_{bulb}{F}_{1-2}}+\frac{1-{ϵ}_{Al}}{{ϵ}_{Al}{A}_{up}}}\hfill \\ ={\stackrel{-}{h}}_{up,out}{A}_{up}\left({\stackrel{-}{T}}_{up}-{\stackrel{-}{T}}_{fluid}\right)\hfill \\ +\sigma ·{ϵ}_{up}·A_{up}·\left({\stackrel{-}{T}}_{up,out}^4-{\stackrel{-}{T}}_{surr}^4\right)\hfill \end{array} \]$

(16)

$\[ \begin{array}{c}{\stackrel{-}{h}}_{lens,in }{A}_{lens }\left({\stackrel{-}{T}}_1-{\stackrel{-}{T}}_s\right)\hfill \\ +\sigma ·\frac{{\stackrel{-}{T}}_{bulb }^4-{\stackrel{-}{T}}_{lens }^4}{\frac{1-{ϵ}_{bulb }}{{ϵ}_{bulb }{A}_{bulb }}+\frac{1}{A_{bulb }{F}_{1-2}}+\frac{1-{ϵ}_{lens }}{{ϵ}_{lens }{A}_{lens }}}+q_{trans }\hfill \\ ={\stackrel{-}{h}}_{lens,out }{A}_{lens }\left({\stackrel{-}{T}}_1-{\stackrel{-}{T}}_2\right)\hfill \\ +\sigma ·{ϵ}_{lens }·A_{lens }·\left({\stackrel{-}{T}}_{lens,out }^4-{\stackrel{-}{T}}_{surr }^4\right)+\tau q_{trans }\hfill \\ \hfill \end{array} \]$

(17)

식 (17)의 경우 자연대류, 복사와 함께 투과(q_trans)가 포함되어 있으며, τ는 렌즈의 투과율이다.

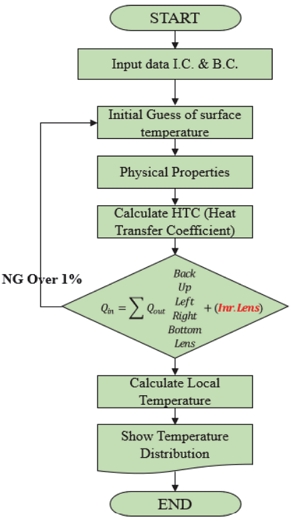
Fig. 8은 개발된 알고리즘 Flow chart이며, 초기 조건과 경계 조건을 입력으로 받은 후, 자연대류와 정상상태 조건에서 입력된 열량과 출력 열량이 모두 수렴할 때까지 열전달 계산을 반복 수행하여 단일 기능에서 각 면의 평균 온도를 계산한다. 이 때 수렴 조건은 식 (18)과 같이 표면 내부 열량과 외부 열량의 차가 1 % 미만일 때이다.

Fig. 8

Flow chart of single function temperature predicting algorithm

(18)

개발된 알고리즘의 Input data에서 램프의 설계 인자가 입력되며, 램프 크기와 전구의 입력 전력, 주변 온도 등이 포함된다. CFD 분석 결과 램프 설계 인자 값들에 따라 램프의 온도 결과가 바뀜을 확인한 바 있으며, 단일 기능 알고리즘에서도 마찬가지이다.

4. 알고리즘 검증

앞서 언급한 것과 같이 일반적으로 CFD 해석에는 모델링, 격자 형성 등의 작업으로 인해 오랜 시간이 소요된다. 또한, 설계된 램프의 온도 예측에 소요되는 시간은 단순히 계산 시간만을 고려했을 때, 길게는 하루까지 긴 시간을 소요한다. 그러나 개발된 알고리즘의 경우, 램프의 사양과 조건을 빠르게 입력하고 변경할 수 있으며, 계산 시간은 10초 이내로 매우 짧다.

개발한 알고리즘의 검증을 위해, 먼저 램프 열전달 현상을 분석하기 위해 생산한 CFD 데이터와 알고리즘 예측 온도를 비교하였다.

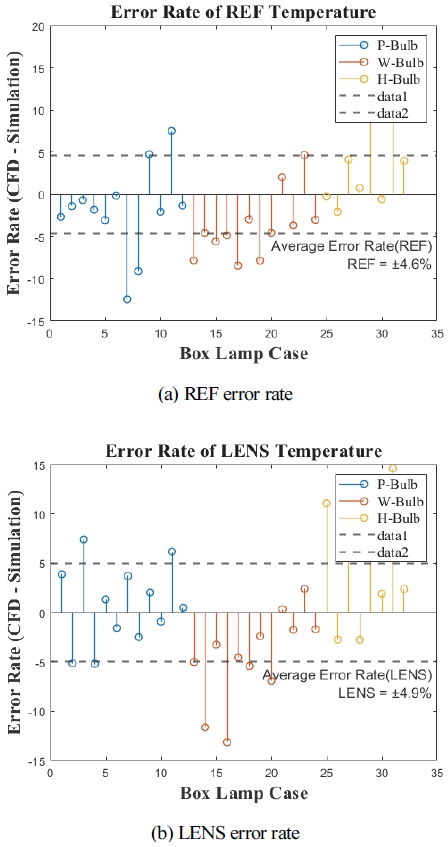
Fig. 9는 생산된 박스형 램프의 CFD 온도 데이터와 알고리즘 결과값을 통해 얻은 온도 예측 오차율을 비교한 그래프이다. REF와 LENS는 각각 평균 ±4.6 %와 ±4.9 %로 낮은 오차율을 나타냄을 확인할 수 있었다.

Fig. 9

Box lamp temperature prediction verification

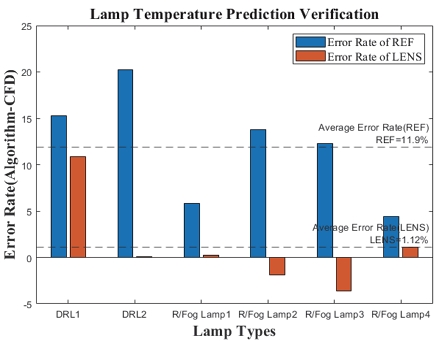
또한, 개발한 알고리즘의 실증을 위해, 에스엘㈜에서 설계 및 제작한 실제 램프 중 2종류인 Daytime Running Lamp(DRL)과 Rear Fog Lamp(R/Fog Lamp)의 CFD 해석 결과와 알고리즘 온도 예측 값을 비교하였다. Fig. 10은 DRL과 R/Fog 램프에서 REF와 LENS의 온도 예측 값의 차이 및 오차율을 나타낸 표이며, DRL과 R/Fog의 REF의 온도 예측 알고리즘 오차율은 평균 ±11.9 %로 나타났으며, LENS의 경우 평균 ±1.12 %로 나타났다.

Fig. 10

Lamp temperature prediction verification

내부 렌즈가 추가된 알고리즘의 경우, 비교 가능한 실제 램프 온도 데이터가 부족하여, Table 4에서 사용된 박스 형태의 CFD 온도 결과만을 알고리즘 예측 온도를 비교하였다.

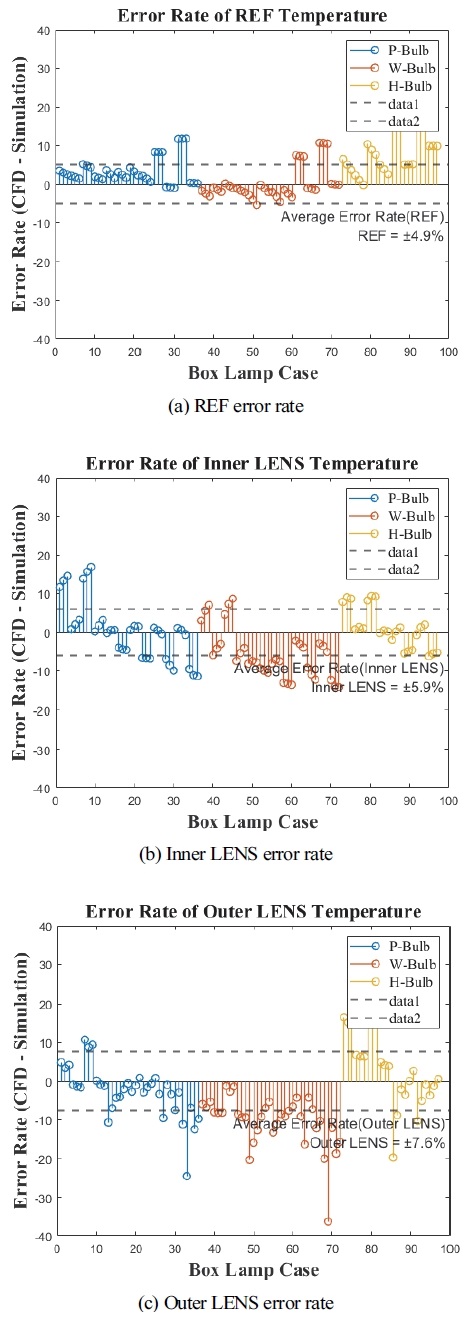
성능 평가 결과는 Fig. 11과 같이 CFD와 알고리즘 예측 최고 온도를 비교하였다. Fig. 11(a)에서 REF면의 경우는 대부분 오차 범위 10 % 내외의 결과가 나타났으나, 램프의 크기가 최대일 때, 오차가 크게 나타났다. 한편 Fig. 11(b)에서 확인할 수 있듯이 내부렌즈 온도의 경우, 대부분 15 % 이내의 오차율을 보였다. Fig. 11(c)의 전구에서 먼 곳에 위치한 외부 렌즈의 경우, 박스 크기 대비 전구의 전력이 작고 주변 온도가 낮을 때 오차가 크게 발생하였다. 이것은 내부렌즈 알고리즘을 구성하는 가중치 변수 γ₁∼γ₃가 램프의 크기와 전구의 전력에 의해 영향을 받기 때문이다.

Fig. 11

Error rate of max temperature between CFD and inner lens algorithm

이런 결과는 실제 전구에서 발생하는 열이 REF면 및 렌즈면에 전체적으로 비슷한 수준의 영향을 주는 것이 아니기 때문일 것으로 판단된다. 이는 현재 개발된 알고리즘이 각 면의 전체 면적과 전구 사이의 열전달 관계를 통해 각 면의 평균 온도를 예측하고, 최고 온도를 계산하도록 되어 있기 때문이다. 추후 실제로 열전달 현상이 주로 일어나는 전구 열원 부근의 ‘유효 면적’을 고려한 알고리즘 개선이 필요하다.

이와 같은 검증 결과에 따라 개발된 온도 예측 알고리즘의 유효성을 확인할 수 있었으며, 추가 연구를 통해 온도 오차율을 ±10 % 이내로 줄이는 것을 목표로 하여야 한다.

5. 결 론

박스형 단일기능 램프 모델을 설계하여 CFD 해석을 통해 내부렌즈 유무에 따른 REF면과 렌즈면에 대한 온도 분포와 열전달 현상을 분석하였다. 단일 기능 램프에서 REF의 최고 온도는 램프의 상단면에서 나타나며, 전구의 중심위치에서 표면의 최고 온도가 나타난다. 렌즈의 최고 온도는 전구의 중심보다 조금 높은 위치에서 표면의 최고 온도가 나타난다. CFD 데이터를 기반으로 하여 각 면의 평균 온도와 최고 온도 사이의 선형 회귀식을 찾았으며, 상단면의 경우, 다변수 다항식의 최고 온도 상관식을 개발하였다. CFD 분석 결과를 바탕으로 단일 기능 최고 온도 예측 알고리즘을 설계하였으며, 예측 오차율은 ±10 % 내외로 나타났으며, 이 때 계산에 소요되는 시간은 10초 이내이다.

차후에는 박스형 단일기능 램프 모델의 알고리즘을 복합기능 및 실제 램프 형상을 반영할 수 있도록 개선할 계획이다. 최종적으로는 실제 램프 모델에 대해 오차율 ±10 % 이내의 내열 온도 예측 정확도를 갖는 차량용 온도 예측 알고리즘을 개발할 계획이다.

References

• J. Wulf and A. Reich, “Temperature Loads in Headlamps,” SAE 2002 World Congress and Exhibition, 2002. [https://doi.org/10.4271/2002-01-0912]
• T. K. Philip, M. Sivapragasam and V. Ravichandran, “Design of an Automotive Headlamp Considering Style and Performance,” SASTECH Journal, Vol.46, No.2, 2013.
• K. F. Sokmen, E. Pulat, N. Yamankaradeniz and S. Coşkun, “Thermal Computations of Temperature Distribution and Bulb Heat Transfer in an Automobile Headlamp,” Heat and Mass Transfer, Vol.50, No.2, pp.199-210, 2013. [https://doi.org/10.1007/s00231-013-1229-5]
• X. Long, J. He, J. Zhou, L. Fang, X. Zhou, F. Ren and T. Xu, “A Review on Light-emitting Diode Based Automotive Headlamps,” Renewable and Sustainable Energy Reviews, Vol.41, pp.29-41, 2015. [https://doi.org/10.1016/j.rser.2014.08.028]
• T. Poorman, J. Bielecki, M. Chang, S. Belsare and F. El-Khatib, “Automotive Lighting Thermal Performance Prediction Methods,” SAE 2001 World Congress, 2001. [https://doi.org/10.4271/2001-01-0858]
• T. Poorman, J. Bielecki and M. Chang, “Methodology to Evaluate Automotive Lamp Venting,” Journal of Passenger Car: Mechanical Systems Journal, Vol.112, pp.753-757, 2003. [https://doi.org/10.4271/2003-01-0648]
• E. W. Liang, R. D. Lillquist, J. P. Gallo, A. J. Poslinski, A. Grimson and B. R. Strauss, “Predicting the Thermal Performance of an Automotive Fog Lamp Reflector,” Journal of Passenger CARS: Part Vol.106, pp.1458-1473, 1997. [https://doi.org/10.4271/970912]
• J. Lee, D. Choi, Y. Kim, S. Choi, Y. Park, J. Lee and K. Lee, “Development of Temperature Prediction Simulation Program for Automotive Headlamp,” KSAE Spring Conference Proceedings, pp.988-994, 2020.
• Y. Chang, M. Kim and B. Ahn, “A Study of Thermal Factor of Automotive Lamps using CFD,” KSAE Annual Conference Proceedings, pp.877-883, 2010.
• B. Choi, C. Lee, M. Ko, S. Lee and O. Kim, “Improving Process and Reliability of Thermal Analysis on Lamp,” KSAE Annual Conference Proceedings, pp.1603-1608, 2012.
• MatWeb, LLC, MatWeb, https://www.matweb.com, , 2020.
• F. P. Incropera and D. P. DeWitt, Fundamentals of Heat and Mass Transfer, 8th Edn., John Wiley & Sons, New York, 2018.