Steer-by-Wire 시스템의 Redundancy 확보를 위한 Steer-by-Brake 시스템 개발

1. 서 론

최근 by-Wire 방식의 차량 섀시 시스템 효율성이 대두됨에 따라 자동차 업계에서는 Steer-by-Wire(SbW), Brake-by-Wire(BbW) 등의 제품들을 활발히 개발 중이다. 특히 SbW 시스템의 경우, 운전자의 Steering wheel 조작과 Rack actuator 동작은 중간에 물리적인 연결(컬럼)없이 전기적 모터 신호로 이루어져있어, 통신 장애와 같은 고장이 발생하게 되면 운전자의 물리적 조작으로 대처가 전혀 불가능하다. 이처럼 운전자(또는 자율주행)의 목표조향 신호 전달에 문제가 발생되면 차량은 곧바로 정상적 주행 궤적을 상실하게 되고, 심각한 교통사고를 야기한다. 이러한 측면에서 SbW 시스템 양산 보급을 앞둔 지금, 고장 시에도 Safety를 확보할 수 있는 Redundancy 기능의 중요성이 대두되고 있다.¹⁾

1990년대부터 편 제동(Differential braking)을 활용한 차량의 조향을 보조 및 대체하는 기능 연구가 지속적으로 진행되어왔다.^2-5) 물리적으로 편 제동은 주행중인 차량에 좌우 종방향 힘 차이를 발생하며, Yaw 모멘트와 횡력이 생성되어 선회에 유리하다. 이때 타이어와 노면 사이에는 조향 Geometry와 관련된 Scrub radius의 영향으로 Wheel angle이 발생한다. 여기서 Scrub radius의 크기와 부호는 Wheel angle 생성 방향(즉, 차량의 횡 모션)에 영향을 미치는 주요 요인 중 하나이다. 이러한 메커니즘을 활용하면 SbW 시스템 Fail과 같은 조향^11,12) 조작이 불가능한 상황에서 차량을 안전한 장소에 정차시키거나, 일정시간 차선을 유지하는 등 최소한의 조향 Redundancy를 확보하는 조향 모션 구현이 가능할 것으로 기대된다.

1998년 초기 연구에서는 Scrub radius 영향이 고려되지 않고 오로지 좌우 편 제동으로 발생하는 모멘트에 초점을 두어 편 제동 제어를 시도하였다.^2,3) Pilutti 연구에서는 조향 선회 시 편 제동으로 추가적인 모멘트를 활용하면 보다 효과적인 선회가 가능하다고 기술하고 있다. 그러나 이는 Wheel angle이 고정(Stuck)인 국한된 경우에만 해당되며, 실제로 운전자의 조향 개입이 없는 상황에서 편 제동을 인가하게 되면 Scrub radius 영향으로 Wheel angle은 고정되지 않고, 한 방향으로 점진적으로 회전(Free-rolling)하여 선회에 영향을 미친다. 이러한 영향은 편 제동 제어시 반드시 고려될 필요가 있다. Dominguez의 연구에서는 조향 Geometry 모형을 반영하여 편 제동 기능을 구현하려는 시도가 있었지만, 그 모형의 근거와 신뢰성은 충분치 못하였으며, 다양한 Scrub radius 값은 고려되었지만 음의 범주로 제한을 두었기 때문에 Steering wheel을 고정한 상태에서 편 제동 제어 시 만족할 만한 결과를 보였다. 이는 SbW 시스템 고장 시 가장 우려되는 Wheel angle의 Free-rolling 현상을 전혀 고려하지 못한다.

근래에 들어 편 제동 제어에 Scrub radius 설정을 반영한 Steer-by-Brake(SbB) 시스템이 등장하였다.⁴⁾ CNXmotion(Continental과 Nexteer 합작사)에서 개발한 이⁷⁾ 시스템은 트레일러가 저속에서 회전 시 자동 제동 제어를 통해 트레일러의 뒤쪽의 축의 Wheel angle을 생성시켜 유리한 회전 반경을 확보하는 것을 목표로 개발되었다. 보편적으로 트레일러 차량에는 추가적으로 뒤축 휠 조향 시스템 장착이 요구되는데, 이 기능을 편 제동 제어로 대체할 수 있다고 설명한다. 이를 위해서는 양의 Scrub radius 설정이 중요하다고 언급하고는 있지만 구체적인 근거는 기술되지 않았다. 또한 이 연구는 산업용 트레일러 차량에 국한 되어있고, 범용적인 SbW 시스템의 Redundancy를 확보하기 위한 기능과는 거리가 있어 보인다.

최근 수행된 Jonasson 연구⁵⁾에서는 자율주행에서 EPS와 같은 조향 시스템 고장 대응을 목표로 편 제동 제어 시스템을 개발하였다. 이 시스템은 카메라 센서 정보를 기반으로 전방 도로 곡률^8-10)을 따르도록 설계되었으며, 운전자의 Steering wheel 조작을 두 가지 방식(Hands-on, -off)을 통해 Wheel angle의 Stuck과 Free-rolling 영향을 모두 고려하여 수행하였다. 이 연구에서 주목할만한 부분은 인가된 편 제동과 동일한 방향의 Wheel steer angle을 확보하기 위해 휠 안쪽에 Spacers를 추가 장착하여 양의 Scrub radius 설정으로 변경한 부분이다. 그럼에도 불구하고 조향 Geometry 모형의 부정확한 설계로 Scrub radius 영향을 제어에 충분히 반영하지 못하였다. 또한 특정 도로 곡률의 제한된 시나리오에서만 그 시스템의 유효성을 확인하였다.

기존 연구들에서 언급한 바와 같이 차량의 편 제동 기반 조향성은 Scrub radius 설계에 크게 기인하는 것을 확인하였다. Scrub radius는 일반적으로 개발되는 차량의 구동 목적에 따라 제조사에 의해 결정되어 설계된다. 예를 들어 RWD(Rear Wheel Drive) 방식이 주로 채택되는 Racing 목적 차량의 경우, 차량 가속 시 유리한 직진성 확보를 위해 전륜 Wheels을 Toe out 설계하고 이를 위해 양의 Scrub radius를 채택하는 경우가 있다. 반면에 양산 보급형 차량의 경우, 다음과 같은 차량 안정성 이유로 음의 Scrub radius로 설계하는 경우가 보편적이다. 일례로 X-split 유형의 제동 시스템에서 Circuit fail이 발생할 경우, 고장 난 Circuit은 제동이 되지 않으며, 남은 한쪽 Circuit으로만 제동력을 전달하는데, 이때 음의 Scrub radius로 설계된 경우에는 편 제동력이 인가된 반대 방향으로 Wheel angle이 회전하면서 차량의 직전성을 확보하게 된다. 이러한 현상은 Split 노면에서 차량의 직진성을 확보하기 위해 동일하게 적용된다.⁴⁾ 하지만 이처럼 편 제동시 Wheel angle이 Yaw 거동과 반대로 생성되는 메커니즘에서는 편 제동으로 발생한 Yaw 모멘트와 횡 이동거리가 상쇄되고, 본 연구에서 제안하는 조향성 확보를 목적으로 하는 편 제동 제어의 성능과 효율을 저하시키는 주요 요인이 될 수 있다.¹³⁾

더욱이 최근 Thyssenkrupp사의 발표⁶⁾에 따르면, SbW 시스템을 차량에 적용하면서 일반 주행에서 토크 스티어를 유발하는 인자인 Scrub radius를 전통적 섀시 설계 방법에서 벗어나 킹핀 앵글 제한으로 줄이는 방향도 제안되고 있으며, Active Front Steering(ASF)의 Capability를 위해 Positive scrub radius를 늘리고, Trail를 줄이는 방향 또한 주장되고 있다. 또한 4륜 독립 조향, In wheel motor 시스템이 적용된 자율 주행 차량에서 극단적인 양의 Scrub radius를 갖는 설계도 보고되고 있다. 이러한 동향을 반영하여 본 연구에서는 양과 음의 Scrub radius 설정을 모두 염두 하였으며, 본 개발 시스템에 유리한 구조를 채택하여 시스템 개발을 수행하였다.

본 연구에서는 SbW 시스템 고장 시(Free-rolling) 편 제동 제어를 통해 차량의 조향성(Steerability)을 확보하는 SbB 시스템 개발을 주요 목표로 한다. 본 논문의 구성은 다음과 같다. 2장에서는 본 시스템의 구성을 설명하고, 차량 동역학 모형을 기반으로 State- feedback 제어기를 3장에서 설계한다. 그리고 4장에서 시험 시나리오 설계, 시뮬레이션 및 실차 시험 평가를 수행하였다. 여기서 우선 Scrub radius 설정에 따라 편 제동 시 생성되는 전륜 휠의 조향성을 분석하였고, 제어에 유리한 설정을 선정하였다. 또한 실차와 시뮬레이션과의 괴리를 최소화하기 위해, 선 수행된 실차 타당성 시험 결과를 기반으로 시뮬레이션 정산(Calibration) 작업을 수행하였다. 마지막으로 결론을 5장에서 정리하였다.

2. 시스템 구성

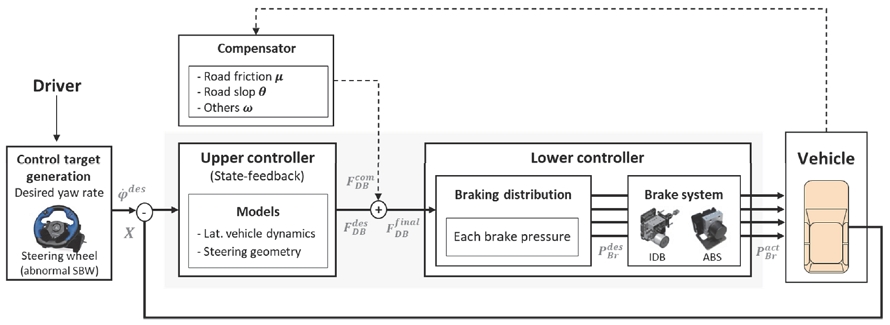
본 연구의 SbB 시스템 구성 개념도는 Fig. 1과 같다. SbB 시스템은 SbW 시스템 내의 통신 고장으로 운전자의 Steering wheel의 조작 신호를 휠 조향 Actuator가 전달받지 못하는 문제가 발생되면 작동한다. 본 연구에서는 SbB 시스템 작동 시 모든 휠의 구동력(Traction force)은 가해지지 않도록 제한하였다. 또한 SbW 시스템 고장 시에도 운전자의 조향 조작 신호는 SbW의 Steering Feedback Actuator(SFA)에 장착된 Steering Wheel Angle Sensor(SAS)를 통해 정상적으로 계측된다고 가정하였다. 즉, 운전자의 SAS 조작량을 기반으로 Desired yaw rate $$ {\dot{\phi }}^{des}$$ 제어목표가 생성된다. 더불어 추후 자율 주행 상황의 경우에는 운전자의 Steering wheel 조작은 차선을 유지하거나 변경이 요구되는 조향각 제어량으로 대체 할 수 있는 범용성을 갖도록 설계하였다.

Fig. 1

Conceptual diagram of SbB system architecture

상위제어기에서는 제어목표와 차량상태와의 차이(Error)를 최소화하는 Desired differential force $$ F_{DB}^{des}$$ 제어 입력을 State-feedback 제어를 통해 실시간으로 산정한다. 단, 이 값은 도로 노면 마찰, 경사 등 다른 외부 요인으로 인해 충분하지 못할 수 있다. 이러한 외부 영향을 제어에 반영하기 위해서 Compensated differential force $$ F_{DB}^{com}$$를 도출하고 이를 $$ F_{DB}^{des}$$에 보상하여 Final differential force $$ F_{DB}^{final }$$를 산정한다. 그러나 본 연구는 개발 초기 단계로 정상 노면 상태(0.9 이상 마찰계수)와 평지(0 경사)를 대상으로 하고있고, 외부 요인이 제어에 미치는 영향은 미비하다는 가정으로 외란 보상기 설계 내용은 본 논문에서는 생략하였다.

하위제어기에서는 상위제어기에서 도출한 $$ F_{DB}^{final }$$를 각 휠의 제동 토크로 변환하고, 각 제동 토크가 생성될 수 있도록, Integrated Dynamic Brake(IDB) 시스템이 제동 압력을 캘리퍼 엑추에이터로 분배한다. 안전을 대비하여 제어 중 휠 슬립이 발생하는 경우에는 IDB 내부의 ABS 및 ESC 로직이 수행될 수 있도록 설계하였다. 본 논문에서는 SbB 시스템의 상위제어기 설계에 초점을 두어 기술하였고, 하위제어기 부분은 제동 토크 및 압력 분배에 관한 내용만 간략히 언급하기로 한다.

3. 제어기 설계

3.2 3-DOF 횡 방향 차량 동적 모형 설계

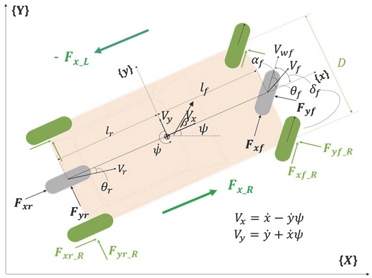
앞 절에서 설명한 제어 목표 Yaw rate에 도달하는 제어 입력 $$ F_{DB}^{des}$$은 차량의 동적 모형 설계를 우선으로 한다. 기존의 횡 방향 차량 동역학 모형은 오로지 횡 거동(횡 이동거리, Yaw)에만 초점을 두었기 때문에 주행 속도, 가속도와 같은 종 방향 속성은 일정(Constant) 하다는 조건을 따른다. 그리고 좌우 편 제동력 영향 또한 반영하지 못하였다. 그러나 SbB 제어가 수행되는 경우, 좌우 편 제동력으로 인한 횡 거동의 영향은 뿐만 아니라 제동력으로 인한 감속 또한 고려될 필요가 있다. 그러므로 본 연구에서는 이와 같은 종 방향 요소를 횡 방향 차량 동역학 모형에 반영하여, 식 (2)와 같이 3-DOF 횡 방향 차량 동적 모형을 설계하였다. 이 모형을 구성하는 파라미터는 Fig. 2와 같다.

$\[ m\left(\ddot{y}+\dot{x}\dot{\psi }\right)=F_{yf}+F_{xf}\cdot {\delta }_f+F_{yr} \]$

(2-1)

$\[ I_z\ddot{\psi }=l_f\cdot F_{yf}+l_f\cdot F_{xf}\cdot {\delta }_f-l_r{F}_{yr}-\frac{D}{2}\left(F_{x_{-}L}-F_{x_{-}R}\right) \]$

(2-2)

Fig. 2

Conceptual diagram of 3-DOF of lateral vehicle dynamics model

여기서, $$ F_{x_{-}L}=F_{x{f}_L}+F_{x{r}_L}, F_{x_{-}R}=F_{x{f}_R}+F_{x{r}_R}$$ 의미한다. 또한 $$ F_{x{f}_L}-F_{x{f}_R}=\mathrm{\Delta }{F}_{xf},{ F}_{x{r}_L}-F_{x{r}_R}=\mathrm{\Delta }{F}_{xr}$$ 로 정리할 수 있다. 이외의 힘은 식 (3)과 같이 정리된다.

$\[ \begin{array}{cc}{F}_{yf}=2\cdot C_{\alpha f}\cdot {\alpha }_f\hfill & where {\alpha }_f={\delta }_f-{\theta }_f\hfill \end{array} \]$

(3-1)

$\[ \begin{array}{cc}{F}_{yr}=2\cdot C_{\alpha r}\cdot {\alpha }_r\hfill & where {\alpha }_r=-{\theta }_r\hfill \end{array} \]$

(3-2)

$\[ \begin{array}{cc}{F}_{xf}=m\cdot a_{wf}\hfill & where a_{wf}=r_{eff}\cdot {\dot{\omega }}_w\hfill \end{array} \]$

(3-3)

여기서 r_eff는 휠의 Effective tire radius이며, $$ {\dot{\omega }}_w$$는 Rotational wheel acceleration을 의미한다, 각 Velocity angle θ_f와 θ_r는 아래 식 (4) 가정으로 추정된다.

$\[ {\theta }_f\simeq \left(\dot{y}+l_f\dot{\psi }\right)/\dot{x} \]$

(4-1)

$\[ {\theta }_r\simeq \left(\dot{y}-l_r\dot{\psi }\right)/\dot{x} \]$

(4-2)

식 (2)에 식 (3)과 (4)를 대입하고 상태변수 $$ \dot{y}$$, $$ \dot{\psi }$$로 정리하면 식 (5)와 같다.

$\[ \ddot{y}\begin{array}{l}=\frac{-2\left(C_{\alpha f}+C_{\alpha r}\right)}{m\dot{x}}\dot{y}+\left\{-1-\frac{2\left(C_{\alpha f }{l}_f-C_{\alpha r }{l}_r\right)}{m{\dot{x}}^2}\right\}\dot{x}\dot{\psi }\hfill \\ +\left(\frac{2C_{\alpha f}+m{r}_{eff}{\dot{\omega }}_w}{m}\right){\delta }_f\hfill \end{array} \]$

(5-1)

$\[ \ddot{\psi }\begin{array}{l}=\frac{-2\left(C_{\alpha f }{l}_f-C_{\alpha r }{l}_r\right)}{I_z\dot{x}}\dot{y}+\frac{-2\left(C_{\alpha f }{l}_f^2+C_{\alpha r }{l}_r^2\right)}{I_z\dot{x}}\dot{\psi }\hfill \\ +\frac{l_f\left(2C_{\alpha f}+m{r}_{eff}{\dot{\omega }}_w\right)}{I_z}{\delta }_f-\frac{D}{2I_z}\left(\mathrm{\Delta }{F}_{xf}+\mathrm{\Delta }{F}_{xr}\right)\hfill \end{array} \]$

(5-2)

SbW 고장 시 조향 각 δ_f는 운전자의 조작과 상관없이 편 제동으로 발생하게 되므로 제어입력으로 사용될 수 없다. 1장에 언급하였듯이, δ_f는 편 제동 시 타이어와 지면 사이의 Scrub radius 영향으로 자연스럽게 발생되고, 이 값의 부호로 휠의 물리적인 회전 방향이 결정된다. 즉, 편 제동에서 제동력이 가해지는 방향으로 차량 Yaw 모션이 발생하는데, 이때 Scrub radius 설정에 따른 δ_f 관계, 즉 조향 기구 Geometry가 동적 모형에 반영되어야만 한다.

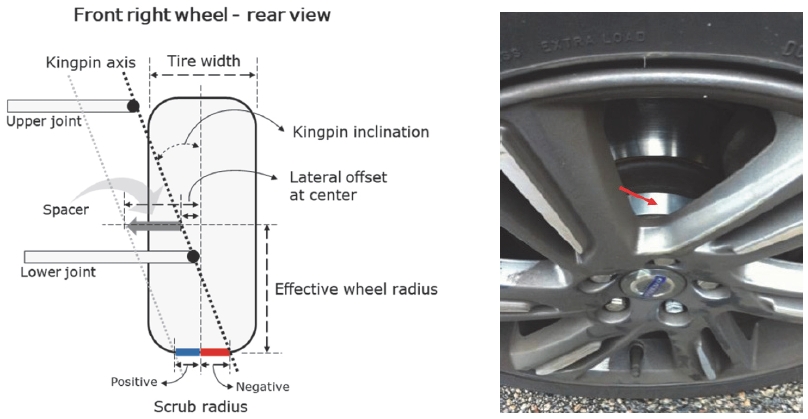
조향 기구 Geometry 설계에 따른 Scrub radius는 Fig. 3과 같다. Scrub radius의 크기와 부호는Kingpin 축의 기울기, 휠 중심에서의 Lateral offset, 유효 휠 크기로 결정된다. 즉, Scrub radius는 Kingpin 축과 지면이 닿는 점으로부터 타이어 중앙까지의 거리를 의미하며, 그림과 같이 음과 양의 값을 갖는다. 1장에 설명하였듯이 편 제동이 인가되는, 즉 Yaw 모멘트가 발생하는 동일한 방향으로 휠 조향각이 발생하는 것이 제어에 유리하다. 이를 위해 본 연구에서는 초기 설계된 음의 Scrub radius를 휠과 브레이크 디스크 사이에 추가적으로 Spacer를 장착하여 양의 Scrub radius 값으로 변경하였다. 다른 대안으로는 Kingpin 축의 기울기를 변경하는 방법도 있지만 이는 기존 설계된 조향 Geometry 구조 변경에 많은 어려움이 따른다.

Fig. 3

Diagram of scrub radius and spacer installation according to mechanical steering geometry

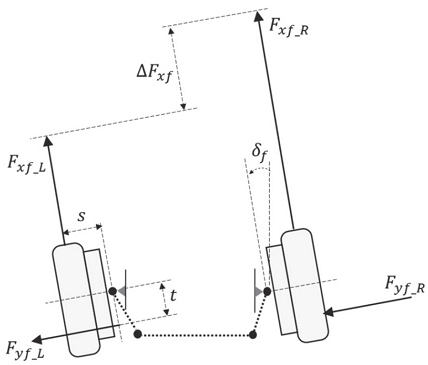
편 제동 시 좌우 종 방향 힘 차이로 인한 δ_f 발생 관계를 조향 Geometry 모형으로 도식하면 Fig. 4와 같고 이를 기반으로 식 (6)을 유도할 수 있다.

$\[ {\delta }_f=\beta +\frac{l_f}{\dot{x}}\dot{\psi }-\frac{s}{2C_{\alpha f}\cdot t}\mathrm{\Delta }{F}_{xf}\text{ where }\beta \simeq \frac{\dot{y}}{\dot{x}} \]$

(6)

Fig. 4

Conceptual diagram of steering angle geometry according to differential braking

여기서 F_{xf_L}, F_{xf_R}은 각각 좌우 종 방향 힘을 뜻하고 ΔF_xf은 그 힘의 차이다. F_{yf_L}, F_{yf_R}는 각각 좌우 횡 방향 힘, s는 Scrub radius, t는 Caster 각으로 인한 Mechanical Trail을 의미한다.

식 (6)의 조향 Geometry 모형을 식 (5)의 3-DOF 횡 방향 차량 동적 모형에 반영하고 이를 상태공간모형 식으로 표현하면 식 (7)과 같다.

$\[ \begin{array}{c}\dot{X}=AX+BU\hfill \\ \begin{array}{cc}\hfill & \frac{d}{dt}\left[\begin{array}{c}\dot{y}\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{cc}\frac{-2C_{\alpha r}+m{r}_{eff}{\dot{\omega }}_w}{m\dot{x}}& \frac{2C_{\alpha r}{l}_r-m{\dot{x}}^2+m{r}_{eff}{\dot{\omega }}_w{l}_f}{m\dot{x}}\\ \frac{2C_{\alpha r}{l}_r+m{r}_{eff}{\dot{\omega }}_w{l}_f}{I_z\dot{x}}& \frac{-2C_{\alpha r}{l_r}^2+m{r}_{eff}{\dot{\omega }}_w{l_f}^2}{I_z\dot{x}}\end{array}\right]\left[\begin{array}{c}\dot{y}\\ \dot{\psi }\end{array}\right]\hfill \\ & +\left[\begin{array}{cc}-\frac{\left(2C_{\alpha f}+m{r}_{eff}{\dot{\omega }}_w\right)s}{2C_{\alpha f}mt}& 0\\ -\left\{\frac{\left(2C_{\alpha f}{l}_f+m{r}_{eff}{\dot{\omega }}_w{l}_f\right)s}{2C_{\alpha f}{I}_{z}t}+\frac{D}{2I_z}\right\}& -\frac{D}{2I_z}\end{array}\right]\left[\begin{array}{c}\Delta F_{xf}\\ \Delta F_{xr}\end{array}\right]\\ & \end{array}\hfill \end{array} \]$

(7)

여기서 횡속도 $$ \dot{y}$$ 와 Yaw rate $$ \dot{\psi }$$ 은 상태변수, ΔF_xf, ΔF_xr는 전륜 및 후륜의 좌우 종방향 힘 차이 즉, 편 제동력으로 제어 입력을 의미한다. 일반적으로 차량 제동 시 전륜과 후륜에 분배되는 제동력의 형상은 비슷하지만, 그 크기는 전륜에 보다 큰 제동력이 가해진다. 이는 제동 시 차량에 Pitch 모션으로 보다 많은 하중이 전륜에 가해지기 때문이며, IDB 시스템으로 전 후륜에 동일 제동 압력을 인가하여도 전륜에 보다 큰 제동력이 가해지도록 설계되었다. 이러한 행태를 반영하여 전, 후륜 사이의 편 제동력을 식 (8)과 같이 정리할 수 있다.

$\[ \mathrm{\Delta }{F}_{xf}=\alpha \mathrm{\Delta }{F}_x,\mathrm{\Delta }{F}_{xr}=\left(1-\alpha \right)\mathrm{\Delta }{F}_x \]$

(8)

여기서 α 는 전, 후륜에 가해지는 편 제동량의 비율이다. 최종적으로 식 (8)을 식 (7)에 적용하여 식 (9)와 같이 3-DOF 횡 방향 차량 동적 모형을 단일 제어입력으로 정리하였다.

$\[ \frac{d}{dt}\left[\begin{array}{c}\dot{y}\\ \dot{\psi }\end{array}\right]\begin{array}{l}=\left[\begin{array}{cc}\frac{-2C_{\alpha r}+m{r}_{eff}{\dot{\omega }}_w}{m\dot{x}}& \frac{2C_{\alpha r}{l}_r-m{\dot{x}}^2+m{r}_{eff}{\dot{\omega }}_w{l}_f}{m\dot{x}}\\ \frac{2C_{\alpha r}{l}_r+m{r}_{eff}{\dot{\omega }}_w{l}_f}{I_z\dot{x}}& \frac{-2C_{\alpha r}{l_r}^2+m{r}_{eff}{\dot{\omega }}_w{l_f}^2}{I_z\dot{x}}\end{array}\right]\left[\begin{array}{c}\dot{y}\\ \dot{\psi }\end{array}\right]\\ +\left[\begin{array}{c}\alpha \left\{-\frac{\left(2C_{\alpha f}+m{r}_{eff}{\dot{\omega }}_w\right)s}{2c_{\alpha f}mt}\right\}\\ -\alpha \left\{\frac{\left(2c_{\alpha f}{l}_f+m{r}_{eff}{\dot{\omega }}_w{l}_f\right)s}{2C_{\alpha f{I}_{z}t}}+\frac{D}{2I_z}\right\}-\left(1-\alpha \right)\frac{D}{2I_z}\end{array}\right]\left[\mathrm{\Delta }{F}_x\right]\end{array} \]$

(9)

4. 시스템 평가

4.1 시나리오 및 파라미터 설정

본 SbB 시스템은 SbW 시스템 고장에 대응하기 위한 목적으로 개발되었기 때문에 고장 발생 시 곡률 변화에 차선을 유지하는 조향(시나리오 A), 직진차로에서 갓길에 정차하기 위한 차선변경 조향(시나리오 B)에서 평가하였다. Table 1과 같이 시험 시나리오는 음과 양의 Scrub radius(Spacer를 장착) 두 가지 설정을 고려하였다. 또한 초기 주행 속도는 약 60, 80 km/h 두 가지 경우로 고려하였고, SbB 제어 수행 시 휠의 구동력 제어를 멈추어 차량이 서서히 정지하는 경우와, 정속 주행(Cruise control)을 유지하기 위한 가속도 제어가 이루어지는 경우 또한 고려하였다.

Table 1

Evaluation scenario

본 연구의 시험 차량은 Genesis g80 EV 세단으로 선정하였고, 속성 값을 정리하면 Table 2와 같다. 여기서 C_af, C_ar, I_z 속성 값은 RT2000 장비를 시험차에 장착하고 여러 차례의 슬라럼 시험 주행 통해 취득한 데이터와 앞서 설계한 동역학 모형을 기반으로 Least square 기법을 적용하여 추정하였다. 이 속성 값들은 정상 노면 상태와 평지 환경에서 고정으로 추정되는 값이며, 본 연구는 초기 개발단계로 해당 조건에서만 평가가 수행되었다.

Table 2

Control parameter value

4.2 시뮬레이션

4.2.1 환경 구축 및 캘리브레이션

본 연구에서 SbB 제어기는 Matlab Simulink R2021b를 사용하여 설계되었고, 실차 시험 이전에 이 제어기를 Carsim 2020.1에 적용하여 시뮬레이션 평가를 수행하였다. 우선적으로 제어기 시뮬레이션 평가 이전에 Carsim에서 설정한 차량 모형의 유효성 검토를 통해 시뮬레이션 파라미터 Calibration을 수행하였다. 시뮬레이션 평가 시 차량 모형의 거동은 실제 차량의 거동과 비슷해야 하고, 차이가 존재할 경우 내부 설정 파라미터 Calibration을 통해 모형 수정이 필수적으로 요구된다. 본 연구에서는 다양한 주행 조건과 편 제동 가진 압력으로 총 60가지 케이스에서 실차 시험을 수행하였다.

이와 동일한 조건으로 시뮬레이션으로 구현하고 각 케이스 별 실차 시험 결과와 비교하며 파라미터 Calibration을 수행하여 차량 모형의 신뢰성을 확보하였다. 특히 조향 Geometry 구조의 속성 값을 조절하여 양과 음의 Scrub radius를 구현하였고, 조향 토크 입력 파라미터의 개입이 생기지 않도록 설계하여 Wheel angle의 Free-rolling 현상 또한 시뮬레이션에 반영하였다.

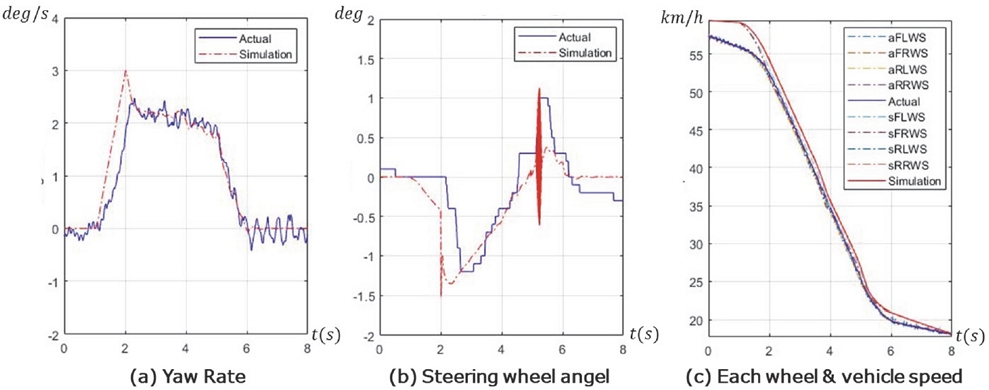
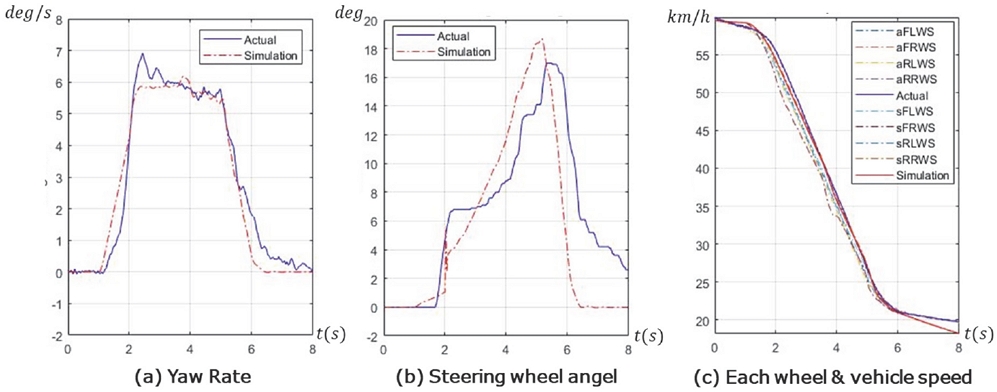
Figs. 5, 6은 시뮬레이션 파라미터 Calibration완료 후, 시뮬레이션과 실차 시험 결과를 비교한 대표적 두 가지 케이스이다. 이는 Scrub radius 설정만 ±20 mm으로 다르고, 약 60 km/h의 초기 속도, 50 bar의 좌측 앞, 뒤 휠 브레이크 압력, Free-rolling 상태 기반 Wheel angle, 휠 구동력 없음으로 나머지 조건이 모두 동일하다. 여기서 (a)는 차량 중심에서 측정한 Yaw rate이며, (b)는 Steering wheel의 각도로 전륜 Wheel angle의 계측을 대신할 수 있다. 그리고 (c)는 각 휠과 차량의 속도이다. 여기서 aFLWS는 Actual Front Left Wheel Speed, sFLWS는 Simulated Front Left Wheel Speed를 뜻하며 다른 휠 속도도 표기하였다. Actual은 실제 시험 차량의 주행 속도이며, Simulation은 시뮬레이션 차량의 주행 속도이다.

Fig. 5

Comparison of actual vehicle and simulation test results according to negative scrub radius(-20 mm)

Fig. 6

Comparison of actual vehicle and simulation test results according to positive scrub radius(+20 mm)

이 시험에서 주목할 점은 편 제동 시 Scrub radius 설정에 따른 Wheel angle의 생성 방향 관계로 이는 Figs. 5(b), 6(b)에서 확인할 수 있다. 음의 Scrub radius 설정 Fig. 5에서는 편 제동이 인가된 방향과 반대로 Wheel angle이 생성되는 경향을 보였다. 두 케이스에서 동일한 편 제동 압력이 인가되었음에도 불구하고 음의 설정에서는 2 deg/s, 양의 설정에서는 6 deg/s으로 약 3배 정도의 Yaw rate 최대값 차이가 발생되는 것을 확인하였다. 이 시험을 통해 SbB 시스템은 양의 Scrub radius 구조에서 제어가 유리할 것으로 판단된다. 또한 두 케이스 모두 실제와 시뮬레이션 차량 거동이 전반적으로 비슷한 형상을 보였고, 이로써 시뮬레이션 파라미터가 합리적인 수준으로 Calibration 되었음을 확인하였다.

4.2.2 시뮬레이션 평가 결과

이 절에서는 개발한 SbB 제어기를 Calibration이 완료된 시뮬레이션 차량 모형에서, 앞서 언급한 8가지 시나리오에서 평가를 수행하였다. 실차 시험을 고려하여 제어기는 Discrete time 신호를 기반으로 0.001초 단위 Iteration으로 이루어지도록 설계하였다. 모든 시나리오에서 Warm-up시간을 초기 5초 동안 정속 주행하고, 이후부터 SbB 제어가 실행된다.

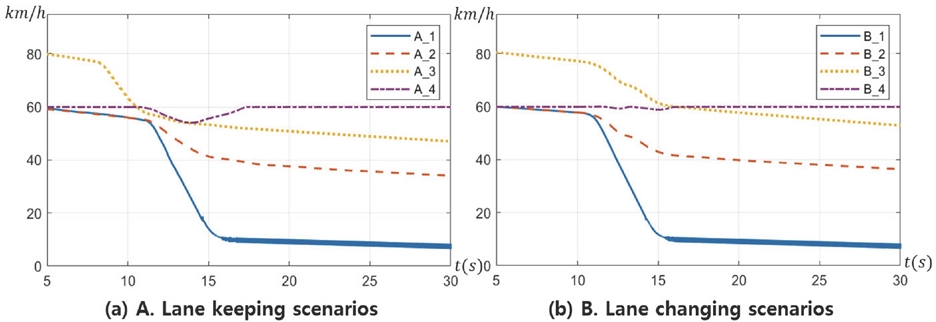
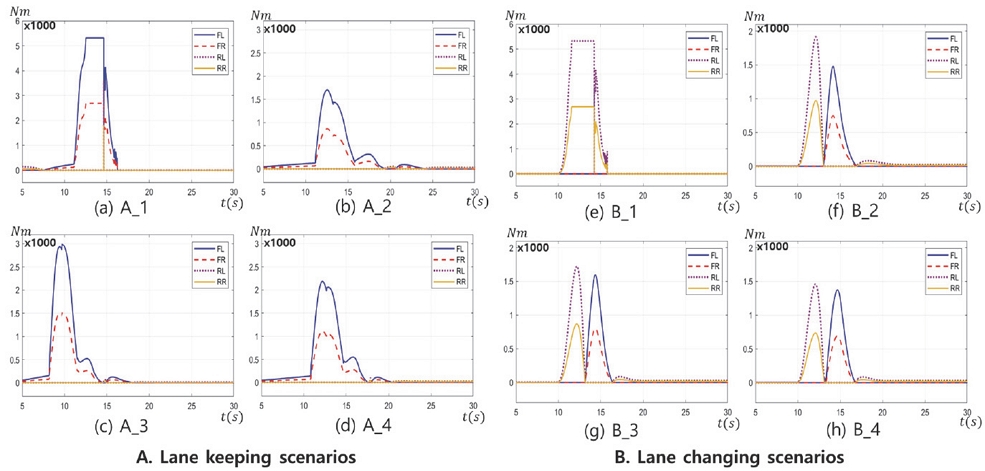
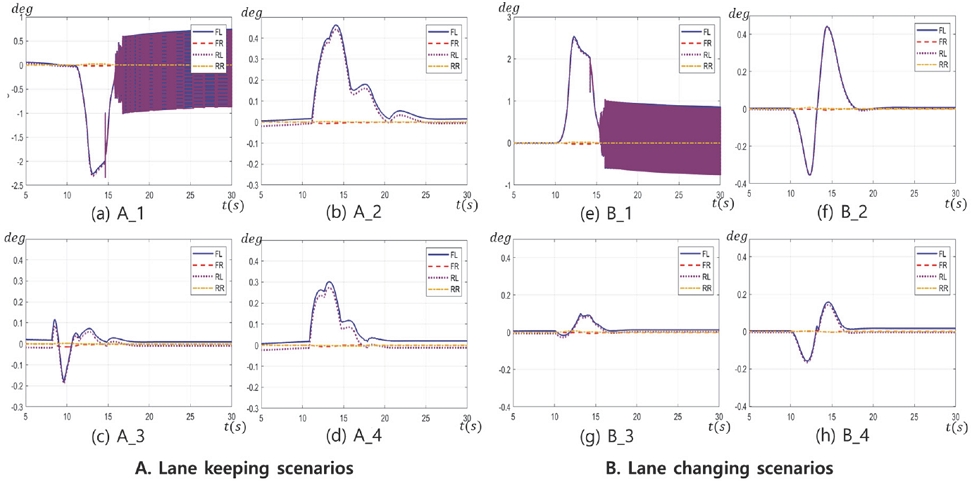
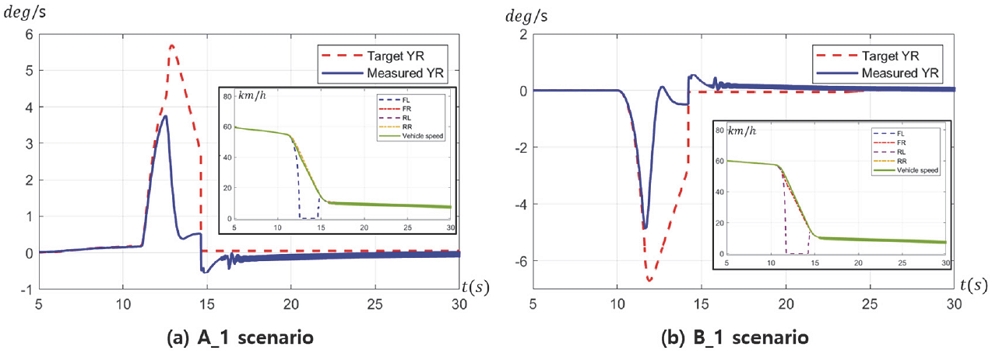
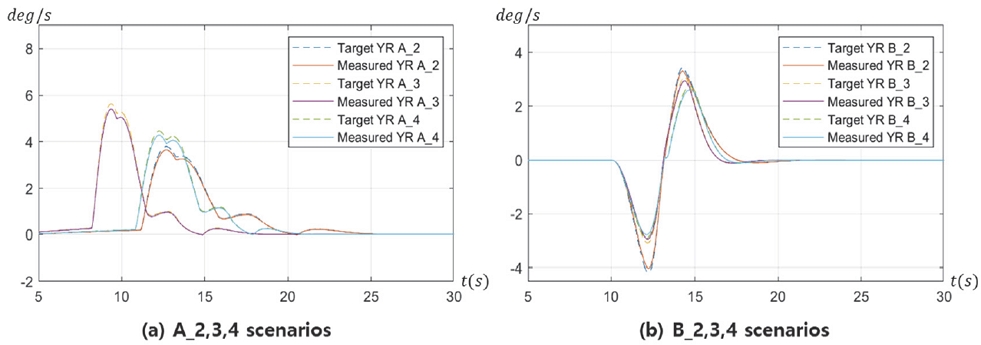
각 시나리오 별 속도 그래프는 Fig. 7과 같다. 그리고 SbB 제어기를 통해 산정된 제어 입력인 각 휠 제동 토크는 각 시나리오 별로 Fig. 8에 정리하였다. 또한 Fig. 9에 시나리오 별 각 Wheel angle의 계측 로그를 정리하였다. 이는 실차에서 계측이 불가하지만, 시뮬레이션 모델에서 측정이 가능하다. 시나리오 A_1, B_1에서의 목표 및 차량 실제 Yaw rate과 휠 각각의 속도를 Figs. 10(a), (b)에 나타내었다. 이외 시나리오 A_2,3,4, B_2,3,4의 yaw rate의 비교 그래프는 Figs. 11(a), (b)와 같다. -20 mm 음의 Scrub radius 설정의 시나리오 A_1, B_1에서 Figs. 9(a), (e)와 같이 SbB 제어 시 전륜의 Wheel angle은 Yaw moment 발생과 반대로 약 2.5 deg 정도 생성되며 이는 차량의 선회에 악영향을 주는 것을 확인하였다. Figs. 10(a), (b)에서와 같이 목표 Yaw rate를 완전히 추종하지 못할뿐더러 휠 락(Wheel lock)이 발생되었고, 목표에 Yaw rate에 도달하기 위해 Figs. 8(a), (e)와 같이 FL에 5000 Nm (약 80 bar) 이상의 과한 제동 토크가 제어입력으로 인가되었음에도 불구하고 제어 목표 Yaw rate에 미달되는 것을 확인할 수 있다. 더불어 약 2.8 m/s²의 감속도(Fig. 7 참고)로 양의 Scrub radius 시나리오 대비 급격이 감소였고, 이러한 구동력 저하 영향이 충분한 Yaw rate를 생성하지 못한 이유로 작용한다. 또한 Figs. 9(a), (e)의 약 17초 부근에서 Wheel angle이 -1~1 deg 정도 진동하는 현상을 보이는데, 이는 10 km/h 이하의 낮은 속도에서 Free-rolling이 반영된 시뮬레이션 설정으로 발생한 에러로 간주 할 수 있다. +20 mm 양의 Scrub radius 설정의 시나리오(A_2,3,4, B_2,3,4)는 Figs. 11(a), (b)와 같이 목표 Yaw rate를 완벽하게 추종하는 것을 확인하였다. 이를 추종하기 위해 Figs. 8(b, c, d), (f, g, h)와 같이 선회하는 방향의 각 휠에 약 2700 Nm 이하의 적절한 제동 토크로 제어 입력이 인가되는 것을 확인하였다. 전륜의 Wheel angle 또한 Free-rolling 조건임에도 양의 Scrub radius 효과로 편 제동 선회 방향과 동일한 방향으로 생성되는 것을 확인하였다.

Fig. 7

Vehicle driving speed according to the scenario

Fig. 8

Vehicle wheel brake torque according to the scenario

Fig. 9

Vehicle wheel angle according to the scenario

Fig. 10

Vehicle yaw rate and wheel speed according to negative scrub radius(-20 mm) scenario(A_1, B_1)

Fig. 11

Vehicle yaw rate according to positive scrub radius(+20 mm) scenario(A_2,3,4, B_2,3,4)

80 km/h 이상의 높은 속도에서 양의 Scrub radius의 영향은 주목할 만하다. Figs. 9(c), (g)와 같이 전륜의 Wheel angle은 편 제동 방향과 미비하게 반대로 형성되는 영향을 보이는 것이 확인되었다. 그러나 이후 속도가 감소되며 선회 방향과 동일한 방향으로 각도가 서서히 생성되며, SbB 제어의 유효성을 확보하였다. 양의 Scrub radius 설정의 모든 시나리오에서는 휠 락이 발생하는 경우는 없었으며, 완전한 제어 안정성을 확보하는 것을 확인하였다. 또한 초기 주행 속도를 유지하는 구동력이 인가된 시나리오 Fig. 7의 A_4, B_4 경우에서 또한 충분한 SbB 제어 성능이 확보되며 편 제동 제어로 인한 약간의 속도 감소가 존재하지만 금세 초기 셋팅 속도에 도달하는 것을 확인하였다.

4.3 실차 시험

4.3.1 시험 환경 구축

본 연구에서 실차 시험을 위해 개발한 SbB 제어기를 Dspace사의 범용 ECU인 MicroAutobox II에 적용하였다. 여기에는 Fig. 1의 목표 Yaw rate을 생성 부분과 상위제어기, 제동 토크 분배 입력을 생성하는 부분이 Matlab Simulink 모형으로 설계되어 담겨있다. 제어에 요구되는 실시간 차량 상태 정보와 제동 토크 제어 입력은 IDB ECU와 MicroAutobox 사이에 CANFD의 PCAN을 통해 실시간으로 송수신되도록 구축하였다. 실제 SbW 고장 시에 개발한 SbB 제어기는 운전자의 Steering wheel 조작으로 조향 의지를 입력 받게 되지, 본 연구에서 사용된 시험 차량은 SbW 시스템을 장착하기 전의 상황으로 기존에 장착된 Steering wheel은 물리적인 조향 컬럼과 랙으로 연결되어 있어 운전자가 조작 시 Wheel angle 움직임에 영향을 주어 SbW 시스템 고장 상태를 모사하지 못한다. 그리하여 본 연구에서는 SAS를 부착한 별도의 Steering wheel 장치를 Fig. 12와 같이 추가적으로 구성하고, 기존 조향 EPS 시스템의 로직에 직진성을 보장하는 Return 제어 기능을 Off 시켜 차량에 장착된 Steering wheel은 조작하지 않는 방법으로 SbW 고장 시 Fee-rolling 상황과 유사하게 모사하였다. 추후 이 구성은 운전석의 EPS 조향 시스템을 SbW 시스템으로 교체되어 시험될 예정이다.

Fig. 12

Configuration of test vehicle set-up

4.3.2 실차 시험 평가 결과

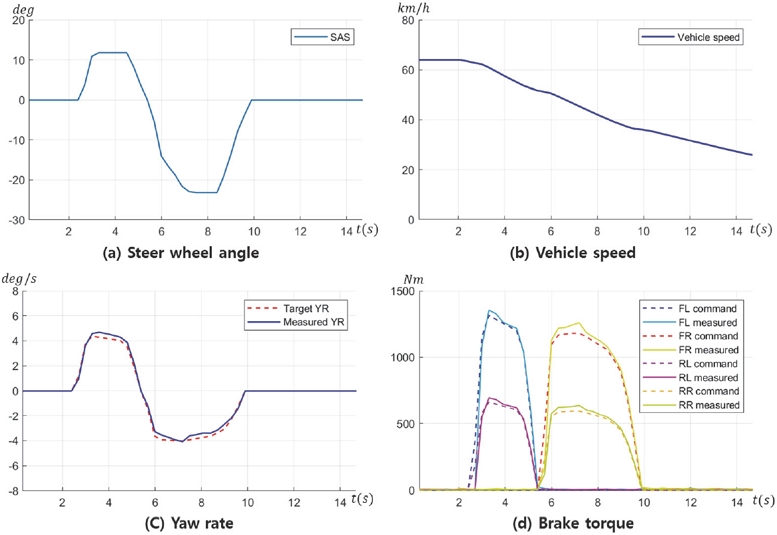
실차 시험은 경기도에 위치한 한국교통안전공단 자동차안전연구원의 높은 마찰 계수의 Dry 아스팔트 공로에서 수행되었다. 평가 시나리오는 Table 1의 8가지시나리오를 포함한 총 64가지 조건으로 구성하여 시험을 진행하였으나, 본 논문에서는 B_3의 차선변경 시나리오와 흡사한 조건에서의 시험 결과만을 대표적으로 언급하기로 한다.

실차 시험은 앞서 진행한 시뮬레이션 시나리오와 동일한 조건에서 진행하였고, 이 중 대표적 두 가지 시나리오 A_2, B_2와 흡사한 조건의 실차 시험 결과를 Figs. 13, 14와 같이 정리하였다. 다만 운전자의 조향 조작이 시뮬레이션과 실차 시험 사이에 어느정도 차이가 있다. 예를 들어 B_2 시뮬레이션에는 완전한 ±12 deg 정도 크기의 Sin파 형태 조향 조작을 입력 받지만, 실차 시험의 경우에는 Fig. 14(a)와 같이 조향각 변경 이후 ±15 deg 정도의 각도를 약 2~3초 정도 유지하는 조향 조작 형태가 입력되었다. 이러한 행태는 실제 운전자가 천천히 차선을 변경하는 조향 조작 행태와 근사하다.

Fig. 13

Vehicle test results in lane keeping scenario(A_2)

Fig. 14

Vehicle test results in lane changing scenario(B_2)

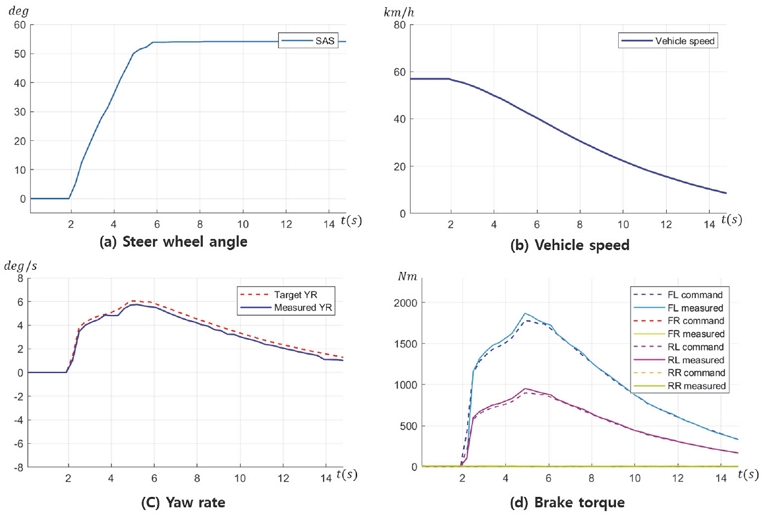
Lane keeping A_2 시험 결과는 Fig. 13과 같다. Fig. 13(c)과 같이 차량의 Yaw rate은 실험자의 조향 조작으로 생성한 목표 Yaw rate에 잘 추종하는 것을 확인할 수 있다. 또한 A_2의 시뮬레이션 결과와 거의 유사한 양의 Yaw rate 이 생성되는 것이 확인되었다. 제동 토크 또한 Fig. 13(d)와 같이 좌측 전륜에 최대 약 1400 Nm, 후륜에 630 Nm 정도로 시뮬레이션 상황보다 약하게 인가되지만, 비슷한 형상으로 발생하는 것을 확인할 수 있다.

Lane Changing B_2 시험 결과는 Fig. 14와 같다. Fig. 14(c)와 같이 목표 Yaw rate에 차량의 거동이 잘 추종하는 것을 확인할 수 있다. 이 또한 Yaw rate은 시뮬레이션과 실차 시험 모두 약 ±3 deg/s 정도의 크기로 비슷한 형상을 보였다.

Fig. 13(d)와 같이 실제 시험에서의 전륜 제동 토크는 최대 1200 Nm 정도로 시뮬레이션 보다 약하지만 유사한 입력 형태를 띄는 것을 확인하였다. 다만 실차 시험에서 약 10초 동안 보다 넓은 범위의 제동 입력이 인가되는 형태로 보아 총 제동량은 시뮬레이션 상황보다 크다고 유추할 수 있다. 그리하여 Fig. 13(b)와 같이 SbB 제어가 수행되는 동안 차량의 속도는 초기 60 km/h에서 20 km/h로 시뮬레이션 보다 과한 감속을 보인다. 이는 시험 차량이 전기차로 구동모터 특성의 회생제동 모드(I-pedal mode) 영향이 연료 차량의 엔진브레이크(기어 Down shift) 현상보다 크게 작용하여 발생하는 원인으로 유추된다. 전, 후륜에 인가되는 제동 토크량의 차이는 3.3장에 언급한 전, 후륜 토크 Factor 비율에서 비롯되고, 이와 같은 균일한 압력 배분으로 승차 이질감, 제어 불안정성 등의 문제는 발생하지 않았다. 이로써 개발한 SbB 제어기의 성능은 실차에 적용할만한 신뢰도 높은 성능이 확보됨을 확인하였다.

5. 결 론

본 연구에서 개발한 SbB 시스템은 SbW 시스템 고장으로 조향 불능 시 운전자 조향 조작 의지를 정도를 편 제동 제어를 통해 고장에 대응이 가능하다. 다양한 시나리오의 시스템 평가를 통해 조향 불능 상황에 충분히 대응 가능한 것을 확인하였다. 다만 본 연구는 시스템 양산 이전에 선행 개발한 수준으로 양의 Scrub radius 설정에서만 제어 유효성이 확보되는 결과를 보였지만, 본 연구를 초석으로 다양한 통합 섀시 제어 시도를 통해 양산되는 대부분 차량에 적용된 음의 Scrub radius 조향 시스템에서도 제어 유효성을 확보 할 수 있을 것으로 기대 할 수 있다. 예를 들어 SbW 시스템 고장 시 가변 서스펜션 제어와 통합하여 전륜 차고(King-pin 각)를 조절하면 음의 Scrub radius를 양으로 변화 시킬 수 있다. 더불어 Rear Wheel Steering(RWS) 시스템제어와의 통합, 구동력 추가 및 분배 방안을 적극 활용하면 음의 Scrub radius가 지닌 구조적 한계를 충분히 극복 가능 할 것으로 기대된다.

더욱이 최근 SbW 시스템이 적용되면서 전통적 섀시 설계 방법에서 벗어나 킹핀 앵글 제한으로 Scrub radius 영향을 줄이는 방향도 제안되고 있으며, Positive scrub radius를 늘리는 방향이 적극 주장되고 있다. 또한 4륜 독립 조향, In wheel motor 시스템이 적용된 자율 주행 차량에서 극단적인 양의 Scrub radius를 갖는 설계도 보고되고 있는 점으로 비추어 보았을 때, 본 연구에서 제시한 양의 Scrub radius 설정에서의 SbB 제어 방안은 유의미하다고 사료된다.

추후 연구로 우리는 SbW 시스템 실물을 장착하고, 칼만필터 기반 상태 추정 및 외란 보상, 관측기를 적용할 예정이며, 저 마찰 노면, 경사로 등과 같은 다양한 상황의 실차 시험 검증을 수행하여 양산 수준의 시스템 성능을 확보할 계획이다.

Acknowledgments

A part of this paper was presented at the KSAE 2022 Fall Conference and Exhibition

References

• K. L. Kim, J. R. Kim and T. Y. Koo, “New Steering Systems for Future Vehicles, Steer-by-Wire into Production Development,” Auto Journal, KSAE, Vol.43, No.2, pp.13-19, 2021.
• T. Pilutti, G. Ulsoy and D. Hrovat, “Vehicle Steering Intervention through Differential Braking,” Journal of Dynamic Systems, Measurement, and Control, Vol.120, No.3, pp.314-321, 1998. [https://doi.org/10.1115/1.2805402]
• A. D. Dominguez-Garcia, J. G. Kassakian and J. E. Schindall, “A Backup System for Automotive Steer-by-wire, Actuated by Selective Braking,” 2004 IEEE 35th Annual Power Electronics Specialists Conference, Vol.1, pp.383-388, 2004.
• Continental Automotive Systems, Vehicle Wheel Steer Control System and Method, US Patent 2021/0086737 A1, Filed September 4, 2020, Published March 25, 2021.
• M. Jonasson and M. Thor, “Steering Redundancy for Self-driving Vehicles Using Differential Braking,” Vehicle System Dynamics, Vol.56, No.5, pp.791-809, 2018. [https://doi.org/10.1080/00423114.2017.1356929]
• I. Szepessy, “Thyssenkrupp Steering: What is Needed for the SbW Breakthrough?,” 14th Automotive Steering Systems Conference, 2022.
• Steering Systemand Method for Controlling Vehicle Direction Through Differential Braking of Left and Right Road Wheels, US Patent 6,021,367, filed August 24, 1994, Issued February 1, 2000.
• M. Kissai, X. Mouton and B. Monsuez, “EPAS Fail-safe Control Using Differential Braking,” Transportation Research Procedia, Vol.52, pp.300-306, 2021. [https://doi.org/10.1016/j.trpro.2021.01.035]
• D. Zhang, B. Lin, A. Kirli and C. Okwudire, “Reduction of Steering Effort in the Event of EPAS Failure Using Differential Braking Assisted Steering,” SAE International Journal of Transportation Safety, Vol.5, No.2, 2017. [https://doi.org/10.4271/2017-01-1489]
• M. Park, S. Lee, M. Kim, J. Lee and K. Yi, “Integrated Differential Braking and Electric Power Steering Control for Advanced Lane-change Assist Systems,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.229, No.7, pp.924-943, 2015. [https://doi.org/10.1177/0954407014547927]
• B. -C. Jang, Y. -H. Yun and S. -C. Lee, “Simulation of Vehicle Steering Control through Differential Braking,” International Journal of Precision Engineering and Manufacturing, Vol.5, No.3, pp.26-34, 2004.
• B. Lee, A. Khajepour and K. Behdinan, “Vehicle Stability through Integrated Active Steering and Differential Braking,” SAE Transactions, pp.948-965, 2006. [https://doi.org/10.4271/2006-01-1022]
• J. Kim, Y. Cho, J. Ryu and S. Ko, “Development of Steer-by-Brake System for Rednndancy of Steer-by-Wire,” KSAE Fall Conference Proceedings, pp.468-469, 2022.