차량 모션 기반 타이어 힘 추정 및 실차 검증

1. 서 론

최근 자율주행 기술의 고도화 및 본격적 상용화를 앞두고, 자율 주행 안전에 관한 문제가 중요한 요소로 대두되고 있다. 사람이 직접 운전할 경우 주행 상황을 운전자가 인지, 판단하여 조향, 가/감속 등을 결정하기 때문에 위험 상황에 대하여 대처가 유연하다. 하지만 상용화를 앞둔 레벨 3 이상의 자율주행의 경우 상당 부분 제어 시스템이 직접 인지, 판단하여 차량의 거동을 제어하기 때문에 시스템이 정확한 노면의 상태, 타이어의 힘 및 슬립 상황의 정확한 예측은 더욱 중요하다. 특히, 타이어 힘은 차량 운동의 근원이며, 선회 시 안정성과 주행 성능에 직접적인 영향을 미친다.

하지만 제어 관점에서 이러한 타이어 힘을 직접 측정하기 위해 차량에 센서를 추가로 장착하는 것은^1,2) 원가 상승을 유발하고 혹독한 실차 주행 환경에서는 여러 측정 오차가 발생할 수 있는 기술적 한계 또한 존재한다. 이러한 이유로 타이어 힘을 차량 동역학 모델에 근거하여 다양한 추정 알고리즘을 통해 추정하려는 노력들이 이어지고 있다. 많은 연구에서 타이어의 수직력을 추정할 때, 주로 저비용 센서들과 Observer를 통하여 수직력을 추정하거나³⁾ UKF(Unscented Kalman Filter)⁴⁾를 사용하여 수직력을 추정하였다. 타이어 모델을 기반으로 추정할 경우 Dugoff 모델과 같은 비선형 타이어 모델들을 기반으로 타이어 힘을 추정하였다. 추정 방법론 또한 EKF(Extended Kalman Filter),^5,6) Sliding mode observer⁷⁾ 등 여러 알고리즘을 사용하고 있다. 타이어 모델은 UA모델,⁸⁾ Magic formula⁹⁾를 비롯한 다양한 비선형 모델들이 활용되고 있으며 많은 연구에서 선형 마찰 영역을 가정하여 타이어 힘을 산출하는 경우가 많았다.¹⁰⁾ 또한, 타이어 모델을 기반으로 타이어 횡력 추정 시, 슬립 관련 상태 변수들의 측정을 위해 GPS 등의 센서를 추가로¹¹⁾ 활용하는 경우도 있었다. 타이어 횡력 추정 관점에서는 Bicycle 모델을 사용해 좌/우 합쳐진 전/후 타이어 힘을 추정하는 식은 많았지만¹²⁾ 상대적으로 본 연구처럼 좌/우 휠의 타이어 힘까지 분리하여 추정하고 이를 실험적으로 검증까지 하는 연구는 매우 적었다.

본 연구에서는 차량의 질량과 무게 중심 위치를 정확히 알거나, 다른 추정 로직에 의해 비교적 정확하게 예측 가능하다고 가정하고, 타이어 모델의 사용없이 차량의 거동을 기반으로 4륜의 모든 수직력과 횡력을 추정하였다. 각 타이어의 수직력 추정 시, 차량을 강체로 가정하여 종/횡방향 가속도 센서 정보를 통해 종/횡방향 하중 전이(Load transfer)량을 예측하여 4륜의 수직력을 추정하였다. 수직력을 추정하는 과정은 비교적 간단하지만 실차 검증 조건에서 타이어 힘을 충분히 정확히 추정하는 성능을 보였다.

각 타이어의 횡력은 타이어 모델, 즉 타이어힘-슬립 관계식을 배제하고 차량 거동 관점에서 횡방향 힘 평형식과 요 모멘트 평형식을 통해 좌/우 합쳐진 전/후 횡력을 우선적으로 추정하였다. 그, 이후 추정된 전/후 횡력을 좌/우로 나누는 과정에서 기존의 방식들은 주로 좌/우의 수직력의 선형 비율로 분배를 하는데 본 연구에서는 실제 차량에서의 횡력-수직력간 비선형 관계를 룩업테이블 형태로 고려하였고, 좌/우 분배 시 큰 오차 요인인 초기 토우각도 적절히 보상하였다. 이부분이 기존 횡력 추정 연구와 큰 차별점으로 볼 수 있다.

차량 휠의 3방향 타이어 힘/모멘트를 계측하는 장비인 6분력계(Wheel force transducer)를 시험 차량 4륜에 부착하여 다양한 선회, 가/감속 실차 시험 시나리오에서 타이어 힘을 계측하였고, 이를 기반으로 제안 추정 로직의 검증 및 성능 육성을 실시하였다.

본 논문의 작성 구조는 다음과 같다. 2장에서 제안 타이어 횡력 및 수직력 추정 로직의 상세 방법을 서술하였고, 기존 타이어 힘 추정 방법들 간의 성능 비교도 실시하였다. 3장에서 실차 주행 데이터를 기반으로 추정 성능을 검증하였고, 4장에서 결론을 맺는 것으로 구성되어 있다.

2. 타이어 힘 추정 로직 개발

본 연구에서는 차량 거동 관점에서 차량의 종/횡방향 가속도 센서 계측치와 차량 질량, 무게중심 정보 기반으로 4륜 타이어의 횡/수직방향 힘을 각각 추정하였다.

수직 방향 타이어 힘은 가속도 센서 계측치 기반으로 예측된 종/횡방향 하중 전이(식 (1))를 기반으로 추정하였고, 타이어 횡력은 차량 횡방향 힘평형식(식 (8)), 요 모멘트 평형식(식 (9))에 대한 연립방정식에 의해 전/후 타이어의 좌/우 합쳐진 횡력을 우선적으로 예측하고, 앞서 추정된 4륜의 수직력과 각 횡력 사이의 비선형성을 고려하여 각 타이어별 횡력을 분리 추정하였다.

2.1 4륜 타이어 수직력 추정 로직

기존 연구에서는 수직력을 추정할 때, 다소 복잡한 수식을 활용해¹³⁾ 추정하였으나, 본 연구에서는 비교적 간단한 대수식으로 신뢰도 높게 모든 타이어의 수직력을 추정할 수 있었다. 수직력 추정 시 차량의 질량과 초기 무게 배분을 알고 있다고 가정하였고, 식 (1)과 같이 차량의 종/횡 가속도 신호 신호를 측정하여 각 바퀴로의 하중 전이를 예측한 후 이를 기반으로 각 타이어별 수직력을 추정하였다.

$\[ \begin{array}{c}{F}_{Z_{-}FL}=F_{Z_{-}FL,nominal}-k_1{a}_y-k_3{a}_x\hfill \\ F_{Z_{-}FR}=F_{Z_{-}FR,nominal}+k_1{a}_y-k_3{a}_x\hfill \\ F_{Z_{-}RL}=F_{Z_{-}RL,nominal}-k_2{a}_y+k_3{a}_x\hfill \\ F_{Z_{-}RR}=F_{Z_{-}RR,nominal}+k_2{a}_y+k_3{a}_x\hfill \end{array} \]$

(1)

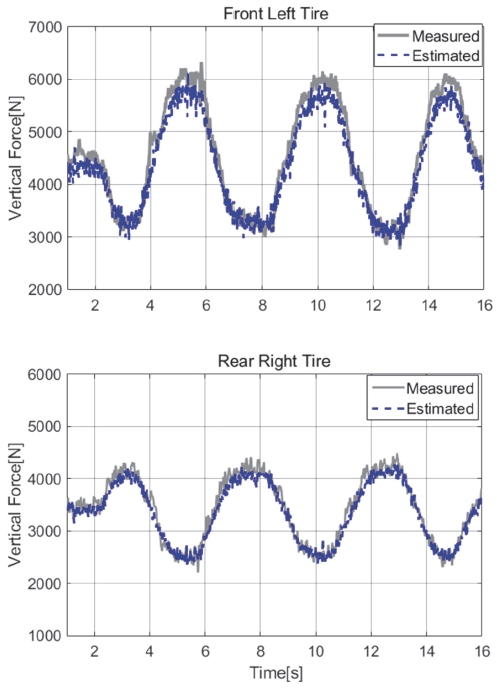
횡방향 가속도 a_y에 차량 전륜에는 계수 k₁, 후륜에는 계수 k₂를 곱하여 횡방향 하중 전이를 계산하였다. 마찬가지로 종방향으로 가/감속 시 차량에 종방향 하중 전이가 발생하며, 종방향 가속도 a_x에 계수 k₃를 곱하여 종방향 하중 전이를 계산하였다. 차량 핸들링 관점에서 주행 시 횡가속도에 의하여, 차량의 전/후륜에 발생하는 횡방향 하중 전이는 서로 다르게 설계되기 때문에 계수 k₁, k₂는 각각 다른 값을 갖는다. 종방향 하중 전이는 좌/우가 동일하기 때문에 계수 k₃는 좌/우 같은 값을 사용한다. 계수, k₁, k₂, k₃는 실측된 수직력 데이터를 기반으로 결정하였으며, k₁=400, k₂=250, k₃=250[N/(m/s²)]로 설정하였다. 계수는 차량에 따라 달라질 수 있으며, 본 연구의 대상 차량은 k₁이 k₂보다 크기 때문에 선회 시 언더스티어 경향으로 전륜 롤 강성이 후륜 대비 더 크게 설계된 것을 확인할 수 있다. Fig. 1은 50 kph, 피크 횡가속도가 4.5 m/s²정도인 슬라럼 조향에 대한 차량의 전륜 좌측 타이어와 후륜 우측 타이어 수직력 추정치와 실제 측정값의 비교이다. 식 (1)과 같은 단순한 수식으로도 각 타이어 수직력을 충분히 정확하게 추정하는 모습을 보여주었다.

Fig. 1

Experimental validation for proposed vertical force (7) estimation logic (slalom, 50 kph)

2.2 4륜 타이어 횡력 추정 로직

2.2.1 기존 타이어 횡 추정 로직의 한계

기존 많은 연구에서^14,15) 비선형 타이어 모델을 활용하여 식 (2)와 같이 타이어 슬립각(α)과 코너링 강성(C_α)을 입력으로 타이어 횡력을 추정하였다.

$\[ F_y=f\left(C_{\alpha },\alpha \right) \]$

(2)

4륜의 타이어 횡력을 추정하기 위한 기존 방법의 문제는 각 휠에서의 타이어 슬립각 및 코너링 강성의 사전 정보가 필요하다는 점이다. 특히, 다음 식 (3) ~ (6)과 같이 각 타이어 별 슬립각을 알기 위해서는 차량에서 측정이 어려운 종속도(V_x), 횡속도(V_y)가 필요하며, 타이어의 코너링 강성 또한, 수직힘, 노면/타이어의 종류 등의 여러 예측이 어려운 비선형적 요인에 의해 결정된다.

$\[ {\alpha }_{FL}=\delta -\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left[\frac{V_y+l_F\dot{\gamma }}{V_x-t\dot{\gamma }/2}\right] \]$

(3)

$\[ {\alpha }_{FR}=\delta -\text{arctan}\left[\frac{V_y+l_F\dot{\gamma }}{V_x+t\dot{\gamma }/2}\right] \]$

(4)

$\[ {\alpha }_{RL}=-\text{arctan}\left[\frac{V_y-l_R\dot{\gamma }}{V_x-t\dot{\gamma }/2}\right] \]$

(5)

$\[ {\alpha }_{RR}=-\text{arctan}\left[\frac{V_y-l_R\dot{\gamma }}{V_x+t\dot{\gamma }/2}\right] \]$

(6)

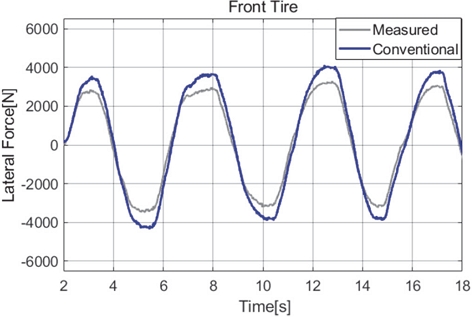
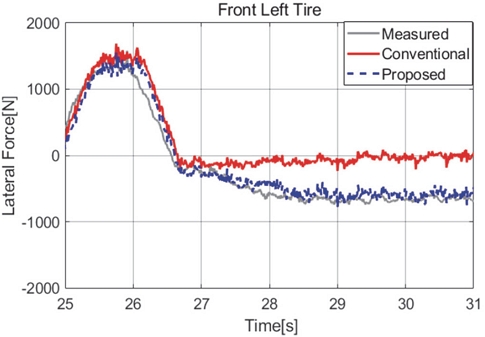
타이어의 코너링 강성은 기본적으로 측정이 어려운 타이어 슬립각의 크기에 비선형적으로 변화하는데, 보통은 식 (7)과 같이 강성을 횡력-슬립각의 Zero슬립 근처의 초기 기울기로 정하는 선형 타이어 횡력 모델을 사용하는데, 슬립각이 증가하게 되면 실제 강성 기울기는 작아지기 때문에 선형 타이어 모델 기반의 횡력 추정의 경우 어느 정도 횡슬립이 발생하는 선회 상황에서는 Fig. 2와 같이 오차가 발생한다.

$\[ F_y=C_{\alpha }\alpha \]$

(7)

Fig. 2

Experimental validation for conventional lateral force estimation method (slalom, 50 kph)

Fig. 2에서는 식 (2)와 같이 코너링 강성과 타이어 슬립각의 곱으로 횡력을 추정한 결과이며, 50 kph, 피크 횡가속도가 4.5 m/s²정도인 슬라럼 주행 상황에서 실제 차량 센서 계측과 비교했을 때 추정 오차가 발생하는 것을 확인할 수 있다(제안 로직의 추정 결과인 Fig. 3 대비). 물론, 이 경우도 슬립각 산출에 필요한 차량의 종/횡속도도 정확히 알 수 있다고 가정했기 때문에 실제 적용 측면에서 기존 방법은 큰 제약이 존재한다.

Fig. 3

Experimental validation for proposed lateral force estimation logic to each axle (slalom, 50 kph)

2.2.2 제안 타이어 횡력 추정 로직

상기 고정된 타이어 모델에 의존하는 기존 방법의 한계를 개선하기 위해 특정 타이어 모델을 사용하지 않고 차량의 거동 관점에서 횡방향 힘 평형식과 요 모멘트 평형 식을 통해 타이어 횡력을 도출하였다.

뉴턴의 운동 제2법칙인 힘과 가속도와 질량과의 관계를 이용하여 차량의 횡 거동이 발생할 때 횡방향 힘 평형식과 요방향 모멘트 평형식은 다음과 같다.

$\[ m{a}_y=F_{y_{-}F}+F_{y_{-}R} \]$

(8)

$\[ I_z\dot{\gamma }=l_F{F}_{y_{-F}}-l_R{F}_{y_{-}R} \]$

(9)

두 평형식에 의해 연립방정식으로 구한 차량의 전/후 횡력(좌/우 합쳐진)을 추정하는 식은 다음과 같다.

$\[ F_{y_{-}F}=\frac{l_{R}m{a}_y+I_z\dot{\gamma }}{l_F+l_R},{ F}_{y_{-}R}=\frac{l_{F}m{a}_y-I_z\dot{\gamma }}{l_F+l_R} \]$

(10)

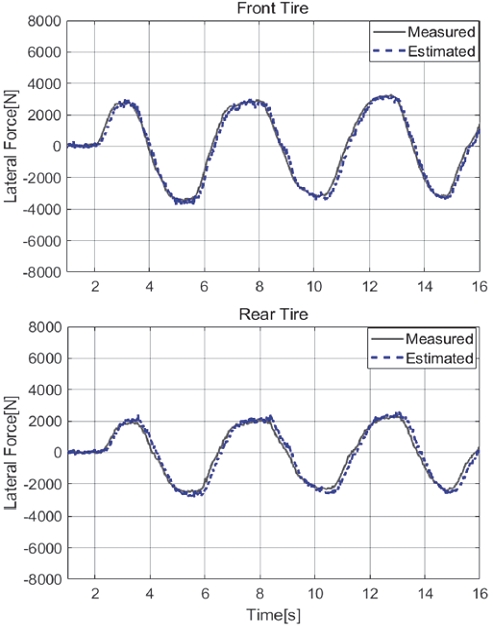
식 (10)에 의해 산출된 전/후 타이어의 횡력을 하나의 대표 주행 시나리오에 대해 Fig. 3과 같이 나타내었다. 전/후륜 타이어 횡력을 매우 높은 정확도로 예측하는 것을 확인할 수 있다.

그 다음은 좌/우륜 합쳐진 횡력을 각각의 좌/우륜로 분리하는 분배부분이다. 가장 단순한 일반적인 방법은¹⁶⁾ 식 (11, 12)과 같이 좌/우 횡력을 좌/우 수직항력의 비율대로 분배하는 것이다.

$\[ F_z=F_{z,Left}+F_{z,Right} \]$

(11)

$\[ F_{y,Left}=\frac{F_{z,Left}}{F_z}{F}_y ,{ F}_{y,Rght}=\frac{F_{z,Right}}{F_z}{F}_y \]$

(12)

하지만 이러한 방식을 실차 계측 데이터에 적용 분석해 본 결과 횡하중 전이에 의한 좌/우 수직력 차이가 증가함에 따라 횡력 추정값의 오차가 크게 발생하는 것을 확인하였다. 따라서, 이를 극복하고자 식 (13)와 같이 Gillespie¹⁷⁾의 연구 결과에 근거하여 타이어의 횡력을 타이어 수직력에 대한 2차식으로 가정하였고, 이를 기반으로 좌/우 타이어 횡력을 분배하였다.

$\[ F_y\approx a{F}_z-b{F_z}^2 \]$

(13)

a, b는 코너링 강성 다항식의 계수로, 실측 데이터 기반으로 결정하였다. 기존의 방식은 수직력에 따른 횡력의 크기가 선형으로 변한다면, 해당 방법은 2차식을 사용하므로 횡력과 수직력이 비선형적인 관계를 가지며 실제 계측 데이터로 검증한 결과 기존 분배 방법 대비 타이어 횡력을 더 정확하게 예측하는 것을 확인하였다. 그러나, 여전히 타이어의 횡력이 매우 큰 경우, 추정값이 실제 값보다 작게 측정이 되거나 횡력이 작은 경우, 실제 값보다 측정이 크게 되는 등 횡력 추정에 오차가 있음을 파악하였다. 이는 실제 차량 현가 시스템의 비선형 특성이 2차식으로 완벽히 표현되기 어렵다는 것을 의미하며 이를 해결하고자 식 (14)와 같이 횡방향 하중전이에 대한 룩업테이블(LUT: Look Up Table) 형태로 좌/우 분배비를 각각 경험적으로 결정하였다. 즉, 기존의 1차식과 2차식은 횡방향 하중 전이 량이 작은 경우(500 ~ 1,500 N)와 큰 경우(2,500 N이상)에서 추정 값과 측정값 간의 오차가 발생하여 이를 개선하고자 실차 계측 데이터를 기반으로 Fig. 4와 같은 룩업테이블을 이용하여 현가시스템의 비선형성을 고려하였다.

$\[ \begin{array}{c}{F}_{y,Left}=LUT\left(\mathrm{\Delta }{F}_z\right)F_y\hfill \\ F_{y,Right}=\left(1-\mathit{LUT}\left(\mathrm{\Delta }{F}_z\right)\right)F_y\hfill \end{array} \]$

(14)

$\[ \begin{array}{c}2\text{Δ}{F}_Z=F_{Z_{-}FL}-F_{Z_{-}FR}\hfill \\ F_{y_{-}FL}\begin{array}{l}=\frac{\left(a{F}_{Z_{-}FL}-b{F}_{Z-FL}{}^2\right)}{\left(a{F}_{Z_{-}FL}-b{F_{Z_{-}FL}}^2+a{F}_{Z_{-}FR}-b{F_{Z_{-}FR}}^2\right)}{F}_{y_{-}F}\hfill \\ =\frac{1}{2}+\frac{a\mathrm{\Delta }{F}_Z-b\mathrm{\Delta }{F}_Z{F}_{Z-F}}{a{F}_{Z_{-}F}-0.5b{F}_{Z_{-}F}{}^2-2b\mathrm{\Delta }{F_Z}^2}{F}_{y_{-}F}\hfill \end{array}\hfill \\ \hfill \end{array} \]$

(15)

$\[ \mathit{LU}\mathrm{T}\left(\mathrm{\Delta }{F}_Z\right)=\frac{1}{2}+\frac{a\mathrm{\Delta }{F}_Z-b\mathrm{\Delta }{F}_Z{F}_{Z-F}}{a{F}_{Z_{-}F}-0.5b{F_{Z_{-}F}}^2-2b\mathrm{\Delta }{F_Z}^2} \]$

(16)

Fig. 4

Proposed distribution ratio of lateral tire force with respect to lateral load transfer

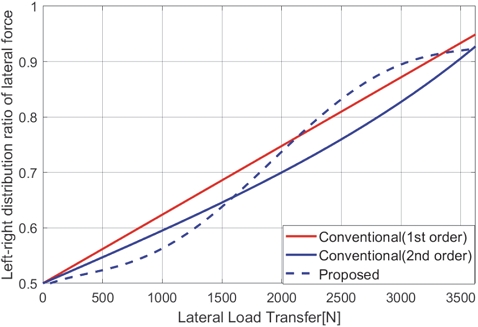
Fig. 4는 횡방향 하중 전이 차이에 따른 횡력 분배 비율을 실제 계측치와 비교하여 결정한 제안 횡력 좌/우 분배비 그래프이다. 횡력 좌/우 분배 비율은 큰 바퀴의 기준에서 해당되는 그래프이며, 횡방향 하중 전이는 절댓값으로 표현하였다. 해당 분배 비율은 전/후 타이어 모두 사용 가능한 비율이다.

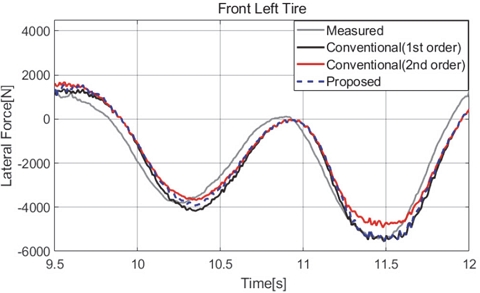
Fig. 5는 기존의 1차식, 2차식에 근거한 분배비와 제안한 분배 비율을 차선변경 주행 상황에서 전륜 왼쪽 타이어 횡력에 적용시킨 그래프이다. 측정값과 비교했을 때 횡력이 커져가면 기존 1차식과 2차식 비율의 경우 제안비율이 적용된 예측보다 오차가 발생함을 보인다.

Fig. 5

Example of the proposed distribution ratio graph of lateral tire force with respect to lateral load transfer

한편, 차량이 감속 시 좌/우 횡력의 추정 오차가 커지는 문제가 발견되었다. 분석 결과, 감속 시 하중이 앞으로 쏠려 다이브 방향으로 피치 거동이 나타나게 되면 특히 전륜에서의 타이어 토우각이 정속 주행 대비 Toe in이 더욱 커지는 경향성이 관찰되었다. 이를 적절히 보상하기 위해 감속 시 감속도에 대한 비례식 형태(ka_x)로 좌/우 횡력을 추가 보상(±ka_x)하여 적용하였다.

Fig. 6에서 타이어 횡력 측정값과 제동 시 토우각 변화를 고려하지 않는 기존 추정 방식과 토우 변화를 고려한 추정 결과를 비교하였다. 슬라럼 주행 이후 후반부 감속 상황에서 Toe in이 발생하여 횡방향으로 힘이 다소 발생하는 현상이 나타났으며 해당 보상 로직을 적용하면 추정 오차가 줄어드는 모습을 확인할 수 있다.

Fig. 6

Estimation accuracy improvement by toe angle compensation (deceleration after slalom)

3. 실차 검증

시뮬레이션 검증에 그쳤던 기존 다수의 연구들과^18,19) 달리 제안 타이어 힘 추정 알고리즘의 양산적용 가능성을 충분히 검증하기 위해 본 연구에서는 실제 차량을 이용하여 검증을 진행하였다. 실험 차량은 4륜에 실제 타이어힘 계측을 위한 6분력계가 장착된 국내 소형 SUV 차량이 활용되었다. 차량의 제원은 Table 1에 나타냈으며 여기서 질량, 무게중심은 6분력계가 포함된 수치이다. 추정 로직의 실차 적용 시에는 6분력계가 배제된 순수 차량의 질량, 무게중심 정보가 적용되어야 한다.

Table 1

Vehicle parameters

3.1 실차 검증 환경

실험 검증은 한국 자동차연구원 주행시험장에서 진행하였으며 데이터 계측 주기는 100 Hz로 독일 dSPACE社의 AUTOBOX를 이용해서 계측하였다. Table 2에 정의된 주행 시나리오로 시험을 수행하였고 제안 추정 로직이 다양한 조향, 속도, 노면 조건에 관계없이 추정을 잘 수행하는지 검증하였다. Case 1을 통해서는 평상 선회 상황에서 제안 타이어 횡력, 수직력 추정 로직을 검증하였고, 좀 더 가혹한 주행 시나리오인 Case 2 ~ 3을 통해서 한계에 근접한 주행상황에서 4륜의 타이어 횡력, 수직력 추정을 잘 이어가는지 확인하였다. 마지막으로 Case 4를 통해 노면 마찰계수가 낮은 환경에서 제안 타이어 힘 추정 정확도를 확인하였다.

Table 2

Driving scenarios for experimental tests

3.2 실차 검증 결과

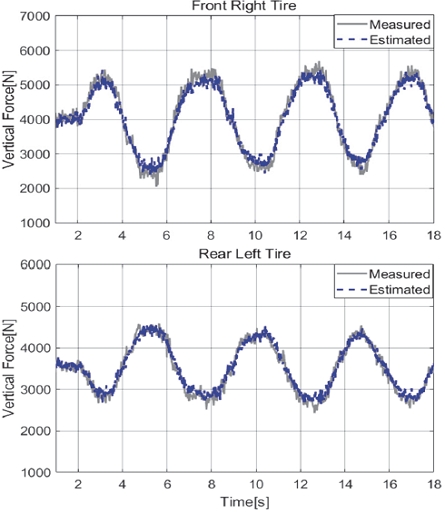
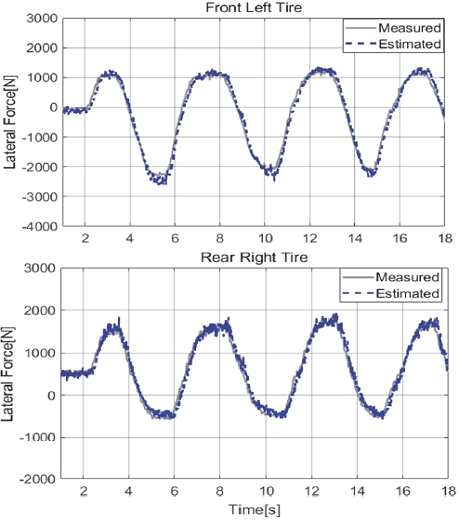
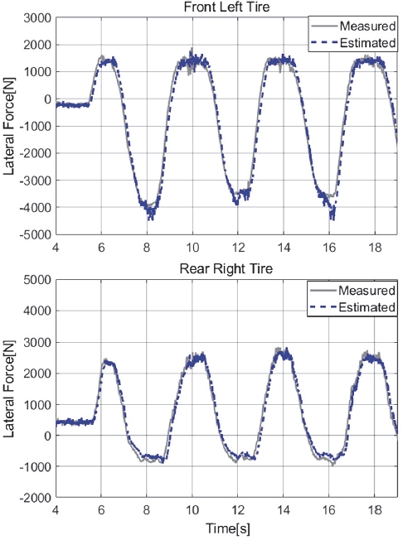
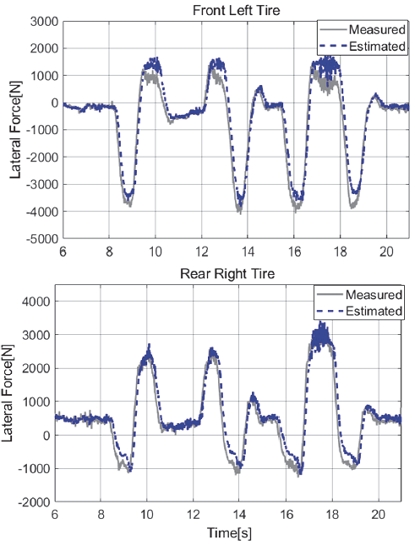
Figs. 7, 8은 Case 1에 대한 타이어 수직력, 횡력 추정 결과이다. 수직력의 경우 우측 전륜쪽, 좌측 후륜를, 횡력의 경우는 좌측 전륜, 우측 후륜에 대한 추정 결과를 나타내었다. Case 1은 상대적으로 다른 Case 대비 차속과 조향각 크기가 다른 시나리오보다 작아 피크 횡가속도가 약 4 m/s²인 상대적으로 마일드한 주행 영역 시험 시나리오에 해당한다. 4륜의 수직력, 횡력 모두 높은 정확도로 추정하는 모습을 보여주었다.

Fig. 7

Vertical tire force estimation results for case1

Fig. 8

Lateral tire force estimation results for case1

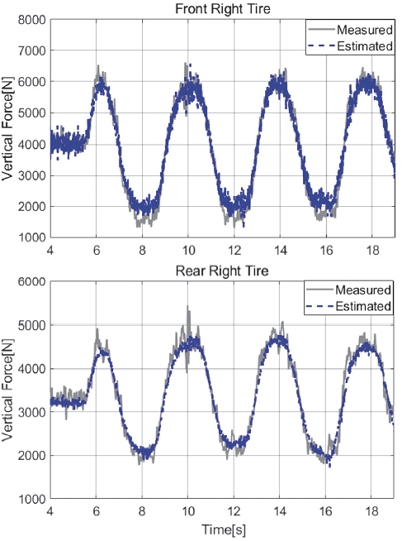
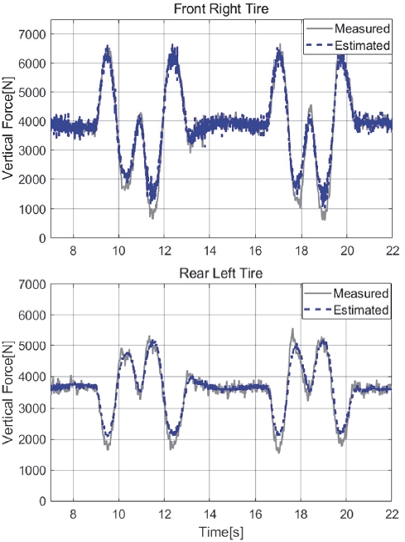
Figs. 9, 10은 Case 2에 대한 타이어 수직력, 횡력 추정 결과이다. Case 2에서는 Case 1보다 높은 80 kph 속도에서의 슬라럼 주행이며 피크 횡가속도가 약 6 m/s²정도이다. Case1 대비 횡방향 하중 전이가 약 1.5배 정도 크게 발생하였으나 여전히 수직력, 횡력 모두 높은 정확도를 유지하고 있음을 확인할 수 있다. 다만, 수직력 추정의 경우 횡방향 하중 전이에 의해 수직력이 낮아지는 쪽에서(8,12,16초 부근) 다소 추종치가 크게 되는 현상이 발생되었다. 이는 차량 롤모션에 의해 수직축의 방향이 계측장비의 수직축과 추정 모델의 수직축이 다른 것이 원인이며, 실제 장비의 수직력 측정 시 수직축은 롤 거동에 의해 지표면 대비 기울어지기 때문에(추정치의 수직축은 여전히 지표면에 수직한 축) 지표면 수직축 방향의 수직력 대비 다소 작게 측정되는 것으로 판단된다.

Fig. 9

Vertical tire force estimation results for case2

Fig. 10

Lateral tire force estimation results for case2

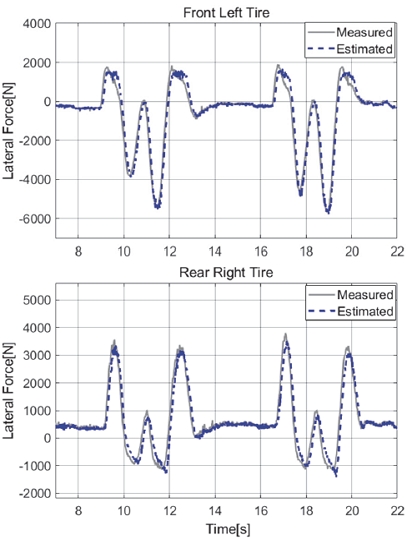
Figs. 11, 12는 Case 3에 대한 타이어 수직력, 횡력 추정 결과이다. Case3은 Case 2와 차량 속도는 같으나 더욱 빠른 조향 속도로 차선 변경하는 상황이다. 횡방향 하중 전이가 Case 2보다 더 높은 한계 선회 상황에서도 높은 추정 정확도를 유지하고 있음을 확인할 수 있다. Case 2에서와 같이 수직력이 작아지는 부분에서 추정치가 계측치보다 큰 상황이 동일하게 발생하였다.

Fig. 11

Vertical tire force estimation results for case3

Fig. 12

Lateral tire force estimation results for case3

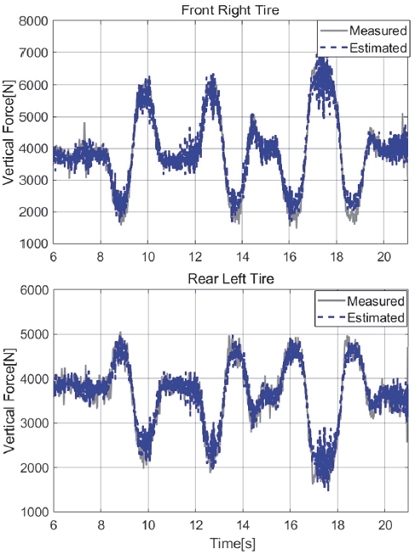
Figs. 13, 14는 저마찰로 차선변경 조건인 Case 4에 대한 타이어 수직력, 횡력 추정 결과이다. 전반적으로 제안된 추정 로직은 추정 원리 상 마찰계수에 의존성이 없기 때문에 결과적으로 낮은 마찰계수에서도, 횡력과 수직력을 잘 추정하고 있음을 보여준다. 한편, Fig. 13을 보면 추정치가 다른 시나리오 대비 노이즈가 많은 것이 관찰되는데 이는 해당 저마찰로가 Basalt 노면에 물이 분무된 상태로, 실제 다소 거친 노면에 해당되어 이로 인해 차량 거동의 진동이 발생하여 실제 가속도 센서 계측치의 고주파 성분이 많아진 것이 원인이다.

Fig. 13

Vertical tire force estimation results for case4

Fig. 14

Lateral tire force estimation results for case4

4. 결 론

본 논문에서는 특정 타이어 모델에 의존하지 않고 차량의 거동에 기반하여 비교적 단순한 방법으로 4륜의 타이어 횡방향, 수직 방향 힘을 추정하는 알고리즘을 제안하였고, 추정의 정확성을 실차 시험을 통해 검증하였다.

우선, 종/횡방향 가속도 센서 계측치를 이용하여 종/횡방향 하중 전이를 예측하여 4륜의 수직 방향 타이어 힘을 산출하였다. 차량의 좌/우 합쳐진 전/후 횡력을 차량 거동 관점인 횡방향힘 평형 식, 요 모멘트 평형식을 통해 도출하였고, 그 이후 좌/우 횡력은 앞서 산출된 수직 방향 힘과 차량의 초기 토우각 정보를 이용하여 좌/우 분리하여 산출하였다.

제안 타이어 힘 추정 로직은 6분력계가 장착된 실차 검증 환경에서 다양한 시나리오의 주행 시험을 통해 검증되었다. 그 결과, 제안 로직은 알고리즘의 단순함에도 불구하고 꽤 정확하게 4륜의 타이어 횡력, 수직력을 예측할 수 있음을 확인하였다.

다만, 검증 시 차량의 질량 및 무게중심을 알고 있다고 가정하였기 때문에, 실차 환경에서 질량 및 무게중심 변화에 대해 높은 견실성을 확보하기 위해서는 해당 변동을 식별하기 위한 별도의 다른 추정 로직이 필요하다는 제약이 존재한다.

마지막으로, 제안된 타이어 힘 추정 로직이 추후 타이어 힘 정보를 활용하는 다양한 차량 제어 알고리즘들의 전체적인 차량 레벨의 성능 개선 전반에 기여할 수 있기를 기대한다.

Acknowledgments

이 연구는 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(‘20015831’). 이 논문은 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2022R1A2C1004405, No.2021R1F1A1050200). 이 논문은 2022학년도 한국기술교육대학교 교육연구진흥과제 지원에 의하여 연구되었음.

References

• K. B. Singh, M. A. Arat and S. Taheri, “An Intelligent Tire Based Tire-Road Friction Estimation Technique and Adaptive Wheel Slip Controller for Antilock Brake System,” Journal of Dynamic Systems Measurement and Control, Vol.135, No.3, Paper No.031002, 2013. [https://doi.org/10.1115/1.4007704]
• B. H. G. Barbosa, N. Xu, H. Askari and A. Khajepour, “Lateral Force Prediction Using Gaussian Process Regression for Intelligent Tire Systems,” IEEE Transactions on Systems Man And Cybernetics Systems, Vol.52, No.8, pp.5332-5343, 2022. [https://doi.org/10.1109/TSMC.2021.3123310]
• K. Jiang, A. Pavelescu, A. Victorino and A. Charara, “Estimation of Vehicle’s Vertical and Lateral Tire Forces Considering Road Angle and Road Irregularity,” IEEE 17th International Conference on ITCS, pp.342-347, 2014. [https://doi.org/10.1109/ITSC.2014.6957714]
• S. W. Kim, Y. W. Jeong, J. S. Kim, S. H. Lee and C. C. Chung, “Estimation of Vertical Load Variation on a Tire Using Unscented Kalman Filter,” Transactions of KSAE, Vol.28, No.1, pp.43-52, 2020. [https://doi.org/10.7467/KSAE.2020.28.1.043]
• G. Baffet, A. Charara and J. Stepahant, “Sideslip Angle, Lateral Tire Force and Road Friction Estimation in Simulations and Experiments,” International Conference on Control Applications, pp.903-908, 2006. [https://doi.org/10.1109/CCA.2006.285967]
• G. Baffet, A. Charara and G. Dherbomez, “An Observer of Tire-road Forces and Friction for Active Security Vehicle Systems,” IEEE/ASME Transactions on Mechatronics, Vol.12, No.6, pp.651-661, 2007. [https://doi.org/10.1109/TMECH.2007.910099]
• S. Moon, M. Choi and S. Kim, “Tire Lateral Force and Cornering Stiffness Estimation Using Sliding Mode Observer,” CICS Annual Conference Proceedings, pp.96-97, 2013.
• Y. Choi and G. Gim, “Improved UA Tire Model as a Semi-empirical Model,” FISITA World Automotive Congress, pp.1-8, 2000.
• H. Hamman, J. K. Hedrick, S. Rhode and F. Gauterin, “Tire Force Estimation for a Passenger Vehicle with the Unscented Kalman Filter,” IEEE Intelligent Vehicles Symposium, pp.814-819, 2014. [https://doi.org/10.1109/IVS.2014.6856391]
• H. Kim, D. Kim, K. Cho, S. Kim and K. Park, “Vehicle Model with Linear or Nonlinear Tire Model and Steering Control,” Proceedings of 2011 ICROS Jeonbuk-Jeju Regional Conference, pp.35-37, 2011.
• S. L. Miller, B. Youngberg, A. Millie, P. Schweizer and J. C. Gerdes, “Calculating Longitudinal Wheel Slip and Tire Parameters Using GPS Velocity,” Proceedings of the American Control Conference, Vol.3, pp.1800-1805, 2001. [https://doi.org/10.1109/ACC.2001.945995]
• J. Kim, “Estimation of Tire Forces using Vehicle Linear Accelerations and Yaw Rate,” Transactions of KSAE, Vol.27, No.10, pp.747-753, 2019. [https://doi.org/10.7467/KSAE.2019.27.10.747]
• Y. Seo and K. Nam, “Development of a Lateral Tire Force Estimation Algorithm Based on Rack Force of Steer-by-Wire Systems,” KSAE Spring Conference Proceedings, pp.287-288, 2021.
• M. Doumiati, A. Victorino, A. Charara and D. Lechner, “A method to Estimate the Lateral Force and Sideslip Angle of a Vehicle: Experimental Validation,” Proceedings of the 10th American Control Conference, pp.6936-6942, 2010. [https://doi.org/10.1109/ACC.2010.5531319]
• N. Chowdhri, L. Ferranti, F. S. Iribarren and B. Shyrokau, “Integrated Nonlinear Model Predictive Control for Automated Driving,” Control Engineering Practice, Vol.106, pp.1-15, 2021. [https://doi.org/10.1016/j.conengprac.2020.104654]
• S. Cheng, L. Li, B. Yan, C. Liu, X. Wang and J. Fang, “Simultaneous Estimation of Tire Side-slip Angle and Lateral Tire Force for Vehicle Lateral Stability Control,” Mechanical Systems and Signal Processing, Vol.132, pp.168-182, 2019. [https://doi.org/10.1016/j.ymssp.2019.06.022]
• T. Gillespie, Fundamentals of Vehicle Dynamics, SAE International, p.215, 1992. [https://doi.org/10.4271/R-114]
• D. Lee, I. Kim and K. Huh, “Tire Lateral Force Estimation System Using Nonlinear Kalman Filter,” Transactions of KSAE, Vol.20, No.6, pp.126-131, 2012. [https://doi.org/10.7467/KSAE.2012.20.6.126]
• H. Hamann, J. K. Hedrick, S. Rhode and F. Gauterin, “Tire Force Estimation for a Passenger Vehicle with the Unscented Kalman Filter,” IEEE Intelligent Vehicles Symposium, pp.814-819, 2014. [https://doi.org/10.1109/IVS.2014.6856391]