상용차 군집주행을 위한 차간거리 제어 전략
Copyright Ⓒ 2023 KSAE / 208-07
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In this study, a novel method for setting a target inter-vehicle distance is developed to enable platooning between heavy-duty vehicles with different loading weight. To this end, the minimum target inter-vehicle distance for a platooning operation is computed by predicting the maximum deceleration in the longitudinal direction after considering the loading weight of all vehicles in the platoon. To prevent control error and delay that may occur due to differences in the loading weight of vehicles, the inter-vehicle distance control strategy of each vehicle is proposed, which compensates the minimum target inter-vehicle distance for longitudinal control error of the preceding vehicle in the platoon. For the longitudinal control of heavy-duty vehicles, an SMC(Sliding Mode Control)-based robust controller is designed to track the computed target inter-vehicle distance. The proposed algorithm is verified through a total of eight scenarios, including four cases in the difference in the loading weight of vehicles and two cases for emergency-braking and acceleration of a leading vehicle in the platoon. Simulation results show that the proposed algorithm can ensure the safety of platooning performance without collision between preceding and following vehicles in the platoon. These results also demonstrate that the proposed algorithm can improve the driving stability of the platoon, compared to existing strategies.
Keywords:
Platooning, String stability, Crash safety, Autonomous driving, CACC(Cooperative Adaptive Cruise Control), V2V Communication키워드:
군집주행, 대열 안정성, 충돌 안전성, 자율주행, 협력적응순항제어기, 차량 간 통신1. 서 론
상용차 군집주행 시스템은 V2V(Vehicle to vehicle) 통신 및 Radar, Camera와 같은 환경 센서를 활용하여 여러 대의 상용차가 군집대열을 형성하여 대열 내 선행차량(PV, Preceding vehicle)과 속도 및 거리 간격을 유지하고, 선두차량(LV, Leading vehicle)의 주행 경로를 추종하여 주행하는 자율주행 기술이다.
군집주행 기술은 LV의 운전자를 제외한 추종차량(FV, Following Vehicle)의 운전자들에게 자율주행을 제공하여 운전자의 편의성을 증대시킬 뿐만 아니라, 차량 간격을 좁게 유지함으로써 군집대열 전체의 공기저항을 낮추어 연비를 향상시킨다.1-4) 또한, Arem 등5)은 개별 상용차량이 수동으로 주행하는 것보다, 한 차선 내 여러 대의 상용차량이 군집을 이뤄 주행하는 것이 교통 혼잡을 줄이고, 교통처리량을 증가시키는 효과가 있음을 보였다.
이렇듯 군집주행 기술은 운전자의 편의성, 연비 향상 및 배기가스 감소, 교통처리량 증가 등의 많은 이점 때문에, 전 세계적으로 군집주행에 관한 많은 연구가 수행되고 있다.
미국의 PATH(Partners for advanced transit and highways)6) 프로젝트에서는 상용차량의 고속 군집주행 기술을 선보이며 약 20 %의 연비를 개선하였다.
유럽의 SARTRE(SAfe Road Trains for the Environment)7) 프로젝트에서는 대형 상용차량과 승용차량이 혼재된 군집주행 기술을 선보이며, 공차중량의 차이가 큰 두 차량이 군집을 형성하는 주행상황에 대해, 대열의 주행 안전성을 확보하기 위한 안전 요구사항을 도출하였다.
또한, ITS 기술을 통한 에너지 절약과 지구 온난화 방지를 목표로 수행되었던 일본의 Energy-ITS8) 프로젝트에서는 대형 상용차량 3대가 10 m 거리 간격을 유지하며 80 kph로 주행하는 군집주행 기술을 선보이며, 약 14 %의 연비를 개선할 뿐만 아니라, 일반주행 대비 이산화탄소 배출량 약 2.1 %가 감소하였다는 것을 증명하였다.
한편 유럽의 ENSEMBLE9) 프로젝트에서는 군집주행 상용화를 목표로 이탈리아 상용차 브랜드인 이베코(IVECO)를 중심으로 다중 브랜드 상용 군집주행 적용을 위한 브랜드 간 상호 운용이 가능한 군집주행 시스템을 개발하였다. 이 프로젝트에서는 이종 브랜드의 차량 동특성 및 제어기 설계 컨셉의 차이가 있음에도 상호 운용이 가능함을 보였다.
마지막으로 한국에서는 상용차 군집주행 기술 내재화를 목표로 한국도로공사를 중심으로 현대자동차, 카카오모빌리티, 국민대학교 등 다수의 기업과 연구기관이 참여하여 TROOP(TRuck platOOning Project)10)를 진행하였다. 이 프로젝트에서는 대형 상용차량 4대가 덕평IC부터 원주IC까지 약 60 km의 고속도로 구간을 90 kph의 속도로 12.5 m의 거리 간격을 유지하며 군집주행을 수행하였다.
이처럼 군집주행 기술 관련하여 많은 연구가 수행되었지만, 군집주행 상용화를 위해서는 여전히 해결해야 할 문제들이 남아있다.
Humphreys 등11), Humphreys과 Bevly12)은 군집을 형성한 차량 간 대열의 간격을 좁게 설정할수록 대열 전체의 연비 및 교통처리량이 향상됨을 증명하였지만, Badnava 등13)은 어느 상황에서도 충돌 안전성이 보장되도록 대열의 적정 차간거리를 유지하기 위한 운영 전략이 수립되어야 한다는 것을 언급하고 있다.
위 두 연구를 통해 군집주행의 이점과 충돌 안전성은 서로 상충 관계에 있음을 알 수 있다. 다시 말해, 충돌 안전성을 확보함과 동시에 군집주행의 이점을 극대화하기 위한 군집대열의 차간거리 설정 전략이 필수적으로 요구되는 기술임을 알 수 있으며, 이와 관련된 연구를 살펴보면 다음과 같다.
Swaroop와 Huandra14)은 차간거리 설정 전략을 고정 차간거리15,16)(CSP, Constant Spacing Policy)와 가변 차간거리17-21)(VSP, Variable spacing policy) 두 가지로 구분하고 있다. CSP의 경우 FV가 전체 대열의 주행상황과는 무관하게 자신의 선행차량인 PV와 고정적인 차간거리를 유지하도록 하는 전략으로, 목표 상대거리를 고정된 상수로 정의한다. 이는, 군집대열의 주행 속도 및 차량의 동특성이 반영되지 않는 차간거리로 인해 대열이 불안정한 상황이 발생할 가능성이 존재한다. VSP는 CSP와 달리, 군집대열의 주행 속도 및 차량의 동특성을 반영하여 PV와 FV 사이의 차간거리를 가변적으로 설정하는 전략으로, 목표 상대거리를 가변 파라미터로 정의한다.
VSP는 고정 타임갭(CTG, Constant time gap)과 고정 안전계수(CSF, Constant safety factor)로 나눌 수 있다. 전자의 경우, 가변 파라미터를 대열 내 후행차량이 일정 거리를 유지하며 선행차량을 추종하고자 할 때 안전을 위해 확보해야 하는 거리를 시간으로 나타낸 지표인 타임갭과 차량 주행 속도의 곱으로 설정한다. 이 결과, 대열의 목표 차간거리가 주행 차속과 비례하게 증가함에 따라 고속 주행 시 차간거리가 증가하여 주행 안정성을 확보할 수 있지만, 차량의 동특성은 여전히 반영되지 않아 군집대열에서의 충돌 안전성은 보장할 수 없다. 후자의 경우에는 차량의 최대 감속 성능을 통해 차량의 정지거리를 예측하여 이 값의 배수를 가변 파라미터로 설정한다. 이 결과, 목표 차간거리는 차량의 예측 정지거리를 반영하기 때문에 충돌 안전성 측면에서는 우수할 수 있으나 개별 차량의 예측 정지거리만을 사용하는 것은 군집대열 내 차간거리가 매우 길어질 수 있으므로, 앞서 설명한 군집대열이 좁은 간격을 유지하며 주행하는 것에 따른 군집주행의 이점은 미비해질 것으로 판단된다. 또한, 군집대열 내 개별 상용차량이 적재량에 따른 주행 성능의 차이가 발생하는 경우 대열이 불안정한 상황이 발생할 수 있다.
이렇듯, 군집주행의 차간거리 설정 전략에 관한 많은 연구가 있었지만, 대다수가 안전성 측면에서 아직 미흡한 것을 알 수 있다.
Zhang 등22)은 군집주행의 안전성을 확보하기 위해 수행되었던 기존 연구들의 대다수가 이상적인 조건이나 특정 시뮬레이션 조건에서 수행되었음을 지적하였으며, 군집주행이 상용화되기 위해서는 실제 도로에서와 같이 적재량이 각기 다른 상용차량으로 구성된 군집주행 상황에서도 기존 연구들이 유효한지 입증하기를 강조하였다.
위와 같은 이전 연구에 대한 고찰을 바탕으로, 본 논문에서는 적재량이 다른 상용 자율차량으로 구성된 군집대열이 급제동과 같은 긴급 상황에서도 충돌 안전성을 확보함과 동시에 주행 안정성을 확보하기 위한 상용차량의 군집주행 차간거리 제어 전략을 제안한다. 본 알고리즘은 크게 두 가지의 내용을 포함하고 있는데 첫째, 군집대열 내 상용차량의 적재량을 고려하여 종방향 한계 감속도를 예측하고, 이를 바탕으로 군집대열 운영을 위한 최소 목표 차간거리를 도출한다. 계산된 최소 목표 차간거리는 군집대열 내 상용차량이 추종해야 할 목표 상대거리로 활용되어 충돌 안전성을 확보하게 된다. 둘째, 적재량에 따른 개별 상용차량의 주행 특성 차이가 군집대열의 주행 안정성에 미치는 영향을 최소화하기 위해, FV는 대열주행을 위한 제어 목표에 PV의 제어 오차만큼을 보상하여 최종 제어 목표를 도출하고 이를 바탕으로 종방향 제어를 수행하게 된다.
본 논문에서 제안하는 알고리즘의 개발 및 검증을 위해 Matlab/Simulink, TruckMaker와 다수의 대상차량에 대한 상호 결합 시뮬레이션을 지원하는 SimNet를 활용하였으며, 대열 내 일부 차량에 대해 적재량의 차이를 두고 LV의 가속과 같이 추종해야 하는 차량의 상태가 변화하는 주행상황과 LV의 급제동 등 대열 내 충돌 위험도를 높이는 주행상황을 시나리오로 구성하여 전체 군집대열의 충돌 안전성과 주행 안정성을 검증하였다.
2. 시스템 아키텍처
군집주행 시스템은 군집주행 운영을 위한 운영 제어기와 차량의 가감속 및 조향 제어를 위한 종⋅횡방향 제어기로 구성된다. 운영 제어기에서는 대열주행을 위한 대상 차량의 운영 모드 결정 및 운영 모드에 따른 제어 목표를 계산하며, 종⋅횡방향 제어기에서는 계산된 제어 목표를 추종하기 위한 가감속 및 조향 제어를 수행한다.
군집주행 시스템 내 차간거리 제어알고리즘은 운영 제어기에서 각각의 운영 모드에 따른 목표 차간거리와 차속 등을 계산하고, 종방향 제어기에서는 대상 차량이 이를 추종할 수 있도록 가감속 제어를 수행해야 한다.
이번 장에서는 본 연구에서 다루고 있는 군집주행 시스템의 전체 구성과 운영 제어기 내 포함된 목표 차간거리 설정 전략에 관한 기존 연구를 설명한다.
2.1 군집주행 시스템 구성
군집주행 시스템은 일반적으로 대열 합류(Join), 유지(Maintain), 이탈(Leave)의 세 가지 동작 모드를 갖는다.
군집주행 시스템의 동작시퀀스는 운전자의 수동주행 또는 운전자가 설정한 속도로 자율주행 중인 대상 차량이 합류하고자 하는 전방 군집대열의 후미에서 숙련된 운전자에 의해 수동주행 중인 대열 내 선두차량 LV에 대열합류를 요청하면서 시작된다. LV는 대상 차량과 전체 군집대열의 주행 상태를 고려하여 대상 차량의 대열합류 요청을 승인한다. 시스템은 승인 즉시 대열합류 모드로 천이되어 대상 차량이 전방 군집대열에 합류할 수 있도록 차량을 제어한다. LV는 전체 군집대열의 주행 안정성을 고려하여 군집대열의 운영 조건인 목표 차간 및 차속을 설정해야 하며, 대상 차량이 대열합류 모드에서 LV가 설정한 군집대열의 운영 조건을 만족한 경우 시스템은 대열합류를 완료하고 대열유지 모드로 천이된다. 대열유지 모드에서는 대상 차량이 군집대열의 목표 차간 및 차속 유지를 위한 차량 제어를 수행한다. 전체 군집대열이 대열유지 주행 중, LV 또는 대상 차량의 운전자가 군집주행 해제를 요청하게 되면 시스템은 대열이탈 모드로 천이되어 대상 차량이 전방 군집대열로부터 이탈할 수 있도록 차량을 제어한다. 대열 이탈모드의 대상 차량은 자신의 선행차량과 시스템이 설정한 특정 차간거리 이상으로 거리 간격이 벌어졌을 경우 군집주행 시스템은 종료되며, 초기 운전자의 수동주행 또는 운전자가 설정한 속도로 자율주행을 재개한다.
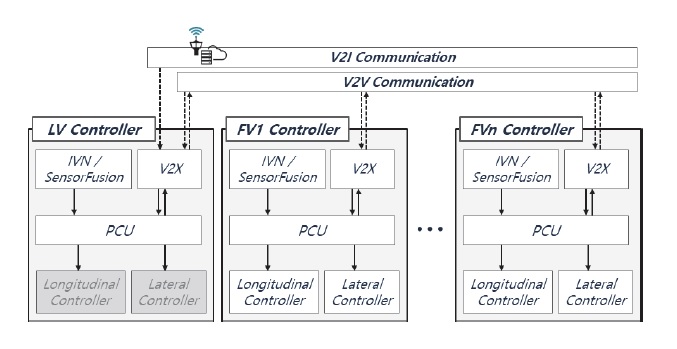
Fig. 1은 이들 세 가지 동작 모드를 운영하기 위한 군집주행 시스템의 전체 구성을 나타낸다.
전체 군집주행 시스템을 구성하는 개별 차량 제어기는 Fig. 1과 같이 V2X 통신을 통한 인프라(V2I Communication) 또는 대열 내 다른 차량 간(V2V Communication) 군집주행을 위한 정보를 송⋅수신하며, 개별 차량의 상태 정보(IVN, In-Vehicle Network)와 레이더 및 카메라 센서로부터 취득한 데이터를 융합(Sensor fusion)하여 얻은 주행 차선 및 전방 선행 차량의 상태 정보를 활용한다.
V2X, 차량의 상태 정보, 센서 계측 정보는 개별 차량의 군집 형성 및 대열주행을 총괄하는 운영 제어기(PCU, Platoon control unit)로 전달된다.
LV의 운영 제어기는 일반주행 상황에는 군집주행을 위한 목표 차간거리를 FV에 전달하여 군집대열 내 각 차량이 목표 차간거리를 유지하며 주행할 수 있도록 한다. 그러나, LV가 비상 정지해야 하는 위험주행 상황에서는 V2I로부터 취득한 인프라 정보 또는 센서 계측 정보를 통해 전방 위험 상황을 인지하여 군집주행의 비상 정지상황을 판단하거나, 차량의 상태 정보 중 운전자의 감속 페달 입력에 따라 군집주행의 비상 정지상황을 판단한다. 만약 전방 위험 상황에 대해 비상 정지가 필요한 경우, LV의 운영 제어기에서는 비상 정지와 동시에 전체 FV에 비상 정지 신호를 전달하여 대열 내 각 차량이 비상 정지 거동을 수행하도록 한다.
FV의 운영 제어기는 일반주행 상황에는 LV로부터 수신한 목표 차간거리만큼 전방 선행 차량에 대한 상대거리를 유지하기 위해 차량의 제어 목표를 계산하여 종방향 제어기(Longitudinal controller)에 전달한다. 대열유지 모드에서는 LV로부터 수신한 목표 차간거리가 차량의 제어 목표가 되지만, 대열합류와 이탈 모드에서는 목표 차간거리까지의 과도 구간에 대한 목표 차간거리 계획을 통해 제어 목표가 결정된다. 또한, LV로부터 비상 정지 신호를 받으면, 제어 목표와 무관하게 차량의 비상 정지 거동을 수행한다.
LV의 종⋅횡방향 제어기는 숙련된 운전자의 수동주행으로 대체되며, FV의 종⋅횡방향 제어기에서는 운영 제어기로부터 전달받은 종⋅횡방향 제어 목표를 추종하기 위한 차량의 가감속 및 조향 제어를 수행한다.
본 논문에서 제안하는 상용차 군집주행 차간거리 제어 전략은 Fig. 1의 전체 군집주행 시스템의 기본 구성을 바탕으로 개발하였다.
2.2 기존 차간거리 설정 전략
군집주행 시스템의 차간거리 설정 전략은 군집주행 기술의 다양한 설계 목표와 밀접한 연관이 있기에 현재까지 많은 방법이 제안되어왔다. 예를 들어, 대열을 구성하는 차량 간 차간거리를 매우 작게 설정할 경우 교통처리량을 증가시킬 수 있지만, 동시에 충돌 안전성은 현저히 감소하게 된다. 반대로 대열을 구성하는 차량 간 차간거리를 매우 길게 설정하는 경우에는 충돌 안전성을 높일 수 있으나 연비개선, 교통처리량 감소 등 군집주행의 이점을 극대화하기는 어려울 것이다.
이처럼, 현재까지 군집주행 시스템의 다양한 설계 목표가 제안되어왔지만 가장 우선시되어야 하는 것은 대열 내 선행 및 후행차량이 대열을 유지하는 동안 서로 충돌하지 않는 범위 내에서 최소 차간거리를 유지할 수 있도록 하는 것이다.
이번 절에서는 기존 연구되어 온 군집주행의 차간거리 설정 전략 중, 가장 많이 알려진 CTG(고정 타임갭) 방식과 CSF(고정 안전계수) 방식에 관해 설명하고, 5장에서는 이 방식들과 본 연구에서 제안하는 차간거리 설정 전략을 비교하여 본 연구에서 제안하는 알고리즘의 우수성을 입증한다.
CTG 방식은 대열 내 선행 및 후행차량이 일정 거리 간격을 유지하며 주행할 때, 안전을 위해 확보해야 하는 거리를 시간으로 나타낸 지표인 타임갭(τ)을 고정된 상수로 표현하는 방식으로, 식 (1)과 같이 나타낼 수 있다.
| (1a) |
| (1b) |
식 (1)의 ci,d는 대열 내 각 차량의 목표 차간거리를 의미하며, c0는 선행 및 후행차량이 모두 정지한 경우에 허용되는 최소 간격을 의미한다. 식 (1)의 V는 식 (1a)와 같이 LV의 속도로 표현하거나, 식 (1b)와 같이 대열 내 선행차량인 PV의 속도로 표현할 수 있다. 이는 군집대열 내 FV가 차량 간 통신을 통해 LV의 상태 정보도 수신 가능하며, 센서 계측 정보를 통해 바로 앞에 위치하여 주행하는 전방 선행 차량인 PV의 상태 정보도 계측 가능한 군집주행 시스템의 구성에 따라 두 가지 방식 모두 적용이 가능함을 의미한다. 식 (1b)와 같이 PV의 속도를 사용하여 목표 차간거리를 설정할 경우, 긴급 제동이 필요한 상황에서 제동 지연으로 인해 대열 후미에 있는 차량이 충돌할 가능성이 크기 때문에 일반적으로 식 (1a)와 같이 LV의 속도를 사용하여 계산한 목표 차간거리를 사용한다.
CSF 방식은 군집주행 시스템에서 충돌 가능성을 최소화하기 위해 고안된 전략으로, 차량의 안전 정지거리에 고정된 상수배의 곱으로 표현하여 식 (2)과 같이 나타낼 수 있다.
| (2) |
| (3) |
식 (2)의 Sb는 차량의 안전 정지거리이며, k는 안전계수를 의미한다. 식 (2)의 Sb는 식 (3)과 같이 LV의 제동거리로 표현할 수 있으며, CSF 방식의 목표 차간거리 설정은 LV 제동거리의 상수배 만큼의 차간을 유지하며 주행하는 전략이다.
소개한 기존 차간거리 전략 두 가지의 공통점은 LV의 주행 상태를 기준으로 목표 차간거리를 결정한다. 다시 말해, 기존 방식들의 대부분이 군집대열을 구성하는 개별 상용차량의 적재량이 다른 경우를 다루지 않고 있으므로 적재량이 다른 차량 간 군집주행에 대한 기존 방식의 유효성이 검증될 필요성 있다.
3. 제안 차간거리 설정 전략
본 연구에서 제안하는 군집주행의 차간거리 설정 전략은 두 가지의 내용을 포함한다. 첫째, 군집대열을 구성하는 개별 상용차량의 적재량이 다른 경우에도 충돌 안전성을 확보할 수 있도록 대열 내 전체 차량의 주행 특성을 반영하여 대열 운영을 위한 최소 목표 차간거리를 계산한다. 둘째, 대열 내 차량의 적재량 차이로 인해 발생할 수 있는 제어 오차 및 지연에도 대열의 주행 안정성 및 군집주행의 이점을 유지하기 위해, 발생하는 제어 오차 및 지연을 보상하는 개별 상용차량의 수정된 목표 차간거리를 계산한다.
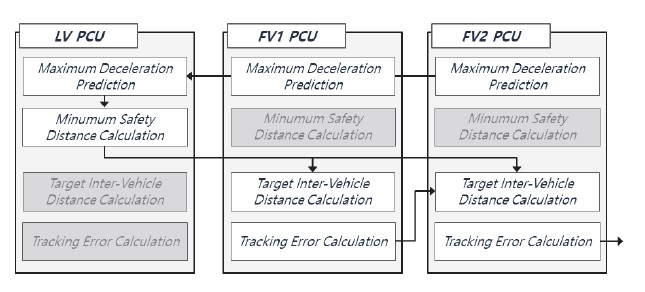
Fig. 2는 위 내용을 포함하는 본 연구의 군집주행 차간거리 설정 전략의 세부 구성을 나타낸다.
위 Fig. 2에서도 알 수 있듯이 제안하는 차간거리 설정 전략은 군집주행 시스템 내 LV의 운영 제어기와 FV의 운영 제어기에서 동작하며, 앞서 언급한 충돌 안전성과 대열의 주행 안정성이라는 해결점에 대해 일대일로 대응되는 두 가지 세부 기능을 가진다. 첫째, 충돌 안전성을 확보하기 위해 FV의 운영 제어기에서는 대상 차량의 재원 및 상태 정보를 기반으로 종방향 한계 감속도를 예측하여 이를 LV의 운영 제어기로 전달하며, LV의 운영 제어기에서는 전달받은 FV의 종방향 한계 감속도를 반영하여 대열 운영을 위한 최소 목표 차간거리를 계산하고 이를 다시 FV의 운영 제어기로 전달한다. 둘째, 대열의 주행 안정성을 확보하기 위해, FV의 운영 제어기에서는 LV의 운영 제어기로부터 전달받은 최소 목표 차간거리와 자신의 선행차량의 운영 제어기로부터 차간거리 제어 오차를 전달받아 오차를 보상하는 대상 차량의 수정 목표 차간거리를 계산한다. 이번 장에서는 차간거리 설정 전략의 두 가지 세부 기능에 관해 설명한다.
3.1 감속 차 기반 차간 전략
대열유지 주행 중인 군집대열 내 공차 상태인 선두차량의 급제동은 대열의 후미에 위치하고 적재를 포함한 총 중량이 큰 상용차량에게 매우 치명적일 수 있다. 상용차량의 총 중량은 적재로 인해 자신의 공차중량 대비 2배 이상으로 커질 수 있기에 제동거리 또한 길어진다. 이는 군집대열 내 선두차량이 급제동하는 상황에서, 대열 후미의 상용차량이 제동 주행을 수행하는 도중 후방충돌로 이어질 가능성이 농후하다. 따라서 본 논문에서는 적재량이 각기 다른 상용차량의 총 중량과 주행 속도에 따라 달라지는 종방향 한계 감속도를 예측하고, 이를 군집대열의 목표 차간거리 계산에 활용하여 어떠한 상황에서도 군집대열이 충돌하지 않을 수 있도록 하는 감속 차 기반 차간거리 설정 전략을 제안한다.
종방향 한계 감속도 예측은 LV를 포함하여 군집대열을 구성하는 모든 차량의 운영 제어기에서 대상 차량을 기준으로 이루어진다.
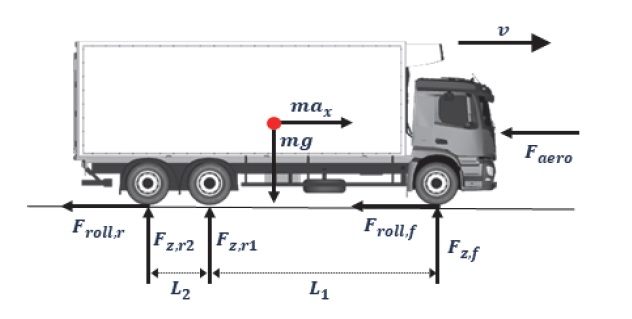
Fig. 3은 종방향 한계 감속도를 예측하기 위해 활용한 상용차량 종방향 모델23)이며, 이를 운동방정식을 나타내면 식 (4)와 같이 표현할 수 있다.
식 (4a)의 m과 ax는 각각 차량의 질량과 종방향 가속도를 의미하며, Fx는 차량의 제동 장치에 의해 생성되는 제동력이다. Faero과 FRolling은 각각 차량의 주행 방향의 역방향으로 생성되는 공기저항에 의한 힘과 구름저항에 의한 힘을 의미한다.
| (4a) |
| (4b) |
| (4c) |
식 (4a)의 Faero과 FRolling는 각각 식 (4b)과 식 (4c)과 같이 정의할 수 있다. 식 (4b)의 Cd는 공기저항계수, ρ는 공기밀도, A는 차량의 전방 단면적, V는 차량의 속도를 의미한다. 식 (4c)의 μ는 구름저항계수, g는 중력가속도를 의미한다. 식 (4b)와 식 (4c)를 각각 k1와 k′2, k′3를 통해 단순화하여, 식 (4a)를 정리하면 최종적으로 식 (5)와 같이 표현할 수 있다.24)
| (5) |
| (6) |
식 (5)로부터 상용차량의 공차중량과 적재량을 구분하여 종방향 감속도를 구하면 식 (6)과 같이 표현할 수 있다. 식 (6)의 m0, ∆m는 각각 차량의 공차중량과 적재량을 의미한다.
공차 상태의 차량이 감속할 경우 제동력은 식 (7)과 같이 표현할 수 있다. 식 (7)의 ax0는 공차 상태의 차량에 대한 감속도를 의미한다.
| (7) |
식 (6)과 식 (7)을 이용하여, 공차 상태의 차량에서 측정된 종방향 한계 감속도를 통해 적재 상태의 차량에 대한 종방향 한계 감속도를 계산하면 식 (8)과 같이 나타낼 수 있다.
| (8) |
식 (8)의 ax,max는 적재 상태의 차량에 대한 종방향 한계 감속도를, ax0,max는 공차 상태의 차량에 대한 종방향 한계 감속도를 의미한다. 예측한 차량의 종방향 한계 감속도를 통해 계산한 적재 상태의 상용차량 제동거리는 식 (9)과 같이 나타낼 수 있다.
| (9) |
| (10) |
| (11) |
적재로 인해 총 중량이 큰 FV가 자신의 선행차량 또는 LV의 급감속에도 충돌이 발생하지 않도록 하기 위해서는 무거운 중량으로 인해 부족해진 FV의 감속도를 제동거리로 보상하여 대열 운영을 위한 최소 목표 차간거리를 결정해야 한다. 이를 위해, 식 (10)과 같이 대열을 구성하는 모든 상용차량에 대해 선행 및 후행차량 간 감속도 차이에 의해 발생하는 제동거리 차이(∆Sb,i)를 계산하여, 식 (11)과 같이 대열 운영을 위한 최소 목표 차간거리(cd)에 보상하였다.
식 (11)의 cd는 식 (10)의 ∆Sb,i 중에서 가장 큰 값(cS)을 기준으로 정의되어 군집대열 내 모든 차량의 충돌 안전성을 확보한다. 식 (11)의 c0는 대열 내 선행 및 후행차량 간 허용되는 최소 간격으로 국제표준 ISO-2217925)을 참고하여 2 m로 설정하였다.
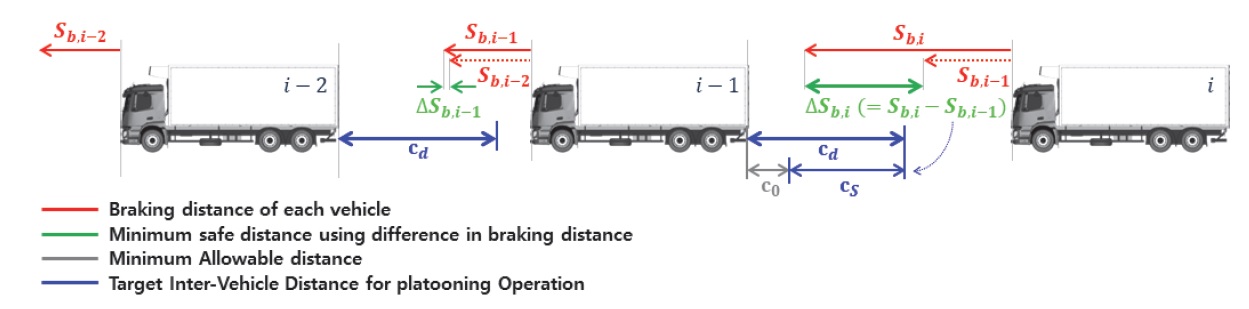
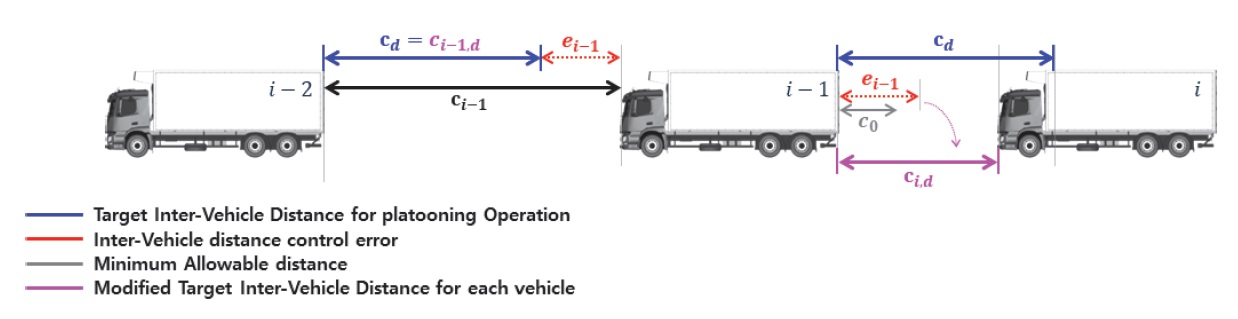
Fig. 4는 식 (11)의 대열 운영을 위한 최소 목표 차간거리(cd)를 포함하여, 대열 내 선행 및 후행차량 간 관계식을 도식화하여 나타내었다. LV는 군집대열을 구성하는 모든 차량으로부터 전달받은 종방향 한계 감속도를 기반으로 계산한 대열 운영을 위한 최소 목표 차간거리를 다시 대열 내 모든 차량에 전달하며, 차량들은 이를 추종하기 위한 종방향 제어를 수행한다.
3.2 허용 최소 간격 가변 전략
군집대열 내 후행차량이 선행차량에 비해 큰 적재량을 가진 경우, 선행차량과의 적재량 차이가 큰 후행차량은 작은 차량에 비해 상대적으로 전방 선행차량을 추종하는데 가속 또는 감속 성능 저하로 인해 더 큰 제어 오차를 가지게 된다. 적재량으로 인해 발생하는 선행 군집대열 추종 제어 오차는 대열의 후미로 갈수록 오차가 전달되거나 누적되어 전체 대열의 주행 안정성을 감소시킬 수 있다. 또한, 전체 군집대열의 길이가 길어지게 되는데, 이는 교통처리량 및 연비개선 등의 군집주행 이점을 잃어버리게 된다.
이번 절에서는 3.1절에서 제안한 감속 차 기반 차간 전략과 더불어, 군집대열이 가속 또는 감속하는 일반주행 상황에서도 적재량 차이에 의한 제어 오차가 군집대열에 미치는 악영향을 감소시키기 위한 개별 차량의 허용 최소 간격 가변 전략을 제안한다.
개별 차량의 허용 최소 간격 가변 차간거리 설정 전략은 3.1 절 식 (11)의 충돌 안전성을 확보하기 위해 제안한 감속 차 기반 차간 전략에서 계산된 대열운영을 위한 최소 목표 차간거리(cd)에 식 (12)와 같이 적재량으로 인한 대열 내 선행차량의 전방차량 추종 제어 오차를 보상한다.
| (12a) |
where
| (12b) |
식 (12a)의 ci,d는 대열 운영을 위한 최소 목표 차간거리(cd)와 대열 내 선행차량의 종방향 제어 오차(ei-1)의 차로 계산된 개별 차량의 수정 목표 차간거리를 의미한다. 식 (12a)의 ei-1는 식 (12b)와 같이 대열 내 선행차량이 자신의 전방차량과 적재량 차이로 인해 발생할 수 있는 종방향 제어 오차 즉, 두 차량 간 상대거리와 대열 운영을 위한 최소 목표 차간거리의 차로 계산된다.
계산한 개별 차량의 수정 목표 차간거리는 전체 군집대열이 가속하는 상황에서 발생할 수 있는 적재량이 큰 차량의 가속 지연이 대열의 후미로 전달되는 현상을 억제하여 전체 군집대열의 주행 안정성을 확보할 수 있을 뿐만 아니라, 전체 대열의 총 길이가 늘어나는 현상을 방지하여 군집주행의 이점을 유지할 수 있도록 한다.
3.1절의 식 (11)과 같이 군집대열 내 상용차량의 최대 제동거리와 대열 내 차량 간 최소 허용 간격의 합으로 계산되는 대열 운영을 위한 최소 목표 차간거리에 식 (12)와 같이 선행차량의 종방향 제어 오차를 보상하고자 할 때, 개별 차량의 수정 목표 차간거리가 대열 내 상용차량의 최대 제동거리보다 작아지는 현상이 발생할 수 있다. 이러한 현상은 전체 군집대열이 가속 중 급감속을 하는 경우, 순간적으로 최대 제동거리보다 작아진 목표 차간거리로 인해 충돌이 발생할 가능성이 존재한다. 이를 위해, 식 (13)과 같이 대열 내 선행차량 종방향 제어 오차의 보상을 최소 허용 간격인 c0 이내로 제한하였다.
| (13a) |
where
| (13b) |
식 (13)의 ce는 c0 이내로 제한한 종방향 제어 오차를 의미하며, 이를 통해 계산된 개별 차량의 수정 목표 차간거리는 군집대열 내 상용차량의 목표 차간거리가 최대 제동거리보다 항상 같거나 큰 상태가 유지되도록 한다.
Fig. 5는 식 (13)의 개별 차량의 수정 목표 차간거리(ci,d)를 포함하여, 대열 내 선행 및 후행차량 간 관계식을 도식화하여 나타내었다. 대열 내 선두차량인 LV를 제외한 모든 FV는 LV로부터 전달받은 대열 운영을 위한 최소 목표 차간거리에서 자신의 선행차량의 종방향 제어 오차를 보상하여 최종 개별 차량의 수정 목표 차간거리를 계산하고, 이를 추종하기 위한 종방향 제어를 수행한다.
군집주행 시스템은 군집대열을 구성하는 개별 차량 간 통신(V2V)을 통해 군집주행 운영을 위한 정보를 송수신해야 한다. Table 1은 본 논문에서 제안하는 두 가지 차간거리 설정 전략을 적용하는 데 필요한 V2V 송수신 신호를 정리하였다. 군집주행 운영을 위한 V2V 신호는 대열 내 모든 FV가 LV에게 전달하는 신호, LV가 모든 FV에게 전달하는 신호, FV의 선행차량인 PV가 FV에게 전달하는 신호 세 가지로 구분된다. 군집대열 내 모든 FV는 자신의 종방향 한계 감속도를 LV에게 전달해야 한다. LV는 전체 군집대열이 긴급 제동을 해야 하는 상황에 대해, 모든 FV에게 긴급 제동을 알리는 플래그 신호를 전달해야 한다. 또한, LV는 대열 내 차량 간 최소 허용 간격과 대열 운영을 위한 최소 목표 차간거리를 모든 FV에게 전달해야 한다. 마지막으로 PV는 자신의 전방차량 추종 제어 오차를 FV에게 전달해야 한다.
4. 상용차량 종방향 제어기 설계
군집대열 내 LV를 제외한 모든 상용차량은 개별 군집주행 운영 제어기에서 계산된 목표 차간거리를 추종하기 위한 종방향 가감속 제어를 수행해야 한다.
이번 장에서는 앞서 3장에서 제안한 본 연구의 두 가지 차간거리 설정 전략에 따라 계산된 목표 차간거리의 유효성을 확인하기 위해, 설계한 종방향 가감속 제어기에 관해 설명한다.
상용차량은 적재에 따라 작게는 수천 킬로그램, 크게는 수만 킬로그램의 총 중량을 가질 수 있다. 다시 말해, 상용차량은 일반 승용차량과 달리 총 중량에 변화가 매우 크기 때문에 모델 불확실성 및 외란에 많은 영향을 받는다. 본 논문에서는 자율주행 분야에서 널리 활용되어 온 많은 제어이론26-29)을 적용해본 가운데, 상용차량에 비교적 좋은 성능을 보이며 모델 불확실성 및 외란에 강인한 성능을 보이는 SMC(Sliding mode control) 제어이론30-34) 기반의 종방향 가감속 제어기를 설계하였다.
SMC 제어이론 적용을 위해, 대열 내 후행차량의 선행차량 추종 제어 오차에 대한 Sliding surface를 식 (14)과 같이 정의하였다.
| (14a) |
where
| (14b) |
식 (14a)의 k1, k2, k3는 Sliding surface의 설계 변수이며, e는 식 (14b)과 같이 선행 및 후행차량 간 차간거리에서 목표 차간거리를 뺀 차간거리 제어 오차를 의미한다. 식 (14)에서 정의한 Sliding surface에 도달하기 위한 조건을 구하기 위해, s에 대한 Lyapunov 함수 V를 식 (15)와 같이 정의하였다.
| (15) |
| (16) |
Lyapunov 함수의 s에 대한 미분은 식 (16)과 같이 Negative semi-definite 조건을 만족해야 하며, 이를 만족시키기 위한 식을 도출하면 식 (17a)과 같고, 이를 등가 조건으로 변환하면 식 (17b)과 같이 나타낼 수 있다.
| (17a) |
| (17b) |
식 (17)의 Sliding condition을 만족하는 제어 입력 u를 구하면 식 (18)과 같다.
| (18) |
| (19) |
식 (18)의 제어 입력 u은 목표 차간거리를 추종하기 위한 대상 차량의 종방향 목표 가속도를 나타낸다. 계산된 제어 입력 u은 대상 차량의 가⋅감속 액추에이터의 입력값으로 인가하여 차량의 종방향 거동을 제어하게 된다. 차량의 가⋅감속 액추에이터는 종방향 목표 가속도만큼의 가⋅감속 제어를 수행하기 위해 차량의 가속페달 및 감속페달에 대한 하위 제어를 수행한다. 본 논문에서는 차량의 액추에이터 제어를 위한 하위 제어기를 별도로 구성하지 않고, 대상 차량에 목표 가속도에 해당하는 제어 입력 u을 인가하여 시뮬레이션을 수행하였다.
또한, λ는 제어이득을 의미하는 설계변수로 본 연구에서는 군집대열의 안전주행을 고려하여 해당 값을 선정하였으며, sign() 함수는 s=0인 지점에서 불연속으로 인한 채터링 현상이 발생할 수 있기에 식 (19)과 같이, sat() 함수를 사용하여 최종 제어 입력 u*를 계산하였다.
5. 주행 시나리오 및 시뮬레이션 결과
제안한 알고리즘을 검증하기 위해 본 연구에서는 적재량이 각기 다른 상용차량으로 이루어진 군집대열이 특정 속도로 대열을 유지하고 있는 상황에서 대열 내 선두차량인 LV가 급제동 또는 가속하는 군집주행 시나리오를 구성하여 시뮬레이션을 수행하였다. 또한, 2.2절에서 제시한 기존 차간거리 설정 전략과의 비교를 통해 기존 연구 대비 제안한 알고리즘의 유효성을 검증하였다. 이번 장에서는 그 결과에 관해 설명하고자 한다.
본 논문에서는 제안한 알고리즘의 개발 및 검증을 위해, Matlab&Simulink, TruckMaker와 SimNet을 활용하였다. IPG 社의 표준 TruckMaker는 하나의 대상 차량 시뮬레이션에 중점을 둔 환경이기 때문에, 3대 이상의 대상 차량을 동시에 시뮬레이션해야 하는 군집주행 시스템을 적용하는 데에는 무리가 있다. 따라서 다수의 대상 차량에 대한 독립적인 시뮬레이션을 지원하고, 각 차량 간 동기화되어 결합된 상호작용을 지원하는 SimNet를 추가로 연동하여 모든 상용 차량에 개발한 군집주행 시스템을 적용하여 평가하였다.
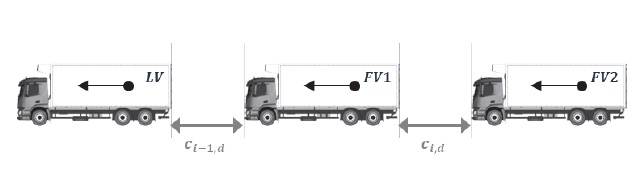
알고리즘 검증을 위해 구성한 군집주행 시나리오에는 Fig. 6과 같이 총 3대의 상용차량 즉 LV, FV1, FV2가 등장한다. LV는 군집대열 내 선두차량을, FV2는 군집대열 내 후미차량을, FV1은 LV와 FV2의 중앙에 위치하여 LV의 후행차량이자 FV2의 선행차량을 의미한다. 구성한 대열의 급제동 및 가속 시나리오는 시뮬레이션 시작 시점에서 총 3대의 차량이 2.2절의 기존 전략과 3장의 제안 전략에 따라 계산된 ci,d의 목표 차간거리를 유지하며 주행한다.
앞서 언급한 것과 같이, 주행 시나리오는 총 두 가지의 조작 변인을 갖는다. 첫 번째 조작 변인은 전체 군집대열에 큰 영향을 미칠 수 있는 LV의 거동 변화로, Table 2에서와 같이 전체 군집대열이 시뮬레이션 초기 80 kph로 대열유지 중인 상황에서 LV가 자신의 최대 감속도로 급제동하는 경우와 초기 50 kph에서 LV가 0.25 m/s2로 70 kph까지 가속하는 경우 두 가지이다. LV의 최대 감속도는 감속 구간 내 평균 6.2 m/s2이다.
두 번째 조작 변인은 Table 3에서와 같이 대열 내 선행 및 후행차량 간 차간거리 유지 성능에 대해 큰 영향을 미칠 수 있는 상용차량의 적재량 차이에 따른 총 중량 차이로, 대열 내 FV1과 FV2가 대상 차량 공차중량(m0=13450)의 50 %, 100 %에 해당하는 적재를 추가한 경우를 총 네 가지로 나누었다. 참고로 시나리오 내 모든 차량은 적재량에 따른 총 중량을 제외한 차량의 모든 제원은 동일한 것으로 가정한다.
Table 3의 네 가지 경우 모두 LV는 공차 상태이다. 1번 대열은 FV1만 공차중량의 100 %에 해당하는 적재량을 포함하는 경우로 공차 상태의 두 차량 사이에 적재 차량이 존재하는 주행상황이다. 2번 대열은 1번 대열과 달리, FV1과 FV2 모두 공차중량의 100 %에 해당하는 적재량을 포함하는 경우로 LV를 제외한 대열 내 모든 차량이 자신의 공차중량만큼을 적재한 상태에서 주행하는 상황이다. 3번과 4번 대열은 각각 FV1과 FV2 공차중량의 50 %, 100 %와 100 %, 50 %의 적재량을 포함하는 경우로 LV를 포함하여 대열 내 모든 차량에서 총 중량의 차이가 존재하는 주행상황이다. 알고리즘의 타당성 검증을 위해 구성한 적재량 차이에 대한 네 가지 경우는 모두 LV를 추종하는 전체 군집대열 내 상용차량의 입장에서 발생할 수 있는 주행상황을 일반화한 경우로, 대다수 군집대열의 적재 주행상황을 포괄하고 있다.
위의 시나리오의 두 가지 조작 변인을 통해 최종 시나리오는 LV의 거동 변화에 대한 두 가지 경우, 대열 내 차량의 총 중량 차이 네 가지의 경우를 조합하여 Table 4와 같이 총 8가지로 구성하였다.
LV가 급제동하는 주행 시나리오(A)에서는 전체 군집대열 내 차량 간 충돌 발생 여부를 통해 제안 전략의 충돌 안전성을 확인한다. 특히 A와 대열 내 차량의 총 중량 차이에 대한 네 가지 경우(1 ~ 4)를 조합하여, 차량의 적재중량 변화가 차간거리 설정 전략의 충돌 안전성에 미치는 영향을 확인한다. LV가 가속하는 주행 시나리오(B)에서는 군집대열 내 차량의 총 중량 차이에 의한 가속 성능 차이가 제어 오차 및 지연을 발생시킬 수 있으므로, B와 1 ~ 4를 조합하여, 차량의 적재중량 변화가 차간거리 설정 전략에 따른 대열의 주행 안정성에 미치는 영향을 확인한다.
추가로 기존 전략 대비 제안 전략의 유효성을 검증하기 위해, 각각의 주행 시나리오에 대해 2.2절의 기존 전략과 3장의 제안 전략을 적용하여 시뮬레이션 결과를 비교하였다. Table 5는 시뮬레이션을 수행한 모든 차간거리 설정 전략을 나타낸다.
시뮬레이션을 수행한 전략은 2.2절의 CTG 방식과 CSF 방식에 대해 설계변수를 달리하여 각각 두 가지씩 총 네 가지의 기존 전략과 3장의 두 가지 제안 전략이다. 아래에서는 총 8가지 시나리오에 대해, 위 6가지 차간거리 설정 전략을 적용한 시뮬레이션 결과를 소개하고 이를 비교 분석한다.
5.1 급제동 시나리오
대열 내 적재 상태의 상용차량을 포함하는 군집주행 상황에서 80 kph로 유지 중인 대열의 LV가 급제동하는 시나리오 A-(1 ~ 4)에 대해 시뮬레이션을 수행한 차간거리 설정 전략은 기존 방식인 CTG(TG=0.5), CTG (TG=1.0), CSF(k=0.25), CSF(k=0.5)와 제안 방식인 PROPOSED1이다. 추가로 적재 상태가 각기 다른 군집대열(1 ~ 4)과 모두 공차 상태의 상용차량으로 구성된 군집대열 간 차량의 제동 거리 차이를 비교하기 위해, 모든 차량이 공차인 상태로 구성된 군집대열의 시나리오 A에 대한 CTG(TG=0.5)를 적용한 시뮬레이션 결과를 추가하여 함께 비교하였다.
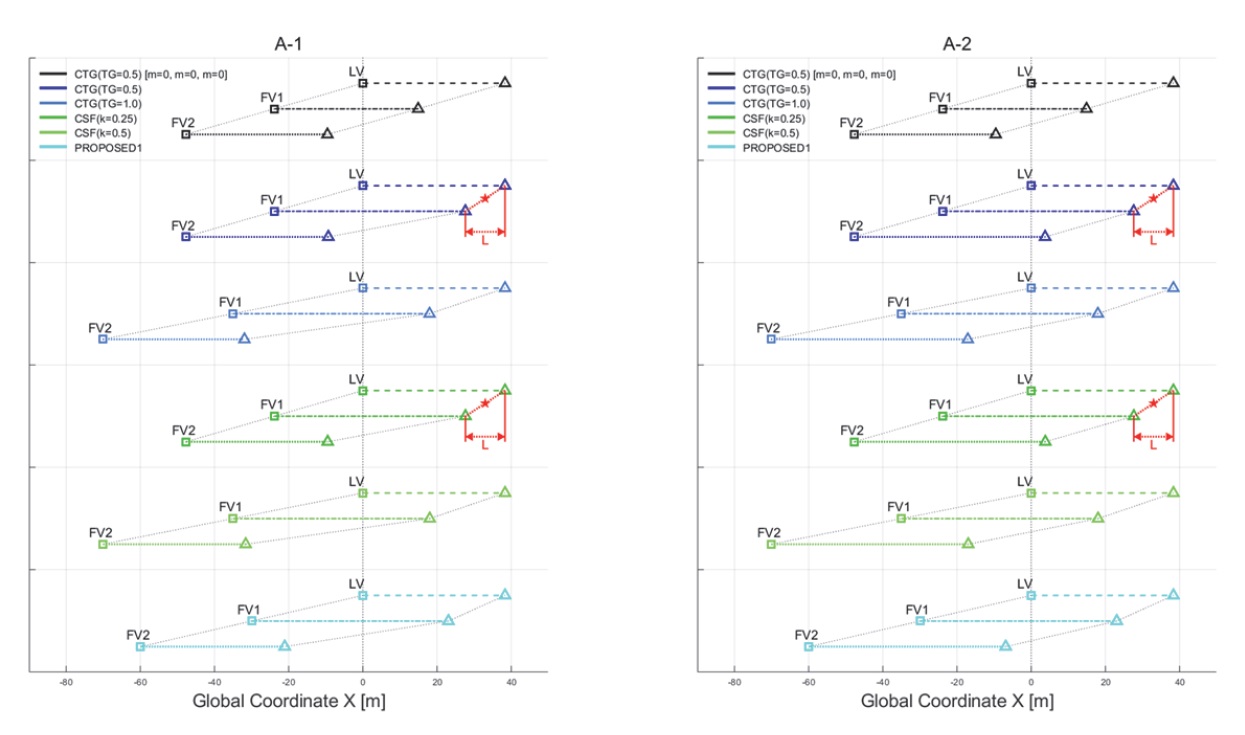
Fig. 7은 시나리오 A-1과 A-2에 대한 시뮬레이션 결과를 나타낸다. 적용한 군집대열의 차간거리 설정 전략별 색을 달리하여 구분하였으며, 시뮬레이션 결과 그래프의 X축은 각 차량의 X축 방향 이동 궤적을 나타낸다. 네모와 세모 마커 지점은 각 차량의 CG점으로, 네모 마커 지점은 LV가 급제동을 시작한 시점을, 세모 마커 지점은 LV의 급제동이 시작된 이후 LV, FV1, FV2 총 3대의 차량이 완전히 정차한 시점을 나타낸다. 따라서 두 지점 사이를 잇는 선은 각 차량의 제동거리를 나타낸다. 각 차량의 네모와 세모 마커 지점은 모두 CG점을 의미하기 때문에, LV가 급제동을 시작하는 시점에서의 각 차량 사이의 차간거리는 네모 마커 지점 사이의 거리와 차량의 길이인 L(=10.7 m)의 차로 계산되며, 세 대의 차량이 모두 정차한 시점에서의 각 차량 사이의 차간거리는 세모 마커 지점 사이의 거리와 L의 차로 계산된다. 따라서, 결과 그래프에서 별 마커는 세모 마커 지점 사이의 거리가 L인 경우로, 이는 대열 내 선행 및 후행 차량이 제동 주행 중 충돌이 발생하여 시뮬레이션이 종료되었음을 의미한다.
시나리오 A-1과 A-2의 시뮬레이션 결과 그래프에서, 가장 상단에 있는 첫 번째 군집대열은 모든 차량이 공차 상태로 구성된 군집대열에 CTG(TG=0.5) 방식을 적용한 경우로서, 모든 차량이 동일한 제원과 중량을 갖기 때문에 LV의 급제동 시작 시점에서 각 차량 사이의 차간거리와 모든 차량이 정차한 시점에서 각 차량 사이의 차간거리는 동일하게 약 13.2 m이다. 이와 달리, 적재량을 포함한 나머지의 경우에서는 적재 상태인 차량의 길어진 제동거리로 인해 LV의 급제동 시작 시점에서의 차간거리와 모든 차량이 정차한 시점에서의 차간거리는 서로 다른 것을 확인할 수 있으며, 이때 공차중량의 100 %를 적재한 차량의 제동거리는 공차 상태의 차량 대비 약 14.7 m만큼 길어진 것을 알 수 있다. 이를 통해, 대열 내 차량의 적재량 차이에 따라 차량별 제동거리에서 차이가 발생하는 상황에 대해 충돌 안전성을 확보하기 위한 차간거리 설정 전략이 필요함을 알 수 있다. 두 시나리오에서는 공통적으로 두 번째 대열과 네 번째 대열에서 각각 LV와 FV1의 충돌이 발생한 것을 확인할 수 있는데, 이는 설계변수가 설계자에 의해 고정된 상수로 정의되는 CTG와 CSF 방식의 특성 때문임을 알 수 있다. 다시 말해, 설계변수를 작게 설정한 경우에는 두 번째와 네 번째 대열의 시뮬레이션 결과와 같이 대열의 좁은 차간거리(약 13.2 m)로 인해 급제동 중 충돌이 발생할 수 있는 반면에 설계변수를 크게 설정할 경우 세 번째와 다섯 번째 대열의 시뮬레이션 결과와 같이, 지나치게 넓은 대열의 차간거리(약 24.3 m)로 인해 군집주행의 이점이 사라질 수 있다. 결과적으로 CTG와 CSF 방식은 차량의 적재량에 따른 최대 제동거리를 고려하지 않고 설계변수에만 의존하는 것을 알 수 있다. 이와 달리, 본 논문의 3.1절에서 제안한 방식을 적용한 두 시나리오의 여섯 번째 대열에서는 LV의 급제동 시작 시점에서 대열의 차간거리(약 19.3 m)를 유지하여 충돌이 발생한 두 번째와 네 번째 대열보다 넓은 차간을, 세 번째와 다섯 번째 대열보다는 좁은 차간을 유지하고 있는 것을 알 수 있다. 또한, 모든 차량이 정차한 시점에서 LV와 FV1의 차간거리는 약 2.5 m로 이 수치는 최소 허용 간격인 2 m를 만족한 것을 확인할 수 있다. 결과적으로, 대열을 구성하는 상용차량의 적재량을 고려한 최대 제동거리를 기준으로 산출하는 본 논문의 차간거리 설정 방식을 적용한 여섯 번째 대열의 경우, 급제동으로 인해 발생할 수 있는 대열 내 차량 간 충돌을 방지하는 범위 내에서 가장 좁은 차간을 유지하는 것을 확인할 수 있었다.
Table 6은 Fig. 7에서 시나리오 A-1의 시뮬레이션 결과를 수치로 정리한 표이다. 시나리오 A-1은 급제동 시나리오 A-(1 ~ 4) 중에서 LV와 FV1의 중량 차이가 가장 큰 대열 형태로, 시나리오 A-1의 결과를 통해 충돌 안전성 확보에 대한 제안 전략의 효과를 직관적으로 확인할 수 있다.
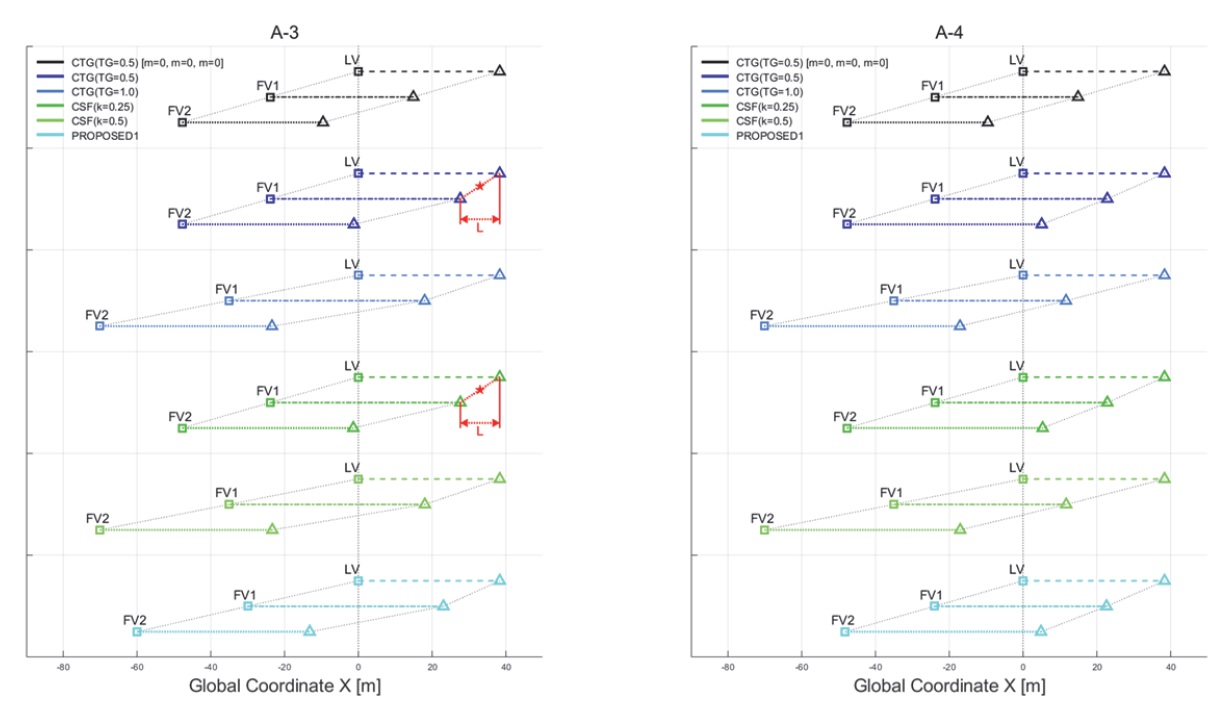
Fig. 8은 시나리오 A-3과 A-4에 대한 시뮬레이션 결과를 나타낸다. 시나리오 A-1과 A-2에서와 같이, 모든 차량이 공차 상태로 구성된 군집대열에 CTG(TG=0.5) 방식을 적용한 그래프 가장 상단에 있는 첫 번째 대열은 LV의 급제동 시작 시점과 모든 차량이 정차한 시점에서 각 차량 사이의 차간거리(약 13.2 m)는 동일하다. 그러나 이를 제외한 적재를 포함한 경우 즉, 시나리오 A-3에서는 자신 공차중량의 100 %, 50 %를 각각 적재한 FV1, FV2와 시나리오 A-4에서는 50 %, 100 %를 각각 적재한 FV1, FV2의 길어진 제동거리로 인해 LV의 급제동 시작 시점과 모든 차량이 정차한 시점에서의 차간거리는 서로 다른 것을 확인할 수 있다. 이때 공차중량의 50 %를 적재한 차량의 제동거리는 공차 상태의 차량 대비 약 8.4 m, 100 %를 적재한 차량의 제동거리는 시나리오 A-1과 A-2에서와 같이, 약 14.7 m만큼 길어진 것을 알 수 있다. 시나리오 A-3에서는 두 번째 대열과 네 번째 대열에서 각각 LV와 FV1의 충돌이 발생한 것을 확인할 수 있는데, 이는 상대적으로 중량이 가벼운 차량의 제동거리가 짧기 때문이며, LV와 FV1의 적재량 차이(13450 kg)에 의한 제동거리 차이(14.7 m)는 충돌 한계치를 넘어선 것으로 예상된다. 반면에 시나리오 A-4에서는 두 번째 대열과 네 번째 대열에서 충돌이 발생하지 않은 것을 확인할 수 있다. 이는 대열 내 LV, FV1, FV2의 적재량이 순차적으로 증가하는 형태이며, LV와 FV1, FV1과 FV2 각각의 적재량 차이(6725 kg)에 의한 제동거리 차이(8.4 m)는 시나리오 A-3과 달리 충돌 한계치를 넘어서지 않은 것으로 예상할 수 있으나, FV1 또는 FV2 적재량의 작은 변화로도 충돌이 발생할 수 있기에 안전하다고 볼 수 없다. 두 시나리오의 세 번째와 다섯 번째 대열은 시나리오 A-1과 A-2에서와 같이, 군집주행의 이점보다는 안전에 중점을 두어 설계변수를 더 크게 설정한 경우로 대열이 더 넓은 차간거리(약 24.3 m)를 유지하여, 두 번째 대열과 네 번째 대열 대비 충돌 안전성 측면에서는 우수할 수 있으나, 교통처리량 증가 및 연비개선 등의 효과를 극대화하기는 어려울 것으로 판단된다. 본 논문의 3.1절에서 제안한 방식을 적용한 시나리오 A-3과 A-4의 여섯 번째 대열 중, 전자의 경우 대열 내 차량 간 최대 적재량 차이인 13450 kg, 후자의 경우 6725 kg에 의해 발생하는 제동거리 차이를 기준으로 대열의 차간거리가 각각 약 19.3 m와 약 13.4 m로 설정되어 LV 급제동 시작 시점에서 대열의 차간거리가 전자가 후자보다 더 긴 것을 확인할 수 있다. 또한, 전자와 후자 모두 모든 차량이 정차한 시점에서 LV와 FV1의 차간거리는 최소 허용 간격인 2 m를 만족하였으며, 후자의 경우에서는 FV1과 FV2의 차간거리도 최소 허용 간격 2 m를 만족한 것을 확인할 수 있다. 결과적으로, 본 논문의 제안 방식을 적용한 각 시나리오의 여섯 번째 대열의 경우, 급제동으로 인해 발생할 수 있는 대열 내 차량 간 충돌을 방지하는 범위 내에서 가장 좁은 차간을 유지하여 대열의 충돌 안전성을 확보하였을 뿐만 아니라, 군집주행의 이점 또한 기존 전략 대비 높아질 것으로 예상된다.
5.2 가속 시나리오
대열 내 적재 상태의 상용차량을 포함하는 군집주행 상황에서 50 kph로 유지 중인 대열의 LV가 70 kph까지 가속하는 시나리오 B-(1 ~ 4)에 대해 시뮬레이션을 수행한 차간거리 설정 전략은 기존 방식인 CTG(TG=1.0), CSF(k=0.5)와 제안 방식인 PROPOSED1과 PROPOSED 2이다. 추가로 적재 상태가 각기 다른 군집대열(1 ~ 4)과 모두 공차 상태의 상용차량으로 구성된 군집대열 간 차량의 가속 성능 차이를 비교하기 위해, 모든 차량이 공차인 상태로 구성된 군집대열의 시나리오 B에 대한 PROPOSED1를 적용한 시뮬레이션 결과를 추가하여 함께 비교하였다.
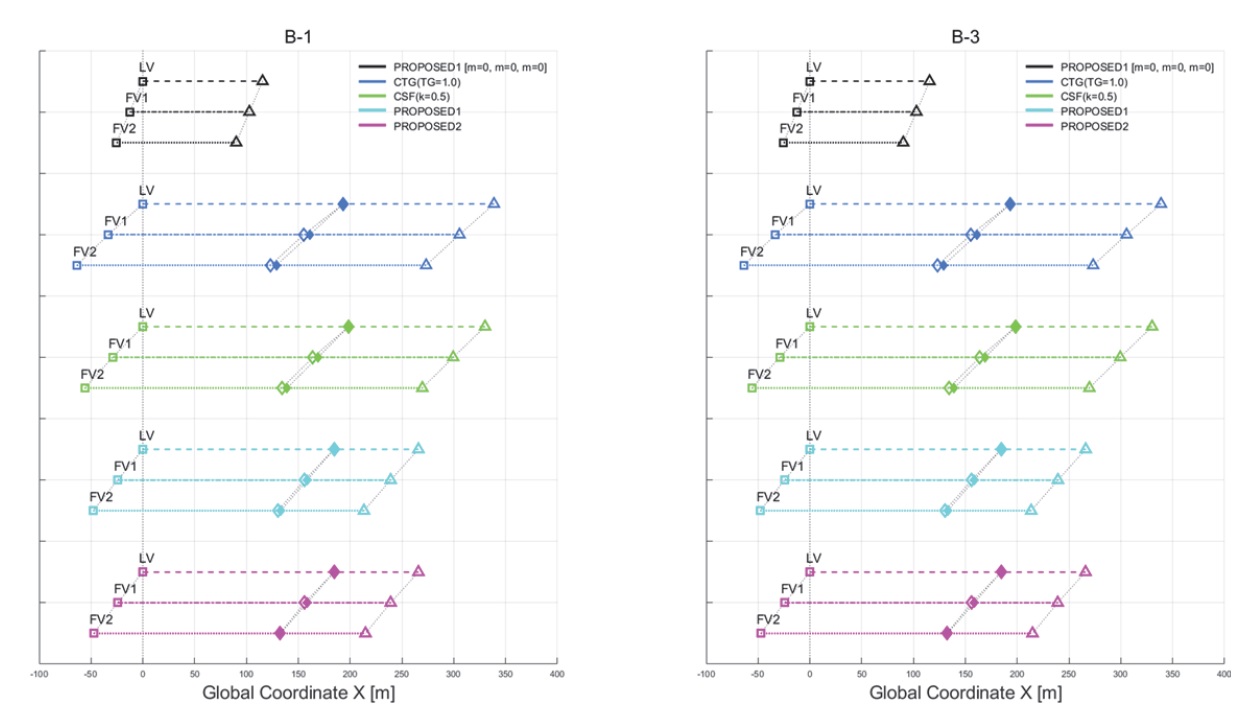
Fig. 9는 시나리오 B-1과 B-3에 대한 시뮬레이션 결과를 나타낸다. 시나리오 A에서와 같이, 적용한 군집대열의 차간거리 설정 전략별 색을 달리하여 구분하였으며, 시뮬레이션 결과 그래프의 X축은 각 차량의 X축 방향 이동 궤적을 나타낸다. 네모와 세모 마커 지점은 각 차량의 CG점으로, 네모 마커 지점은 LV가 초기 50 kph에서 가속하여 65 kph에 도달한 시점으로 대열이 가속 중인 과도 상태이며, 세모 마커 지점은 LV의 가속이 시작된 이후 LV, FV1, FV2 총 3대의 차량이 대열의 목표 차간거리 및 속도 70 kph에 완전히 수렴한 정상상태 도달 시점을 나타낸다. 따라서 두 지점 사이를 잇는 선은 LV의 속도 65 kph에서 각 차량이 가속하는 대열의 과도상태로부터 정상상태에 수렴할 때까지 이동한 거리를 나타낸다. 네모와 세모 마커 지점은 시나리오 A에서와 같이 각 차량의 CG점을 의미하기 때문에, LV가 65 kph에 도달한 시점에서의 각 차량 사이의 차간거리는 네모 마커 지점 사이의 거리와 차량의 길이인 L의 차로 계산되며, 세 대의 차량 모두 정상상태에 도달한 시점에서의 각 차량 사이의 차간거리는 세모 마커 지점 사이의 거리와 L의 차로 계산된다. 또한, 속이 빈 것과 채워진 두 가지의 마름모 마커 지점이 존재하는데, 전자의 경우 대열 내 각 차량의 목표 차간거리와 실제 차간거리의 차로 계산되는 추종 제어 오차가 가장 크게 발생한 지점을 의미하며, 후자의 경우 해당 시점에서 제어 오차가 발생하지 않았을 때 각 차량이 실제 위치해야 할 지점을 의미한다. 다시 말해, 전자와 후자의 두 지점 사이의 거리가 각 차량의 추종 제어 오차임을 알 수 있다. 네모와 세모 마커 지점과 동일하게 마름모 마커 지점 또한 각 차량의 CG점으로, 최대 추종 제어 오차를 갖는 시점에서의 각 차량 사이의 차간거리는 같은 마름모 마커 지점 사이의 거리와 L의 차로 계산된다. 각 시점에서 전체 군집대열의 총 길이는 LV의 마커 지점과 FV2의 같은 마커 지점 사이의 거리와 L의 차로 계산된다.
시나리오 B-1과 B-3의 시뮬레이션 결과 그래프에서, 가장 상단에 있는 첫 번째 군집대열은 모든 차량이 공차 상태로 구성된 군집대열에 본 논문 3.1절의 제안 방식(PROPOSED1)을 적용한 경우로서, 모든 차량이 동일한 제원과 중량을 갖기 때문에 대열 내 LV, FV1, FV2의 차간거리는 최소 허용 간격(2 m)을 만족하며 주행하는 것을 확인할 수 있다. 또한, 첫 번째 군집대열에서 마름모 마커 지점이 생략된 것을 알 수 있는데 이는 3대의 차량 모두 동일한 추종 제어 오차를 가지며 그 값이 0에 수렴하기 때문이다. 이와 달리, 적재량을 포함한 나머지의 경우에서는 FV1과 FV2 각 차량의 적재량에 따라 두 차량의 가속 성능 저하가 발생하여 추종 제어 오차가 커진 것을 확인할 수 있다. 이를 통해, 대열 내 차량의 적재량 차이에 따른 가속 성능 차이가 대열의 주행 안정성에 미치는 영향을 최소화하기 위한 차간거리 설정 전략이 필요함을 알 수 있다. 두 시나리오에서 공통적으로 적용한 4가지 전략은 모두 차간거리 설정을 위해 대열 내 차량의 속도를 반영한다. 기존 전략인 CTG와 CSF 방식을 각각 적용한 두 번째 대열과 세 번째 대열의 경우 LV의 속도를 반영하여, 50 kph로 주행 중인 LV가 가속을 시작한 시점에서는 차간거리가 각각 약 15.9 m와 10.6 m였으며, 모든 차량이 70 kph로 주행 중인 정상상태 도달 시점에서의 차간거리는 각각 약 21.5 m와 20.0 m이다. 제안 방식을 적용한 네 번째와 다섯 번째 대열의 경우 대열 내 차량의 최대 제동거리를 산출하는 과정에서 모든 차량의 속도를 반영하여, LV가 가속을 시작한 시점에서는 차간거리가 약 8.6 m였으며, 모든 차량이 정상상태 도달 시점에서의 차간거리는 약 15.1 m이다. 이를 통해, 두 시나리오의 모든 대열에서는 LV의 속도가 증가함에 따라, LV가 가속을 시작한 시점보다 모든 차량이 정상상태에 도달한 시점에서 차간거리가 더 길어지는 것을 확인할 수 있다. 그러나, 제안 방식을 적용한 네 번째와 다섯 번째 대열이 기존 방식을 적용한 두 번째와 세 번째 대열 대비 약 65 m 앞서 정상상태 도달한 것을 확인할 수 있는데, 이는 제안 방식이 임의의 설계변수의 상수 배로 계산되는 기존 방식과 달리 대열 내 선행 및 후행차량 간 제동거리 차이의 최대치를 기준으로 설정한 차간거리를 활용하였기 때문이며, 그 결과 50 kph에서의 목표 차간거리와 70 kph의 목표 차간거리의 차가 기존 방식 대비 작은 것을 확인하였다. 결과적으로 작은 차간거리의 변화폭으로 인해 정상상태 수렴 속도가 향상되었다. 제안 방식을 각각 적용한 네 번째와 다섯 번째 대열에서의 차이점은 과도 구간 내 최대 추종 제어 오차 시점에서의 전체 군집대열 길이로, 전자의 경우 약 54.1 m이며 후자의 경우 약 52.1 m임을 확인할 수 있다. 대열 전체의 길이에서 전자와 후자가 약 2.0 m의 차이가 발생한 이유는 네 번째 대열에서 선행차량의 추종 제어 오차가 후행차량으로 누적되었으며, 다섯 번째 대열에서는 본 논문 3.2절의 제안 전략인 대열 내 선행차량의 추종 제어 오차를 후행차량에 보상하는 방식을 적용하여 오차 보상이 이루어졌기 때문이다. 따라서, 대열이 가속하는 과도 구간에서 다섯 번째 대열이 기존 전략 및 3.1절의 제안 전략 적용한 나머지 대열 대비 대열의 총 길이가 가장 짧은 것을 확인할 수 있었다. 시나리오 B-1과 B-3의 차이점은 FV2의 적재량으로, 전자에서는 0 kg(공차 상태), 후자에서는 6725 kg이다. 13450 kg의 가장 무거운 적재량을 포함하여 가속 성능의 저하가 가장 큰 FV1을 추종하는 시나리오 B-1의 FV2와 시나리오 B-3의 FV2 사이의 추종 제어 오차의 차이가 0 m에 수렴할 정도로 매우 작은 것을 확인할 수 있는데, 이는 가장 무거운 적재량으로 인해 가속 성능의 저하가 가장 큰 FV1를 추종하기에 두 차량의 가속 성능 및 그 성능의 차이는 전혀 지장이 없음을 의미한다. 이를 통해, 대열 내 차량의 적재량 차이뿐만 아니라 적재 차량의 배치 방법도 중요한 하나의 군집주행의 안전성을 높일 수 있는 고려 요소임을 알 수 있다.
Table 7은 Fig. 9에서 시나리오 B-1의 시뮬레이션 결과를 수치로 정리한 표이다. 시나리오 B-1은 가속 시나리오 B-(1 ~ 4) 중에서 LV와 FV1의 중량 차이가 가장 큰 대열 형태로, 시나리오 B-1 결과를 통해 적재량 차이에 의한 FV1의 추종 제어 오차 발생 시, 군집대열의 주행 안정성 확보에 대한 제안 전략의 효과를 직관적으로 확인할 수 있다. 추가로, 추종 제어 최대 오차 지점에서 PROPOSED1과 PROPOSED2의 FV1과 FV2 사이의 차간거리는 최소 허용 간격인 2 m만큼의 차이가 나는 것을 확인할 수 있다.
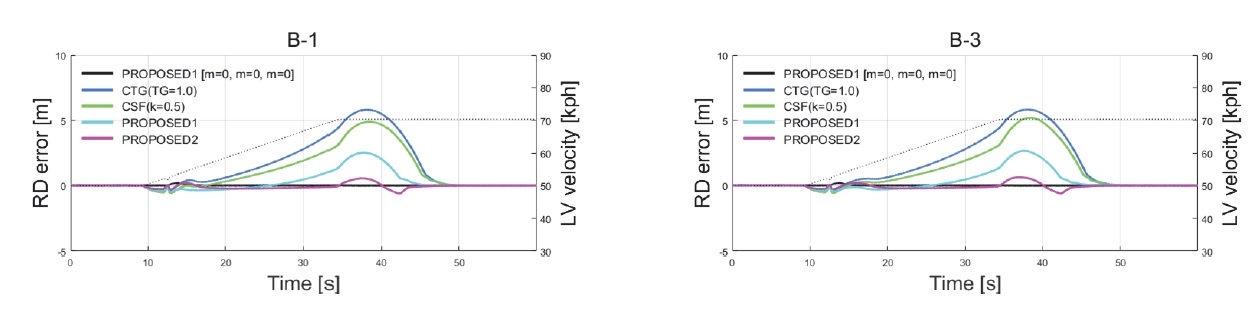
Fig. 10은 시나리오 B-1과 B-3에서 FV2의 전략별 추종 제어 오차에 관한 결과 그래프를 나타낸다. 추종 제어 오차는 LV에서 계산된 목표 차간거리에 따라 FV2가 위치해야 하는 지점에 대한 오차로 계산하였다. 이는 적재량에 의해 발생한 FV1의 제어 오차와 무관하게 군집주행 대열의 운영 목표에 대한 추종 제어 오차를 의미하며, 이 결과를 통해 군집대열의 주행 안정성을 향상시키기 위한 제안 전략의 유효성을 판단할 수 있다. 그래프에서 LV가 50 kph에서 70 kph까지 가속하는 구간의 최대 오차 지점은 Fig. 9의 마름모 지점에 해당한다.
결과적으로, 대열이 가속하는 주행상황에서 본 논문의 3.1절의 제안 방식을 적용한 시나리오 B-1과 B-3의 네 번째와 다섯 번째 대열이 가속 시 차간거리 변화폭도 가장 작아 정상상태 수렴 속도가 기존 전략 대비 가장 빠르며, 특히 3.2절의 제안 방식을 적용한 다섯 번째 대열의 경우는 군집주행 대열의 운영 목표에 대한 추종 제어 오차 및 전체 군집대열의 총 길이도 가장 짧아, 군집주행의 이점을 극대화할 수 있을 것으로 판단된다.
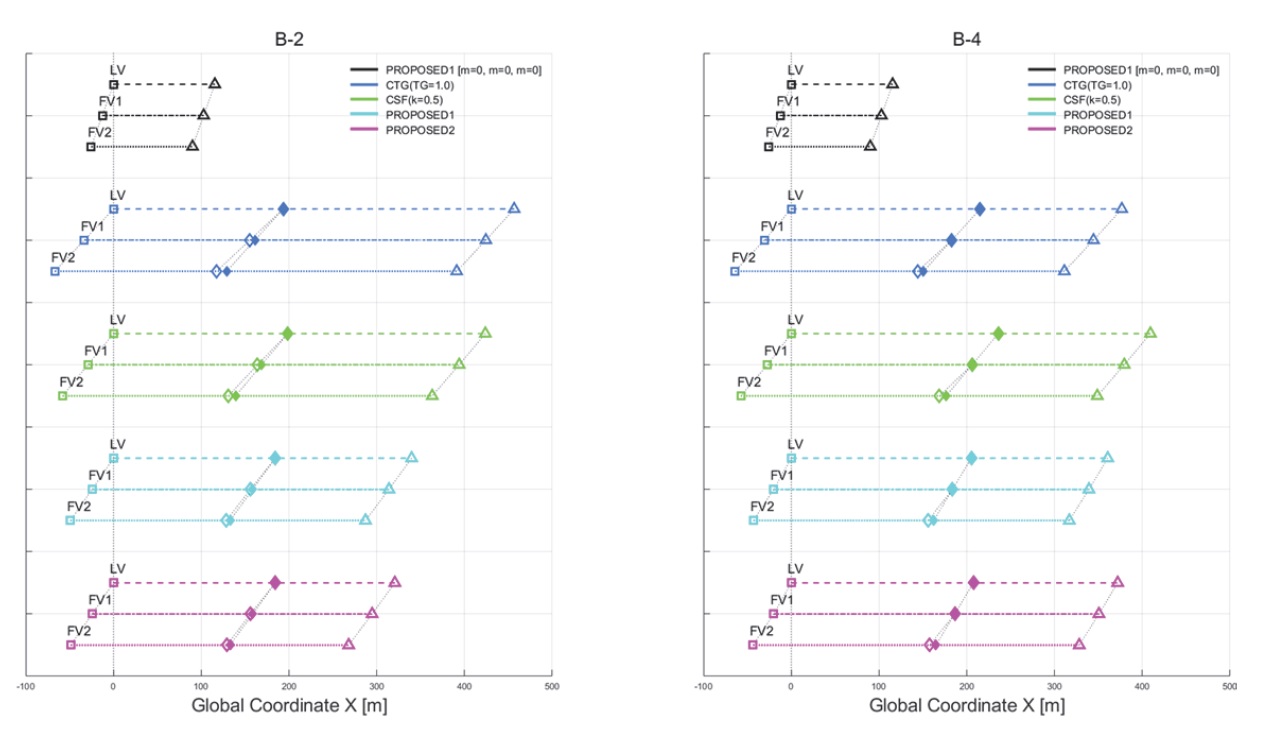
Fig. 11은 시나리오 B-2와 B-4에 대한 시뮬레이션 결과를 나타낸다. 시나리오 B-1과 B-3에서와 같이, 모든 차량이 공차 상태로 구성된 군집대열에 본 논문 3.1절의 제안 방식(PROPOSED1)을 적용한 그래프 가장 상단에 있는 첫 번째 대열은 차량 간 최소 허용 간격인 2 m의 차간거리를 유지하며, 이 간격은 대열이 50 kph에서 70 kph로 가속하는 과정에서도 동일하다. 이와 달리, 적재량을 포함한 나머지의 경우에서는 시나리오 B-1과 B-3에서와 같이 각각의 전략별 차간거리 설정 방식에 따라 차간거리가 변화한다. 두 시나리오에서는 공통적으로 FV1이 FV2보다 적재량이 크기 때문에, FV2는 FV1보다 가속 성능의 저하가 더 크다. 따라서, 본 논문 3.1절의 제안 방식을 적용한 네 번째 대열에서 FV1의 제어 오차와 FV2의 제어 오차는 시나리오 B-2의 경우 각각 약 2.6 m, 4.5 m, B-4의 경우 각각 0.5 m, 6.5 m로 두 시나리오에서 모두 FV1의 제어 오차보다 FV2의 제어 오차가 더 큰 것을 알 수 있다. 이러한 대열 내 FV2의 제어 오차가 가장 큰 경우에 대해, 대열 내 선행차량의 추종 제어 오차를 보상하는 본 논문 3.2절의 제안 방식을 적용한 다섯 번째 대열에서는 군집대열의 주행 안정성을 향상시키기 위한 차간거리 설정 전략의 유효성을 판단하기 어렵다. 그러나, 두 시나리오에서는 시나리오 B-1과 B-3에서와 같이 제안 방식을 적용한 네 번째와 다섯 번째 대열이 기존 방식을 적용한 두 번째와 세 번째 대열 대비 시나리오 B-2의 경우 약 90 m 이상, 시나리오 B-4의 경우 약 25 m 이상 앞서 정상상태 도달하는 것을 확인할 수 있다. 이는 대열 내 후행차량이 선행차량보다 더 무거운 적재량을 포함하는 경우에서도 기존 방식 대비 차간거리의 변화폭을 줄일 수 있게 되어 정상상태 수렴 속도가 향상되는 특성이 여전히 유효하다고 할 수 있다. 결과적으로 본 논문의 제안 방식이 군집대열의 충돌 안전성을 확보함과 동시에, 대열의 차간거리를 기존 방식 대비 짧게 유지하여 군집주행의 이점인 교통처리량 및 연비개선 등이 가장 두드러질 것으로 판단된다.
6. 결 론
상용차량의 군집주행 기술은 운전자의 편의성 및 교통처리량 개선, 연비 향상 등의 이점으로 인해 전 세계의 많은 국가에서 연구가 진행되었지만, 상용차량의 적재량 차이가 군집주행에 미치는 영향에 관한 연구는 여전히 부족한 실정이다.
본 논문에서는 적재량이 각기 다른 상용차량이 군집주행을 수행하는 상황에서도 충돌 안전성을 확보하고, 적재중량에 의한 제어 오차 및 지연 현상과 같은 대열주행의 악영향을 미치는 요소를 줄일 수 있는 목표 차간거리 설정 전략을 제안하였다. 이를 위해, 군집대열 내 모든 차량의 종방향 한계 감속도를 예측하여 대열 운영을 위한 최소 목표 차간거리를 계산하였으며, 계산된 목표 차간거리에 대열 내 선행차량의 종방향 제어 오차를 보상하여 최종 개별 차량의 수정 목표 차간거리를 도출하였다. 또한, 대열 내 개별 상용차량이 계산된 목표 차간거리를 추종하기 위한 SMC 기반의 종방향 제어기를 설계하였다.
본 논문에서 제안한 알고리즘의 유효성을 검증하기 위해, 대열의 충돌 안전성을 평가하기 위한 시나리오와 대열의 주행 안정성을 평가하기 위한 시나리오를 구성하여, 기존 방식과 함께 비교 분석하였다. 충돌 안전성 평가 시나리오는 LV가 급제동하는 주행상황에서, 대열의 주행 안정성 평가 시나리오는 LV가 가속하는 주행상황에서 각각 평가되었으며, 평가는 대열을 구성하는 LV, PV, FV의 적재량 차이에 따라 조합한 네 가지의 군집대열을 대상으로 평가하였다. 본 연구의 차간거리 설정 전략은 기존 방식 대비 우수한 효과를 보였으며, 조합한 네 가지의 군집대열 모두 LV가 급제동하는 주행상황에서도 충돌 안전성이 확보됨을 확인하였고, LV가 가속하는 주행상황에서도 적재량 차이가 미치는 대열주행의 제어 오차 및 지연이 현저히 저하됨을 확인할 수 있었다.
Acknowledgments
본 연구는 산업통상자원부 (한국산업기술진흥원)의 “새만금지역 상용차 자율주행 테스트베드 구축사업” (과제번호 P0013841)의 지원을 받아 수행된 연구임.
References
- M. Zabat, N. Stabile, S. Frascaroli and F. Browand, The Aerodynamic Performance of Platoons: A Final Report, UC-Berkeley Institute of Transportation Studies, UCB-ITS-PRR-95-35, 1995.
- J. Patten, B. McAuliffe, W. Mayda and B. Tanguay, Technical Report: Review of Aerodynamics Drag Reduction Devices for Heavy Trucks and Buses, National Research Council Canada, CSTTHVC-TR-205, 2012.
-
A. Alam, B. Besselink, V. Turri, J. Mårtensson and K. Johansson, “Heavy-Duty Vehicle Platooning for Sustainable Freight Transportation: A Cooperative Method to Enhance Safety and Efficiency,” IEEE Control System Magazine, Vol.35, No.6, 2015.
[https://doi.org/10.1109/MCS.2015.2471046]

-
M. P. Lammert, A. Duran, J. Diez, K. Burton and A. Nicholson, “Effect of Platooning on Fuel Consumption of Class 8 Vehicles over a Range of Speeds, Following Distances, and Mass,” SAE Int. J. Commercial Vehicles, Vol.7, No.2, 2014.
[https://doi.org/10.4271/2014-01-2438]

-
B. Arem, C. Driel and R. Visser, “The Impact of Cooperative Adaptive Cruise Control on Traffic-Flow Characteristics,” IEEE Transactions on Intelligent Transportation Systems, Vol.7, No.4, pp.429-436, 2006.
[https://doi.org/10.1109/TITS.2006.884615]

- T. Robinson, E. Chan and E. Coelingh, “Operating Platoons on Public Motorways: An Introduction To The SARTRE Platooning Programme,” 17th ITS World Congress, 2010.
- N. Christopher, S. Steven E, L. Xiao-Yun, T. Deborah and K. Aravind, Cooperative Adaptive Cruise Control (CACC) for Truck Platooning: Operational Concept Alternatives, UC-Berkeley Institute of Transportation Studies, 2015.
-
S. Tsugawa, S. Kato and K. Aoki, “An Automated Truck Platoon for Energy Saving,” IEEE International Conference on Intelligent Robots and Systems, San Francisco, 2011.
[https://doi.org/10.1109/IROS.2011.6094549]

- L. Konstantinopoulou, A. Coda and F. Schmidt, “Specifications for Multi-Brand Truck Platooning,” ICWIM 8-8th International Conference on Weigh-In-Motion, Prague, 2019.
- KAIA(Korea Agency for Infrastructure Technology Advancement), Final Report: Development of Operation Technology for V2X Truck Platooning, https://www.kaia.re.kr/portal/landmark/readTskView.do?tskId=147674&yearCnt=1&menuNo, , 2021.
-
H. L. Humphreys, J. Batterson, D. Bevly and R. Schubert, “An Evaluation of the Fuel Economy Benefits of a Driver Assistive Truck Platooning Prototype Using Simulation,” SAE 2016-01-0167, 2016.
[https://doi.org/10.4271/2016-01-0167]

-
H. Humphreys and D. Bevly, “Computational Fluid Dynamic Analysis of a Generic 2 Truck Platoon,” SAE 2016-01-8008, 2016.
[https://doi.org/10.4271/2016-01-8008]

-
S. Badnava, N. Meskin, A. Gastli, M. A. AI-Hitmi, J. Ghommam, M. Mesbah and F. Mnif, “Platoon Transitional Maneuver Control System: A Review,” IEEE Access, Vol.9, pp.88327-88347, 2021.
[https://doi.org/10.1109/ACCESS.2021.3089615]

-
D. Swaroop and R. Huandra, “Intelligent Cruise Control System Design Based on a Traffic Flow Specification,” Vehicle System Dynamics, Vol.30, No.5, pp.319-344, 1998.
[https://doi.org/10.1080/00423119808969455]

- D. Swaroop and K. R. Rajagopal, “A Review of Constant Time Headway Policy for Automatic Vehicle Following,” IEEE Intelligent Transportation Systems Conference Proceedings, Oakland, 2001.
-
H. Chehardoli and MR. Homaeinezhad, “Third-Order Leader-Following Consensus Protocol of Traffic Flow Formed by Cooperative Vehicular Platoons by Considering Time Delay: Constant Spacing Strategy,” SAGE Journal of Systems and Control Engineering, Vol.232, No.3, pp.285-298, 2018.
[https://doi.org/10.1177/0959651817750521]

-
W. Junmin and R. Rajamani, “Should Adaptive Cruise-Control Systems be Designed to Maintain a Constant Time Gap between Vehicles?,” IEEE Transactions on Vehicular Technology, Vol.53, No.5, pp.1480-1490, 2004.
[https://doi.org/10.1109/TVT.2004.832386]

-
S. Moon, I. Moon and K. Yi, “Design, Tuning, and Evaluation of a Full-Range Adaptive Cruise Control System with Collision Avoidance,” ELSEVIER Control Engineering Practice, Vol.17, No.4, pp.442-455, 2009.
[https://doi.org/10.1016/j.conengprac.2008.09.006]

-
J. Marzbanrad and N. Karimian, “Space Control Law Design in Adative Cruise Control Vehicles Using Model Predictive Control,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.225, No.7, pp.870-884, 2011.
[https://doi.org/10.1177/0954407011400819]

-
R. J. Caudill and W. L. Garrard, “Vehicle-Follower Longitudinal Control for Automated Transit Vehicles,” IFAC Proceedings Volumes, Vol.9, No.4, pp.195-209, 1976.
[https://doi.org/10.1016/S1474-6670(17)67295-1]

-
S. E. Shladover, C. Nowakowski, X. Y. Lu and R. Ferlis, “Cooperative Adaptive Cruise Control: Definitions and Operating Concepts,” SAGE Journal of the Transportation Research Board, Vol.2489, No.1, pp.145-152, 2015.
[https://doi.org/10.3141/2489-17]

-
L. Zhang, F. Chen, X. Ma and X. Pan, “Fuel Economy in Truck Platooning: A Literature Overview and Driections for Future Research,” Journal of Advanced Transportation, Vol.2020, 2020.
[https://doi.org/10.1155/2020/2604012]

-
R. Rajamani, Vehicle Dynamics and Control, 2nd Edn., Springer, New York, 2012.
[https://doi.org/10.1007/978-1-4614-1433-9]

- J. Y. Wong, Theory of Ground Vehicles, 3rd Edn., Wiley, New York, 2001.
- ISO 22179, Intelligent Transport Systems – Full Speed Range Adaptive Cruise Control(FSRA) Systems – Performance Requirements and Test Procedures, 2009.
-
S. Kim, D. Kim, S. Lee, J. Shin, S. Cho, B. Moon and K. Park, “A Study on the Development Methodology of Functional Safety Evaluation Scenario for V2V Communication of Urban Cooperative Autonomous Driving System,” Transactions of KSAE, Vol.29, No.5, pp.437-449, 2021.
[https://doi.org/10.7467/KSAE.2021.29.5.437]

-
T. Oh, W. Son, T. Ahn, Y. Lee and K. Park, “Development of Automated Lane Change Algorithm Considering Safety of Surrounding Vehicles,” Transactions of KSAE, Vol.29, No.5, pp.391-405, 2021.
[https://doi.org/10.7467/KSAE.2021.29.5.391]

- Y. C. Ha, Design of Integrated Autonomous Driving System that Incorporates Chassis Controller for Improvement Ride Comfort, M. S. Thesis, Kookmin University, Seoul, 2020.
-
T. Ahn, Y. Lee and K. Park, “Design of Integrated Autonomous Driving Control System That Incorporates Chassis Controllers for Improving Path Tracking Performance and Vehicle Stability,” MDPI Electronics, Vol.10, No.2, 2021.
[https://doi.org/10.3390/electronics10020144]

-
J. Liu and X. Wang, Advanced Sliding Mode Control for Mechanical Systems: Design, Analysis and MATLAB Simulation, Springer, Heidelberg, 2011.
[https://doi.org/10.1007/978-3-642-20907-9_3]

- H. S. Roh, Development of the Longitudinal Control for Truck Platooning, M. S. Thesis, Kookmin University, Seoul, 2019.
-
D. H. Kim, Y. C. Ha, S. H. Kim, S. Y. Lee, K. H. Park, H. B. Park and J. S. Jeon, “Development of Cooperative Autonomous Driving Algorithm Using V2V Communication for Convoy Driving,” Transactions of KSAE, Vol.29, No.4, pp.307-319, 2021.
[https://doi.org/10.7467/KSAE.2021.29.4.307]

- J. Y. Yoo, A Study on Truck Platooning Longitudinal Control System considering the Dynamics of Truck, M. S. Thesis, Kookmin University, Seoul, 2020.
- K. S. Huh, J. Y. Yoo, Y. K. Lee and K. H. Park, “Development of Variable Inter-Vehicle Distance Control According to Truck Platooning Use-case,” KSAE Fall Conference Proceedings, p.603, 2020.