[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 31, No. 1, pp.19-27

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jan 2023

Received 29 Sep 2022 Revised 14 Oct 2022 Accepted 17 Oct 2022

DOI: https://doi.org/10.7467/KSAE.2023.31.1.019

주행 시간 및 에너지 소비 최소화를 위한 모델예측제어 기반 전기차 속도 및 충전 계획 알고리즘 연구

김선우

; 이원형

; 김광기^*

인하대학교 전기컴퓨터공학과

Model Predictive Control for Speed and Charge Planning of Electric Vehicles in Minimizing Trip-time and Energy-consumption

Sunwoo Kim

; Wonhyung Lee

; Kwang-Ki K. Kim^*

Department of Electrical and Computer Engineering, Inha University, Incheon 22212, Korea

Correspondence to: ^*E-mail: kwangki.kim@inha.ac.kr

Copyright Ⓒ 2023 KSAE / 206-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

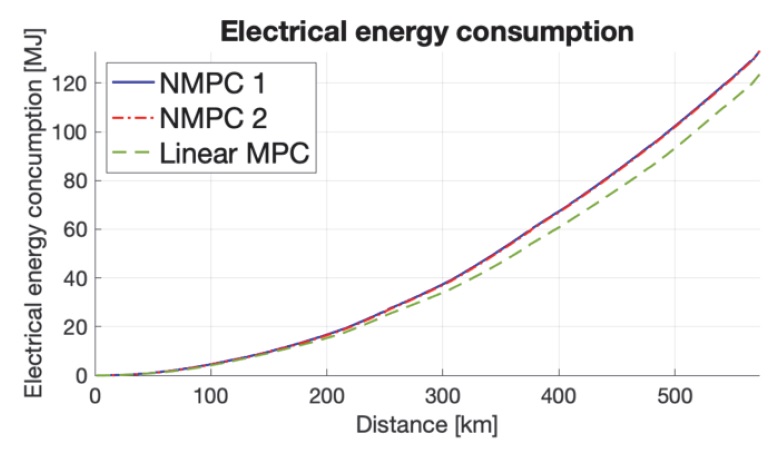
This paper presents different methods of model predictive control(MPC) for optimal decision-making on EV charging and speed planning. The goal of high-level planning is to minimize trip time and energy consumption for which EV charging planning, i.e., knowing where it will be charged and how much charge it needs, is explicitly considered, as well as energy-efficient speed planning. We propose both non-convex and convex optimization problem formulations for MPC-based, high-level planning of vehicle speed and charging in a spatial domain. A problem in linear MPC is presented as a convex quadratic programming approximation(i.e., convexified quadratic program) of the original nonlinear MPC. In the proposed linear MPC, the square of the vehicle speed is considered as a state variable, battery dynamics is simplified, and the powertrain constraint is convexified. To assess the conservatism of a convexified MPC problem and its solution, we will compare the performances of nonlinear and linear MPC solutions in a driving simulation of a Munich-Cologne trip (573 km) with four charging stations. The optimality of a linear MPC is shown as comparable to nonlinear counterparts, whereas its computation speed is one order of magnitude faster. This implies that the proposed linear MPC can be also used in short-term replanning, in which improved energy efficiency and increased reduction in trip time could be achieved in real driving conditions.

Keywords:

Eco-driving, Electric vehicles, Speed planning, Charging planning, Optimal control, Model predictive control, Nonlinear programming, Quadratic programming

키워드:

경제주행, 전기자동차, 속도계획, 충전계획, 최적제어, 모델예측제어, 비선형계획법, 이차계획법

1. 서 론

환경 규제 준수에 대한 범세계적인 관심과 그 필요성이 증대됨에 따라, 모빌리티 업계에 적용되는 환경 규제 역시 강화되고 있다.¹⁾ 특히 이산화탄소 및 질소산화물과 같은 온실가스 배출에 대한 규제는 심화되고 있기에, 이에 대한 해결 방안으로 내연기관 차량을 대체하는 전동화 차량의 개발 및 성능 개선이 차량 제조사들의 주도로 진행되고 있으며, 전동화 차량에 대한 에너지 효율 기준 역시 강화되고 있다. 한편, 순수 전기차 및 플러그인 하이브리드 차량, 연료전지 자동차와 같은 전동화 차량의 시장 보급에 대해 걸림돌이 되는 것은 내연기관 차량에 비해 상대적으로 낮은 배터리의 에너지밀도와 미비한 충전 인프라이다. 이는 운전자의 Range anxiety를 야기시켜 전기차의 확대 보급을 저해하는 중요한 요인 중에 하나이다.

이러한 에너지 충전 관점에서의 전기차의 단점을 보완하는 방법으로서 최적제어 기법을 기반으로 차량의 에너지 효율을 높이고, 항속거리를 늘리는 Eco-Driving 기술에 대한 연구개발 결과들이 발표되어 왔다. 전기차 또는 전동화 차량의 효율적인 에너지 운영을 위한 계층적 제어 구조에서 다음의 연구 결과들이 진행되어 왔다:

(i) Eco routing²⁾

(ii) Eco planning(Eco-driving)^3-6)

(iii) Eco tracking(supervisory control)⁷⁾

여기서 (i) Eco-routing은 출발점에서 도착점까지의 여러 경로들 중에서 최적의 에너지를 사용하는 경로를 선택하는 방법이고, (ii) Eco planning은 정해진 주행 경로 상에서 도로의 경사 정보, 도로의 정체 상황, 신호등 정보 등을 커넥티비티 기술을 이용하여 획득하고 이를 반영한 전방 주행 환경 예측을 통하여 최적의 에너지를 사용하는 차량의 속도를 결정하는 방법이며, 그리고 (iii) Eco tracking은 정해진 또는 계획된 또는 운전자가 요구하는 속도를 추적하는 연전비 향상을 위한 하이브리드 차량의 파워트레인 제어 기술을 일컫는다.

본 논문에서 다루는 Eco-driving 기술은, 주행 경로가 이미 선택된 상황에서 전체 예측 계획 구간에 걸쳐 주행 시간, 에너지 소모량, 운전자의 편안함 등을 다목적 비용함수(Cost)로 설정하고 운전 계획 구간에서 이를 최소화하는 차량의 속도 프로파일을 결정하는 방법이다. Eco-driving의 해를 구하는 방법으로는 기본적으로 최적제어 해를 구하는 방법들이 모두 적용될 수 있다. 예를 들면, 모델 예측 제어,^7-10) (근사)동적 계획법,^11-16) 강화학습^17-19)의 접근법을 적용한 연구가 활발하게 진행되어 왔다.

본 연구에서 저자는 순수 배터리 전기차((B)EV)의 전비 향상과 동시에 주행시간 단축을 목적으로 하는 선형 모델예측제어(Model Predictive Control, MPC)기반 속도 계획 방법과 이차계획법(Quadratic Programming, QP)을 사용한 볼록 최적화(Convex Optimization) 해를 제시한다. 여기서 총 주행시간에는 충전소에서의 충전 시간을 포함하였다. 속도 및 충전 계획을 동시에 결정하기 위한 최적제어 문제를 정의하고, 해당 문제를 해결하기 위한 비볼록 그리고 볼록 최적화의 해를 구하는 방법을 제시하고, 이로부터 얻어진 결과의 성능 시험을 위하여 시뮬레이션을 수행하였다. 또한 본 연구와 관련된 비선형 모델 예측 제어 방법에 관한 선행 연구^9,10)와의 비교를 위하여, 최적화 성능 그리고 연산 시간 등을 계산한 결과를 제시하였다.

서론 이후의 논문 구성은 다음과 같다. ‘2장 모델링’에서는 시간 및 공간 영역에서의 차량의 동역학 모델 및 모터 출력 제약조건에 대한 모델링 방법을 소개하고, ‘3장 최적제어 문제 정의’에서는 기존의 비선형 최적제어 문제와 이차계획법 접근 방법을 위해 새롭게 정의한 선형 최적제어 문제를 제시한다. 그리고 ‘4장 최적화 방법론’에서는 최적제어 문제의 해를 구하기 위한 비볼록 그리고 볼록 최적화 방법을 제시하고 비볼록 최적화 문제의 볼록화 과정을 설명한다. ‘5장 시뮬레이션 및 결과’에서는 세 가지 서로 다른 최적제어 문제와 그 해들을 시뮬레이션 결과를 통하여 비교한다, 그리고 마지막으로 ‘6장 결론 및 향후 연구 계획’으로 논문을 마무리한다.

2. 모델링

2.1 연속시간 차량 동역학 모델

전기차 속도의 동적 제어시스템 모델링을 위해, 다음과 같은 차량의 종방향 동역학 모델을 고려한다:

m v ˙ (t) = F m (t) - F b (t) - F r (t)

(1)

여기서 $F r t = F a t + F a (t)$ 는 결합 하중력(Combined load force)이며, F_a(t)는 차량에 종방향으로 작용하는 공기역학적 항력이다. 풍속이 상대적으로 작다고 가정하면, 차량에 작용하는 공기역학적 항력(Air drag force)은 다음과 같이 나타낼 수 있다.

F a (t) = 12 ρ a C d A f v 2 (t)

(2)

여기서 F_a(t)는 차량에 작용하는 중력 및 타이어에 작용하는 구름저항의 결합력을 의미하며, 식 (3)과 같이 나타낼 수 있다.

F α (t) = m g s i n ⁡ (α (s (t))) + C r c o s ⁡ (α (s (t)))

(3)

여기서 α(s(t))는 차량의 위치 s(t)의 도로 경사각(Road slope angle)이다.

2.2 이산시간 차량 동역학 모델

본 논문에서는 연속시간 차량 동역학 모델로부터 이산시간 모델을 구성하기 위해, Euler Forward 방법을 적용하였다.

v t + Δ t k = v (t) + F m (t) - F b (t) - F r (t) m Δ t k

(4)

위의 식 (4)는 다음과 같이 다시 쓸 수 있다.

v t k + 1 = v t k + F m t k - F b t k - F r t k m Δ t k

(5)

한편, 식 (5)에서 $v k ∶ = v t k$ 로 정의하면, (5)의 식으로부터 (6)의 식을 얻을 수 있다.

v k + 1 = v k + F m, k - F b, k - F r, k m Δ t k

(6)

여기서 결합 하중력은 식 (7)과 같이 정의된다.

F r, k = 12 ρ a C d A f v k 2 + m g s i n ⁡ α s k + C r c o s ⁡ α s k

(7)

2.3 공간영역 차량 동역학 모델

시간 영역에서의 차량 동역학 모델을 바탕으로, 차량의 이동거리(또는 간격기반 전방 이동거리의 인덱스)를 독립변수로 갖는 공간 영역에서의 차량 동역학 모델을 정의할 수 있다. 우선 아래와 같이 사다리꼴 규칙(Trapezoidal rule)를 이용하여 공간간격변수와 시간간격변수 사이의 관계를 다음과 같이 정의하고

Δ s k : = s t k + 1 - s t k = v t k + v t k + 1 2 Δ t k

(8)

시간간격변수를 다음과 같이 나타낼 수 있다:

Δ t k = 2 Δ s k v k + v k + 1

(9)

식 (6)에 식 (9)를 대입하면, 공간 영역에서의 차량 종방향 동역학 모델을 다음과 같이 얻을 수 있다.

v k + 1 2 = v k 2 + 2 Δ s k m F m, k - F b, k - F r, k v k 2, α k

(10)

2.4 모터 출력 제약조건

전동화 차량의 파워트레인 내 모터의 물리적인제약조건을 다음과 같이 고려한다. 전동화 차량에 사용되는 AC 모터의 견인 전동력은 모터가 발생시킬 수 있는 최대 기계적 토크 또는 모터의 회전축에 연결된 차량의 바퀴의 회전 속도, 즉 차량의 속도에 의해 제한되며, 이는 다음의 식으로 나타낼 수 있다:

F - m, k = m i n F - m, F - m, k c p v k, F - m, k c p v k = P - m v k

(11)

여기서 $F - m, k c p v k$ 는 위치 k에서 차량의 속도에 따라 제한되는 모터의 최대 구동력이며, 이는 모터의 최대 출력 $P - m$ 을 차량의 속도 v_k > 0로 나눈 값으로 계산된다.

3. 최적제어 문제 정의

3.1 주행 시간 감소를 위한 비용함수 정의

본 연구에서는, 시간영역 또는 공간영역에서의 주행 시간 최소화의 목적으로 다음의 총 운행시간 t_N을 목적함수로 고려한다.

t N = ∑ k = 0 N - 1 Δ t k + ∑ k ∈ K τ c h, k = ∑ k = 0 N - 1 Δ s k v k + ∑ k ∈ K τ c h, k

전체 주행 시간은 차량이 이동 중에 있는 운전 시간과 k번째 위치에 있는 충전소에서 배터리를 충전하는 충전 시간 $τ c h, k$ 의 합으로 나타낼 수 있으며, 이를 최적제어 문제의 비용함수의 일부로서 설정하여 차량으로 하여금 주행시간을 최소화하도록 한다.

3.2 시간영역 비볼록 최적제어 문제

본 연구에서는, 전기차의 주행 경로상 정해진 수의 충전소가 정해진 위치에 있음을 가정하고, 주행 시간을 최소화함과 동시에 제한 속도 범위 내에서 정해진 배터리 SoC(State of Charge)의 범위를 유지하며 주행하는 시나리오²⁰⁾를 가정한다.

이러한 전기차 충전 및 속도 계획을 위하여, 선행 연구⁹⁾에서 제시된 다음의 비선형 최적제어 문제를 고려한다.

m i n t N + ∑ k = 0 N - 1 ω d δ k + ω e F m, k 2 + ω b F b, k 2 s . t . v k + 1 = 2 Δ s k m e q F m, k - F b, k - F r, i + v k 2 t k + 1 = t k + Δ s k v k + τ c h, k ζ k + 1 = ζ k - Δ s k η k E c a p F m, k + P c h, k E c a p τ c h, k v_≤ v k ≤ v ¯ k ζ_- δ k ≤ ζ k ≤ ζ ¯ + δ k 0 ≤ τ c h, k ≤ τ ¯ c h, k 0 ≤ F m, k ≤ F ¯ m, k 0 ≤ F b, k ≤ F ¯ b 0 ≤ δ k x 0 = x i n i t

(12)

여기서 차량 내 모터의 구동 효율과 충전 속도는 상태변수와 제어변수에 의해 결정되며, 이는 다음과 같이 나타낼 수 있다.

η k = η k F m, k, v k, P c h, k = P c h, k ζ k

또한, 본 문제에서는 여유 변수 δ를 도입하여 배터리의 SoC에 대한 제약조건의 완화를 허용한다. 이는 실시간 최적화에서, 배터리 충전량이 낮은 상태에서 장거리 운행 계획 시, 주어진 Hard constraint를 만족시키는 속도 계획의 해가 없는 문제를 해결하기 위한 것이다. 가중치 ω_d를 충분히 크게 설정하면, 이러한 제약조건의 완화는 Hard constraint를 만족시키는 계획이 있을 경우에 최적 해에 영향을 미치지 않는다.

비용함수의 각 항에 대한 가중치 ω_d, ω_e, ω_b는 각각 여유변수, 모터의 기계적 힘, 브레이크 힘에 대한 가중치이며, 가중치를 조절함에 따라 최적화 문제를 풀 때 주행 시간과 에너지 사용량의 중요도를 조절할 수 있다. 주행 시간과 에너지 소모량은 상충 관계(Trade-off)에 있으며, 따라서 주행 시간 감소를 고려한 비용함수 항의 가중치를 증가시키면 에너지 사용량은 증가한다. 반면 에너지 사용량 감소를 고려한 비용함수 항에 대한 가중치를 증가시키면 주행 시간이 증가한다.

3.3 이차 비용함수를 갖는 공간영역 비볼록 최적제어 문제

본 절에서는 Eco-driving을 위해 이차 비용함수를 갖는 공간영역에서 정의된 비선형 최적제어 문제를 다음과 같이 정의한다.

m i n - ∑ k = 0 N - 1 ω t x k Δ s k 2 + ∑ k ∈ K τ c h, k + ∑ k = 0 N - 1 ω d δ k + ω e F m, k 2 + ω b F b, k 2 s . t . x k + 1 = 2 Δ s k m e q F m, k - F b, k - F r, k x k + x k ζ k + 1 = ζ k - Δ s k η k E c a p F m, k + Γ c h, k E c a p τ c h, k x_≤ x k ≤ x - k ζ_- δ k ≤ ζ k ≤ ζ - + δ k 0 ≤ τ c h, k ≤ τ - c h, k 0 ≤ F m, k ≤ F - m, k 0 ≤ F b, k ≤ F - b 0 ≤ δ k x 0 = x i n i t

(13)

여기서, $F - m, k$ 는 아래와 같이 정의한다.

F - m, k = m i n F - m, F - m, k c p x k, F - m, k c p x k = P - m x k ≈ c 0 + c 1 x k

위 문제에서는 물리적인 전체 주행시간과 충전 시간, 그리고 구동 에너지와 기계적 제동으로 손실되는 에너지를 비용함수로 고려하였고, 여유변수 δ를 최소화하기 위한 목적으로 비용함수에 δ를 포함하였다. 또한 상태변수 x_k는 k번째 위치(또는 Distance)에서의 차량 속도의 제곱 $v k 2$ 로 정의하며, 이에 따라 주행 시간 최소화를 고려하는 시간 영역에서의 비용함수 항 t_N은 공간 영역에서의 비용함수 항 $x k Δ s k 2$ 로 변환된다. 차량에 작용하는 결합 하중력은 x_k에 대해 Affine 하며 다음과 같이 쓸 수 있다.

F r, k x k = c r m v g c o s ⁡ α k + m v g s i n ⁡ α k + 12 c a A f ρ a x k

또한, 위 문제에서 차량이 충전소가 있지 않은 구간을 지날 때 (k∉K), $τ - c h, k = 0$ 로 정하며, 새롭게 도입한 계수 ω_t는 주행시간에 대한 가중치이다. 위 문제의 상태변수와 제어변수를 정리하면 다음과 같다.

상 태 변 수 : X k : = x k, ζ k T 제 어 변 수 : U k : = F m, k, F b, k, τ c h, k, δ k T

3.4 이차 계획법 기반 접근방법을 위한 공간영역 볼록 최적제어 문제

본 절에서는 이차 계획법(Quadratic programming) 기반 접근법을 위해 공간영역에서 볼록 최적제어 문제를 다음과 같이 정의한다.

m i n - ∑ k = 0 N - 1 ω t x k Δ s k 2 + ∑ k ∈ K τ c h, k + ∑ k = 0 N - 1 ω d δ k + ω e F m, k 2 + ω b F b, k 2 s . t . x k + 1 = 2 Δ s k m e q F m, k - F b, k - F r, k x k + x k ζ k + 1 = ζ k - Δ s k η k E c a p F m, k + P c h, k E c a p τ c h, k x_≤ x k ≤ x - k ζ_- δ k ≤ ζ k ≤ ζ - + δ k 0 ≤ τ c h, k ≤ τ - c h, k 0 ≤ F m, k ≤ F - m, k 0 ≤ F b, k ≤ F - b 0 ≤ δ k x 0 = x i n i t

(14)

위 문제에서 모터의 효율과 배터리 충전 속도는 상수 값으로 고정한다.

η k = 0.85, P c h, k = 45 [k W]

한편, 엄밀하게는 모터의 견인과 기계적 감속이 동시에 작동하지 않도록 하는 모터 힘과 기계적 브레이크의 제동력에 대한 제약조건 F_m,k⋅F_{b, k}≤0을 고려해야 하지만, 식 (13)의 최적제어 문제에서는 F_m,k≥의 조건으로 모터의 회생제동을 고려하지 않았기 때문에 해당 제약조건은 F_m,k⋅F_{b, k=}0이 된다. 여기서 비용함수의 F_m,k와 F_{b, k}의 양의 제곱항들로 인하여, F_m,k⋅F_{b, k=}0조건을 직접적으로 고려하지 않아도 최적해는 조건을 항상 만족하게 된다.

4. 최적화 방법론(Solution Methods)

4.1 비선형 모델 예측 제어 방법

3.2, 3.3절에서 제시된 비볼록 최적제어 문제의 최적해를 얻기 위해, 비선형 모델예측제어 방법을 적용한다. 이를 위해, Quasi-newton interior point 알고리즘을 기반으로 하는 비선형 계획법의 수치적 방법을 사용하여 해를 구하였다.

4.2 선형 모델 예측 제어 방법

3.4절에서 제시된 볼록 최적제어 문제의 최적해를 얻기 위해, 선형 모델예측제어 방법을 적용한다. 이를 위해, Active-set 방법 또는 Quasi-newton interior point 알고리즘을 기반으로 하는 이차 계획법의 수치적 방법을 사용한다.

4.3 시간 영역 및 공간 영역에서의 속도계획 방법

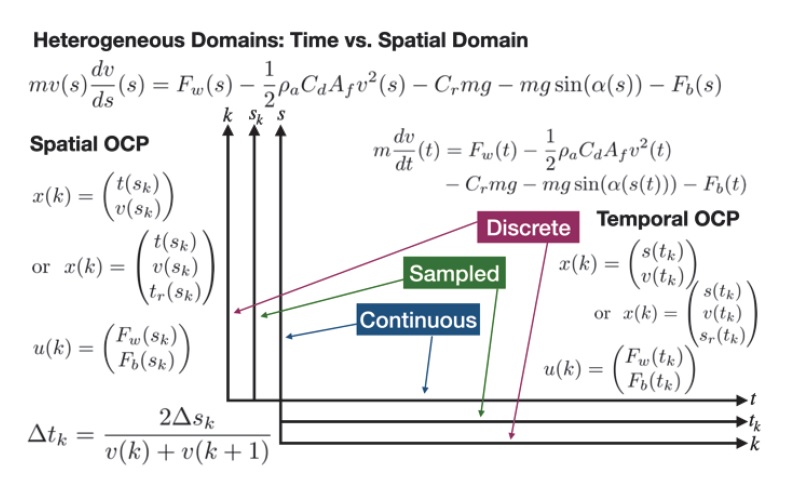
Fig. 1은 연속 및 이산, 시간 및 공간 영역에서의 상태 변수 및 제어 입력변수 간의 관계를 나타낸 그림이다. 이에 따라, 공간 영역의 속도계획법은 시간 영역에서의 속도 계획법으로 다음의 과정을 통해 변환할 수 있다. 현재의 속도 $v t k = v s k$ 와 다음 Space에서의 속도 $v * S k + 1$ 가 주어졌을 때, 시점 $t ∈ t k, t k + 1$ 에서의 목표 속도 v_target은 다음과 같이 결정할 수 있다.

v t a r g e t (t) = v s k + v * 2 s k + 1 - v 2 s k 2 Δ s k t - t k

여기서 다음 샘플링 시점 t_k+1은

t k + 1 = t k + 2 Δ s k v * s k + 1 + v s k

로 결정된다. 위의 시간 영역에서의 목표 속도 설정은 파워트레인(모터) 피드백 제어의 기준 값으로 사용될 수 있다.

Fig. 1

State and control inputs in time and space domain

5. 시뮬레이션 및 결과

이전 장에서 제시된 최적제어 문제의 해를 각각 비선형계획법 및 이차계획법으로 얻고, 최적해로부터 차량의 에너지 효율 및 주행시간을 도출하기 위한 시뮬레이션을 진행한다.

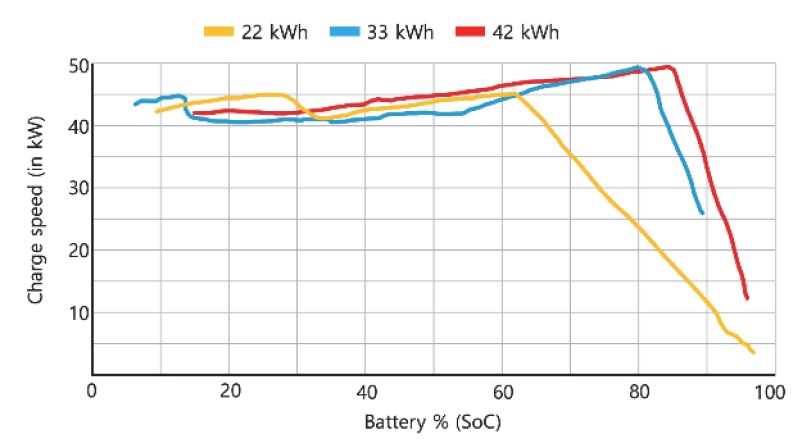
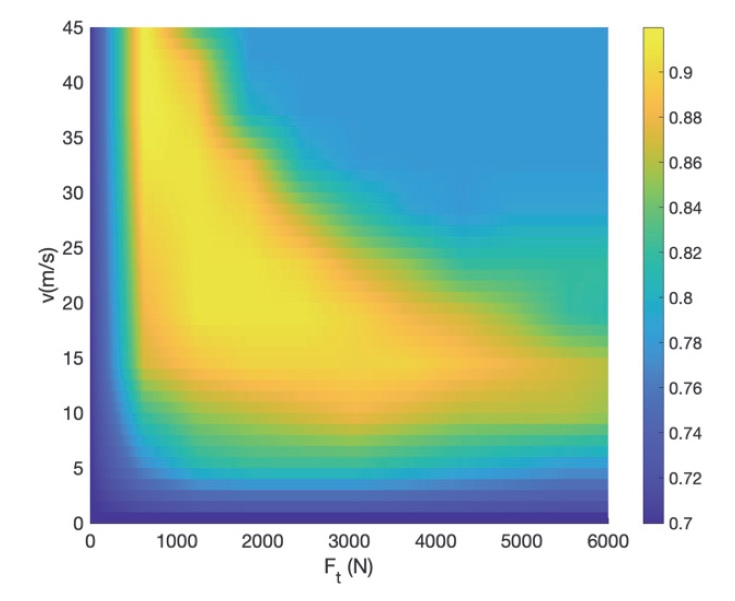
시뮬레이션을 위해, 충전소가 4개 있는 뮌헨-쾰른 간 573 km의 주행 경로를 가정하였다. 차량 배터리의 초기 SoC는 75 %로 설정하였으며, 배터리의 충전 모델 및 모터 효율 모델은 3.2절 및 3.3절의 비선형 최적제어 문제에 대해서는 Fig. 2에 제시된 BMW i3 42 kWh 모델의 충전 프로파일과 Fig. 3에 제시된 효율 지도(Efficiency map)의 데이터를 사용하였으며, 선형 최적제어 문제에 대해서는 충전 프로파일 P_ch(ζ)과모터 효율 η을 각각 45 kW와 0.85로 고정하였다. 시뮬레이션에 사용한 차량 파라미터는 Table 1의 내용과 같다. 또한 여유변수를 사용하여, SoC에 대한 제약조건이 0 ≤ ζ ≤ 1로 완화될 수 있도록 하였다. 이는 MPC 최적화 문제의 해를 구하기 위한 수치연산 기반의 Solver가 제약조건을 만족시키는 해가 없는 경우에, Infeasible의 결과를 내지 않고 완화된 조건으로 해를 구할 수 있도록 하기 위함이다. 수치 해의 δ 값을 확인하여 원하는 조건이 만족되었는지 판단할 수 있다.

Fig. 2

Actual charging profile of BMW i3 as a function of vehicle’s SoC

Fig. 3

An example of motor efficiency η(Ft, vt)map of EV

Table 1

Vehicle parameters for simulation

5.1 Nonlinear MPC 1(NMPC 1)

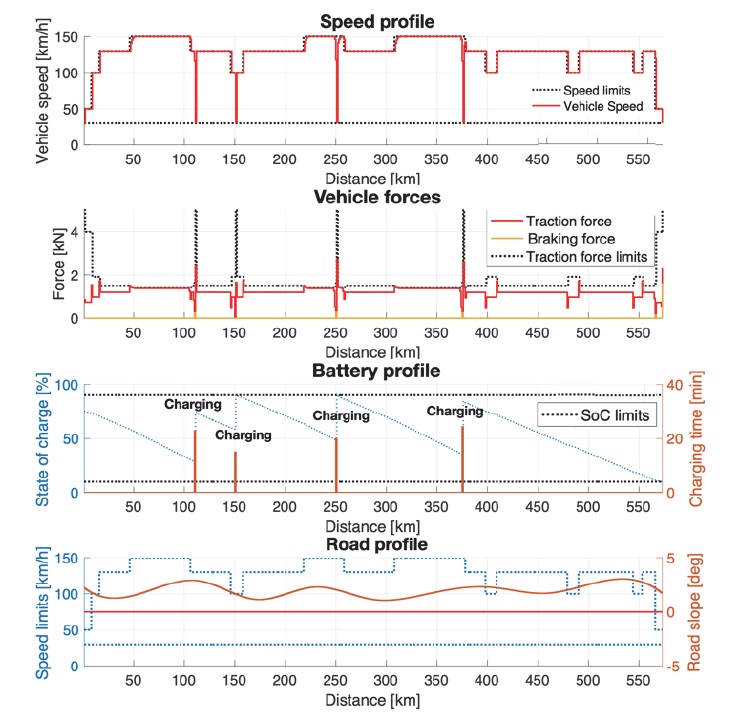
NMPC 1의 시뮬레이션에서는 3.2절에서 제시된 시간영역 비선형 최적제어 문제의 해를 찾기 위해 비선형 모델예측제어 방법을 적용하였으며, 비용함수의 각 항에 대한 가중치는 ω_d = 1 × 10⁶, ω_e = 1 × 10^-7, ω_b = 1 × 10^-6와 같이 설정하였다. 이로부터 시뮬레이션을 진행한 결과 차량이 모든 충전소에서 배터리를 충전하는 결과를 얻었다. NMPC 1의 경우, 차량은 충전소 1,3,4에서 거의 비슷한 시간을 충전에 사용한다. 또한 주행을 마쳤을 때 허용된 SoC 범위(0.1 ~ 0.9)의 하한에 도달하는데, 이로부터 전체 주행 시간 중 충전 시간이 차지하는 비율이 최소화 될 것임을 추측할 수 있다. 또한 차량이 에너지 사용을 줄이기 위해 의도적으로 감속하여 주행 시간과 충전 시간 사이의 균형을 달성하는 것을 시사한다.

Fig. 4

Comparison of travel time between MPCs

Fig. 5

Comparison of energy consumption

Table 2

Comparison of travel time and energy consumption

5.2 Nonlinear MPC 2(NMPC 2)

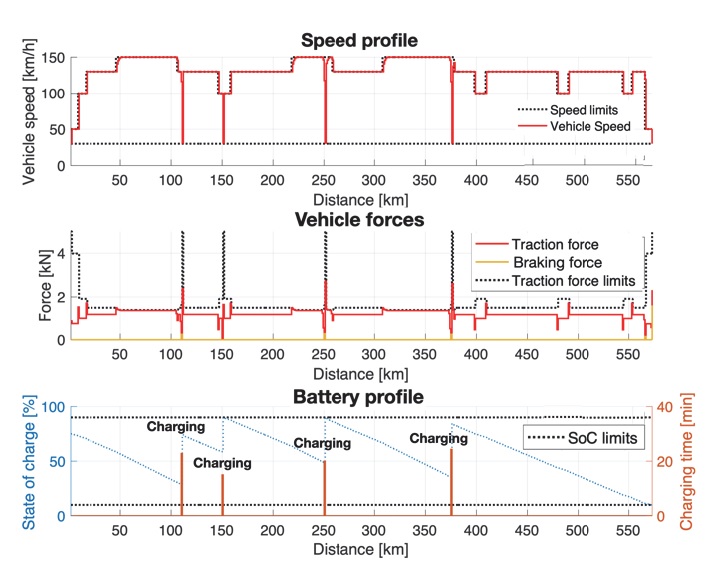
NMPC 2의 시뮬레이션에서는 3.3절의 공간영역 비선형 최적제어 문제의 해를 얻기 위해 비선형 모델 예측 제어 방법을 적용하였다.

또한 비용함수의 각항들에 대한 가중치는 ω_t = 1 × 10⁶, ω_d = 1, ω_e = 1 × 10^-5, ω_b = 1 × 10^-5와 같이 설정하였다. 그 결과로 차량은 NMPC 1의 결과보다 약 0.15 % 적은 주행 시간을 기록하였고, 충전 시간은 약 0.9 % 증가, 전기적 에너지 사용량은 약 0.02 % 감소하였다. 한편, Fig. 7의 배터리 SoC 프로파일에서 SoC가 허용된 범위를 넘어 충전 및 방전하는데, 이는 여유변수 ζ의 도입이 배터리 SoC에 대한 제약조건을 완화하는 것을 의미한다.

Fig. 6

Solution trajectories obtained from nonlinear MPC with nonconvex OCP11) (NMPC 1)

Fig. 7

Solution trajectories obtained from nonlinear MPC with quadratic costs13) (NMPC 2)

Fig. 8

Solution trajectories obtained from linear MPC with convex OCP14) (Linear MPC)

5.3 Linear MPC

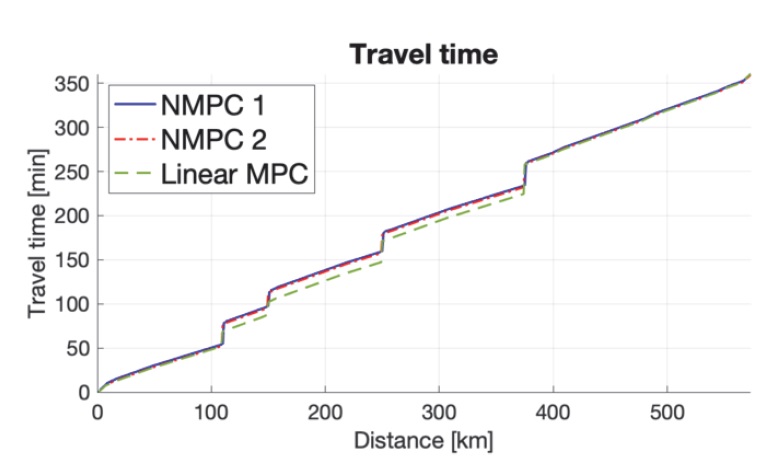
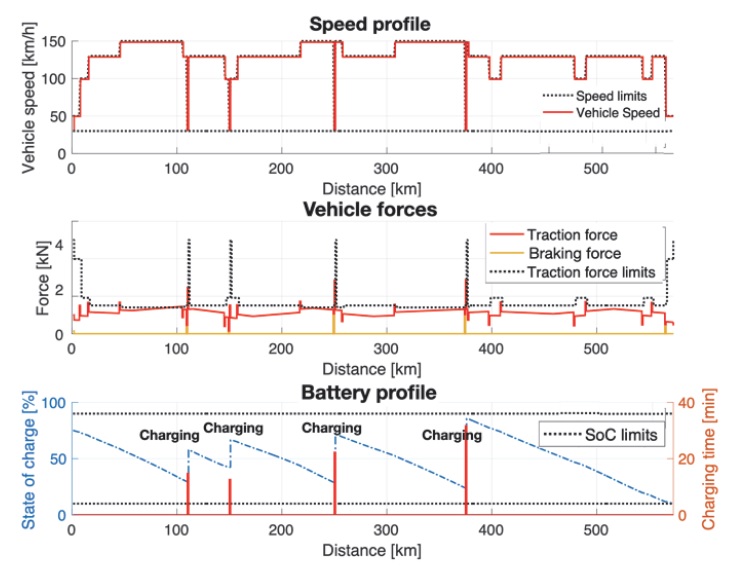
Linear MPC의 시뮬레이션에서는 3.4절의 공간영역 볼록 최적제어 문제의 해를 얻기 위해 이차 계획법 기반 접근 방법을 사용하였고, 비용함수의 각 항에 대한 가중치는 NMPC 2 시뮬레이션에 적용된 값을 사용한다. 그 결과 NMPC 1 대비 총 주행시간은 약 0.14 % 증가하였고, 충전 시간은 약 1 % 감소하였으며, 전기적 에너지 사용량은 약 7.21 % 감소하였다.

한편, Linear MPC 시뮬레이션 결과의 경우, NMPC 시뮬레이션의 결과보다 에너지 사용량이 상대적으로 낮은데, 이는 모터 효율이 상대적으로 높은 속도 및 Traction force 영역에서 차량이 주행하기 때문에 나타나는 현상으로 해석된다.

또한 연산시간(CPU Time)를 비교한 결과는, Linear MPC의 경우 평균 29.49초, NMPC 1의 경우 평균 54.54초, NMPC 2는 평균 43.17초의 계산시간이 소요되어, 3.4절에서 제시한 볼록화 기반 Linear MPC 방법이 NMPC 1과 NMPC 2 방법들과 비교하여 각각 약 46 % 그리고 32 % 만큼 계산시간이 감소하였다.

6. 결 론

본 논문에서는 충전시간을 포함한 전기자동차의 주행시간과 에너지 사용량을 동시에 최소화 할 수 있는 주행 기법인 Eco-Driving을 목적으로 하는 새로운 모델예측제어 기반 속도 및 충전 계획 방법을 제시하였다. 선행 연구에서 제시된 비선형 최적제어 문제를 이차 계획법으로 공식화한 선형 최적제어 문제로 근사하는 볼록화 방법을 제시하였다. 또한 각 최적제어 문제의 해를 얻기 위한 시뮬레이션 결과로부터 확인할 수 있듯이, 해당 볼록 선형 최적제어 문제의 해는 총 주행 시간 및 에너지 소비 측면에서 비선형 최적제어 문제에서 얻은 것과 유사한 결과를 나타내며, 계산 시간 면에서도 유의미한 시간 단축 효과를 제공한다. 연산 시간의 단축과 최적제어 문제의 볼록화는 계획 알고리즘의 임베디드화에 유리함과 더불어 주행 상황 및 환경 변화에 따른 실시간 속도 및 충전 계획의 재설정에 용이하므로, 커넥티비티 그리고 자율주행 기술과 결합하여 중요한 전기차 서비스 항목이 될 수 있을 것으로 기대한다.

Nomenclature


m :	vehicle mass, kg
v(t) :	vehicle speed, m/s
F :	force, N
ρ_a :	mass density of air, kg/m³
C_d :	aerodynamic drag coefficient
A_f :	frontal area of the vehicle, m²
g :	gravitational acceleration, m/s²
C_r :	rolling resistance coefficient
s(t) :	travel distance or distance index at time t, km
α :	road slope, deg
$F -$ :	maximum force limit, N
$P -$ :	maximum power limit, N
τ_ch,k :	charging time at location k, sec
K :	a set of index where the charging station is located

Subscripts


m :	motor (traction)
b :	brake
elec :	electric (power, force)
mech :	mechanical (power, force)
ch :	charging
cap :	capacity
w :	wheel

Acknowledgments

이 논문은 2022년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0017124, 2022년 산업혁신인재성장지원사업).

References

K. U. Seok and H. J. Yoon, “Study on the Strategy of CO₂ Reduction Technology in Vehicle According to CO₂ Emissions Regulation in EU – Focusing on Auxiliary Energy-improvement,” Transactions of KSAE, Vol.23, No.2, pp.230-238, 2015. [https://doi.org/10.7467/KSAE.2015.23.2.230]
D. Watzenig and B. Brandstatter, Comprehensive Energy Management: Eco Routing & Velocity Profiles, Springer, New York, 2017. [https://doi.org/10.1007/978-3-319-53165-6]
A. Sciarretta, G. De Nunzio and L. L. Ojeda, “Optimal Ecodriving Control: Energy-efficient Driving of Road Vehicles as an Optimal Control Problem,” IEEE Control Systems, Vol.35, No.5, pp.71-90, 2015. [https://doi.org/10.1109/MCS.2015.2449688]
J. Guanetti, Y. Kim and F. Borrelli, “Control of Connected and Automated Vehicles: State of the Art and Future Challenges,” Annual Reviews in Control, Vol.45, pp.18-40, 2018. [https://doi.org/10.1016/j.arcontrol.2018.04.011]
A. Vahidi and A. Sciarretta, “Energy Saving Potentials of Connected and Automated Vehicles,” Transportation Research Part C: Emerging Technologies, Vol.95, pp.822-843, 2018. [https://doi.org/10.1016/j.trc.2018.09.001]
L. Guzzella and A. Sciarretta, Vehicle Propulsion Systems: Introduction to Modeling and Optimization, Springer Berlin, Heidelberg, 2013. [https://doi.org/10.1007/978-3-642-35913-2]
A. Weißmann, D. Görges and X. Lin, “Energy-optimal Adaptive Cruise Control Based on Model Predictive Control,” IFAC-PapersOnLine, 20th IFAC World Congress, Vol.50, No.1, pp.12563-12568, 2017. [https://doi.org/10.1016/j.ifacol.2017.08.2196]
H. Lim, C. C. Mi and W. Su, “A Distance-based Two-stage Ecological Driving System using an Estimation of Distribution Algorithm and Model Predictive Control,” IEEE Transactions on Vehicular Technology, Vol.66, No.8, pp.6663-6675, 2017. [https://doi.org/10.1109/TVT.2017.2667723]
Y. Jia, R. Jibrin, Y. Itoh and D. Görges, “Energy-optimal Adaptive Cruise Control for Electric Vehicles in Both Time and Space Domain Based on Model Predictive Control,” 9th IFAC Symposium on Advances in Automotive Control AAC, IFAC-PapersOnLine, Vol.52, No.5, pp.13-20, 2019. [https://doi.org/10.1016/j.ifacol.2019.09.003]
Y. Jia, R. Jibrin and D. Görges, “Energy-optimal Adaptive Cruise Control for Electric Vehicles Based on Linear and Nonlinear Model Predictive Control,” IEEE Transactions on Vehicular Technology, Vol.69, No.12, pp.14173-14187, 2020. [https://doi.org/10.1109/TVT.2020.3044265]
C. Sun, J. Guanetti, F. Borrelli and S. J. Moura, “Optimal Eco-driving Control of Connected and Autonomous Vehicles through Signalized Intersections,” IEEE Internet of Things Journal, Vol.7, No.5, pp.3759-3773, 2020. [https://doi.org/10.1109/JIOT.2020.2968120]
E. Ozatay, S. Onori, J. Wollaeger, Ü. Özgüner, G. Rizzoni, D. Filev, J. Michelini and S. D. Cairano, “Cloud-based Velocity Profile Optimization for Everyday Driving: A Dynamic-programming-based Solution,” IEEE Transactions on Intelligent Transportation Systems, Vol.15, No.6, pp.2491-2505, 2014. [https://doi.org/10.1109/TITS.2014.2319812]
D. Kim, J. S. Eo and K. -K. K. Kim, “Parameterized Energy-optimal Regenerative Braking Strategy for Connected and Autonomous Electrified Vehicles: A Real-time Dynamic Programming Approach,” IEEE Access, Vol.9, pp.103167-103183, 2021. [https://doi.org/10.1109/ACCESS.2021.3098807]
D. Kim, J. S. Eo and K. -K. K. Kim, “Service-Oriented Real-Time Energy-Optimal Regenerative Braking Strategy for Connected and Autonomous Electrified Vehicles,” IEEE Transactions on Intelligent Transportation Systems, Vol.23, No.8, pp.11098-11115, 2022. [https://doi.org/10.1109/TITS.2021.3099812]
J. W. Bae and K. -K. K. Kim, “Gaussian Process Approximate Dynamic Programming for Energy-optimal Supervisory Control of Parallel Hybrid Electric Vehicles,” IEEE Transactions on Vehicular Technology, Vol.71, No.8, pp.8367-8380, 2022. [https://doi.org/10.1109/TVT.2022.3178146]
K. Kim, C. Kang, W. Lim and. S. Cha, “Optimization of Vehicle Speed in Urban Road Using Dynamic Programming,” Transactions of KSAE, Vol.27, No.9, pp.687-692, 2019. [https://doi.org/10.7467/KSAE.2019.27.9.687]
H. Lee, N. Kim and S. W. Cha, “Model-based Reinforcement Learning for Eco-driving Control of Electric Vehicles,” IEEE Access, Vol.8, pp.202 886-202 896, 2020. [https://doi.org/10.1109/ACCESS.2020.3036719]
M. Zhou, Y. Yu and X. Qu, “Development of an Efficient Driving Strategy for Connected and Automated Vehicles at Signalized Intersections: A Reinforcement Learning Approach,” IEEE Transactions on Intelligent Transportation Systems, Vol.21, No.1, pp.433-443, 2020. [https://doi.org/10.1109/TITS.2019.2942014]
M. Wegener, L. Koch, M. Eisenbarth and J. Andert, “Automated Eco-driving in Urban Scenarios using Deep Reinforcement Learning,” Transportation Research Part C: Emerging Technologies, Vol.126, pp.102967, 2021. [https://doi.org/10.1016/j.trc.2021.102967]
FORCESPRO Chapter 11.19 High-level interface: Optimal EV Charging and Speed Profile Example, https://forces.embotech.com/Documentation/examples/high_level_ev_speed_management/index.html, , 2022.

Symbol	Description	Value
m_v	Vehicle mass	1350 [kg]
e_I	Mass factor	1.06 [-]
A_f	Frontal projected area of vehicle	2.38 [m²]
ρ_α	Air density	1.206 [kg/m³]
c_a	Air drag coefficient	0.29 [-]
c_r	Rolling resistance coefficient	0.01 [-]
$F - m$	Maximum traction force	5 [kN]
$F - b$	Maximum braking force	10 [kN]
E_cap	Battery’s energy capacity	37.9 [kWh]
$P - c h$	Maximum charging power	50 [kWh]
$v_$	Minimum vehicle velocity	30 [km/h]
$v ¯$	Maximum vehicle velocity	150 [km/h]
$ζ_$	Minimum SoC	0.1 [-]
$ζ ¯$	Maximum SoC	0.9 [-]

	t_N [min] (%)	$∑ τ c h, k$ [min] (%)	E_mech [MJ] (%)	E_elec [MJ] (%)
NMPC 1	360.17 (100.00)	81.94 (100.00)	117.72 (100.0)	133.16 (100.0)
NMPC 2	359.64 (99.85)	82.68 (100.90)	117.66 (99.95)	133.14 (99.98)
Linear MPC	360.66 (100.14)	81.12 (99.00)	110.05 (93.48)	123.56 (92.79)