사회적 규범 내에서 여유 변수를 활용한 커넥티드 카의 자연스러운 속도 계획법

2.1 사회적 규범과 위반 행동

오래 전부터 사람들은 특정 상황에서 규칙 위반이 자연스러운 사회적 규범을 형성해왔다.⁵⁾ 이때 규범은 사회적 현상이며, 이는 특정 상황에서 사람들에 의해 정의되고 명명되는 것이다.⁶⁾ 이러한 위반 행동은 이때 범죄 행동을 포함하지 않는 단어이다.

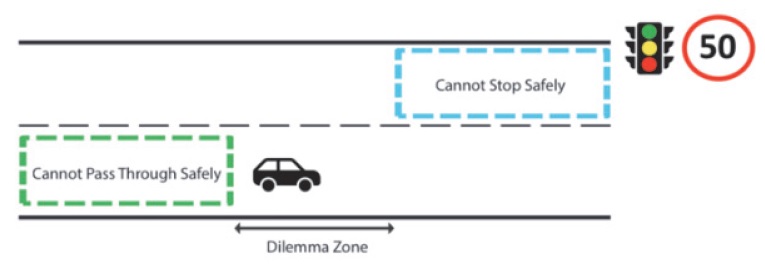
Fig. 1과 같이 혼잡한 도로에서 위반 행동은 일반적으로 차량 운행 중에서 흔히 볼 수 있는데, 신호등이나 횡단보도 앞에서 정지선을 넘어 정차하는 예를 볼 수 있다. 또한 신호등 앞에서 노란 불을 보자마자 어떤 운전자는 속도를 증가시켜 신호등을 지나고, 어떤 운전자는 정지할 수도 있다. 자율주행차량의 경우 동일한 상황에서 급정거를 하여 신호 규약을 준수할 것인지 아니면 정해진 제한속도보다 과속하더라도 신호등이 황색 등인 상태에서 통과하여 전체 교통흐름을 원활하게 하고, 후방충돌을 방지할 것인지 등에 대한 고민이 필요 할 것이다.

Fig. 1

Congested traffic flow at intersection(Source: http://stock.adobe.co.kr/)

신호등 체계가 있는 일반적인 도로에서는 신호등 앞에서 다음 Fig. 2와 같이 안전하게 정지할 수 없는 구간, 안전하게 지나갈 수 없는 구간, 그리고 마지막으로 그 어디 구간에도 속하지 않는 딜레마 존이 있다. 본 연구는 딜레마 존에서 여유 변수를 도입한 최적화 기법을 이식한 제안한 행동 패턴을 실험하고 주행 시간 단축을 목적으로 한다.

Fig. 2

Dilemma zone at signalized single-lane roads

2.2 커넥티드 카의 통신 기술

Fig. 3과 같이 커넥티드 카는 주변에 위치한 차량, 신호등과 같은 구조물, 그리고 보행자 간의 통신을 활용할 수 있다. 통신 기술을 활용한 연결성은 커넥티드 카에서 판단/제어 시에 필요한 정보들을 선 취득하게 함으로 주행 목적에 맞게 유리하게 작용한다. 예를 들어, 유인 운전차량과 Vehicle-To-Vehicle(V2V) 통신 기술을 활용하여 선행 주행하는 차량의 정보들을 취득함으로써 커넥티드 카의 속도 궤적을 목적에 맞고 적절하게 계획하고 이를 제어할 수 있다.

Fig. 3

Illustration of connected and automated vehicle(Source: http://stock.adobe.co.kr/)

신호등 위상 및 신호(Signal-Phase-and-Timing, SPaT) 정보를 Vehicle-To-Infrastructure(V2I) 통신 기술을 적극적으로 활용하여 신호등 정보들을 미리 취득함으로 차량 사고를 미연에 방지하는 적절한 판단/제어 전략을 세울 수 있다. 이때 V2X 통신을 활용한 속도 궤적을 계획하는 연구들이 제안되었는데 예를 들어, 녹색 신호등 구간을 적절히 지나가거나,^7,8) 실시간 SPaT 정보를 활용한 계층적 속도 계획법이 제시되었다.⁹⁾ 따라서 본 연구에서는 V2I와 같은 구조물과의 통신 기술을 적극 활용하여 SPaT 정보를 커넥티드 카에 취득하게 함으로써 사회적 규범 내에서 위반 행동을 내포하는 현실적인 운전자 행동 패턴을 모사할 것이다.

3.1 시스템 모델링

본 연구는 시스템을 다음과 같은 단순화된 차량의 종방향 역학을 적용하고자 한다.

여기서 s는 차량의 위치, v는 종방향 속도, a_x는 시스템의 제어 입력 u로 사용되는 차량의 종방향 가속도를 나타낸다. 이때 일반적인 선형 비가변 상태-공간 모델은 다음과 같다.

이때 x=[s v]^T이며, 상태-공간을 구성하는 A, B, 그리고 C 행렬들은 다음과 같다.

그리고 위와 같은 상태-공간 모델은 Euler 기법을 활용하여 다음과 같이 이산화 되는데,

이때 A_d, B_d, 그리고 C_d는 이산화 된 상태 행렬들을 나타낸다.

식 (3a)와 (3b)을 가지고 본 연구에서는 전형적인 최적화 문제를 3.2절에서 논의하고자 한다.

3.2 추종 모델 예측 제어

해당 절에서는 제약 조건을 만족하며 도로 제한 속도를 추종하기 위한 목적으로 일반적인 추종 모델 예측 제어 문제를 논의한다. 기준 신호, r^ref인 도로 제한 속도를 추종하기 위해 제어 목적을 구성하고자 한다.

그 결과, 우리는 다음과 같이 변형된 목적 함수를 고려하고자 한다.

이때 $$ \begin{array}{c}\Delta u_k=u_k-u_{k-1},e_k=y_k-r_k,Q_e^T=Q_e\in ,\\ R^{n_x\times n_x}>0,R_e^T=R_e=R^{n_u\times n_u}>0,P_{\mathrm{\infty }}>0.\end{array}$$

이때 출력 기준 신호를 추종하는 목적을 고려하면,

해당 최적화 기법에서 사용되는 증강 시스템에서 확장된 상태는 다음과 같이 정의하는데, $$ {z_k=\left[\begin{array}{c}{x}_k\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{u}_{k-1}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{r}_k\end{array}\right]}^T$$,

이때 A_x, B_x는 증강된 시스템을 구성하는 상태 행렬들이다.

증강된 시스템에서, 우리는 다음과 같이 추종 오차를 시스템 출력으로 정의할 수 있다.

전통적인 추종 모델 예측 제어는 다음과 같은 최적 제어 문제에 기반하여 정의할 수 있는데,

때 MPC 피드백은 첫번째 최적 값에 기반하여 정의할 수 있는데, $$ \mathrm{\Delta }{u}_0^{*}$$, 즉,

이때 우리는 실제 제어 입력, u_k가 아닌 제어 입력 증분, ∆u_k를 적용하였다. 이는 시스템 출력을 0이 아닌 값으로 유지하기 위해 정상 상태에서 명령된 값으로 적용했기 때문이다. x_k가 현재의 상태, u_k-1이 이전의 제어 입력, 그리고 $$ r_k^{ref }$$는 현재의 추종 입력이라고 가정한다. 그 결과 다음과 같은 제어 행동이 결정된다.

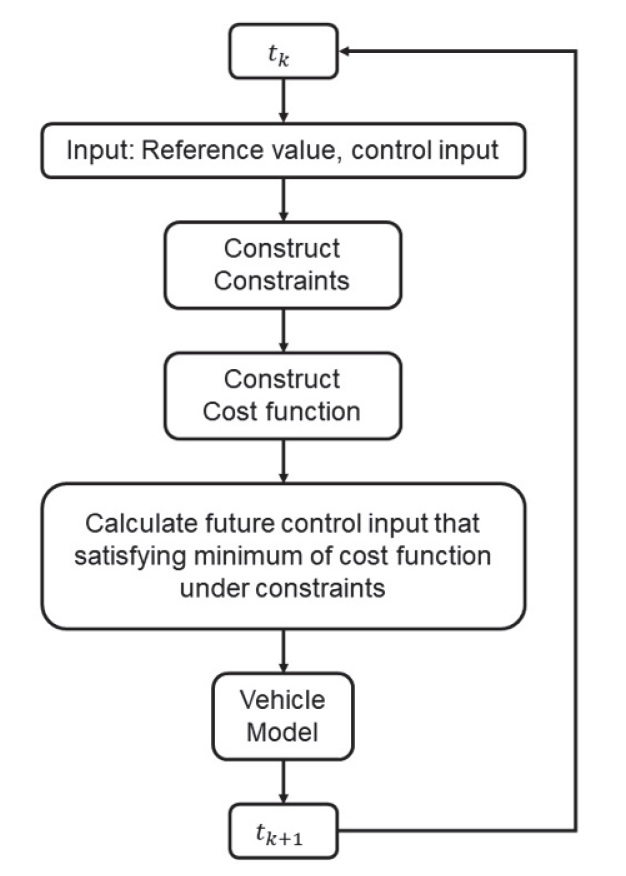
이때 추종 모델 예측 제어 기법을 개요도로 나타내면 다음 Fig. 4와 같다. t_k 시점부터 시작하는데, 입력으로 상태의 목표값과 제어값을 입력으로 받는다. 다음으로 제약 조건 및 비용 함수를 구성하는데, 이때 일반적인 제약 조건 및 추종 모델에 맞는 오차를 기반으로 한 비용 함수를 구성한다. 그 다음으로 제약 조건 하에서 오차값으로 구성된 비용 함수의 최소화를 만족하는 미래 제어값을 계산한다. 마지막으로, 계산된 미래 제어값은 차량 모델에 들어가게 된다.

Fig. 4

Flow chart of tracking model predictive control

다음 절에서 가변 제약 조건을 가진 추종 모델 예측 제어 기법을 논의하고자 한다.

4.1 느슨한 제약 조건을 가진 추종 모델 예측 제어

만약 제약 조건들이 느슨할 경우, 상태 제약 조건은 시스템의 작동에 타당하지 않을 수 있다. 즉, 약간의 위반은 발생 가능하지만 이는 치명적인 결과(예: 차량 사고)로 이어지지 않는다. 그래서 추종 모델 예측 제어 기법의 동작 원리에서 잠재적으로 알맞지 않은 부분을 여유 변수를 통해 제어할 수 있다. 상태 제약 조건을 느슨하게 만들어 주는 여유 변수는 다음과 같다.

이때 ϵ은 최적화 문제에서 조작 가능한 변수이다.

느슨한 제약 조건을 가진 추종 모델 예측 제어 문제는 다음과 같이 구성되는데,

이때 여유 변수의 가중치 µ > 0은 큰 값이다.

그 결과 제어 행동은 다음과 같이 정의된다.

다음 절에서 여러 시뮬레이션 환경에서 이루어진 결과에 대해 논의한다.

4.2 가변 제약 조건 모델 예측 제어

조작가능한 변수 ϵ에 대해 본 연구는 가변적으로 여유 변수를 적용하는 기법에 대해 소개하고자 한다.

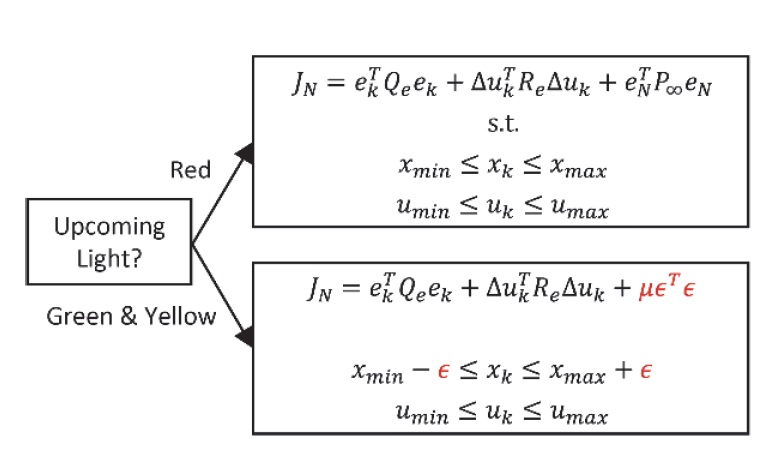
Fig. 5에서 볼 수 있듯이 만약 다가오는 신호등의 위상이 녹색과 황색일 때, 추종 모델 예측 제어의 목적 함수와 상태 제약 조건에 여유 변수를 둔다. 이와 반대로 다가오는 신호등의 위상이 적색일 때, 전통적인 추종 모델 예측 제어 기법을 적용한다. 앞서 언급한 바와 같이 상태 제약 조건에 여유 변수를 시간에 따라 가변적으로 설정한다.

Fig. 5

Diagram of variational constrained MPC algorithm

해당 제어 기법은 일반적인 목적 함수에 여유 변수를 더함으로써 적색 위상일 때 완전한 정지를 하지 않을 수 있다. 그 결과, 본 연구는 해당 오점을 해결하고자 적색 위상에 도달할 경우에 전통적인 추종 모델 예측 제어 기법을 적용한다. 이와 반대로 다른 위상에 도달할 경우에는 여유 변수를 적용하여 사회적 규범 내에서 과속하는 경향을 내포하는 행동 패턴을 제안하고자 한다.

다음 절에서 해당 제어 기법을 이식한 커넥티드 카의 제안한 행동 패턴의 다양한 시뮬레이션 결과에 대해 논의한다.

5.1 시뮬레이션 환경

본 실험에서 앞서 언급한 세 가지 제어 기법들을 매트랩 2021b, 그리고 Intel(R) Core(TM) i7-11700F @ 2.50 GHz CPU, 32 GB RAM, NVIDIA GeForce GTX 3060 Ti GPU가 연산에 사용되었다. 이러한 설정에서 본 논문에서는 단일 도로에서 신호등 체계를 구축하고, 속도제한 표지판 또한 임의로 배치하였다. 이때 신호등 위치는 MATLAB 명령어 randi()를 활용하여 랜덤으로 배치하고, 배치에 따른 3가지 도로에서 시뮬레이션한다.

예를 들어, Fig. 6과 같이 신호등 배치에 대한 알고리즘을 확인할 수 있다. 이때 입력으로 R은 랜덤씨드 수, M은 종착지의 위치, N은 배치할 신호등의 수, P_y는 황색 신호등의 지속 시간이다. 출력으로는 L인 배치된 신호등의 위치 정보이다. 1번째 줄에서 우선 랜덤씨드 수를 주어, 랜덤화를 고정한다. 2번째 줄에서 종착지의 위치와, 배치할 신호등의 수를 활용하여 첫번째로 배치된 신호등의 위치 정보, 즉, L_rng를 얻는다. 3번째 줄에서 첫번째로 얻은 L_rng를 활용하여 정렬한다. 마지막으로 4번째 줄에서 정렬된 L_sorted를 활용하여 겹치지 않는 유니크한 위치 정보만 출력으로 내보낸다.

Fig. 6

Algorithm of arrangement of traffic light systems

5.2 거리 결과

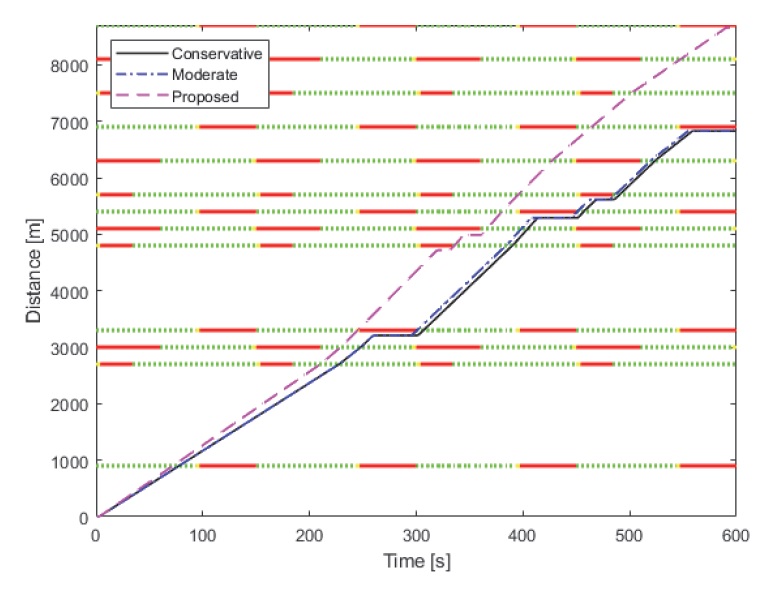
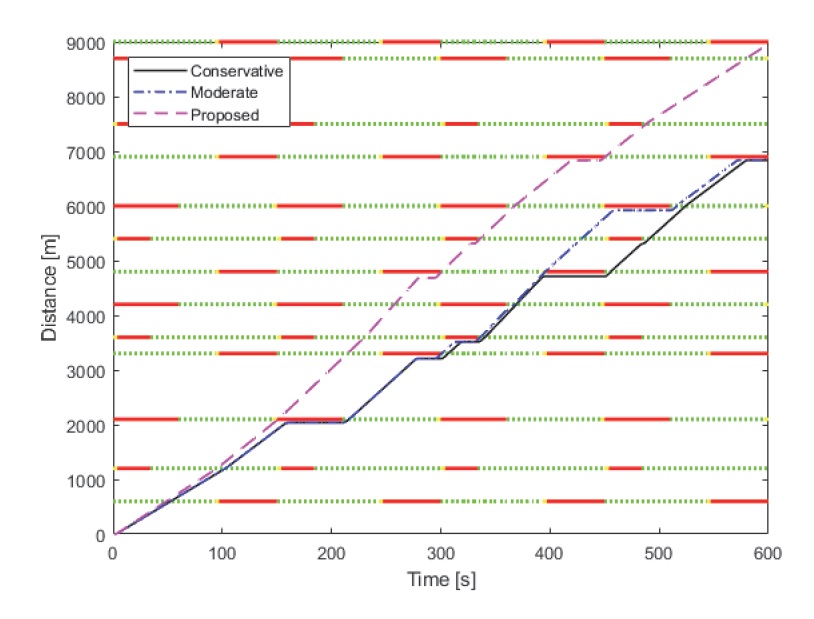
본 절에서는 거리 결과에 대해 논의하고자 한다. 거리 결과 그래프에서는 시간-거리 그래프에서 세 가지 행동 패턴의 위치 궤적을 보인다. 그래프 상의 가로 선은 해당 거리에 배치된 신호등을 의미하며, 가로 선의 색 변화는 시간에 따라 적색, 황색, 그리고 청색 신호등이 번갈아가며 켜지는 것을 나타낸다. Fig. 7은 해당 시간에 따른 거리 결과를 보여주는데, 전 구간에 걸쳐 느슨한 제약 조건을 가진 제안한 운전자 행동 패턴은 첫번째 신호등 구간부터 가속하여 이를 지나가는 것을 볼 수 있다.

Fig. 7

Space-time diagram in each of behaviors at first arrange-ment

제안한 행동은 시뮬레이션 시작부터 기울기를 보았을 때, 도로 제한 속도보다 과속하는 것을 관측할 수 있다. 각각의 운전자 행동 패턴들의 주행 거리는 상대적으로 8,677 m, 6,862 m, 6,828 m로 제안한 행동, 일반적인 행동, 그리고 보수적인 행동 패턴의 순이다. 이러한 결과는 일반적인 행동 패턴은 황색 신호등 구간(딜레마 존)일 때 과속은 하지만, 8번째 신호등 구간에서 정지하고, 녹색 신호등 구간에서 도로 제한 속도를 준수하여 다음 신호등에서 대기하므로 종래에는 보수적인 운전자 행동 패턴과 유사하게 주행한다. 이와 반대로 전 구간에 걸쳐서 제약조건에 여유 변수를 부과한 제안한 행동 패턴은 사회적 규범 내에서 용인되는 과속을 통해 시기 적절히 신호등을 통과하여 종래에 가장 긴 주행 거리를 얻을 수 있었다. 예를 들어 4번째 신호등 구간 전부터 과속을 하여 해당 신호등이 황색등일 때 지나감으로써 5, 6번째 신호등에서 정지함에도 불구하고, 제안한 행동 패턴이 가장 긴 주행 거리를 얻을 수 있었다.

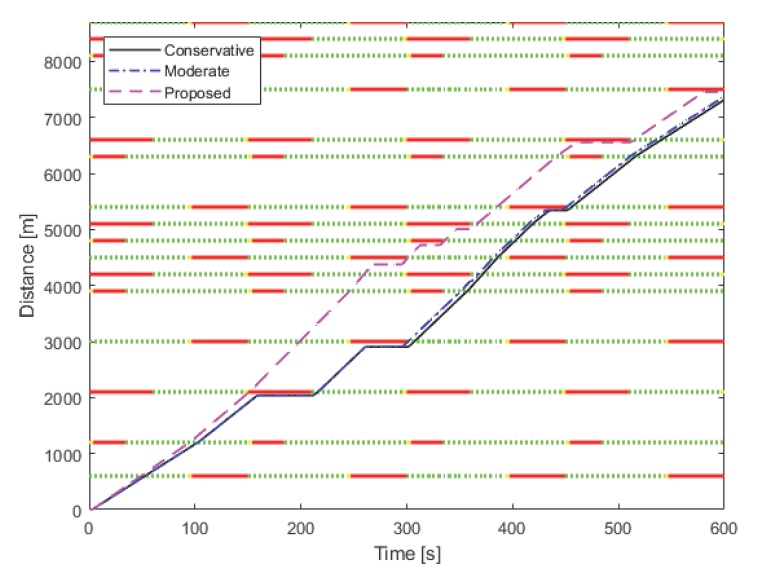
Fig. 8은 Fig. 7과 달리 랜덤 씨드 수를 바꾸어 신호등을 배치시킨 그림이다. 그림에서 볼 수 있다시피 3번째 신호등 구간부터 각기 다른 제어 기법이 이식된 행동 패턴들의 주행 결과가 판이하게 나타난다. 예로써 해당 신호등 구간에서 제안한 행동 패턴은 황색 신호등 구간일 때 과속하여 지나가는 것을 관측할 수 있지만 이와 반대로, 다른 행동 패턴들은 정지하는 것을 볼 수 있다. 따라서 제안한 행동이 3번째 신호등 구간 전부터 과속하여 해당 신호등이 황색등일 때 통과하여 지나감으로써 비교군과 다른 주행 거리 결과를 얻을 수 있었다. 따라서 가장 긴 주행 거리를 획득함과 더불어 또한 4번째 신호등 위치에 도달하였을 때 주행 시간을 비교해보면 다음과 같다. 상대적으로 215초, 300초, 그리고 306초로 제안한 행동, 일반적인 행동, 마지막으로 보수적인 행동이다.

Fig. 8

Space-time diagram in each of behaviors at second arrangement

Fig. 9는 또 다른 랜덤 씨드 수에 따른 신호등 배치에 따른 거리 결과를 보여주는데, 제안한 행동은 3번째 신호등에서 황색 신호등이 켜져 있을 때 과속하여 해당 신호등을 통과하는 것을 관측할 수 있다. 하지만 7번째 신호등 구간부터 정지하는 것을 관측할 수 있는데, 이는 과속을 함에도 불구하고, 통과할 수 없는 신호등의 배치로 인한 것이다. 따라서 종래에는 비교군으로 설정한 일반적인 행동과 보수적인 행동 패턴과 크게 다르지 않은 거리 결과를 얻을 수 있다.

Fig. 9

Space-time diagram in each of behaviors at third arrange-ment

5.3 속도 결과

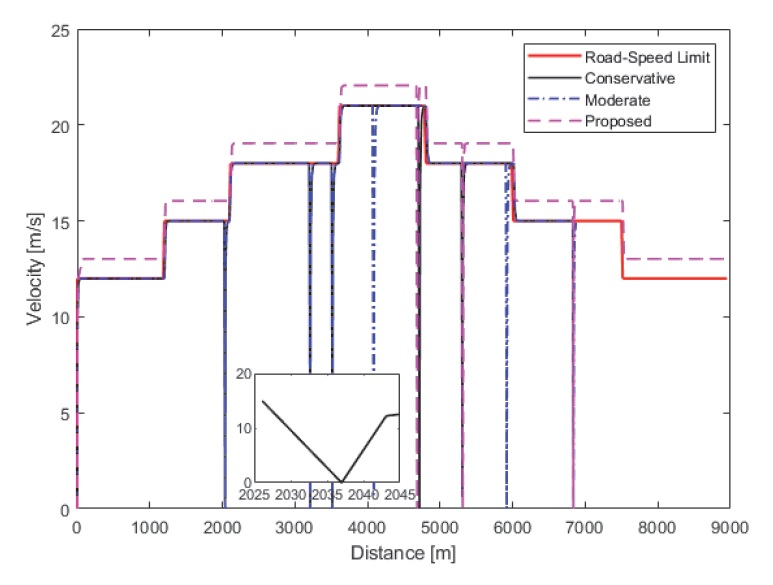
Fig. 10은 두번째 시나리오(Fig. 8)에서 거리에 따른 속도 결과를 보여주는데, 적색 실선은 속도 제한을 표현한 것이다.

Fig. 10

Velocity-space diagram in each of behaviors at third arrangement

그림에서 제안한 행동은 모든 구간에 걸쳐서 속도 제한을 준수하지 않는 결과를 보여주는데, 속도 제한 값에 따른 위반 정도가 다른 것은 상태 제약 조건을 느슨하게 만드는 여유 변수, ϵ값이 해당 제한 값과 연관되어 있게, 즉 도로 제한 속도의 10 %로 설정하였기 때문이다. 그 결과, 보수적인 운전자 행동인 유인 운전 차량은 속도 제한을 엄격히 준수하며, 적색 신호 구간일 때 정지하는 것을 확인할 수 있다. 예를 들어, 제안하고자 하는 행동은 5,000 m 부근에 위치한 신호등까지 과속하며 주행하다가 해당 신호등에서 처음으로 정지하는 것을 관측할 수 있다. 그 다음으로 2번 정도 더 정지하다가 종착 지점까지 연속하여 주행하는 것을 확인할 수 있다. 이와 반대로 비교군들은 신호등 앞에서 수시로 정지하며 제한 속도를 준수하는 결과를 얻을 수 있다. 또한, 부가적인 그래프에서 볼 수 있다시피, 0으로 튀는 값들을 관측할 수 있지만 실제로 튀는 값들이 아님을 볼 수 있다. 그 이유로 x축이 거리로 설정되어 있으므로 0으로 수렴하는 구간을 충분히 표현하지 못 할만큼 긴 거리로 설정되어 있기 때문이다.