등가정하중법을 이용한 비선형 동적 시스템의 파라미터 식별 및 모델 간소화
Copyright Ⓒ 2022 KSAE / 205-06
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
A parameter identification method of nonlinear dynamic systems is proposed. The error function of the finite element model is defined by the given input/output data and is minimized through structural optimization. In general, nonlinear dynamic response optimization is costly. This study uses the equivalent static load method to perform nonlinear dynamic response optimization for the identification. After identification is completed, the error function is reduced since the simulation value is close to the experimental value. Eventually, the finite element model becomes more accurate. The proposed method is applied to three numerical examples. The results indicate that the proposed method can minimize the model error through parameter identification.
Keywords:
Parameter identification, Structural optimization, Nonlinear dynamic response optimization, Equivalent static loads method, Finite element model키워드:
파라미터 식별, 구조최적설계, 비선형 동적 해석, 등가정하중법, 유한요소모델1. 서 론
자동차 차체 등의 설계와 다양한 제품의 설계 단계에서 유한요소법(Finite element method)이 점차 많이 활용되고 있다.1-4) 이에 따라서 성능이 우수한 유한요소모델(Finite element model)들을 효과적으로 제작하는 기법들이 요구된다. 구조최적화(Structural optimization) 분야는 최적화 이론을 유한요소해석 등의 컴퓨터 시뮬레이션과 접목한다.5-7) 일반적으로 연비 등을 중시하는 자동차 설계에서는 질량을 목적함수로 정의하고 최소화한다. 제한조건은 설계 목적에 따라서 유한요소해석의 각종 응답으로 정의될 수 있다. 최적화 과정에서는 민감도(Sensitivity)라는 일종의 기울기 함수가 필요하다. 민감도의 계산에는 미분 방정식 해결이 필요하기 때문에, 비선형/동적 해석을 고려한 최적화에서는 상당히 어려워질 수 있다.8) 그러므로 구조최적화는 주로 선형 정적 응답 최적화(Linear static response optimization) 분야가 잘 발전하였다.6) 그러나 자동차와 같은 실제 구조물은 비선형 동적 응답을 따르는 경우가 많다. 민감도를 직접 계산하지 않는 근사 최적화(Approximate optimization) 기법들이 있으나, 설계변수가 많을수록 근사모델 생성에 비용이 증가한다.9)
등가정하중법(ESLM, Equivalent static loads method)은 비선형 동적 응답 최적화(Nonlinear dynamic response optimization) 기법으로 대두되는 이론이다.10,11) 등가정하중(ESLs, Equivalent static loads)은 비선형 동적 해석의 결과로부터 얻어진 변위장(Displacement field)과 동일한 변위장을 이용하여 수학적으로 계산된다.12) 선형 정적 응답 해석에서 등가정하중을 외력으로 사용하였을 때, 비선형 동적 응답과 같은 변위가 얻어진다. 등가정하중법은 이를 활용하여 선형 정적 응답 최적화에서 비선형 동적 응답을 고려할 수 있다. 차량 충돌을 고려하는 등의 비선형 동적 응답 최적화를 수행하는 등가정하중법 연구들이 수행되어 왔다.11,13-15)
한편, 유한요소해석은 주어진 모델과 입력 데이터(Input data)로부터 출력 데이터(Output data)를 얻는 과정이다. 이와 반대로 알려진 바가 없는 미지의 시스템을 확인하기 위해 실험이나 경험 등에 의해 주어진 입/출력 데이터를 활용하는 역설계 문제도 있다. 시스템 식별(System identification)은 주어진 실험값(Experimental value)를 이용하여 시스템을 근사 수학 모델로 표현하는 방법이다.16-18) 모델의 해석값(Simulation value)이 실험값과 잘 일치하면 식별이 잘 수행된 것이다. 시스템이 알려져 있는 경우, 실험값과 해석값의 오차를 최소화하기 위해 종종 최적화 기법을 적용하기도 한다. 시스템의 파라미터를 결정하는 이러한 과정은 파라미터 식별(Parameter identification)이라고도 한다.
본 연구에서는 등가정하중법을 활용하여 비선형 동적 시스템의 파라미터 식별을 수행하는 방법을 제안한다. 기존 연구에서는 차량 충돌 문제에 대한 파라미터 식별 등을 적절하게 수행하고 파라미터를 결정하였으나, 미지의 시스템을 집중 질량 모델(Lumped mass model)로 간주하거나 시스템의 일부를 집중 질량 요소로 보았다.19,20) 제안한 방법에서는 기존의 유한요소법 이론이 이미 수학적으로 잘 정립된 이론1-4)에 근거하므로 유한요소를 변경하거나 단순화하지 않고 그대로 사용한다. 시스템의 식별이 이미 적절히 이루어진 것으로 간주한다. 비선형 동적 해석 결과가 주어진 실험값을 만족하도록 유한요소모델의 파라미터 식별을 수행한다. 비선형 동적 해석 결과를 최적화에서 고려하기 위해 등가정하중법을 활용한다. 제안한 방법은 세 가지 수치 예제에 적용된다. 첫번째는 간단한 평판으로 이루어진 예제이다. 제안한 방법으로 비선형 동적 시스템의 파라미터 식별이 가능함을 결과로부터 알 수 있다. 두번째는 차량 전방 구조물의 정면충돌 예제이다. 복잡한 비선형 응답을 갖더라도 해석값을 실험값에 잘 일치하도록 오차를 최소화한다. 세번째는 실제 유한요소모델이 주어져 있지 않는 배터리의 식별 예제이다. 예제의 결과는 시스템이 알려져 있지 않더라도 제안한 방법이 파라미터 식별을 통해 모델의 오차를 최소화할 수 있음을 보여준다.
2. 배경 이론
2.1 시스템 식별 및 파라미터 식별
현실 세계에서의 거동은 수학적으로 잘 표현되지 않는 복잡한 현상들이 많다. 유한요소법은 다양한 분야에서 활용되고 있으나, 유한요소모델도 근사모델이므로 실제 구조물의 거동을 완벽하게 나타낼 수는 없다. 그러나 유한요소 이론이 실제 구조물의 거동을 매우 유사하게 모사하는 이유는 수학적으로 잘 정립된 방정식을 활용하여 유한요소모델이 생성되기 때문이다.2)
시스템 식별은 미지의(Unknown) 시스템을 근사 수학 모델로 표현하고자 하며, 시스템과 상호작용하는 입/출력 데이터를 활용한다.18) 시스템은 다항함수 등으로 표현될 수 있으며, 시스템의 해석 결과와 주어진 데이터의 오차가 적을수록 시스템이 잘 식별된 것이다. 수학 모델에서 오차 e는 다음과 같이 표현된다.
| (1) |
b는 파라미터를 나타내며 Sgiven와 Smath는 각각 주어진 데이터와 수학 모델의 해석 결과를 가리킨다.
어떤 시스템이 수학 모델이 아니라 유한요소모델로 표현이 가능하다면, 식 (1)을 다음과 같이 다시 표현할 수 있다.21)
| (2) |
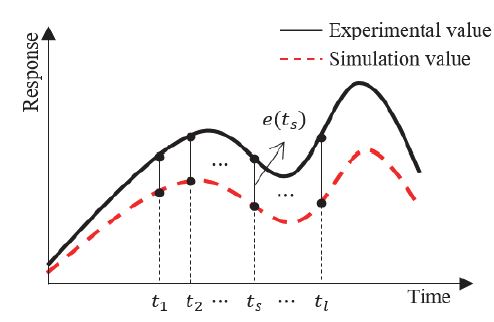
Sexp는 실험이나 측정 등을 통한 관찰에서 얻어진 구조물의 응답으로 실험값(Experimental value)으로 간주된다. Ssim는 모델의 해석 결과이며, 해석값(Simulation value)이다. 각각의 응답곡선과 오차를 Fig. 1에서 살펴볼 수 있다.
시스템에 대해 관심을 갖는 시간 영역이 0 ≤ t ≤ T로 주어진다면, 해석값의 오차도 해당 시간 영역에서 모두 고려되어야 한다. 오차방정식은 다음과 같이 정의될 수 있다.
| (3) |
오차방정식 f는 해당 시간 영역에서 두 응답곡선에 둘러쌓이는 면적을 나타낸다.
시스템의 식별을 유한요소모델의 생성 과정으로 대응했다면, 모델에서 요소의 크기나 재료의 영률과 같은 여러 파라미터들의 결정과정은 파라미터 식별에 해당된다. 해석 결과의 오차를 최소화함으로써 파라미터 식별을 할 수 있다.
2.2 등가정하중법
비선형 동적 응답을 고려하는 최적화 방법으로 등가정하중법(ESLM, Equivalent static loads method)을 간략하게 소개하고자 한다.10) 등가정하중법은 크게 해석영역(Analysis domain)과 설계영역(Design domain)으로 이루어진다. 해석영역에서는 비선형 동적 응답 해석이 먼저 수행된다. 해석 결과로부터 변위장을 산출하면, 이를 활용해서 등가정하중을 계산한다. 설계영역에서는 계산된 등가정하중을 활용하여 선형 정적 응답 최적화를 수행한다. 해석영역과 설계영역을 반복하는 과정을 설계주기(Design cycle)라 한다.
등가정하중은 다음과 같이 정의된다.
| (4) |
s는 시절점을 나타내며, l은 시절점의 수이다. 등가정하중 는 시간 ts에서 계산된 변위장 z(ts)을 사용하여 계산된다. KL은 비선형 동적해석에 사용된 모델과 동일한 모델의 선형화된 강성 행렬이다.12)
해석영역에서 계산된 등가정하중을 설계영역의 선형 정적 응답 최적화에서 다음과 같이 활용한다.
| (5) |
b는 설계변수 벡터이며, F(b)는 목적함수이다. zL는 선형 정적 응답의 변위이며, g(b, zL)는 부등제한조건(Inequality constraint)을 나타낸다. 계산된 등가정하중 들은 다중하중조건(Multiple loading cases)으로 동시에 처리된다.22) 선형 정적 응답 최적화가 완료되면, 설계변수를 갱신하고 수렴 조건을 확인한다. 만약 수렴하지 않으면 수렴할 때까지 설계주기를 반복한다.
기존의 일반적인 등가정하중법을 간략하게 소개하였다. 등가정하중법은 다양한 차량 충돌 문제에 적용하는 연구14,23-25)들이 진행되고 있으며, 상용소프트웨어에 탑재되어 있으므로 사용이 용이하다. 매우 적은 수의 비선형 해석만으로도 우수한 최적해를 제공하는 등의 장점도 크다. 그러나 아직까지 이론의 수학적인 근거에 대한 논란도 있다. 만약, 등가정하중법이 수렴한 경우에는 원래의 비선형 동적 응답 최적화 문제의 최적해를 보장할 수 있음을 보이는 등의 활발한 연구들이 지속되고 있다. 비선형 동적 응답을 고려하지만, 대부분은 변위 응답만을 고려하고 있는 점은 한계로 나타난다. 속도와 가속도 등을 고려하기 위해서 각 시절점의 변위의 차이를 이용하여 계산하는 방법 등이 있으나, 과정이 상당히 복잡해진다.24)
3. 파라미터 식별을 위한 등가정하중법 활용
등가정하중법을 활용하여 비선형 동적 시스템의 파라미터를 결정하는 방법을 제안한다. 알려진 데이터는 절점의 변위이며, δexp이다. 식별될 파라미터는 재료의 영률(Young’s modulus)과 쉘(Shell)의 두께 등이며, 비선형 동적 응답을 고려한 최적화에서 설계변수로 고려된다. 해석 결과로부터 산출된 절점의 변위는 δsim으로 표현된다.
파라미터 식별을 위한 최적화 과정에서 수렴을 빠르게 하고, 식별의 정확도를 높이기 위해 여러 절점의 변위를 동시에 고려한다. 그러므로 목적함수는 각 절점에서 계산된 오차들의 총합으로 한다. 비선형 동적 응답을 갖는 유한요소모델의 파라미터 결정을 위한 정식화는 다음과 같다.
| (6) |
b는 설계변수이며, 목적함수 f는 오차들의 합이다. p는 응답을 고려할 절점의 번호들을 나타내며 w는 고려한 절점들의 수이다. 는 절점 p에서의 실험값과 해석값을 나타낸다. 실험값은 변위에 해당하므로 비선형 동적 해석의 결과로부터 변위 Z로 직접 얻어진다.
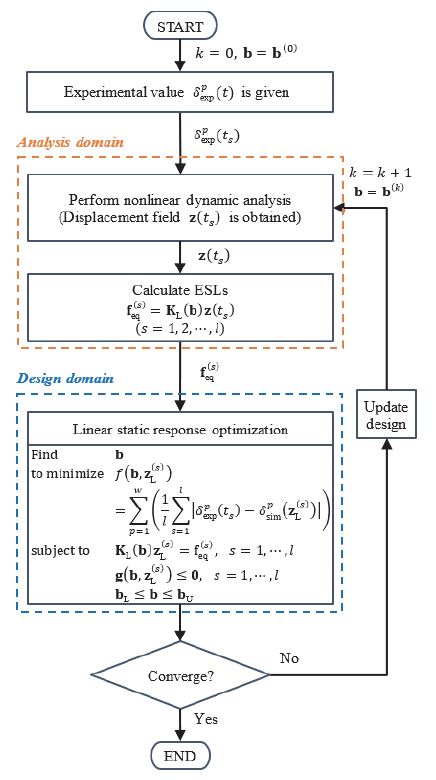
비선형 동적 응답 최적화로 표현된 파라미터 식별이 식 (6)으로 주어졌을 때, 제안하는 방법의 전체 흐름도는 Fig. 2에 나타나 있다. 시스템의 입/출력 데이터에 해당하는 실험값들이 주어져 있다고 가정한다. 먼저, 해석영역에서 비선형 동적 해석을 수행하고 결과로부터 변위 z(ts)를 산출해낸다. 여기서 등가정하중을 활용하기 위해 고려하는 시절점 t=ts에서만 응답을 산출한다. 그리고 식 (4)의 과정을 통해 등가정하중을 각 시절점에서 계산한다.
설계영역에서는 계산된 등가정하중을 활용하여 선형 정적 응답 최적화를 다음과 같이 수행한다.
| (7) |
등가정하중을 활용하기 위해 각 시절점에서만 응답들을 고려한다. 그러므로 오차방정식은 Fig. 1에 나타난 두 응답곡선이 둘러싼 면적이 아니라, 각 시절점에서 오차의 평균으로 재정의된다. 응답을 고려할 w개 절점에서 계산된 오차방정식의 총합이 목적함수이다. 제한조건으로는 각 응답들의 상/하한을 함께 고려했다.
각 세부 단계는 다음과 같이 요약된다.
- - Given: 시스템에 대한 유한요소모델과 입/출력 데이터가 주어져 있다. 실험값 가 함께 주어진다. 설계주기의 수는 k=0이다. 초기 파라미터 b=b(0)을 설정한다.
- - Step 1: 해석영역(Analysis domain)에서 비선형 동적 해석을 수행하고, 시절점 s=1,⋯,l에서 변위 응답 z(ts)들을 얻는다.
- - Step 2: 등가정하중 을 각 시절점에서 변위 응답 z(ts)을 활용하여 산출한다.
- - Step 3: 설계영역(Design domain)에서 선형 정적 응답 최적화를 수행한다. 외력으로 등가정하중을 다중하중조건으로 적용한다.
- - Step 4: 최적화 결과로부터 수렴조건을 확인한다. 수렴했으면 설계를 종료하고, 수렴하지 않았으면 설계주기 및 설계변수를 각각k=k+1, b = b(k)으로 갱신하고 Step 1으로 되돌아간다.
식별 이후에 해석 결과가 제한조건을 만족하고 오차도 잘 줄이면 식별이 잘 되는 것이다. 연구에서는 비선형 동적해석을 위해 LSTC(Livermore Software Technology Corporation)사의 LS-DYNA26)를 활용하고, 등가정하중 계산과 선형 정적 최적화 과정에는 Altair사의 OptiStruct27)를 활용한다.
4. 파라미터 식별 사례
4장에서는 세 가지 파라미터 식별 예제를 소개한다. 각 예제는 단순한 평판 구조물, 차량 전방 구조물, 전기차용 배터리 모듈에 대한 간소화된 모델의 파라미터 식별을 수행한다.
4.1 평판 구조물의 파라미터 식별
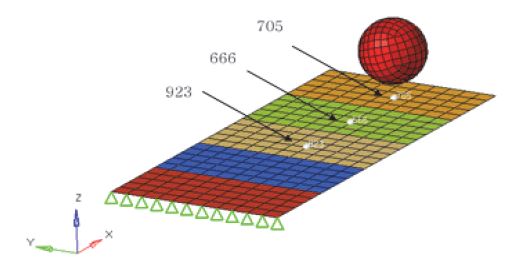
평판 구조물 예제에서는 Fig. 3에 그려진 구조물의 두께와 영률을 파라미터로 고려하고 식별한다. 평판의 한쪽은 고정되어 있고, 반대쪽은 강체 공과 충돌한다. 공의 속도는 50 mm/ms이다. 구조물의 길이, 폭, 두께는 각각 250 mm, 110 mm, 4 mm이며, 재료 특성은 밀도가 7830 ton/m3, 영률은 190 GPa, 푸아송비는 0.3이다.
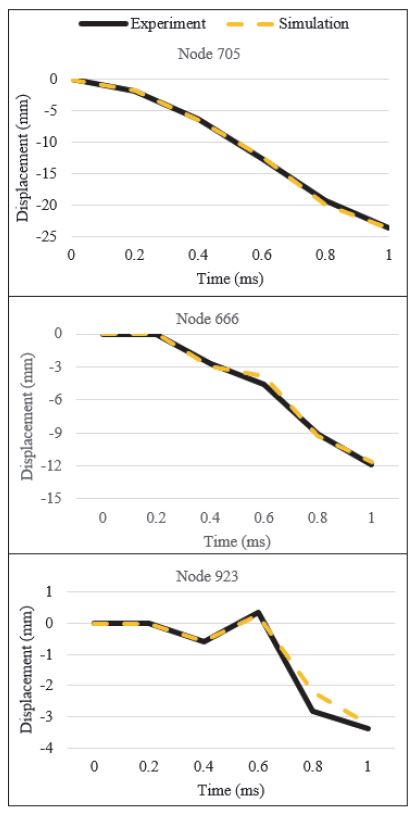
주어진 것으로 가정한 모델과 실험값은 Fig. 3의 모델과 약간 다른 실제 유한요소모델을 참고로 한다. 실험값을 제공하는 실험모델(Experiment model)의 두께는 5 mm, 영률은 207 GPa이다. 식별을 위한 응답으로 세 절점의 변위를 고려한다. 666번, 705번, 923번 절점들이며, 705번은 공과 최초로 맞닿는 절점이다. 주어진 실험값들은 Table 1에 정리하였다.
모델에는 다섯 개의 평판이 있다. 각 평판의 두께와 영률이 모두 파라미터이다. 식별을 위한 최적설계 정식화는 식 (7)을 활용한다. 최적화 전, 후의 각 파라미터의 값들이 Table 2에 나타나 있다. 최종 설계에서 세 절점의 변위가 Fig. 4에 비교되어 있다. 목적함수는 설계 결과에서 0.7이 되었다. 간단한 평판 구조물에 대해 제안한 방법을 통한 식별을 수행하였다. 등가정하중법을 이용하여 비선형 동적 해석 문제의 파라미터에 대한 결정이 가능하다는 것을 확인했다. 주어진 예제를 수행하는데 여섯 번의 설계주기가 반복되었으며 비선형 동적 해석도 여섯 번 수행되었다. 비선형 동적 응답 최적화를 위해 실험계획법이나 근사모델을 사용하는 경우와 비교한다면, 상당히 적은 횟수의 비선형 해석만을 요구한다.
4.2 전면충돌하는 차량 전방 구조물의 식별
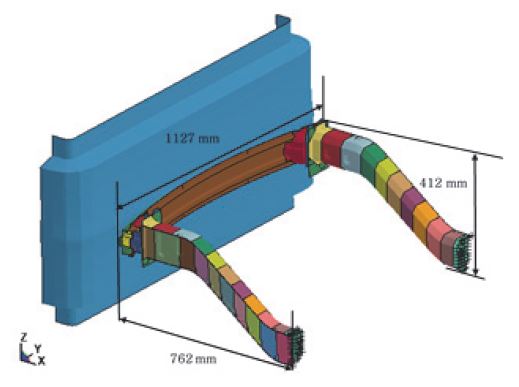
두번째 예제는 Fig. 5에 그려진 자동차 범퍼 구조물이다. 모델은 9045개의 절점, 8529개의 쉘 요소를 사용하여 29개의 부재로 구성된다. x, y, z 방향으로 각각 길이가 762 mm, 폭이 1127 mm, 높이가 412 mm이다. 왼쪽에 위치한 Pendulum이 2.2 m/s으로 범퍼에 충돌한다. 첫번째 예제와 마찬가지로 실험값은 주어진 모델의 파라미터들을 변경하여 생성한 실험모델의 해석 결과로부터 정의하였다.
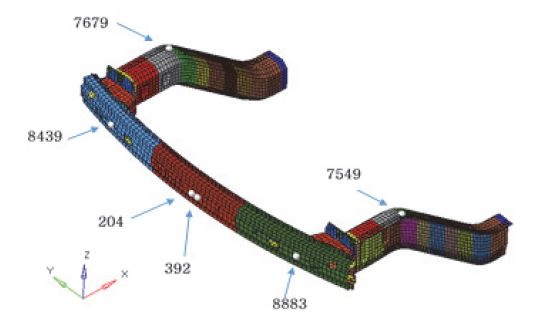
식별 문제는 Fig. 6에 표시된 여섯 개의 절점에서 x방향 변위의 오차를 최소화하도록 수행된다. 결정할 파라미터는 고정된 하나의 쉘을 제외한 28개 쉘 부재의 두께이다. 비선형 동적 응답 최적화는 식 (6)을 따르지만 제안한 방법에서는 등가정하중을 사용하므로 식 (7)을 사용한다.
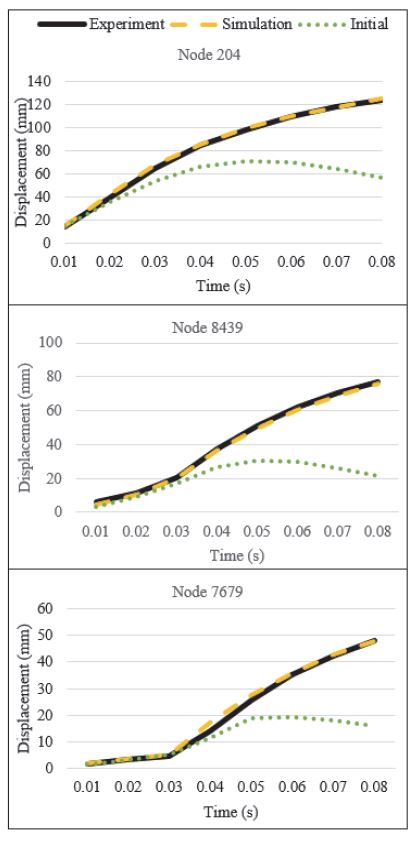
목적함수의 결과는 0.86으로 나타났고, 각 설계변수는 실험모델과 상당히 유사해진다. 오차가 매우 작아졌기 때문에, 여섯 개의 절점에서의 변위 응답들도 첫번째 예제처럼 실험값과 매우 유사해졌다. 대칭인 여섯 점들 중, 세 점의 변위가 Fig. 7에 나타나 있다. 대칭성으로 인해 나머지 세 점의 변위도 거의 같으므로 생략하였다. 두번째 예제를 통해 비선형성이 크면서, 모델의 규모와 설계변수의 수가 증가한 문제에서도 모델의 파라미터들을 잘 식별할 수 있음을 검증하였다.
4.3 배터리 모델의 파라미터 식별
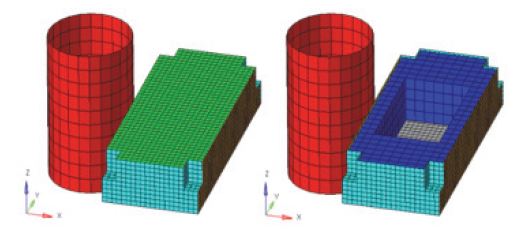
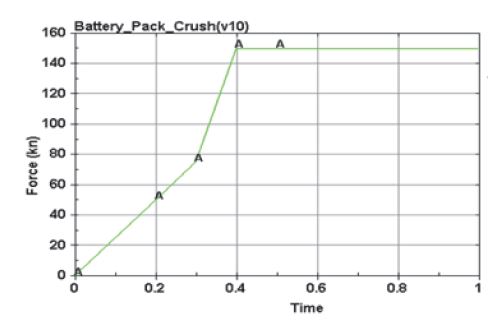
세번째 예제는 Fig. 8에 나타나 있는 전기자동차 배터리 모델을 식별한다. 실제 전기차의 배터리 모듈(Battery module)은 내부에 여러 개의 셀(Cell)로 들어차 있다. 그러나 Fig. 8의 모델에서는 모듈 내부를 상세히 생성하지 않고, 솔리드(Solid) 요소를 사용하여 간단하게 생성했다. 만일 주어진 실험값이나 관심 영역이 배터리 모듈의 겉면에서 일어나는 거동에만 초점을 맞추고 있다면, 모델 내부를 예제와 같이 단순화할 수도 있을 것이다.
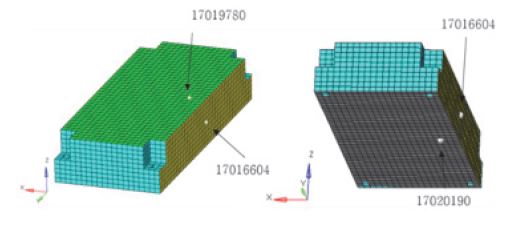
모델의 길이, 폭, 높이는 각각 395.4 mm, 173.7 mm, 76.1 mm이다. 설계에서 관심 영역이 아닌 배터리 모듈 안쪽은 Fig. 8의 오른쪽 그림에서 보이듯이 솔리드 요소를 사용해서 단순화되었다. 왼쪽 그림과 같이 윗면을 포함한 모든 겉면은 쉘 요소로 둘러싸여 있다. 지름 150 mm의 강체 기둥은 배터리를 측면에서 압축시킨다. 해석 시간은 1 s이며, 기둥에 작용하는 힘은 Fig. 9와 같다. 솔리드 요소의 영률은 6.97 GPa이고, 쉘 요소의 영률은 69.7 GPa이다. 쉘 요소는 알루미늄과 비슷한 재료이며 솔리드 요소는 10배 정도 무른 재질이다. 쉘의 두께는 모두 2 mm이다.
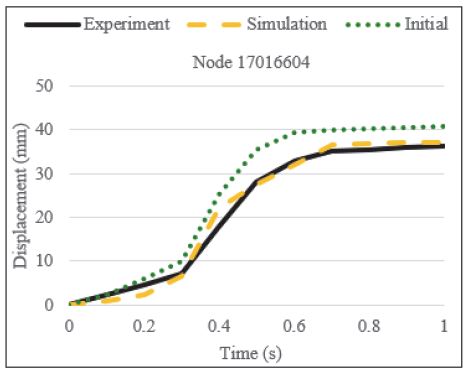
이전 예제들과 마찬가지로 주어진 유한요소모델과 유사한 실험모델로부터 가상의 실험값을 얻었다. 실험모델에서 솔리드 요소의 영률은 10.5 GPa이다. 모델의 식별에 고려하는 절점들은 Fig. 10과 같이 기둥에 접하는 면에 가까우면서 서로 다른 면에 위치한 세 개의 절점들이 채택되었다.
파라미터 식별 과정의 최적화에 대한 정식화는 동일하게 식 (7)을 이용한다. 시절점은 0.1 s부터 0.1 s마다 1 s까지 선택하여 총 10개를 고려한다. 충격을 받는 면과 반대쪽 면, 윗면과 아랫면까지 네 개의 쉘 부재에 대한 두께 및 영률을 파라미터로 고려한다.
목적함수 결과는 4.01로 나타났다. 설계변수의 초기값은 실험모델과 식별하는 모델이 서로 같다. 그러나 내부의 솔리드 요소가 서로 다른 영률을 갖기 때문에 초기에 변위는 크게 다르다. 기둥과 충돌하는 측면에 위치한 절점에서의 변위를 Fig. 11에 나타내 보였다. 이 예제는 내부에 가상의 솔리드 요소를 배치하는 것으로 유한요소모델을 간소화했고, 간소화된 모델을 사용하여 쉘 부재의 두께와 영률에 대한 파라미터 식별이 잘 이뤄짐을 보여주고 있다.
5. 결 론
본 연구에서는 비선형 동적 응답을 갖는 구조물의 미지 파라미터에 대한 식별 방법을 제안했다. 시스템이 갖는 오차를 표현하기 위한 오차방정식을 정의하고, 오차를 최소화하는 방법으로 파라미터를 결정하였다. 비선형 동적 응답을 고려하는 최적화 방법으로 등가정하중법을 활용하는 방법을 제시했으며, 4장에서는 세 가지 예제를 통해서 방법을 검증하였다.
기존의 시스템 식별을 이용한 유한요소모델 구성 방법들이 집중 질량 요소를 사용하여 시스템을 구현한데 반해, 제안한 방법은 유한요소를 변경하거나 단순화하지 않고 비선형 시스템의 파라미터 식별을 수행한다. 따라서 시스템의 특성을 보다 잘 모사할 수 있을 것으로 사료되며, 식별된 모델의 해석 결과가 주어진 입/출력 데이터와 상당히 일치하는 것이 예제들의 결과로부터 확인된다. 예제들의 목적함수는 식별하는 시스템이 갖는 응답과 실험값의 오차를 계산하는 과정에서 절대값을 사용하여 표현했지만, 설계자의 판단에 따라서는 편차의 제곱을 사용할 수도 있을 것이다. 최적화 알고리즘에 따라서는 절대값의 취급이 곤란할 수 있기 때문이다. 단, 변동의 폭이 큰 시스템의 응답에 대해서는 제곱항이 목적함수를 지나치게 증가시킬 수 있음을 고려해야 한다.
소개된 세 가지의 파라미터 식별 예제는 제안한 방법이 변위에 대한 오차를 상당히 줄어들게 할 수 있는 것으로 보이나, 오차가 0이 되지는 않는다. 따라서 얻어진 식별 결과가 완벽하다고 볼 수는 없다. 또한 비선형 동적 응답을 고려하여 파라미터 식별을 수행했는데, 비교적 간단한 구조물들을 통해서만 검증이 된 것이다. 예제보다 비선형성이 크고 요소가 많은 모델을 잘 식별할 수 있을지 연구가 필요하다. 또한 유한요소모델의 규모와 복잡성, 설계변수의 수, 고려할 응답의 종류와 수, 등가정하중 계산을 고려할 시절점의 위치나 수 등 다양한 요인에 따라 식별의 정확도가 달라질 수 있다.
그러나 제안한 방법은 실제 실험을 통해 응답을 확인하거나 직접 파라미터를 측정하는 것이 어려운 시스템을 식별하는데 여전히 유효한 방법이다. 비선형 동적 시스템의 변위 응답을 파라미터 식별에 직접 고려할 수 있는 것이 장점이다. 비선형 동적 응답 최적화를 위해 근사모델 등을 활용하는 일반적인 방법 대신, 등가정하중법을 사용하여 비교적 매우 적은 횟수의 실험 및 해석만 필요하다. 근사모델을 사용하지 않으므로 식별할 파라미터의 수에 해당하는 설계변수의 수에 대한 제약은 거의 없는 것과 같고, 유한요소모델의 정확성 및 해석 결과의 신뢰성이 근사모델보다 우수하다. 모델의 규모가 상당히 큰 경우에는 모델을 축소 또는 간소화하더라도 적용할 수 있음을 확인했다. 따라서 제안한 파라미터 식별 방법은 자동차의 충돌안전성능이나 내구성 예측과 같은 높은 정확도가 요구되는 동시에 복잡한 시스템의 파라미터 식별에 활용하기에 충분히 유용할 것이라고 기대된다.
Acknowledgments
이 연구는 2022년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20017248).
References
- O. C. Zienkiewicz, R. L. Taylor and J. Z. Zhu, The Finite Element Method: Its Basis and Fundamentals, Elsevier, 2005.
- K. -J. Bathe, Finite Element Procedures, Klaus-Jurgen Bathe, 2006.
- R. D. Cook, Concepts and Applications of Finite Element Analysis, John Wiley & Sons, 2007.
- J. N. Reddy, Introduction to the Finite Element Method, McGraw-Hill Education, 2019.
- G. J. Park, Analytic Methods for Design Practice, Springer Science & Business Media, Berlin, 2007.
-
J. S. Arora, Introduction to Optimum Design, Elsevier, Amsterdam, 2011.
[https://doi.org/10.1016/B978-0-12-381375-6.00004-8]

- R. T. Haftka and Z. Gürdal, Elements of Structural Optimization, Springer Science & Business Media, Berlin, 2012.
- K. K. Choi and N. -H. Kim, Structural Sensitivity Analysis and Optimization 1: Linear Systems, Springer Science & Business Media, 2004.
-
M. Avalle, G. Chiandussi and G. Belingardi, “Design Optimization by Response Surface Methodology: Application to Crashworthiness Design of Vehicle Structures,” Structural and Multidisciplinary Optimization, Vol.24, No.4, pp.325-332, 2002.
[https://doi.org/10.1007/s00158-002-0243-x]

-
Y. I. Kim and G. J. Park, “Nonlinear Dynamic Response Structural Optimization using Equivalent Static Loads,” Computer Methods in Applied Mechanics and Engineering, Vol.199, No.9-12, pp.660-676, 2010.
[https://doi.org/10.1016/j.cma.2009.10.014]

-
G. J. Park, “Technical Overview of the Equivalent Static Loads Method for Non-linear Static Response Structural Optimization,” Structural and Multidisciplinary Optimization, Vol.43, No.3, pp.319-337, 2011.
[https://doi.org/10.1007/s00158-010-0530-x]

-
B. S. Kang, W. S. Choi and G. J. Park, “Structural Optimization under Equivalent Static Loads Transformed from Dynamic Loads Based on Displacement,” Computers & Structures, Vol.79, No.2, pp.145-154, 2001.
[https://doi.org/10.1016/S0045-7949(00)00127-9]

-
A. Karev, L. Harzheim, R. Immel and M. Erzgräber, “Free Sizing Optimization of a Front Hood using the ESL Method: Overcoming Challenges and Traps,” Structural and Multidisciplinary Optimization, Vol.60, No.4, pp.1687-1707, 2019.
[https://doi.org/10.1007/s00158-019-02285-9]

-
Y. M. Lee, Y. H. Han, S. O. Park and G. J. Park, “Vehicle Crash Optimization Considering a Roof Crush Test and a Side Impact Test,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.233, No.10, pp.2455-2466, 2019.
[https://doi.org/10.1177/0954407018794259]

-
J. Triller, R. Immel, A. Timmer and L. Harzheim, “The Difference-based Equivalent Static Load Method: An Improvement of the ESL Method’s Nonlinear Approximation Quality,” Structural and Multidisciplinary Optimization, Vol.63, No.6, pp.2705-2720, 2021.
[https://doi.org/10.1007/s00158-020-02830-x]

-
R. Ghanem and M. Shinozuka, “Structural-System Identification. I: Theory,” Journal of Engineering Mechanics, Vol.121, No.2, pp.255-264, 1995.
[https://doi.org/10.1061/(ASCE)0733-9399(1995)121:2(255)]

-
L. Ljung, System Identification, In Signal Analysis and Prediction, Springer, pp.163-173, 1998.
[https://doi.org/10.1007/978-1-4612-1768-8_11]

-
K. J. Keesman, System Identification: An Introduction, Springer, 2011.
[https://doi.org/10.1007/978-0-85729-522-4]

-
C. Kim and J. S. Arora, “Development of Simplified Dynamic Models using Optimization: Application to Crushed Tubes,” Computer Methods in Applied Mechanics and Engineering, Vol.192, No.16-18, pp.2073-2097, 2003.
[https://doi.org/10.1016/S0045-7825(03)00242-1]

-
W. Pawlus, H. R. Karimi and K. G. Robbersmyr, “Development of Lumped-parameter Mathematical Models for a Vehicle Localized Impact,” Journal of Mechanical Science and Technology, Vol.25, No.7, pp.1737-1747, 2011.
[https://doi.org/10.1007/s12206-011-0505-x]

-
K. W. Lee, T. H. Chong and G. -J. Park, “Development of a Methodology for a Simplified Finite Element Model and Optimum Design,” Computers & Structures, Vol.81, No.14, pp.1449-1460, 2003.
[https://doi.org/10.1016/S0045-7949(03)00084-1]

-
W. S. Choi and G. J. Park, “Structural Optimization using Equivalent Static Loads at all Time Intervals,” Computer Methods in Applied Mechanics and Engineering, Vol.191, Nos.19-20, pp.2105-2122, 2002.
[https://doi.org/10.1016/S0045-7825(01)00373-5]

-
W. H. Choi, Y. M. Lee, J. M. Yoon, Y. H. Han and G. J. Park, “Structural Optimization for Roof Crush Test using an Enforced Displacement Method,” Int. J. Automotive Technology, Vol.19, No.2, pp.291-299, 2018.
[https://doi.org/10.1007/s12239-018-0028-x]

-
J. M. Yoon, Y. M. Lee, S. O. Park, Y. H. Han and G. J. Park, “Crash Optimization Considering the Head Injury Criterion,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.233, No.11, pp.2879-2890, 2019.
[https://doi.org/10.1177/0954407018809298]

-
M. -H. Jeong, Y. -I. Kim and G. -J. Park, “Nonlinear Dynamic Response Structural Optimization for the Structure Integrating the Body-In-White and Battery Pack of an Electric Vehicle Considering a Side Pole Impact Test,” Transactions of KSAE, Vol.29, No.7, pp.683-691, 2021.
[https://doi.org/10.7467/KSAE.2021.29.7.683]

- J. O. Hallquist, LS-DYNA Theory Manual, 2006.
- Altair, Hyperworks 2020 User’s Manual, 2020.