자동 변속기 시스템에서 비틀림 진동 저감을 위한 토크 컨버터 원심 진자 댐퍼 성능 해석에 관한 연구

1. 서 론

자동 변속기 차량 동력 전달계에서 발생되는 비틀림 진동은 엔진에서 발생하는 토크 변동 성분이 가진원으로 작용하여 구동계에 전달되는 과정에서 발생한다. 특히, 연비 향상과 효율 증대를 위해 토크 컨버터 내부에 장착된 록업 댐퍼로 인해 직결되어 전달된 변동 토크가 자동변속기에 전달되어 NVH 문제를 발생시키며, 차량의 구조 수명에 영향을 일으킬 수 있다.

차량 운전자의 정숙성 및 안락한 승차감에 대한 욕구가 높아지고 차량 경량화, 토크 증대, 다운사이징, 복잡한 기어박스 구조 등 구동계 및 차체 진동에 현저히 불리해지면서 토크 컨버터의 기존 1단 록업 댐퍼는 한계에 도달했으며, 터보차저 엔진의 높은 배기량에는 충분하지가 않다. 이를 극복하기 위해 직렬 2단 스프링에 원심 진자가 장착된 시스템에 대한 개발이 이루어지고 있다. 특정 주파수가 아닌 전 운전 주파수 영역에서 댐핑 성능을 가지는 원심 진자는 수십 년 전에 발명되어 연구가 진행되고 있다. 비틀림 진동을 줄이기 위해 제작된 항공기 엔진의 크랭크축으로 회전하는 원심진자 연구,¹⁾ 고성능 항공기의 비선형 진동 감소를 위해 비필라형 진자 흡진기에 관한 연구,²⁾ 왕복 4기통 엔진 크랭크축 진자 흡진기에 관한 연구,³⁾ 입력 토크 균형을 맞추기 위해 설계된 캠 기반 원심 진자 흡진기에 관한 연구,⁴⁾ 원심 진자의 최적 공진 조율에 관한 연구,⁵⁾ DMF가 장착된 차량 시스템에서 원심진자에 관한 연구⁶⁾ 등 여러 연구가 이루어지고 있다.

본 연구는 직렬 2단 스프링에 원심 진자가 장착된 시스템에서 차량 주행 시 발생한 문제를 해결하기 위하여 모달해석을 근거로 주행 시 발생되었던 문제를 해석적으로 접근하여 설계 변수를 제안하였다.

2. 본 론

2.1 구동계 시스템 비틀림 진동

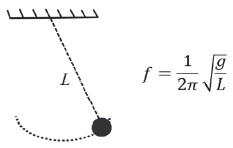
Fig. 1은 거리(L)와 중력(g)에 따라 변하는 진동 주파수를 가지는 푸고진자(Foucault pendulum)를 나타낸다. 회전기계에서 중력에 의해 주어지는 가속도는 구심 가속도 Rω²로 대체되며, 여기서 ω는 회전 속도이다.

Fig. 1

Foucault’s pendulum

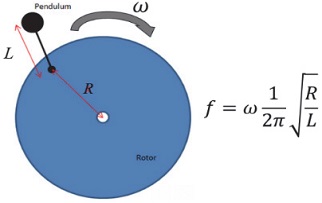
Fig. 2에서 알 수 있듯이, 원심 진자의 고유 진동수는 항상 회전 속도 ω에 비례한다. 따라서 알맞은 R과 L를 선택을 함으로써 엔진 폭발 오더의 고유 진동수와 반대의 위상을 가지는 원심 진자 흡진기를 얻을 수 있다. 즉, 원심 진자의 공진 조율 오더는 진자의 길이와 반경을 조율하여 엔진 오더에 맞게 설정할 수 있다.

Fig. 2

Centrifugal pendulum

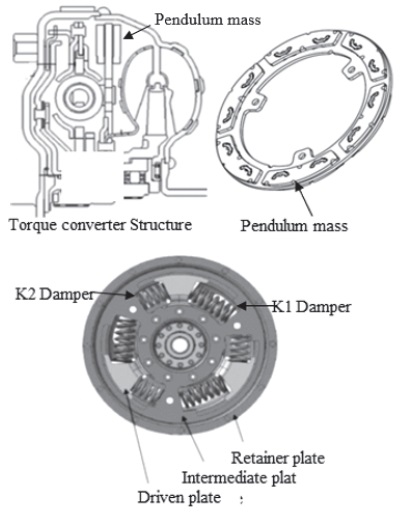
본 연구를 위해 고려된 차량은 후륜으로 8단 자동 변속 장치와 최대 엔진 토크가 440 Nm인 4기통 가솔린 엔진이 장착된다. Fig. 3에 표시된 토크 컨버터 진자 흡진기의 구조는 기존의 펌프, 스테이터 및 터빈 구성 요소로 이루어지며, 원심 진자는 두 개의 댐퍼를 연결하는 중간 플레이트에 장착된다. Retainer plate에 전달된 엔진 동력이 Drive plate, K1 Damper, Intermediate plate, K2 Damper 순으로 전달되며, 두 개의 댐퍼가 직렬 작동되어 낮아진 등가 강성으로 더 나은 필터링이 가능하게 된다.

Fig. 3

Torque converter pendulum

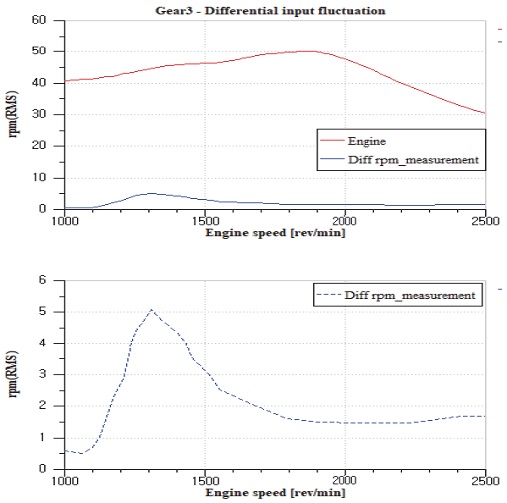
Drive조건에서 엔진측 플라이휠과 디퍼렌셜 입력에 비접촉 자기 센서를 통해 받은 측정 신호는 상용 진동 분석 장비인 LMS Test. Lab으로 입력된다. 비틀림 진동을 분석하기 위해 계측된 값은 0~200 Hz 저주파 필터를 적용 후 회전속도에 따른 차수 분석을 실시하여 Fig. 4와 같이 엔진의 입력 각속도에 대한 디퍼렌셜의 각속도 크기를 산출하였다. 디퍼렌셜 속도 변동 값이 통상적으로 본 연구에 차량의 개발 목표수준인 각속도 변동량 4 rpm(RMS)이상으로 부밍 소음이 발생되었다. 본 연구에서는 원심 진자 흡진기의 주 작동 구간인 2,000 rpm 이하에서 이상진동이 발생한 원인을 조사하고 속도 변동을 줄이기 위한 매개 변수를 제안하였다.

Fig. 4

Torsional vibration level from measurement

따라서 본 연구의 구성 내용은 다음과 같다.

• - 상용 파워트레인 해석 프로그램인 AMESim을 이용하여 수치 계산을 수행하기 위한 드라이브 라인 모델링을 구축하였다.
• - 시스템 모달 해석을 통해 이상 진동에 대한 원인을 분석하였으며, 동력전달계의 고유진동수과 비틀림 진동 수준을 검토하여 저속에서의 비틀림 진동을 감소시키는 영향 계수에 대한 연구를 수행하였다.
• - 비틀림 진동이 감소될 수 있는 원심 진자 흡진기가 장착된 직렬 2단 강성 토크 컨버터에 대한 설계 변수를 제안하였다.

2.2 시스템 모델링 및 모달 해석

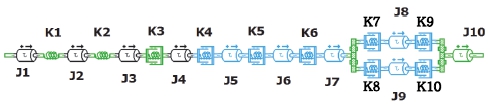
리어 휠 구동은 자유도에 의해 관성의 질량 모멘트와 비틀림 강성에 의해 Fig. 5와 같이 모델링 된다. 차량의 뒷바퀴를 구동하기 위해 엔진 및 기어박스에서 추진축으로 전달된 다음 디퍼렌셜 및 리어휠로 전달된다.

Fig. 5

Amesim modal analysis model

펌프와 연결된 엔진 크랭크축의 관성은 하나의 질량으로 간주하였다. 록업 댐퍼 1단과 2단 스프링 강성은 중간 플레이트에 의해 상호 연결되며 중간 플레이트에 원심 진자가 장착된다. 기어박스는 각 단별 기어 관성, 구동 및 종동축으로 구성되어 있으며, 각각의 기어를 하나의 관성 모델로 등가 시킨 단일 질량 시스템으로 모델링하였다. 유성기어박스, 출력축 및 관련 회전 부품은 각각의 기어비를 고려하여 하나의 관성 모델로 등가 하여 모델링하였다. 리어 디퍼렌셜은 강성에 의해 연결된 입력 및 출력 질량으로 모델링되며, 리어 디퍼렌셜 기어비가 이 구성 요소에 고려된다. 좌측 및 우측 휠 타이어 시스템은 구동축 강성에 의해 디퍼렌셜과 연결된다. Table 1은 10자유도 각각에 대한 부품명을 나타낸다. 다자유도에 대한 운동방정식은 다음과 같이 작성된다.

$\[ J\ddot{x}+C\dot{x}+Kx=F \]$

$\[ X={\left[{\theta }_1 {\theta }_2 {\theta }_3 {\theta }_4 {\theta }_5 {\theta }_6 {\theta }_7 {\theta }_8 {\theta }_9 {\theta }_{10}\right]}^{\text{T}} \]$

Table 1

Parameter of the vehicle

구성 요소의 각 부품 관성은 J₁, J₂, ..., J₉, K₁, K₂, ..., J₁₀는 회전 스프링 상수, θ₁, θ₂, ..., θ₁₀는 각 요소의 각도 변위, F는 토크 벡터, 위첨자 T는 전치행렬을 나타낸다. x는 각도 변위 벡터, J는 관성 행렬, C는 댐핑 행렬이다.

질량 행렬은 다음과 같이 표현된다.

$\[ J=\left[\begin{array}{cccccccccc}{J}_1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& J_2& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& J_3& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& J_4& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& J_5& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& J_6& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& J_7& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& J_8& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& J_9& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& J_{10}\end{array}\right] \]$

강성 행렬은 다음과 같이 표현된다.

$\[ \text{K}=\left[\begin{array}{cccccccccc}{K}_1& {-K}_1& 0& 0& 0& 0& 0& 0& 0& 0\\ -K_1& \left(K_1+K_2\right)& -K_2& 0& 0& 0& 0& 0& 0& 0\\ 0& -K_2& \left(K_2+K_3\right)& -K_3& 0& 0& 0& 0& 0& 0\\ 0& 0& -K_3& \left(K_3+K_4\right)& -K_4& 0& 0& 0& 0& 0\\ 0& 0& 0& -K_4& \left(K_4+K_5\right)& -K_5& 0& 0& 0& 0\\ 0& 0& 0& 0& -K_5& \left(K_5+K_6\right)& -K_6& 0& 0& 0\\ 0& 0& 0& 0& 0& -K_6& \left(K_6+K_7+K_8\right)& -K_7& -K_8& 0\\ 0& 0& 0& 0& 0& 0& -K_7& \left(K_7+K_9\right)& 0& -K_9\\ 0& 0& 0& 0& 0& 0& -K_8& 0& \left(K_9+K_{10}\right)& -K_{10}\\ 0& 0& 0& 0& 0& 0& 0& -K_9& -K_{10}& \left(K_9+K_{10}\right)\end{array}\right] \]$

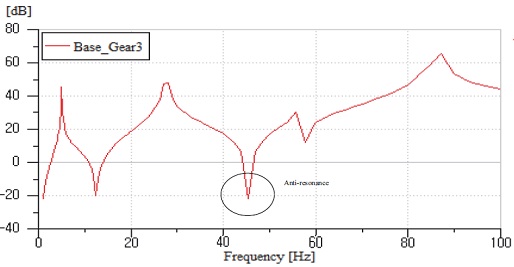
모든 구성 요소의 감쇠 없이 선형 모달 분석을 수행하여 Table 2와 같이 고유 주파수를 얻었지만 기어 3단 조건에서 1,300 rpm대역의 저조한 성능에 대해서 설명할 수 있는 고유 주파수가 존재하지 않았다. Fig. 6과 같이 중간 플레이트의 입력 토크와 가속 출력 사이의 주파수 응답 함수(FRF)를 확인했을 때 45 Hz에 반공진 주파수가 있었으며, 부밍 소음 발생 지점과 근접한 것을 알 수 있었다.

Table 2

Resonance frequency in drive condition

Fig. 6

Frequency response function

2.3 구동계 시스템 해석

2.3.1 주행 해석 검토

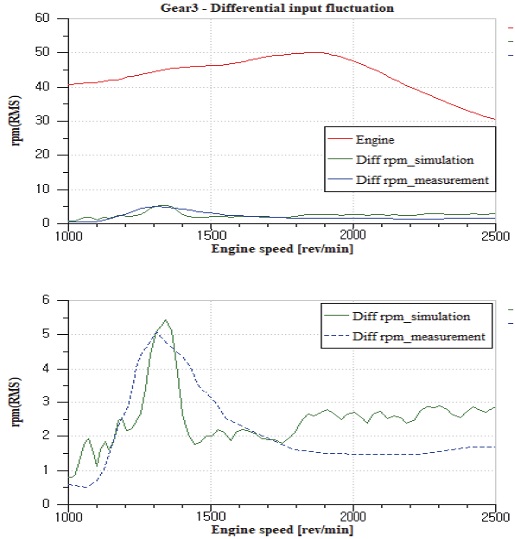
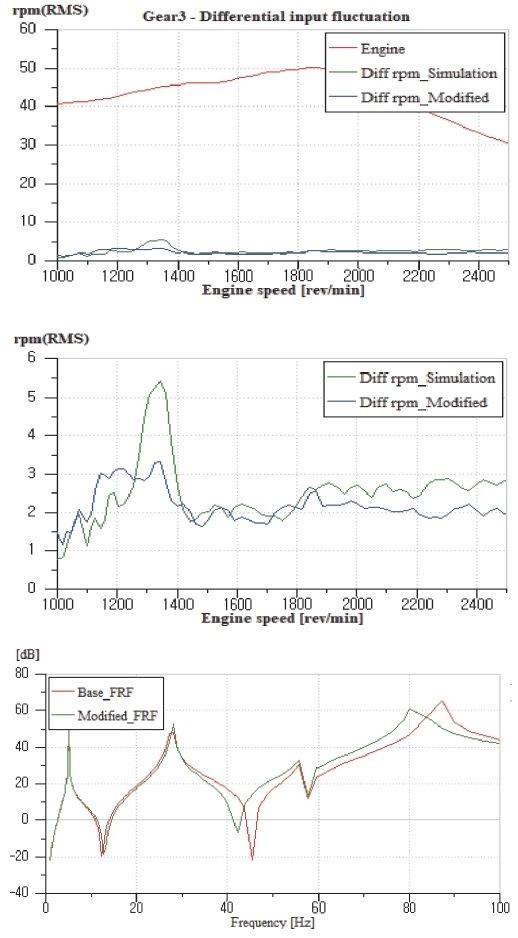
댐퍼의 히스테리시스와 각 구성 요소의 댐핑을 고려한 모델링 및 해석을 수행하였다. 구동계 시스템의 가진력인 엔진 입력 토크는 실제 차량에서 계측된 각속도 값을 토크로 산출하여 적용하였다.⁷⁾ 실차 계측과 해석 결과의 진동 값을 Fig. 7에 나타내었으며, 해석 결과 1,350 rpm엔진 속도에서 각속도 변동값 5.5 rpm(RMS)수준으로 실차 계측 결과와 동일한 영역대에서 부밍 진동이 발생한 것을 확인하였다.

Fig. 7

Correlation result of torsional vibration level

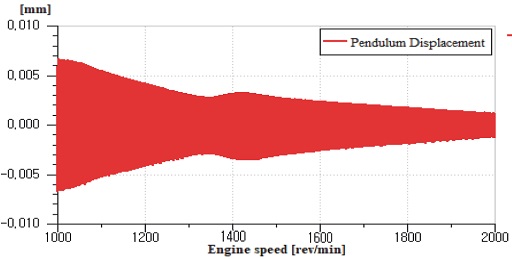
엔진 속도에 따른 원심진자의 작동 변위는 Fig. 8에 나타내었다. FRF에서 확인된 반공진 지점인 1,350 rpm에서 원심진자의 작동 변위가 감소되면서 필터링 성능이 떨어진 것으로 판단된다.

Fig. 8

Pendulum displacement during run-up

2.3.2 원심 진자 흡진기 특성 검토

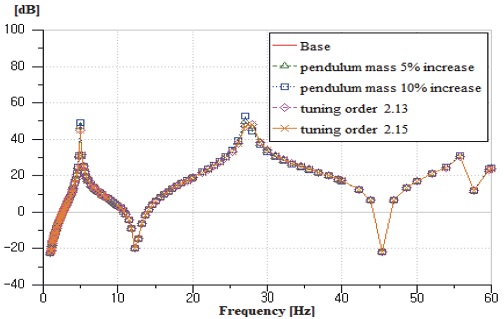
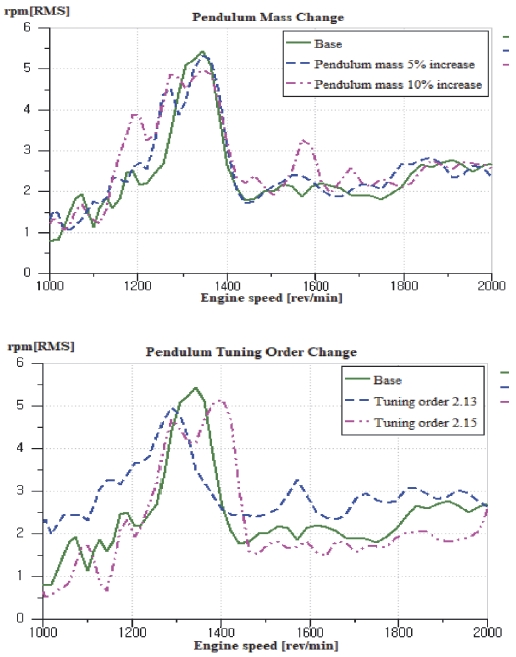
원심 진자 댐퍼의 성능을 개선하기 위해 원심진자 무게, 공진 조율 오더에 대한 해석을 수행하였다. Fig. 9는 원심진자 무게와 공진 조율 오더 변화에 따른 FRF결과이다. 원심진자 무게와 공진 조율 오더는 반공진주파수에 영향을 미치지 않았다. Fig. 10은 원심진자 무게와 공진 조율 오더 변화에 따른 후륜 디퍼렌셜측의 비틀림 진동 수준이다. 저속에서 발생된 반공진에 의한 부밍은 원심 진자의 작동 성능에 영향을 주었으며 원심 진자의 개선으로 목표 속도 변동을 충족하기에는 충분하지 않음을 알 수 있었다.

Fig. 9

FRF result by pendulum parametric variation

Fig. 10

Torsional level by pendulum parametric variation

2.3.3 록업 댐퍼 특성 검토

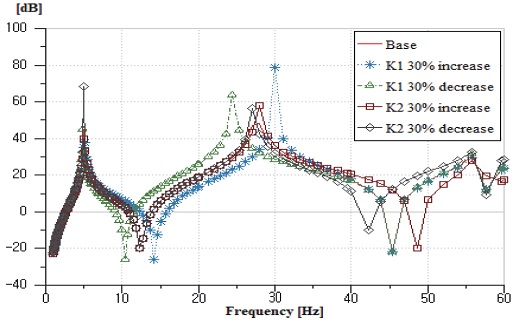
Fig. 11은 록업 댐퍼의 강성에 따른 FRF결과이다. K1 강성은 댐퍼모드의 공진 주파수에 영향을 미치지만 반공진점 위치는 45 Hz로 고정된다. K2 강성 변경시 반공진 주파수가 이동하는 것을 확인할 수 있었다. 두 개의 댐퍼가 직렬로 작동되기 때문에 토크 용량을 유지한 채 K2 강성만 변경이 불가하다. 따라서 설계 허용 범위내 토크 용량을 만족하는 K1과 K2의 강성비 조합을 산출하기 위해 설계 변수를 설정하였다.

Fig. 11

FRF result by damper stiffness variation

토크 용량을 만족하는 댐퍼의 등가 강성은 20.2 Nm/deg이며, 1단과 2단의 강성비를 1에서 5까지 0.25 간격으로 범위를 설정하였다. 강성비에 따른 강성값을 Table 3에 나타내었다.

$\[ 1,\mathrm{ }2\mathrm{단}\mathrm{강}\mathrm{성}\mathrm{비}\mathrm{ }\mathrm{r}atio\left(K2/K2\right)=1:5:0.25 \]$

(1)

$\[ \mathrm{등}\mathrm{가}\mathrm{ }\mathrm{강}\mathrm{성}\mathrm{ }{K}_{eq}=20.2Nm/deg \]$

(2)

$\[ 1\mathrm{단}\mathrm{ }\mathrm{강}\mathrm{성}\mathrm{ }K1=K_{eq}\times \frac{\left(1+ratio\right)}{ratio} \]$

(3)

$\[ 2\mathrm{단}\mathrm{ }\mathrm{강}\mathrm{성}\mathrm{ }K2=ratio\times K1 \]$

(4)

Table 3

Damper spring at various condition

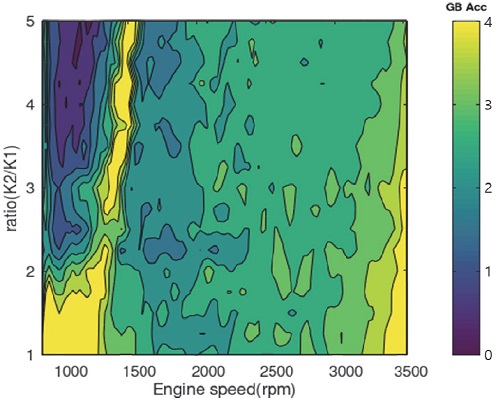
Fig. 12는 록업 댐퍼 강성비에 따른 엔진 속도당 디퍼렌셜 속도 변동량을 나타낸 등고선도이다. 개발 목표를 초과할 경우 노란색음영으로 나타냈으며, 1단과 2단의 강성비가 2.5일 때 목표수준을 만족하는 것으로 확인되었다. 만족하는 강성값을 Table 4에 정리하였다.

Fig. 12

Contour plot of DOE result

Table 4

Damper spring modification

3. 결 론

본 연구에서는 토크 컨버터 원심 진자가 장착된 자동변속기 후륜 구동시스템에서 고유치 및 동해석을 수행하였다. 주행평가를 통해 해석결과의 절연 성능을 비교하였으며, 해석 모델에 대한 검증을 하였다. 저속 범위에서 발생한 공진 문제에 대한 조사를 바탕으로 다음과 같은 결론을 얻었다.

• 1) 토크 컨버터 원심 진자가 장착된 자동변속기 후륜 구동시스템에서 고유치 및 동해석을 수행하였다. 주행평가를 통해 해석결과의 절연 성능을 비교하였으며, 해석 모델에 대한 검증을 하였다.
• 2) 선형 모달 분석 및 FRF로부터 직렬 2단 스프링에 원심 진자가 장착된 시스템에서 차량 주행시 저속에서 발생한 문제는 댐퍼의 반공진와 관련 있는 것으로 나타났다.
• 3) 원심 진자의 주요 파라미터인 중량 및 공진 조율 오더에 대한 연구결과 원심 진자의 수정만으로 개선은 제한적인 것으로 나타났다.
• 4) 반공진점 위치의 변경을 통해 진자 성능을 향상시킬 수 있었으며, 반공진점 위치 변경은 댐퍼 강성 변경에 의해 가능하다.
• 5) 댐퍼 강성에 대한 최적화 해석을 통해 개선된 필터링 결과를 Fig. 13에 보여준다.

Fig. 13

Improved pendulum performance

References

• E. S. Taylor, “Eliminating Crankshaft Torsional Vibration in Radial Aircraft Engines,” Technical Report, SAE 360105, 1936. [https://doi.org/10.4271/360105]
• D. E. Newland, Nonlinear Vibrations: A Comparative Study with Application to Centrifugal Pendulum Vibration Absorbers, Ph.D. Thesis, Massachusetts Institute of Technology, 1963.
• V. Borowski, H. Denman, D. Cronin, S. Shaw, J. Hanisko, L. Brooks, D. Milulec, W. Crum and M. Anderson, “Reducing Vibration of Reciprocating Engines with Crankshaft Pendulum Vibration Absorbers,” SAE 911876, 1991. [https://doi.org/10.4271/911876]
• A. S . Alsuwaiyan a nd S . W. Shaw, “Performance and Dynamic Stability of General-path Centrifugal Pendulum Vibration Absorbers,” Journal of Sound and Vibration, Vol.252, No.5, pp.791-815, 2002. [https://doi.org/10.1006/jsvi.2000.3534]
• C. Shi, R. G. Parker and S. W. Shaw, “Tuning of Centrifugal Pendulum Vibration Absorbers for Translational and Rotational Vibration Reduction,” Mechanism and Machine Theory, Vol.66, pp.56-65, 2013. [https://doi.org/10.1016/j.mechmachtheory.2013.03.004]
• Y. H. Jang, S. K. Jayachandran and S. K. Lee, “Study on Centrifugal Pendulum DMF Performance in Automotive Application during the Driving,” Transactions of KSAE, Vol.27, No.10, pp.771-776, 2019. [https://doi.org/10.7467/KSAE.2019.27.10.771]
• M. D. Hur and S. K. Lee, “The Research of Torsional Vibration Analysis for HF Application in Powertrain,” KSAE Symposium, pp.73-78, 2007.