다구치 기법을 이용한 디젤 기관 시뮬레이션의 최적화에 관한 연구

1. 서 론

효과적인 내연기관 시뮬레이션을 위해서는 기관의 각 부분에 대한 적절한 모델링이 선행되어야 하며 모델링에 포함된 적절한 상숫값들이 주어져야 한다. 이 상숫값들이 실험적으로 주어지게 된다면 이상적이지만, 실제의 경우에서는 그렇지 못한 경우가 대부분이다. 그래서 지금까지 진행한 연구에서는 해석에 필요한 상수를 결정할 때 프로그램에서 추천하는 값을 그대로 적용하거나 추천하는 값 주변으로 일정 범위 내의 상수를 선택하여 서로 조합한 후 모든 경우의 수를 시뮬레이션하는 방법을 사용하여 최적의 결과를 도출하였다.^1-7) 이 방법을 사용하게 되면 경우의 수가 너무 많이 발생하게 되고¹⁾ 연구에 따르는 시간과 경비의 증가로 이어지게 된다.

상수 결정에 따르는 경우의 수를 줄이면서 최적의 결과를 도출할 수 있다면 내연기관의 시뮬레이션을 수행하는 데 있어서 아주 효과적이라 할 수 있다. 정해진 실험 수를 줄이면서 최적의 결과를 도출하는 방법 중에 많이 사용되는 방법이 실험계획법(DOE: Design of Experiments)이다. 실험계획법은 문제를 해결하기 위해 문제에 직간접적으로 미치는 요인을 파악하고 그 인과관계를 수학적 관계식으로 규명한 후 이 수학적 관계식을 활용하여 문제를 효과적으로 해결하는 계획적인 활동을 의미한다. 효과적으로 활용 가능한 실험계획법은 실험의 결과물이라 할 수 있는 특성치와 특성치에 영향을 주는 요인에 따라 요인배치법, 분할법, 교락법, 일부 실시법, 불완전 블럭계획법, 반응표면계획법 등 다양한 방법이 존재한다.^8-10)

요인배치법 중 하나인 다구치 기법(Taguchi method)은 손실함수의 개념을 도입해 특성치의 특성에 따라 다른 손실함수를 사용하며, SN비(Signal to Noise ratio)를 사용하여 특성치의 최적값을 도출할 수 있게 하는 방법이다. 특히 직교배열표(Orthogonal array)를 적극적으로 활용하여 실험수를 획기적으로 줄여 인자의 수가 많아 경우의 수가 많아지는 실험에 적용을 할 경우 효과적인 방법이다.^10-12) 이러한 다구치 기법은 다양한 분야에서 활발히 활용되고 있으며 내연기관 및 차량의 개발에도 적용되고 있다.^13-15) 하지만 이들 대부분은 다구치 기법을 설계 변수를 찾는데 적용하고 있으며 상수 결정 방법으로서의 적용은 드물다. 아울러 다수개의 목적함수를 동시에 만족하는 최적 조합을 찾는 것이 아닌 각각의 목적함수에 대해 개별적 최적 조합을 찾는 것이 대부분이다.

본 연구에서는 선박용으로 사용하는 16기통 V형 디젤 기관을 대상으로 하여 내연기관 해석용 상용 시뮬레이션 소프트웨어인 AVL사의 BOOST를 이용하여 시뮬레이션을 수행하고자 한다. 일반적으로 기관에 대한 시뮬레이션은 실린더 내에서의 시뮬레이션과 흡⋅배기 계통에서의 시뮬레이션으로 나뉜다. 먼저 실린더 내에서의 시뮬레이션은 연소해석과 실린더 내에서의 열전달 해석으로 나뉘며 AVL사의 BOOST 프로그램은 디젤기관에 대한 연소해석의 경우 Wiebe Function Model, Double Wiebe Function Model, Woschni-Anisits Model, Hiroyasu et al Model, AVL MCC Model, 정압 연소 모델 등의 연소해석 모델을 제공한다. 그리고 열전달 해석의 경우 Woschni 1978 Model, Woschni 1990 Model, Hohenberg Model, Lorenz Model, AVL 2000 Model 등의 여러 모델을 제공한다. 본 연구에서는 여러 가지 연소해석 모델 중 실험에 의존하는 상수가 비교적 적고 현장에서 접근하기 용이하면서도 그 유용성이 널리 입증된 Wiebe Function Model⁵⁾을 적용하고자 하였다. 이 모델은 다른 모델들에 비해 실험 상수에의 의존이 적은 편이나 여전히 몇 개의 상수를 포함하고 있으며 이를 결정하는 것이 이 논문의 주요 목적 중 하나이다. 실린더 내 과정을 정확히 해석하기 위해서는 실린더의 상류 및 하류가 되는 흡⋅배기 계통에서의 정확한 유동 해석이 선행되어야 한다. 이를 위해 준정상 모델(Quasi-steady Model), Filling and Emptying Model 등이 제시된 바 있으나¹⁾ AVL BOOST에서는 관내에서의 시간 및 공간적 효과를 반영하여 압력파의 유동을 정확히 고려하여 반영하는 Wave Action Model을 제공하고 있다. 흡⋅배기 계통의 시뮬레이션은 다시 흡⋅배기관 자체에서의 유동해석과 각 관의 경계에서의 유동해석으로 나뉜다. 흡⋅배기관 내의 유동은 벽면과의 마찰, 단면적 변화, 열전달 및 엔트로피의 변화를 갖는 1차원 비정상 압축성 유동으로 간주하여 연속방정식, 운동방정식 및 에너지방정식을 유한체적법의 개념에 기초한 ENO Scheme을 사용하여 수치적인 해를 구한다.^16,17) 각 관의 경계에서의 유동해석은 여러 가지의 다양한 경계조건 – 대기와 접한 경계, 에어 클리너, 터보 과급기, 공기 냉각기, 단면적이 다른 관의 접속부, 여러 관들의 분기점, 흡기 및 배기 밸브를 통한 입출입 유동 등 - 에 대해 각각 적절한 모델을 설정하여 적용하였다. 이에 관한 상세한 설명은 저자들의 이전의 연구를 포함한 참고문헌^1-4,6,7)에 상세히 소개되어 있다.

대상 기관을 구성하는 각 계통에 대한 모델링은 이전의 연구를 통해 도출된 최적화된 모델링 방법을 적용한다. 실린더 최고압력과 제동평균유효압력(BMEP : Brake Mean Effective Pressure)에 주요한 영향을 미치는 연소 모델의 경우 디젤 기관의 시뮬레이션에 많이 사용되어 온 Wiebe Function Model^5,16,17)을 사용한다. 열전달 모델의 경우에서는 Woschni 1990 Model^16-19)을 적용한다.

본 연구에서는 이들 해석 모델에 포함되는 주요한 실험 상수들 중 연소모델에 포함되는 Wiebe 형상 계수(Wiebe Shape Parameter)와 연소지속기간(Combustion duration) 및 열전달 모델에 포함되는 열전달 보정 계수(Heat transfer multiplier)의 최적의 조합을 찾고자 한다.

지금까지는 이들 상수들을 BOOST에서 추천한 값을 기준으로 5가지 정도로 변화를 주고 조합하여 모든 경우의 수에 대해 시뮬레이션을 진행하여 목표값에 가장 근접한 값을 도출하는 상수들의 조합을 찾는 방법을 사용하였다.

본 연구에서는 이들 상수의 값을 정하기 위해 다구치 기법을 사용하고자 한다. 즉 주어진 운전조건에서 실린더 최고압력과 제동평균유효압력이 주어졌을 경우 이 두 인자들을 목적함수로 하여 주어진 목표값이 나오도록 하는 실험 상수들의 최적 조합을 찾고자 한다. 먼저 첫 번째 단계는 이전의 연구들에서 수행해왔던 방식으로서 가능한 모든 경우의 수에 대해 시뮬레이션을 수행하고 결과값을 도출한다. 이를 전역 탐색(Global search)이라 한다.

두 번째 단계는 다구치 기법을 적용하여 최적화된 인자의 조합을 찾는다. 다구치 기법을 적용할 때는 크게 두 가지 방법을 이용하여 결과를 찾고자 한다. 조합된 제어인자의 모든 수준을 한번에 탐색하는 일괄 탐색(Single-step search)과 탐색 범위 내의 몇 가지 수준에 대해 탐색한 후 영역을 좁혀 나가는 다단계 탐색기법(Multi-step search)을 사용하고자 한다. 특히 다단계 탐색 기법의 경우 주어진 범위 내에서 인자의 최적값을 탐색하는 고정 영역 다단계 탐색(Fixed-range multi-step search)과 함께 주어진 범위 밖으로도 범위를 확장하여 탐색하는 가변 영역 다단계 탐색(Variable-range multi-step search) 기법을 사용하여 최적의 결과를 도출하고자 한다.

이러한 연구를 통해 앞으로 새로운 기관의 개발이나 개선작업을 위해 기관 시뮬레이션을 할 때 미리 선정한 범위와 상관없이 최소의 실험을 통해 최적의 시뮬레이션 결과를 도출할 수 있는 새로운 연구 방법을 구축하고자 한다.

2. 기관 시뮬레이션 모델링

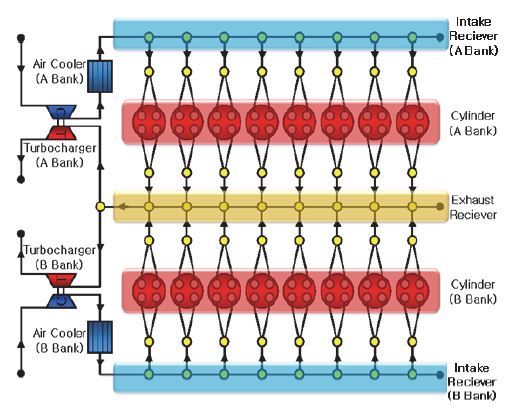
본 연구에서 대상으로 하는 기관은 Fig. 1에 나타낸 것과 같이 16개의 실린더를 갖는 선박용 V형 압축 착화 기관이다. 이 기관은 8개의 실린더가 그룹을 지어 각각 A-Bank와 B-Bank를 형성한다.

Fig. 1

Schematic diagram of 16-cylinder V-type engine

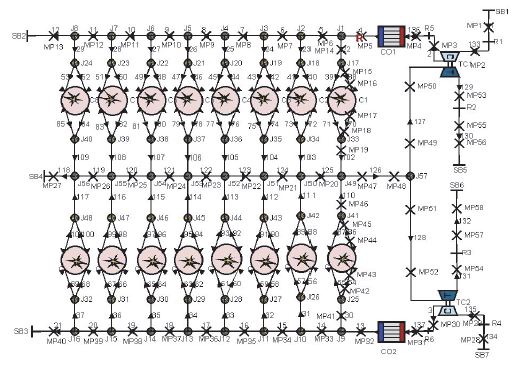
이 기관에서는 각각의 Bank에서 에어클리너를 통해 공기를 흡입한 후 터보과급기의 압축기와 공기 냉각기를 거쳐 흡기 Receiver로 유입하고 여기서 각 실린더로 연결되는 흡기 Runner로 분배된다. 실린더 직전에서 흡기 포트는 2개로 분기되어서 2개의 흡기 밸브를 통해 실린더로 유입한다. 실린더로부터 나오는 배기가스는 2개의 배기 밸브 각각에 연결된 배기 포트를 지나 한 개의 배기 러너로 연결되고 각각의 러너는 두 Bank에 공통된 하나의 배기 Receiver를 통해 터빈으로 유입한 후 배기관을 거쳐서 유출된다. Fig. 2는 BOOST에서 모델링한 기관의 모습을 나타내고 있다. 그림에 나타난 것처럼 흡기관계와 배기관계를 실제의 형상을 거의 그대로 반영하여 모델링하였다. 특히 흡기 리시버와 배기 리시버는 관들의 조합으로서 모델링하였으며 이 결과 총 132개의 관으로 구성되었다.

Fig. 2

Modeling configurations using AVL BOOST

3. 전통적인 방법 – 전역 탐색

실린더 최고 압력과 제동평균유효압력은 기관 성능의 척도라 할 수 있다. 이들에 영향을 미치는 인자들 중 가장 주요한 인자로서 Wiebe 형상 계수, 연소지속기간 및 열전달 보정 계수를 선정하였다.^5,7) 이 3가지 인자들을 BOOST에서 추천하는 값을 기준으로 하여 일정 범위 내에서 변화를 주면서 시뮬레이션을 시행하였다. 시뮬레이션의 결과값 중에서 실린더 최고 압력과 제동평균유효압력의 실험값과 계산값을 비교하여 최적의 결과를 도출하는 인자들의 조합을 찾는 동시에 인자들이 실린더 최고 압력과 제동평균유효압력에 미치는 영향을 파악하고자 하였다.

Wiebe 형상 계수를 0.8, 1.0, 1.2, 1.4, 1.6으로, 연소지속기간을 63°, 64°, 65°, 66°, 67°로 하였다. 마지막으로 열전달 보정계수를 0.5, 0.75, 1.0, 1.25, 1.5로 변화시키면서 종전의 연구에서와 같이 이들의 가능한 모든 조합인 125번의 경우에 대해 시뮬레이션을 진행하였다. 이를 전역탐색(Global Search)라 이름하였다. Table 1에 제어인자를 정리하였다.

Table 1

Summary of control variables

Fig. 3은 연소지속기간이 해당 기관에 대한 BOOST 추천 값인 67°인 경우 Wiebe 형상 계수와 열전달 보정계수의 변화에 따른 실린더 최고 압력과 제동평균유효압력을 계산한 값의 변화를 나타내고 있다. 이 논문에서 그림을 제시하지 않은 다른 연소지속기간의 경우와 함께 살펴보면 전체적인 경향은 열전달 보정계수가 커질수록 실린더 최고 압력은 작아지고, Wiebe 형상 계수가 커질수록 실린더 최고 압력은 역시 작아지는 것을 나타내고 있다. 제동평균유효압력은 열전달 보정계수가 커질수록, 또한 Wiebe 형상 계수가 커질수록 작아지는 것을 나타내고 있다.

Fig. 3

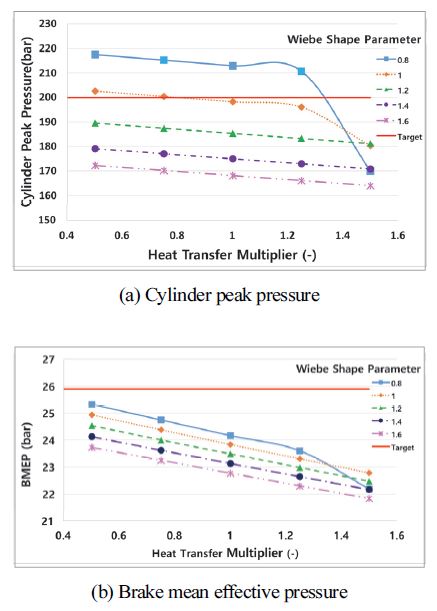
Effect of heat transfer multiplier and Wiebe shape parameter on the cylinder peak pressure and brake mean effective pressure(combustion duration 67 degrees)

Fig. 4는 연소지속기간이 실린더 최고 압력과 제동평균압력에 미치는 영향을 열전달 보정계수가 0.5인 경우에 대해 나타낸 것이다. 이 그림에서 연소지속기간이 증가함에 따라 실린더 최고 압력은 선형적으로 작아지는 경향을 보이고 제동평균유효압력 역시 미미하게 작아지는 경향을 보인다.

Fig. 4

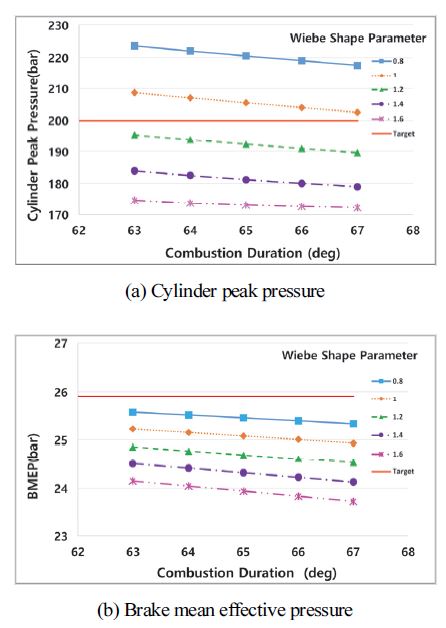
Effect of Wiebe shape parameter and combustion duration on the cylinder peak pressure and brake mean effective pressure(heat transfer multiplier 0.5)

Fig. 5는 Wiebe 형상계수가 실린더 최고 압력과 제동평균압력에 미치는 영향을 연소지속기간 67°인 경우 나타낸 것이다. 이 그림에서 모든 열전달 계수에서 Wiebe 형상계수가 증가함에 따라 실린더 최고 압력은 작아지는 경향을 보이고 제동평균유효압력 역시 선형적으로 작아지는 경향을 보인다.

Fig. 5

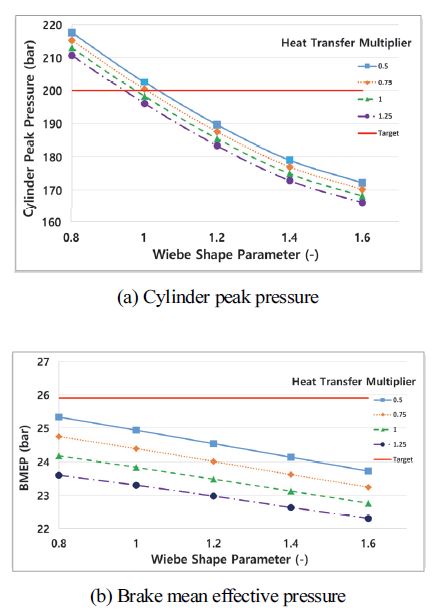
Effect of Wiebe shape parameter and heat transfer multiplier on the cylinder peak pressure and brake mean effective pressure(combustion duration 67 degrees)

이 그림들과 함께, 여기서 제시하지 않은 다른 경우들의 그림을 종합해서 분석하면 실린더 최대 압력에 가장 큰 영향을 미치고 있는 인자는 Wiebe 형상 계수이고 Wiebe 형상 계수가 증가 할수록 실린더 최대 압력은 감소한다. Wiebe 형상 계수는 최대 변화 범위 내에서 실린더 최대 압력은 약 25 % 정도의 영향을 미치고 있다. 두 번째로 영향을 미치고 있는 인자는 열전달 보정계수이고 선형적인 변화범위에서는 약 4 % 정도 내외의 영향을 미치고 있다. 연소지속기간은 최대 변화범위 내에서 약 2~3 % 정도의 영향을 미치고 있어 실린더 최대 압력에 미치는 영향은 작다. 제동평균유효압력에 가장 큰 영향을 미치고 있는 인자는 열전달 보정계수이고 열전달 보정계수가 증가할수록 제동평균유효압력은 감소한다. 열전달 보정계수의 최대 변화 범위 내에서 제동평균유효압력은 일정 구간동안은 약 9~13 % 정도의 영향을 미치고 있으며 선형 변화 구간에서는 8 % 내외의 영향을 미친다.

두 번째로 영향을 미치고 있는 인자는 Wiebe 형상 계수이고 최대 변화범위 내에서 약 6 % 정도의 영향을 미치고 있다. 연소지속기간의 경우 최대 변화범위 내에서 1 % 정도의 영향을 미치고 있다.

대상 기관에서의 최적의 조합을 찾아보면 실린더 최고 압력과 제동평균유효압력의 실험값에 접근하는 것은 열전달 보정계수가 0.5 부근이며, Wiebe 형상 계수는 1.0~1.2 부근, 연소지속기간은 66°부근인 것으로 나타난다. 실험값과 가장 근접한 조합은 Table 2와 같다.

Table 2

Optimal combination of factors using global search

4. 다구치 기법 적용 결과

최적화된 인자들을 찾는데 다구치 기법을 적용하게 되면 실험의 가지 수를 줄이면서 최적화된 인자들을 찾을 수 있다. 다구치 기법을 적용하는데 있어서는 전역탐색 방법과의 정확한 비교를 위해 우선 인자의 탐색 범위를 Table 1에 나타난 것으로 고정하였다. 이를 고정 영역 탐색(Fixed-range search)이라 한다.

이러한 탐색에는 하나의 직교배열표를 사용하여 전체 인자와 수준수를 한번에 적용하는 고정영역 일괄 탐색 방법(Fixed-range single-step search)과, 몇 단계에 걸쳐 범위를 좁혀가며 최적 인자를 찾아가는 고정영역 다단계 탐색 방법(Fixed-range multi-step search)을 설정하여 적용하였다. 이렇게 얻은 결과들을 앞에서 적용한 전역 탐색 방법을 통해 얻은 결과와 비교하였다.

이상의 과정을 통해 다구치 방법의 효용성을 검토한 후에는 다단계 탐색을 적용하면서, 인자를 미리 설정한 범위 내에서만 적용하지 않고 필요할 경우 범위 밖의 인자도 고려 대상에 넣어 보다 좋은 결과를 얻을 수 있는 가능성을 모색하였다. 이 방법을 가변 영역 다단계 탐색 방법(Variable-range multi-step search)이라 부른다.

이와 함께 목표값인 실린더 최고압력과 제동평균유효압력에 미치는 영향이 큰 인자들을 정량적으로 찾기 위해 분산분석법(ANOVA: ANalysis of VAriance)^11,12)을 활용하였다. 분산분석법을 이용해 나온 결과를 앞에서 나온 결과들과 비교하고자 한다.

목적함수는 실린더 최고압력과 제동평균유효압력이 최적화 결과의 유효성에 미치는 영향이 지배적임을 고려하여 이 두 개의 값을 목적함수로 선정하였다. 일반적으로 다구치 기법의 경우 한 개의 목적함수를 갖는 최적화 문제에 적용되기 때문에 두 개의 목적함수를 동시에 고려하여 다구치 기법을 적용하기 위하여 다음 식과 같이 실린더 최고압력과 제동평균유효압력의 예측에 대한 상대오차율의 평균을 손실함수로 정의하였다.

여기서, f(i)는 i번째 실험 결과에 대한 손실함수, p_c,i는 i번째 실험의 실린더 최고압력, p_c는 실린더 최고압력의 목표값(실험값), p_b,i는 i번째 실험의 제동평균유효압력, 그리고 p_b는 제동평균유효압력의 목표값(실험값)이다.

손실함수는 가급적 작은 오차를 가져야 하므로 망소특성(Smaller-the-better characteristics)을 가져야 한다. 망소특성의 SN비 계산식은 다음과 같다.^11,12)

여기서 y_i는 i번째의 특성값을 의미하며, n은 전체 자료값의 갯수를 의미한다.

4.1 고정 영역 일괄 탐색

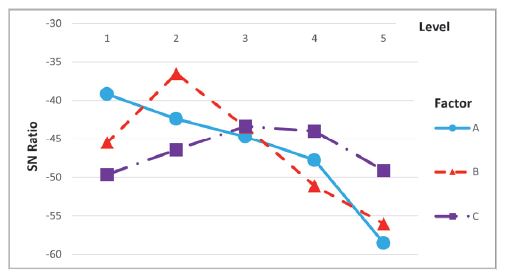
대상 기관의 경우 제어 인자는 3인자이며 인자에 따른 모든 수준은 5수준이다. Table 3은 고정 영역 일괄 탐색을 적용하기 위한 제어인자와 수준을 정리한 표이다. Table 3을 바탕으로 하여 고정 영역 일괄 탐색을 적용하기 위한 직교배열표를 Table 4에 나타내었다. 직교배열표를 바탕으로 계산하여 주효과도를 나타내면 Fig. 6과 같다. 이 그림에서 보면 가장 큰 값을 가지는 조건은 A인자의 경우 1수준에서, B인자의 경우에는 2수준에서, C인자의 경우에는 3수준에서 나타낸다.

Table 3

Control variables and control levels for fixed-range single-step search

Table 4

Orthogonal array table for global search

Fig. 6

Main effect diagram using fixed-range single-step search

고정 영역 일괄 탐색을 적용하여 수행한 실험 수는 총 25개이며, 이를 통해 나온 최적인자 조합은 A인자의 경우 0.5, B인자의 경우는 1.0, C인자는 65°라는 결과를 얻었다. 이 결과는 전역탐색을 통해 얻어내 결과 값 중 3순위에 해당하는 값으로 1순위의 조합과는 불과 0.45 %포인트의 차이를 나타나고 있다.

이어서 실린더 최고압력과 제동평균유효압력에 미치는 인자의 영향을 정량적으로 알아보기 위해 분산분석을 적용하였다. Table 5는 실린더 최고압력에 대한 분산분석표이며 Table 6은 제동평균유효압력에 대한 분산분석표이다. 분산분석을 통해 B인자가 정량적으로 가장 큰 값을 가지고 있으므로 실린더 최고압력에 가장 큰 영향을 미치는 것은 B인자인 Wiebe 형상 계수 라고 할 수 있다. B인자에 비해 A인자와 C인자가 미치는 영향은 작다. 제동평균유효압력에 가장 큰 영향을 미치는 것은 A인자인 열전달 보정 계수이며, B인자와 C인자가 미치는 영향은 작다. 이는 앞서 전역탐색을 통해 얻은 결과와 동일하다.

Table 5

ANOVA table for cylinder peak pressure (fixed-range single-step search)

Table 6

ANOVA table for brake mean effective pressure (fixed-range single-step search)

4.2 고정 영역 다단계 탐색

4.2.1 1차 탐색

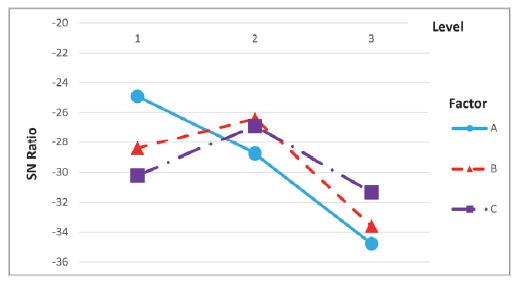
고정 영역 다단계 탐색에서는 각 인자별로 3개의 수준만을 고려한다. 1차 선정에서는 1수준과 3수준은 인자들 중에서 가장 작은 값과 가장 큰 값으로, 2수준의 경우 중간 값으로 선정하여 탐색한다. 1차 탐색을 위해 선정된 제어인자는 Table 7과 같다. Table 7을 기준으로 수준을 설정하여 L₉(3⁴) 직교배열표로 나타내면 Table 8과 같다. 직교배열표에 나타난 결과값을 기준으로 주효과도를 나타내면 Fig. 7과 같다. 이 주효과도에서 A인자는 1수준에서, B와 C인자는 2수준에서의 합이 가장 큰 값을 가지므로 최적의 조합은 A₁B₂C₂라 할 수 있다. 따라서 1차 선정에서 열전달 보정 계수는 0.5, Wiebe 형상 계수는 1.2, 연소지속기간은 65°로 한다.

Table 7

Control variables and levels for the 1st step trial

Table 8

Orthogonal array table for the 1st step trial

Fig. 7

Main effect diagram using fixed-range multi-step search(the 1st step)

4.2.2 2차 탐색

제어인자의 2차 선정을 위해 1차 선정에서 최적의 조합으로 선정된 인자들을 기준으로 하여 더 세밀하게 나누어 2차 선정을 위한 제어 인자를 Table 9와 같이 설정하였다. A인자의 경우 1차 탐색에서 선정된 0.5를 2수준으로 하고 이 값보다 작은 것을 1수준으로 선정하여야 하나, A인자의 변화 범위를 0.5에서 1.5로 고정하고 탐색을 수행하므로 A인자의 1차 선정값을 1수준으로 하고 그와 인접한 값들을 2, 3 수준으로 하였다. 선정된 제어인자를 이용하여 Table 8과 같은 L₉(3⁴) 직교배열표로 작성하고 이에 따라 주효과도를 작성하여 분석하면 2차 탐색에서의 제어인자의 최적의 조합은 A₁B₁C₂로 나타난다. 즉 열전달 보정계수는 0.5, Wiebe 형상 계수는 1.0, 연소지속기간은 65°로 하여 2차 선정을 마친다.

Table 9

Control variables and control levels for the 2nd step trial

이어서 실린더 최고압력과 제동평균유효압력에 미치는 인자의 영향을 정량적으로 알아보기 위해 분산분석을 적용하였으며, 이 결과 앞에서와 동일한 결과를 나타내고 있다.

4.2.3 3차 탐색

제어인자의 3차 선정을 위해 2차 선정에서 최적의 조합으로 선정된 인자들을 기준으로 하여 보다 세밀하게 나누어 3차 선정을 위한 제어 인자를 Table 10과 같이 선정하였다. 선정된 제어인자를 이용하여 L₉(3⁴) 직교배열표와 이에 따른 주효과도를 작성하면 A는 1수준, B인자는 2수준, C인자는 3수준으로 제어인자의 최적의 조합은 A₁B₂C₃로 나타난다. 즉 열전달 보정계수는 0.5, Wiebe 형상 계수는 1.0, 연소지속기간은 64°로 하여 3차 선정을 마친다.

Table 10

Control variables and control levels for the 3rd step trial

4.2.4 최종 선정

3번의 다단계 탐색을 통해 최적의 조합을 찾을려고 시도하였으나, 2차 선정에서 3차 선정으로 진행함에 있어 A인자와 B인자는 최적값이 0.5와 1.0으로 고정이 되고 C인자만 변동이 되었다. 따라서 A인자와 B인자는 고정을 하고 C인자만 모든 수준에 대해 실험한 결과값들을 비교하여 최적의 값을 찾고자 하였다. Table 11은 A인자와 B인자를 고정하고 C인자의 모든 수준에 대해 실험한 결과값을 정리하고 있다. 표에서 보면 C인자가 67°일 때 가장 작은 평균오차율을 나타내고 있다. 따라서 A인자 0.5, B인자 1.0, C인자 67°를 최적의 인자로 선정하였으며, 이 값은 전역탐색의 1순위와 동일한 값이며 총 수행한 실험 수는 29개이다. 총 실험수가 3번의 다단계 탐색을 통한 27회와 마지막 실험 5회를 합해서 32개가 아닌 29개인 이유는 32번의 실험 중 3번의 실험이 중복되므로 실제로는 29회의 실험이 수행되었다.

Table 11

Comparison of result during combustion duration variance(heat transfer multiplier : 0.5, Wiebe shape parameter : 1.0)

이어서 실시한 분산분석에 있어서도 앞서와 동일한 결과를 얻을 수 있었다.

4.3 가변 영역 다단계 탐색

지금까지는 각 인자별로 주어진 범위 내에서 다구치 기법을 적용하였다. 예를 들면 열전달 보정 계수는 0.5~2.5까지 0.5간격으로 주어졌다. 고정 영역 다단계 탐색을 통해 1차 탐색 결과가 0.5인 경우 0.5보다 적은 값이 없기 때문에 다음 단계 적용에서 0.5라는 열전달 보정 계수 값을 2수준에 놓고 계산하지 못하고 1수준에 놓고 계산을 하였다. 즉 0.5보다 작은 범위의 계산을 고려하지 않았기 때문이다. 가변 영역 다단계 탐색의 경우는 1차 탐색에서는 종전의 방식과 같이 하고 1차 탐색에서 미리 설정한 범위의 경계값이 최적값으로 나왔을 경우 그것을 2수준으로 놓고 이전의 탐색에서 적용한 범위 밖에 있는 수준값을 1 또는 3 수준으로 설정한다.

4.3.1 1차 탐색

1차 선정은 고정 영역 다단계 탐색과 동일하게 하고 진행하기 때문에 그 결과 역시 동일하게 나오게 된다. 선정된 제어인자와 수행을 위한 직교배열표 그리고 결과를 산출하기 위한 주효과도는 Table 7, Table 8 및 Fig. 7과 동일하다. 그리고 산출된 결과는 A₁B₂C₂로 열전달 보정 계수는 0.5, Wiebe 형상 계수는 1.2, 연소지속기간은 65°가 된다.

4.3.2 2차 탐색

1차 선정의 결과에서 최적의 조합은 A₁B₂C₂로서 열전달 보정 계수인 인자 A의 경우 최적 값이 가장 작은 값인 0.5가 되었다. 따라서 B, C인자는 그대로 2수준에 놓고 A인자는 1차 선정에서 최적 값인 0.5를 2수준으로 놓고 원래 인자의 변화 범위에 있지 않은 0.4라는 새로운 값과 0.6이라는 새로운 값을 1수준과 3수준에 놓고 다단계 탐색을 적용한다. 그리고 B인자의 경우에서도 범위를 좁혀 0.1간격으로 새로운 값을 적용하였다. Table 12는 새로운 인자 조합을 나타내고 있으며 선정된 제어인자를 이용하여 L₉(3⁴)직교배열표를 작성하고 주효과도를 통해 최적의 조합을 찾아보면 A인자와 B인자, C인자 모두 1수준으로 나타나며 2차 선정에서 최적의 조합은 열전달 보정계수는 0.4, Wiebe 형상 계수는 1.1, 연소지속기간은 64°이다.

Table 12

Control variables and levels for the 2nd step trial

4.3.3 3차 탐색

2차 선정에서 나온 A인자와 B인자가 또다시 최저값을 가지므로 한번 더 가변영역 다단계 탐색을 적용하였다. 2차 선정에서 나온 최적의 제어인자를 2수준으로 놓고 1수준과 3수준의 제어인자를 새로 설정하였다. Table 13은 새로운 인자 조합을 나타내고 있으며 선정된 제어인자를 이용하여 L₉(3⁴)직교배열표를 작성하고 주효과도를 통해 최적의 조합을 찾아보면 A인자와 B인자는 2수준으로 C인자는 3수준으로 나타나며 3차 선정에서 최적의 조합은 열전달 보정계수는 0.4, Wiebe 형상 계수는 1.1, 연소지속기간은 65°이다.

Table 13

Control variables and levels for the 3rd step trial

4.3.4 최종 선정

3번의 가변영역 다단계 탐색을 적용하면 총 수행한 실험 수는 총 27개이며, 이를 통해 나온 최적인자 조합은 A인자의 경우 0.4, B인자의 경우는 1.1, C인자는 65°라는 결과를 얻었으며, 이 결과는 전역탐색을 통해 얻어내 결과 값 중 1순위보다 더 우수한 값이다. 구체적으로 전역탐색의 1순위 조합값의 평균오차율이 2.53 %인데 비해 가변영역 다단계 탐색을를 통해 얻어낸 결과의 평균오차율은 1.62 %이다. 따라서 범위 밖에서 존재하는 더 좋은 인자들의 최적 조합값을 찾아 낼 수 있었다.

가변영역 다단계 탐색을 시행하는 각 단계마다 실린더 최고압력과 제동평균유효압력에 미치는 인자의 영향을 정량적으로 알아보기 위해 분산분석을 적용하였다. 그 결과 앞서의 분산분석에 있어서와 동일한 결과를 나타냄을 확인할 수 있었다.

4.4 결과비교

전역 탐색을 통해 얻은 결과와 다구치 기법을 고정 영역 일괄 탐색, 고정 영역 다단계 탐색 및 가변 영역 다단계 탐색을 적용하여 얻은 결과를 Table 14에 정리하였다. 전역 탐색을 통해 총 125번의 실험을 통해 얻었던 결과를 다구치 기법을 통해 고정 영역 일괄 탐색의 경우는 25번의 실험을 통해 전역 탐색의 2순위에 해당하는 우수한 결과를 찾았다. 고정 영역 다단계 탐색을 통해서는 29번의 실험을 통해 전역 탐색의 2순위에 해당하는 우수한 결과를 도출하였다. 특히 가변 영역 다단계 탐색를 통해 27번의 실험으로 전역 탐색의 1순위 보다 더 오차가 적은 우수한 결과를 찾아낼 수 있었다.

Table 14

Comparison of result

5. 결 론

본 연구에서는 기관의 성능 해석에 가장 큰 영향을 미치는 상수를 설정하고, 실험계획법을 통해 상수를 선정함으로써 상수값 선정에 요구되는 시간과 비용을 최소화하고자 하였다. 이를 위해 실험계획법의 하나인 다구치 기법을 고정 영역 일괄 탐색과 고정 영역 다단계 탐색 및 가변 영역 다단계 탐색의 방법을 각각 적용하여 요구되는 실린더 최고 압력과 제동평균유효압력을 얻게 하는 최적의 상수 조합을 도출하였다. 다구치 기법을 적용하여 얻은 결과를 기존의 방법을 통해 찾은 결과와 비교하여 다음과 같은 결론을 얻었다.

• 1) 모든 가능한 상수들의 조합을 검토한 결과 압축착화 기관의 실린더 최고압력에 가장 큰 영향을 미치는 인자는 Wiebe 형상계수로 나타나고 있다. 제동평균유효압력에 가장 큰 영향을 미치는 인자는 열전달 보정계수로 나타나고 있다. 다른 인자들의 효과는 이 인자들에 비해 비교적 적게 나타나고 있다. 이 결과는 다구치 기법을 이용한 분산분석에 있어서도 현저하게 적은 실험횟수로서 동일하게 확인할 수 있었다.
• 2) 각 상수들의 변화 범위를 동일하게 하고 다구치 기법의 일괄 탐색과 다단계 탐색을 시행하고 그 결과를 가능한 모든 상수의 조합에 대해 계산한 결과와 비교한 결과 실험횟수를 크게 줄이면서 거의 유사한 정확도로서 최적의 상수 조합을 도출할 수 있었다.
• 3) 다단계 탐색을 시행할 경우 주어진 범위 밖의 상수를 고려대상에 넣을 수 있었고 이 경우 기존의 방법보다 실험횟수를 크게 줄이면서 더 정확도가 우수한 상수의 조합을 찾을 수 있었다.

References

• R. S. Benson, “The Thermodynamics and Gas Dynamics of Internal Combustion Engines,” Clarendon Press, Oxford, Vol.1, pp.479-570, 1982.
• N. Miyamoto, T. Chikahisa, T Murayama and R. Sawyer, “Description and Analysis of Diesel Engine Rate of Combustion and Performance Using Wiebe’s Functions,” SAE 850107, 1985. [https://doi.org/10.4271/850107]
• S. N. Lee, N. Miyamoto, T. Murayama and S. S. Noh, “Analysis of Combustion and Performance of Diesel Engine by Wiebe’s Combustion Function,” Transactions of the Korean Society of Mechanical Engineers, Vol.9, No.3, pp.353-359, 1985.
• B. C. Yoo, B. H. Lee and K. S. Yoon, “Study on the Prediction of Performance and Emission in a 4-Cylinder 4-Stroke Cycle Turbocharged Gasoline Engine(First Paper),” Transactions of KSAE, Vol.10, No.6, pp.25-38, 1988.
• J. Gohjel, “Review of the Development and Applications of the Wiebe Function : A Tribute to the Contribution of Ivan Wiebe to Engine Research,” International Journal of Engine Research, Vol.11, No.4, 2010. [https://doi.org/10.1243/14680874JER06510]
• W. J. Choi, S. P. Ryu and K. S. Yoon, “Simulation for the Prediction of Indicated Performances of a Gasoline Engine Using GT-POWER,” Journal of the Korean Society of Marine Engineering, Vol.39, No.4, pp.368-373, 2015. [https://doi.org/10.5916/jkosme.2015.39.4.368]
• C. S. Jeong, S. K. Woo, S. P. Ryu and K. S. Yoon, “Study on the Simulation of a Spark Engine Using BOOST,” Journal of the Korean Society of Marine Engineering, Vol.40, No.9, pp.733-742, 2016. [https://doi.org/10.5916/jkosme.2016.40.9.733]
• S. H. Park, Modern Design of Experiments, 2nd Edn., Min-Yeong-Sa, Seoul, 2012.
• I. M. Yang, K. T. Oh, C. B. Yoo and I. K. Hwang, Design and Analysis of Experiments, 1st Edn., Min-Yeong-Sa, Seoul, 2015.
• T. H. Woo, J. H. Park, Y. W. Jo and K. M. Yang, Design of Experiments, 3rd Edn., Publisher of Hyeong-Seol, Pajoo, 2013.
• S. B. Lee, Taguchi Method Easy to Understand, 3rd Edn., Publisher of Sang-Jo, Seoul, 2003.
• R. K. Roy, A Primer on the Taguchi Method, 2nd Edn., Society of Manufacturing Engineers, Southfield, 2010.
• G. B. Park, Y. B. Lee, I. G. Cho and D. H. Choi, “Design of Automotive Fuel Tank for Preventing Liquid Carry Over Using Taguchi Method and Approximate Optimization,” Transactions of the Korean Society of Marine Engineering, Vol.37, No.8, pp.1059-1067, 2013. [https://doi.org/10.3795/KSME-A.2013.37.8.1059]
• C. W. Lee, W. S. Lim, Y. I. Park and J. M. Lee, “Analysis of a Vechicle Performance Using Taguchi Method: How does a Torque Converter Affect the Vehicle Performances,” Transactions of the Korean Society of Marine Engineering, Vol.26, No.6, pp.1085-1091, 2002. [https://doi.org/10.3795/KSME-A.2002.26.6.1085]
• V. H. Wilson and Udayakumar, “Optimization of Diesel Engine Parameters Using Taguchi Method and Design of Evolution,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol.34, No.4, pp.423-428, 2012. [https://doi.org/10.1590/S1678-58782012000400001]
• AVL, BOOST version 2010 User Guide, AVL, Graz, 2010.
• AVL, BOOST Theory version 2010, AVL, Graz, 2010.
• G. Woschni, “A Universally Applicable Equations for the Instantaneous Heat Transfer Coefficient in the Internal Combustion Engine,” SAE 670931, 1967. [https://doi.org/10.4271/670931]
• G. Woschni and J. Fieger, “Determination of Local Heat Transfer Coefficients at the Piston of a High Speed Diesel Engine by Evaluation of Measured Temperature Distribution,” SAE 790834, 1979. [https://doi.org/10.4271/790834]