차량상태 오차를 이용한 경로추종 보정제어 알고리즘

1. 서 론

자율주행 자동차는 4차 산업혁명 시대의 핵심 기술로서, 최근까지 기술적인 연구와 개발만이 아닌 관련 법규와 제도 개정 등이 활발히 진행되고 있다. 이전에는 차선 유지 보조 시스템(Lane Keeping Assistance System; LKAS)이나 지능형 순항 제어(Smart Cruise Control; SCC), 차선 변경 보조(Lane Change Assist; LCA) 수준의 주행보조 또는 이용 편의를 위한 부분 자율주행 수준이었다면, 현재는 완전 자율주행을 위한 연구가 활발히 진행되고 있다.^1,2)

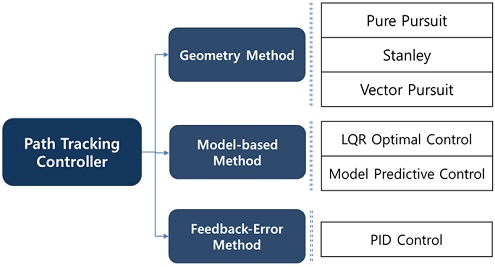
완전 자율주행 연구는 주요 시스템인 측위, 인식, 판단, 제어 부분으로 나뉘어 진행되고 있다. 이 중에서, 자율주행 자동차를 최종적으로 움직이게 하는 기술인 경로 추종 제어는 가장 중요하면서도 안정적이어야 하는 부분이다. 자율주행 자동차의 경로 추종 제어 기술은 실시간 차량 위치 좌표로부터 나오는 기준 경로(Reference Path)를 추종하는 제어기로, Fig. 1과 같이 크게 기하학적 방법과 모델기반 방법, 피드백 에러 방법으로 나눌 수 있다.^3-5)

Fig. 1

Path tracking control method

Pure-Pursuit(PP) 제어기와 Stanley 제어기로 대표되는 기하학적 방법의 경우, Single-Input- Single-Output(SISO)의 간단한 모델을 사용함으로써 제어의 실시간성 보장과 좋은 성능을 가진다. 그러나 간단한 모델인 만큼 실제 적용에 있어서 많은 제약이 있다. 로컬 경로(Local Path) 사용에 있어서 경로 형상에 문제가 발생하거나, 각 제어기의 한계점을 극복하는 정밀한 추종을 위해서는 많은 튜닝 과정이 필요하다.^3,5-7) 이러한 한계점을 극복하기 위해 2가지의 다른 제어기들을 복합적으로 사용되는 연구가 진행되었다.^8-10) 모델기반 방법의 경우, 차량 모델을 기반으로 하여 튜닝에 있어서 많은 노력이 필요 없고, 속도 또는 조향에 따른 특성 변화 문제도 해결할 수 있기 때문에, Linear Quadratic Regulator(LQR)이나 Model Predictive Control(MPC) 등으로 다양한 연구^11-15)가 진행되었다. 에러 피드백 방법의 경우, 차량의 움직임을 반영할 수는 있지만 동특성의 활용에는 한계가 있어, PP기반에 PID와 Low-pass Filter를 활용한 연구처럼 복합적인 사용을 위한 연구가 진행되었다.^16,17) 그러나 상기 기술한 제어기들은 시뮬레이션 기반 검증으로 실제 주행 환경에서 발생하는 하드웨어 딜레이 현상이나 차량의 슬립 현상, 실제 차량의 동특성 등을 고려하지 못하였고,^4,8,9,12-14) 특정 조건이 되면 게인(Gain) 값을 천이하는 스위칭 방식의 복합 제어기의 경우 불연속적인(Discrete) 부분에서 튀는 현상이 발생할 수 있어 주행 안전성에 불리하다.^9,10)

따라서 본 논문에서는 앞선 시뮬레이션 연구와 다르게 실제 도로 환경인 상암 DMC 자율주행 테스트베드(Testbed)에서 정밀지도 기반의 경로를 실제 차량으로 주행하며 앞선 한계점을 극복하고자 하였다. 제안된 방법은 계산이 간단하고 외란에도 안정적인 Pure-Pursuit 기반 제어 알고리즘에 모델기반 차량 상태 Feedback 제어인 LQR을 보정용으로 이용하여 더욱 정밀한 추종 능력을 갖고, 승차감에서도 개선되는 경로 추종 보정 복합 제어 알고리즘을 제시한다.

2. 실험 환경 구성

2.1 실험 차량 시스템 구성

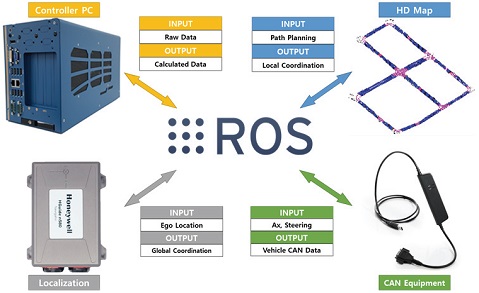
본 논문에서 사용한 실험 차량의 경우, SUV 전기차인 KIA의 Niro EV이다. 차량에는 Photo. 1처럼 지붕에는 주변 환경 인식을 위한 Ouster LiDAR 1개와 전,후방 카메라를, 트렁크에는 전원공급 장치인 위한 배터리, 인버터와 전체 시스템 실행 제어를 하는 Nuvo-8108GC_NX, 측위를 위한 cm급 오차 장비인 Honeywell INS-GPS, 제어를 위한 Kvaser CAN 통신 장비를 설치하였다. 각 센서로부터 받는 모든 데이터 처리 및 제어 입력은 Robot Operating System(ROS)을 기반으로 하였으며 실험 차량의 시스템 구조는 Fig. 2와 같다.

Photo. 1

Test vehicle - KIA Niro EV

Fig. 2

ROS system architecture

2.2 정밀지도 기반 경로 생성

정밀지도(High-Definition Map; HD Map)는 도로와 주변 시설 정보를 정확히 표현한 지도로서, 기상 상황이 나쁘거나 GPS 센서 불량 등 환경적 요인이 좋지 못한 상황에서도 차량의 위치를 더욱 정밀히 파악하게 도와준다. 이는 지역 경로를 실시간 생성할 필요 없이 주어진 정밀지도 좌표를 경로로 사용할 수 있게 해준다. 구성 데이터로는 지형지물, 도로 표시, 시설물 등의 정적 지도 정보와 도로 변화 상황을 실시간 적용해주는 동적 지도 정보로 되어 있다. 자율주행 기술이 발전함에 따라, 정밀지도 구축이 늘어나고 관련 연구들^18,19)도 다양해지고 있어 정밀지도가 자율주행 차량의 상용화를 위한 핵심 인프라로 자리 잡을 것으로 보인다.

본 논문에서는 경로 생성에 있어 국토지리정보원에서 제공하는 지리 공간 벡터 데이터 형식인 Shp 파일의 정밀지도 데이터를 사용하였다. 차량의 주행 경로, 차선, 도로 마크 등 지리적 정보만으로 경로 데이터를 먼저 추출하고, 얻어낸 정보와 실험 차량과의 연동을 위해 위경도 좌표계(WGS84)에서 UTM 좌표계(UTM52N)로 좌표계 변환을 하였다. 이렇게 얻은 위치 데이터를 QGIS 소프트웨어에서 제공하는 벡터 도형 도구를 통해 꼭짓점을 추출한 뒤, 해당 소프트웨어의 필드 계산기를 통해 전역 좌표를 생성하고, 이를 교차로 부분과 일반 도로 부분으로 나누어 경로로써 활용하였다.

Fig. 3

K-city map in KATRI

3. 경로추종 보정제어 알고리즘 전략

3.1 기하학적 제어 알고리즘

3.1.1 Pure-Pursuit Controller

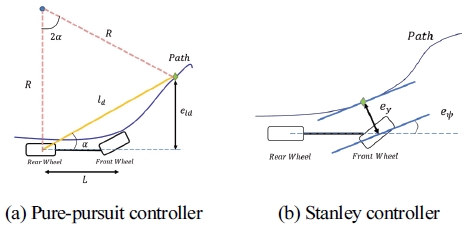
Pure-Pursuit 제어기는 외란에 안정적이고, 간단하면서도 승차감이나 추종 능력에서 좋은 성능을 보장하는 것으로 널리 사용되는 경로 추종 제어기이다. 이 제어기는 Fig. 4(a)와 같이 차량 후륜 위치와 전방 경로의 목표 지점 예견점(Look-ahead Point)을 연결하는 원호를 통해 조향값을 얻어낸다. 예견점과 헤딩 방향 사이의 각도 α를 sin법칙을 통해 유도하고, 예견점과 차량 후륜 사이의 거리 l_d를 애커만 조향각 모델(Ackerman Steering Angle Model)에 적용하면 목표 조향 각(δ_PP)이 식 (1)과 같이 도출된다.

$\[ {\delta }_{PP}={\tan }^{-1}\left(\frac{2L \sin \alpha }{l_d}\right) \]$

(1)

Fig. 4

Geometry explanation of geometry control algorithm

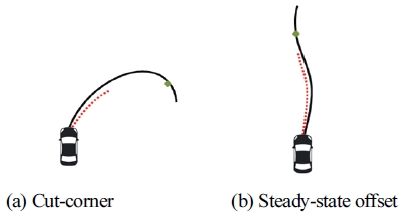
Pure-Pursuit 제어기의 경우, 예견점 선정이나 차량 속도 영향에 따라 차량의 Oversteer와 Understeer 현상이 발생하는데, 이를 보완하기 위해 차량 속도에 비례한 예견점 튜닝을 실시한다.^5-7) 그러나 이 또한 매개 변수 한 개만을 다루기 때문에 정밀한 추종과 관련해서는 한계가 있다. Fig. 5(a)와 같이 곡률이 큰 도로에서는 안쪽을 파고드는 Cut-corner 현상이나 Fig. 5(b)와 같이 수렴하지 않고 일정한 오차를 유지하며 주행하는 Steady-State Offset이 대표적인 한계이다.

Fig. 5

Limitation of pure-pursuit controller

3.1.2 Stanley Controller

Stanley 제어기는 2005 DARPA Grand Challenge에서 Stanford University가 처음 개발한 제어기로, 차량 전륜 축으로부터 목표 경로까지 가장 가까운 점을 기준으로 하여 제어하는 방법이다. 차량의 헤딩 방향과 기준점의 접선 방향의 차이를 헤딩 에러 e_ψ, 차량 전륜 축과 기준점 사이 거리를 횡 방향 오차를 e_y, 차량 속도 V_x로 하여 목표 조향 각도를 식 (2)와 같이 계산한다.

$\[ {\delta }_{Stanley}=e_{\psi }+{\tan }^{-1}\left(\frac{k•e_y}{V_x}\right) \]$

(2)

Stanley 제어기의 경우, 기준점이 차량과 가깝게 위치하기 때문에 하드웨어 반응성의 영향에 따라 고속이나 경로 곡률이 큰 경우 발산 가능성이 존재한다. 또한, 정밀한 추종을 위해 급격한 이동이 생기고 이로 인해 승차감에 있어서 좋지 못한 점도 있다.

$\[ \left\{\begin{array}{c}\ddot{y}=-\frac{2C_{\alpha f}+{2C}_{\alpha r}}{m{V}_x}\dot{y}-\left(v_x+\frac{2C_{\alpha f}{l}_f-{2C}_{\alpha r}{l}_r}{m{V}_x}\right)\dot{\psi }+\frac{2C_{\alpha f}}{m}\delta \hfill \\ \ddot{\psi }=-\frac{2C_{\alpha f}{l}_f-2C_{\alpha r}{l}_r}{I_z{V}_x}\dot{y}-\frac{2C_{\alpha f}{l}_f^2+{2C}_{\alpha r}{l}_r^2}{I_z{V}_x}\dot{\psi }+\frac{2C_{\alpha f}{l}_f}{I_z}\delta \hfill \end{array}\right. \]$

(3)

$\[ \left[\begin{array}{c}\dot{y}\\ \ddot{y}\\ \dot{\psi }\\ \ddot{\psi }\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{2C_{\alpha f}+{2C}_{\alpha r}}{m{V}_x}& 0& -v_x-\frac{2C_{\alpha f}{l}_f-{2C}_{\alpha r}{l}_r}{m{V}_x}\\ 0& 0& 0& 1\\ 0& -\frac{2C_{\alpha f}{l}_f-2C_{\alpha r}{l}_r}{I_z{V}_x}& 0& -\frac{2C_{\alpha f}{l}_f^2+{2C}_{\alpha r}{l}_r^2}{I_z{V}_x}\end{array}\right]\left[\begin{array}{c}y\\ \dot{y}\\ \psi \\ \dot{\psi }\end{array}\right]+\left[\begin{array}{c}0\\ \frac{2C_{\alpha f}}{m}\\ 0\\ \frac{2C_{\alpha f}{l}_f}{I_z}\end{array}\right]\delta \]$

(4)

$\[ \begin{array}{cc}\left\{\begin{array}{c}{\dot{e}}_y=\dot{y}+V_x\left(\psi -{\psi }_{des}\right)\hfill \\ {\dot{e}}_{\psi }=\dot{\psi }-{\dot{\psi }}_{des}\hfill \end{array},\right.\hfill & \left\{\begin{array}{cc}\dot{x}=Ax+Bu+v& \left(\therefore u=\left[\delta \right]\right)\end{array}\right.\end{array} \]$

(5)

$\[ \left[\begin{array}{c}{\dot{e}}_y\\ {\ddot{e}}_y\\ {\dot{e}}_{\psi }\\ {\ddot{e}}_{\psi }\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{2C_{\alpha f}+{2C}_{\alpha r}}{m{V}_x}& \frac{2C_{\alpha f}+{2C}_{\alpha r}}{m}& -\frac{2C_{\alpha f}{l}_f-{2C}_{\alpha r}{l}_r}{m{V}_x}\\ 0& 0& 0& 1\\ 0& -\frac{2C_{\alpha f}{l}_f-2C_{\alpha r}{l}_r}{I_z{V}_x}& \frac{2C_{\alpha f}{l}_f-2C_{\alpha r}{l}_r}{I_z}& -\frac{2C_{\alpha f}{l}_f^2+{2C}_{\alpha r}{l}_r^2}{I_z{V}_x}\end{array}\right]\left[\begin{array}{c}{e}_y\\ {\dot{e}}_y\\ e_{\psi }\\ {\dot{e}}_{\psi }\end{array}\right]+\left[\begin{array}{c}0\\ \frac{2C_{\alpha f}}{m}\end{array}\right. \]$

(6)

3.2 모델기반 제어 알고리즘

3.2.1 Vehicle Dynamic Model

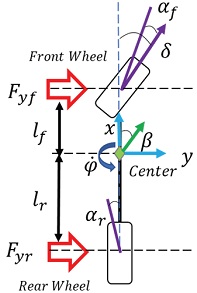
모델기반 제어 알고리즘의 경우, 차량 동역학 모델(Vehicle Dynamic Model)을 적용하여 최종 조향 식을 만들어 낸다. 먼저 차량 횡-동역학 모델은 Fig. 6과 같고, 식 (3), (4)로 정리된다. 본 논문에서는 식 (5)의 차량 상태 오차와 조향각을 횡-동역학 모델에 적용하여 식 (6)과 같은 Error-Based Dynamic Model¹²⁾을 도출하였다.

Fig. 6

Bicycle-lateral dynamic model

m은 차량의 질량, V_x는 차량의 종방향 속도, $$ \dot{\psi }$$는 요레이트(Yaw rate), I_z은 요(Yaw) 관성 모멘트, l_f, l_r은 중심점으로부터 전,후까지의 거리, C_αf, C_αr은 전,후 코너링 강성을 나타낸다. 위 식들에서 사용되는 차량 파라미터 값들은 Table 1에 나타내었다.

Table 1

Test vehicle parameters

3.2.2 Linear Quadratic Regulator

LQR의 경우 최적 제어 알고리즘으로, 상태 가중치 행렬인 Q와 R 선정을 통해 식 (7)의 Cost Function이 최소가 되게 하는 최적 Gain K를 얻어내는 것이다. Q와 R에 의해 Gain K가 정해지므로, LQR에서 가장 기본적이자 중요한 것은 원하는 목표와 주행 능력에 맞추어 최적 Q와 R을 선정하는 것이다.

$\[ J={\int }_0^{\infty }\left(x^T{Q}_x+u^{T}Ru\right)dt \]$

(7)

$\[ x=\left[\begin{array}{cccc}{e}_y& {\dot{e}}_y& e_{\psi }& {\dot{e}}_{\psi }\end{array}\right] \]$

(8)

$\[ A^{T}P+PA-PB{R}^{-1}{B}^{T}P+Q=0 \]$

(9)

$\[ K=R^{-1}{B}^{T}P \]$

(10)

$\[ u=-Kx \]$

(11)

Q와 R 행렬을 원하는 조향 목표에 맞게 선정한 후, 주행하면서 Reference Pose와 Current Pose를 비교하여 얻은 상태 오차 행렬 x를 식 (8)과 같이 구한다. 이를 Algebraic Riccati Equation으로 알려져 있는 식 (9)와 식 (10)에 대입하여 최적 Gain K를 얻어내고, 최종으로 계산된 K를 이용하여 식 (11)과 같은 제어 입력인 조향각 u를 계산한다. 여기서 행렬 A와 B는 앞서 Error-Based Dynamic Model 식 (5)에 해당하는 부분과 같다.

3.3 오차 보정 경로추종 제어 전략

앞서 소개한 단일 경로 추종 제어 알고리즘들은 속도에 따른 차량 동특성 변화나 모델에 따른 연산 실시간성 확보 불확실성, 실제 주행 시 발생하는 하드웨어 딜레이 같은 문제들로 인해 성능이 저하되는 문제점이 있다. 이러한 문제를 극복하기 위해 각 제어기에 따라 추가적인 파라미터 최적화 작업^3-5)을 수행해야 한다. 예를 들어 Stanley 제어기의 경우, 헤딩 에러와 횡 방향 오차에 의한 제어 부분에 각각 게인 k_ψ, k_y을 적용한 식 (12)를 만들고, 이를 실험적 튜닝을 통해 더욱 정밀한 추종을 하게 할 수 있다.

$\[ {\delta }_{Stanley}=k_{\psi }•e_{\psi }+k_y•{\tan }^{-1}\left(\frac{k•e_y}{v_x}\right) \]$

(12)

그러나 이와 같은 추가적인 단일 제어기 최적화를 진행해도 한계는 존재한다. 기하학적 제어 알고리즘의 경우, 간단한 구성과 기준 경로에 절대적으로 의존적인 만큼 차량 상태와 경로의 특징에 민감하고, 단순 속도나 게인에 대한 튜닝으로는 차량 동특성을 적용하지 못하는 한계가 존재한다. 이는 곧, 실험을 수행했던 차량이 아닌 다른 차량으로 주행하게 되면 파라미터 수치를 처음부터 모두 바꾸어야 하는 것을 의미한다. 이와 반대로 모델기반 제어 알고리즘의 경우, 다른 차량으로 주행하게 되어도 차량 특성 파라미터 값만 맞추어 변경해주면 특별한 추가 튜닝 과정 없이도 안정적인 주행을 할 수 있다. 그러나 실제 차량 주행 환경에서 실시하면 계산의 실시간성 확보 문제로 인해 경로 곡률이 크거나 속도가 높은 경우 경로를 크게 도는 현상인 Overshoot 현상이 발생하는 문제가 있고, 모델의 정확도와 차량 상태 오차에도 영향을 많이 받아 성능 보장에 있어 불확실성이 존재한다.

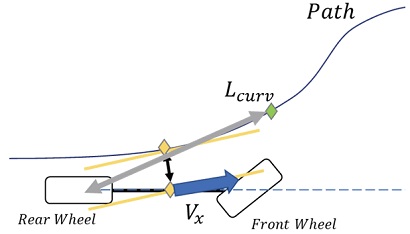
본 논문에서 제안하는 알고리즘 전략은, 서로 다른 방법의 제어기를 병렬적으로 구성하는 것으로, 안정적인 주행과 승차감을 보장하는 기하학적 방법에 추종에 있어서 차량 동특성을 고려하는 모델기반 제어기를 이용하여 부족한 추종 능력을 보완시켜주는 상호 보완적 제어기를 개발하는 것이다. 보정 방법은 Pure-Pursuit 기반 주행에 차량 오차 상태와 전방 경로의 로컬 곡률(Local Curvature)에 따른 LQR 조향 값을 비례 적용하는 것이다. 보정을 위한 파라미터 구성은 Fig. 7과 같이 전방 경로 곡률 판단 위치(L_curv)에서의 곡률과 현재 차량 상태 오차로 하였고, 보정 게인(k_LQR) 정의는 식 (13), (14)와 같다. 앞선 식들을 활용하여 얻어낸 최종 조향식은 식 (15)와 같다. 전방 경로 곡률이 조건보다 크다고 여겨지는 구간이나 보정용 게인(k_LQR)값이 0.3보다 크게 되는 구간에서는 게인 k_LQR가 0.3을 넘지 못하도록 했는데, 이는 실험적으로 보정 값이 높다고 하여 수렴이 빠르게 되는 것이 아니었고, 가속 구간에서는 수렴에 있어서 불안정한 결과를 초래했기 때문이다.

$\[ L_{curv}=2.7+0.3 V_x \]$

(13)

$\[ \begin{array}{c}{k}_{LQR}=\left|e_y\right|+0.1\left|e_{\psi }\right|\hfill \\ \left(\therefore k_{LQR}\le 0.3 \mathrm{i}\mathrm{f} {\kappa }_{L_{curv}}\times 1000>60\right)\hfill \end{array} \]$

(14)

$\[ {\delta }_{Correct}=\left(1-k_{LQR}\right)•{\delta }_{PP}+k_{KQR}•{\delta }_{LQR} \]$

(15)

Fig. 7

Correction parameter configuration

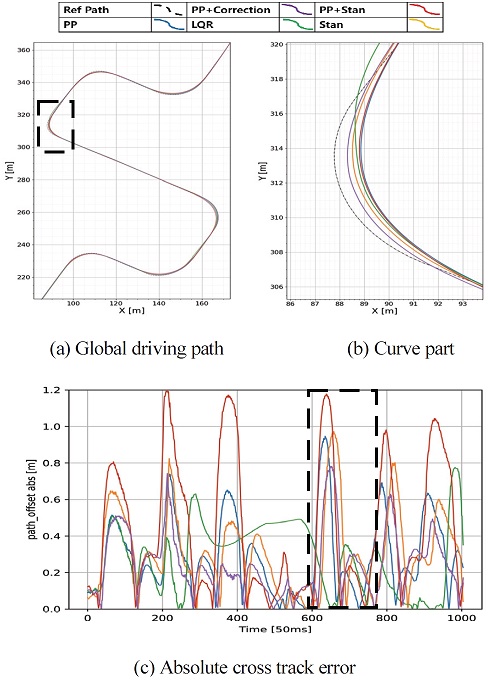
본 논문에서 제안한 제어기의 성능 검증 및 비교 분석을 위해 Fig. 3과 같은 자동차안전연구원에 위치한 K-city를 총 5가지의 제어기(PP, Stanley, LQR, PP + Stan, PP + Correction)로 주행하였다. PP + Stan 제어기는 곡률 및 경로 각도 오차에 따른 게인 스위칭 방식을 적용하였다.^9,10) Fig. 8은 곡률이 큰 구간인 田부분을 속도 23~42 kph로 주행한 결과이고, K-city 전체 구간을 속도 23~63 kph로 주행하여 얻은 결과는 Table 2와 같다. 주행 성능 기준으로는 Cross Track Error와 Heading Error를 사용하였고, 횡 제어 승차감 판단으로는 횡 이동 후 직진으로 들어가는 부분에서 횡 가속도의 변화가 적을수록 승차감에 있어서 좋은 결과를 가질 것이라 판단하여, 상대적 승차감 기준으로 횡방향 가가속도(Lateral Jerk) [m/s³]를 사용하였다. 최종 분석 결과 평균 Cross Track Error는 PP + Correction > LQR > Stanley > PP + Stan > PP 순의 결과가 나왔다. 평균 Heading Error의 경우 PP + Stan > LQR > PP + Correction > Stanley > PP, 평균 Jerk의 경우는 PP > PP + Correction > PP + Stan > Stanley > LQR가 조사되었다. 이를 종합적으로 보았을 때, 주행 성능과 승차감에 있어서 PP + Correction이 개선된 것을 확인할 수 있었다.

Fig. 8

Tracking performance result in K-city

Table 2

Control test results – K-city total

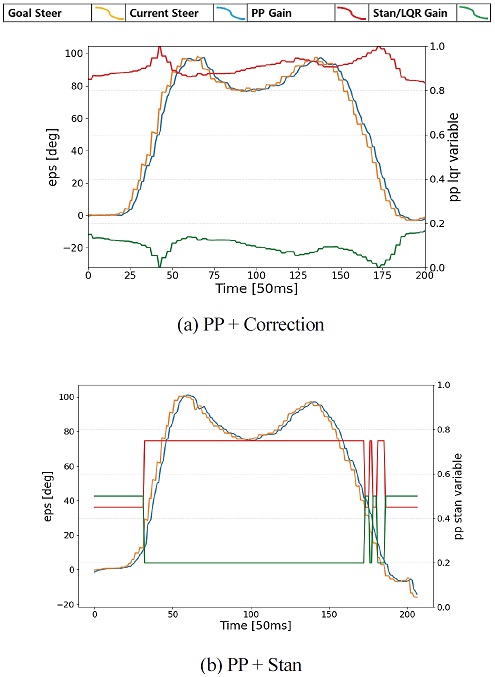
Fig. 8(b)구간에서 PP + Correction과 PP + Stan 제어기의 조향각과 게인 천이 과정을 보면, PP + Correction는 Fig. 9(a)처럼 연속적인 게인 수치를 갖는 반면, (b) PP + Stan 스위칭 방식은 천이 과정에서 급격한 게인 변화가 있었다. 이는 실제 주행 중 센서 미세 오차에 따른 전방 경로 곡률 계산 오류나 실제 곡률이 변할 때 생기는 게인 천이 과정으로, 스위칭 방식이 불연속적으로 변하는 현상으로 인해 주행 안정성 확보에서 불리하다는 것을 보여준다.

Fig. 9

Steering angle and gain transition

4. 주행 실험 및 결과

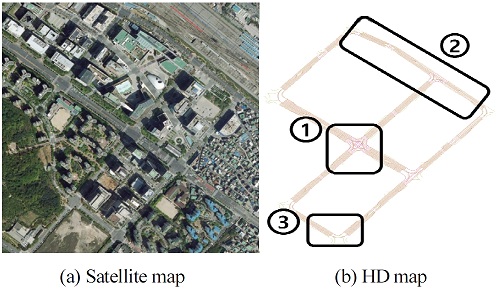
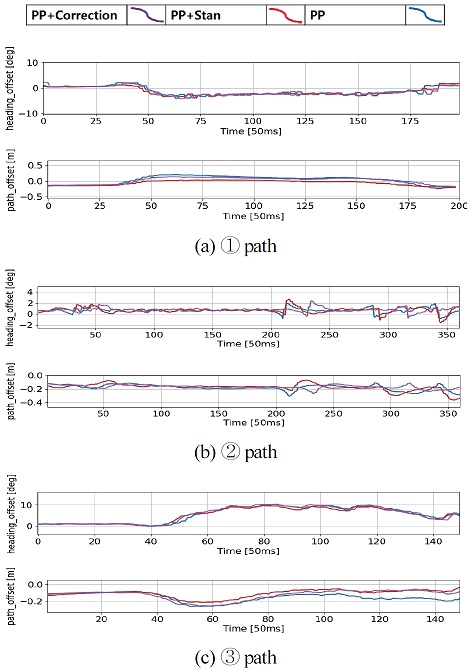
실험은 Fig. 10의 자율주행 테스트베드인 상암 DMC에서 25~55 kph로 주행하였고, 경로 생성에 있어서는 국토지리정보원에서 제공하는 정밀지도 데이터를 사용하였다. 여러 상황 별 분석을 위해 좌회전 구간 ①, 직선 구간 ②, 우회전 구간 ③, 총 3개의 구간으로 나누어 분석하였고, 비교 제어기로는 PP, PP + Stan, PP + Correction을 사용하였다.

Fig. 10

Sangam DMC autonomous vehicle testbed

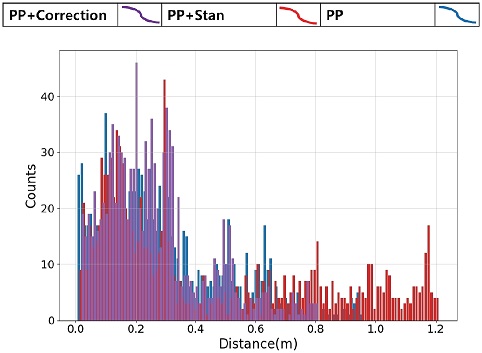
주행 결과로, 주행 성능을 나타내는 횡 오차와 헤딩 오차는 Fig. 11, 종합하여 정리된 결과는 Fig. 12와 Table 3과 같다. 구간 별로 분석해 보면 낮은 곡률의 ①구간의 경우, 30~40 kph으로 주행하여 모든 면에서 타 제어기와 비슷한 성능을 보였고, ③구간에서는 25 kph 저속으로 주행하여 추종 성능이 다른 복합 제어기와 비슷하였지만, Fig. 9와 같은 조향 변화에 의해 제안한 제어기가 승차감에서 더욱 좋은 결과를 가졌다. ② 구간의 경우 직진 후 약간 꺾이는 구간이 존재하는데, 55 kph의 고속임에도 불구하고 꺾인 후 다시 수렴하는 구간에서 가장 좋은 성능을 보였다.

Fig. 11

Compare the tracking performance of different path section

Fig. 12

Absolute cross track error histogram in sangam DMC

Table 3

Control test results – sangam total

5. 결 론

본 논문에서 제안한 제어기는 안전한 주행 능력과 부드러운 승차감이 장점인 Pure-Pursuit 제어기 기반에 LQR 제어기를 결합시키는 경로추종 보안 제어기를 제안하였다. 이는 다양한 주행 상황에 따른 동특성을 고려하며 정밀한 추종을 하는 LQR 제어기를 이용하여 P-P 제어기의 부족한 추종 제어 능력을 보완시켜줄 수 있다.

측위, 인식 센서 등의 오차가 없는 이상적인 시뮬레이션 기반 검증과 달리, 속도에 따른 차량 동특성 변화, 경로의 곡률 특성, 액츄에이터의 동특성 및 컴퓨팅 시스템의 한계 등 여러 문제가 발생하는 실제 주행 환경 속에서 검증 및 분석을 수행하였다.

실험 결과, K-city와 상암 DMC의 다양한 도로 상태에서 P-P 제어기나 P-P+Stanley 제어기와 비교했을 때, 제안된 제어기가 더욱 향상된 추종 능력과 승차감을 가지는 것을 주행 결과 데이터로 확인할 수 있었다. 이는 기존의 단순 Trial & Error 튜닝 방식과 다르게, 정밀지도의 도로 정보 및 차량 모델의 특성을 사용하는 제어기이기 때문에 향후 활용도 측면에 있어서도 더욱 가치가 있을 것으로 기대한다.

Acknowledgments

이 논문은 산업통상자원부 ‘산업전문인력역량강화사업’의 재원으로 한국산업기술진흥원(KIAT)의 지원(2021년 친환경자동차(xEV) 부품개발 R&D 전문인력양성사업, 과제번호 : P0017120)과 과학기술정보통신부 및 정보통신기획평가원의 대학ICT연구센터육성지원사업의 연구결과로 수행되었음(IITP-2021-2018-0-01426).

References

• S. J. Jang, “Trend of SW Technology Related to Autonomous Vehicles,” Information and Communications Magazine, Vol.33, No.4, pp.27-33 2016.
• J. K. Lee, “Direction and Task of Self-driving Car Industrial Technology,” The Journal of The Korean Institute of Communication Sciences, Vol.35, No.5, pp.13-20, 2018.
• C. Kim, D. Lee and K. Yi, “Vehicle Steering System Analysis for Enhanced Path Tracking of Autonomous Vehicles,” Journal of Auto-vehicle Safety Association, Vol.12, No.2, pp.27-32, 2020.
• J. M. Snider, Automatic Steering Methods for Autonomous Automobile Path Tracking, Robotics Institute, Pittsburgh, Carnegie Mellon University, CMU-RITR-09-08, 2009.
• S. Bacha, M. Ayad, R. Saadi, A. Aboubou, M. Bahri and M. Becherif, “Modeling and Control Technics for Autonomous Electric and Hybrid Vehicles Path Following,” 5th International Conference on Electrical Engineering- Boumerdes(ICEE-B), 2017. [https://doi.org/10.1109/ICEE-B.2017.8191998]
• D. Y. Yu, C. H. Park and S. H. Hwang, “Autonomous Vehicle Control Systems using Look-Ahead Points,” The Korean Society of Mechanical Engineers Conference Proceedings, pp.2027-2031, 2019.
• H. J. Joo and K. B. Lee, “Changes in Path Tracking Performance of Autonomous Vehicle According to Design Feedback Gain and Look-ahead Distance of Pure-pursuit Algorithm,” Transactions of KSAE, Vol.29, No.9, pp.839-846, 2021. [https://doi.org/10.7467/KSAE.2021.29.9.839]
• D. Y. Yu, D. G. Kim, H. S. Choi and S. H. Hwang, “Hybrid Control Strategy for Autonomous Driving System using HD Map Information,” Journal of Drive and Control, Vol.17, No.4, pp.80-86, 2020.
• M. Cibooglu, U. Karapinar and M. T. Soylemez, “Hybrid Controller Approach for an Autonomous Ground Vehicle Path Tracking Problem,” 25th Mediterranean Conference on Control and Automation(MED), 2017. [https://doi.org/10.1109/MED.2017.7984180]
• D. G. Kim, Pure Pursuit based Hybrid Path Following Control Algorithm with Path Angle Error Compensation, Ph. D. Dissertation, Sungkyunkwan University, Suwon, 2020.
• K. Vivek, M. A. Sheta and V. Gumtapure, “A Comparative Study of Stanley, LQR and MPC Controllers for Path Tracking Application (ADAS/AD),” IEEE International Conference on Intelligent Systems and Green Technology(ICISGT), 2019.
• C. Piao, X. Liu and C. Lu, “Lateral Control Using Parameter Self-Tuning LQR on Autonomous Vehicle,” International Conference on Intelligent Computing, Automation and Systems(ICICAS), 2019. [https://doi.org/10.1109/ICICAS48597.2019.00197]
• M. M. Sherif, A. M. Ahmed, A. M. Moustafa and M. Moness, “Optimal Control of Lane Keeping System Using Simulated Annealing and Linear Quadratic Regulator,” 15th International Computer Engineering Conference (ICENCO), 2019. [https://doi.org/10.1109/ICENCO48310.2019.9027294]
• S. H. Lee, S. K. Lim, M. W. Sho, J. J. Kwon, T. W. Hong and K. H. Park, “Development of Steering Control Algorithm for High Speed Autonomous Vehicle Base,” KSAE Annual Conference Proceedings, pp.780-787, 2013.
• J. Y. Lee and K. S. Yi, “MPC based Steering Control using a Probabilistic Prediction of Surrounding Vehicles for automated Driving,” Journal of Institute of Control, Robotics and Systems, Vol.21, No.3, pp.199-209, 2015. [https://doi.org/10.5302/J.ICROS.2015.14.9012]
• Y. Chen, Y. Shan, L. Chen, K. Huang and D. Cao, “Optimization of Pure Pursuit Controller based on Pid Controller and Low-pass Filter,” 21st International Conference on Intelligent Transportation Systems (ITSC), 2018. [https://doi.org/10.1109/ITSC.2018.8569416]
• M. Park, S. Lee, and W. Han, “Development of Steering Control System for Autonomous Vehicle Using Geometry‐based Path Tracking Algorithm,” ETRI Journal, Vol.37, No.3, pp.617-625, 2015. [https://doi.org/10.4218/etrij.15.0114.0123]
• D. G. Kim, G. S. Gwak and S. H. Hwang, “HD Map Data Processing Algorithm For Real-Time Localization,” KSAE Fall Conference Proceedings, p.666, 2019.
• Y. S. Na, S. K. Kim, Y. S. Kim, J. Y. Park, J. M. Jeong, K. C. Jo, S. J. Lee, S. J. Cho, M. Y. Sunwoo and J. M. Oh, “HD Map Usability Verification for Autonomous Car,” Transactions of the KSAE, Vol.28, No.11, pp.797-808, 2020. [https://doi.org/10.7467/KSAE.2020.28.11.797]