공간적 자기상관성을 고려한 자동차검사 부적합률의 지역적 영향요인 분석

1. 서 론

자동차검사는 차량의 성능을 주기적으로 검사하여 교통사고를 예방하고 배출가스를 감소하는 등 자동차 운행질서를 확립하기 위한 목적으로 1962년부터 시행되어 오고 있다.⁵⁾ 자동차검사는 빅데이터를 통계적으로 분석 후 원인을 추론하여 예방하는 방식과는 다르게 결함에 대한 사후처리 및 관리에 집중하고 있다. 자동차검사 데이터를 활용하여 차량결함에 영향을 미치는 근본적인 원인을 규명할 수 있다면, 차량결함을 예방함으로써 교통사고가 발생할 가능성을 최소화할 수 있기 때문에 자동차검사 데이터를 통계적으로 활용하는 것은 매우 의미 있는 일이라 할 수 있다.

2019년도 자동차검사 통계로 제시된 자동차검사 부적합률을 지역별로 살펴보면 서울, 대전, 강릉은 부적합률이 높게 나타난 반면 경북, 경남은 낮은 부적합률을 보이는 등 지역별 자동차검사 부적합률에 차이가 존재하는 경향을 보이고 있다. 또한 지역별 자동차검사 부적합률은 인접 지역 간 유사한 경향을 보이는 군집적인 특성을 보이기도 하는데, 이는 자동차검사 부적합률 역시 공간적 속성을 기반으로 하는 공간데이터의 한 종류이기 때문에 나타난 결과라고 볼 수 있다.

일반적으로 인접한 지역 간에는 지역적 특성이 유사한 경향을 나타내기 때문에 인접한 지역 간 자동차검사의 부적합률에도 서로 영향을 주고받는 상호연관성, 즉 공간적 의존성이 존재하는 것으로 볼 수 있다. 그 이유로는 차량의 운행범위가 한 지역 내로 국한되지 않는다는 것을 고려할 때, 자동차의 운행상태는 다수 지역의 지형적 특성 및 기후 등에 의해 영향을 받게 되기 때문이다. 그러므로 이러한 특성을 고려하지 않은 분석은 공간적 의존성을 가지고 있는 변수들의 관계를 잘못 규명하는 결과로 이어질 수 있다.

지리학자인 Waldo Tobler가 주장한 지리학 제1법칙(The First Law of Geography)^*에 의하면 공간상에 분포되어 있는 객체들은 임의적으로 존재하는 것이 아니라 객체 간에 서로 영향을 주고받는 상태로 존재하는데, 이것이 곧 지리정보과학의 틀을 이루는 가장 기본적 개념 중 하나인 공간적 의존성 또는 공간적 자기상관을 의미한다.¹²⁾

일반적으로 공간객체를 포함하는 공간 데이터에는 이와 같은 공간적 의존성(또는 자기상관)(Spatial dependence or autocorrelation) 외에도 공간적 이질성(Spatial heterogeneity)이라는 두 가지 특성이 내재되어 있기 때문에, 선형회귀분석과 같은 계량경제모형을 적용하고자 할 때에는 이 두 가지 특성이 미치는 영향을 적절하게 통제하는 것이 필요하다.³⁾ 공간적 의존성의 영향을 적절하게 통제하지 못한 상태에서 일반선형회귀모형을 예측할 경우, 통상최소자승법(Ordinary least square)을 통해 예측된 회귀계수는 더 이상 최선불편추정량(Best linear unbiased estimator)의 속성을 가지지 못하는 편의된 추정량(Biased estimators)이 되며, 공간적 이질성은 추정된 회귀계수의 효율성을 저하시켜 올바른 통계적 추론을 하지 못하도록 영향을 미치는 주요한 요인으로 작용한다.^6,20)

공간 데이터가 가지고 있는 이런 문제점을 해결하기 위한 대안으로 공간계량분석기법이 나타나게 되었는데, 현재까지 공간객체를 다루는 다양한 분야에서 공간계량분석기법이 사용되어 오고 있다. 대표적으로 주택가격 추정을 위한 연구,^3,14) 폭력범죄의 특성에 관한 연구,^23,24) 교통사고 발생 특성 분석^6,7) 등 공간적 분포 특성에 따른 이질성 및 공간적 의존성 연구에 폭넓게 활용되어 오고 있다.

따라서 본 연구는 자동차검사데이터와 공간데이터를 결합하여 자동차검사 부적합률 자료에 공간적 자기상관성이 존재하는지 여부를 확인하고, 자동차 부적합률에 영향을 주는 변수들을 공간계량모형을 통해 분석하여 차량 및 환경요인으로 인해 발생하는 교통사고에 대한 대책 마련에 기초적인 정보를 제공하는 것을 목적으로 한다.

2. 연구방법

2.2 연구방법

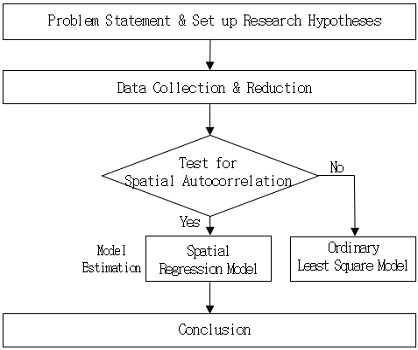
본 연구의 연구 과정은 Fig. 1과 같다. 먼저 자동차검사 부적합률의 공간데이터는 지역별로 편차가 클 뿐 아니라 군집적인 특성을 나타내고 있기 때문에 공간적으로 인접성을 가진다는 가설을 정립하였다. 그 다음 수집된 자료를 기반으로 공간적 자기상관이 있는지를 검토한 후, 공간적 자기상관성이 유의한 경우 공간계량분석기법을 적용하여 분석을 실시하고, 최종적으로 자동차검사 부적합률에 영향을 주는 지역적 특성을 규명하고 이에 대한 결론을 도출한다.

Fig. 1

Research procedure

2.2.1 GIS Data Format

한국교통안전공단에서 제공하는 자동차검사데이터는 차량의 개별특성과 검사판정에 대한 내용을 담고 있다. 본 연구에서는 분석을 위해 한국교통안전공단(2018∼2019)의 검사판정 중 1부 부적합, 2부 부적합, 1부 부적합+시정권고, 2부 부적합+시정권고와 같은 4가지 판정결과를 받은 차량을 부적합 차량으로 규정하여 종속변수로 활용하였다.

독립변수는 개별 차량의 속성을 나타내는 변수와 지역적 특성을 대변할 수 있는 변수 2가지 유형으로 구분하였다. 개별차량 데이터는 기존 연구에서 자동차의 결함에 영향을 준다고 밝혀진 평균 차령,^18,22) 경유차량 비율,⁹⁾ 사업용차량 비율⁶⁾을 자동차검사데이터(2018∼2019)에서 산출하였다.

지역적 특성으로는 자동차검사데이터에서 산출한 민간검사소비율과 기상청¹⁷⁾의 평균기온 및 강수량, KOSIS¹⁰⁾의 도로포장률이 있다. 먼저 연합뉴스²⁵⁾에서 보도된 바와 같이 민간검사소의 합격률이 공단검사소보다 높아 검사가 허술하다는 지적을 기반으로 부적합률에 영향을 준다고 가정하였으며, 장마철 수막현상과 공기압 때문에 열이 과다하게 발생하여 차량결함이 발생한다는 연구¹¹⁾를 통해 강수량이 자동차 결함에 영향이 있다는 추론을 하였다. 또한 긴급출동 건수는 겨울철인 12월∼1월이 가장 많았고 기온이 영하로 떨어지는 날씨에 연료의 파라핀 성분이 응고되어 점성이 더욱 높아지면서 자동차 연료의 필터를 막아 자동차 결합을 유발한다는 연구²⁾를 근거로 기온이 자동차 결함에 영향이 있다는 가설을 정립하였다.

한국교통안전공단⁸⁾의 자동차검사소 현황 주소와 통계청²¹⁾의 경계선을 포함한 공간 파일을 활용하여 공간데이터를 구축하였다. 구축된 공간데이터와 종속변수 및 독립변수를 결합하여 공간적 자기상관성 분석에 필요한 GIS data format을 구축하였다.

Table 1은 종속변수와 독립변수의 기술통계량이다. 종속변수인 자동차검사 부적합률은 최솟값인 충청남도 계룡시의 5.7 %와 최댓값인 미추홀구의 41.1 %간 격차가 35.4 %로 상당하였다. 독립변수인 평균기온은 강원도 평창군이 4.3 °C, 대구 수성시가 16.4 °C이며, 강수량은 파주시가 1,009.5 mm, 거제시가 2,507.6 mm으로 지역별로 기후의 차이가 발생하였다. 도로 포장률은 경상남도 의령군이 62.1 %로 가장 적은 수치로 분석되었다. 민간검사소의 비율은 평균 93 %로 분석되었고 검사차량의 평균차령은 서울시 용산구 2.2년과 강원도 정선군 11.7년간에 9.6년의 격차가 발생했다. 사업용 차량의 비율은 최솟값인 강원도 양구군과 최댓값인 전라남도 보성군의 격차가 69 %, 경유차량의 비율은 최솟값인 서울시 용산구와 최댓값인 전라남도 신안군의 격차가 57.3 %로 상당하였다.

Table 1

Descriptive statistics of variable

종속변수와 독립변수의 기술통계량을 분석한 결과 각 변수들이 지역별로 편차가 발생하고 특정지역에 높고 낮음이 군집하는 경향이 밝혀졌다.

2.2.2 공간가중행렬(Spatial Weights Matrix)

공간가중행렬이란 연구대상지역 내 지점 간에 서로 공간적으로 인접하고 있는가의 여부를 파악할 수 있도록 행렬 형태로 나타낸 것으로, n×n 차원의 정사각행렬로 이루어진다.⁴⁾ 공간 간의 상호작용 정도를 정의하고 i 지역과 j 지역이 인접하면 행렬의 구성요소인 W_ij는 1이 된다. 공간가중행렬을 어떻게 구축하는지에 따라 공간계량모형의 연구결과가 상이하기 때문에 공간가중행렬의 인접지역에 대한 정의는 중요한 단계인데, 구축 방법은 인접성 방식(Contiguity weight), 거리 방식(Distance weight), 근접 지점수 방식(K-Nearest neighbors)으로 구분된다.⁴⁾

인접성 방식(Contiguity weight)은 일반적으로 두 지역이 한 변을 공유하는 Rook형, 두 지역이 한 모서리를 공유하는 Bishop형, 두 구역이 한 변 또는 한 모서리를 공유하는 Queen형의 3가지 방식으로 분류된다. 거리방식(Distance weight)은 일정거리 이하에 위치하면 인접한 지역으로 정의하는 방식이며, 근접 지점수 방식(K-Nearest neighbors)은 일정개수 이하의 지역만 인접한 지역으로 정의하는 방식이다.

서만훈 등¹⁵⁾의 연구에서는 도서지역을 포함하기 위해 거리방식(Distance weight)을 적용하였지만, 본 연구는 도서 지역을 제외한 220개의 시⋅군⋅구로 연구의 공간적 범위를 설정하였기 때문에 인접성 방식(Contiguity weight)인 Rook형을 적용하였다.

2.2.3 공간적 자기상관성(Spatial Autocorrelation)

공간적 자기상관성이란 특정 관측치가 일정 변수에 의한 영향을 받을 뿐만 아니라 공간적인 특성에 영향을 받아 변량의 크기가 유사한 지역이 서로 밀집하는 현상이다. 일반적으로 공간 데이터 상에서 공간적 자기상관성이 존재하는지의 여부는 크게 전역적 자기상관성과 국지적 자기상관성 방식으로 검토된다.⁴⁾

전역적 자기상관성(Global autocorrelation)은 분석대상지역 내에서 유사한 값들의 전반적인 군집 경향을 하나의 지표로 나타낸 것으로 Moran¹⁶⁾이 제안하는 I지수와 Geary¹⁹⁾가 제안하는 G지수가 보편적으로 이용된다. I지수는 높은 값들의 군집과 낮은 값들의 군집을 구분하지 못하고 유사한 값들의 군집을 지수에 적용하나, G지수는 높은 값과 낮은 값의 군집을 구분하여 반영한다.⁴⁾ 본 연구는 군집한 지역의 높고 낮음의 차이보다는 일정 지역에 군집한 경향을 파악하여 공간적으로 자기상관성이 있음을 검증하는 것을 목적으로 하기 때문에 Moran이 제안하는 I지수를 활용하여 자기상관성 검증을 실시하였다. Moran’s I 지수는 -1과 1 사이의 값을 가지는데, 1의 경우 완전한 양의 자기상관성을, -1은 완전한 음의 자기상관성임을 나타낸다. 유사한 값들을 가진 값들이 지역적으로 인접해있는 경우 1에 가까운 값을 가지게 되고, 높고 낮은 값들이 고르게 분포해있는 경우 –1에 수렴한다. I지수의 산정 식은 식 (1)과 같다. 여기서, N은 관측치의 수, Y_i와 Y_j는 각 지역의 관측치, $$ \overline{Y}$$는 관측값들의 평균값이며, W_ij는 열의 합을 1로 하는 공간가중행렬 W의 (i, j)번째 원소값이다.

$\[ I=\frac{N\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}\left(Y_i-\overline{Y}\right)\left(Y_j-\overline{Y}\right)}{\left(\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}\right)\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2} \]$

(1)

국지적 자기상관성(Local autocorrelation)은 특정지역을 중심으로 유사한 값들을 보이는 공간적 군집패턴을 세부적으로 나타내는 통계량을 의미한다. 전역적 자기상관성에서는 분석대상 지역 전체의 공간적 자기상관성을 하나의 값으로 나타낸다는 한계가 있다. Anselin¹⁾은 국지적 차원에서의 공간적 자기상관성을 측정하기 위해 Local Indicator of Spatial Association(LISA) 지수를 제안하였고 공간적 군집지역인 HH(High-High) 및 LL(Low-Low)과 공간적 이례지역인 HL(High-Low) 및 LH(Low-High)로 구분하였다. LISA지수의 경우 특정 지역의 값과 주변 지역들이 가지는 값의 가중평균이 서로 유사하면 정적인 자기상관, 차이가 크게 나타나면 부적인 자기상관으로 정의하며, 산정 식은 식 (2)와 같다. 여기서, n은 관측횟수, y_i와 y_j 각 지역의 관측치, $$ \overline{Y}$$는 관측값들의 평균값이며, W_ij는 i 위치와 j 위치 사이의 행렬을 의미한다.

$\[ I_i=\frac{n^2}{\left(\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}\right)}\times \frac{\left(y_i-\overline{Y}\right)\sum _{j=1}^n{w}_{ij}\left(y_j-\overline{Y}\right)}{\sum _{i=1}^n{\left(y_i-\overline{Y}\right)}^2} \]$

(2)

2.2.4 공간회귀모델

일반선형회귀모델(Ordinary Least Squares, OLS)에서는 종속변수의 관측치와 오차값이 서로 독립되어 있다고 가정하며, 회귀식에 의해 설명되지 않은 잔차는 공간적 상관성이 없다고 가정한다. 따라서 공간적 의존성으로 인해 공간적 자기상관성이 통계적으로 유의미하게 나타난다면 선형회귀모델의 가정에 위반하게 되고 추정된 회귀계수가 편기되는 결과를 얻는다.⁴⁾ 따라서 공간적 자기상관성의 분석기법으로 선형회귀모델을 적용하는 것은 적절치 않고 대체모델로 공간회귀모델을 적용한다.

공간회귀모델(Spatial regression model)이란 공간데이터의 특성으로 인해 선형회귀모델의 가정에 위반하여 발생하는 문제를 해결하여 모델의 추정결과에 대한 신뢰도를 높이는 분석기법으로 공간시차모델과 공간오차모델이 있다.

공간시차모델(Spatial lag model)은 종속변수가 공간적 자기상관성을 가지는 경우 적용하는 분석기법이다. 주변지역들이 종속변수에 미치는 영향을 변수화하고 새로운 독립변수로 추가하여 인접한 관측치에 대한 영향력을 통제하는 것으로, 모형식은 식 (3)과 같다. 여기서, W는 공간가중행렬, ρ는 공간자기회기계수로 벡터 Y가 이웃하고 있는 관측개체들의 공간가중된 평균값에 의해 설명되는 정도이며, X는 주택 속성별 변수 벡터, ε는 오차항을 의미한다.

$\[ \begin{array}{cc}Y=\rho WY+X\beta +ϵ,& ϵ~MNV\left(0,{\sigma }^2{I}_n\right)\end{array} \]$

(3)

공간오차모델(Spatial error model)은 오차에서 공간적 자기상관성이 존재하는 경우 적용하는 대안이다. 각각의 오차 공분산을 만들어 오차들 사이에 존재하는 공간적 종속성을 통제하고 휘귀모델내에서 공간적 상호작용의 영향을 고려한다. 공간오차모델은 식 (4)와 같이 표현되며, 공분산구조를 활용하기 때문에 선형회귀모델에 비해 신뢰도 있는 결과를 얻을 수 있다. 여기서, X는 주택 속성별 변수 벡터, ε는 오차항을 의미한다.

$\[ Y=X\beta +ϵ\left(\begin{array}{cc}ϵ=\lambda W\mu +\mu ,& ϵ~MNV\left(0,{\sigma }^2{I}_n\right.\end{array}\right) \]$

(4)

3. 연구결과

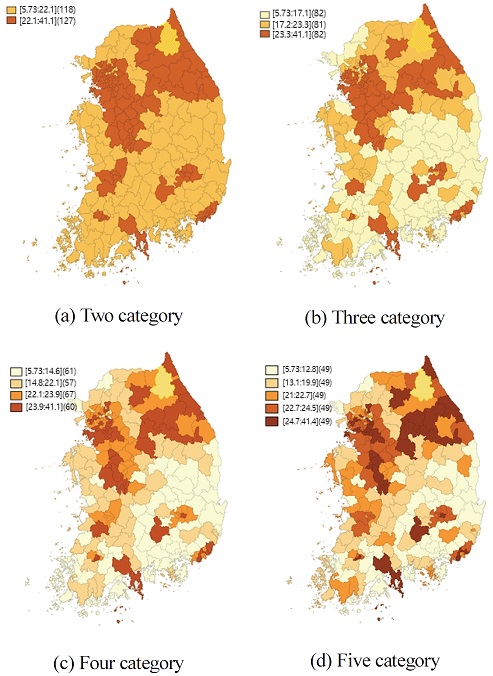
자동차검사 부적합률의 공간적 분포를 범주 개수에 따라 시각화한 결과는 Fig. 2와 같다.

Fig. 2

Quantile map by range number

범주를 2개로 구분한 (a)를 보면 자동차검사 부적합률이 지역별로 높고 낮음이 군집되어 분포하고 있는 것을 명확하게 확인할 수 있는데, 서울, 경기, 강원지역에 자동차검사 부적합률이 높았고 경북, 경남, 전북 지역에 낮은 것으로 분석되었다. 범주 개수가 3, 4, 5개인 (b), (c), (d) 지도를 비교한 결과 역시 자동차검사 부적합률의 높고 낮음이 일정 지역을 중심으로 점진적으로 확산되는 경향을 보이고 있음을 알 수 있다. 따라서 자동차검사 부적합률은 공간적 자기상관성이 있다는 연구가설을 정립하고 공간적 자기상관성 검증을 실시하였다.

3.1 전역적 자기상관성

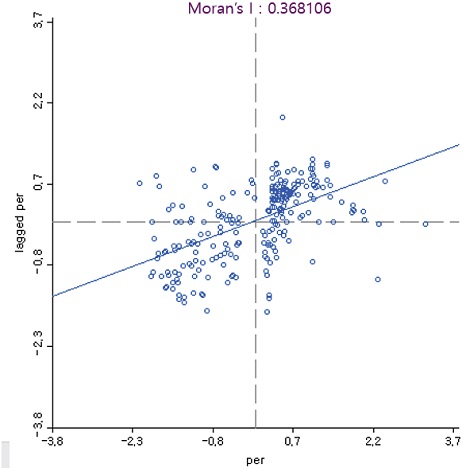
자동차검사 부적합률 자료에 공간적 자기상관성이 존재하는지 여부를 확인하기 위한 Moran’s I 분석을 실시하였으며, 그 결과는 Fig. 3과 같다. Moran’s I 통계량이 0이상이면 공간적 자기상관성이 존재한다고 판단할 수 있는데,⁴⁾ 자동차검사 부적합률의 Moran’s I 통계량은 0.37로 공간적 자기상관성이 존재한다는 결과를 얻을 수 있다.

Fig. 3

Moran’s I factor of global autocorrelation

3.2 국지적 자기상관성

공간적으로 부적합률의 높고 낮음이 분포되어있는 지역을 세부적으로 분석하기 위해 국지적 자기상관성 검증을 실시하였다. 국지적 자기상관성 검증은 크게 5개 유형으로 구분되는데, 부적합률이 높은 지점끼리군집한 HH(High-High)유형, 반대로 부적합률이 낮은 지점끼리 군집한 LL(Low-Low)유형, 높은 지점 주변에 낮은 지점이 존재하는 HL(High-Low)유형, 낮은 지점 주변에 높은 지점이 존재하는 LH(Low-High), 특이사항이 없는 지점인 Not significant로 구분된다.

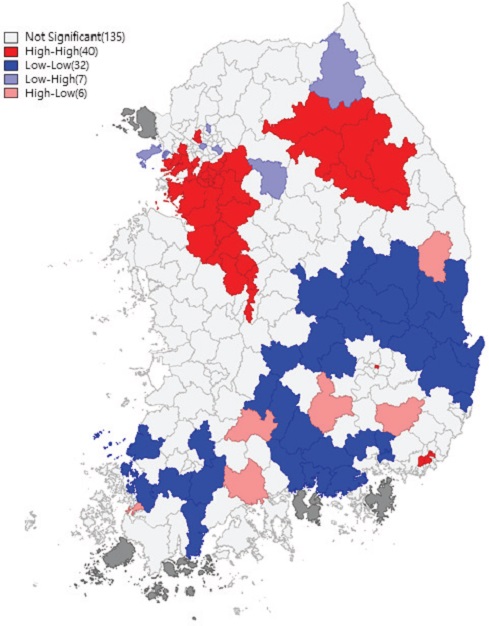
국지적 자기상관성을 분석한 결과 Table 2와 같이 HH(High-Low) 40곳, LL(Low-Low) 32곳, HL(High-Low) 6곳, LH(Low-High) 7곳, Not significant 135곳으로 구분되었다.

Table 2

Number by local autocorrelation type

부적합률이 높은 지역끼리 군집한 HH유형으로 구분된 40개 시⋅군⋅구는 주로 서울, 경기, 대전, 강원지역에 밀집하고 있는 것으로 분석되었고, 반대로 부적합률이 낮은 지역끼리 군집한 LL유형은 경북, 경남, 전북을 중심으로 분포하고 있는 것을 Fig. 4에서 확인 할 수 있다.

Fig. 4

Lisa cluster map of vehicle inspection incongruity

3.3 공간회귀모델

공간회귀모델을 적용하기 전 선형회귀모델 분석을 통해 변수의 적절성을 평가하였으며, 추정결과는 Table 3과 같다. CONDITIONNUM이 30이하로 다중공선성의 심각성이 없고 Jarque-Bera 검증결과 유의수준 내에 기각할 수 없어 오차항이 정규분포를 따르고 있다.⁴⁾ 오차항의 분산이 일정하지 않음을 의미하는 이분산성을 검증한 결과 Breush-Pagan을 제외한 두 검정에서는 유의수준에서 귀무가설을 기각할 수 없어 오차항에 이분산이 존재하지 않는 것으로 판단된다. 선형회귀모델 추정 결과 종속변수와 독립변수의 데이터는 회귀분석을 적용하는데 적절하며, 자동차검사 부적합률의 분산에 영향을 미치는 것은 독립변수에 의해서만이 아닌 이웃하는 주변 지역들의 영향을 받는 것으로 분석되었다.

Table 3

Estimation result of OLS

본 연구에서는 최적합 분석모델을 선정하기 위해 Lagrange Multiplier(LM) 검증을 실시하였다. LM 검증에서 LM-Lag와 LM-Error 모두 유의한 결과를 얻었으나, Robust LM검증에서 Robust LM-Lag만 유의한 결과를 얻어 본 연구의 분석모델로 공간오차모델은 적절하지 않은 것으로 판단되었다. 따라서 본 연구에서는 공간시차모델을 최적합 분석모델로 선정하였다.

자동차검사 부적합률에 영향을 주는 지역별 특성을 선형회귀모델과 공간회귀모델로 분석한 결과는 Table 4와 같다. 일반적으로 공간회귀모델의 추정은 최대우도법(Maximum likelihood method)으로 이루어지기 때문에 모델의 설명력을 결정계수인 R²로 진단하지 않는다.¹⁵⁾ 따라서 공간회귀모델과 선형회귀모델의 설명력 비교는 Log Likelihood(LL), Akaike Information Criterion(AIC), Schwarz Criterion(SC) 통계량으로 실시하였다. 공간시차모델의 LL통계량이 -695.6으로 공간오차모델 -699.62보다 크고 AIC, SC통계량이 각각 1407.2, 1435.21로 가장 적은 것으로 나타나 최적합 모델은 공간시차모델인 것으로 결론내릴 수 있다.¹⁵⁾

Table 4

Result of spatial regression models

최적합모델로 선정된 공간시차모델을 중점으로 자동차검사 부적합률에 영향을 주는 변수를 살펴보면, 평균기온(Average temperature), 민간 검사소 비율(Percentage of private inspection stations), 검사차량의 평균차령(Average vehicle age), 경유차량비율(Percentage of diesel vehicles inspected), 강수량(Amount of precipitation)이 유의한 변수로 나타났다. GM²⁾의 연구와 유사하게 평균기온이 낮은 지역일수록 자동차검사 부적합률이 높았고 민간검사소의 비율이 높을수록 부적합이 낮다는 결과를 얻었다. Washburn 등²²⁾과 Bin¹⁸⁾의 연구는 차량이 오래될수록 결함이 많이 발생한다는 변수 간의 단순한 관계를 규명한 것과 달리, 본 연구에서는 공간적 특성을 고려하여 오래된 차량이 많은 지역일수록 자동차의 결함이 많이 발생한다는 결과를 얻었다. 최경임 등⁹⁾의 연구와 유사하게 경유차량의 비율이 높은 지역일수록 자동차검사 부적합률이 높다는 분석결과가 나타났다. 장마철 수막현상과 공기압 때문에 열이 과다하게 발생하여 차량결함이 발생한다는 연구¹¹⁾와 유사하게 강수량이 많을수록 자동차 결함이 더 발생하는 것으로 나타났다.

강수량은 모델에 따라 검증 결과가 다르게 분석되었다. 선형회귀모델과 공간오차모델에서는 유의 수준을 벗어났지만, 공간시차모델에서 유의한 것으로 나타났다. 최적합 모델로 선정된 공간시차모델과 선형회귀모델 및 공간오차모델의 결과가 다른 것은 공간적 자기상관성을 가시는 종속변수에 대한 모델 선택의 중요성을 시사한다.

4. 결 론

본 연구는 자동차검사 부적합률의 공간적 자기상관성을 검증하였고 공간적 자기상관성 검증 결과를 기반으로 자동차검사 부적합률에 영향을 주는 지역적 특성을 공간회귀모델로 추정하였다.

References

• L. Anselin, “Local Indicator of Spatial Association-LISA,” Geographical Analysis, Vol.27, No.2, pp.93-115, 1995. [https://doi.org/10.1111/j.1538-4632.1995.tb00338.x]
• GM, Analysis of Cause of Vehicle Defects in Winter, Incheon, 2012.
• H. J. Chun, “A Study on the Comparison of Housing Price Models Using Spatial Metrics and GIS,” KREA, Vol.64, pp.46-56, 2016.
• H. Y. Lee and S. C. No, Advanced Statistic Analysis Theory, Moon Woo Sa, Gyeonggi, pp.634-657, 2013.
• J. H. Sul and J. H. Kim, Analysis of Cost and Effectiveness of Automobile Inspection System, Policy Research Report, KOTI, pp.1-15, 1998.
• J. W. Lee and T. H. Kim, “Examing the Characteristics of Traffic Accidents Involving Elderly Drivers in Seoul,” The Korea Spatial Planning Review, Vol.102, pp.19-34, 2019. [https://doi.org/10.15793/kspr.2019.102..002]
• K. A. Rhee, Traffic Accident Analysis Using Spatial Econometrics: A Case of Seoul, Ph. D. Dissertation, Seoul National University, Seoul, 2016.
• Korean Transportation Safety Authority, Vehicle Inspection Data, Gimcheon, 2018-2019.
• K. I. Choi, T. H. Kim and S. I. Lee, “Traffic Accident Risk Classification on the Vehicle Inspection Code Utilizing Data Mining(CHAID),” Korea Institute of Intelligent Transport System: 2012 Spring Conference, pp.440-445, 2012.
• Kosis, Road Pavement Rate by City, County and District, South Korea, 2019.
• Hankook Tire, Suggestions for Safe Driving in the Rainy Season, https://www.donga.com/news/article/all/20210705/107793394/2, , 2021.
• K. K. Kemp, Encyclopedia of Geographic Information Science, SAGE, California, p.146, 2008. [https://doi.org/10.4135/9781412953962]
• Ministry of the Interior and Safety, Local Government Administrative Districts and Population, Sejong, pp.4-205, 2018.
• M. S. Choi and S. Y. Byeon, “Comparison on Forecasting Performance of Housing Price Prediction Models in Seoul,” Seoul Studies, Vol.17, No.3, pp.75-89, 2016.
• M. W. Seo, J. S. Lee and Y. Choi, “Estimation of the Natural Damage Dissaster Considering the Spatial Autocorrelation and Urban Characteristics,” KSCE Journal of Korea Society of Civil Engineers, Vol.36, No.4, pp.723-733, 2016. [https://doi.org/10.12652/Ksce.2016.36.4.0723]
• P. A. P. Moran, “The Interpretation of Statistical Maps,” Journal of the Royal Statistical Society. Series B (Methodological), Vol.10, No.2, pp.243-251, 1948. [https://doi.org/10.1111/j.2517-6161.1948.tb00012.x]
• Korea Meteorological Administration, Average Annual Value of Domestic Climate (During 30 Years), http://www.weather.go.kr/weather/climate/shortcut/shortcut_05.jsp, , 2019.
• O. K. Bin, “A Logit Analysis of Vehicle Emissions Using Inspection and Maintenance Testing Data,” Transportation Research Part D: Transport and Enviroment, Vol.8, No.3, pp.215-227, 2003. [https://doi.org/10.1016/S1361-9209(03)00004-X]
• R. C. Geary, “The Contiguity Ratio and Statistical Mapping,” The Incorporated Statistician, Vol.5, No.3, pp.115-145, 1954. [https://doi.org/10.2307/2986645]
• S. W. Lee, S. D. Yoon, J. Y. Park and S. D. Min, Spatial Measurement Model Application, Pybook, Seoul, 2006.
• Statistics Korea, 2019 Administrative District Boundary: City, County and District, Geographic Information Service, Sejong, 2019.
• S. Washburn, S. Joseph and F. Mannering, “Statistical Modeling of Vehicle Emissions from Inspection Maintenance Testing Data,” Transportation Research Part D, Vol.6, No.21, pp.21-36, 2001. [https://doi.org/10.1016/S1361-9209(00)00011-0]
• Y. H. Yeom, “Spatial Regression Analyses on the Relationship between Alcohol Outlet and Violent Crime Rates,” The Journal of Police Science, Vol.18, No.3, pp.109-132, 2018.
• Y. H. Yeom, “Analysis on Structural Covariates and Spatial Heterogeneity of Violent Crimes in Application of Geographically Weighted Regression Model,” The Journal of Police Science, Vol.18, No.4, pp.9-40, 2018.
• Yonhap New Agency, Private Auto Inspection Center Foolish Inspection Detected Ignoring Fine Dust Emission, https://www.yna.co.kr/view/AKR20190709065851004, , 2019.