[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 29, No. 12, pp.1147-1159

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Dec 2021

Received 26 Apr 2021 Revised 17 Aug 2021 Accepted 29 Sep 2021

DOI: https://doi.org/10.7467/KSAE.2021.29.12.1147

주행 경로의 곡률 특성 반영을 통해 추종 성능을 향상시킨 가변 지평선 Model Predictive Control

최윤석¹⁾

; 이원우¹⁾

; 유진우^*^{, 2)}

1)국민대학교 자동차공학전문대학원
2)국민대학교 자동차IT융합학과

A Variable Horizon Model Predictive Control Based on Curvature Properties of Vehicle Driving Path

Yoonsuk Choi¹⁾

; Wonwoo Lee¹⁾

; Jinwoo Yoo^*^{, 2)}

1)The Graduate School of Automotive Engineering, Kookmin University, Seoul 02707, Korea
2)Department of Automobile and IT Convergence, Kookmin University, Seoul 02707, Korea

Correspondence to: ^*E-mail: jwyoo@kookmin.ac.kr

Copyright Ⓒ 2021 KSAE / 193-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

This paper proposes a novel model predictive control(MPC) algorithm that increases the path tracking performance based on the driving path. The proposed algorithm reduces the path tracking errors of the MPC by utilizing the curvature of each driving step to update the prediction horizon for the path, and also updates the control horizon according to the latest prediction horizon. We will construct a scenario where straight and curved paths are combined, and then calculate curvatures according to the path at each step. In other words, we will update both the prediction horizon and the control horizon through the calculated curvature at each step. The results of the experiment will verify the tracking performance between the basic MPC and the proposed algorithm via Matlab simulations. Hence, we will demonstrate that the proposed MPC algorithm can improve the path tracking performance compared to the basic MPC.

Keywords:

Model predictive control, Autonomous driving, Path tracking, Prediction horizon, Variable horizon

키워드:

모델 예측 제어, 자율주행, 경로 추종, 예측 지평선, 가변 지평선

1. 서 론

최근 자동차 업계에서 자율주행 자동차와 차량 부품의 전장화가 화두로 떠오름에 따라 차량의 많은 부품이 전기 장치로 바뀌고 있다. 이에 따라 Model Predictive Control(MPC)를 활용하여 자율주행 자동차에 접목하여 차량의 주행 경로를 추종하거나 엔진, 변속기, 배기가스, 모터 등의 효율을 최적화하는 연구가 활발히 진행되고 있다.

MPC는 1960년대 초, Kalman이 제약 없는 2차 목적 함수를 최소화하도록 설계한 선형 2차 조절기(LQR)을 사용하면서 연구가 진행되었다. 하지만 MPC는 실제 산업 프로세스의 비선형성에 대한 문제 때문에 산업에 응용되기까지 오랜 시간이 걸렸다. MPC가 산업 프로세스 제어에 응용된 것은 1978년이다.¹⁾ 당 해에 화학 공학자들이 MPC를 화학 공정에 적용해 다른 제어 기법에 비해 이점이 있다는 것을 입증하며, 다양한 산업 분야에서 MPC를 활용하게 되었다.

MPC가 다양한 산업 분야에서 활용되면서 1990년 대 초 자동차 산업 분야에도 적용되었다. Ford Motor Company에서 MPC를 기반으로 한 제어 기술을 탐구하기 시작하면서 Direct injection stratified charge engines²⁾과 Traction control³⁾ 등에 대해 MPC를 적용했고, 다양한 자동차 분야에 MPC가 적용되면서 ADAS⁴⁾와 자율주행 분야까지 확장되어 최적의 궤적이나 충돌 회피 궤적을 설계하는 연구가 이루어졌다.^5,6) 또한, 도로의 곡률 정보를 기반으로 MPC의 Reference data를 다시 설정하여 추종 성능을 높이는 MPC,⁷⁾ 도로의 곡률 정보를 기반으로 차량의 속도를 제어하는 MPC,⁸⁾ 타이어의 지면 마찰과 도로의 곡률을 활용하여 제약 조건을 다시 설정한 후, 경로 추종 성능을 높이는 MPC⁹⁾처럼 차량의 상태만 고려하는 것이 아닌 도로의 곡률 등 외부 정보도 고려하여 차량의 추종 성능을 높이는 MPC에 대한 연구가 이루어지고 있다.

MPC는 Non-linear MPC를 통해 차량 모델의 비선형성을 고려하거나, Robust MPC처럼 상태 제약 조건을 더 강화하여 추종 성능을 높이는 방향으로 발전되었다. 이러한 연구에서는 Horizon의 크기를 고정해서 MPC가 실행되었고, Horizon의 크기를 경험적으로 설정해왔다. 하지만 고정된 Horizon을 활용하는 MPC는 Prediction horizon과 Control horizon의 크기에 따라 Horizon의 크기가 큰 경우에는 추종 성능은 좋지만, 계산 부하가 생긴다. 반대로 Horizon의 크기가 작은 경우에는 계산 시간은 빠르지만, 추종 성능이 부족해지는 단점이 있다. 이 방법은 다양한 시나리오에서 다양한 동작을 취해야 하는 자동차에는 맞지 않는다는 단점이 있다.

위의 단점을 보완하기 위해 Horizon의 크기를 변수로 설정하는 연구가 진행되었다. 하지만 이 또한, 도로가 직선인 지, 곡선인 지 판단하여, Prediction horizon의 크기를 길 때와 짧을 때, 2가지로 설정하여 선택하는 2-stage horizon 방법이거나 특정 조건이 만족하면, 미리 설정해 놓은 Horizon을 대입하는 방법이기 때문에 차량이 항상 적절한 수준의 Horizon으로 주행하기에는 무리가 있다.^10,11)

따라서, 본 논문에서는 주행 경로에서 곡률의 변화량에 따라 Prediction Horizon을 새롭게 갱신하고, 갱신한 Prediction horizon에 따라 Control horizon도 적절한 수준으로 갱신하여 주행하는 연구를 진행하였다. 기존 연구에서 Horizon을 일정한 상수로 설정하여 주행하는 것과는 다르게 Horizon을 변수로 설정해서 주행 경로의 곡률에 따라 Horizon을 변경하여 주행하게 함으로써 차량의 경로 추종 성능을 향상시켰다.

2. MPC 설계

이 장에서는 MPC를 설계한다. 2.1절에서는 차량의 동역학적 특성을 바탕으로 한 Bicycle 모델을 제시한다.¹²⁾ 다른 절에서는 MPC를 설계하기 위한 이산 선형 차량 모델, 비용 함수, 제약 조건에 대해 소개한다.

2.1 차량의 동역학적 모델

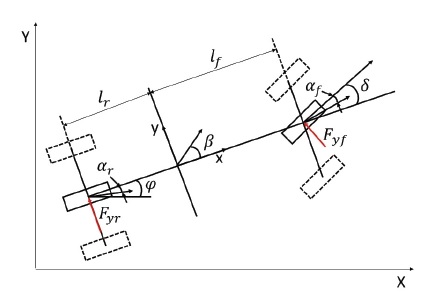
이 절에서는 MPC 설계에 사용한 차량의 Bicycle model에 대해 설명한다. 차량의 모델을 구할 때, 다음과 같은 가정을 한다. 1) 차량의 종방향 속도는 일정하다. 2) 앞바퀴, 뒷바퀴는 각각 좌우 바퀴가 하나의 바퀴로 뭉쳐있다. 3) 현가장치의 움직임, 미끄러짐 현상, 공기 역학적 영향은 매우 작다. 4) 뒷바퀴의 조향각은 0이다.¹³⁾ 위 가정을 통해 Fig. 1과 같이 차량의 선형 모델을 뉴턴의 법칙을 사용하여 구할 수 있다.

m V β ˙ + ψ ˙ = F x f + F x r,

(1)

I z ψ ¨ = l f F x f - l r F x r,

(2)

Fig. 1

Bicycle model of vehicle

여기서 F_xf와 F_xr은 아래와 같다.

F x f = C f × α f = C f × δ - β - l f ψ ˙ V,

(3)

F x r = C r × α r = C r × - β + l r ψ ˙ V

(4)

식 (3), (4)를 식 (1), (2)에 대입하면 아래와 같이 Sideslip angle(β)과 Yaw rate( $Ψ ˙$ )에 대한 차량 모델 식으로 표현할 수 있다.

β ˙ = - C r + C f m V β + C r l r - C f l f m V 2 - 1 ψ ˙ + C f m V δ

(5)

ψ ¨ = C r l r - C f l f I z β - C r l r 2 + C f l f 2 I z V ψ ˙ + C f l f I z δ .

(6)

식 (5), (6)을 활용하면 상태 방정식을 구할 수 있다

MPC의 상태 방정식은 식 (7), (8)과 같이 쓸 수 있다.

X ˙ c = A c X c + B c δ,

(7)

Y c = C c X c

(8)

여기서 δ는 MPC의 입력인 조향각을 의미한다.

X c = P y β ψ ψ ˙ T,

(9)

여기서 P_y는 차량의 횡방향 위치, β는 차량의 Side slip angle, Ψ는 차량의 Yaw angle, $Ψ ˙$ 는 차량의 Yaw rate를 의미한다.

A c = 0 V V 0 0 - C r + C f m V 0 C r l r - C f l f m V 2 - 1 0001 0 C r l r - C f l f I z 0 - C r l r 2 + C f l f 2 I z V,

(10)

B c = 0 C f m V 0 C f l f I z, C c = 100001000001 .

(11)

식 (9), (10), (11)은 각각 연속 시간 상태 방정식에서 고려할 차량의 상태, 상태 행렬, 입력 행렬, 출력 행렬을 나타낸다.

2.2 MMPC¹³⁾를 위한 이산 선형 차량 모델

본 논문에서는 입력 제약 조건과 상태의 제약 조건을 체계적으로 처리할 수 있는 기능 때문에 다중 제약 조건이 있는 MPC를 계획된 궤적을 추적하기 위해 사용했다.¹³⁾ 앞 절에서 소개한 연속 시간 상태 방정식을 재귀 방정식의 형태로 바꾸기 위해 T_s의 주기로 이산 시간 상태 방정식을 구한 값은 다음과 같다.¹⁴⁾

X d k + 1 = A d X d k + B d u k,

(12)

A d = e A c T s, B d = ∫ 0 T s e A c r B c d τ .

(13)

MPC의 출력은 아래와 같다.

Y d k = C d X d k,

(14)

여기서,

Y d k = P y k β k ψ ˙ k,

(15)

C d = C c = 100001000001 .

(16)

경로 추종 문제에서 추종 성능을 높이기 위해 식 (12), (15)를 식 (17), (18)과 같이, 입력의 증분에 대한 형태로 변경한다.

X a k + 1 = A a X a k + B a ∆ u k,

(17)

Y a k = C a X a k,

(18)

여기서,

X a k = ∆ X d k Y d k,

(19)

A a = A d O d T C d A d I d, B a = B d C d B d,

(20)

C a = O d I d,

(21)

O d = 000000000000, I d = 100010001 .

(22)

식 (19), (20), (21)은 증강된 상태 방정식에 대한 변수, 입력, 출력에 대한 행렬이고, O_d는 출력 변수의 개수를 행의 개수로 가지고 상태 변수의 개수를 열의 개수로 가지는 0행렬이다. I_d는 출력 변수의 개수를 행과 열의 개수로 가지는 단위행렬이다.

2.3 MMPC의 비용 함수

비용 함수를 간략화하여 나타내기 위해 Reference 데이터와 MPC를 통해 예측한 데이터를 벡터화해서 표현한다.

∆ U m = ∆ u k, …, ∆ u k + m, …, ∆ u k + N C - 1 T

(23)

X m k = X a k,

(24)

Y m k = F m X m k + G m ∆ U m k, = Y a k + 1 … Y a k + N P T

(25)

여기서,

F m = C a A a C a A a 2 … C a A a N C … C a A a N P 3 N P × 7, T

(26)

G m = C a B a 0 ⋯ 0 C a A a B a C a B a ⋯ 0 ⋮ ⋮ ⋯ 0 C a A a N C - 1 B a C a A a N C - 2 B a ⋯ C a B a ⋮ ⋮ ⋱ ⋮ C a A a N P - 1 B a C a A a N P - 2 B a ⋯ C a A a N P - N C B a 3 N P × N C

(27)

MPC의 비용 함수는 상태 변수의 목표값과 최적화된 입력으로 계산된 상태 변수의 차이를 최소화하는 입력을 구하도록 만들어진다. 따라서 구성한 MPC의 비용 함수는 아래와 같다.

J = R r k - Y m k T R r k - Y m k + ∆ U m T R - ∆ U m

(28)

여기서,

R r k = P y r k + 1 β r k + 1 ψ ˙ r k + 1 ⋮ P y r k + N P β r k + N P ψ ˙ r k + N P, Y m k = P y k + 1 β k + 1 ψ ˙ k + 1 ⋮ P y k + N P β k + N P ψ ˙ k + N P .

(29)

비용 함수가 최솟값을 가지려면 비용 함수를 미분한 값이 0이어야 한다.

∂ J ∂ X m = 0, ∂ J ∂ U m = 0 .

(30)

식 (30)을 정리한 후, 식 (28)에 대입하면 아래와 같이 ∆U_m에 대한 비용 함수를 얻을 수 있다.¹⁰⁾

J = 12 Δ U m T E m ∆ U m + ∆ U m T K m,

(31)

여기서,

E m = 2 G m T G m + R -

(32)

K m = - 2 G m T R r k - F m X m k .

(33)

본 논문에서는 선형 제약 조건을 고려해 2차 비용 함수를 계산하기 위해 MATLAB의 quadprog함수를 사용했다.

2.4 MMPC의 제약 조건

MPC는 주어진 비용 함수, 상태 변수와 제약 조건에 따라 최적화된 제어 입력을 계산하므로 상태 변수, 입력 등에 대한 제약 조건을 설정한다. 본 논문에서는 입력 조건인 전륜 조향각, 출력으로 설정한 상태 변수인 횡방향 위치, Sideslip angle(β)과 Yaw rate( $Ψ ˙$ )에 대한 제약 조건을 설정했다. 비용 함수를 ∆U_m에 대한 식으로 수정하였으므로, 제약 조건도 ∆U_m에 관한 식으로 나타내어야 한다.¹⁵⁾

입력 벡터에 대한 제약 조건은 아래와 같다.

U min ≤ U m ≤ U max,

(34)

- U m ≤ - U min, U m ≤ U max .

(35)

식 (34)를 두 가지 불평등 제약 조건식으로 나타내면 식 (35)와 같고, 이를 행렬로 나타내면 다음과 같다.

- I I U m ≤ - U min U max .

(36)

U_m은 아래와 같은 식으로 표현할 수 있으므로

u k u k + 1 u k + 2 ⋮ u k + N C - 1 = I I I ⋮ I u k + 1 + I 00 ⋯ 0 I I 0 ⋯ 0 I I I ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ I I I ⋯ I ∆ u k ∆ u k + 1 ∆ u k + 2 ⋮ ∆ u k + N C - 1

(37)

식 (37)을 식 (36)에 대입하면 아래와 같은 제약 조건을 얻을 수 있다.

- C 2 C 2 ∆ U m ≤ - U min + C 1 u k - 1 U max - C 1 u k - 1,

(38)

여기서,

C 1 = 111 ⋮ 1 N C × 1, C 2 = I 00 ⋯ 0 I I 0 ⋯ 0 I I I ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ I I I ⋯ I N C × N C .

(39)

입력의 증분과 출력에 대해서 같은 과정을 거치면 아래와 같은 불평등 제약 조건을 얻을 수 있다.

- I I ∆ U m ≤ - ∆ U min ∆ U max,

(40)

- G m G m ∆ U m ≤ - C 3 P min β min ψ ˙ min + F m X m k C 3 P max β max ψ ˙ max - F m X m k .

(41)

식 (38), (40), (41)을 통해 MPC의 제약 조건을 완성한다.

M 1 M 2 M 3 ∆ U m ≤ N 1 N 2 N 3 .

(42)

3. Variable Horizon Model Predictive Control Based on Path Curvature

N_P는 예측된 미래 시간 단계의 수로 어느 시점까지 예측할 것인지를 의미한다. 즉, N_P가 너무 작은 경우에는 미래 상황에 대한 대처가 미흡해지고 너무 큰 경우에는 계산 부하가 걸리기 때문에 상황에 따라 적절한 값을 설정해야 한다. 따라서 본 논문에서는 자율주행 자동차가 주어진 시나리오를 주행할 때 추종 성능을 증가시킬 수 있도록 Variable horizon MPC based on path curvature를 제안한다.

3.1 Variable Horizon MPC Based on Path Curvature의 알고리즘

Variable horizon MPC based on path curvature는 단계마다 Horizon을 다르게 하여 각각의 주행 상황을 반영한 Horizon을 설정하여 주행하도록 설계되었다.¹⁶⁾

Variable horizon MPC based on path curvature의 기본 알고리즘은 아래와 같다. 직선 구간에서는 짧은 N_P를 유지하여 직선 구간을 안정적으로 따라갈 수 있도록 설계하고, 곡선 구간에서는 N_P를 길게 하여 곡률의 변화에 잘 대응하도록 설계한다.

Table 1은 Variable horizon MPC based on path curvature 알고리즘의 Pseudo code이다. 이는 다음 단계에 주행할 경로의 곡률을 계산하고, 계산한 곡률의 변화량을 기반으로 N_P,present, N_C,present 등을 계산하여 MPC에 적용하는 알고리즘이다.

Table 1

Pseudo code of Variable horizon MPC based on path curvature algorithm

3.2 Variable Horizon MPC Based on Path Curvature의 계산식

이 절에서는 Variable horizon MPC based on path curvature에서 N_P와 N_C를 설정할 때, 사용한 계산식에 대해 설명한다.

N P, p r e s e n t = N P, p a s t + s g n x e a x + e - a x - 2 + 12

(43)

여기서, N_P,past는 바로 전 단계에서 상태를 예측할 때 사용한 N_P이고, N_P,present는 현재 단계에서 상태를 예측할 때 사용할 N_P이다. x는 곡률의 변화량을 의미하고, a는 곡률의 변화량 값이 계산식 안에서 적절한 효과를 낼 수 있도록 보정하는 상수이다. 이 실험에서 a는 계산을 통해 나온 곡률의 최대값에 역수를 취하여 설정했다. 따라서, 곡률의 변화량이 클수록 N_P의 변화량은 전 단계에 비해 크다.

식 (43)은 곡률이 증가함에 따라 N_P도 증가하고, 곡률이 감소함에 따라 N_P도 감소하는 것을 나타낸다. 또한, N_P를 정수화하기 위해 x에 관한 식을 반올림하여 계산한다.

곡률의 변화량은 주행 경로가 직선에서 곡선으로 바뀌는 구간을 기점으로 다시 곡선에서 직선으로 바뀌는 구간에 진입할 때까지 증가하고 감소하는 경향이 반복된다. 여기서 지수 함수는 음의 구간에서 출력의 영향력이 많이 떨어지기 때문에 이를 보정하기 위해서 지수 함수와 지수 함수의 역수를 더한 꼴로 계산식을 나타낸다.

N C, p r e s e n t = 0.5 N P, p r e s e n t .

(44)

식 (44)는 N_P가 변화함에 따라 예측 단계에서 N_C를 계산하는 식이다. 본 논문에서는 N_C를 N_P의 0.5배로 설정했다.⁸⁾

4. 시나리오 구성 및 실험 결과

이 실험은 아래 환경에서 진행되었다.

ㆍCPU: AMD Ryzen 7 3800XT 8-Core Processor 3.90 GHz
ㆍRAM: 32.0 GB
ㆍGPU: NVIDIA GeForce RTX 3070
ㆍTool: Matlab 2020b, Autonomous Driving Toolbox

실험은 차량, 트럭, 보행자 등 다양한 Actor의 전장, 축거, 속도 등 다양한 파라미터를 추가할 수 있고, 센서를 활용해 주행 데이터를 수집할 수 있는 MATLAB의 Autuonomous driving toolbox와 MATLAB을 연동해 사용했다. Reference 데이터는 Autuonomous driving toolbox 상 Lead vehicle의 주행 데이터를 Reference data로 활용했다.

Table 2는 MPC를 구성하는데 활용된 차량의 파라미터이다.

Table 2

MPC parameter

4.1 시나리오 1 구성 및 실험 결과

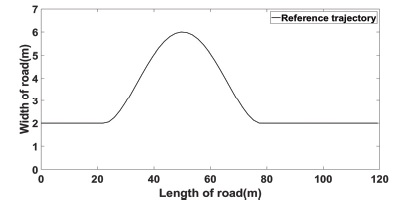
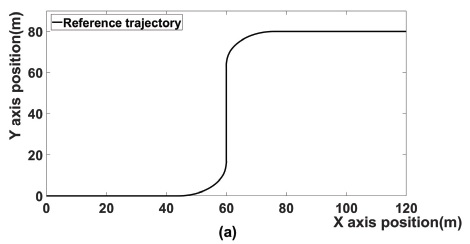
시나리오 1은 Fig. 2와 같다. 차량은 2차선 도로의 2차선을 주행한다. 시작 지점에서 약 50 m 거리에서 장애물을 감지한 후 첫 번째 차선으로 전환하고 장애물을 지나면 두 번째 차선으로 복귀한다. 차량의 초기 속도는 20 m/s이고 샘플링 시간은 0.1로 설정한다. 또한 실험은 horizon(60, 15 및 variable horizon)에서 진행된다. 다른 horizon을 가진 세 가지 MPC 알고리즘의 결과를 비교하여 각 알고리즘의 추적 성능을 평가한다.

Fig. 2

The trajectory of scenario 1

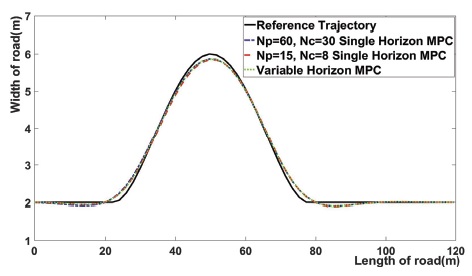
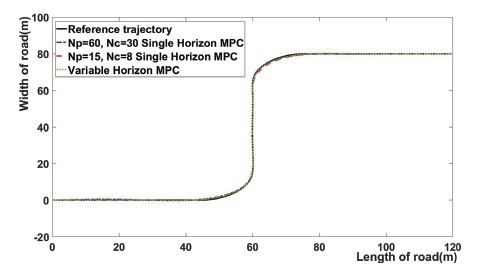
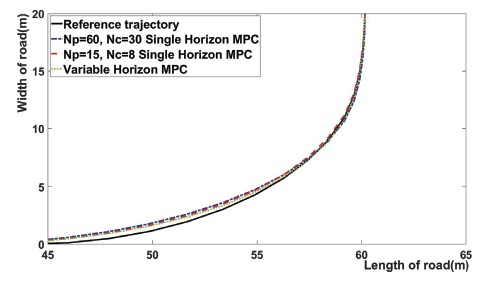
Fig. 3은 3개의 MPC의 궤적을 비교한다. 여기서 검은색 점선으로 표시된 부분은 Reference trajectory, 파란색일점쇄선으로 표시된 부분은 N_P = 60인 단일 Horizon MPC, 빨간색 파선으로 표시된 부분은 N_P = 15인 단일 Horizon MPC, 초록색 점선으로 표시된 부분은 Variable horizon MPC based on path curvature를 의미한다. 위에서 볼 수 있듯이 Variable horizon MPC based on path curvature가 Reference Trajectory를 가장 근접하게 추종한다.

Fig. 3

Comparison for Trajectory of 3-type MPCs

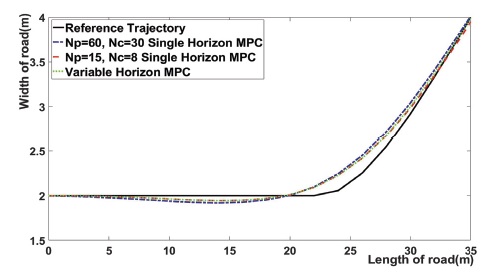
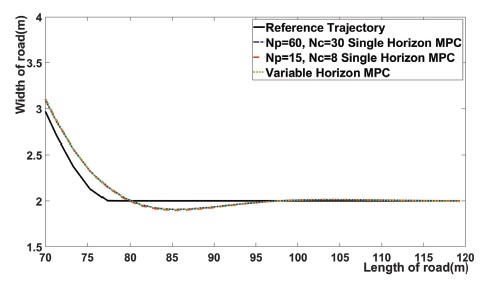
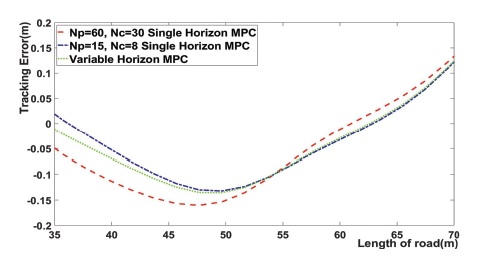
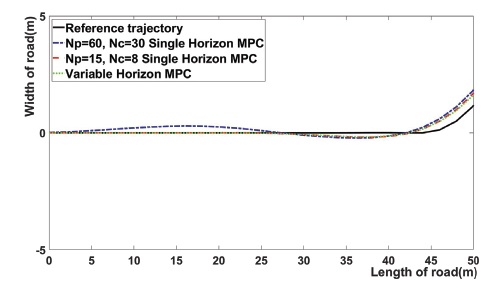
Fig. 4는 Fig. 2에서 직선 주행 구간과 직선에서 곡선으로 바뀌는 구간을 확대한 결과이다. 이 결과는 직선 구간과 직선에서 곡선으로 바뀌는 구간에서 제안한 MPC를 통해 얻은 Trajectory는 N_P = 15, N_C = 8일 때의 단일 Horizon MPC의 Trajectory와 거의 흡사하다. 이 구간에서는 제안한 MPC와 N_P = 15일 때의 단일 MPC의 Trajectory가 N_P = 60, N_C = 30일 때의 단일 Horizon MPC의 Trajectory에 비해 추종 성능이 높아지는데, 그 원인은 제안한 MPC의 효과로 직선 구간에서는 짧은 N_P가 적용되었기 때문이다. 또한, 위의 결과는 직선 구간에서 N_P를 일정 수준 이상 크게 설정하면 직선 경로를 주행하는 시점에서 미래의 곡선 경로까지 고려하므로 곡선 경로를 잘 추종하기 위해 미리 곡선 경로를 준비해 직선 경로에서 추종 오차가 커지는 문제점이 발생하고, 제안한 MPC를 통해 직선 구간에서 Trajectory의 오차가 생기는 것을 방지할 수 있다는 것을 의미한다.

Fig. 4

Comparison for Trajectory of 3-type MPCs in region that changes from straight to curve path

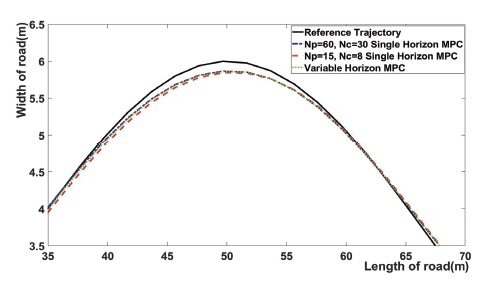
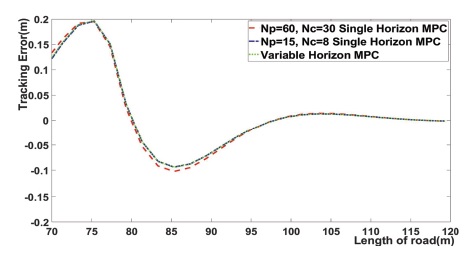
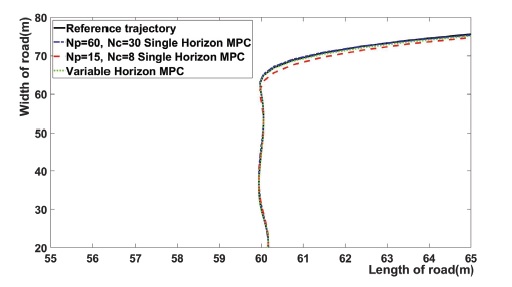
Fig. 5는 Fig. 2의 곡선 주행 구간을 확대한 결과이다. 이 결과는 곡선 구간에서 제안한 MPC를 통해 얻은 Trajectory는 N_P = 60, N_C = 30일 때의 단일 Horizon MPC의 Trajectory와 같다. 이 구간에서는 제안한 MPC와 N_P = 60일 때의 단일 MPC의 Trajectory가 N_P = 15, N_C = 8일 때의 단일 Horizon MPC의 Trajectory에 비해 추종 성능이 높아지는데 그 원인은 제안한 MPC의 효과로 곡선 구간에서 긴 N_P가 적용되었기 때문이다. 또한, 위의 결과는 곡선 구간에서 N_P를 짧게 설정하면 곡선 경로를 주행할 때 예측 구간이 적기 때문에 곡선 경로를 추종 성능이 부족하다. 제안한 MPC는 곡선 구간에서 곡률에 따라 N_P를 증가시키기 때문에 이러한 문제점을 해결할 수 있다.

Fig. 5

Comparison for Trajectory of 3-type MPCs at curve path

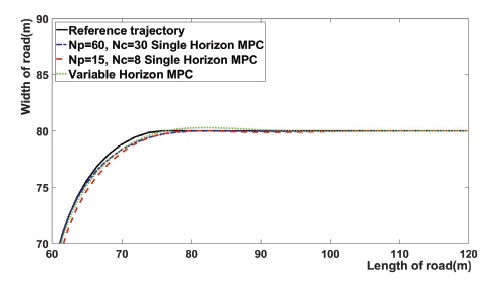
Fig. 6은 Fig. 3에서 곡선 주행 구간과 직선에서 곡선으로 바뀌는 구간을 확대한 결과이다. 이 결과는 Fig. 4에서 설명한 것과 같은 효과를 지닌다.

Fig. 6

Comparison for Trajectory of 3-type MPCs in region that changes from curve to straight path

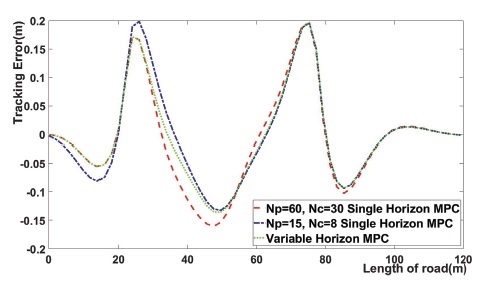
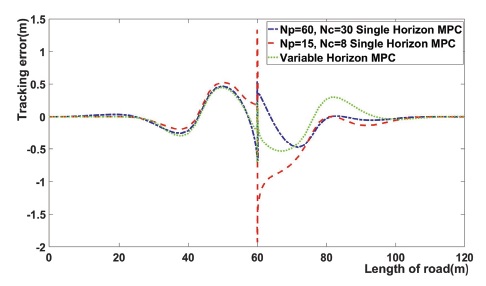
Fig. 7은 3개의 MPC의 추종 오차를 비교한다. Tracking error는 0에 가까울수록 추종 성능이 좋다는 것을 의미한다. 위의 그림에서 Variable horizon MPC의 Tracking error가 거의 모든 구간에서 나머지 2개의 단일 MPC보다 0에 가깝게 나타난다. 이는 Variable horizon MPC based on path curvature의 추종 성능이 가장 높음을 의미한다.

Fig. 7

Comparison for tracking errors of 3-type MPCs

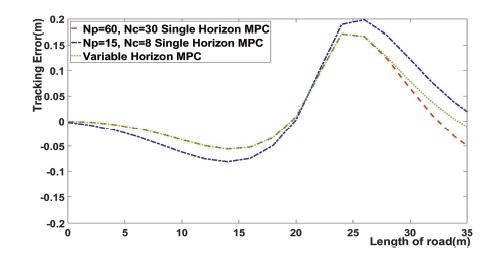
Fig. 8은 직선 구간과 직선에서 곡선으로 바뀌는 구간의 Tracking error를 확대한 것이다.

Fig. 8

Comparison for tracking errors of 3-type MPCs in region that changes from straight to curve path

Fig. 9는 곡선 구간에서의 Tracking error를 확대한 것이다.

Fig. 9

Comparison for tracking errors of 3-type MPCs at curve path

Fig. 10은 곡선 구간과 직선에서 곡선으로 바뀌는 구간의 Tracking error를 확대한 것이다.

Fig. 10

Comparison for tracking errors of 3-type MPCs in region that changes from curve to straight path

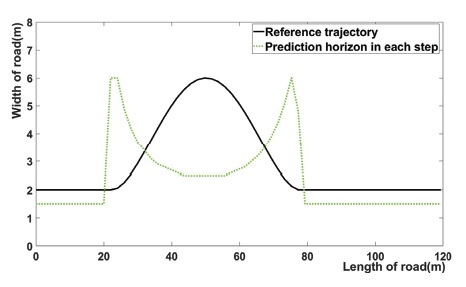
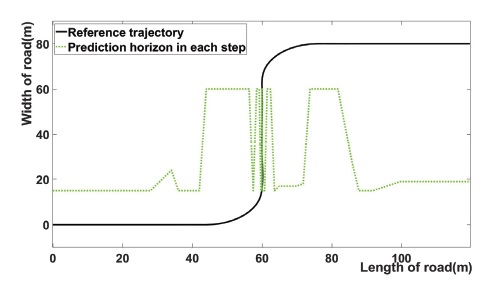
Fig. 11은 차량이 주행할 때 각각의 주행 경로에서의 prediction horizon의 크기를 나타낸다. Prediction horizon은 Figure의 가시성을 높이기 위해 0.1배 해서 나타내었다. Fig. 11을 살펴보면 곡선 주행 경로에 들어서는 순간, prediction horizon이 증가하고, 곡률이 줄어드는 구간인 약 30~70 m 구간에서는 Prediction horizon이 감소한다. 또한, 직선 구간에서는 주행 시작 시 설정했던 Prediction horizon으로 돌아오면서 제안한 알고리즘의 효과가 있음을 보인다.

Fig. 11

Prediction horizon in each step

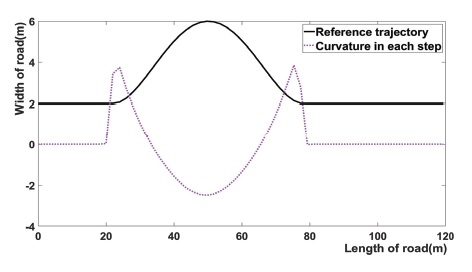
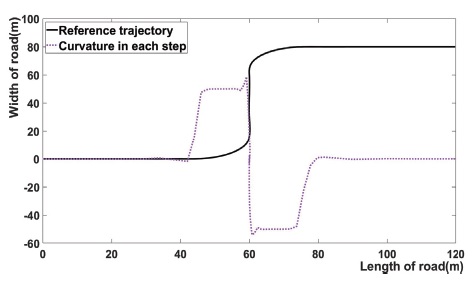
Fig. 12는 차량이 주행할 때 각각의 주행 경로에서의 곡률을 나타낸다. 가시성을 위해 기존 곡률의 크기에 200을 곱하여 나타냈다. 논문에서 곡률의 변화를 기반으로 Prediction horizon을 다르게 설정했으므로, 곡률의 그래프와 Prediction horizon이 유사하게 나타난다.

Fig. 12

Curvature in each step

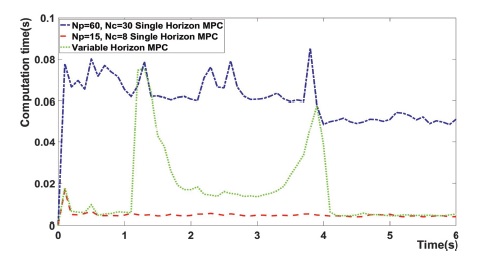
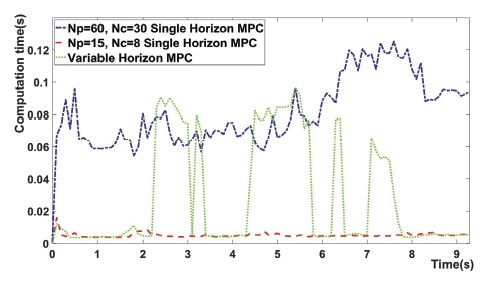
Fig. 13은 각 단계 별 MPC가 구동하는데 걸리는 시간을 의미한다. 제안한 MPC 알고리즘의 경우, 단계마다 걸리는 시간이 직선 구간에서는 N_P가 15인 MPC와 유사해 전체적인 계산 시간을 줄이고, 곡선 구간에서도 역시 N_P가 60인 MPC에 비해 확연히 줄어듦을 확인할 수 있다.

Fig. 13

Computation time in each step

Table 3은 시나리오를 모두 마쳤을 때 평균 추종 오차를 계산하여 표로 나타낸 것이다. 제안한 Variable horizon MPC based on path curvature는 단일 Horizon MPC에 비해 평균 추종 오차가 감소하였으므로 제안한 MPC를 통해 추종 성능이 향상되었음을 보여준다.

Table 3

Average tracking errors at each MPC

Table 4는 MPC의 계산 시간을 나타낸다. 이는 Reference 궤적을 생성하는 부분을 제외한 순수 MPC가 시작 구간인 0 m부터 도착 구간인 120 m까지 모든 구간을 주행했을 때 시간을 나타낸다. 이 결과는 Horizon의 크기가 계산 시간에도 큰 영향을 미치는 것을 나타낸다. 제안한 알고리즘은 단일 Horizon MPC에 비해 추종 성능을 높였고, 계산 시간도 단일 Horizon MPC에서 상대적으로 높은 추종 성능을 보이는 N_P = 60일 때 보다 감소함을 확인했다.

Table 4

Computational time at Each MPC

MPC에서 Horizon이 큰 경우, 추종 성능은 좋아진다는 장점이 있지만, 계산 시간이 증가한다는 단점이 있다. 반대로 Horizon이 작은 경우, 추종 성능은 좋지 않다는 단점이 있지만, 계산 시간은 짧다는 장점이 있다. Table 3과 4의 결과에서 제안한 Variable horizon MPC는 Horizon이 큰 MPC에 비해 108 % 추종 성능이 증가하고, 계산 시간이 273 % 감소함을 보였다.

4.2 시나리오 2 구성 및 실험 결과

두 번째 시나리오는 Fig. 14와 같다. 차량은 두 개의 곡선 도로를 연속적으로 주행한다. 처음에 차량은 길이 40 m의 직선 도로를 주행하다가 회전 반경 20 m의 곡선 주행 구간으로 좌회전한다. 이어 40 m 직선구간을 달리다가 선회반경 20 m의 (우회전) 곡선구간으로 진입한다. 우회전 곡선 구간을 지나면 40 m 직진 구간을 지나면 시나리오가 종료된다. 차량의 초기 속도는 20 m/s이고 샘플링 시간은 0.1로 설정한다. 또한 실험은 다른 Horizon(60, 15 및 Variable horizon)을 갖는 3가지 MPC를 비교한다.

Fig. 14

The trajectory of scenario 2

Fig. 15는 3개의 MPC의 궤적을 비교한다. 여기서 검은색 점선으로 표시된 부분은 Reference Trajectory, 파란색 일점쇄선으로 표시된 부분은 N_p = 60인 단일 Horizon MPC, 빨간색 파선으로 표시된 부분은 N_p = 15인 단일 Horizon MPC, 초록색 점선으로 표시된 부분은 Variable horizon MPC based on path curvature를 의미한다. 위에서 볼 수 있듯이 Variable horizon MPC based on path curvature가 Reference trajectory를 가장 근접하게 추종한다.

Fig. 15

Comparison for Trajectory of 3-type MPCs

Fig. 16은 직선 주행 구간과 직선에서 곡선으로 바뀌는 구간을 확대한 결과이다. 이 결과는 직선 구간과 직선에서 곡선으로 바뀌는 구간에서 제안한 MPC를 통해 얻은 Trajectory는 N_P = 15, N_C = 8일 때의 단일 Horizon MPC의 Trajectory와 거의 흡사하다. 이 구간에서는 제안한 MPC와 N_P = 15일 때의 단일 MPC의 Trajectory가 N_P = 60, N_C = 30일 때의 단일 Horizon MPC의 Trajectory에 비해 추종 성능이 높아지는데, 그 원인은 제안한 MPC의 효과로 직선 구간에서는 짧은 N_P가 적용되었기 때문이다.

Fig. 16

Comparison for Trajectory of 3-type MPCs in region that changes from straight to curve path

Fig. 17에서는 제안한 MPC를 통해 얻은 Trajectory는 N_P = 60, N_C = 30일 때의 단일 Horizon MPC의 Trajectory와 같다. 이 구간에서는 제안한 MPC와 N_P = 60일 때의 단일 MPC의 Trajectory가 N_P = 15, N_C = 8일 때의 단일 Horizon MPC의 Trajectory에 비해 추종 성능이 높아지는데 그 원인은 제안한 MPC의 효과로 곡선 구간에서 긴 N_P가 적용되었기 때문이다.

Fig. 17

Comparison for Trajectory of 3-type MPCs at curve path

Fig. 18은 직선에서 곡선으로 바뀌는 구간이다. 이 결과는 Fig. 16에서 설명한 것과 같은 효과를 지닌다.

Fig. 18

Comparison for Trajectory of 3-type MPCs in region that changes from straight to curve path

Fig. 19는 곡선에서 직선으로 바뀌는 구간이다. 이 결과는 곡선 구간에서 N_P가 가장 작은 N_P = 15, N_C = 8일 때의 단일 Horizon MPC의 Trajectory는 Reference trajectory에 가장 멀고, N_P=60인 MPC와 제안한 MPC는 거의 유사한 경향을 보인다. 그 원인은 제안한 MPC의 효과로 곡선 구간에서는 긴 N_P가 적용되었기 때문이다.

Fig. 19

Comparison for Trajectory of 3-type MPCs in region that changes from curve to straight path

Fig. 20은 3개의 MPC의 추종 오차를 비교한다. Tracking error는 0에 가까울수록 추종 성능이 좋다는 것을 의미한다. 직선 주행 구간에서는 N_P가 60인 MPC의 추종 오차가 가장 크지만, 곡선 주행 구간에 진입하면서 N_P가 15인 MPC의 추종 오차가 가장 커진다. 제안한 MPC는 이 두 가지 MPC의 장점을 취해, 직선 구간에서는 N_P가 15인 MPC와 유사한 성능을 보이고, 곡선 구간에서는 N_P가 60인 MPC와 유사한 성능을 보인다.

Fig. 20

Comparison for tracking errors of 3-type MPCs

Fig. 21은 차량이 주행할 때 각각의 주행 경로에서의 Prediction horizon의 크기를 나타낸다. Fig. 21을 살펴보면 곡선 주행 경로에 들어서는 순간, Prediction horizon이 증가하고, 곡률이 줄어드는 구간 Prediction horizon이 감소한다. 또한, 직선 구간에서는 주행 시작 시 설정했던 Prediction horizon으로 돌아오면서 제안한 알고리즘의 효과가 있음을 보인다.

Fig. 21

Prediction horizon in each step

Fig. 22는 차량이 주행할 때 각각의 주행 경로에서의 곡률을 나타낸다. 가시성을 위해 기존 곡률의 크기에 800을 곱하여 나타냈다. 논문에서 곡률의 변화를 기반으로 Prediction horizon을 다르게 설정했으므로, 곡률의 그래프와 Prediction horizon이 유사하게 나타난다.

Fig. 22

Curvature in each step

Fig. 23은 각 단계 별 MPC가 구동하는데 걸리는 시간을 의미한다. 제안한 MPC 알고리즘의 경우, 단계마다 걸리는 시간이 직선 구간에서는 N_P가 15인 MPC와 유사해 전체적인 계산 시간을 줄이고, 곡선 구간에서도 역시 N_P가 60인 MPC에 비해 확연히 줄어듦을 확인할 수 있다.

Fig. 23

Computation time in each step

Table 5는 시나리오를 모두 마쳤을 때 평균 추종 오차를 계산하여 표로 나타낸 것이다. 제안한 Variable horizon MPC based on path curvature는 단일 Horizon MPC에 비해 평균 추종 오차가 감소하였으므로 제안한 MPC를 통해 추종 성능이 향상되었음을 보여준다.

Table 5

Average tracking errors at each MPC

Table 6은 MPC의 계산 시간을 나타낸다. 이는 Reference 궤적을 생성하는 부분을 제외한 순수 MPC가 시작 구간인 0 m부터 도착 구간인 120 m까지 모든 구간을 주행했을 때 시간을 나타낸다. 이 결과는 Horizon의 크기가 계산 시간에도 큰 영향을 미치는 것을 나타낸다. 제안한 알고리즘은 단일 Horizon MPC에 비해 추종 성능을 높였고, 계산 시간도 단일 Horizon MPC에서 상대적으로 높은 추종 성능을 보이는 N_P = 60일 때 보다 감소함을 확인했다.

제안한 Variable horizon MPC는 추종 성능이 높은 N_P = 60인 MPC에 비해, 더 좋은 추종 성능을 보인다. 하지만 계산 시간을 약 313 % 감소시켰다. 또한, 추종 성능이 낮은 N_P = 15인 MPC에 비해서 추종 성능이 약 241 % 감소함을 보였다.

Table 6

Computational time at Each MPC

5. 결 론

본 논문에서는 주행 경로의 곡률에 따라 N_P와 N_C를 바꿔가며 주행하는 MPC 알고리즘을 개발하였다. 단일 Horizon MPC에서 N_P를 작게 설정하면 최적화를 하는 과정에서 곡선 구간에 대한 예측을 늦게 하기 때문에 직선 구간에서는 안정적이지만 곡선 구간을 따라가지 못하는 한계점이 있고, N_P를 크게 설정하면 최적화 과정에서 미리 예측된 곡선 구간을 따라가기 위해 직선 구간이 불안정하다는 한계점이 있다.

본 논문에서는 이러한 한계점을 보완하기 위해서 각 단계마다 N_P와 N_C를 변경하며 주행하는 Variable horizon MPC based on path curvature 알고리즘을 제시했고, Matlab 환경상에서 제안한 MPC와 2개의 단일 Horizon MPC의 추종 성능을 비교함으로써 제안한 MPC를 사용했을 때 추종 성능이 증가함을 검증했다.

Nomenclature


A_a :	state matrix for augmented state space model
A_c :	state matrix for continuous state space model
A_d :	state matrix for discrete state space model
B_a :	control matrix for augmented state space model
B_c :	control matrix for continuous state space model
B_d :	control matrix for discrete state space model
C_a :	output matrix for augmented state space model
C_c :	output matrix for continuous state space model
C_d :	output matrix for discrete state space model
C_f :	cornering stiffness of front wheels, [N/deg]
C_r :	cornering stiffness of front wheels, [N/deg]
F_x_f :	front tire force, [N]
F_x_r :	rear tire force, [N]
I_z :	yaw moment inertia, [kgm²]
J :	cost function.
N_C :	control horizon
N_c,PRE :	control horizon of next step
N_p :	prediction horizon
N_P,past :	prediction horizon of past step
N_P,present :	prediction horizon of present step
P_y :	lateral position, [m]
T_s :	sampling time, [s]
V :	vehicle velocity, [m/s²]
l_f :	c.g distance to front wheels, [m]
l_r :	c.g distance to rear wheels, [m]
m :	vehicle mass, [kg]
u :	input
α_f :	tire slip angle of front wheels, [deg]
α_r :	tire slip angle of rear wheels, [deg]
β :	sideslip angle, [deg]
Ψ :	yaw angle, [deg]
$Ψ ˙$ :	yaw rate, [deg/s]
δ :	front steering angle, [deg]

Acknowledgments

A part of this paper was presented at the KSAE 2021 Spring Conference

이 논문은 산업통상자원부 ‘산업 전문 인력 역량 강화사업’의 재원으로 한국산업기술진흥원(KIAT)의 지원을 받아 수행된 연구(2021년 미래형자동차 R&D 전문인력 양성사업, 과제번호: N0002428)임. 이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(과제번호: NRF-2021R1F1A1062153, NRF-2019R1G1A1100532).

References

J. Richalet, A. Rault and J. Papon, “Model Predictive Heuristic Control,” Automatica, Vol.14, No.5, pp.413-428, 1978. [https://doi.org/10.1016/0005-1098(78)90001-8]
N. Giorgetti, G. Ripaccioli, A. Bemporad, I. Kolmanovsky and D. Hrovat, “Hybrid Model Predictive Control of Direct Injection Stratified Charge Engines,” IEEE/ASME Transactions on Mechatronics, Vol.11, No.5, pp.499-506, 2006. [https://doi.org/10.1109/TMECH.2006.882979]
N. Giorgetti, A. Bemporad, H. E. Tseng and D. Hrovat, “Traction Control Hybrid Model Predictive Control Application towards Optimal Semi-active Suspension,” International Journal of Control, Vol.79, No.5, pp.521-533, 2005. [https://doi.org/10.1080/00207170600593901]
J. Hwang, K. Huh, H. Na, H. Jung, H. Kang and P. Yoon, “Development of a Model Based Predictive Controller for Lane Keeping Assistance System,” Transactions of KSAE, Vol.17, No.3, pp.54-61, 2009. [https://doi.org/10.4271/2008-01-1454]
A. Gray, Y. Gao, J. K. Hedrick and F. Borrelli, “Robust Predictive Control for Semi-autonomous Vehicles with an Uncertain Driver Model,” IEEE Intelligent Vehicles Symposium (IV), Australia, pp.208-213, 2013. [https://doi.org/10.1109/IVS.2013.6629472]
S. Cho and K. Yi, “Vehicle Stop and Go Cruise Control Using a Vehicle Trajectory Prediction Method,” Transactions of KSAE, Vol.10, No.5, pp. 206-213, 2002.
C. Dai, C. Zong and G. Chen, “Path Tracking Control Based on Model Predictive Control with Adaptive Preview Characteristics and Speed-assisted Constraint,” IEEE Access, Vol.8, pp.184697-184709, 2020. [https://doi.org/10.1109/ACCESS.2020.3029635]
H. Zhou, J. Gao and H. Liu, “Vehicle Speed Preview Control with Road Curvature Information for Safety and Comfort Promotion,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.235, No.6, pp.1527-1538, 2021. [https://doi.org/10.1177/0954407020972851]
L. Yang, M. Yue and T. Ma, “Path Following Predictive Control for Autonomous Vehicles Subject to Uncertain Tire-ground Adhesion and Varied Road Curvature,” International Journal of Control, Automation and Sys tems, Vol.17, No.1, pp. 193-202, 2019. [https://doi.org/10.1007/s12555-017-0457-8]
B. Zhang, C. Zong, G. Chen and G. Li, “An Adaptive-prediction-horizon Model Prediction Control for Path Tracking in a Four-wheel Independent Control Electric Vehicle,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.233, No.12, pp.3246-3262, 2019. [https://doi.org/10.1177/0954407018821527]
H. Chaofang and Z. Lingxue, “Overtaking Control Strategy Based on Model Predictive Control with Varying Horizon for Unmanned Ground Vehicle,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.235, No.1, pp.78-92, 2021. [https://doi.org/10.1177/0954407020947515]
R. Rajamani, Vehicle dynamics and control, 2nd Edn., Springer Science & Business Media, New York Dordrecht Heidelberg London, pp.27-31, 2011.
J. Ji, A. Khajepour, W. W. Melek and Y. Huang, “Path Planning and Tracking for Vehicle Collision Avoidance Based on Model Predictive Control with Multiconstraints,” IEEE Transactions on Vehicular Technology, Vol.66, No.2, pp.952-964, 2016. [https://doi.org/10.1109/TVT.2016.2555853]
L. S. Shieh, H. Wang and R. E. Yates, “Discrete Continuous Model Conversion,” Applied Mathematical Modelling, Vol.4, No.6, pp.449-455, 1980. [https://doi.org/10.1016/0307-904X(80)90177-8]
L. Wang, Model Predictive Control System Design and Implementation Using MATLAB®, Springer Science & Business Media, New York Dordrecht Heidelberg London, pp.47-50, 53-68, 2009.
Y. Choi, W. Lee, K. Choi and J. Yoo, “Variable Horizon Model Predictive Control Based on Path Curvature for the Tracking Performance,” KSAE Spring Conference Proceedings, p.344, 2021.

Symbol	Description	Value [units]
m	Vehicle mass	2020 [kg]
l_f	C.g. distance to front wheel	1.40 [m]
l_r	C.g. distance to rear wheel	1.65 [m]
I_z	Yaw moment of inertia	3234 []
C_af	Front wheel cornering stiffness	1420 [N]
C_ar	rear wheel cornering stiffness	1420 [N]
V	Velocity of vehicle	20 [m/s]
T_s	Sampling time	0.1 [s]

Abstract

Keywords:

키워드:

1. 서 론

2. MPC 설계

2.1 차량의 동역학적 모델

2.2 MMPC13)를 위한 이산 선형 차량 모델

2.3 MMPC의 비용 함수

2.4 MMPC의 제약 조건

3. Variable Horizon Model Predictive Control Based on Path Curvature

3.1 Variable Horizon MPC Based on Path Curvature의 알고리즘

3.2 Variable Horizon MPC Based on Path Curvature의 계산식

4. 시나리오 구성 및 실험 결과

4.1 시나리오 1 구성 및 실험 결과

4.2 시나리오 2 구성 및 실험 결과

5. 결 론

Nomenclature

Acknowledgments

References

Fig. 1

Fig. 2

Fig. 3

Fig. 4

Fig. 5

Fig. 6

Fig. 7

Fig. 8

Fig. 9

Fig. 10

Fig. 11

Fig. 12

Fig. 13

Fig. 14

Fig. 15

Fig. 16

Fig. 17

Fig. 18

Fig. 19

Fig. 20

Fig. 21

Fig. 22

Fig. 23

Table 1

Table 2

Table 3

Table 4

Table 5

Table 6

2.2 MMPC¹³⁾를 위한 이산 선형 차량 모델