다층 신경망을 이용한 통합형 Axle 캠버 횡강성 시험-해석 코릴레이션
Copyright Ⓒ 2021 KSAE / 192-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
One of the chassis products, namely, the integrated axle, must meet the camber strength criteria in the development stage. Camber strength performance verification is mainly conducted by testing and finite element analysis. Recently, the test was replaced by the finite element analysis to verify integrated axle camber strength performance and reduce product development cost and time. However, in order to replace the test with a simulation, the test/analysis correlation must be done beforehand. Therefore, this study proposes the integrated axle camber strength test/analysis correlation method through a multi-layer neural network. The result of the test/analysis correlation using a multi-layer neural network showed that the average error between the test and the analysis is about 10 %. This result proves the effectiveness of this research method, and suggests that the camber strength test could be replaced by the finite element analysis.
Keywords:
Back propagation, Camber strength, Correlation, Finite element analysis, Forward propagation, Multi-layer neural network키워드:
오차역전파법, 캠버 횡강성, 상관관계 분석, 유한요소해석, 순전파법, 다층 신경망1. 서 론
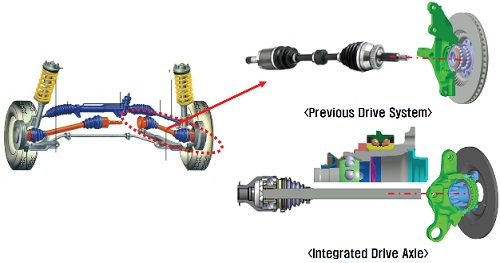
통합형 Axle은 Fig. 1과 같이 기존 등속조인트와 허브베어링을 하나의 구동시스템으로 통합시킨 차세대 동력전달 부품이다. 기존 Axle과 같이 새롭게 개발되는 통합형 Axle 또한 구조와 형태에 따라 차량의 주행 및 선회 성능이 결정되기 때문에 개발 시 캠버 횡강성 성능 검증이 필수로 이루어진다. Axle의 캠버 횡강성 성능은 주로 Axle의 허브베어링 사양(PCD, Pitch, Ball size, Ball 개수, 재료 물성 등)에 따라 좌우되며, 캠버 횡강성 시험 또는 유한요소해석을 통해 성능을 평가한다.1) 시험을 통한 Axle의 캠버 횡강성 성능 평가가 가장 보편적으로 이루어지며, 실물을 통한 성능 평가이기 때문에 신뢰성 또한 매우 뛰어나다. 하지만 실물을 통한 캠버 횡강성 성능 평가는 시제품 제작비용 때문에 제품 개발 비용이 증가되며, 시제품 제작 기간 및 평가 기간 때문에 차량 개발 기간을 지연시킬 수 있다.
Integrated Drive Axle(IDA)
반면 유한요소해석을 이용한 Axle의 캠버 횡강성 성능 평가는 가상 환경에서 3D 모델을 이용하여 설계 단계에서부터 성능을 예측하기 때문에 제품의 개발 기간 및 비용을 절감할 수 있다.2) 이러한 유한요소해석의 강점 때문에 Axle 캠버 횡강성 시험 평가를 해석 평가로 대체하려는 여러 연구가 진행되었다. 김기헌 등1)은 Axle의 캠버 횡강성 시험을 유한요소모델로 모사하여 시험 결과와 비교를 통해 해석적 평가방법의 유효성을 증명하였다. 또한 이승표 등3)은 유한요소해석을 통해 Axle의 캠버 횡강성 평가 방법을 제시하였고, Axle의 부품 중 허브베어링이 캠버 횡강성에 미치는 영향이 가장 크다는 것을 해석적으로 증명하였다.
기존 연구들은 시험 결과와 해석 결과 사이의 오차를 줄이기 위해 실제 시험과 같이 유한요소모델 및 해석 조건을 모델링하였다. 이러한 유한요소모델의 해석 결과는 시험 결과와 유사한 경향을 보이나 해석 시간과 비용을 증가시키는 단점이 있다. 유한요소모델과 해석 조건을 단순화 하면 해석 시간 및 비용은 줄어드나 시험 결과와 해석 결과 사이의 오차가 발생한다. 해석 조건을 단순화함과 동시에 시험 결과와 유사한 해석 결과를 얻기 위해선 해석 조건과 해석 결과 사이의 상관관계 분석을 통해 시험 결과와 유사한 해석 결과를 얻을 수 있는 최적의 해석 조건을 도출해야 한다. 이광섭 등4)은 차량의 시트 벨트 엥커리지의 시험 평가 방법을 유한요소모델로 단순히 모델링한 뒤 해석의 Damping 계수와 해석 결과 사이의 상관관계를 파악하여 시험 결과와 유사한 해석 결과를 얻을 수 있는 Damping 계수를 확보하였다. 김학영과 최성현5)은 유한요소모델로 단순화된 차량 로암 정강도 해석에 다구찌 강건설계 개념을 응용하여 시험 결과와 유사한 해석 결과를 얻을 수 있는 최적의 해석 조건을 도출하였다. 그 결과 해석 신뢰도를 약 38 % 이상 개선하였으며, 시험/해석 코릴레이션 방법론을 제시하였다. 이처럼 기존 연구들은 해석 조건과 해석 결과 사이의 상관관계를 분석하여 시험과 해석 결과 사이의 오차를 줄였다.
하지만 기존 연구들은 1개 또는 2개 이상의 해석 조건과 1개의 해석 결과 사이의 상관관계를 분석하여 시험/해석 코릴레이션 연구를 수행하였다. 캠버 횡강성 시험/해석 코릴레이션은 2개 이상의 해석 조건과 2개 이상의 해석 결과 사이의 상관관계를 분석해야 하기 때문에 기존의 연구 방법을 적용하기엔 한계가 있다. 따라서 본 연구에서는 다층신경망을 이용하여 2개 이상의 해석 조건과 2개 이상의 해석 결과 사이의 상관관계를 분석할 수 있는 방법을 제시하고, 캠버 횡강성 시험/해석 코릴레이션에 적용하여 시험과 동일한 해석 결과를 도출하는 최적 해석 조건을 예측 하고자 한다.6) 또한, 예측된 최적의 해석 조건을 유한요소모델로 모델링하여 해석한 뒤 그 결과와 시험 결과를 비교함으로써 예측된 최적 해석 조건의 유효성을 검증하고자 한다.7)
2. 다층 신경망
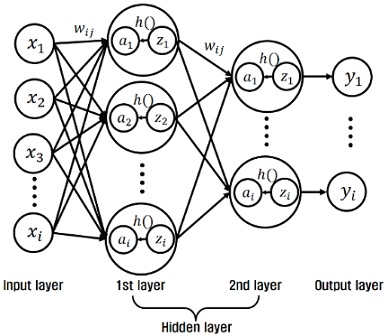
다층 신경망은 데이터 학습을 통해 2개 이상의 입⋅출력값 사이의 상관관계를 분석할 수 있으며, 이는 주로 이진 판단, 선택 분류 그리고 예측(회귀)에 관련된 공학 문제 해결에 이용된다. 다층 신경망의 개념도는 Fig. 2와 같이 입력층, 하나 이상의 은닉층, 출력층으로 구성되어 있으며, 각 층 사이에 존재하는 가중치 wij와 편향 bi를 데이터 학습을 통해 갱신하여 입력값과 출력값 사이의 상관관계를 분석한다.
Structure of neural network
이를 수식으로 나타내면 식 (1)과 같고, [x1, x2, ⋯, xi]는 다층신경망의 입력값을, [y1, y2, ⋯, yi]는 출력값을 나타낸다. 이렇게 입력값과 출력값으로 구성된 데이터셋 을 이용하여 가중치 wij와 편향 bi를 특정 알고리즘을 이용하여 학습시킨 뒤, 각종 공학 문제 해결에 사용한다.8)
| (1) |
- Y = XW+B
- where xi : input valu
- yi : output data
- wij : neural network weight
- bi : neural network bias
2.1 다층 신경망 학습
다층 신경망 학습은 순전파와 오차역전파를 통해 이루어진다. 순전파 단계에서는 식 (2)와 같이 데이터셋 입력값 a0 = x1 를 이용하여 기댓값을 계산한다.
| (2) |
- where h( ) : relu activate function
순전파 단계에서 기댓값을 구하기 위해 각 은닉층에서는 활성화 함수(본 연구에서는 Relu 활성화 함수 이용)를 이용하며, 마지막 출력층에서는 활성화 함수 대신 항등 함수를 사용해 최종 기댓값 등 함수를 사용해 최종 기댓값 을 도출한다. Relu 활성화 함수는 식 (3)과 같다.
| (3) |
이렇게 도출된 기댓값은 식 (4)와 같이 평균제곱오차(MSE, Mean Square Error) 알고리즘을 이용하여 오차를 산출하게 되고 이 오차를 출력층에서 입력층 방향으로 역전파 시키며(오차역전파법) 가중치와 편향값을 학습시킨다.
| (4) |
- where yk : true output value from dataset
- tk : expected value
가중치와 편향 학습에 대한 많은 이론들이 존재하지만 본 연구에서는 경사하강법을 이용하였으며, 경사하강법은 식 (5)와 같다.
| (5) |
- where η: learning rate
2.2 다층 신경망 성능 검증
학습이 완료된 다층 신경망은 성능 검증이 필요하다. 성능 검증을 위해 본 연구에서는 식 (6)과 같이 오차의 절댓값평균(MAE, Mean Absolute Error)을 사용하여 학습된 신경망의 성능을 검증하였다.
| (6) |
- Accuracy = 1 - EMEA
2.3 다층 신경망을 이용한 해석 조건 예측
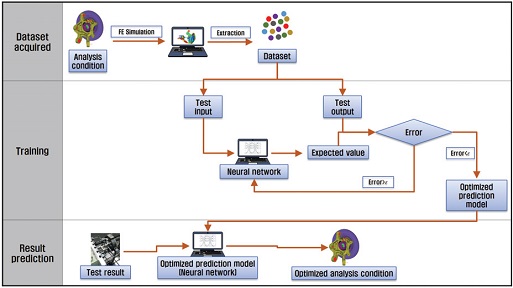
Fig. 3은 다층 신경망을 이용하여 통합형 Axle 캠버 횡강성 시험/해석 코릴레이션 프로세스를 나타낸 것이다. 첫번째 단계에서는 유한요소모델과 실험계획법을 이용하여 데이터셋을 구성하였다. 두번째 단계에서는 데이터셋과 식 (1)~(6)을 이용하여 다층 신경망을 학습시켰으며, 학습된 신경망의 성능을 검증 하였다. 마지막 단계에서는 학습된 신경망을 이용하여 최종적으로 시험 결과와 유사한 해석 결과를 얻을 수 있는 최적의 해석 조건을 예측하였다.
The process of result prediction
3. 통합형 Axle 캠버 횡강성 시험 및 해석
3.1 통합형 Axle 캠버 횡강성 시험
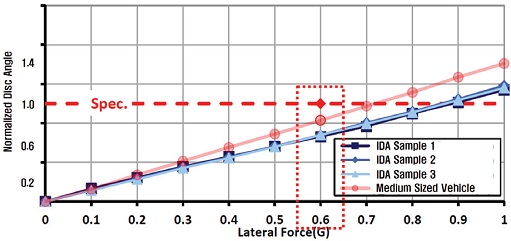
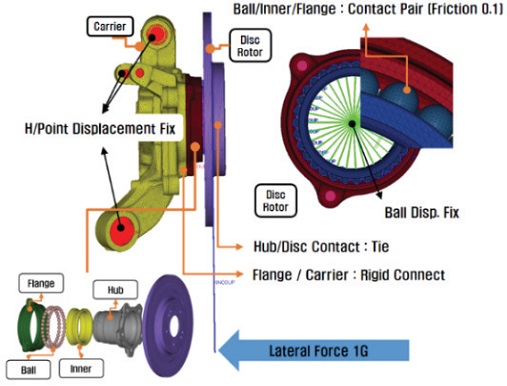
서론에서 언급했듯이 섀시 제품 중 하나인 통합형 Alxe은 개발 단계에서 캠버 횡강성 시험 조건을 만족해야 한다. 캠버 횡강성 시험은 차량의 주행 성능과 선회 성능을 Axle 단위에서 측정하는 시험으로, 실차 조건을 모사하여 Fig. 4와 같이 Axle 단위 시험으로 구성된다. 시험 조건은 Axle의 마운팅 부분을 Jig에 장착한 뒤, 차량 휠 모사 Jig를 조립한 후 타이어와 지면이 맞닿는 부분(Tire patch)에서 차량 내측 방향으로 1 G 하중을 가하는 것이다. 캠버 횡강성 시험 평가 결괏값은 차량 내측 하중 방향에 대한 디스크 로터의 변위 각도(캠버각)이며, 시험 기준은 0.6 G 하중 입력 시 차량 사이즈별로 일정 수준 이하여야 한다. 통합형 Axle은 고성능 차량을 타깃으로 개발된 제품으로 Fig. 5와 같이 일반 준중형 차량 대비 0.6 G 하중에서 캠버 횡강성은 약 30 % 이상 높은 수준이다.
Camber strength test of vehicle axle
IDA camber strength test result compared to general vehicle camber strength test result
3.2 통합형 Axle 캠버 횡강성 해석
통합형 Axle 캠버 횡강성 시험을 유한요소모델로 모사하여 해석을 진행하기 위해 Carrier, Flange, Ball, Inner, Hub 그리고 Disc rotor를 유한요소모델로 생성하였다. 해석 효율을 고려하여 필수적인 부품만 유한요소모델로 구성하였으며, 시험결과를 바탕으로 모든 요소를 탄성모델로 모델링 하였다. 유한요소모델은 Altair사의 HyperMesh를 이용하여 생성했으며, 요소는 약 12,000~43,000개, 절점 개수 약 48,000~188,000개 수준이다. 요소의 크기는 평균 3 mm이며, 타입은 Abaqus C3D4 이다.
초기 해석 조건은 시험 조건과 해석 시간을 고려하여 Fig. 6과 같이 설정하였다. Carrier 각 마운팅부 H/Point를 강체로 연결하여 변위 구속시켰으며, 각 부품들의 접촉 부위를 고려하여 ABAQUS contact pair(마찰계수 0.1) 조건을 설정하였다. 허브베어링의 플랜지부와 Carrier는 Bolt 체결 대신 강체 연결로 모사하였으며, 디스크 로터와 허브베어링은 실제 연결 구조를 고려하여 Tie 조건으로 설정하였다. 하중은 디스크 로터 제동부면에서 Tire patch점까지 강체 요소로 연결한 뒤 차량의 1 G 하중을 부여하였다. 해석 Solver는 ABAQUS/Implicit solver를 이용하였다.
IDA camber strength structural analysis boundary and contact condition
3.3 통합형 Axle 캠버 횡강성 시험/해석 결과
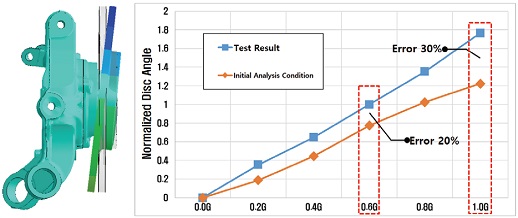
통합형 Axle 캠버 횡강성의 초기 해석 결과와 시험 결과는 Fig. 7과 같다. 캠버 횡강성 시험/해석 결과를 시험 기준인 0.6 G 하중점에서 비교한 결과 약 20 % 이상의 오차를 보이며, 최대 하중점(1 G 하중)에서는 약 30 % 오차를 보인다. 유한요소해석 조건은 시험 조건 대비 간단하게 모델링 되었고, 물성 또한 탄성 영역만 사용하여 두 결과 사이에 오차가 발생하는 것으로 판단된다. 이러한 오차 수준은 실제 시험을 대신하여 가상 환경(유한요소해석 또는 시뮬레이션)에서 제품의 성능을 평가하기엔 한계가 있다. 따라서 해석 조건과 해석 결과 사이의 상관관계를 다층 신경망을 통해 분석한 뒤, 시험 결과와 유사한 해석 결과를 도출할 수 있는 최적의 해석 조건을 도출 하여 시험/해석 결과 사이의 오차 수준을 좁히고자 한다.
IDA camber strength structural analysis result and the graph comparing between analysis result and test result
4. 데이터셋 생성 및 다층 신경망 학습
다층 신경망을 이용하여 해석 조건과 해석 결과 사이의 상관관계를 분석하여 최적의 해석 조건을 도출 하기 위해선 식 (1)과 같이 다수의 해석 조건과 해석 결과로 이루어진 데이터셋이 필요하다. 다수의 데이터셋은 2절에서 설명한 이론을 통해 다층 신경망을 학습 키시며, 학습이 완료된 다층 신경망은 시험 결과와 유사한 해석 결과를 도출할 수 있는 해석 조건을 예측하는데 사용 된다.
4.1 데이터셋 생성
다수의 데이터셋을 생성하기 위해서는 다수의 해석 조건과 이에 상응하는 해석 결과가 필요하다. 다수의 해석 조건을 만들기 위해 실험계획법의 완전요인배치설계를 이용하였으며, 앞선 연구와 자체 해석 결과를 바탕으로 통합형 Axle 허브베어링(Flage, Inner, Outer, Ball)의 탄성계수와 실제 시험에서 오차를 수반할 수 있는 항목을 고려하여 6개의 해석 조건을 완전요인배치설계의 인자로 선정했다. 선정된 6개의 인자 및 수준은 Table 1과 같으며, 각 인자의 조합을 통해 35×41=972개의 해석 케이스를 구성했다. 972개의 해석 케이스에 상응하는 해석 결과를 산출하기 위해 HyperStudy를 이용하여 자동으로 해석을 수행하였으며, Python 코드를 통해 자동으로 해석 결과를 수집했다. 해석 결과는 각 하중(0.2 G, 0.4 G, 0.6 G, 0.8 G, 1.0 G)에 대한 캠버각으로 총 5개의 값을 갖는다. 이렇게 만들어진 972개의 해석 조건 케이스와 해석 결과는 데이터 학습을 위해 각각 입력값 xi, 출력값 yi로 나눴으며, 본 연구에서는 시험 결과와 가장 유사한 해석 결과를 도출할 수 있는 해석 조건을 예측해야 하기 때문에 해석 조건을 출력값으로 설정 하였다. 이와 반대로 각 해석 조건에 따른 해석 결과를 예측하고 싶다면 해석 결과를 출력값으로 설정하면 된다. 다층 신경망 학습을 위해 최종적으로 수집된 데이터셋은 Table 2와 같이 Maxtrix 형태로 나타낼 수 있으며, 각 값은 정규화 하여 표현하였다. 입력값은 시험 결괏값을 1로 기준으로 하여 정규화 하였으며, 출력값은 각 인자의 최대수준의 값을 1로 기준으로 하여 정규화 하였다.
Factors of full factorial design
Dataset of camber strength result of full factorial design
4.2 다층 신경망 학습 및 정확도 검증
생성된 데이터셋을 이용하여 다층 신경망을 학습시키기 위해선 은닉층의 크기와 다층 신경망의 하이퍼파라미터를 설정해 줘야 된다. 본 연구에서 사용된 하이퍼파라미터는 Table 3과 같으며, 다층 신경망은 3층(1층 : 5×20, 2층 : 20×10, 3층 : 10×6)으로 구성하였다. 다층 신경망 학습 시 미니배치 크기는 20으로 설정 하였으며,9) 학습된 다층 신경망의 정확도를 확인하기 위해 Epoch을 2,000으로 설정하였다.10) 그 결과 학습된 다층 신경망의 정확도는 약 90 % 수준이다.
Hyper parameter
5. 해석 조건 예측
5.1 학습된 신경망 이용한 해석 조건 예측
통합형 Axle 캠버 횡강성 시험/해석 코릴레이션을 위한 해석 조건을 예측하기 위해 입력값으로 캠버 횡강성 시험값을 입력했다. 이는 연구에서 사용된 다층 신경망이 해석 결과(입력값)와 해석 조건(출력값)으로 구성된 데이터셋을 통하여 학습되었기 때문이다. 이에 따라 시험 결과를 학습된 신경망에 입력하여 최적의 해석 조건을 예측한 결과는 Table 4와 같다. 초기 해석 조건 대비 신경망을 통해 예측된 해석 조건은 Damping factor에서 최대 50 % 이상 변화율을 보이며, 다른 Factor들은 약 -1 %~2 % 사이의 변화율을 보인다.
The comparison of initial analysis condition and predicted analysis condition
5.2 예측된 해석 조건 검증
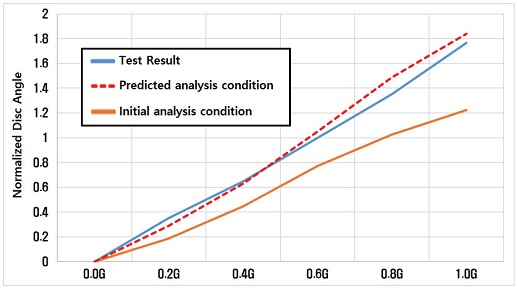
학습된 신경망을 통해 예측한 해석 조건의 유효성을 검증하기 위해 예측된 해석 조건과 같이 유한요소모델을 구성하였다. 유한요소모델 구성 시 요소 사이즈와 종류는 초기 해석 델과 동일하게 설정 하였으며, 해석 조건만 다층 신경망을 통해 예측된 해석 조건을 사용하였다. 예측된 해석 조건을 적용하여 유한요소모델을 해석한 결과는 Fig. 8과 같으며, 초기 해석 결과와 시험 결과를 시험 기준인 0.6 G 캠버 횡강성값을 기준으로 정규화 하여 함께 나타냈다. 또한 Table 5와 같이 각 하중점에 대한 정규화된 캠버 횡강성 값을 시험 결과, 예측된 해석 조건 적용 결과, 초기 해석 결과 순으로 비교하여 나타냈다. 시험 결과 대비 초기 해석 조건 적용 결과는 시험 기준점인 0.6 G에서 약 22 %의 오차율을 보이며, 다른 하중점에서도 약 20 % 이상의 오차율을 보인다. 반면, 예측된 해석 조건 적용 결과는 시험 기준점인 0.6 G에서 약 5 % 수준의 오차율을 보이며, 0.2 G 하중에 대한 캠버 횡강성 값 (17.78 %)을 제외하고는 모두 10 % 이내의 오차율을 보인다. 0.2 G 하중에 대한 캠버 횡강성 오차율이 다른 하중에 비해 큰 이유는 캠버 횡강성 절댓값이 매우 작음으로 작은 오차에도 오차율이 크게 변화되기 때문으로 판단된다.
The comparison graph of test, predicted analysis condition and initial analysis condition result
The comparison of test, predicted analysis condition and initial analysis condition result
6. 결 론
본 연구에서는 다층 신경망을 이용하여 통합형 Axle 캠버 횡강성 시험/해석 코릴레이션을 수행하였다. 972개의 해석 데이터를 이용하여 다층 신경망을 학습시켰으며, 학습된 신경망을 이용하여 시험 결과와 유사한 해석 결과를 얻을 수 있는 최적의 해석 조건을 예측하였다. 예측된 해석 조건을 유한요소모델로 재구성하여 각 하중점에 대한 캠버 횡강성 값을 시험 결과와 비교한 결과 시험 기준인 0.6 G 하중 점에서 오차가 10 % 이내였다. 이러한 연구 내용과 결과를 바탕으로 다음과 같은 결론을 얻을 수 있었다.
- 1) 다층 신경망과 해석 데이터를 이용하여 시험/해석 코릴레이션 방법을 제안하였고, 통합형 Axle 캠버 횡강성 시험/해석 코릴레이션 사례를 통해 유효성을 검증하였다.
- 2) 다층 신경망을 이용하여 2개 이상의 해석 조건과 2개 이상의 해석 결과 사이의 상관관계 분석이 가능하다는 것을 증명하였다.
- 3) 기존 시행착오 방식에 의한 시험/해석 코릴레이션이 아니라 체계적인 방법에 의해 수행되기 때문에 보다 빠르고 신뢰할 수 있는 해석 조건을 도출할 수 있다.
- 4) 부품 개발 시 진행되는 다수의 시험 평가 방법을 본 연구에서 제시한 방법을 통해 해석 평가로 대체할 수 있을 것으로 사료된다.
- 5) 다만, 본 연구는 단일 Axle 형상에 대해서만 다층 신경망을 학습시켜 최적 해석 조건을 예측했기 때문에 Axle 형상 변경 시 다층 신경망을 재 학습시켜 최적 해석 조건 다시 예측해야 된다. 이러한 한계점은 다양한 Axle 형상까지 고려한 다층 신경망을 이용한다면 해결할 수 있을 것으로 판단되며, 추후 이와 관련된 연구를 진행할 예정이다.
Nomenclature
| xi : | input value |
| yi : | output value |
| wij : | neural network weight |
| bi : | neural network bias |
| h( ) : | relu activation function |
| η : | learning rate |
Acknowledgments
A part of this paper was presented at the KSAE 2020 Fall Conference and Exhibition
References
- K. H. Kim, S. K. Lee and C. I. Park, “Study on the Design Parameter of Corner Module that Affect Camber Stiffness,” KSAE Fall Conference Proceedings, pp.532-537, 2017.
-
H. W. Yoon and S. K. Lee, “Analysis of Influence of Oil Pan Structure Modification on Radiation Noise of an Engine Using FEM,” Transactions of KSAE, Vol.25, No.5, pp.573-580, 2017.
[https://doi.org/10.7467/KSAE.2017.25.5.573]
- S. P. Lee, I. H. Lee, B. C. Kim and Y. W. Lee, “Stiffness Analysis for Automotive Wheel Bearing Including Corner Module,” KSPE Annual Conference Proceedings, pp.109-110, 2013.
- K. S. Lee, H. J. Kim, D. M. Jeong, J. C. Hwang, K. M. Cho and B. Y. Choi, “Improvement of the Correlation between Seatbelt Anchorage FEA and Test,” KSAE Spring Conference Proceedings, p.26, 2019.
- H. Y. Kim and S. H. Choi, “Test/Analysis Correlation Process Development Using Design of Experiment and Analysis Accuracy Improvement,” KSAE Fall Conference Proceedings, pp.474-475, 2018.
-
E. A. Sim, S. H. Lee and J. H. Lee, “Prediction of Static and Dynamic Behavior of Truss Structures Using Deep Learning,” Journal of the Korean Association for Spatial Structures, Vol.18, No.4, pp.69-80, 2018.
[https://doi.org/10.9712/KASS.2018.18.4.69]
- H. S. Cho, B. Y. Oh and H. Y. Kim, “Test-Analysis Correlation of Integrated Axle Camber Strength by Structure Analysis and Back Propagation Neural Network,” KSAE Fall Conference Proceedings, p.369, 2020.
-
Y. R. Li, T. Zhu, Z. Tang, S. N. Xiao, J. K. Xie, Z. B. Liu and S. D. Xiao, “Inversion Prediction of Back Propagation Neural Network in Collision Analysis of Anti-Climbing Device,” Advances in Mechanical Engineering, Vol.12, No.5, pp.1-13, 2020.
[https://doi.org/10.1177/1687814020922050]
- D. H. Yoon, Python Nal Coding for Deep Learning, Hanbit Media, Seoul, 2019.
- S. Goki, Deep Learning from Scratch, Hanbit Media, Seoul, pp.141-196, 2017.