전자식 조향 시스템의 병렬연결 상호 다중 모델을 이용한 고장진단 알고리즘

1. 서 론

최근 자율주행 자동차의 시장이 지속적으로 확대되면서 첨단 운전자 보조 시스템인 ADAS(Advanced Driver Assistance System) 기술이 발전하고 있다. ADAS는 첨단센서와 제어장치를 통해 운전자를 보조해 운전미숙이나 갑작스러운 사고 등으로부터 안전성을 향상시킬 뿐만 아니라 운전의 편의성도 높여준다. 기술의 편의성과 필요성에 의해 많은 ADAS 어플리케이션이 연구되고 있으며 특히 차선유지시스템 LKS(Lane Keeping System)는 대표적인 횡방향제어로써 전자식 조향 시스템인 EPS(Electric Power Steering)로 제어하게 된다. 최근에는 환경문제와 기술의 발전으로 인해 EPS는 많은 신차에서 기존의 유압식 조향 시스템 방식인 HPS(Hydraulic Power Steering)를 대체하고 있다. 이처럼 EPS 시스템의 중요성이 높아짐에 따라 자율주행차량의 횡방향제어를 위한 다양한 제어기법들이 제안되었다.^1-4)

EPS 시스템은 많은 장점들을 가지는 운전자 조향 보조 시스템이지만 향상된 기술에는 언제나 제어안정성이 보장되어야 한다. EPS 시스템을 구성하는 여러 가지 기계 또는 전기장치에서 예상치 못한 고장이 발생해 시스템의 특성이 갑자기 변하는 경우 안정적인 제어를 못 하게 될 가능성이 커지면서 운전자에게 나쁜 영향을 미칠 수 있다. 이를 방지하기 위해 시스템의 안정성과 운전자의 안전성을 보장하기 위한 고장진단 알고리즘을 연구하는 것은 매우 중요하며 실제로도 플랜트 모델을 기반으로 한 연구들,^5-7) 그리고 최근에는 SVM(Support Vector Machine)과 같은 인공지능을 접목한 고장진단 연구⁸⁾들도 많이 이루어지고 있다. 하지만 인공지능기반 고장진단 알고리즘의 경우, 좋은 성능을 내기 위한 학습 시간도 오래 걸리고 아직까지는 모델을 기반으로 한 알고리즘과 비교했을 때 확연한 성능차이를 내기는 어렵다.

본 논문에서는 EPS 시스템의 기계적, 전기적으로 고장이 났을 때 어떠한 고장인지 판단해주는 알고리즘으로 상호 다중 모델 IMM(Interacting Multiple Model)을 적용한다. 병렬적으로 구성된 모델들의 상호작용을 통해 어떠한 고장상태가 가장 적합한지 확률적으로 알 수 있으므로 고장 제어를 빠르고 정확하게 할 수 있다. 이는 단일 관측기만을 사용할 때보다 시스템 예측 정확도가 높아 여러 외부요인의 영향을 받을 때나 알 수 없는 상황에 처했을 때도 시스템의 상태를 추정하여 안정적인 제어가 가능하도록 한다. 더 나아가 기존의 IMM 알고리즘에서 고장진단 성능 향상을 위한 새로운 구조의 설계방식을 제시한다. 다수의 IMM 추정기들이 확률에 기반한 값을 업데이트하도록 설계하여 더 복잡하고 복합적인 상황에서 추정신뢰도를 높일 수 있다.

2. EPS 시스템의 고장진단

2.1 EPS 시스템 모델

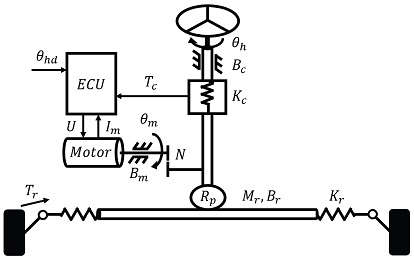
Fig. 1은 스티어링 컬럼에 모터가 위치한 C-EPS(Column Type EPS) 시스템의 구조를 나타낸다. 여기서는 자율주행차량의 EPS 시스템이라고 하고 운전자 토크 T_d를 0으로 가정한다. 제어 레퍼런스인 θ_hd를 전자제어장치인 ECU(Electronic Control Unit)에 입력하면 모터의 전압 U를 조절하여 모터 토크를 생성하고 기어에 의해 스티어링 컬럼으로 전달, 결과적으로는 스티어링 휠 각도 θ_h가 θ_hd를 추종하게 된다.

Fig. 1

Structure of the C-EPS system

2.1.1 확장 동역학 모델

EPS 시스템에 뉴턴법칙을 적용하여 스티어링 컬럼, 모터, 기어, 랙/피니언의 기계적, 전기적 파라미터들을 고려해 동역학 모델을 표현할 수 있다.^2,3,16)

$\[ \begin{array}{c}{J}_c{\ddot{\theta }}_h=-K_c{\theta }_c-B_c{\dot{\theta }}_c+\frac{K_c}{N}{\theta }_m+T_d\hfill \\ J_{eq}{\ddot{\theta }}_m=\frac{K_c}{N}{\theta }_h-K_N{\theta }_m-B_{eq}{\dot{\theta }}_m+K_t{I}_m-\frac{1}{N}{T}_r\hfill \\ \dot{L_m{I}_m}=-R_m{I}_m-K_t{\dot{\theta }}_m+U\hfill \end{array} \]$

(1)

여기서 $$ J_{eq}=J_m+\left(R_p^2/N^2\right)M_r, K_N=\left(K_c+K_r{R}_p^2\right)/N^2, B_{eq}=B_m+\left(R_p^2/N^2\right)B_r$$이다.

EPS 시스템의 모터에 의해 바퀴가 좌우로 움직이게 되면 그에 해당하는 힘이 지면으로부터 작용하게 되는데, 이때 외란 T_r(Road reaction torque on the rack and pinion)이 발생한다. 하지만 T_r은 측정이 불가능한 값이므로 관측기를 통한 추정을 위해 상태변수가 확장된 모델을 구성한다.

Extended state observer로 T_r을 추정하기 위해 상태 벡터 x=[θ_h ω_h θ_m ω_m I_m d]^T와 입력 u=U를 가지는 동역학 모델을 구성한다. 이때 d=T_r이다. $$ \dot{d}=0$$이라고 가정했을 때, 증강된 상태공간 방정식은 식 (2)와 같이 나타낼 수 있다. 아래 모델에 관측기를 사용한다면, 알 수 없는 외란 파라미터 T_r도 함께 추정할 수 있게 된다.

$\[ \begin{array}{c}\dot{\mathbf{\text{x}}}\left(t\right)=A\mathbf{\text{x}}\left(t\right)+Bu\left(t\right)\hfill \\ \mathbf{\text{y}}\left(t\right)=C\mathbf{\text{x}}\left(t\right)\hfill \end{array} \]$

(2)

$\[ A=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ -\left(\frac{K_c}{J_c}\right)& -\left(\frac{B_c}{J_c}\right)& \frac{K_c}{J_{c}N}& 0& 0& 0\\ & 0& 0& 1& 0& 0\\ \frac{K_c}{J_{eq}N}& 0& -\left(\frac{K_N}{J_{eq}}\right)& -\left(\frac{B_{eq}}{J_{eq}}\right)& \frac{K_t}{J_{eq}}& -\left(\frac{1}{J_{eq}N}\right)\\ 0& 0& 0& -\left(\frac{K_t}{L_m}\right)& -\left(\frac{R_m}{L_m}\right)& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right] \]$

$\[ B={\left[\begin{array}{cccccc}0& 0& 0& 0& \frac{1}{L_m}& 0\end{array}\right]}^T \]$

$\[ C=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\end{array}\right] \]$

2.2 다중 모델 기반 고장진단 알고리즘

EPS 고장에 대한 안정성과 신뢰성을 확보하기 위해서 고장 발생 시 고장을 진단하고 분류할 수 있는 알고리즘이 필요하다. 본 논문에서는 여러 고장상태의 시스템모델들을 설계하고 다중 필터가 병렬적으로 관측을 하는 다중 모델 구조(Multi model structure)를 설계한다.

2.2.1 칼만 필터

다중 모델은 Zero-Order Hold(ZOH)를 이용해 이산화된 모델에 Kalman filter를 적용한 필터모델들로 구성되었다. Extended state observer로써 사용된 Kalman filter는 과거의 정보와 새로운 측정값을 이용하는 알고리즘이다. 예측과 추정단계가 시스템에 대하여 재귀적으로 작용하여 실제 출력값에 가까워지도록 반복적으로 값을 업데이트한다. 그와 동시에 Gaussian noise의 영향을 고려하여 최적화된 관측기 이득을 통해 상태변수를 추정할 수 있다.^9-11)

2.2.2 상호 다중 모델

고장이 발생한 특정 파라미터를 찾기 위해 IMM을 기반으로 Markov chain rule을 따르는 확률적 다중 모델의 병렬 구조를 설계한다. Markov 확률 분포를 가지는 시스템에 Bayesian 이론에 근거한 상호작용을 만드는 IMM 추정기는 가장 간단하고 비용 효율적인 시스템 추정 알고리즘 중 하나이다.^12,13)

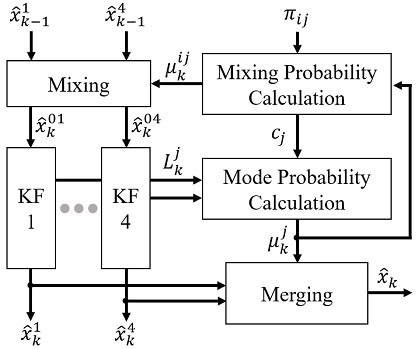
Fig. 2의 구조는 4개의 Kalman Filter(KF) 모델로 구성된 IMM이다. 서로 다른 모드에서 가장 가능도(Likelihood)가 높은 모드를 추정하게 되는데, 이때 모드확률(Mode probability)과 전이확률(Transition probability)에 따라 모드 i에서 가장 확률이 높은 모드 j로 모드 간 전환이 일어나고 병렬적으로 필터링 된다. 이러한 IMM 추정기는 Mixing, Filtering의 반복적인 과정과 Merging 과정을 통해 최종 추정값을 도출하며, 다음과 같은 재귀적 알고리즘을 수행한다.^12-15)

Fig. 2

Structure of interacting multiple model

2.2.2.1 Mixing

현재 각 모델의 확률인 모드확률 $$ {\mu }_{k-1}^i$$과 전이행렬 π_ij에 의해 Mixing probability $$ {\mu }_k^{ij}$$를 정의할 수 있다. $$ {\mu }_k^{ij}$$는 전체 n개의 모델 간에 상호작용이 일어날 확률이 정의된 행렬이다.

$\[ \begin{array}{c}{\mu }_k^{ij}=\frac{1}{c_j}{\pi }_{ij}{\mu }_{k-1}^i\hfill \\ c_j=\sum _{i=1}^n{\pi }_{ij}{\mu }_{k-1}^i\hfill \end{array} \]$

(3)

여기서 c_j는 Normalization factor이며, 상호작용 후의 상태변수와 공분산인 Mixed state $$ {\widehat{x}}_k^{0j}$$와 Mixed covariance $$ {\Sigma }_k^{0j}$$는

$\[ \begin{array}{c}{\widehat{x}}_k^{0j}=\sum _{i=1}^n{\mu }_k^{ij}{\mu }_{k-1}^i\hfill \\ {\Sigma }_k^{0j}==\sum _{i=1}^n{\mu }_k^{ij}\left[{\Sigma }_{k-1}^i+\left({\widehat{x}}_{k-1}^i-{\widehat{x}}_k^{0j}\right){\left({\widehat{x}}_{k-1}^i-{\widehat{x}}_k^{0j}\right)}^T\right]\hfill \end{array} \]$

(4)

이다. 여기서 $$ \left({\widehat{x}}_{k-1}^i-{\widehat{x}}_k^{0j}\right){\left({\widehat{x}}_{k-1}^i-{\widehat{x}}_k^{0j}\right)}^T$$는 모델의 불확실성을 의미한다. 이 과정에서는 Filter의 Correction 과정으로부터 나온 모델별 추정값인 Estimated state $$ {\widehat{x}}_{k-1}^i$$와 Estimated covariance $$ {\Sigma }_{k-1}^i$$ 가 $$ {\mu }_k^{ij}$$에 의해 전체적인 모델 간에 확률적인 보정이 일어난다.

2.2.2.2 Filtering

Kalman filter는 예측과 추정단계를 재귀적으로 반복하는 관측기이다. 단일 Kalman filter와의 차이점은 예측단계에서 Mixing 과정의 상호작용에 의해 확률적 보정이 일어난 값으로 예측을 한다는 것이다.

$\[ \begin{array}{c}Prediction\hfill \\ {\overline{x}}_k^j={\Phi }_k^j{\widehat{x}}_k^{0j}+{\Gamma }_k^j{u}_k\hfill \\ {\overline{\Sigma }}_k^j={\Phi }_k^j{\overline{\Sigma }}_k^{0j}{\left({\Phi }_k^j\right)}^T+Q_k^j\hfill \end{array} \]$

(5)

$\[ \begin{array}{c}Correction\hfill \\ u_k^j=u_k-{\overline{y}}_k^j\hfill \\ S_k^j=C_k^j{\overline{\Sigma }}_k^j{\left(C_k^j\right)}^T+R_k^j\hfill \end{array} \]$

(6)

$\[ \begin{array}{c}{K}_k^j={\overline{\Sigma }}_k^j{\left(C_k^j\right)}^T+{\left(S_k^j\right)}^{-1}\hfill \\ {\widehat{x}}_k^j={\overline{x}}_k^j{+K}_k^j{v}_k^j\hfill \\ {\Sigma }_k^j={\overline{\Sigma }}_k^j{-K_k^j{S}_k^j\left(K_k^j\right)}^T\hfill \end{array} \]$

(7)

2.2.2.3 Mode Probability Update

새로운 측정값 y_x와 예측된 값인 $$ {\overline{y}}_k^j$$의 차이를 Kalman filter로부터 식 (6)과 같이 구할 수 있다. 모든 모델의 오차와 오차 공분산을 따져 측정값에 가장 적합한 모델을 선정할 수 있는데, 이때 모델들의 가능도를 가능도 함수(Likelihood function)를 통해 구할 수 있다.

$\[ {\Lambda }_k^j=\frac{1}{{\left|2\pi S_k^j\right|}^{1/2}}\exp \left[-\frac{1}{2}{\left(v_k^j\right)}^T{\left(S_k^j\right)}^{-1}{v}_k^j\right] \]$

(8)

모델들의 가능도 $$ {\Lambda }_k^j$$에 의해 현재 시스템에 대한 적합도라 할 수 있는 모드확률 $$ {\mu }_k^j$$는 다음과 같다.

$\[ {\mu }_k^j=\frac{c_j{\Lambda }_k^j}{\sum _{i=1}^n{c}_i{\Lambda }_k^i} \]$

(9)

모드확률 $$ {\mu }_k^j$$와 Estimated state $$ {\widehat{x}}_k^j$$, Estimated covariance $$ {\Sigma }_k^j$$는 재귀적으로 다음 Step에서 다시 모델 간 Mixing이 일어난다.

2.2.2.4 Merging

이 과정에서는 모든 모델의 확률을 기반으로 최종 추정값을 도출하며, 필터의 추정값이 필요할 때 구하게 된다. 각 모델의 추정값들의 모드확률에 대한 기댓값이 최종 추정값 $$ {\widehat{x}}_k$$이다.

$\[ \begin{array}{c}{\widehat{x}}_k=\sum _{j=1}^n{\mu }_k^j{\widehat{x}}_k^j\hfill \\ {\Sigma }_k=\sum _{j=1}^n{\mu }_k^j\left[{\Sigma }_k^j+\left({\widehat{x}}_k^j-{\widehat{x}}_k\right){\left({\widehat{x}}_k^j-{\widehat{x}}_k\right)}^T\right]\hfill \end{array} \]$

(10)

3. PCIMM 기반 고장진단 구조

IMM의 고장진단과 상태변수 추정 성능을 조금 더 개선하기 위해 PCIMM(Parallel Connected Interacting Multiple Model) 구조를 제시한다. 하나의 IMM 내에서 Kalman filter들이 서로 상호작용하듯이 새로운 방식은 다수의 IMM 추정기들이 병렬적인 구조로 구성되어 IMM 간에 확률에 기반한 값을 업데이트하여 서로 상호보완 하도록 설계한다. 이러한 PCIMM 구조를 사용하면 IMM의 상태추정성능을 향상시켜 더 복잡하고 복합적인 상황에서 상태 추정이 가능하다.

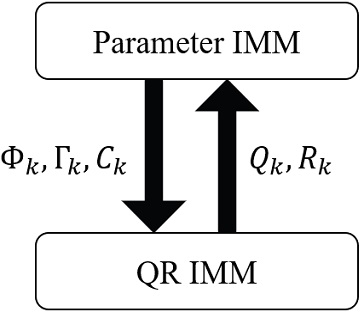
2개의 IMM으로 구성된 PCIMM의 구조는 Fig. 3과 같다. 먼저 Parameter IMM에서는 모드확률을 고려해 현재의 시스템상태에 가장 잘 맞는 시스템행렬을 찾아서 QR IMM으로 업데이트한다. 그리고 QR IMM에서는 Parameter IMM에서 받은 시스템행렬을 활용해 QR IMM 내의 모드확률을 고려한 Q(System noise covariance), R(Output noise covariance) 값을 찾아준다. 이후에는 Q, R 값이 다시 Parameter IMM에서 활용될 수 있도록 업데이트하는 방법으로 반복적으로 상호작용한다.

Fig. 3

Structure of PCIMM(Parallel Connected Interacting Multiple Model)

3.2 Q, R Update

QR model에서는 모든 모델이 동일한 파라미터 행렬을 가진다. 모드확률을 고려한 모델들의 System noise covariance Q_x, Output noise covariance R_x를 Parameter model에 업데이트한다. 이때 Parameter update와 Q, R update는 동일한 Step에서 병렬적으로 일어난다.

Table 1

PCIMM pesudo code

4. 모의 실험 결과

4.1 고장상태 모델링

EPS 시스템에서 발생할 수 있는 파라미터 고장의 종류는 크게 기계적 고장, 전기적 고장으로 나눌 수 있다. 하지만 많은 기계, 전기장치들로 구성되어 있기 때문에 각 시스템의 파라미터 변화에 의한 고장상태를 모델링 해주기 위해서는 여러 요인을 고려해주어야 한다. 본 논문에서는 스티어링 컬럼, 모터, 랙/피니언 시스템에 대한 고장을 대표적으로 선정했다. 먼저, 스티어링 컬럼과 랙/피니언 시스템에서 갑작스러운 외부요인에 의해 마찰력이 증가하게 되는 경우 각각의 댐핑인 B_c, B_r의 변화가 일어나는 것으로 기계적 고장을 나타냈다. 그리고 모터에서 저항 R_m이 증가하게 될 경우 모터에 흐르는 전류에 변화가 생기므로 시스템에 미치는 영향이 크다. 따라서 이를 전기적 고장으로 나타냈다.

정상적으로 동작하는 EPS 시스템 모델을 Model 1로 정하고, 스티어링 컬럼의 댐핑 B_c가 증가하는 고장상태를 Model 2, 모터에서 저항 R_m이 증가하는 고장상태를 Model 3, 랙/피니언에서 댐핑 B_r이 증가하는 경우를 Model 4로 Table 2와 같이 총 4개의 모델을 구성했다. 여기서 $$ B_c^1$$, $$ R_m^1$$, $$ B_r^1$$은 Model 1의 파라미터값들이다.

Table 2

Fault modeling in EPS system

4.2 실험 환경 설정

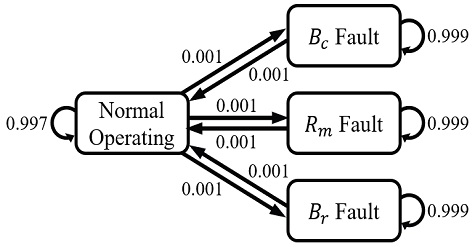
각 모드의 확률들의 합과 전이행렬의 행의 합은 1을 유지하도록 모드확률의 초기값 $$ {\mu }_0^i$$와 전이행렬 π_ij를 설정해주어야 한다. 본 논문에서는 모드확률의 초기값을 4개의 모델에 대하여 0.25로 모두 동일한 확률을 주었으며, 전이행렬은 정상 동작 상태에서 세 가지의 고장상태로 전환될 수는 있지만 어떠한 특정한 고장상태에서는 정상상태로만 전환될 수 있도록 설계했다.

$\[ \begin{array}{c}{\mu }_0^i=\left[\begin{array}{cccc}0.25& 0.25& 0.25& 0.25\end{array}\right]\hfill \\ {\pi }_{ij}=\left[\begin{array}{cccc}0.997\hfill & 0.001& 0.001& 0.001\\ 0.001& 0.999& 0& 0\\ 0.001& 0& 0.999& 0\\ 0.001& 0& 0& 0.999\end{array}\right]\end{array} \]$

(11)

Fig. 4

Block diagram for switching between models

4.3 Single Kalman Filter와 IMM 성능 비교

고장진단 성능을 검증하기 위해 정상 동작 중에 20초 부근부터 한 종류의 고장이 발생하며, 이때 알고리즘적으로 적합한 모델의 가능도가 증가하면서 모드확률이 증가하게 된다. 결과적으로는 세 가지의 고장에 대해서 모두 노이즈 성분을 줄이면서 상태변수를 추정할 수 있었다.

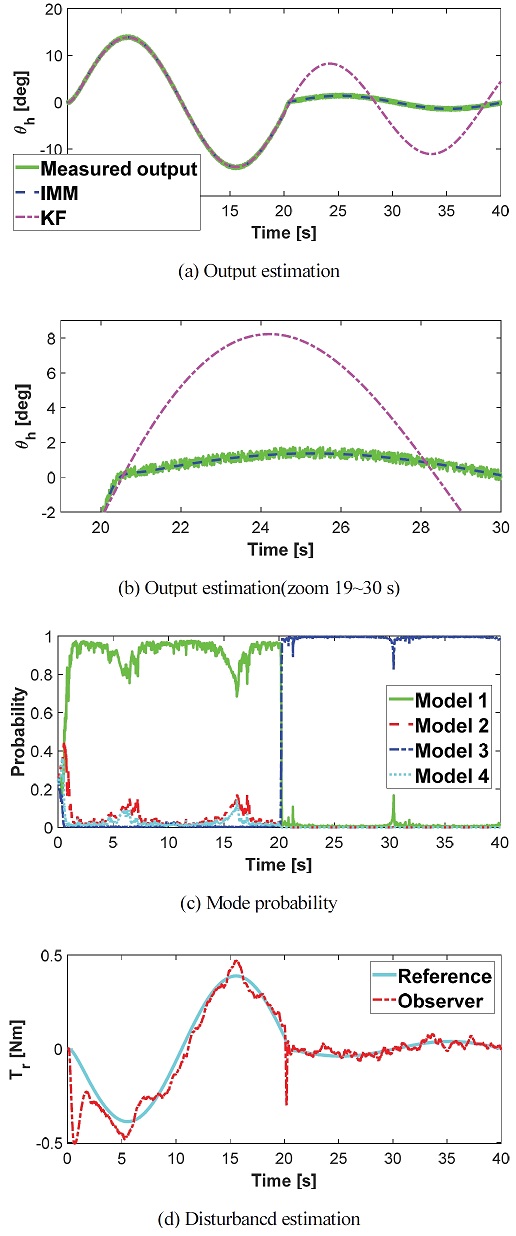
Fig. 5는 대표적으로 모터의 전기적 고장상황을 가정하여 R_m이 7배만큼 증가하는 경우에 대한 모의 실험 결과이다. IMM에 각기 다른 네 가지 타입의 Kalman filter 모델로 구성되어 확률적으로 추정값을 보정하므로 단일 Kalman filter를 사용할 때보다 고장검출 성능에서 차이가 있었다. Fig. 5(a)와 (b)를 봤을 때, 고장을 분류하고 진단하는 데 있어서 IMM은 단일 Kalman filter를 사용할 때보다 훨씬 좋은 성능을 보여준다. Kalman filter 외에 Unscented Kalman filter나 Extended Kalman filter와 같은 단일 필터는 정상상태의 시스템 모델 파라미터를 기반으로 추정하기 때문에 여러 필터 모델을 포함하는 IMM에 비해 고장 추정 성능이 떨어질 수밖에 없다.¹⁴⁾ 단일 필터들은 갑자기 변한 시스템을 따라가기 힘든 반면, IMM은 고장난 시스템의 출력값을 거의 정확히 추정한다.

Fig. 5

IMM simulation result with motor fault

또한 Fig. 5(c)와 같이 시스템이 변화함과 동시에 그에 해당하는 Model 3의 확률은 상승하지만 해당하지 않는 고장상태의 모드확률은 유효확률인 50 %를 넘어가지 않았다. 따라서 시스템이 크게 변하더라도 IMM은 여러 Kalman filter 모델의 확률적인 상호작용에 의해 단일 관측기에 비해 지속적으로 상태를 추정하는 능력이 탁월하여 빠르고 정확한 고장검출을 하는 것을 확인할 수 있었다.

여기서 Extended state observer를 사용하여 외란 T_r을 추정한 결과는 Fig. 5(d)와 같다. T_r은 바퀴의 방향이 회전함으로써 생기는 반발력 토크이므로 Steering wheel angle θ_h에 반대 방향으로 작용하는 토크값을 임의로 발생시켰으며 이때의 추정값이 실제 필터에 적용되었다.

4.4 PCIMM 성능 검증

본 논문에서는 2개의 IMM으로 구성된 PCIMM에 대한 모의 실험을 한다. Parameter IMM 모델은 Table 2와 동일하고 QR IMM의 모델들은 Table 3과 같다. IMM 추정기는 기본적으로 출력을 받아서 필터링을 하는 알고리즘이기 때문에 센서노이즈와 관련된 R의 변화에 따라 QR 모델을 선정했다.

Table 3

QR IMM modeling

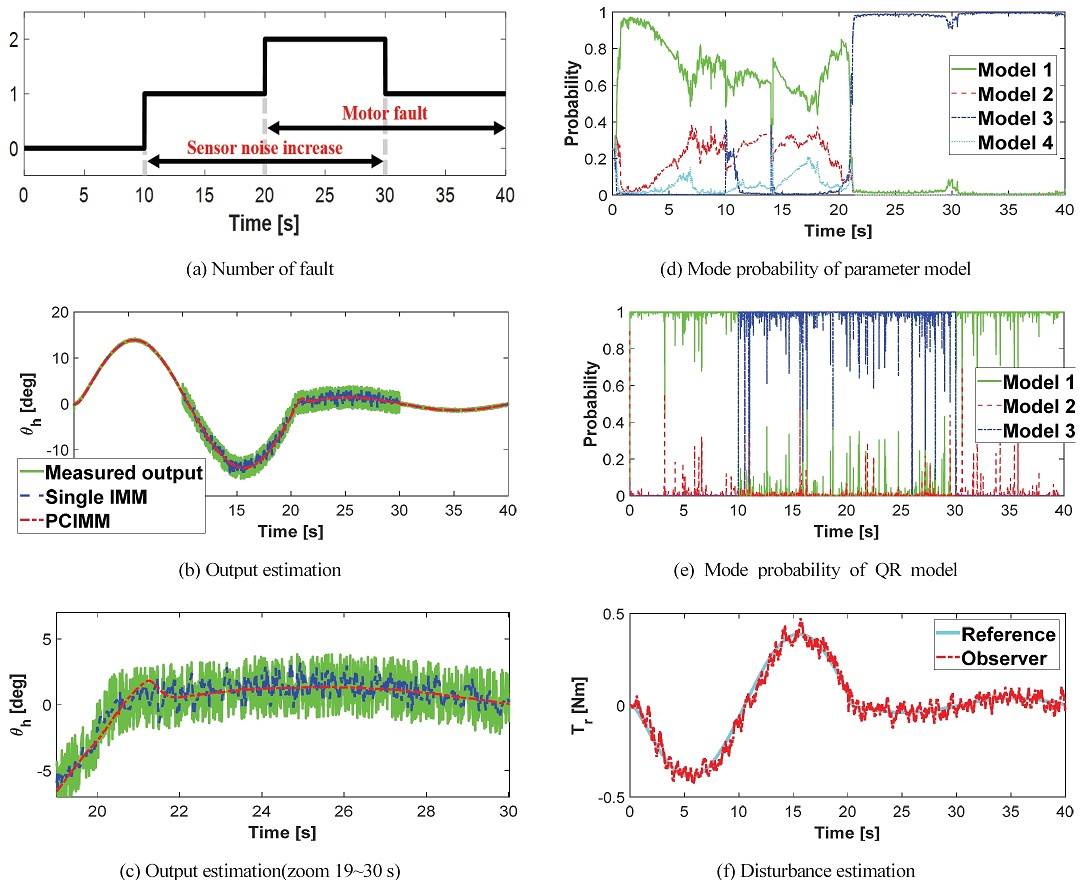
이러한 모델을 기반으로 앞선 실험 환경과는 다른 고장상황에서 모의 실험을 진행했다. 20초 부근부터 한 종류의 파라미터 고장이 발생하는 것은 같으나 추가적으로 10초에서 30초 사이에 센서노이즈 R이 정상상태의 60배가 증가하는 복합적 고장상황을 가정했다. 단일 고장이 아닌 두 가지의 고장상황이 발생했음에도 불구하고 IMM 추정기 모델들의 확률적인 상호작용을 통해 서로의 고장상황에 대한 가능도를 보정하여 노이즈에 상관없이 변화하는 시스템특성을 잘 추정할 수 있었다. Table 4를 보면 단일 IMM을 사용할 때보다 추정 정확도가 높아져 RMSE 값이 크게 줄었음을 알 수 있다.

Table 4

RMSE comparison of single IMM and PCIMM

Fig. 6

PCIMM simulation result

5. 결 론

본 논문에서는 횡방향제어의 안정성을 향상시키기 위해 고장진단 알고리즘을 적용하여 EPS 시스템의 고장상황에 대한 신뢰성을 높이고자 하였다. 바퀴와 지면 사이에서 발생하는 외란 T_r을 고려한 확장 동역학 모델을 제시하고 EPS 시스템의 기계적, 전기적 고장들을 분석하여 여러 고장상황을 모델링함으로써 EPS 시스템에 적합한 다중 모델을 설계할 수 있었다.

IMM은 Kalman filter의 여러 모델이 병렬 구조로 구성되어 확률적인 상호작용을 통해 빠르게 변하는 시스템 특성을 추정하는 것이 가능하며, 단일 Kalman filter를 적용하는 것보다 시스템을 추종하는 관점에서 더 강력한 성능을 보여주었다. 또한 IMM의 복합적인 고장상황에서의 성능을 향상시킬 수 있는 PCIMM을 제시하고 검증하였다. 향후 연구에서는 제시된 방법의 추가적인 모델들을 분석하고 개선하여 고장진단 알고리즘의 성능향상을 기대할 수 있을 것이다.

Acknowledgments

이 연구는 정부의 자동차 산업 핵심 기술 개발사업(그린카)[20007447-초소형 전기차 주행 안정성 향상을 위한 전동식 조향시스템 기술 개발] 및 2020년 대한민국 교육부와 한국연구재단의 지원(NRF-2020R1F1A1071547)을 받아 연구를 수행하였습니다.

References

• C. M. Kang, S. H. Lee and C. C. Chung, “Kinematic Vehicle Lateral Motion Model based Lane Estimation System,” KSAE Spring Conference Proceedings, pp.1154-1155, 2016.
• W. Kim, Y. S. Son and C. C. Chung, “Torque-Overlay-Based Robust Steering Wheel Angle Control of Electrical Power Steering for a Lane-Keeping System of Automated Vehicles,” IEEE Transactions on Vehicular Technology, Vol.65, No.6, pp.4379-4392, 2016. [https://doi.org/10.1109/TVT.2015.2473115]
• A. Marouf, M. Djemai, C. Sentouh and P. Pudlo, “A New Control Strategy of an Electric-Power-Assisted Steering System,” IEEE Transactions on Vehicular Technology, Vol.61, No.8, pp.3574-3589, 2012. [https://doi.org/10.1109/TVT.2012.2209689]
• C. M. Kang, W. Kim and H. Baek, “Cascade Backstepping Control With Augmented Observer for Lateral Control of Vehicle,” IEEE Access, Vol.9, pp.45367-45376, 2021. [https://doi.org/10.1109/ACCESS.2021.3066444]
• R. Ghimire, C. Sankavaram, A. Ghahari, K. Pattipati, Y. Ghoneim, M. Howell and M. Salman, “Integrated Model-Based and Data-Driven Fault Detection and Diagnosis Approach for an Automotive Electric Power Steering System,” IEEE Autotestcon, pp.70-77, 2011. [https://doi.org/10.1109/AUTEST.2011.6058760]
• J. S. Kim, W. G. Hwang and W. S. Lee, “Development of a Fault-Tolerant Steer-By-Wire Control System,” Transactions of KSAE, Vol.14, No.5, pp.1-8, 2006.
• K. Oh and K. Yi, “Model based Fault Detection and Robust Steering Control Algorithm for Autonomous Vehicle Using Sliding Mode Observer,” Transactions of KSAE, Vol.25, No.6, pp.732-741, 2017. [https://doi.org/10.7467/KSAE.2017.25.6.732]
• T. P. Banerjee and S. Das, “Multi-Sensor Data Fusion Using Support Vector Machine for Motor Fault Detection,” Information Sciences, Vol.217, pp.96-107, 2012. [https://doi.org/10.1016/j.ins.2012.06.016]
• R. E. Kalman, “A New Approach to Linear Filtering and Prediction Problems,” Journal of Fluids Engineering, Vol.82, No.1, pp.35-45, 1960. [https://doi.org/10.1115/1.3662552]
• G. Welch and G. Bishop, “An Introduction to the Kalman Filter,” UNC-CH Computer Science Technical Report 95041, 1995.
• D. S. Yun and H. S. Yu, “Development of the Optimized Autonomous Navigation Algorithm for the Unmanned Vehicle Using Extended Kalman Filter,” Transactions of KSAE, Vol.16, No.3, pp.7-14, 2008.
• H. A. P. Blom and Y. Bar-Shalom, “The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients,” IEEE Transactions on Automatic Control, Vol.33, No.8, pp.780-783, 1988. [https://doi.org/10.1109/9.1299]
• E. Mazor, A. Averbuch, Y. Bar-Shalom and J. Dayan, “Interacting Multiple Model Methods in Target Tracking: A Survey,” IEEE Transactions on Aerospace and Electronic Systems, Vol.34, No.1, pp.103-123, 1998. [https://doi.org/10.1109/7.640267]
• V. Judalet, S. Glaser, D. Gruyer and S. Mammar, “Fault Detection and Isolation via the Interacting Multiple Model Approach Applied to Drive-By-Wire Vehicles,” Sensors, Vol.18, No.7, Paper No.2332, 2018. [https://doi.org/10.3390/s18072332]
• C. M. Kang, S. H. Lee and C. C. Chung, “Vehicle Lateral Motion Estimation with Its Dynamic and Kinematic Models Based Interacting Multiple Model Filter,” IEEE 55th Conference on Decision and Control(CDC), pp.2449-2454, 2016. [https://doi.org/10.1109/CDC.2016.7798629]
• S. Lee, W. Jung, D. Bae and M. Lee “A Study on the Application of Hollow P-EPS to a Micro-Electric Vehicle Using a Simulator,” Transactions of KSAE, Vol.28, No.12, pp.875-882, 2020. [https://doi.org/10.7467/KSAE.2020.28.12.875]