핸들링 목표 성능 달성을 위한 타겟 캐스케이딩 기반 서스펜션 설계

1. 서 론

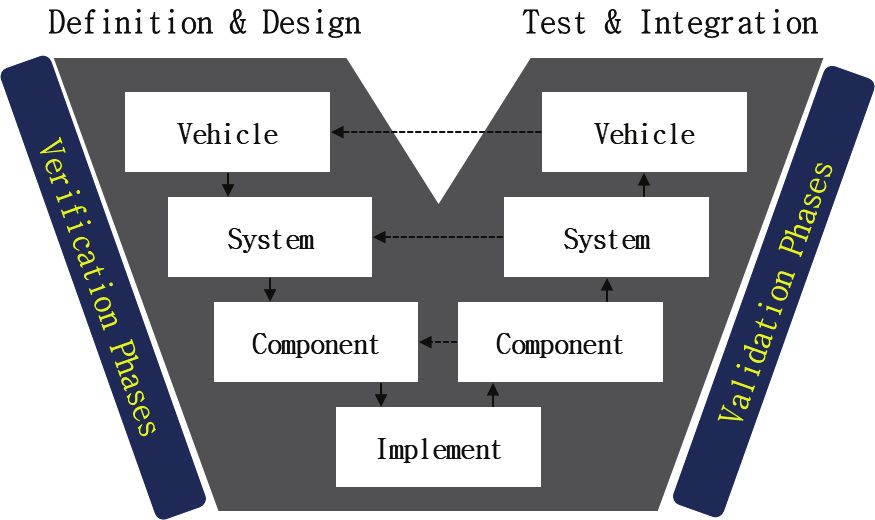
차량을 개발하는데 있어 엔지니어링 제약 조건을 준수하면서 성능 목표를 만족시키기 위하여 단일화된 설계 문제만으로는 차량과 같이 복잡성이 높은 제품의 성능을 만족하기 어렵다. 이를 해결할 수 있는 방법으로 제안된 것이 타겟 캐스케이딩 설계 방법으로 전체 프로세스는 다음과 같다. 먼저 전체 시스템의 계층을 분해하여 Fig. 1과 같이 V-모델을 구성하고, 최상위 레벨의 성능 목표를 수립한 후 하위 시스템으로 목표를 전파한다. 이 때 상, 하위 시스템의 상호 관계를 해석 모델로 구성하고, 목적 함수 및 설계 변수를 이용하여 수학적 표현으로 정의한 설계 문제를 최적화 전략에 의해 해결하는데 사용한다. 마지막으로 설계 결과를 바탕으로 목표 값이 올바로 추종됐는지 확인한다.

Fig. 1

V-model of vehicle development

이러한 방법론은 2001년 제안되었으며 본 논문에서는 차량의 핸들링 성능 개발을 위한 서스펜션 설계에 적용하였다.¹⁾ 타겟 캐스케이딩 설계를 통해 시스템 전체가 최상위 레벨의 핸들링 성능 목표를 만족하는 일관되고 실현 가능한 설계가 될 수 있도록 계층별 소규모 설계 문제에 대해 적절한 목표를 설정하고, 목표를 만족하기 위한 하위 계층의 설계 값을 최적화 전략에 따라 결정함으로써 차량 개발 초기 일정 수준 이상의 성능 목표를 달성할 수 있다.²⁾ 타겟 캐스케이딩 방법에 의한 핸들링 성능 개발에 있어서 중요한 부분 중 하나는 최상위 레벨에서의 성능 목표를 설정하는 것이고, 또 다른 하나는 상, 하위 계층 간 상호작용을 상세히 모델링하면서도 초기 설계 도구로써 해석이 신속하게 수행될 수 있도록 연산 속도가 빠른 해석 모델을 개발하는 것이 필요하다.³⁾

본 논문에서는 최상위 계층인 차량 레벨에서의 핸들링 성능 목표 설정을 위하여 크리깅 방법으로 주⋅객관 평가 상관 모델을 생성하고, 이 모델을 이용하여 주관 성능 목표를 객관 성능 목표로 변환하는 방법을 제시하였다. 또한 연산 시간 단축을 위해 함수형 현가장치 모델과 메타 휴리스틱 최적화 알고리즘을 사용하여 타겟 캐스케이딩 설계를 실시하고 이를 검증하였다.

2. 타겟 캐스케이딩 기법

타겟 캐스케이딩 기법은 목표를 상위 레벨에서부터 하위 레벨까지 전개시켜가며 설계 변수를 결정하는 설계 접근 방법이다. 이와 같이 설계 대상을 계층화하여 분해하고, 분해된 계층의 최상위 레벨에서의 설계 목표를 최하위 레벨로 단계적으로 전개시켜 설계 효율성을 향상시킬 수 있다.

타겟 캐스케이딩 기법은 특히 자동차 시스템 설계와 같이 복잡한 시스템을 설계할 때 유용하다. 복잡한 하나의 문제를 단계를 나눠 작고 단순한 문제로 전환한다면 조금 더 쉽게 문제를 해결할 수 있기 때문이다. 또한 최적화할 하나의 시스템에 대해서 전반적인 성능을 결정하는 여러 하위 시스템들 간의 더 나은 관계와 절충을 이해하는 데에도 도움을 줄 수 있다.⁴⁾

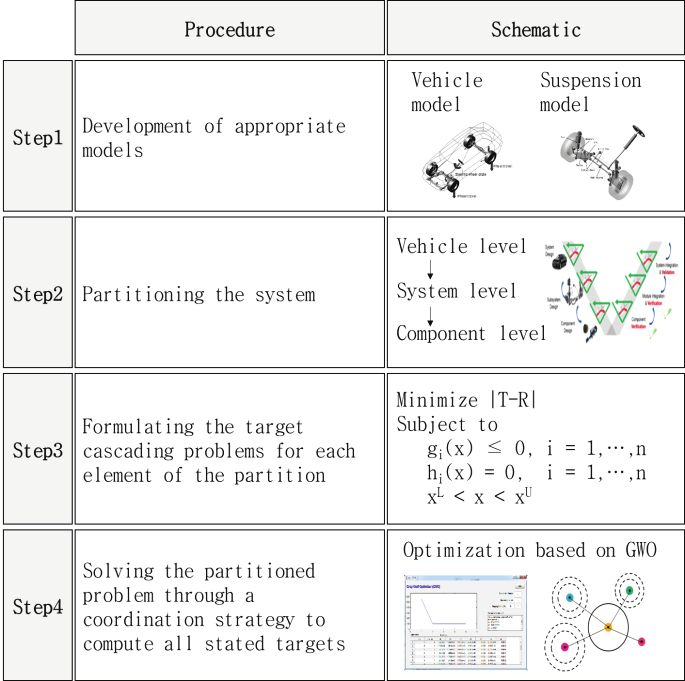
타겟 캐스케이딩 설계의 일반적인 절차는 Fig. 2와 같다. 첫째 적합한 해석 모델 개발 단계이다. 타겟 캐스케이딩 설계는 차량 개발 단계에서 차량이 완성되기 전 가상의 시뮬레이션 환경을 기반으로 성능을 확인하고 설계 변수를 결정하는 방식으로 진행되기 때문에 실차 성능을 예측할 수 있는 해석 모델 개발이 필요하다.

Fig. 2

Target cascading in vehicle design

둘째 시스템 계층 분해 단계이다. 앞서 기술한 것과 같이 수많은 부품으로 이루어진 복잡한 차량 성능에 대해 시스템 단위, 부품 단위로 계층을 분해하여 설계 문제를 간소화하고, 차량, 시스템, 부품으로 연계되는 성능과 설계 변수 간의 관계를 분석할 수 있도록 하는 작업이 필요하다.

셋째 각 계층 요소에 대하여 설계 문제를 수학적으로 정의하는 단계이다. 일반적인 설계 문제는 설계 제약 조건을 만족하면서 설계 목표와 현재의 성능 지수 불일치를 최소화하는 문제로 표현이 가능한데 이때 목적 함수, 제약 조건, 설계 변수에 해당하는 파라미터를 수학적인 구조로 표현하는 단계이다. 이를 통해 해석 모델에 해당 파라미터를 인가하여 시뮬레이션 기반의 최적 설계가 가능하도록 구성한다.

넷째 계층별 목표 성능을 설정하고 정의된 설계 문제를 해결하기 위하여 최적화 전략을 통해 설계 변수를 결정하는 단계이다. 최적화 전략은 목표 값과 추종 값과의 차이가 설정한 범위 이내에 들어올 때까지 설계 변수 값을 변경하여 반복적으로 해석을 수행하면서 목표 값을 추종하는 방법에 대한 내용이며 목표 추종성과 정확성을 모두 갖춰야 한다.

2.1 해석 모델

타겟 캐스케이딩 설계 프로세스에서는 구분된 계층 요소의 성능에 대하여 정량적이고, 분석적인 모델의 존재를 가정한다. 적합한 모델이 없을 경우 모델 개발이 필요한데 차량, 시스템, 부품으로 계층화된 설계 문제를 해결하기 위해서는 차량 단위의 핸들링 성능 해석 모델과 시스템 단위의 전, 후륜 서스펜션의 키네매틱 & 컴플라이언스(이하 K&C) 특성 해석을 위한 모델 구축이 필요하다.

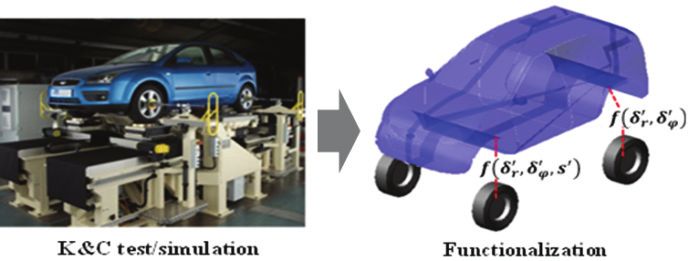
핸들링 성능 해석을 위한 전 차량 모델의 경우 기존 다물체 차량 동역학 모델을 이용하면 실차 정합성 측면에서는 유리하지만 큰 자유도로 인하여 실시간 해석이 어렵기 때문에 최적 설계에 적합하지 않다. 따라서 본 논문에서는 함수형 현가장치 모델을 활용하여 해석 모델의 신뢰성을 확보하는 동시에 연산 시간을 단축시킴으로써 실시간 수준으로 반복적인 시뮬레이션에 의한 최적 설계가 가능하게 하였다.⁵⁾ 함수형 현가장치 모델은 Fig. 3과 같이 현가장치 특성 시험기(이하 SPMD) 평가 또는 Adams 해석을 통해 얻어진 K&C 특성 데이터를 활용하여 3차원 공간에서 운동하는 차량을 차체와 4개의 휠, 총 5개의 강체로 모델링을 하고, 각 휠이 차체에 대하여 상대운동을 하도록 함수 형태로 모델링한 차량 동역학 모델이다. 차량의 운동은 관성 좌표계에 대해 차체와 각 휠에 고정된 좌표계 위치와 회전에 의하여 표현될 수 있도록 모델을 구성하였다. 이 모델의 경우 11자유도의 상미분 방정식으로 운동방정식을 기술하기 때문에 해석을 수행하는데 걸리는 시간이 다물체 차량 동역학 모델과 비교하여 훨씬 절약될 수 있다. 또한 SPMD 평가 결과나 Adams 해석 결과를 활용하여 모델링함으로써 비선형 방정식을 풀지 않기 때문에 시간적 측면의 효율성이 증가하여 실시간 차량 동역학 해석이 가능한 장점이 있다.

Fig. 3

Functional suspension model

K&C 특성 해석을 위한 기구 정역학 모델 역시 해석 정합성과 연산속도를 모두 고려해 모델링해야 한다. 이를 위해 본 논문에서는 차체와 휠 사이 각종 현가 기구의 연결 구조와 조인트, 부시와 같은 힘 요소 특성을 모델에 포함하면서 효율적인 수식 유도가 가능하도록 모델링하였다.⁶⁾ 부시를 포함한 다물체 현가장치 모델은 상대좌표계로 모델링할 경우 부시를 조인트로 모델링한 현가장치 모델에 비해 현가 장치를 이루는 강체 간의 기구학적 연결 구조가 단순화 된다. 즉 휠에 기구학적으로 연결된 현가 링크가 차체와는 부시로 연결되어 루프를 이루고 있지 않으며 트리 구조 형태를 취한다. 기구학적으로 개루프를 띄고 있는 기구의 경우 조인트 상대 운동을 일반 좌표로 취할 경우 구속조건식이 없어진다. 이처럼 상대 조인트 좌표계를 사용하면 직교 좌표계를 사용하는 Adams 등에 비해 현가장치 기구 정역학 해석 시에 기구학적 구속조건식이 없어져서 방정식의 규모가 작아지고 해석 과정이 더 단순하여 안정적인 해석이 가능하다.

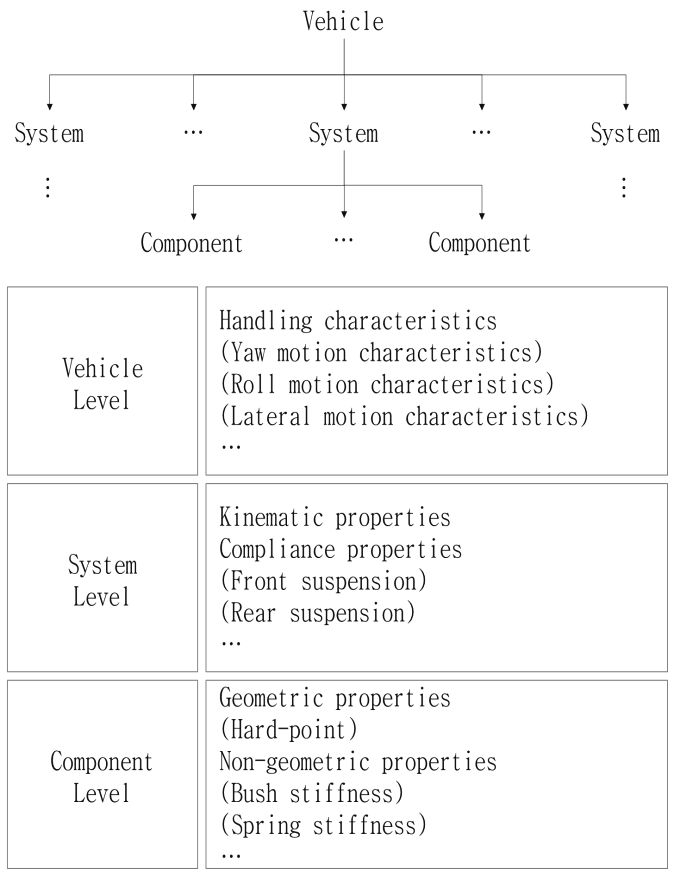
2.2 시스템 계층 분해 및 타겟 캐스케이딩 설계

앞 절에서 구축한 해석 모델을 이용하여 타겟 캐스케이딩 설계 방법으로 핸들링 성능 목표를 만족하는 서스펜션 설계를 진행하기 위하여 Fig. 4와 같이 차량, 시스템, 부품 세 단계로 계층을 분해하였다. 계층 분해 작업을 통하여 총 두 번의 최적화 모듈을 가지게 되며, 첫번째 차량 단계에서의 최적화에서는 핸들링 성능을 만족하는 K&C 특성 변수를 결정한다. K&C 특성 변수는 차체와 각 휠의 상대적인 위치 변화에 따른 휠의 토우 각, 캠버 각, 캐스터 각 등의 변화로 계산되는 기구학적 특성과 타이어 접지면에 작용하는 힘과 모멘트에 의한 휠의 얼라인먼트 변화로 계산되는 컴플라이언스 특성을 4차 다항식으로 모사하여 추출한 1, 2차 계수 값을 사용하고, 여기에 전, 후륜 스프링 강성, 댐퍼 감쇠력, 스태빌라이저바 강성을 포함한다.⁷⁾

Fig. 4

Hierarchy of vehicle models in target cascading

차량 단계에서의 설계 문제는 식 (1)과 같이 나타낼 수 있다.

$\[ \begin{array}{l}\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} ‖T_{veh}-R_{veh}‖\\ x \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} R_{veh}=r_{veh}\left(x\right)\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}\\ \begin{array}{cc} g_{v,i}\left(x\right)\le 0, & i=1,\dots ,m_i\end{array}\\ \begin{array}{cc} h_{v,j}\left(x\right)\le 0, & j=1,\dots ,m_j\end{array}\\ \begin{array}{cc} x_k^{lower}\le x_k\le x_k^{upper} , & k=1,\dots ,n\end{array}\end{array} \]$

(1)

설계 제약 조건인 g_ν,i(x)와 h_ν,i(x)를 만족하는 동시에 설계 목표 T_νeh와 전 차량 해석 모델에 의한 해석 결과 R_νeh의 차이를 최소화하는 목적 함수와 시스템 레벨의 K&C 특성 설계 변수로 표현 가능하다. 3절에서 자세히 다루겠지만 본 논문에서는 핸들링 성능으로 정의된 7개 항목인 정상상태 롤 각, 롤 게인, 정상상태 요 각속도, 요 각속도 응답시간, 요 각속도 오버슛, 횡가속도 응답시간, 조향 민감도를 설계 목표로, K&C 특성값을 설계 변수로 설정하여 최적 설계를 진행하였다. 여기서는 핸들링 성능으로 정의된 7개 항목을 모두 설계 목표로 설정하였으나, 필요 시 설계 제약 조건을 따로 설정할 수도 있다.

두번째 시스템 단계에서의 최적화는 앞선 차량 단계의 설계 문제로부터 결정된 K&C 특성 변수를 다시 목적 함수로 설정하여 부품 단위의 설계 변수를 결정하게 된다. 이때 부품 단위의 설계 변수는 전, 후륜 서스펜션 및 스티어링 시스템의 지오메트리 특성을 나타내는 값으로 부품의 하드포인트 좌표와 부시 강성과 같은 설계 값으로 정의된다.

시스템 단계에서의 설계 문제 역시 아래와 같이 식 (2)의 형태로 표현할 수 있다.

$\[ \begin{array}{l}\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} ‖T_{sys}-R_{sys}‖\\ x \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} R_{sys}=r_{sys}\left(x\right)\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}\\ \begin{array}{cc} g_{s,i}\left(x\right)\le 0, & i=1,\dots ,m_i\end{array}\\ \begin{array}{cc} h_{s,j}\left(x\right)\le 0, & j=1,\dots ,m_j\end{array}\\ \begin{array}{cc} x_k^{lower}\le x_k\le x_k^{upper} ,& k=1,\dots ,n\end{array}\end{array} \]$

(2)

차량 레벨에서 전파된 설계 목표, 본 논문에서는 K&C 특성 함수의 1, 2차 계수를 사용하여 현재 모델이 가지고 있는 계수 값과의 차이를 최소화하도록 목적 함수를 설정하고, 하드포인트 및 부시 강성과 같은 부품 레벨의 설계 변수를 결정하도록 시스템 단계 설계 문제를 정의하였다. 이때 차량 단계에서의 설계 문제와 마찬가지로 설계 제약 조건 g_s,i(x)와 h_s,i(x)를 설정하는 것이 가능하다.

2.4 최적 설계 전략

앞선 단계에서 설계 문제를 정의하고 최상위 레벨에서의 성능 목표를 설정하였다면 그 다음 단계로 설계 문제를 해결하기 위한 최적 설계 전략을 수립해야 한다. 최적 설계 전략 중 자연의 원리나 구조에서 영감을 받아 문제를 해결하는 방법을 메타 휴리스틱 알고리즘이라고 하는데 본 논문에서는 메타 휴리스틱 알고리즘 중 하나인 Grey Wolf Optimizer(이하 GWO)를 사용하여 최적 설계를 진행하였다.

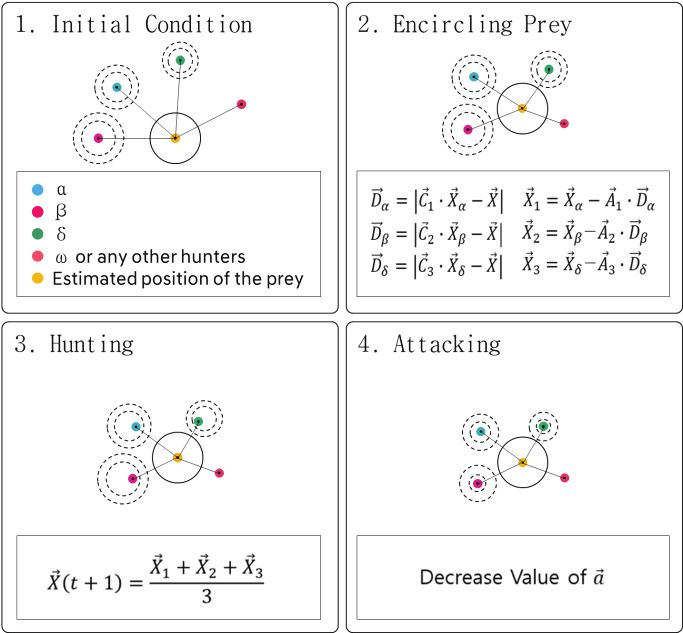
이 알고리즘은 2014년 Mirjalili가 제안한 것으로 자연에서 회색 늑대들의 지배 체계와 사냥 메커니즘을 모방한 최적 설계 알고리즘이다.¹³⁾ 늑대의 지배 계급은 크게 네 가지 유형으로 분류되는데 리더이자 의사 결정 계급인 알파, 알파의 의사 결정을 돕는 조력자 계급인 베타와 델타, 그리고 이 세 그룹을 제외한 나머지 계급인 오메가는 리더의 의사 결정에 따라 움직이는 추종 집단이다. 이러한 지배 구조에 따라 Fig. 5에서와 같이 사냥감을 찾아 포위하고 공격하는 사냥 단계를 최적 설계에 적용하여 수학적으로 모형화할 수 있다.

Fig. 5

Grey wolf optimizer algorithm

초기 위치에서부터 사냥감을 포위하는 첫번째 과정은 식 (10), (11)과 같이 표현한다.

$\[ \overrightarrow{D}=\left|\overrightarrow{C}\cdot {\overrightarrow{X}}_p\left(t\right)-\overrightarrow{X}\left(t\right)\right| \]$

(10)

$\[ \overrightarrow{X}\left(t+1\right)=\left|{\overrightarrow{X}}_p\left(t\right)-\overrightarrow{A}\cdot \overrightarrow{D}\right| \]$

(11)

여기서 t는 목표물을 찾아가기 위한 여러 번의 학습 과정 중 현재의 학습 횟수를 나타내며, $$ {\overrightarrow{X}}_p\left(t\right)$$는 t번째 학습과정에서의 목표물의 위치 벡터, $$ \overrightarrow{X}\left(t\right)$$는 회색 늑대의 위치 벡터이다. $$ \overrightarrow{A}$$와 $$ \overrightarrow{C}$$는 벡터로 표현된 보정 계수로써 식 (12), (13)과 같이 정의한다. 이때 $$ \overrightarrow{a}$$는 진화가 거듭될수록 2에서 0까지 선형적으로 줄어드는 계수이다.

$\[ \overrightarrow{A}=2\overrightarrow{a}\cdot rand\left(\mathrm{0,1}\right)-\overrightarrow{a} \]$

(12)

$\[ \overrightarrow{C}=2\cdot rand\left(\mathrm{0,1}\right) \]$

(13)

사냥감을 포위한 후 점차 사냥감에 근접해가면서 본격적인 사냥, 즉 최적 해를 탐색하는 과정이 두 번째 과정이다. 이때 실제 최적 해 $$ {\overrightarrow{X}}_p$$를 모르기 때문에 진화 대상이 되는 개체의 위치를 식 (14)와 같이 최적 해에 가장 근접한 3개 해의 위치 벡터 평균값을 통해 결정한다.

$\[ {\overrightarrow{X}}_{t+1}=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3} \]$

(14)

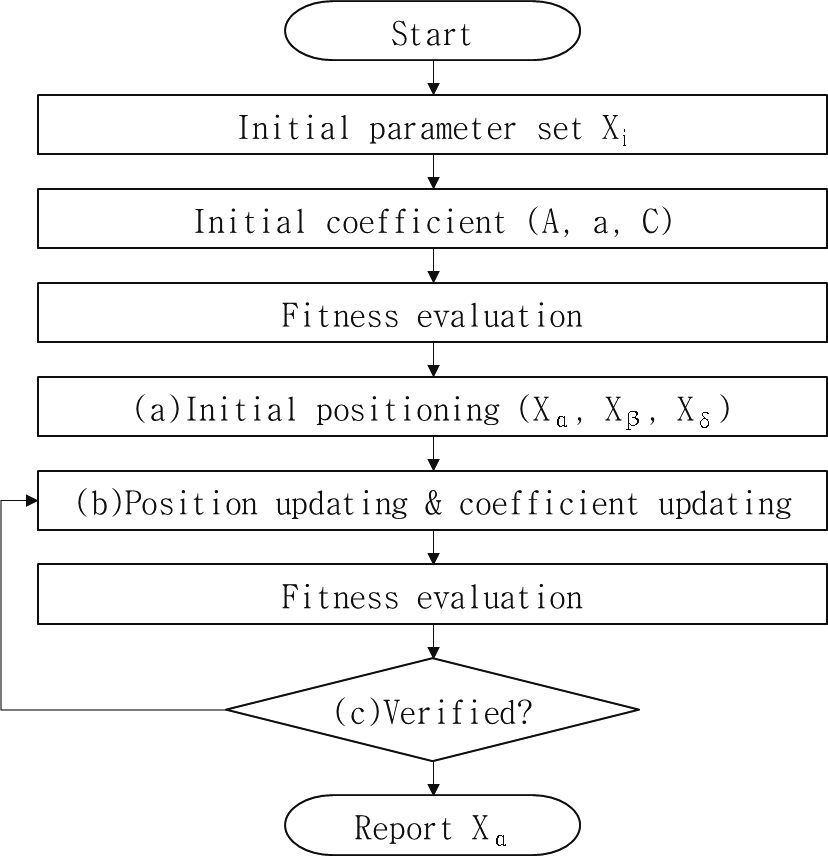
이러한 일련의 진화 과정을 반복함으로써 알파, 베타, 델타의 위치가 업데이트되면서 나머지 개체들의 위치는 점차 최적 해 방향으로 접근하게 되고 최종적으로 오차 범위에 들어오는 최적 해 $$ {\overrightarrow{X}}_{\alpha }$$값을 도출할 수 있다. Fig. 6은 GWO 최적 설계 알고리즘의 전체 동작 순서도이다.

Fig. 6

Flowchart of GWO algorithm

3. 타겟 캐스케이딩 기법에 의한 서스펜션 설계 및 검증

2장에서 서술한 타겟 캐스케이딩 절차를 실제 서스펜션 설계에 적용하고, 그 결과를 검증하기 위하여 차량 단위 설계와 시스템 단위 설계, 두 단계로 계층을 구분하여 설계 문제를 정의하였다. 차량 단위 설계에서의 해석 모델은 함수형 현가 장치 모델을 사용하여 실차 평가 방법에 기반한 해석 조건으로부터 성능 지수들을 계산한다. 최적 설계를 위한 목적 함수는 해석 모델로부터 조향 입력에 따른 차량의 동적 응답 특성을 정량적으로 계산한 핸들링 성능 지수에 대하여 목표 값과 해석 값의 차이를 최소화하도록 설정하고, 설계 변수는 시스템 레벨의 K&C 특성으로 설정하여 핸들링 목표 성능을 만족하는 K&C 특성을 결정한다. 이때 핸들링 목표 성능은 경쟁차량의 객관 성능 지수로 설정할 수도 있고, 주⋅객관 평가 상관 모델을 이용하여 목표 주관 점수로부터 객관 성능 지수를 예측하여 그 값을 목표로 사용할 수도 있다. 본 논문에서는 주⋅객관 평가 상관 모델을 활용하여 핸들링 목표 설정을 진행하고, 목표 성능을 달성하기 위하여 타겟 캐스케이딩 기법을 적용하여 서스펜션 부품을 설계하였다.

우선 목표 설정을 위하여 차량 거동의 과도 상태와 정상 상태 특성을 모두 확인할 수 있는 스텝 스티어 1개 시나리오에 대한 객관 성능 지수를 선정하였다. 스텝 스티어 평가의 경우 정상 상태 및 과도 상태에서의 차량 롤거동과 요 각속도 및 횡 가속도 크기와 지연감 등에 대하여 해석이 가능하며 이를 지수화한 7개 항목은 정상상태롤 각, 롤 게인, 정상상태 요 각속도, 요 각속도 응답시간, 요 각속도 오버슛, 횡가속도 응답시간, 조향 민감도이다. 여기에 주관 평가 항목은 평가 결과의 신뢰성 확보를 위해 유럽 잡지사의 핸들링 성능과 관련된 평가 항목을 사용하였으며 AutoBild의 Stability와 Agility, AMS의 Handling과 Steering, 총 4개 항목을 선정하였다. 그리고 동일한 차급에 해당하는 4대의 차량(A∼D)에 대하여 객관 성능 지수 7개 항목과 주관 성능 지수 4개 항목에 대한 평가 데이터를 Tables 1, 2와 같이 확보하였다. 크리깅 방법을 적용하여 $$ \widehat{y}\left(x\right)=f^T\left(x\right)\widehat{\beta }+r^T\left(x\right)R^{-1}\left(y_s-F\widehat{\beta }\right)$$와 같은 형태의 주⋅객관 평가 상관 모델을 생성하기 위하여 이 데이터들을 가지고 GWO 알고리즘을 통해 계수값을 결정하여 모델을 생성하고, 설계 대상 차량의 객관 평가 결과로부터 Table 3의 Initial과 같이 주관 평가 점수를 예측하였다.

Table 1

Objective metrics data for correlation model

Table 2

Subjective assessments data for correlation model

Table 3

Subjective assessment targets

설계 대상 차량의 경우 아직 개발 중인 차량으로 잡지사의 주관 평가 점수가 없기 때문에 이 방법을 사용하여 주관 평가 점수를 예측하였으며 그 결과 열세로 예측된 Agility와 Handling 항목의 점수를 각각 3점, 5점 상향하는 것을 목표로 다시 상관 모델을 사용하여 Table 4의 Target과 같은 목표 객관 성능 지수를 도출하였고 이 값을 차량 레벨 설계 목표로 설정하였다.

Table 4

Vehicle level targets from correlation model

그 다음 설정한 목표 값과 해석 모델의 시뮬레이션 결과값과의 차이를 최소화하도록 설계 문제를 정의하고, 설계 변수를 설정한다.

설계 변수는 초기 토우 각, 캠버 각과 같은 기구학적 특성 값과 전, 후륜 스프링 강성, 댐퍼 감쇠력, 스태빌라이저바 강성 및 4차 다항식 형태로 표현된 K&C 특성에 대한 1, 2차 계수 값, 여기에 조향계 특성 및 타이어 특성 등을 포함시킨 후 민감도 분석을 통해 스크리닝 과정을 진행하였다. 그 결과 Table 5와 같이 총 26개 항목을 설계 변수로 설정하였다. 이 설계 문제에서 핸들링 성능 목표는 주⋅객관 평가 상관 모델로부터 목표 주관 점수를 달성하기 위한 객관 성능 지수 7개 항목에 대한 예측 값이고, 해석 모델에 입력되는 설계 변수는 초기 설정 값에서부터 GWO 알고리즘에 따라 값을 계속해서 업데이트해 가면서 최종적으로 시뮬레이션 결과 값이 목표 값에 근접할 때의 설계 변수를 최종적으로 결정하게 된다.

Table 5

Design variables of vehicle level

최적 설계를 진행한 결과는 Table 6에서 볼 수 있듯이 정상상태 요 레이트는 변화가 없었고, 나머지 6개 성능에 대하여 목표 값 대비 최대 6 % 이내 오차율로 목표 값을 추종하는 방향으로 설계가 진행된 것을 확인하였다. 또한 설계 변수인 K&C 특성 변화는 롤 스티어 및 횡력스티어에 의한 선회 특성 변화가 약 언더스티어 경향의 특성을 갖도록 설계되어 핸들링 성능 향상 목표를 달성하도록 초기 값 대비 설계 값이 변경된 것을 확인할 수 있었다.

Table 6

Vehicle level optimization result

두번째로 시스템 레벨에서의 설계 문제는 Table 7과 같이 차량 레벨 설계 문제로부터 결정된 K&C 특성 다항식의 1, 2차 계수를 목표 값으로 설정하여 이 목표를 만족하는 하드포인트 및 부시 강성 등의 부품 특성을 결정하는 문제이다. 차량 레벨 설계 문제와 마찬가지로 설정한 목표 값과 해석 모델의 시뮬레이션 결과 값과의 차이를 최소화하도록 설계 문제를 정의하였다. 시스템 레벨에서의 해석모델은 앞 절에서 서술한 것과 같이 전, 후륜 현가 장치에 대하여 상대 조인트 좌표계를 사용하여 방정식을 유도한 기구 정역학 모델을 사용하여 K&C 특성 해석을 진행한다.

Table 7

System level targets

해석 모델로부터 계산되는 K&C 특성은 키네매틱 해석인 범프, 롤, 스티어링 모드 해석과 컴플라이언스 해석인 횡 방향, 전후 방향 모드 해석의 결과이다. 시스템 레벨 최적 설계 문제의 목적함수는 차량 레벨 설계로부터 결정된 시스템 특성 값 중에서 하위 부품 계층을 포함하지 않는 초기 토우 각, 캠버 각, 전, 후륜 스프링 강성, 댐퍼 감쇠력, 스태빌라이저바 강성을 제외하고, K&C 특성 함수의 1, 2차 계수 값만 사용한다.

목표값 설정 후 다음 단계로 설계 변수를 설정하였다. 이때 변수로 사용할 하드포인트 및 부품 강성에 대한 인자가 과다하여 차량 레벨에서의 최적화 과정과 마찬가지로 전, 후륜 현가장치의 하드포인트 및 부품 강성에 대한 민감도 분석을 통해 Table 8과 같이 전륜의 하드포인트 및 부시 강성 27개 항목, 후륜의 부시 강성 11개 항목, 총 38개 항목으로 스크리닝한 설계 변수에 대하여 GWO 알고리즘을 사용하여 최적 설계를 진행하였다. 하드포인트 및 부시 강성에 대한 상세 설정 값은 대외비로 논문에서는 생략한다.

Table 8

Design variables of system level

최적 설계 결과 Table 9와 같이 K&C 특성 계수의목표를 추종하는 결과를 얻었다. K&C 최적화의 경우 영향도가 큰 타이어에 대한 변수가 포함되지 않았는데 설계 변수를 추가로 설정하거나 설계 제한 조건을 확장하여 최적화를 진행하면 추종성은 더 개선될 것으로 판단된다. 부품 최적 설계 방향 역시 하드포인트 및 부시 강성에 대한 값들이 롤 스티어 및 횡력 스티어에 의한 선회 특성 변화가 약 언더스티어 경향의 특성을 갖는 방향으로 설계되어 핸들링 성능 향상 목표를 추종하는 방향으로 설계가 진행된 것을 확인할 수 있었다.

Table 9

System level optimization result

최적 설계에 대한 검증은 타겟 캐스케이딩 설계를 통해 결정된 K&C 특성 값과 부품 특성 값을 가지고 해석 모델을 모델링 하고, 핸들링 성능 지수를 계산하여 목표 값과 비교함으로써 결과를 검증하였다. 성능 지수 비교를 위하여 차량 레벨 최적 설계 단계에서 결정된 K&C 특성 값을 전 차량 모델로 해석한 핸들링 성능 지수를 R_νeh라고 명시한다.

또한 시스템 레벨 최적 설계 단계에서 결정된 하드포인트 및 부시 강성 값을 기구 정역학 모델로 해석하고, 해석한 K&C 특성 값을 다시 전 차량 모델로 핸들링 성능 지수를 해석하여 R_sys라고 명시한다. 비교 결과는 Table 10과 같이 7개 성능 지수에 대한 값들이 목표 값을 추종하는 방향으로 해석된 것을 확인할 수 있다. 객관 성능 지수를 주⋅객관 평가 상관모델을 이용하여 주관 평가 점수로 변환한 결과는 Table 11과 같다. 주관 평가 항목에 대해서도 시스템 레벨까지 최적 설계를 진행하였을 때 Agility와 Handling 성능 향상 목표를 추종하는 방향으로 부품 특성이 설계 되었다.

Table 10

Objective metrics from optimization result

Table 11

Subjective assessments from optimization result

4. 결 론

본 논문에서는 차량 전체 시스템에 대하여 계층을 분해하고, 차량에서 시스템, 시스템에서 부품으로 연계되는 타겟 캐스케이딩 기반의 설계 문제를 해결하는 방법을 제안하였다. 제안한 방법을 통해 핸들링 성능을 만족하는 서스펜션 부품을 설계하였으며 다음과 같은 결과를 얻을 수 있었다.

첫째, 차량 레벨에서의 핸들링 목표 성능 설정을 위해 크리깅 기법을 이용하여 주⋅객관 평가 상관 모델을 생성하고, 이 모델로부터 주관 성능 점수를 객관 성능 지수로 변환하는 정량화된 핸들링 목표 성능 설정 방법을 제안하였다. 이를 통해 개발 중인 C세그 차량의 핸들링 성능 가운데 열세 항목에 대하여 주관 평가 점수를 약 3점향상시킬 수 있도록 정량 목표를 설정하고 해석을 통해 검증 하였다.

둘째, 타겟 캐스케이딩 방법을 적용하여 핸들링 성능을 만족하는 K&C 특성 변수를 결정하고, 결정된 K&C 특성을 목표로 서스펜션 부품 특성을 결정하는 설계 방법을 제안하였다. 특히 목표 값에 대한 수렴성과 수렴 속도를 모두 고려하여 차량 단위의 함수형 현가 장치 모델과 시스템 단위의 상대 조인트 좌표계로 방정식을 유도한 기구 정역학 모델을 이용하여 성능을 예측하고, GWO 알고리즘에 의해 최적 값을 탐색하는 방법을 사용함으로써 기존 Trial & Error 방식 대비 개발 비용 및 시간을 단축할 수 있는 프로세스 기반을 마련하였다. 이 방법을 C세그 차량에 적용하여 핸들링 성능을 평균 18 % 개선할 수 있도록 지오메트리 및 K&C 설계 변수를 도출하였다.

셋째, 차량 핸들링 성능에 대한 주관 평가 점수를 향상시키는 방향으로 목표 성능을 설정하고 타겟 캐스케이딩 방법으로 설계를 진행한 결과 약 언더스티어 경향의 특성을 가지면서 설정한 목표 값을 추종하도록 시스템 및 부품 특성이 설계된 것을 확인함으로써 타겟 캐스케이딩 기반 서스펜션 설계 타당성을 검증하였다.

본 논문에서 제시한 설계 방법을 통하여 차량 전체 개발 기간을 단축하고 설계 효율성을 증대하는데 기여할 수 있을 것으로 기대된다.

References

• H. M. Kim, Target Cascading in Optimal System Design, Ph. D. Dissertation, University of Michigan, Ann Arbor, 2001.
• K. Shintani, A. Abe and Y. Yamamoto, “A Target Cascading Method Using Model Based Simulation in Early Stage of Vehicle Development,” SAE 2019-01-0836, 2019. [https://doi.org/10.4271/2019-01-0836]
• D. O. Kang, S. J. Heo, M. S. Kim, W. C. Choi and I. H. Kim, “Robust Design Optimization of Suspension System by Using Target Cascading Method,” Int. J. Automotive Technology, Vol.13, No.1, pp.109-122, 2012. [https://doi.org/10.1007/s12239-012-0010-y]
• J. Blanco and L. Munoz, “Methodology for the Design of a Double-Wishbone Suspension System by Means of Target Cascading: Problem Statement,” SAE 2013-01-0973, 2013. [https://doi.org/10.4271/2013-01-0973]
• S. S. Kim and P. H. Park, “Development of Functional Suspension Vehicle Dynamics Model with Suspension Roll Coupling Effects,” KSAE Annual Conference Proceedings, pp.973-980, 2012.
• S. K. Kim and S. S. Kim, “An Analysis of Handling Characteristics Dispersion due to Suspension Hard-point Tolerance,” KSAE Annual Conference Proceedings, pp.958-967, 2012.
• S. Wu, Y. Hou, L. Li, Y. Zhang and L. Chen, “Special Analytical Target Cascading for Handling Performance and Ride Quality Based on Conceptual Suspension Model and Multi-body Model,” SAE 2009-01-1455, 2009.
• I. A. Badiru and M. W. Neal, “Optimization of the Customer Experience for Routine Handling Performance,” SAE 2015-01-1588, 2015. [https://doi.org/10.4271/2015-01-1588]
• D. Crolla, Encyclopedia of Automotive Engineering, John Wiley & Sons, New York, pp.2199-2216, 2015.
• M. S. Hyun, G. W. Lee and S. J. Heo, “Study on Modeling Method of Correlation between Subjective and Objective Performance of Handling and Steering Feel,” Transactions of KSAE, Vol.28, No.9, pp.597-603, 2020. [https://doi.org/10.7467/KSAE.2020.28.9.597]
• J. P. Costa, L. Pronzato and E. Thierry, A Comparison Between Kriging and Radial Basis Function Networks for Nonlinear Prediction, NSIP, 1999.
• J. S. Ryu, M. S. Kim, K. J. Cha, T. H. Lee and D. H. Choi, “Kriging Interpolation Methods in Geostatistics and DACE Model,” KSME International Journal, Vol.16, No.5, pp.619-632, 2002. [https://doi.org/10.1007/BF03184811]
• S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey Wolf Optimizer,” Advances in Engineering Software, Vol.69, pp.46-61, 2014. [https://doi.org/10.1016/j.advengsoft.2013.12.007]