모델 기반 재생 온도 제어 방법을 적용한 제어 정확도 향상에 관한 연구

1. 서 론

현재 양산 중인 디젤엔진은 배기가스 규제를 만족하기 위해 매연포집장치(Diesel Particulate Filter, 이하 DPF)를 필수적으로 장착하고 있다. DPF 내 포집된 PM(Particulate Matter)을 태우기 위해서는 별도의 재생모드를 주기적으로 사용한다. 재생모드에 진입하게 되면 엔진의 배기가스 온도를 PM의 산화 온도 이상으로 증가시키기 위해 공기제어와 연료분사 패턴을 변경하고, 엔진과 DPF 사이에 장착되어 있는 산화촉매(DOC or LNT)의 발열반응을 활용하기 위하여 후분사를 적용한다. 포집된 PM을 적절하게 태우기 위해서는 DPF 전단온도 기준 최소 600 ^oC 이상의 온도로 정밀하게 제어가 되어야 한다. 제어 온도가 낮은 경우에는 불완전 재생이나, 재생 시간 증가에 의한 오일 증가 등의 문제가 발생할 수 있고, 제어온도가 너무 높은 경우에는 촉매 열화 손상에 의해 NOx, CO 등 다른 배기가스들의 정화율 저하 문제가 발생하거나 DPF 내부의 비정상 재생 등에 의한 하드웨어 손상문제를 야기할 수 있는 위험성을 가지고 있다.¹⁾ 최근 기술 트렌드를 보면 물리적인 모델을 제어 로직으로 구현하여 보다 정밀한 제어를 구현하는 사례들이 많아지고 있고,^2-5) 내연기관의 다양한 분야에서도 적극적으로 활용되고 있다.

본 논문에서는 열역학 법칙과 에너지 방정식을 활용한 모델 기반 재생온도 제어방법에 대하여 상세하게 기술하고자 한다.

2. 배기가스 온도 모델링

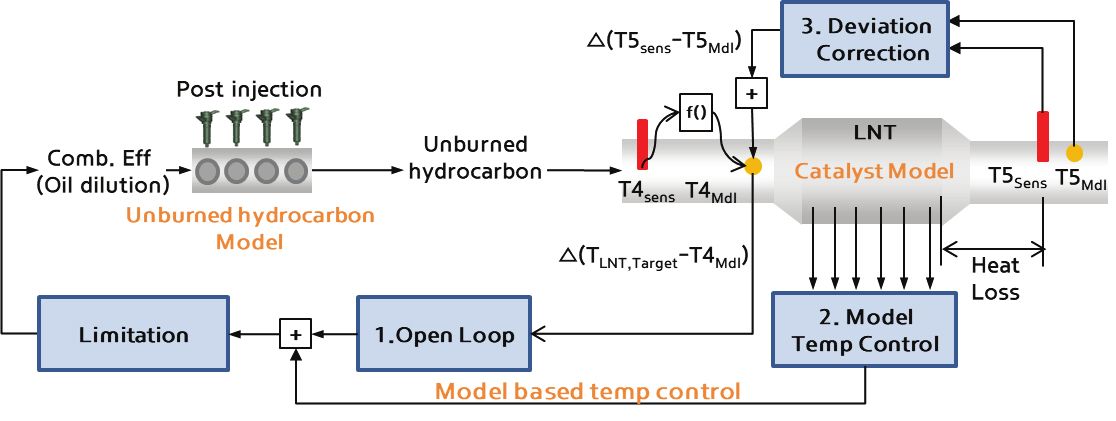
Fig. 1은 모델기반 재생온도 제어 흐름도를 나타낸다. 모델 기반 재생 온도 제어를 실행하기 위해서는 배기가스 온도의 예측 모델링이 선행되어야 한다. 산화 촉매 전단 온도(이하 T4온도)로부터 촉매 내부의 발열 및 열전달 과정을 거치고, 후단 배기파이프 내에서의 열손실을 고려하여 DPF 전단온도(이하 T5온도)를 예측하는 과정이다. 온도 제어는 온도 예측 모델을 역으로 활용하게 된다. 즉, 목표온도와 산화촉매 전단온도의 차이로부터 산화촉매 내의 발열 및 열전달에 필요한 목표 연료량을 계산하는 과정이다. 온도 예측 모델링은 크게 산화 촉매 내에서 환원제로 사용되는 미연탄화수소 예측단계, 산화 촉매 내 발열 및 열전달 모델, 산화촉매 후단 파이프 열손실 모델 등 세 단계로 나뉘어진다.

Fig. 1

Schematic of model-based DPF temperature control

2.1 엔진에서 배출되는 미연탄화 수소 예측

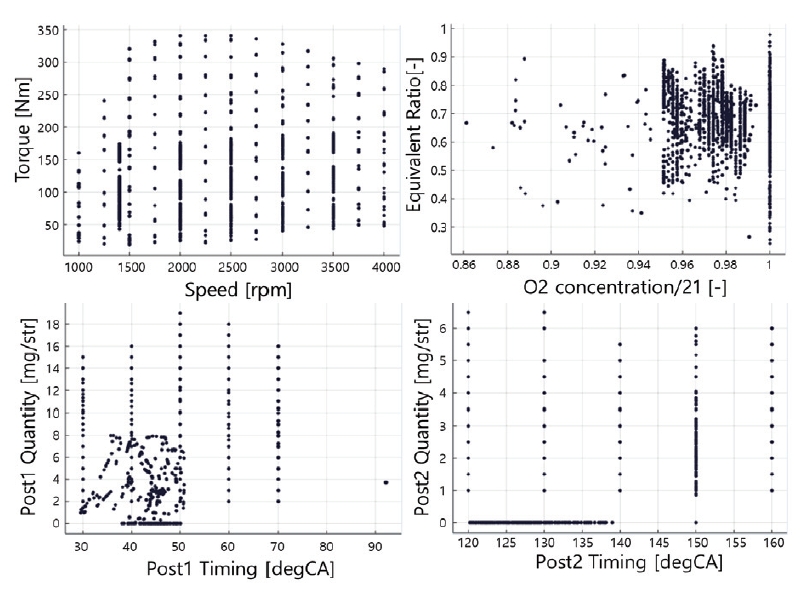
엔진으로부터 배출되는 미연 탄화수소 예측은 실린더 내 분사된 연료의 연소 효율 예측을 의미한다. 실린더 내에서 완전 연소되지 않은 연료는 미연탄화 수소 형태로 배기밸브를 통해 배출되게 된다. 미연탄화 수소 예측 모델 구성을 위해 연소 효율에 영향이 큰 변수들을 미리 선정한 후에 실험적인 방법을 통해 예측 모델을 구성하였다. 엔진 운전 조건 중 다양한 상황을 반영하기 위한 실험계획은 Table 1과 같이 설정하였고, 측정된 입력변수에 대한 결과는 Fig. 2에 나타내었다.

Table 1

Design of Experiment for modeling unburned HC

Fig. 2

Test results obtained for conducting unburned HC modeling

미연탄화수소와 연소효율을 예측하는 것은 궁극적으로 산화촉매 내 발열온도를 예측하기 위한 것이므로, 엔진에서 측정된 발열 온도로부터 열역학 법칙을 이용하여 미연탄화수소와 연소효율을 예측하고자 하였고 이는 에 식 (1)~(3)에 나타내었다. 이때 복사에 의하여 외부로의 열손실의 변화는 미세하다는 가정하에 무시하였다.

$\[ ∆{\mathit{Q}}_{\mathit{e}\mathit{x}\mathit{o}}-∆{\mathit{Q}}_{\mathit{r}\mathit{a}\mathit{d}}=\dot{\mathit{m}}\cdot \mathit{C}\cdot \left({\mathit{T}}_{\mathit{L}\mathit{N}\mathit{T}}-{\mathit{T}}_4\right)\cdot ∆\mathit{t} \]$

(1)

$\[ \dot{q_{rg}}\cdot H=\dot{m}\cdot C\cdot \left(T_{LNT}-T_4\right)\cdot ∆t+∆Q_{rad} \]$

(2)

$\[ {\eta }_{cmb}=\frac{\dot{q_{total}}-\dot{q_{rg}}}{\dot{q_{total}}} \]$

(3)

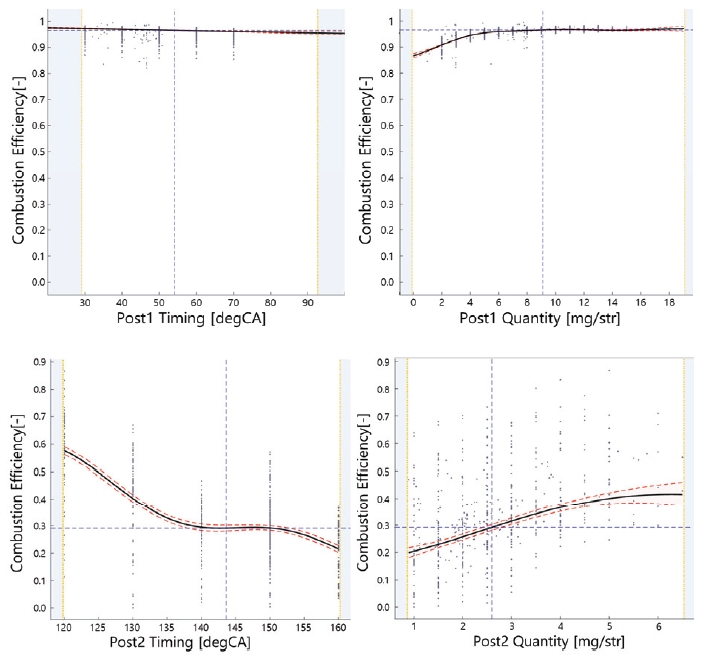
실험 결과는 단계적으로 ASC Gaussian Process Model을 활용하여 분석하였다.⁶⁾ 먼저 연소효율에 가장 민감하게 영향을 미치는 것으로 알려진 분사시기와 분사량에 대해 모델링을 진행하였다. 분사에 근접하게 분사하는 Post1의 분사시기 스윙을 통해 ATDC 30~70 °CA에서의 연소효율을 모델링하였고, 배기밸브가 열리는 시점인 ATDC 120~160 °CA에서는 Post2의 분사시기 스윙을 통해 모델을 구성하였다. 그리고 미세한 조정 작업을 거쳐 두 영역에서의 모델을 연결하여 전체 분사시기 및 연료량에 대한 연소효율을 모델링하였다. 이때 ATDC 20 °CA 이전에 분사되는 연료는 99%이상 연소가 된다고 가정하여 튜닝을 진행하였다. Post1/2 스윙에 의한 모델링 과정은 Fig. 3에 나타내었다.

Fig. 3

Combustion efficiency model according to inj. timing/quantity

이렇게 정의된 분사량과 분사시기에 의한 연소효율을 제외한 후, EGR율과 당량비 그리고 엔진회전수와 엔진 부하에 대한 연소효율은 각 변수들의 영향도를 고려하여 측정 오차를 최소화하는 방향으로 모델링하였다.

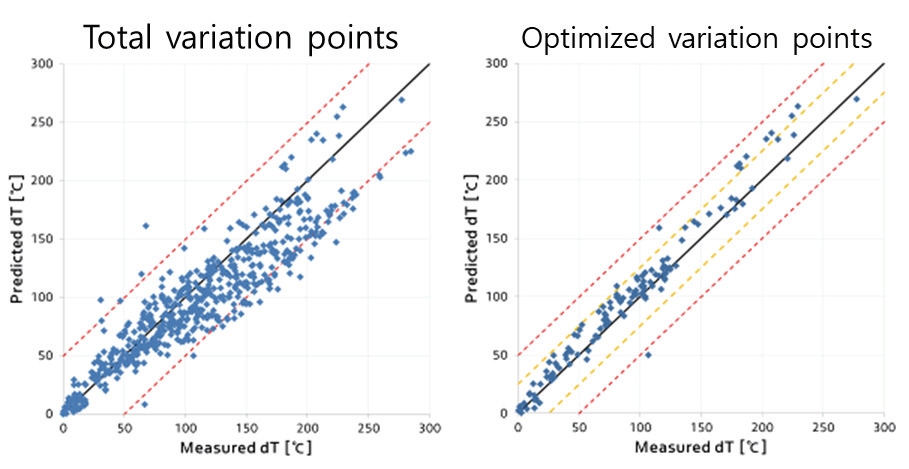
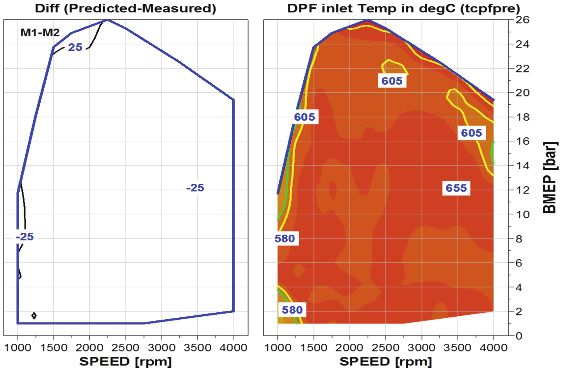
모델링을 완료한 결과는 Fig. 4와 Fig. 5에 나타내었다. Fig. 4의 좌측 그림은 각 입력변수들의 전체 스윙시험 결과에 대한 모델링 결과이고, 우측 그림은 입력변수들을 최적화한 후에 전 엔진 운전 영역에서의 모델링 결과를 보여준다. 각 입력변수들의 전체 스윙시험 결과들에 대해서는 약 ±50 ^oC 수준의 모델 편차를 보이고 있고, 입력변수들의 최적화 매핑 이후 전체 엔진 운전 영역에서의 모델 편차는 약 ±25 ^oC수준을 보이고 있다. 이때 T5온도 분포는 대부분의 엔진 운전 영역에서 605~655 ^oC 수준으로 상당히 정밀하게 조정된 결과를 확인할 수 있다.

Fig. 4

Accuracy of unburned HC(Combustion efficiency) model

Fig. 5

The regeneration temperature in the whole operating area

2.2 산화촉매 내부 열교환 과정

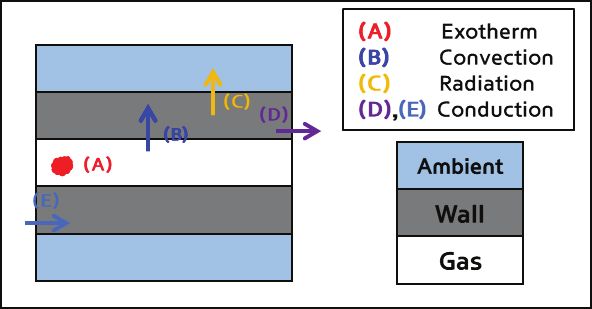
산화촉매 내부 열 교환 과정을 상세히 모델링하기 위해 길이 방향으로 가상의 몇 개의 슬라이스로 나누어 계산한다. 열 교환 과정은 Fig. 6에 나타난 것과 같이 촉매 벽면과 배기가스 사이의 대류과정, 앞 슬라이스와 뒷 슬라이스 사이의 전도과정, 촉매 벽면과 외부공기 사이의 복사과정으로 나눌 수 있다.

Fig. 6

Heat transfer inside oxidation catalyst

2.2.1 미연탄화수소에 의한 촉매 내부 발열

엔진으로부터 배출되는 미연탄화수소는 촉매 내부에서 발열반응을 일으키게 되는데, 촉매 전환 효율을 고려한 열역학 법칙을 수식으로 나타내면 식 (4)와 같다.

$\[ ∆T_{exo,k}=\frac{{\eta }_{cnv,k}\cdot \dot{q_{rg,k}}\cdot H}{C_{p,gas}\cdot \dot{m_{gas}}} \]$

(4)

2.2.2 배기가스와 촉매 벽면의 대류 열전달

산화촉매 내 진입한 배기가스와 촉매 표면의 온도는 과도 구간의 각각의 상태에서 실시간 차이가 발생하게 되기 때문에 대류 열전달이 일어나게 된다. 식 (5)는 단위 시간 당 각 슬라이스에서의 대류 열전달량을 나타내고, 이는 열전달 계수, 가스와 촉매 표면의 온도 차이, 그리고 촉매 내부 채널들의 총 표면적의 합으로 계산된다. 가스와 촉매 표면 사이의 온도차는 전단 가스 온도로부터 발열온도가 더해진 값과 촉매 표면의 온도 차이를 의미하며, 식 (6)과 같이 나타낼 수 있다.⁷⁾

보통 비열이 더 큰 촉매의 온도변화가 더 작기 때문에 과도 상태에서는 전단 슬라이스와 후단 슬라이스에서의 열전달 형태가 달라지게 된다. 즉, 촉매 온도가 높은 상태에서 배기가스 온도가 낮아지게 될 경우 대류 열전달에 의해 전단부 배기가스 온도는 승온될 것이며, 반대의 경우에는 전단부의 높은 가스온도에서 차가운 촉매 온도 쪽으로 대류열이 전달되어 촉매 표면의 온도가 승온될 것이다. 따라서 대류열전달을 적용하면 각 슬라이스 별로 시간에 따른 온도 추이를 일부 변화 시킬 수 있다.

$\[ ∆Q_{conv}={\alpha }_{EX,Wall,k}\cdot ∆T_{gas,Wall,k}\cdot \frac{A_{chn}}{n_{SI}}\cdot ∆t \]$

(5)

$\[ \begin{array}{c}\begin{array}{cc}{T}_{gas,k}=T_{gas,k-1}+∆T_{exo,old} ,& T_{gas,k}=T_{gas,DS,k-1}\end{array}\\ ∆{\mathit{T}}_{\mathit{g}\mathit{a}\mathit{s},\mathit{W}\mathit{a}\mathit{l}\mathit{l},\mathit{k}}={\mathit{T}}_{\mathit{g}\mathit{a}\mathit{s},\mathit{k}-1}+∆{\mathit{T}}_{\mathit{e}\mathit{x}\mathit{o},\mathit{o}\mathit{l}\mathit{d}}-{\mathit{T}}_{\mathit{W}\mathit{a}\mathit{l}\mathit{l},\mathit{k},\mathit{o}\mathit{l}\mathit{d}}\\ ={\mathit{T}}_{\mathit{g}\mathit{a}\mathit{s},\mathit{k}}-{\mathit{T}}_{\mathit{W}\mathit{a}\mathit{l}\mathit{l},\mathit{k},\mathit{o}\mathit{l}\mathit{d}}\end{array} \]$

(6)

2.2.3 전후단 슬라이스 사이의 열전도

전단 슬라이스와 후단 슬라이스 사이에서는 길이 방향으로 열전도가 일어나는데 이를 식 (7)과 같이 열전도율, 슬라이스 사이 온도차이, 단면적과 단위 슬라이스 당 길이의 식으로 나타낼 수 있다. 그리고 열전도에 의한 온도 변화는 열전달량과 촉매 비열을 통해 식 (8)과 같이 나타낼 수 있다. 열전도량은 전단 슬라이스 온도 변화와 후단 슬라이스 온도 변화의 위상 차이를 직접적으로 결정하는 인자이다. 촉매 내부에 길이 방향으로 여러 가지 온도센서를 장착한 후 촉매 전단온도가 Step으로 변화할 때 각 슬라이스에서의 모델온도를 실제온도와 비교하여 촉매 내부 모델 온도의 변화 속도를 결정하게 된다. 이는 최종적으로 촉매 후단 가스 온도의 변화 속도를 결정하게 되므로, 과도 상태에서의 온도 변화 정도를 모델링할 수 있다.

$\[ ∆Q_{cond}=C_5\cdot \left(T_{Wall,k,old}-T_{Wall,k+1}\right)÷\frac{l_{comp}}{n_{SI}}\cdot A_{face} \]$

(7)

$\[ ∆T_{cond,ax,k}=\frac{∆Q_{cond,ax,k}}{C_{p,SI,k}} \]$

(8)

2.2.4 촉매와 외기에 의한 복사열전달

촉매는 복사열전달에 의해 외기에 열을 빼앗기게 된다. 복사 열전달량과 복사에 의한 온도 손실량은 식 (9)~(10)에 나타내었다. 외기로의 단위 시간당 열손실은 배기가스 유량이 작을수록 그리고 외기온이 낮을수록 더 커지게 된다. 계산되는 열손실량에 따라서 촉매 내부에서 최대온도를 나타내는 슬라이스의 위치가 달라질 수 있다. 복사열전달을 고려하지 않는다면 촉매 내 발열에 의해 통상 맨 끝단 슬라이스에서 최대 온도가 나타나게 된다. 그런데 복사열전달에 의한 촉매 내부에서의 열손실이 고려된다면, 엔진 운전 조건에 따라 중간 슬라이스에서도 최대 온도를 나타낼 수 있게 되어 촉매 내부의 실제 온도 거동을 더 상세히 모사할 수 있게 된다. 이 후 온도 제어 측면에 있어서도 복사에 의한 열손실을 고려하여 각 슬라이스에 따른 촉매 내부 목표 온도 프로파일이 결정되게 된다.

$\[ ∆Q_{rad}=k_k\cdot \frac{\left(T_{wall,k,old}-T_{amb}\right)}{R_{insul}}\cdot \frac{A_{surf}}{n_{SI}}\cdot ∆t \]$

(9)

$\[ ∆T_{rad,k}=\frac{∆Q_{rad,k}}{C_{p,SI,k}} \]$

(10)

2.2.5 촉매 내 에너지 방정식

각 슬라이스에서의 촉매와 가스 온도는 각각의 에너지 방정식에 의해 계산될 수 있다. 먼저 촉매 내 채널 벽면을 검사체적으로 가정하여 에너지 방정식을 세울 수 있다. 촉매로 들어오는 열은 전단 슬라이스에서의 열전도와 가스로부터의 대류열전달이 있고, 촉매에서 나가는 열은 복사열전달에 의한 열손실과 후단 슬라이스로의 열전도가 있다. 이를 수식으로 나타내 보면 식 (11)과 같고, 맨 앞단 슬라이스로부터의 열전달과 맨 끝단에서의 열전달은 0으로 가정하여 계산한다.

마찬가지로 촉매 내 배기가스 온도를 계산하기 위해 촉매 내부 가스가 지나가는 채널공간을 하나의 검사체적으로 생각하여 에너지 방정식을 세울 수 있다. 이 때 배기가스의 온도는 촉매 벽면과의 대류열전달과 발열온도만 고려하면 된다. 따라서 각 슬라이스 끝단부 배기가스 온도는 식 (12)와 같이 슬라이스 시작부 온도로부터 대류 열전달에 의해 빼앗기는 온도를 고려하여 계산한다. 식 (4), (8), (10)의 온도 변화량을 식 (11)~(12)의 촉매와 가스온도 계산식에 대입하여 촉매 전단 가스온도로부터 순차적으로 계산하면 각 슬라이스에서의 촉매 및 가스 온도는 시간에 따라 차례대로 결정된다.

$\[ \begin{array}{c}{T}_{SI,k}=T_{SI,k,old}+\left(∆T_{cond,ax,k-1}+∆T_{conv,ax,k}-∆T_{rad,k}\right.\\ \left.-∆T_{cond,ax,k}\right)\end{array} \]$

(11)

$\[ \begin{array}{c}{T}_{gas,DS,k}=T_{gas,k-1}+∆T_{exo,old}-∆T_{conv,k}\\ =T_{gas,k-1}+∆T_{exo,old}-\frac{∆Q_{conv}}{C_{p,gas}\cdot \dot{m_{gas}}\cdot ∆t}\\ T_{gas,DS,0}=T_4\end{array} \]$

(12)

2.3 산화촉매 후단 파이프 열손실 과정

당사에서 신규 개발한 3세대 1.6리터 급 엔진에서는 최신 트렌드의 후처리 장치 레이아웃을 활용하여 촉매의 크기는 최대화였으나, 산화촉매와 DPF 사이의 U자 형상의 챔버형 파이프로 인해, 온도 손실을 수반하게 되었다. 보다 정확한 DPF 온도 제어를 위해서 파이프에서 발생하는 온도 손실을 예측하는 모델링이 필요하였으며, 파이프 온도 손실 모델값은 산화촉매에 필요한 미연 탄화수소를 계산하는 모델 기반 제어 로직에도 동시에 반영된다. 엔진 및 차량 조건에서 발생하는 온도 손실은 엔진 회전수, 배기유량, 차량 속도에 따라 다르며, 파이프에 전달된 에너지와 외기로의 열손실을 파이프 벽면 온도를 중심으로 하는 에너지 방정식으로부터 손실 온도를 계산할 수 있다. 엔진에서는 이를 수식으로 정리하면 식 (13)~(16)과 같다.

$\[ Q_{\to tube}=C_{p,gas}\cdot \dot{m_{exh}}\cdot \left(T_{in}-T_{out}\right)\cdot ∆t \]$

(13)

$\[ \begin{array}{c}\begin{array}{cc}{Q}_{tube\to }=\alpha \cdot A\cdot \left(T_{Wall}-T_{amb}\right)\cdot ∆t,& \alpha \cdot A={\beta }_{loss}\end{array}\\ \frac{T_{in}-T_{out}}{T_{in}-T_{Wall}}={\beta }_{add}\end{array} \]$

(14)

$\[ T_{Wall}=\frac{C_{p,gas}\cdot \dot{m_{exh}}\cdot {\beta }_{add}\cdot T_{in}+{\beta }_{loss}\cdot T_{amb}}{C_{p,gas}\cdot \dot{m_{exh}}\cdot {\beta }_{add}+{\beta }_{loss}} \]$

(15)

$\[ T_{out}=T_{in}-{\beta }_{add}\cdot \left(T_{in}-T_{wall}\right) \]$

(16)

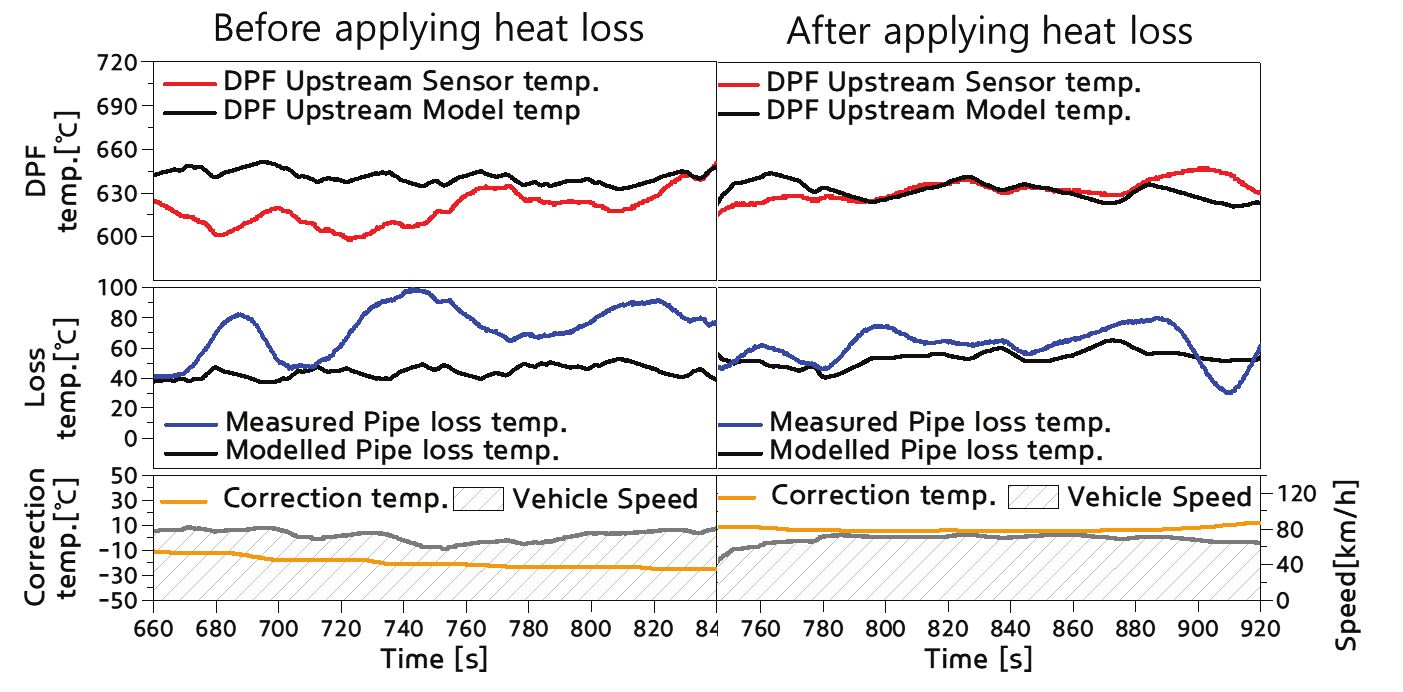
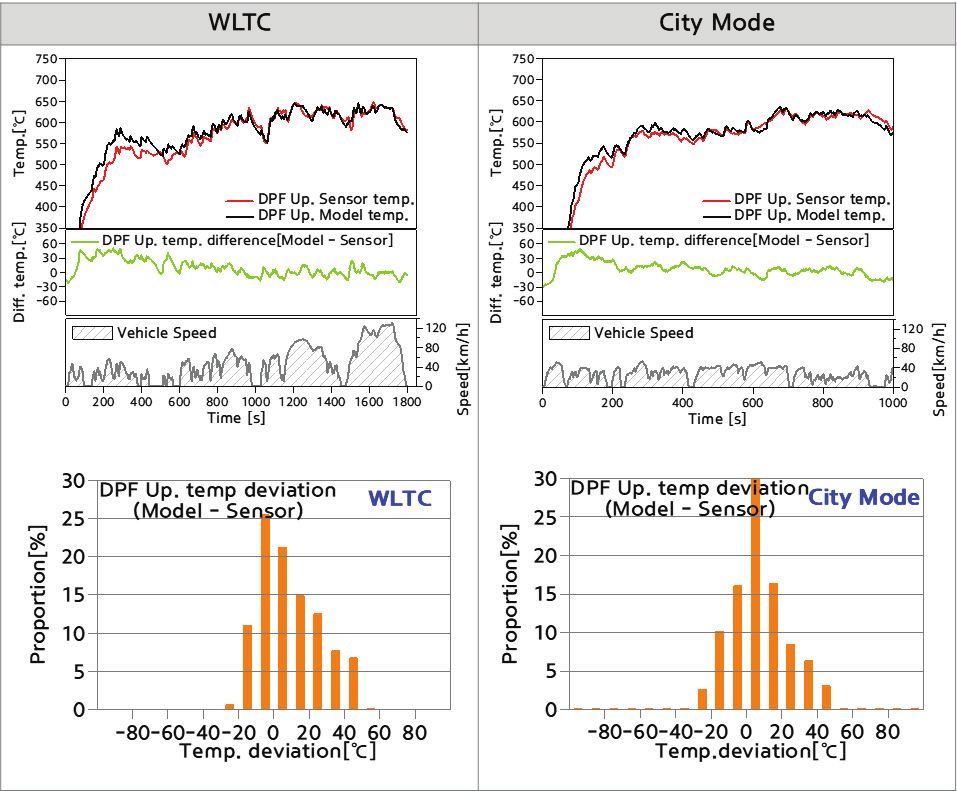
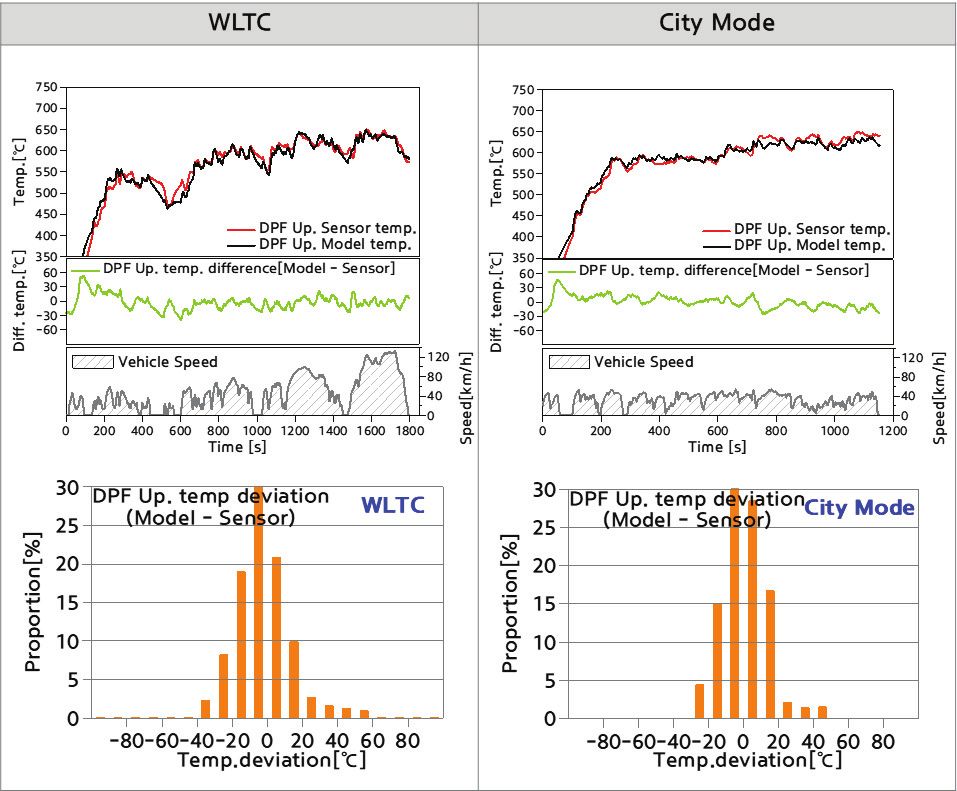
차량속도에 따른 열손실 적용 유무에 따른 측정 결과를 Fig. 7에 나타내었다. 좌측 그림을 보면 차속 조건 미적용으로 인해 파이프 손실 온도 모델값이 실제대비 부족하고 DPF 전단 온도는 모델 온도 대비 낮게 제어되지만, 차량속도에 따른 열손실을 추가 적용 시에는 우측 그림과 같이 DPF 온도 제어가 보다 정확히 되고 있음을 확인할 수 있었다.

Fig. 7

Comparison results before and after applying heat loss in pipe

3. 모델 기반 재생 온도 제어 방법

모델 기반 재생 온도 제어는 앞에서 구성한 촉매 모델링을 역으로 활용하여 재생목표온도와 전단온도의 차이를 통해 목표 연료량을 Open loop으로 계산하고, 실제 T5 온도를 목표 재생온도에 맞추기 위한 피드백 제어까지의 과정을 의미한다. 이는 크게 촉매 내부 목표 온도 프로파일 결정 및 목표 연료량 계산과 정밀한 제어를 위한 T4 다이나믹 모델 및 제어 오차 피드백 보상으로 나눌 수 있다.

3.1 촉매 내부 목표 온도 프로파일 결정

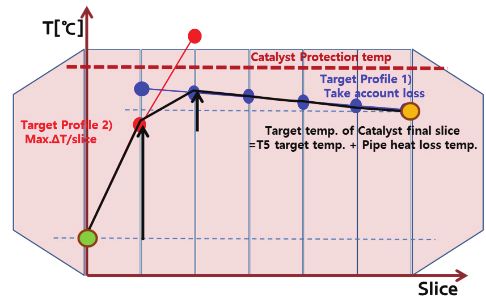
촉매 내부 각 슬라이스들의 목표 온도를 결정할 때는 세 가지를 고려해야 한다. 우선 앞쪽 슬라이스에서의 각 목표 온도는 전환 가능한 최대 미연 탄화수소량에 의한 발열온도를 넘어설 수는 없다. 최종단 슬라이스의 목표온도는 DPF 입구온도로부터 파이프 열손실 온도를 더한 값으로 계산된다. 최종단으로부터 앞쪽으로 이동할수록복사열전달에 의한 손실온도가 목표 온도에 더해질 수 있다. 중간 슬라이스에서는 앞 단에서부터의 목표온도와 끝단으로부터의 목표온도에 촉매 내부 H/W 한계온도가 추가로 고려되어 세가지 목표온도 중 가장 작은 값으로 선택되게 된다. 이는 Fig. 8에 그림으로 나타내었다.

Fig. 8

Profile of target temperature

3.3 T4 다이나믹 모델

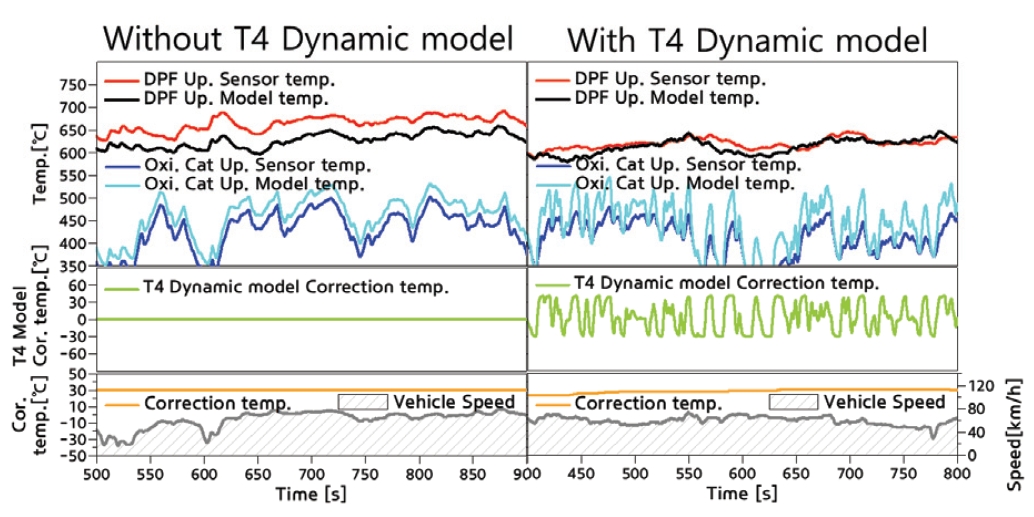
모델기반 재생온도 제어의 가장 중요한 입력인자인 촉매 전단 T4 온도는 차량에 장착된 센서가 가지는 열관성(Thermal inertia)때문에 반응성이 실제보다 느린 것이 일반적이다. 상대적으로 느린 센서값을 기준으로 목표 연료량을 계산하게 되면 과도 구간에서 제어 오차를 야기할 수 있다. 따라서 T4 온도 센서의 거동을 보다 빠르게 예측하도록 Dynamic 모델링을 실시함으로 인해 과도 구간에서 발생하는 연료량 계산 오차를 개선할 수 있고, 보다 정밀한 제어를 실현할 수 있다. Fig. 9와 같이 T4 Dynamic 모델을 적용하여 T4 온도 변화가 빈번한 모드에서도 DPF전단 온도 제어가 안정적으로 되는 것을 확인할 수 있다.

Fig. 9

Regeneration temperature with and without T4 Dynamic model

3.4 모델 제어 오차 피드백 보상 방법

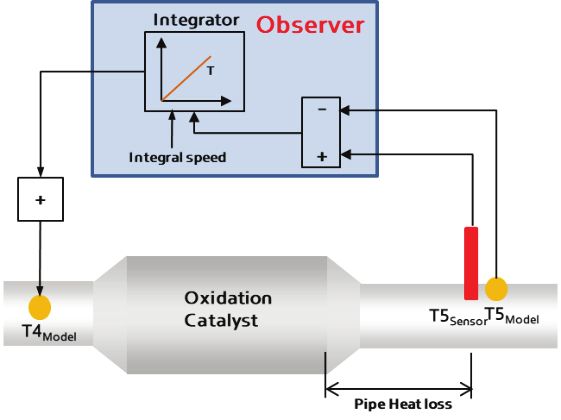
모델에 의해 Open loop으로 계산된 연료량에 의한 재생온도는 필연적으로 모델 오차를 가지게 된다. 모델 오차는 엔진 각 영역에서의 모델링 편차 뿐 아니라 촉매의 귀금속량과 열화정도, 엔진에서 분사되는 연료량 오차 등에 의해 발생할 수 있다. 따라서 모델 오차는 엔진에 장착된 T5 센서를 통해 피드백 보상을 해야한다. T5 피드백 보상 개략도를 Fig. 10에 나타내었다. 파이프 열손실을 고려한 DPF 전단 모델을 기준으로 하여 센서에서 측정된 온도값과의 차이를 촉매 전단 온도 보정한다. 보정된 촉매 전단 모델 온도는 목표 연료량 계산에 이용된다. T5 피드백 보상은 실시간 운전영역에서 발생하는 재생 온도의 누적 편차를 천천히 보정하며, 최종 보정값은 학습값으로 영구 저장되어 엔진 단품 별 시스템의 편차를 보상할 수 있다.

Fig. 10

Schematic of regeneration temperature observer

4. 차량 검증 결과

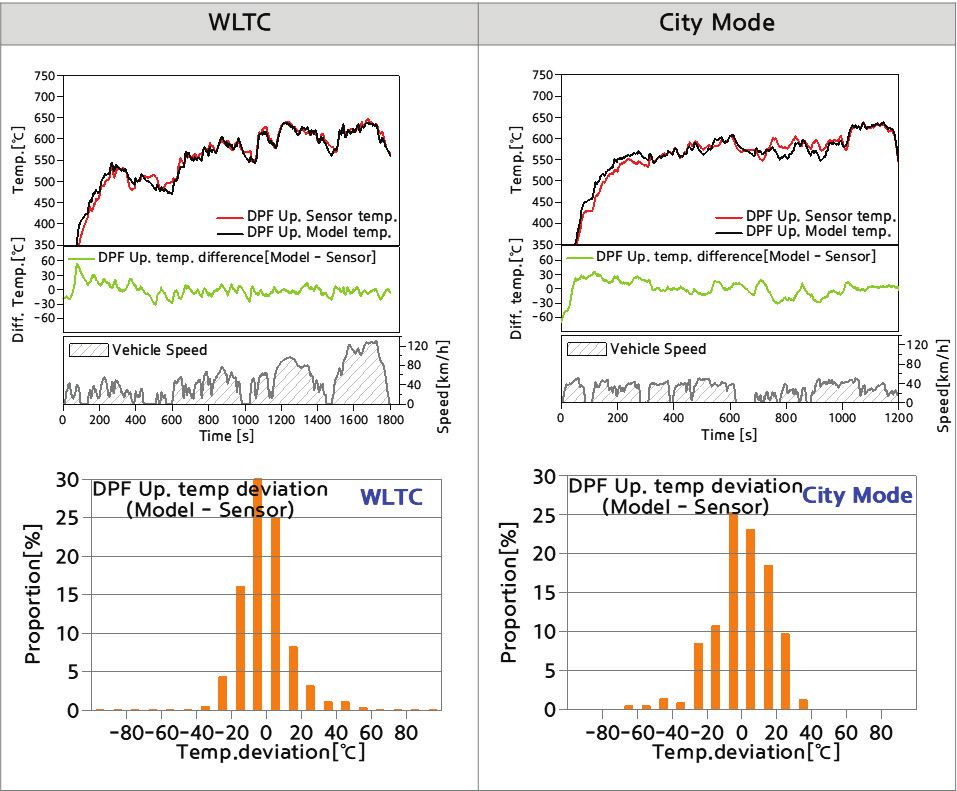
최종 튜닝된 모델 기반 제어 방법을 적용하여 실차에서 WLTC(Worldwide harmonized Light duty driving Test Cycle) 모드를 비롯한 극도심 모드 등 다양한 환경과 주행조건에서 검증 평가를 실시하였다. 아이들이나 타행 주행 조건 등 엔진 부하가 낮은 조건에서는 오일희석이나 산화촉매 내부온도 한계로 인한 분사 연료량 제한이 적용되어 목표 재생온도에 미치지 못하는 구간이 다소 존재하지만, 이런 경우에서 조차 모델은 정상적으로 동작하면서 전체적으로 T5 측정값과 모델값과의 편차는 대부분 영역에서 약 ±25 ^oC 수준의 정밀하게 제어가 되고 있음을 확인할 수 있었다.

Fig. 11

Validation results in B-seg. vehicle

Fig. 12

Validation result in C-seg. vehicle

Fig. 13

Validation results in D-seg. vehicle

또한 동일한 엔진과 후처리 장치가 탑재된 다양한 종류의 차량에서도 검증이 진행되었다. B-seg 부터 D-seg까지 동일한 하드웨어를 장착한 차량에는 모두 동일한 재생온도 모델을 적용하여 평가가 진행되었는데, 차종과 관계없이 모두 유사한 수준의 제어 정밀도를 확인할 수 있었다. 따라서 강건한 모델이 구축되면 차량 종류, 주행 모드 등 외부 조건이 변화하더라도 모델에 기반하여 목표 온도를 추종하기 위한 목표 연료량 값이 자동으로 변경되어 계산되므로, 최종적으로 일정한 제어 정밀도 결과를 얻을 수 있다는 장점을 확인할 수 있었다.

5. 결 론

전단 온도로부터 후단 온도를 예측하는 온도 모델링과 이를 역으로 활용하는 제어 모델을 구성하였고, 이를 바탕으로 하는 모델 기반 재생온도 제어 방식을 양산차 개발에 적용하였다. 다양한 실험을 통해 재생온도 제어 정밀도를 검증하였고, 다음과 같은 결론을 얻을 수 있었다.⁸⁾

• 1) 실험적인 방법을 통해 다양한 입력변수의 변화에 따른 연소효율 모델을 구성하였다.
• 2) 열역학 법칙을 활용한 촉매 발열 모델과 전도, 대류, 복사열전달의 에너지 방정식을 적용하여 촉매 내부 모델을 구성하였다.
• 3) 모델 기반 제어를 위해 촉매 내부 목표온도 프로파일을 설정하였고, 목표 연료량을 실시간 도출하도록 제어 모델을 구성하였다.
• 4) 센서 반응성을 고려한 T4 다이나믹 모델을 적용하여 제어 모델의 정밀도를 향상시켰고, T5 피드백 제어를 통해 제어 오차 및 차종간 편차를 줄일 수 있었다.
• 5) 실차에서 다양한 환경 및 주행 조건에서 검증한 결과 재생 온도는 모델과 편차 약 ±25 ^oC 수준에서 정밀한 제어가 가능하였다.
• 6) 본 모델 기반 재생 제어 방식을 통해 B seg.부터 D seg.까지 다양한 차급에 동일한 모델링으로 양산 개발 완료하였다.

References

• J. H. Lee, C. I. Kwon, S. J. Kim and G. K. Yeo, “Control of Diesel Catalyzed Particulate Filter System I (The CPF System Influence Assessment According to a Regeneration Condition),” SAE 2005-01-0661, 2005.
• K. Bencherif, F. Benaicha, S. Sadaï and M. Sorine, “Diesel Particulate Filter Thermal Management Using Model-Based Design,” SAE 2009-01-1082, 2009. [https://doi.org/10.4271/2009-01-1082]
• J. Castellano, A. Chaudhari and J. Bromham, “Adaptive Temperature Control for Diesel Particulate Filter Regeneration,” SAE 2013-01-0517, 2013. [https://doi.org/10.4271/2013-01-0517]
• C. Depcik, C. Langness and J. Mattson, “Development of a Simplified Diesel Particulate Filter Model Intended for an Engine Control Unit,” SAE 2014-01-1559, 2014. [https://doi.org/10.4271/2014-01-1559]
• H. W. Noh, M. K. Park, J. H. Kim, S. W. Ju, K. S. Choi and W. K. Moon, “A Study of DPF Regeneration Temperature Control Technology Based on Exhaust Gas Temperature Model for Catalyst for Passenger Diesel Engine,” KSAE Fall Conference Proceedings, pp.13-14, 2016.
• S. L. Wang, Predicting the Performance of Automatically Scalable Computation (ASC), The Degree of Bachelor of Arts, Harvard College, Massachusetts, 2016.
• F. P. Incropera and D. P. Dwitt, Fundamentals of Heat and Mass Transfer, 5th Edn., John’s Wiley & Sons, New York, 2001.
• D. H. Hur, J. H. Jung, J. J. Lee, S. Kim, J. K. Lee and J. H. Lee, “A Study of Model-Based DPF Temperature Control Method,” KSAE Fall Conference Proceeding, pp.63-70, 2020.