CFD를 활용한 동력분산식 고속전철용 감속기의 오일 처닝 해석
Copyright Ⓒ 2021 KSAE / 189-07
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
For the purpose of sufficient lubrication and cooling of the gear unit when it comes to temperature increase due to frequent acceleration/deceleration, it is important to establish an optimum gear box design, such as oil path holes and baffles. In order to predict them and pursue design improvement, CFD simulation was carried out by using the Moving/Deforming Mesh(MDM) technique employed in Ansys Fluent for rotating geometries and Volume of Fluid(VOF) for the modeling of the multiphase flow regime. In the present study, the power distribution type reduction gear unit, which is being manufactured currently for installation in EMU-250 and EMU-300 high-speed trains(260~320 km/h grades) was employed. As a result, the transient nature of highly violent multiphase flow by gear churning was simulated successfully with the suggested numerical schemes. Additionally, the temperature prediction of each part according to convective heat transfer induced by oiling flow and surface heat flux by gear loss assumption is described.
Keywords:
Reduction gear unit, CFD, MDM(Moving Deforming Mesh), VOF, Convective heat transfer coefficient, EMU키워드:
감속기, 전산유체역학, 동적변형격자, Volume of Fluid, 대류열전달계수, KTX-이음1. 서 론
동력분산형 고속전철에 적용되는 주요장치는 부품 표준화 요구사항에 따라 감속기의 경우 EMU250과 EMU300에 동일한 모델이 적용된다. EMU250의 경우 운행속도가 260 km/h, EMU300의 경우 운행속도가 320 km/h로 결정되면서 동일한 모델을 적용하기 위한 설계검토가 진행되었다. 차량의 운행 요구조건에 따라 적합한 시스템 설계를 위해서는 추진시스템과 대차 및 감속기 등의 주요 장치는 상호 연관성과 인터페이스를 고려해서 설계되어야 한다. 특히, 오일 순환에 의한 기어 및 베어링 부의 윤활이나 냉각 성능의 확보는 감속기의 성능과 내구성에 직접적인 영향을 주는 요소이므로, 오일 경로 및 내부 격벽 등의 설계 변경 인자를 고려하여 설계 초기 단계에 다양한 검토가 이루어질 수 있어야 한다. 하지만, 모형이나 시작품 등의 제작을 통한 설계 검증은 시간과 비용 측면에 있어서 여러 설계 변수를 고려하기에는 무리가 있다. 따라서, 전산 모사를 통해 이러한 기존 검증 방법의 단점을 극복하고 다양한 설계 및 작동 조건에 따른 결과를 예측할 수 있다. 철도차량용 감속기와 같은 동력전달장치, 기어 박스류 등에 대한 이전 연구 사례는 효율, 손실, 윤활 및 냉각 등 목적에 따라 이론적, 실험적 방법뿐만 아니라 수치 기법의 신뢰성 및 전산 리소스의 확장성에 대한 뒷받침으로 인해 해석적 접근도 비교적 최근에 들어서 다양하게 이루어지고 있다. Liu 등1) 및 Imtiaz2)는 대표적인 FZG 기어를 이용하여 오일의 점도 및 회전수 변화에 따른 처닝 손실 해석을 통해 모델링 기법 및 해석 기법의 타당성을 입증하는 연구를 수행하였다. 최종락 등3)은 비교적 복잡한 스파이럴 베벨 기어가 장착된 동력전달장치에 대해 다양한 설계 변수에 따른 다상유동의 유체역학적 특성 분석과 설계 검증을 시도하였고, Patel과 Anto4)는 해석 기법과 작동 조건에 따른 처닝 손실 예측에 대한 연구를 수행하였다. Liu 등5)은 비교적 단순한 형상의 1단 평기어 이긴 하나 회전수에 따른 고체 영역 온도의 시간 변화율을 예측하는 복합열전달 해석까지 고려한 연구를 수행하였으며, Cho 등6)은 다수의 중첩 영역을 포함하는 유성기어에 대해 오일 수위 별 대류열전달계수 결과를 고려한 시간에 따른 유동장의 온도 변화 예측 연구를 수행하였다. 하지만, 다상유동과 함께 기어 형상의 동적변형과 중첩을 동시에 고려해야 하므로 모사 기법이 복잡하고, 전산 리소스 및 계산 소요 시간 또한 방대하므로 실물에 대한 해석 연구, 특히, 열전달까지 동시에 고려하는 연구는 아직까지도 드문 실정이다. 따라서 본 연구에서는, 동력분산형 고속전철 감속기에 대해 고충실도(High-fidelity) 수치 모델 구성과 실제 운행조건의 모사를 통해 내부 오일 순환 구조의 설계 평가 및 오일의 거동에 따른 대류열전달계수의 변화가 최종적으로 온도 분포에 미치는 영향 또한 예측하고자 시도하였다.
2. 본 론
2.1 설계 조건
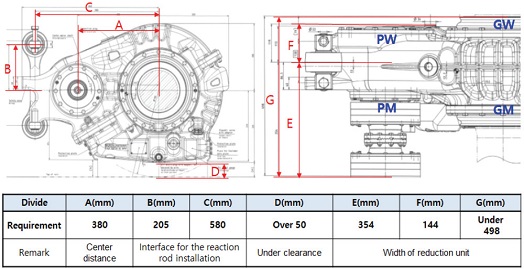
감속기는 동력 대차에 설치되며, Fig. 1에서와 같이 설치 요구 조건이 주어지며, 주어진 공간에 간섭없이 설치되어야 한다. 감속기 설치와 관련하여 중심거리(A)는 피니언과 휠 기어의 설계를 제한하게 되며, Under clearance(D)는 휠 기어의 크기와 기어 케이스의 설계를 제한하게 된다. B, C는 리액션 로드의 설계와 관련이 있고, 폭(E, F, G)은 기어의 치폭과 감속기 케이스의 폭 방향 설계를 제한하는 요소로 작용하게 된다.
Dimension requirement for reduction gear unit
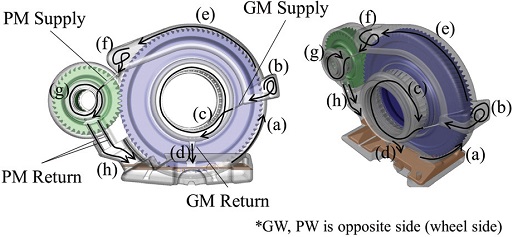
Fig. 1에 표현된 GW, GM, PW, PM 등은 감속기의 조립 방향과 위치를 구분하는 것으로, GW는 휠 기어에서 휠이 조립되는 방향을, GM은 휠 기어에서 모터가 조립되는 방향을, PW는 피니언 기어에서 휠이 조립되는 방향을, PM은 피니언 기어에서 모터가 조립되는 방향을 의미한다.
2.2 해석 방법
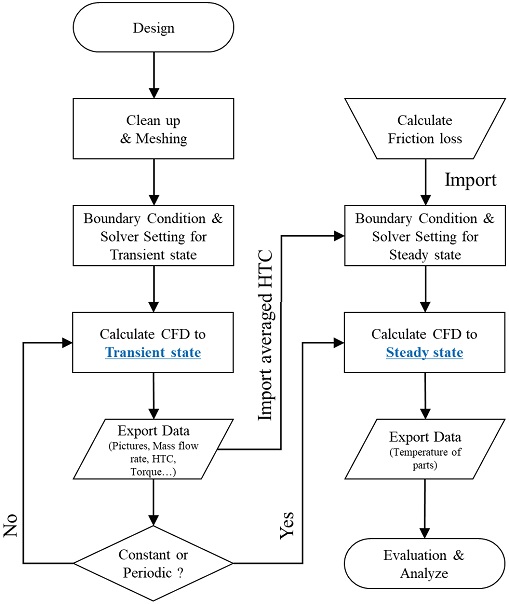
기어의 회전에 의한 오일의 거동과 그에 따른 온도 분포를 예측하기 위해 Fig. 2와 같은 프로세스에 따라 해석을 수행하였다. 오일의 거동을 모사하기 위한 비정상 유동해석을 통해 기어에 작용되는 토크나 오일 순환을 위한 관로 내에서의 유량, 외부로의 누유량, 각 부품들의 대류열전달계수를 산출하게 되며, 이 데이터들의 일정함 혹은 주기적인 경향을 통해 수렴 여부를 판단하였다. 그 다음, 산출된 대류열전달계수와 기어의 예측 동력 손실이 전부 열로 변환된다고 가정하여, 각 부품의 열 경계조건으로 입력한 뒤 정상상태 에너지 방정식 계산을 수행하였으며, 최종적으로 감속기의 온도 분포를 확인할 수 있게 된다. 자세한 해석 방법은 뒷장에서 각각 기술한다.
Analysis flow chart
2.2.2.1 다상유동 해석
오일의 거동, 즉 다상유동을 모사하기 위해, Ansys Fluent에서 제공하는 해석 기법 중, 공기-물과 같이 두 개 이상의 상에 대해 0과 1 사이의 체적 분율 계산을 통해 계면을 추적하여 유체의 거동을 모사하는 Volume of Fluid(VOF) 기법을 활용하였다.
VOF 기법은 각 격자의 경계에 걸쳐 있는 계면을 추적 또는 포착하기 때문에 계면이 격자의 경계에 걸쳐 있지 않고 물방울과 같은 형태로 완전히 격자 안에 들어오게 되면 해석의 정확성과 수렴성이 떨어지게 된다. 따라서, VOF 해석을 위해서는 조밀한 격자 생성이 필요하게 된다.
감속기의 오일은 앞서 Table 1에 기재된 바와 같이 물에 비해 약 170배의 높은 점성을 가지고 있긴 하지만 기어 처닝에 의한 오일 및 공기의 거동은 회전 관성이 지배적인 매우 불규칙적이고 복잡한 유동장을 형성하게 된다. 즉, 회전체 접선 방향 속도를 대표 속도로 봤을 때, 유동이 회전체 r-방향으로 발달할 수 있는 거리는 하우징 벽면까지이다. 이 대표 속도와 특성 길이를 기준으로 하는 레이놀즈 수는 약 49,000에 해당하며, 따라서 본 해석에서는 URANS Realizable k-epsilon 난류 모델 및 표준 벽함수를 적용하여 난류 유동 모사 및 첫 번째 격자점의 위치가 벽 근처 경계층 내부의 로그(Log-law) 영역에 해당하는 y+ <200에 포함되도록 모델링을 수행하였다. 압력-속도 연계는 ANSYS Fluent에서 제공하는 Coupled 알고리즘을 적용하였으며, 압력항 보간은 PRESTO!, 운동량 및 난류 운동-소산항 전달방정식의 이산화는 2차 상류 도식을 적용하였다.
2.2.2.2 동적변형격자
기어의 회전과 같이 회전 운동을 모사하기 위한 대표적인 해석 기법은 MRF(Moving Reference Frame), 슬라이딩 격자(Sliding mesh) 기법이 있으며, 강체의 6-자유도(6-DOF) 운동 혹은 기어와 같이 중첩되는 물체의 운동을 모사하기 위한 방법으로는 대표적으로 중첩격자 기법(Overset mesh)2-4,6)과 동적변형격자 기법(Moving deforming mesh, MDM)1,5)이 있다. 중첩격자 기법의 경우, VOF와 함께 적용할 시 배경 격자(Background mesh)와 해석 대상 격자(Component mesh) 사이 인터페이스에서 정보전달 오차가 발생하는 단점7)으로 인해 본 연구에서는 동적변형격자 기법(MDM)을 적용하였다. 베어링의 회전 영역에 대해서는 슬라이딩 격자 기법을 적용하였다.
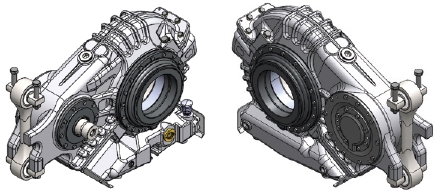
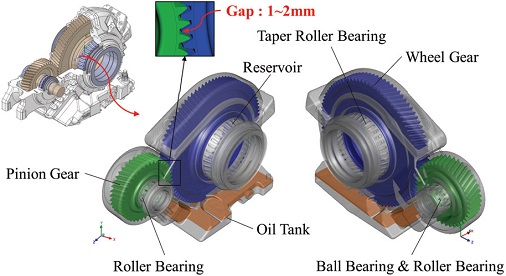
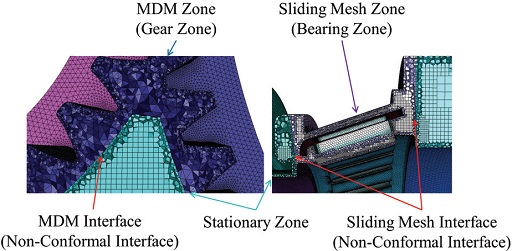
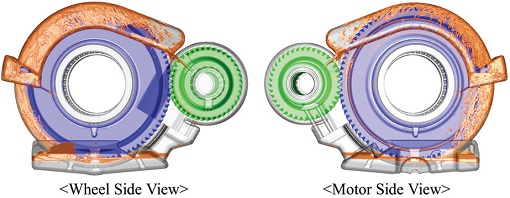
해석에 사용된 모델은 고속철도용 부품 장치 국산화의 일환으로 개발하고 있는 감속기로 Fig. 3과 같으며, 감속기 내부의 오일 순환 구조 및 해석을 위한 내부(유동)영역은 Fig. 4와 같다. 유한체적법(FVM) 기반 해석에 있어서는 기어 간 접촉 및 간섭하게 될 경우 해석이 불가능하며, 혹은 백래쉬(Backlash) 간격이 매우 작을 경우 공간 격자의 품질 문제 및 해의 특이점 발생 등을 유발할 수 있게 된다. 따라서 휠 기어와 피니언 기어 사이에 발생하는 공간 격자의 동적변형이 발생할 때, 격자 품질을 유지함과 동시에 공간 분해능을 확보해야 할 필요가 있다. 하지만, 격자의 크기와 수는 많은 전산 리소스의 소모를 필요로 하기 때문에 목적에 맞게 여러 격자 생성 기법을 활용하여 효율적으로 격자를 생성할 필요가 있다고 판단하였다. Liu 등1)에 따르면 2 % 이내의 기어 치형의 스케일 축소는 오일의 비산 및 처닝 손실에 영향을 끼치지 않는다. Imtiaz2)의 경우, 9~20 % 스케일 축소와 그에 따른 공간 크기에 대한 민감도 해석을 수행하였다. 또한 Mettichi 등8)에 따르면 유동저항에 의한 기어의 동력손실 중에서 휠 기어와 피니언 기어의 압착(Squeezing) 현상은 무시해도 될 만큼 적다는 결과를 보였다. 이러한 선행연구들을 참조하여 치형에 대한 스케일 축소를 통해 휠 기어와 피니언 기어 사이의 간격을 1~2 mm 정도 확보하였다. Fig. 5는 감속기 내부에 격자를 생성한 모습이다. 유동영역은 기어를 포함하고 있는 MDM 영역과 베어링을 포함하고 있는 슬라이딩 격자 영역, 그 외 정지(Stationary) 영역으로 크게 세 가지로 분리하여 격자를 생성하였다. MDM 영역은 과도 해석 매시간 단위마다 격자의 재생성이 이루어져야 하기 때문에 사면체 격자로 구성하였다. 그 외 영역은 다면체, 하우징 내부 공간은 육면체 격자로 구성함으로써, 형상을 최대한 왜곡하지 않는 범위 내에서 격자의 수를 효율적으로 구성하였다. 각 격자 영역은 비공형(Non-Conformal) 인터페이스를 통해 유동정보를 주고받게 된다. 표면 격자의 경우 BETA CAE사의 ANSA, 체적 격자의 경우 Ansys fluent meshing을 사용하여 생성하였으며, 최종적으로 해석에 적용된 격자수는 총 36,800,000개이다.
CAD model of reduction gear unit
Computational domain of reduction gear unit
Volume mesh generation w.r.t MDM & sliding zones
2.2.4.1 감속기 작동 조건
피니언 기어를 축 중심으로 감속기의 최대 견인 토크가 발생하는 입력 속도인 1,325 rpm으로 회전하도록 하였으며, 휠 기어와 각종 베어링들은 그에 상응하는 회전방향과 회전수를 적용하였다. 감속기에서 외부와 통하는 각종 틈새에는 외기가 유입되거나 오일이 누유될 수 있도록 역류를 허용하는 압력 출구 조건(∆P=0)을 적용하였다.
과도 해석에서 수렴성이나 정확성에 영향을 미치는 요인 중 하나는 과도 시간간격(∆t) 크기로서, 물리적 시간의 분해능이라고 할 수 있다. 본 해석에서는 식 (1)의 CFL수를 기준 조건으로 식 (2)와 같이 시간간격 크기를 산출하였는데, 여기서, ω는 회전 각속도로서 특성 속도를, N은 기어의 전체 잇수, n은 단위 시간 간격 동안 임의로 회전시킬 기어 잇수를 나타내다. 본 해석에서는 매시간 간격마다 회전 각속도가 기어 1칸(n=1)에 해당하는 회전 거리(특성 길이)를 넘지 못하도록 시간 간격을 설정하였다.
| (1) |
| (2) |
- CFL : courant-friedrichs-lewy condition
- u : characteristic velocity, m/s
- t : time step size, sec
- x : spatially discretized length, m
- ω : angular velocity, rad/s
- n : predetermined quantity of rotated tooth
- N : total number of teeth of gears
또한 앞 장에서 언급한 동적변형격자 기법의 특성에 맞게 매 과도 시간간격 마다 회전하는 기어 표면을 따라서 발생되는 격자 변형에 대해, 비대칭도(Skewness)가 0.95보다 높아지면 격자를 재생성(Remeshing)을 하여 격자의 품질이 유지되도록 설정하였다.
2.2.4.2 발열량 산출
열전달 해석을 통한 온도 결과값을 계산하기 위해서 감속기 각 부분에서 발생하는 발열량을 먼저 산출하여야 한다. 본 연구에서는 우선 감속기의 최대 견인 토크 사양에 해당하는 입력 속도(rpm)와 입력 토크(N-m)에 따른 이론적 출력에 대해, 기계적 마찰에 의한 손실은 전부 열에너지로 소산되는 것으로, 즉 발열량으로 가정하였다.
기어의 동력 손실에 대한 연구는 이론적, 실험적 검증을 통해 많은 연구가 진행되어 왔으며,9-11) 헬리컬 기어의 경우 기어비의 범위에 따른 효율을 고려하여 역산하면 약 2~6 %9)에 해당된다. 여기서, 전체 손실은 기어 간 마찰에 의한 기계적 손실과 풍손/처닝 손실 및 씰링부 손실과 같은 회전 관성에 의한 손실로 크게 나뉘어지며, 이는 각 부품 별 손실의 비율로 구분될 수 있다. 본 연구에서는 손실을 구하는 과정을 생략하기로 하고, 위 손실 범위의 중간값인 4 %로 가정하였다. 그리고 나서, 헬리컬 기어 각 부분에서의 손실을 이론적 계산과 함께 실험과의 상관관계 및 비교를 수행한 문헌10)을 참조하여, 각 부분 손실의 비율(%)에 대해 추정 및 그에 상응하는 발열량을 Table 2에 나타내었다. 이 값들은 단위 면적당 열유속의 해석 입력 조건으로 사용되며, 이 때, 풍손 및 펌프 손실은 무시하고 기어 및 베어링의 마찰에 의한 손실만 고려한다.
Predicted gear losses
3. 해석 결과
3.1 오일의 거동
감속기가 작동되는 동안 오일이 Fig. 6과 같이 순환될 수 있도록 설계되었다. 휠 기어가 회전하면서 오일 탱크에 고여 있는 오일을 끌어올리게 된다(a). 끌어올려진 오일의 일부는 리저버에 포집 되었다가 중력에 의해 GM, GW supply 경로를 지나 TRB(Taper Roller Bearing)에 공급된다(b)~(c). TRB의 윤활 및 냉각 작용을 하고 난 오일은 다시 중력에 의해 GM, GW Return 경로를 지나 오일 탱크로 회수된다(d).
The process of oil circulation
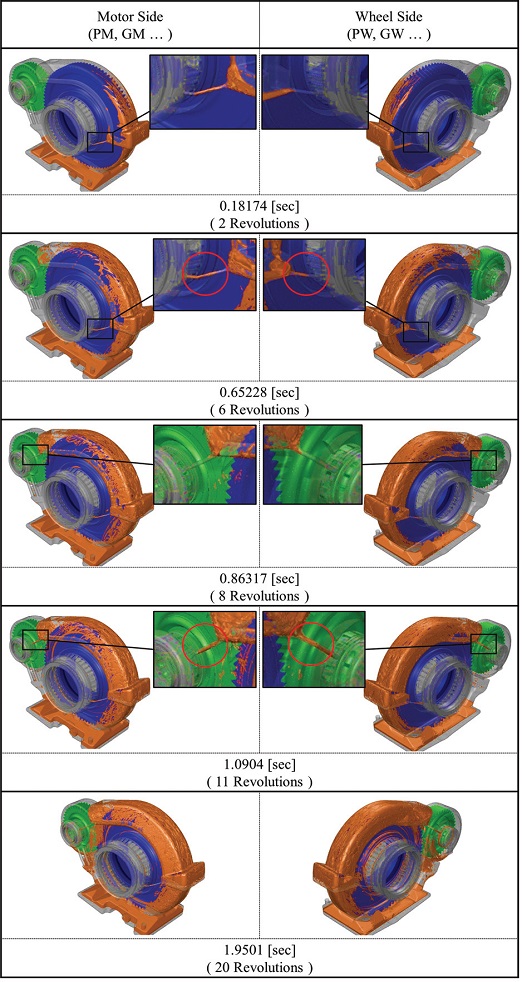
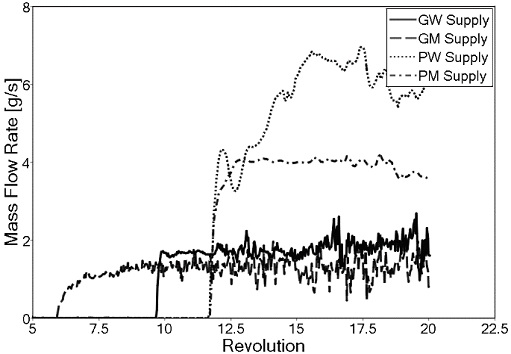
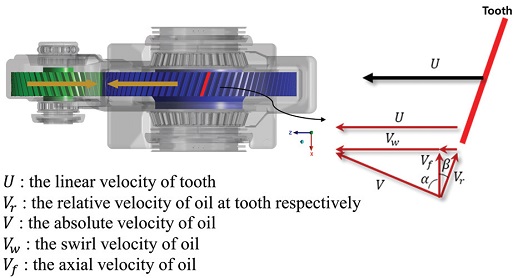
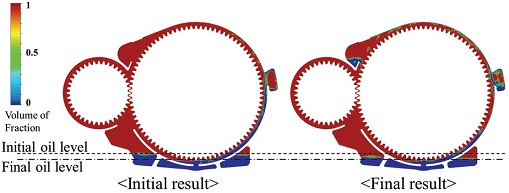
리저버에 포집되지 않은 나머지 오일은 상부로 향하게 된다(e). 상부에 고여 있는 오일은 중력에 의해 PM, PW supply 경로를 지나 볼 베어링과 롤러 베어링에 공급된다(f)~(g). 볼 베어링과 롤러 베어링의 윤활 및 냉각 작용을 하고 난 오일은 다시 중력에 의해 PM, PW Return 경로를 지나 오일 탱크로 회수된다(h). Fig. 6은 모터 측만 나타냈으며, 반대쪽인 휠 측도 유사한 구조를 갖는다. 해석을 통해 이러한 설계 취지에 맞게 전체적인 오일의 거동과 시간에 따라 각 경로를 지나는 오일의 양을 확인할 필요가 있다. 시간에 따른 오일의 거동을 Fig. 7에 나타내었다. 휠 기어에 의해 비산된 오일의 일부는 오일 리저버에 쌓이게 된다. 일정량 이상 쌓이게 되면 오일 경로들(GM supply, GW supply)을 통해서 휠 기어용 TRB에 공급되어 윤활과 냉각을 원활하게 한다. 오일 리저버에 쌓이지 않은 오일은 하우징의 상부까지 도달하여 다른 오일 경로들(PM supply, PW supply)을 통해서 피니언 측의 볼 베어링과 롤러 베어링에 공급된다. 그 이후 유동은 완전발달상태가 되어 오일의 순환이 연속적으로 이루어지며 순환 및 냉각을 유지하게 된다. 초기에 GM supply가 GW supply 보다 먼저 오일이 공급되는 이유는 휠 기어의 양쪽 측면이 서로 다른 위상을 갖는 헬리컬 기어이기 때문이다. 헬리컬 기어의 GM 측(Motor side) 위상이 반대쪽보다 앞서 있기 때문에 먼저 오일을 비산 시킬 수 있지만 이러한 현상이 시간당 오일의 공급량과는 관계가 없다는 것을 Fig. 8을 통해 알 수 있다. Fig. 8을 확인해 보면 GM supply에 먼저 오일이 공급되지만 특정시간 이후에는 GW supply와 PW supply의 유량이 평균적으로 더 높게 나타났다. 그 원인은 Fig. 9의 속도삼각형으로 설명할 수 있다. 헬리컬 기어는 양쪽 측면의 위상차로 인해 각 이빨들이 회전축에 대해 β 만큼의 각도를 갖게 되는데, 이 구배로 인해 마치 팬처럼 유체에 축 방향으로의 속도(Vf)를 유발한다. Fig. 10을 통해 동시간대에 양쪽 측면의 오일을 확인해보면 휠 측의 벽면에 더 많은 오일이 묻어 있는 것을 확인할 수 있다. 더불어, 휠 기어가 회전하는 동안 외부로의 누유는 없는 것으로 확인되었다. Fig. 11은 Y-Z 평면에서 상의 분율을 통해 공기-오일의 계면 및 체적 분포를 나타내었다. 여기서 VOF=0은 오일을 나타내고, VOF=1은 공기를 나타낸다. 휠 기어가 오일을 비산시키면서 하부 탱크의 오일 높이가 약 15 mm 감소하였고, 이 비산된 오일이 오일 리저버와 하우징의 상부에 상당량 고여 있는 것을 확인할 수 있다.
Transient behavior of oil inside gear unit
Mass flow rate of oil through supply paths
Velocity triangle on gear tooth
Comparison of transient oil distribution
Initial oil level changes by gear churning
3.2 열전달 계수 및 온도 분포
기어의 회전과 같이 강한 처닝에 의한 강제대류가 지배적인 열전달 시스템에서의 대류열전달계수는 기어 및 베어링 등의 발열량 및 표면의 온도와 무관하게 유동장에 의해 결정될 수 있다.12,13) 따라서, 앞선 2.2.1절과 Fig. 2의 해석 과정에서 표면의 대류열전달계수를 구하기 위한 방법으로 임의의 열유속(Dummy heat flux) 경계 조건을 감속기 모델 표면에 적용하여 유동장 및 에너지 지배방정식을 풀게 되면, 아래의 식 (3)에 의해 각 부품의 대류열전달계수를 산출할 수 있게 된다.13)
| (3) |
- htc : convective heat transfer coefficient, W/m2∙K
- qw : dummy wall heat flux, W/m2
- Tw : temperature on the wall, K
- Tref : reference bulk temperature, K
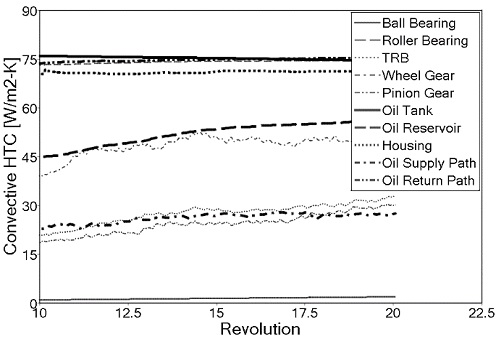
단, 형상에 따라 대류열전달계수는 불균일하게 분포되므로, 다음 단계의 해석 과정을 위해 부품의 모델링 구분을 충분히 세분화할 필요는 있다. Fig. 12에서는 시간에 따른 각 부품들의 대류열전달계수 결과를 나타내었다. 기어, 베어링을 비롯한 대부분의 내부 부품들의 대류열전달계수는 회전이 거듭됨에 따라, 즉 과도 시간이 지남에 따라 일정한 값을 나타내는데, 이 값의 일정한 상태를 통해 해석의 수렴성 및 완전발달상태를 판단하고, 그 값을 반영하여 정상상태의 온도분포를 계산하였다. 이 때, 부품 표면의 경계 조건 입력을 위한 대류열전달계수는 최종 3회전의 평균값으로 사용하였다.
Convective heat transfer coefficient of each parts
고체의 열전도를 고려한 열전달 해석에 있어서, 고체 내부의 온도 구배를 무시한다면, 에너지 평형 개념을 통하여 고체 내부의 에너지 변화율은 고체 표면에서의 열손실과 균형을 이루게 된다.14) 발산정리(Divergence theorem)와 함께 이러한 이론은 엔지니어링 문제에 있어서 유용하게 활용된다. 따라서, 앞서 산출한 발열량을 각각의 부품 전체 체적에서 발생한 에너지라고 가정하면, 부품 표면을 통하여 발산되는 발열량과 균형을 이루고, 이 값을 표면의 단위면적당 열유속 경계 조건으로 입력할 수 있다.
하우징과 외부와의 열전달은 외부 주행풍이 없는 실험실 조건으로서 자연대류에 의해 하우징 외벽을 통해 열이 발산하는 것으로 가정하였으며, 주위 및 발열체의 온도 등의 환경에 따라 그 값은 5~25 W/m2-K의 범위를 나타낸다.14) 본 연구에서는 앞서 설명된 대류열전달계수를 구하는 방법과 동일하게 하우징 최외곽 벽면의 면적 가중치 평균값을 계산하여 7.91 W/m2-K로 적용하였으며, 이 값은 위 문헌에서 언급된 통상적인 자연대류 조건에서의 열전달계수 범위 내에 위치하게 된다.
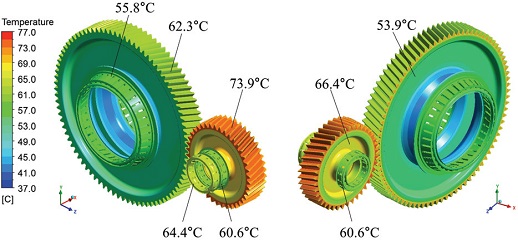
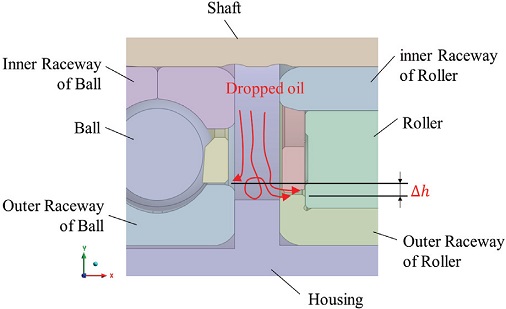
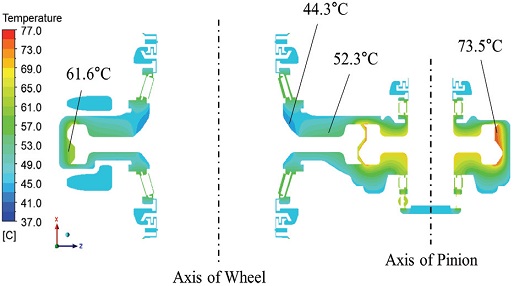
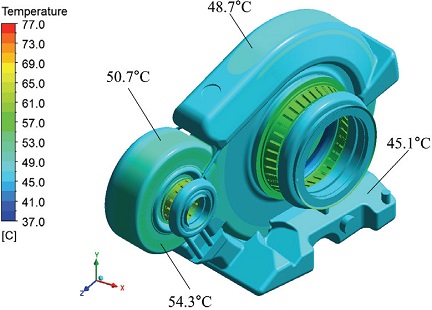
이와 같이 계산된 대류열전달계수와 열유속을 적용한 열전달 해석을 통해 각 부품의 온도를 예측하였으며, Fig. 13에 기어와 베어링 부의 온도 분포 결과를 나타내었다. 기어의 경우 휠 기어와 피니언 기어의 접촉이 주 발열원이기 때문에 다른 부위보다 높은 온도가 나타난다. 휠 기어의 경우 오일 처닝 및 편류(Windage)에 의한 냉각 효과로 인해 피니언 기어보다 온도가 낮게 나타난다. 이것은 Fig. 12에서 휠 기어의 대류열전달계수가 피니언 기어보다 크게 나타나는 것으로도 알 수 있다. 이로 인해 휠 기어는 피니언 기어보다 11~12 oC 정도 온도가 낮게 나타났다. 베어링의 경우 전체적으로 크기나 종류에 상관없이 유사한 온도분포를 나타냈으나 볼 베어링의 온도가 비교적 높게 나타났다. 그 원인은 Fig. 14를 통해 알 수 있는데, 볼 베어링과 롤러 베어링의 외륜의 높이 차이로 인해 볼 베어링에는 상대적으로 적은 오일이 공급되기 때문인 것으로 판단된다. Figs. 15~16을 통해 기어와 베어링에서 발생한 열이 하우징에 전달되는 것을 알 수 있다.
Temperature contours of gears and bearings
Section view of bearing at pinion axis
Temperature contours at center section of axis
Temperature contours of housing
4. 결 론
동력분산형 고속전철에 적용되는 감속기의 내부 오일 순환 구조 설계에 대한 해석적 평가를 위해 VOF와 MDM 해석 기법 및 다상유동-열전달 해석의 방법을 제시하였으며, 이를 활용하여 감속기 내부의 오일 거동을 모사하였다. 또한 열해석을 통해 각 부품들의 온도 분포를 예측하였으며, 주요 고찰은 다음과 같다.
- 1) 처닝에 의한 오일의 비산은 가시적으로 모터 측(GM, PM) 보다는 휠 측(GW, PW)에 더 많이 분포하고, 각종 오일 경로들을 통한 유량 결과를 통해서도 확인할 수 있었다.
- 2) 열해석을 통한 온도 분포는 휠 기어보다 피니언 기어가 더 높은 온도가 발생한다는 것을 확인할 수 있었다. 이는 손실에 의한 발열량이 입력축인 볼 베어링과 롤러 베어링이 가장 높은 반면 냉각을 유도하는 오일의 처닝 및 비산은 상대적으로 적기 때문인 것으로 판단된다.
- 3) 열해석을 위한 발열량 산정은 이전 연구들을 단순 참조하여 적용한 조건이므로 실제 감속기 내부의 발열량과 다소 다를 수 있다. 또한 고체 영역 내부의 온도 계산에 대해, 고체 내부 에너지 변화율이 고체 표면에서의 열손실과 균형을 이룬다는 가정을 통해 수행되었으므로, 따라서 최종적으로 확인하고자 하는 감속기의 시간에 따른 온도 변화와 냉각 성능은 실험을 통한 해석 결과와의 상관관계 도출 및 검증이 필요한 부분이다.
향후 이러한 해석 기법 및 결과들을 활용하여 감속기 내부의 오일 순환 구조를 위한 오일 관로 및 하우징 등 감속기의 사전 설계 평가 및 성능 확보를 위한 설계 개선의 가이드라인으로 제시할 수 있을 것으로 기대된다.
Acknowledgments
본 논문은 2020년도 국토교통부 철도기술개발사업(18RTRP-B148870-02) 고속철도 부품 장치 국산화 기술 개발 과제의 “동력분산식 고속철도용 고내구성 감속기 기술개발 과제”의 지원으로 수행되었습니다.
References
-
H. Liu, T. Jurkschat, T. Lohner and K. Stahl, “Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method,” Lubricants, Vol.6, No.2, 2018.
[https://doi.org/10.3390/lubricants6020047]
- N. Imatiaz, CFD Simulation of Dip-Lubricated Single-Stage Gearboxes through Coupling of Multiphase Flow and Multiple Body Dynamics, an Initial Investigation, Examensarbete, Linkoping University, Linkoping, 2018.
-
J. Choi, H. J. Shin, W. Kim and N. Hur, “Numerical Simulations of Lubrication Behavior with Various Positions of Hydraulic Suction Pipe in a Tractor Transaxle,” Journal of Computational Fluids Engineering, Vol.23, No.2, pp.72-78, 2018.
[https://doi.org/10.6112/kscfe.2018.23.2.072]
-
H. Patel and M. Anto, “Oil Splash Simulation in Final Drive with Overset Mesh,” SAE 2019-26-0274, 2019.
[https://doi.org/10.4271/2019-26-0274]
-
W. Liu, Ho. Fu and Y. Chen, “A Novel Method for Gear Reducer’s Transient Temperature Field Analysis Based on Thermo-Fluid Interaction,” 3rd International Conference on Machinery, Materials and Information Technology Application(ICMMITA 2015), pp.1702-1711, 2015.
[https://doi.org/10.2991/icmmita-15.2015.317]
- J. Y. Cho, N. Hur, J. R. Choi and J. W. Yoon, “Numerical Simulation of Oil and Air Two-Phase Flow in a Planetary Gear System using the Overset Mesh Technique,” International Symposium on Transport Phenomena and Dynamics of Rotating Machinery(ISROMAC 2016), 2016.
- M. J. Kim, Y. T. Kim, W. T. Kim, S. C. Jung, J. W. Kim and S. Y. Choi, “A Numerical Investigation to Predict Structural Integrity of Wheel Guard on Passenger Vehicle under Wading Conditions,” KSAE Fall Conference Proceedings, p.1026, 2019.
- M. Z. Mettichi, Y. Gargouri, P. H. L. Groenenboom and F. Khaldi, “Simulating Oil Flow for Gearbox Lubrication using SPH,” Proceedings of the 10th International SPHERIC Workshop, pp.237-243, 2015.
- A. Bhatia, Basic Fundamentals of Gear Drives, Course No: M06-031, Continuing Education and Development, Inc, 2012.
- D. Mba and P. Heingartner, “Determining Power Losses in the Helical Gear Mesh: Case Study,” Gear Technology, Vol.22, No.5, pp.32-37, 2005.
- B. Y. Kim, K. S. Lee, Y. H. Kim and K. H. Kim, “A Theoretical Approach of Power Losses in Hyundai Hybrid Transmission,” KSAE Annual Conference Proceedings, pp.2991-3001, 2010.
-
B. K. Choi, J. H. Park, M. R. Kim and B. J. Ahn, “Development of the Virtual Test Technology for Evaluating Thermal Performance of Disc Brake,” Transactions of KSAE, Vol.17, No.4, pp.40-47, 2009.
[https://doi.org/10.4271/2009-01-0857]
- Ansys Fluent Theory Guide, Release 2020R2, Ansys Inc., 2020.
- F. P. Incropera and D. P. DeWitt, Fundamentals of Heat and Mass Transfer, pp.174-177, 2nd Edn., John Wiley & Sons, Hoboken, New Jersey, 1985.