[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 29, No. 8, pp.751-763

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Aug 2021

Received 10 Mar 2021 Revised 14 Apr 2021 Accepted 14 Apr 2021

DOI: https://doi.org/10.7467/KSAE.2021.29.8.751

CNG-디젤 이종연료 엔진에서 학습 조건이 엔진 블록 진동을 이용한 실린더 내부압력 예측 DNN 모델의 정확성에 미치는 영향

박찬수¹⁾

; 김경곤¹⁾

; 김우영¹⁾

; 전지연²⁾

; 전미연²⁾

; 배충식^*^{, 1)}

1)한국과학기술원 기계공학과
2)한국조선해양 디지털기술연구소

The Effect of Training Conditions on the Accuracy of In-cylinder Pressure Prediction DNN Model Using Engine Block Vibration in a CNG-Diesel Dual Fuel Engine

Chansoo Park¹⁾

; Gyunggon Kim¹⁾

; Wooyung Kim¹⁾

; Jeeyeon Jeon²⁾

; Miyeon Jeon²⁾

; Choongsik Bae^*^{, 1)}

1)Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, Daejeon 34141, Korea
2)Digital Technology Research Institute, Korea Shipbuilding & Offshore Engineering, 55 Bundang-ro, Bundang-gu, Seognam-si, Gyeonggi 13591, Korea

Correspondence to: ^*E-mail: csbae@kaist.ac.kr

Copyright Ⓒ 2021 KSAE / 189-06
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

A deep neural network(DNN) model was developed in order to predict in-cylinder pressure. Engine block vibration signal and in-cylinder pressure measured by accelerometer and pressure transducer were used as the input and output of the model, respectively. The test engine was a single cylinder compressed natural gas-diesel(CNG-diesel) dual fuel compression ignition engine. In order to evaluate the effect of training conditions on the accuracy of the model, CNG substitution ratio, diesel injection timing, and intake air pressure were changed while maintaining an engine load of 0.6 MPa. Test conditions were composed of unseen engine conditions in the training conditions to avoid overfitting problems. Basically, the coefficient of determination(R²) between the predicted and measured in-cylinder pressure trace was used as an indicator of the model performance. Peak in-cylinder pressure was also included in the analysis. The results showed different prediction accuracies depending on the different intake air pressure and statistically biased test conditions compared to the training conditions.

Keywords:

Effect of training condition, CNG-diesel dual-fuel engine, Deep neural network, Engine block vibration, In-cylinder pressure prediction, Accelerometer

키워드:

학습조건의 영향, 천연가스-디젤 이중연료 엔진, 딥 뉴런 네트워크, 엔진 블록 진동, 실린더 내부 압력 예측, 가속도센서

1. 서 론

이종연료(Dual Fuel, DF) 혼합 연소 기술은 착화 특성이 다른 두 개의 연료를 혼합하여 연소하는 기술이다. 주로 자발화 성능이 낮은 저 세탄가 연료(Low-cetane fuel)와 자발화 성능이 높은 고 세탄가 연료(High-cetane fuel)를 혼합하여 사용한다. 가장 일반적인 연료 혼합 방법은 엔진의 흡기포트에 저 세탄가 연료를 분사하여 공기와 저 세탄가 연료의 예혼합기(Premixed mixture)를 형성하고, 실린더 내로 예혼합기를 흡입한 후 압축하는 과정에서 고 세탄가 연료를 착화제로 실린더 내부에 직접 분사하는 방식이다. 저 세탄가 연료는 가솔린(Gasoline), 천연가스(Natural gas), 수소(Hydrogen)를 주로 사용하고, 고 세탄가 연료는 디젤(Diesel)과 바이오 디젤(Bio-diesel)을 주로 사용한다. 두 연료의 반응성 차이를 이용하여 연료 혼합 비율 조절을 통해 연소 시작 시점을 제어할 수 있다는 측면에서 기존의 신･연소 전략의 고질적인 문제점이었던 연소상(Combustion phase) 제어가 가능하다는 장점이 있다.^1-3)

하지만 낮은 실린더 내부 전역 당량비 조건에서 고 세탄가 연료의 반응성 성층화 감소는 연소 불안정성 증가 문제를 발생시켰다. 이로 인한 실린더 내부 최대 압력 변동성 증가 문제는 엔진의 안정성과 직결되어 있으므로, 현재 대형 이종연료 혼소 엔진들의 경우 모든 실린더에 고성능 압전 소자(Piezo) 방식의 압력센서가 설치되고 있는 실정이다. 이는 정확한 연소 압력 측정을 통해 실시간으로 고 세탄가 연료의 분사시기와 분사량을 제어하기 위함이다. 하지만 피에조 압력센서의 높은 가격과 잦은 고장으로 인한 엔진 비용 상승과 높은 유지비용은 대형 DF 엔진이 극복해야 할 문제로 남아있다.

이러한 문제를 해결하기 위해 대형 DF 엔진의 실린더 내부 압력을 대체 측정하는 연구가 오랜 기간 있어 왔다. 주요 연구 방법으로는 엔코더(Encoder)을 이용하여 엔진 크랭크 각속도 및 각가속도 변화를 측정하는 방법,⁴⁾ 스트레인 게이지(Strain gauge)를 이용하여 실린더 라이너(Liner)의 팽창을 측정하는 방법,⁵⁾ 가속도 센서(Accelerometer)를 이용하여 엔진 블록 진동을 측정하는 방법에 대한 연구를 들 수 있다.⁶⁾

세 방법 모두 연소에서 발생되는 압력파가 실린더 헤드, 벽면, 그리고 피스톤을 밀어내는 힘에 의해 나타나는 엔진의 반응(Response)을 측정한 후, 역 변환 함수를 이용하여 실린더 내부 압력을 역으로 예측한다는 공통점이 있다. 하지만 스트레인 게이지는 열부하에 취약하며, 엔코더 신호는 8기통 이상의 엔진에서는 크랭크 각도(Crank Angle Degree, CAD) 단위에서 연소 시기가 중첩되어 엔코더 신호만으로는 엔진 기통 별 연소 압력을 분리해내기 어렵다는 문제점이 있다. 이로 인해 엔진 블록의 진동을 가속도 센서 또는 노킹(Knocking)센서의 신호를 이용하여 대체 측정하는 연구가 대형 DF 엔진들을 중심으로 진행되고 있다.

엔진 블록 진동을 이용한 실린더 내부 압력 대체 측정 방법의 역 변환 함수로는 크게 이론적 지식을 이용한 방법(Analytic method)과 경험적 지식을 이용한 방법(Empirical method)이 있다.⁷⁾ 이론적 지식을 이용한 방법은 실린더 벽면이 받는 힘이 실린더 내부 기체의 압력 변화와 비례한다는 기본적인 원리에서 착안한 방법이다. 그리고 이 힘이 엔진 블록의 진동 신호와 서로 연관되어 있다는 원리(Coupling)를 이용한 것이다.⁸⁾ 이는 식 (1)과 식 (2)의 가장 기본적인 힘과 진동의 관계식을 통해 확인할 수 있다. 물론 가속도 센서에서 실시간으로 측정되는 엔진 블록 진동 신호는 실린더 내부 압력파가 실린더 벽면에 가하는 충격(Impact)의 결과로 나타나는 엔진 블록의 고유 진동 신호(Natural response), 실린더 내부 압력과 부피의 변화에 따른 압력파 진동(Oscillation), 엔진내 다른 부품의 충격, 마찰, 회전에 의한 기계적인 진동에 의한 신호를 동시에 포함한다.

P c y l ∝ A c y l F g

(1)

where P_cyl : In-cylnder pressure,
　　　A_cyl : In-cylnder surface area,
　　　F_g : gas force to wall

M X ¨ θ + C X ˙ θ + K X θ = F θ

(2)

where M : mass, C : damping, K : stiffness matrix
　　　 $X ¨, X ˙, X$ : Acceleration, velocity, displacement

여기서 엔진 블록의 고유 진동 신호는 일반적으로 엔진의 높은 강성(Stiffness)으로 인해 고주파수 진동으로 나타나며, 실린더 내 압력파 진동 신호는 상대적으로 저주파수 진동으로 나타난 다. 두 신호의 강도는 모두 실린더 내부 압력 변화에 따른 동적 하중의 크기에 비례하여 나타나게 되는데, 이는 식 (3)과 같이 실린더 내부 압력의 상승률의 제곱에 비례한다.⁹⁾

I ∝ P m a x d P d θ m a x 2

(3)

where I : Intensity of combustion vibration,
　　　P_max : peak pressure,
　　　 $d P d θ m a x$ : maximum pressure rise rate

하지만 엔진 블록의 고유진동 신호 자체는 주로 엔진의 구조적 특성을 반영하고 있기 때문에 연소에 대한 정확한 정보를 담고 있지 않다. 그러므로 연소실 내부의 압력파 진동과 관련된 저 주파수 신호의 측정이 연소 압력 예측에 중요한 것으로 알려져 있다.^10,11) 하지만 엔진 연소의 비선형성과 각종 회전체와 보기류에서 발생되는 노이즈 진동 신호들로 인해 이러한 이론적 접근법의 정확성은 낮은 것으로 알려져 있다. 또한, 하나의 엔진 운전 조건에서는 높은 정확성을 보이는 예측 모델이 다른 운전 조건에서는 잘 맞지 않는 문제점이 다수 보고된 바 있다.¹²⁾

이러한 문제점들을 해결하기 위해 선행연구자들은 다양한 운전조건에서 수 많은 엔진 실험을 통해 축적된 엔진 블록 진동 신호와 실린더 내부 압력 신호의 경험적 기계학습(Machine learning)을 이용한 실린더 내부 압력 대체측정 연구를 수행해오고 있다.^13-15) 기계학습 분야는 2010년대 초반 딥 뉴런 네트워크(Deep neuron network, DNN) 기술의 비약적인 발전으로 인해 주목받는 기술이다.

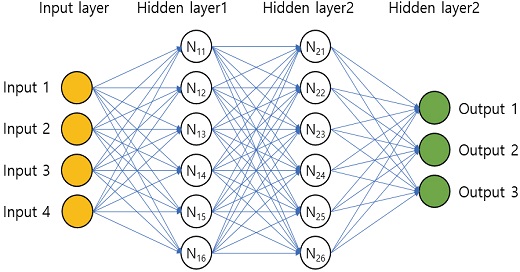
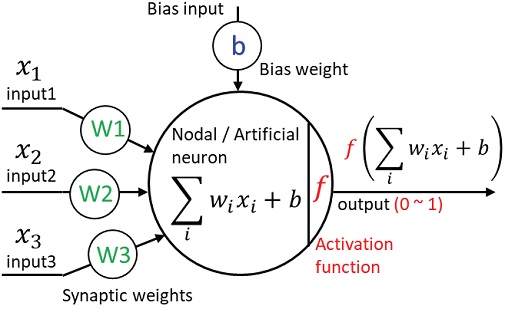
기본적으로 입력층(Input layer)과 출력층(Output layer) 사이에 1개 이상의 은닉층(Hidden layer)으로 구성되며, 각 층별로 정보를 담을 노드(Node)의 개수를 지정하여 모델의 뼈대를 형성한다. 층 간의 노드를 모두 연결(Fully connected)하여 네트워크 망을 구성하고 모든 네트워크 연결망에 가중치(Weight)를 부여하여 입력 값과 가중치의 행렬 곱 연산을 수행하게 된다. 그 후 각 노드 별로 편중치(Bias)를 합하고 활성화 함수(Activation function)를 거쳐 다음 층으로 결과를 전달하게 된다. Fig. 1은 이러한 DNN 모델의 구조의 한 예이며, Fig. 2는 각 노드 지점에서 작동되는 연산 방식의 예를 나타낸다.¹⁶⁾ DNN 모델은 다양한 학습 조건의 입력 값을 받아들여 출력 값을 계산하고, 예측된 출력 결과와 실제 값(Label)과의 차이를 계산하여 그 차이를 최소화하는 방향으로 반복적으로 가중치과 편중치를 갱신하게 된다. 모델의 정확성은 학습 데이터의 측정 정확성, 학습 조건의 구성과 관련된 모델 외적인 변수와 모델의 구조, 학습률, 손실함수 정의, 최적화 알고리즘 등의 모델 내적 변수에 의해 결정된다.

Fig. 1

Example of typical deep neural network model structure

Fig. 2

Weight, bias, and activation function operation in node points

2010년대 중반 이후, 급격히 발전한 DNN 모델은 구조가 간단하고, 연산량을 줄일 수 있으면서도 높은 정확도를 보여 주목받고 있다. 최근 Wesche 등¹⁷⁾은 노킹(Knocking) 센서를 이용하여 선박용 중속 엔진의 실린더 내부 압력 대체 측정 및 NOx 배출량 예측을 DNN 모델 통해 수행하였다. 실린더 헤드에 설치한 2개의 노킹센서에서 측정한 엔진 블록 진동 신호를 DNN 모델로 학습하여 전체 실린더의 연소 압력을 예측하였으며, 예측된 연소 압력 결과를 바탕으로 NOx 배출량 또한 예측하였다.

하지만 기계학습을 이용하여 연소실 내부 압력을 예측한 대부분의 연구들의 경우 단일 연료를 사용하여 엔진을 구동하였기 때문에 연소 특성이 단순하였다.¹⁵⁾ 그리고 학습 조건이라고 할 수 있는 엔진 운전 변수의 구성을 명확하게 밝히고 있다고 하더라도, 학습 조건의 변화에 따른 모델의 예측 성능을 비교 분석한 연구가 드물어 DF 엔진의 연소 압력 예측 기계학습 모델 개발을 위한 학습 조건 구성에 대한 정보를 얻기 어려웠다.

본 연구에서는 6 L급 디젤엔진을 개조한 단기통 천연가스-디젤 이종연료 압축착화 엔진에서 DNN 모델을 이용하여 엔진 블록 진동 신호를 통해 실린더 내부 압력을 예측하는 연구를 수행하였다. 엔진 부하를 고정한 상태에서 천연가스 대체 비율, 디젤 연료 분사시기, 흡기 압력을 변화시켜가며 다양한 운전 조건에서 실험을 수행하였다. 특히 학습 조건 변화에 따른 DNN 모델의 예측 정확성을 알아보기 위해, 서로 다른 학습 조건에서 학습된 모델을 이용하여 학습 조건에 전혀 포함되지 않은 엔진 운전 조건들의 연소 압력을 예측하는 연구를 수행하였다.

2. 실험 장치 및 DNN 모델

2.1 실험 장치

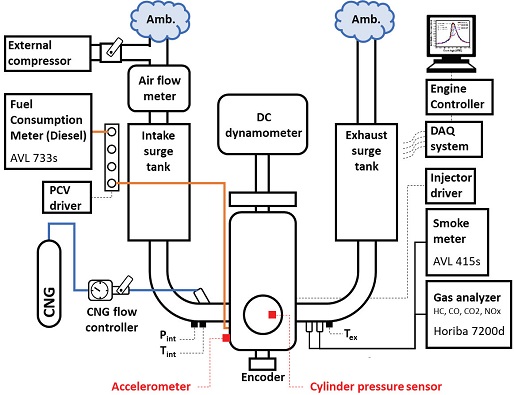
Fig. 3은 엔진 실험 장치의 계략도를 나타낸 것이다. 본 실험은 건설기계용 6기통 디젤 엔진을 단기통 엔진으로 개조한 엔진이다. 엔진에 대한 상세한 정보는 Table 1에서 확인할 수 있다.

Fig. 3

Schematic of experiment engine and measurement systems

Table 1

Engine specification

엔진속도는 AC 동력계(RDL1611Y, UNICO)로 제어하였으며, 연료 공급을 위해 디젤 및 CNG 연료라인을 별도로 구축하여 엔진에 공급하였다. 디젤의 경우 인젝터 드라이버를 제작하여 연료 분사 시기와 연료 분사 기간을 제어하였다. 연료 압력은 100 MPa로 고정하였고 커먼레일(Common rail) 시스템을 이용하여 연료 인젝터에 공급하였다. 사용된 디젤 연료량은 연비계(AVL, 733 s)를 이용하여 질량 단위[g]로 측정하였다. CNG의 경우에는 별도의 연료 인젝터를 설치하지 않고 흡기포트에 지속적으로 연료를 흘려주어 흡기와 충분히 섞이도록 하였다. CNG의 공급압력은 0.5 MPa로 유지하여 외부 컴프레서(EQ75, Nawootec)를 이용한 과급 시에도 공급에 문제가 없게 하였다. 흡기 유량은 공기 유량계(IN-Flow, Bronkhost)를 이용하여 측정하였으며, CNG 분사량은 전자식 유량 제어기(EL-Flow, Bronkhorst)를 통해 제어하여 질량 단위로 디젤 대비 CNG의 분사량으로 정의된 CNG 대체율(Substitution Ratio, SR)을 약 1 % 오차 내로 제어하였다. 흡기 압력(P_int)과 흡기 온도는 흡기 포트에서 피에조 압력센서(4045A5, Kistler)와 K-type 열전대를 이용하여 측정하였다.

DNN모델의 입력값인 엔진 블록 진동은 Fig. 4와 같이 엔진 헤드 흡기 쪽에 별도의 어뎁터(Adapter)를 설치하여 엔진의 XYZ 3축 모두의 진동을 가속도센서(8763B250BT, Kistler)를 이용하여 측정하였다. 이 중 가장 S/N(Signal to noise) 비율이 높았던 Z축 결과를 입력값으로 사용하였다. 엔진 실린더 내부 압력은 피에조 압력센서(6052C, Kistler)를 이용하여 측정하였으며, 실험 결과 측정 값으로 모델 예측 결과의 학습 목표로 설정하였다.

Fig. 4

Accelerometer installation position and sign convention of the sensor

모든 실험 결과는 0.2 CAD 단위로 출력되는 엔코더(E40S8-1800-3-T-24, Autonics) 각도 신호를 기준으로 동기화하여 데이터 입출력 시스템(cRIO-9234, National instrument)을 통해 실험 조건별로 100 엔진 사이클씩 취득하였다.

2.2 DNN 모델

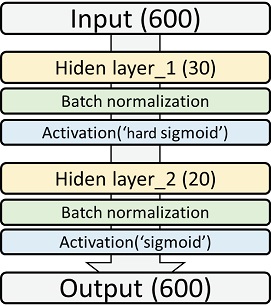
DNN 모델은 오픈 소스 개발 환경인 Python을 이용해 제작되었다. Tensorflow keras 라이브러리 환경에서 모델을 구축하였고, 데이터 전처리와 결과 확인을 위해 Pandas, numpy, matplotlib, sklearn, scipy, seaborn 등의 라이브러리를 사용하였다. DNN 모델의 구성은 Fig. 5와 같다. 먼저 입력단과 출력단의 노드 수는 600개로 설정하고 0.2 CAD 단위로 취득된 진동 신호와 실린더 내부 압력 신호를 입력단과 출력단에 공급하였다. 학습에 사용된 CAD 시기는 다수의 시행착오 과정(Trial and error)을 거쳐 30 CAD bTDC(Before top dead center)에서 90 CAD aTDC(After top dead center)까지로 설정하였다. 이는 압축 TDC 주변 CAD 에서의 진동 정보가 연소 압력의 정보를 가지고 있었기 때문이다.

Fig. 5

Deep neural network(DNN) model architecture

은닉층은 총 2층으로 구성하였다. 첫번째 은닉층은 30개의 노드를 배치하였고, 두번째의 은닉층에는 20개의 노드를 배치하였다. 각 은닉층의 후단에는 Batch normalization 층과 활성화 함수 층을 배치하였다. Batch normalization 층은 각 은닉층에서 계산된 결과가 편중된 분포를 보이지 않도록 하여 모델의 예측 성능을 높여주는 것으로 알려져 있다. 활성화 함수는 Hard sigmoid 함수와 Sigmoid 함수를 사용하였다. 은닉층의 개수, 각 은닉층의 노드 개수, 그리고 활성화 함수는 다양한 조합으로 시행착오방식으로 모델을 제작하여 결과를 비교한 후 가장 결과가 좋았던 시행을 최종 모델로 선정하였다.

모델의 손실함수(Loss function)는 평균 제곱 오차(Mean Square Error, MSE)로 정의하였고, 최적화 함수(Optimization function)는 RMSprop을 사용하였다. 학습률은 0.002로 설정하였다. RMSprop 함수는 AdaGrad 함수를 개선한 함수로써 모델의 역방향 전파(Back propagation) 시 손실함수 기울기의 제곱이 누적되어 계산되던 AdaGrad 함수와 달리 지수 가중 이동 평균(Exponentially weighted moving average)를 통해 최신 기울기를 더 크게 반영하도록 한 함수이다. 모델에 투입되는 입력 값인 진동 신호의 경우 각 CAD 별로 전체 데이터의 평균과 표준편차를 구해서 정규화 하여 투입하였다.

모델의 예측 성능은 결정계수(Coefficient of determination, R²)를 통해 분석하였다. 결정계수는 예측한 회귀함수 결과와 실제 측정 결과의 상호 관계를 파악하기 위한 지표이다. 특히 선형회귀분석(Linear regression analysis)에서 회귀직선의 적합도(Goodness of fit)을 평가하는 문제에 주로 활용된다. 0에서 1사이의 값을 가지며, 1에 가까울수록 결과들 사이의 상관성이 높음을 나타낸다. 식 (4)~(8)은 모델에 사용된 활성화 함수, 최적화 함수, 정규화 함수, 그리고 결정계수의 식이다.

S x = 1 1 + e - x

(4)

where S(x) : Sigmoid function

H S x = max ⁡ 0, m i n 1, x + 1 2

(5)

where HS(x) : Hard sigmoid function

h i ← ρ h i - 1 + 1 - ρ ∂ L i ∂ W ⨀ ∂ L i ∂ W

(6)

where h : Accumulated square of loss gradient,
　　　ρ : hyper parameter,
　　　L : Loss function,
　　　W : Weight

S t a x = x - m σ

(7)

where Sta(x) : Standardized x,
　　　m : mean of x,
　　　σ : Standard deviation of x

R 2 = 1 - ∑ y i - y^i 2 ∑ y i - y ¯ 2

(8)

where R² : Coefficient of determination,
　　　 $y^i$ : ith predicted result,
　　　 $y ¯$ : mean of measured result,
　　　y_i : ith measured result,

3. 실험 조건

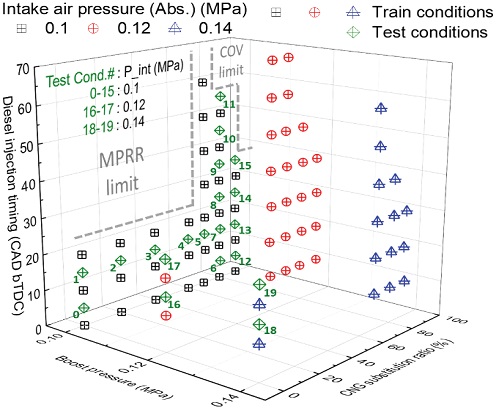
Table 2는 모든 실험 조건에서 공통적으로 동일한 실험 통제 변수들을 나타낸 것이다. 실험 조건은 Tables 3~4와 같이 총 2개의 학습 조건과 1개의 테스트 조건으로 구성되었다. 학습 조건(A)의 경우 과급 조건이 포함되지 않은 자연 흡기 조건만을 학습 조건에 포함하였다. 따라서 흡기 압력이 0.1 MPa로 고정되었다. 연료 분사시기의 경우 압축 행정 TDC에서 10 CAD씩 분사시기를 진각(Advance)하는 방식으로 변화시켰다. CNG SR의 경우 주요 운전영역인 60 % 이상의 SR에서는 10 % 단위로 SR을 변경하였고 그 이하의 영역에서는 20 % 단위로 변경하였다. 엔진의 구조적 안정성 확보를 위해 최대 압력 상승률(Maximum Pressure Rise Rate, MPRR)이 5를 넘지 않는 조건을 유지하였으며, 연소 불안정성의 지표인 도시 유효 평균 압력의 변동 계수(Coefficient of Variation of Indicated Mean Effective Pressure, COV IMEP) 역시 5 %가 넘지 않도록 하였다.

Table 2

Common engine operation condition

Table 3

Engine operation parameters for train conditions

Table 4

Engine operation parameters for the test condition

학습 조건(B)에는 학습 조건(A)의 자연 흡기 압력 대비 20 %와 40 %의 흡기 압력 상승조건들을 추가하여 학습 조건을 구성하였다. CNG SR은 주요 운전 조건인 60 % 이상 조건과 대조군인 0 % 조건만 수행하였으며, 이는 과급 조건에서 SR 60 % 이하로 운전되는 조건은 실질적으로 불필요한 운전 조건이기 때문이다. 연료 분사시기는 학습 조건(A)에서와 같이 MPRR, COV IMEP 제한을 넘지 않는 조건에서만 10 CAD 단위로 변화시켰다.

테스트 조건의 경우 Fig. 6을 통해 구체적으로 확인할 수 있다. 총 20개 조건에 대하여 흡기 압력, 연료 분사시기, CNG SR 변화에 대한 모델의 예측 정확도 변화를 분석하였다. 모델의 학습 데이터에 대한 과적합(Overfitting) 문제를 미연에 차단하기 위해, 테스트 조건의 연료 분사시기의 경우 학습 조건과 다르게 5 CAD bTDC를 기준으로 10 CAD씩 진각하여 학습 조건과 겹치는 조건이 없도록 하였다.

Fig. 6

Train and test conditions for deep neural network model development and evaluation

학습 조건 별 비교 DNN 모델 성능 분석은 학습 조건의 구성에 따른 테스트 조건 별 R²의 차이를 비교하는 방식으로 수행하였다. 학습 조건 변화가 테스트 조건의 예측 정확성에 어떤 영향을 미치는지 정확한 원인 분석을 하기 위해서 테스트 조건은 무작위로 데이터를 뒤섞지(Shuffle) 않고 각 조건의 데이터 들을 순차적으로 나열하는 방식으로 도시하였다. 학습 조건의 경우 무작위로 뒤섞어서 모델에 공급하였지만, 결과 확인을 위해 다시 순서대로 정리하여 학습 조건 별 학습 정확도를 분석하였다. 그 결과 학습 조건에 대한 DNN 모델들의 예측 정확도는 모든 조건에 대해 R² 기준으로 0.99를 달성하였다.

마지막으로 테스트 조건들 중 반복적으로 낮은 예측 정확도를 보이는 조건들의 결과 분석을 위해 조건 별 실린더 내부 압력 신호의 형태 분석을 수행하였다. 이를 위해, 식 (9)~(10)과 같이 실린더 내부 압력의 신호의 첨도(Kurtosis)와 왜도(Skewness)를 정의하였다. 첨도는 양의 값이 클 수록 정규분포 대비 중심축을 기준으로 뾰족한 그래프를 나타내며, 왜도는 양의 값이 클수록 정규분포 대비 왼쪽으로 치우친 그래프를 나타낸다.

K u r t X = E X - E X 4 E X - E X 2 2 - 3

(9)

where Kurt(X) : Kutrosis of X matrix,
　　　E(X) : Expectation of X matrix

S k e w X = E X - E X 3 E X - E X 2 3 / 2

(10)

where Skew(x) : Skewness of matrix X

4. 실험 결과

4.1 학습 조건 (A)와 학습 조건 (B)로 학습한 DNN 모델의 예측 결과 비교

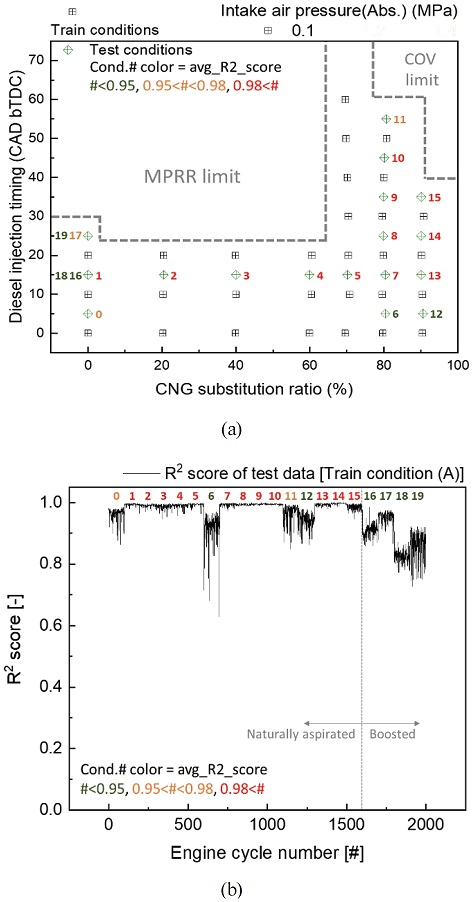
Fig. 7(a), (b)는 과급 조건이 포함되지 않은 학습 조건(A)로 학습한 DNN 모델(DNN 모델(A))을 이용하여 테스트 조건들의 실린더 내부 압력을 예측한 결과의 성능을 R²로 평가한 것이다. 테스트 조건은 Fig. 6에서와 같이 자연 흡기 및 과급 조건을 모두 포함하고 있으며, 테스트 조건 0-15번은 자연 흡기 조건을 나타내고 16-19번은 과급 조건을 나타낸다. 테스트 결과에서 자연 흡기 조건 중 테스트 조건 0, 6, 11, 12번의 예측 정확도가 낮았으며, 과급 조건인 16-19번의 예측 정확도가 낮았다.

Fig. 7

R2 performances for test conditions of DNN model trained with Train condition (A)

결과 분석에 있어서 테스트 조건의 예측 정확도를 높이기 위해서는 학습 조건의 엔진 운전 범위가 테스트 조건의 운전 범위를 포함하고 있어야 한다는 가정을 하면, DNN 모델(A)의 테스트 조건 별 예측 결과를 이해하는데 도움이 된다. 이 가정을 따를 경우, 과급 조건의 예측 정확도가 낮은 이유는 학습 조건 내에 흡기 압력이 과급된 엔진 운전 조건이 없어 과급에 의해 모터링 압력이 상승하는 조건에 대한 학습이 이루어지지 않았기 때문이다. 동일한 방법으로 테스트 조건 0, 6, 11, 12번의 경우 학습 조건(A) 영역 밖의 운전 조건이거나 학습 조건 가장자리에 위치하여 비슷한 운전 조건이 적었기 때문에 예측 정확도가 낮았던 것으로 유추할 수 있다.

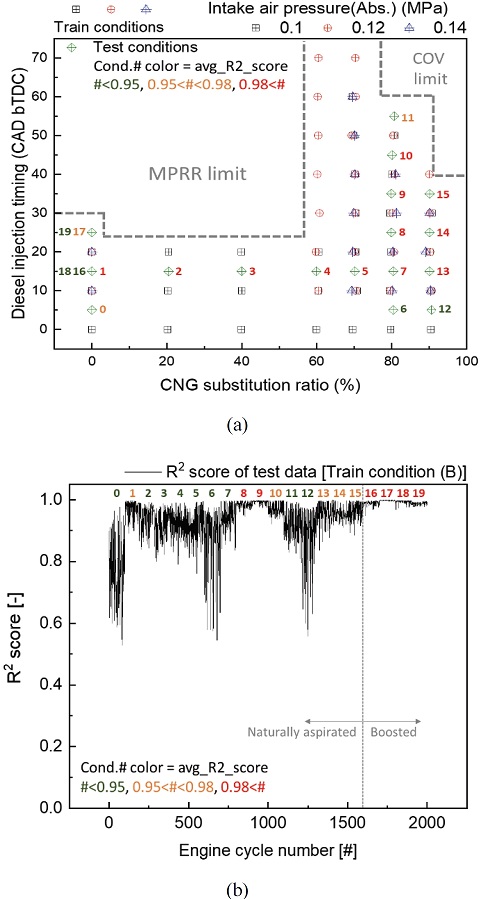
Fig. 8(a), (b)는 과급 조건이 학습 조건에 포함된 학습 조건(B)로 학습한 DNN 모델(DNN 모델(B))을 이용하여 동일한 방법으로 모델의 성능을 R²로 평가한 것이다. DNN 모델(A)의 예측 결과와 큰 차이를 보였는데, 특히 과급 조건인 16번에서 19번 테스트 조건의 예측 정확성이 크게 향상되고 반대로 자연 흡기 조건들의 예측 정확성이 크게 하락한 것을 확인할 수 있다. 이는 DNN 모델(A)의 테스트 조건 0, 6, 11, 12번 결과와 동일한 문제로 생각할 수 있다. 학습 조건(B)에는 0.12 MPa와 0.14 MPa의 총 2단계에 걸친 과급 조건이 존재하기 때문에 기존의 자연 흡기 학습 조건은 새로운 차원의 변수에 대하여 가장자리 조건으로 밀려나기 때문이다.

Fig. 8

R2 performances for test conditions of DNN model trained with Train condition (B)

또한, 학습 조건(B)의 경우, 과급 조건의 개수가 전체 학습 조건의 약 58 %로 자연 흡기 조건에 비해 조건 수가 많이 때문에, 이것이 학습에 영향을 주어 테스트 조건의 자연 흡기 조건들의 예측 정확도가 하락한 것으로 생각할 수 있다.

이러한 결과는 엔진 운전 변수를 기준으로 테스트조건에 인접한 학습 조건이 부족한 경우에서 더욱 두드러지며, DNN 모델(A)에서 낮은 예측 정확도를 보였던 테스트 조건 0, 6, 11, 12번의 경우 더욱 큰 예측 정확도 하락을 관찰할 수 있었다. 또한 기존의 DNN 모델(A)에서는 높은 예측 정확도를 보였던 테스트 조건 1, 2, 3, 4, 5의 경우 DNN 모델(B)로 테스트한 경우 예측 정확도가 크게 하락하였다. 이는 학습 조건(B)의 SR이 대부분 60 % 이상이고, 연료 분사 시기가 20 CAD 이전으로 진각된 조건들이 많았기 때문에 상대적으로 학습 조건이 부족해진 것이 그 원인으로 판단된다.

Fig. 9는 학습 조건에 따른 모델의 예측 정확성 차이가 두드러진 테스트 조건 중 3번 조건의 엔진 블록 진동, 실린더 내부 압력, 그리고 DNN 모델(A), (B)의 실린더 내부 압력 예측 결과를 비교한 것이다. 100 엔진 사이클 단위로 취득된 데이터를 앙상블 평균(Ensemble average)하여 진한 색으로 표시하였고, 개별 사이클 결과는 연하게 표시하였다.

Fig. 9

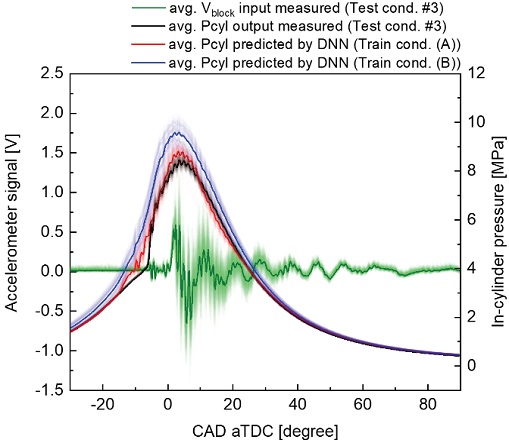
DNN model performance comparison for test condition #3 and measured engine block vibration and in-cylinder pressure

테스트 조건 3번에 대하여 DNN 모델(A)의 예측 결과의 R²는 0.986이었고, DNN 모델(B)의 예측 결과의 R²는 0.922였다. 이러한 결과를 반영하듯이 DNN 모델(A)의 결과가 실제로 측정한 목표 실린더 내부 압력에 더욱 근접한 결과를 보였다. DNN 모델(B)의 경우 연소가 시작되기 전의 모터링 압력부터 잘 예측하지 못하였고 전체적인 연소 압력 역시 목표 실린더 내부 압력 대비 과대 예측한 결과를 보였다. 또한 예측 결과의 변동성이 DNN 모델(A)보다 상승하는 것을 확인할 수 있었다. 이는 학습 조건(B)의 과급 조건들의 영향이 반영되었기 때문으로 판단된다.

앞서 가정한 학습 조건의 범위와 편중에 따른 DNN 모델 별 예측 정확도 차이 분석은 어느 정도 일리 있는 가정이라고 할 수 있지만 정확한 검증이 필요하다. 왜냐하면, DNN 모델은 학습 조건의 주요 변수인 연료 분사시기, SR, 흡기 압력의 의미를 알지 못하고 실제로 학습 입력 값과 출력 값의 신호 형태만을 가지고 학습하기 때문이다. 즉, 테스트 조건의 진동 신호를 이용하여 실린더 내부 압력을 예측할 때, DNN 모델은 테스트 조건의 진동 및 압력 신호와 비슷한 형태의 진동 및 압력 신호를 학습 조건에서 학습함으로써 테스트 조건의 결과를 잘 예측하게 된다고 볼 수 있다. 또는 완전히 비슷한 형태의 신호를 학습 조건에서 찾지 못하더라도, 주변 학습 조건 중에 유사한 형태의 신호들 중 크기가 다른 신호들을 학습한 인공 신경망의 조합을 통해 테스트 조건의 결과를 예측하게 되는 것으로 볼 수 있다. 따라서 학습 조건이 특정 변수에 대하여 편중되면 예측 결과가 편중된 신호 형태에 영향을 받아 전체적으로 이동(shift)되고 형태적으로 변형되는 것이다. 이를 확인하기 위해 모델에 관계없이 예측 정확도가 낮거나 높은 테스트 조건들을 선정하여 이와 관련 있을 것으로 판단되는 학습 조건들의 실린더 내부 압력 신호의 형태를 비교 분석하였다.

4.2 학습 조건 구성이 테스트 조건 예측 성능에 미치는 영향

Fig. 10, Fig. 11은 학습 조건과 테스트 조건 전체의 실린더 내부 압력 신호의 형태를 분석하여 첨도와 왜도로 표현한 것이다. 학습 조건과 테스트 조건 모두 100 엔진 사이클별로 데이터를 취득하였기 때문에 100 엔진 사이클 단위로 비슷한 결과들이 군집을 이루고 있는 것을 확인할 수 있다. 각 군집 내에서 형태의 변동성이 적은 조건은 연소 안정성이 높은 조건이며, 형태의 변동성이 큰 조건은 연소 안정성이 낮은 조건이다.

Fig. 10

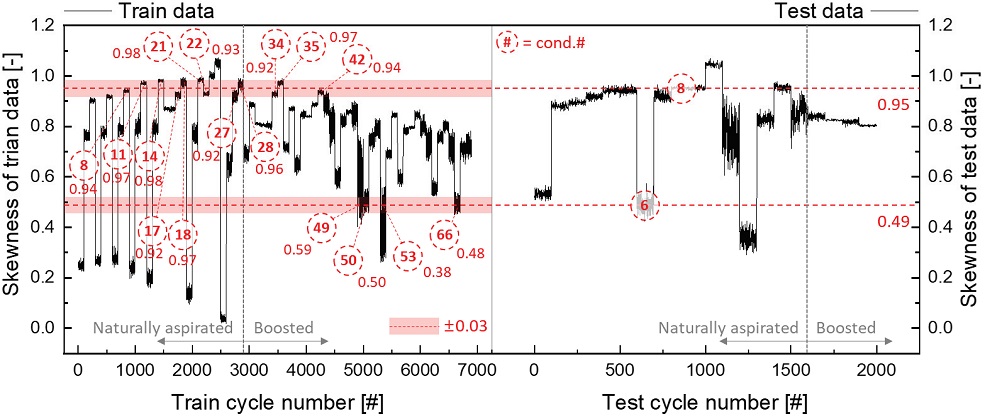
In-cylinder pressure shape comparison using similarity analysis of Skewness of (A) Train conditions and (B) Test conditions

Fig. 11

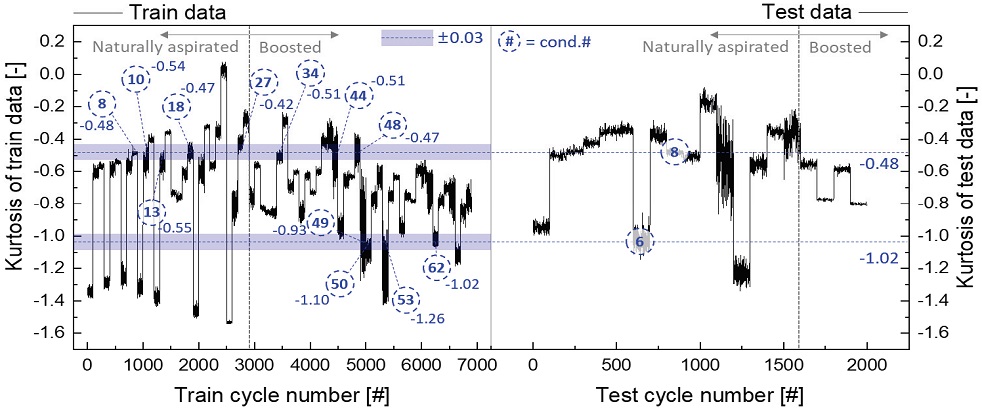
In-cylinder pressure shape comparison using similarity analysis of Kurtosis of (A) Train conditions and (B) Test conditions

연소 특성에 따라 각 운전 조건별로 첨도와 왜도가 큰 차이를 보이는데, 이는 착화 시작 시기, 착화지연 시간, 연료/공기 혼합기의 균질도 및 반응성, 착화 시 실린더 내부 온도와 압력에 영향에 의한 것이다. 물리적 의미에서 각 엔진 운전 조건의 연소 특성은 매우 다르기 때문에 정규 분포와 실린더 내부 압력의 형태적 차이를 비교한 첨도와 왜도 분석 수행 결과가 조건 별로 큰 차이를 보이는 것을 확인할 수 있다. 하지만 본 연구에서는 DNN 모델의 예측 정확도와 실린더 내부 압력의 형태적 상관성에 집중하기 위해, 물리적 해석보다는 형태적 해석에 집중하도록 한다.

테스트 조건들 중, 0, 6, 12번 조건의 첨도와 왜도가 다른 조건들과 확연한 차이를 나타내는데, 공교롭게도 이 조건들의 연소실 내부 압력 예측 정확도는 DNN 모델(A)와 (B)에서 모두 낮았다. 그 원인을 분석하기 위해, 대표적으로 6번 조건의 첨도와 왜도의 평균값을 계산한 후, 비슷한 학습 조건들을 Fig. 10, Fig. 11과 같이 검색하였다. 6번 조건의 첨도는 -1.02였고, 왜도는 0.49였다. 이 값들의 ±0.03 수준의 검색 범위(Searching window) 내에 조건 평균값이 들어오거나, 조건 평균은 이 범위 밖이지만 낮은 연소 안정성으로 인해 이 범위에 내에 결과가 포함된 학습 조건들을 검색하여 그 형태를 비교 분석하였다. 또한, 반대로 학습 조건에 관계없이 예측 결과가 R² 기준 0.98 이상이었던 테스트 조건 8번에 대해서도 동일한 분석법을 적용하여, 예측 성공률이 높았던 이유에 대해 분석하였다.

이 중 테스트 조건 6번과 첨도 또는 왜도가 비슷한 학습조건 49, 50, 53, 62, 66번의 실린더 내부 압력을 Fig. 12(a)를 통해 확인할 수 있다. 그리고 테스트 조건 8번과 첨도 또는 왜도가 비슷한 학습조건 8, 10, 11, 13, 14, 17, 18, 21, 22, 27, 28, 34, 35, 42, 44, 48번의 실린더 내부 압력을 Fig. 12(b)를 통해 확인할 수 있다.

Fig. 12

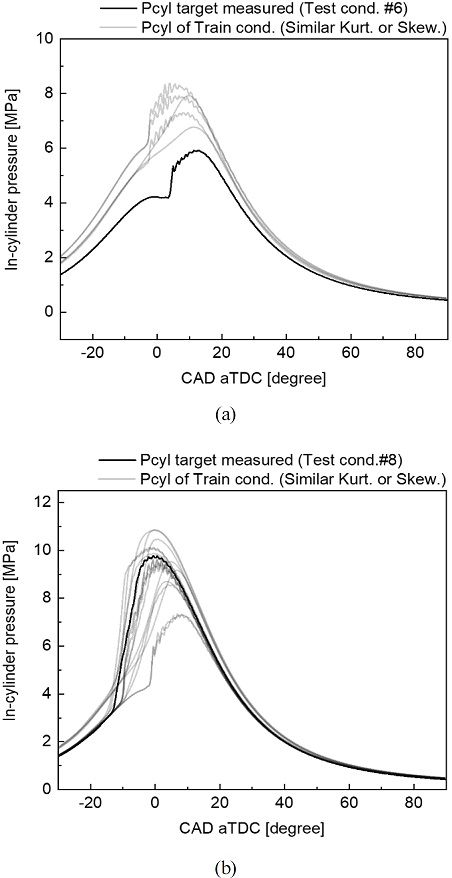
In-cylinder pressure shape comparison of (a) low R2 test condition #6 and (b) high R2 test condition #8 and train conditions which have similar shape, respectively

그 결과, 테스트 조건 6번의 예측 정확도가 낮은 이유를 확인할 수 있다. 이는 Fig. 12(a)와 같이 학습 조건의 실린더 내부 압력이 첨도와 왜도를 기준으로 형태적으로는 테스트 조건 6번과 비슷하지만, 엔진 운전 조건 차이로 인해 CAD를 기준으로 연소 압력의 위치가 다르고, 그 크기 역시 다르기 때문이다. 비슷한 형태의 학습 조건들 모두 흡기 압력이 테스트 조건 6번과 달리 과급 조건이었고, 연료 분사시기에서 차이로 인해 연소 압력 발생 시기가 다르거나 전혀 다른 연소 형태를 보이고 있었다. 따라서 결과적으로 학습 조건에서 비슷한 형태의 실린더 내부 압력이 없는 것이 테스트 조건 6번의 낮은 예측 정확도의 이유라고 할 수 있다.

반대로 학습 조건 8번의 경우, Fig. 12(b)와 같이 첨도와 왜도를 기준으로 비슷한 형태의 실린더 내부 압력을 보이는 학습 조건이 풍부하게 있었다. 그리고 학습 조건의 실린더 내부 압력들이 테스트 조건 8번의 실린더 내부 압력을 상하좌우로 감싸고 있었다. 즉, 학습 조건에서 완전히 동일한 형태의 실린더 내부 압력은 없으나, 비슷한 형태의 압력 선도들을 DNN 모델이 학습한 것이 테스트 조건 8번의 높은 예측 정확도의 이유라고 할 수 있다.

이러한 분석에 대해 더욱 명확한 근거를 얻기 위해, 실린더 내부 압력의 형태가 아닌 엔진 운전 변수를 기준으로 테스트 조건 6, 8번과 인접한 학습 조건들의 실린더 내부 압력 형태를 비교 분석하였다. Fig. 13은 학습 조건(A) 중, 테스트 조건 6번에 인접한 학습 조건들의 연소실 내부 압력과 DNN 모델(A)로 예측한 테스트 조건 6번의 실린더 내부 압력결과를 나타낸다. Fig. 13에서는 Fig. 12(a)에서와는 달리 흡기압력은 모두 동일하였지만, 이번에도 비슷한 형태의 학습 조건을 찾을 수 없었다. 이는 엔진 운전 변수를 기준으로 테스트 조건 6번과 인접한 학습 조건들이 테스트 조건 6번을 예측하는데 도움이 되지 못했다는 것을 의미한다.

Fig. 13

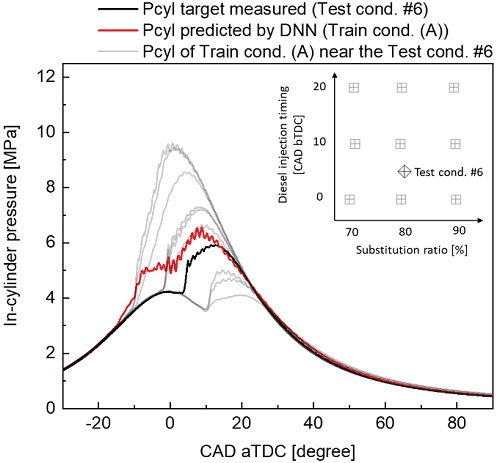
Shape comparison of measured and predicted in-cylinder pressure with Train condition (A) located near the measured condition, Test condition #6

마지막으로 Fig. 14는 학습 조건 (B) 중, 테스트 조건 6과 인접한 학습 조건의 실린더 내부 압력과 DNN 모델(B)로 예측한 테스트 조건 6번의 실린더 내부 압력 결과를 나타낸다. 학습 조건에 과급 조건이 추가됨에 따라 모터링 압력 예측 값에서 오차가 발생하는 것을 확인할 수 있었다. 그리고 과급 조건의 연소 압력은 자연 흡기 조건 대비 상승하는 것을 확인할 수 있는데, 이는 과급된 공기의 압축에 따른 내부 온도 증가 및 점화 지연 감소로 인한 연소상 진각 및 연소실 내부 압력 증가에 의한 것이다. 이로 인해, 학습 조건(B)의 평균적인 실린더 내부 압력의 형태는 학습 조건(A) 대비 테스트 조건 6번과 더 멀어졌다고 할 수 있다.

Fig. 14

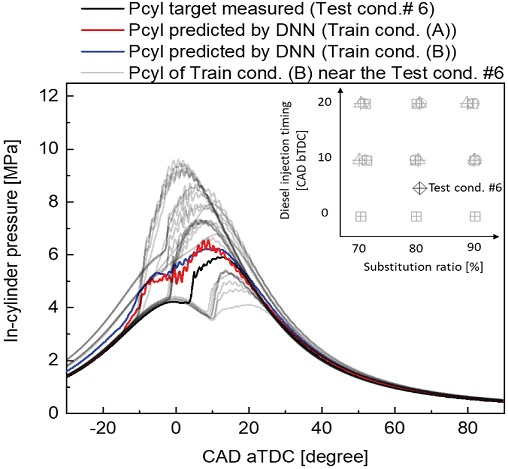
Shape comparison of measured and predicted in-cylinder pressure with Train condition (B) located near the measured condition, Test condition #6

DNN 모델(A)와 (B) 모두 실린더 내부 압력을 목표 결과보다 과대 예측하였는데, 이는 테스트 조건 6번과 인접한 학습 조건 (A)와 (B)의 학습 조건들의 평균적인 실린더 내부 압력이 테스트 조건 6번보다 높았기 때문으로 판단된다. 그리고 DNN 모델 (B)의 예측 결과가 DNN 모델 (A)보다 악화된 이유는 학습 조건(B)의 실린더 내부 압력이 평균적으로 더 높았기 때문으로 판단된다.

정리하자면, 연소실 내부 압력의 형태 분석과 테스트 조건과 인접한 학습 조건 분석을 통해 다음의 결론에 이를 수 있다. DNN 모델의 정확도 향상을 위해서는 엔진 운전 변수를 기준으로 테스트 조건과 인접한 학습 조건을 학습하는 것이 중요한 것이 아니라, 테스트 조건의 실린더 내부 압력과 비슷한 형태를 보이는 학습 조건들을 학습하는 것이 중요하다. 그러므로 학습 조건을 구성할 때, 실린더 내부 압력의 형태를 기준으로 학습 조건을 구성해야 한다.

동일한 분석 방법으로 테스트 조건 8번을 분석하면 다음과 같다. Fig. 15와 Fig. 16은 테스트 조건 8번의 학습 조건 (A), (B)에 따른 DNN 모델 예측 정확도를 나타낸다. Fig. 15의 경우 인접한 학습 조건(A)의 왜도가 테스트 조건 8번과 큰 차이를 보이지 않았으며, 첨도 역시 비슷한 조건이 많이 포함되었다. 즉, 이 경우는 테스트 조건 6번의 경우와 달리 테스트 조건과 인접한 학습 조건의 실린더 내부 압력의 형태가 테스트 조건의 실린더 내부 압력의 형태와 비슷한 것이다. 또한 학습 조건에 테스트 조건 8번 대비 점화 지연이 짧은 조건과 긴 조건이 동시에 포함되었고, 연소 압력 역시 테스트 조건 8번 대비 높은 조건과 낮은 조건이 고르게 분포되어 있었다.

Fig. 15

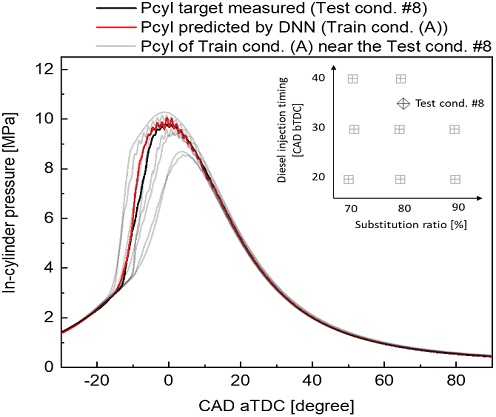
Shape comparison of measured and predicted in-cylinder pressure with Train condition (A) located near the measured condition, Test condition #8

Fig. 16

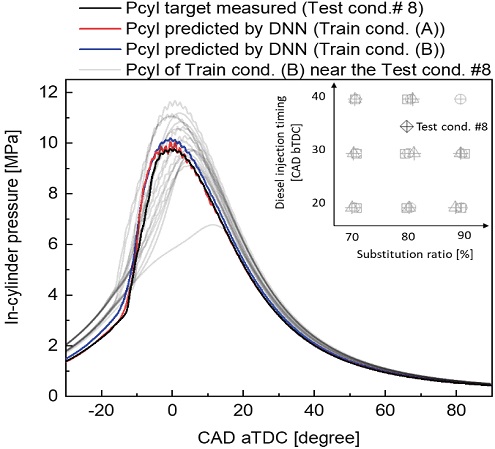
Shape comparison of measured and predicted in-cylinder pressure with Train condition (B) located near the measured condition, Test condition (a) #6, (b) #8

Fig. 16의 DNN 모델(B)의 경우, 학습 조건(B)의 과급 조건들로 인해 모터링 압력 예측이 영향을 받아 과대 예측되었고, 연소 압력 역시 DNN 모델(A)에 비해 과대 예측되었다. 이는 테스트 조건 6번에서와 같이 학습 조건에 높은 연소압력을 보이는 조건이 많이 포함되었기 때문으로 판단된다.

하지만 DNN 모델(B)의 성능이 0.98 이상으로 유지될 수 있었던 이유는, 학습 조건(B)의 과급 조건들에서도 실린더 내부 압력의 형태가 테스트 조건 8번과 유사하면서, 그 크기가 테스트 조건 8번에 비해 높은 조건과 낮은 조건이 동시 존재하여 일방적인 예측 결과 상승을 막았기 때문이다.

이러한 사실들을 통해 진동 신호를 이용하여 연소실 내부 압력을 재구성하는 회귀문제를 DNN으로 해결하고자 할 때, 기존의 엔진 실험 방법에 따라 학습 조건을 특정 운전 변수들의 단순 변화를 통해 구성해서는 안된다는 사실을 더욱 명확히 알 수 있다.

이상적으로는 매우 광범위한 범위에서 다양한 운전 변수를 매우 작은 단위(Step)로 변화시켜가며 실린더 내부 압력의 형태 변화를 체계적으로 기록하고 정리하여 목표로 하는 테스트 조건의 실린더 내부 압력과 비슷한 형태의 운전 조건들을 추출하여 학습하는 것이 예측 정확도를 높이는데 유리하다. 또는 실제 엔진 운전 조건들을 고려하여, 발생가능한 모든 운전 지점을 포괄할 수 있는 방대한 학습 조건을 구성하는 것이 바람직하다. 하지만 이것은 데이터베이스 구성에 시간적, 금전적 자원이 많이 소비된다는 단점이 있다.

따라서 향후 연구에서는 엔진 실 운전 조건에서 진동신호를 이용하여 실린더 내부 압력을 효율적으로 예측하기 위해 필요한 최적의 학습 조건 구성 방법에 대한 연구가 이어져야 할 것이다.

5. 결 론

본 연구에서는 건설기계용 6기통 대형 디젤 엔진을 개조한 단기통 CNG-디젤 이종연료 혼소 엔진에서 엔진 블록 진동 신호를 이용한 실린더 내부 압력 대체 측정 연구를 수행하였다. 엔진 블록 진동 신호는 가속도 센서(Accelerometer)를 이용하여 측정하였으며, 실린더 내부 압력 신호는 압력 센서를 이용하여 측정하였다. 엔진 블록 진동 신호에서 실린더 내부 압력 신호로의 신호 변환 함수로는 DNN(Deep Neural Network) 모델을 이용하였다.

특히 본 연구에서는 학습 조건의 구성에 따른 테스트 조건에 대한 DNN 모델의 예측 정확도 변화를 알아보는 것은 목표로 하였다. 주요 엔진 운전 변수는 연료 분사시기, CNG(Compressed Natural Gas)의 디젤(Diesel) 연료 대체 비율(Substitution Ratio, SR), 그리고 흡기 압력(Intake pressure)이었다. 흡기 압력이 대기압 조건으로만 구성된 학습 조건(A)로 학습한 DNN 모델(A)와 대기압 및 과급 압력으로 구성된 학습 조건(B)로 학습한 DNN 모델(B)로 동일한 테스트 조건에 대한 실린더 내부 압력 예측 정확도를 비교하였다. 이를 통해, 학습 조건이 DNN 모델을 이용한 실린더 내부 압력 예측 정확도에 미치는 영향을 비교 분석하였다. 본 연구의 주요 결과는 아래와 같다.

1) 테스트 조건의 엔진 운전 조건이 학습 조건의 범위를 벗어날 경우, DNN 모델의 예측 정확도가 낮아짐.
2) 테스트 조건의 엔진 운전 조건이 학습 조건의 범위 내에 있더라도 테스트 조건에 인접한 학습 조건이 부족한 경우, DNN 모델의 예측 정확도가 낮아짐.
3) 실린더 내부 압력 신호의 형태를 첨도와 왜도로 정량화 하여, 테스트 조건의 실린더 내부 압력 신호 형태와 비슷한 형태를 가진 학습 조건의 유무가 DNN 모델의 예측 정확도에 영향을 미침을 밝힘.
4) 테스트 조건의 실린더 내부 압력 신호와 비슷한 형상을 가지는 인접한 학습 조건들이 포괄적으로 테스트 조건 주변에 배치될 경우, DNN 모델의 예측 정확도가 향상됨을 밝힘.

Nomenclature


CAD :	crank angle degree
CNG :	compressed natural gas
CNN :	convolutional neural network
COV :	coefficient of variation
DNN :	deep neural network
DF :	dual fuel
IMEP :	indicated mean effective pressure
MPRR :	maximum pressure rise rate
MSE :	mean square error
NOx :	nitrogen oxide
PM :	particulate matter
RBFNN :	redial basis function neural network
RNN :	recurrent neural network
R² :	coefficient of determination
SR :	substitution ratio

Subscripts


DNN model(A) :	DNN model trained with Train condition(A)
DNN model(B) :	DNN model trained with Train condition(B)

Acknowledgments

본 연구는 한국조선해양(Korea shipbuilding & offshore engineering) 산학연구과제(개별 실린더 내부 압력 대체 측정 및 연소 분석 기술개발)의 금전적 기술적 지원에 의해 수행되었으며, 이에 감사드립니다.

References

H. Park, E. Shim, Y. Hwang and C. Bae, “Diesel Injection Strategy in a Premixed Charge Compression Ignition Engine under a Low Load,” Transactions of KSAE, Vol.26, No.3, pp.295-303, 2018. [https://doi.org/10.7467/KSAE.2018.26.3.295]
H. Park, E. Shim and C. Bae, “Improvement of Combustion and Emissions with Exhaust Gas Recirculation in a Natural Gas-diesel Dual-fuel Premixed Charge Compression Ignition Engine at Low Load Operations,” Fuel, Vol.235, pp.763-774, 2019. [https://doi.org/10.1016/j.fuel.2018.08.045]
E. Shim, H. Park and C. Bae, “Intake Air Strategy for low HC and CO Emissions in Dual-fuel(CNG-diesel) Premixed Charge Compression Ignition Engine,” Applied Energy, Vol.225, pp.1068-1077, 2018. [https://doi.org/10.1016/j.apenergy.2018.05.060]
C. Bennett, J. F. Dunne, S. Trimby and D. Richardson, “Engine Cylinder Pressure Reconstruction Using Crank Kinematics and Recurrently-trained Neural Networks,” Mechanical Systems and Signal Processing, Vol.85, pp.126-145, 2017. [https://doi.org/10.1016/j.ymssp.2016.07.015]
R. Amirante, C. Casavola, E. Distaso and P. Tamburrano, “Towards the Development of the In-Cylinder Pressure Measurement Based on the Strain Gauge Technique for Internal Combustion Engines,” SAE 2015-24-2419, 2015. [https://doi.org/10.4271/2015-24-2419]
M. S. Hossain, O. Z. Chao, Z. Ismail, S. Noroozi and S. Y. Khoo, “Artificial Neural Networks for Vibration Based Inverse Parametric Identifications: A Review,” Applied Soft Computing, Vol.52, pp.203-219, 2017. [https://doi.org/10.1016/j.asoc.2016.12.014]
A. Singh, S. Bharadwaj and S. Narayan, “Analysis of Various NVH Sources of a Combustion Engine,” Technical Bulletin, Vol.10, Nos.1-2, pp.29-37, 2016.
G. Chiatti, O. Chiavola, E. Recco, A. Magno, E. Mancaruso and B. M. Vaglieco, “Accelerometer Measurement for MFB Evaluation in Multi-cylinder Diesel Engine,” Energy, Vol.133, pp.843-850, 2017. [https://doi.org/10.1016/j.energy.2017.04.148]
S. Shih, S. Kuan, C. Keeney and R. Ledesma, “Heavy and Medium Duty Vehicle Powertrain Virtual Prototyping,” SAE 982824, 1998. [https://doi.org/10.4271/982824]
J. Zhu, “Investigation on Fault Diagnosis of Diesel Engines from Engine Surface Vibration,” 15th International Congress on Sound and Vibration, pp.2004-2011, 2008.
H. Choi, S. Lee, Y. Kim, I. Jung, J. Lee and K. Min, “An Experimental Research of separating Combustion-Induced Component from Cylinder Block Vibration Signal in HSDI Diesel Engine,” KSAE Spring Conference Proceedings, pp.18-21, 2013.
O. Chiavaola, G. Chiatti, L. Arnone and S. Manelli, “Combustion Characterization in Diesel Engine via Block Vibration Analysis,” SAE 2010-01-0168, 2010. [https://doi.org/10.4271/2010-01-0168]
R. Johnsson, “Cylinder Pressure Reconstruction Based on Complex Radial Basis Function Networks from Vibration and Speed Signals,” Mechanical Systems and Signal Processing, Vol.20, pp.1923-1940. 2006. [https://doi.org/10.1016/j.ymssp.2005.09.003]
K. Bizon, G. Continillo, E. Mancaruso and B. Vaglieco, “Reconstruction of In-cylinder Pressure in a Diesel Engine from Vibration Signal Using a RBF Neural Network Model,” SAE 2011-24-0161, 2011. [https://doi.org/10.4271/2011-24-0161]
L. Jia, J. Naber and J. Blough, “Accelerometer-Based Combustion Metrics Reconstruction with Radial Basis Function Neural Network for a 9L Diesel Engine,” Journal of Engineering for Gas Turbines and Power, Vol.136, No.3, 2014. [https://doi.org/10.1115/1.4025886]
M. Yoon, S. Park, M. Sunwoo and S. Lee, “A Study on the System Identification based on Neural Network for Modeling of S.I. Engines,” Transactions of KSAE, Vol.10, No.5, pp.29-34, 2002.
C. Wesche, S. Bernhardt, T. Schwarz and K. Schmid, “Cylinder-individual Exhaust Gas Emission of Natural Gas Engine Using Structure-borne Sound Signals,” 11th Dessau Gas Engine Conference, pp.290-303, 2019.

Component	Specification
Cylinder number	1
Displacement[cc]	982
Valve per cylinder	4
Bore x Stroke [mm]	100 x 125
Compression ratio	17.4 : 1
Fuel system	DI: Diesel, PFI: CNG
Boosting system	External boosting

Common parameter	Condition
*IMEP: Indicated mean effective pressure
Engine speed [rpm]	1200
Engine load [MPa ^*IMEP]	0.6
Coolant temperature [K]	353
Oil temperature [K]	353
Intake air temperature [K]	303

Control parameter	Condition
NA: naturally Aspirated, MPRR: maximum pressure rise rate *COV IMEP: coefficient of variation of IMEP
Train condition (A) intake air pressure [MPa]	0.1 (# of ^*NA cond. = 29)
Train condition (B) intake air pressure [MPa]	0.1, 0.12, 0.14 (# of NA + Boosting cond. = 6 9 )
Fuel injection timing [CAD]	0, 10, 20, 30, 40, 50, 60, 70 (until MPRR, ^**COV IMEP limit)
CNG substitution ratio [%]	0, 20, 40, 60, 70, 80, 90

Control parameter	Condition
Test condition intake air pressure [MPa]	0.1 (cond.# 00-15) 0.12 (cond.# 16-17) 0.14 (cond. # 18-19)
Fuel injection timing [CAD]	5, 15, 25, 35, 45, 55
CNG substitution ratio [%]	0, 20, 40, 60, 70, 80, 90