고용량 리튬이온 배터리의 주파수 응답특성을 반영한 임피던스 기반 온도 추정 연구
Copyright Ⓒ 2021 KSAE / 189-05
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Recently, research and development have been actively conducted in order to increase the mileage of electric vehicles(EVs). The performance change of lithium-ion battery, the main power source of EV, is related to battery life. This is directly related to EV mileage. One of the factors affecting the change in battery performance is temperature, and to effectively manage the battery temperature, it is necessary to be able to estimate the temperature. A heating factor is needed to estimate the battery temperature. Since the heating factor extracted through the electrical characteristic experiment that has been studied so far does not reflect the electrochemical change inside the battery, it is impossible to estimate the temperature with high accuracy. Therefore, in this paper, for high-accuracy temperature estimation, we extracted the heating factor reflecting the internal frequency response characteristic of the battery, and used it to derive the heat generation rate in the electrical-thermal analysis.
Keywords:
Electric vehicle, Heating factor, Temperature, Frequency response characteristic, Heat generation rate키워드:
전기자동차, 발열인자, 온도, 주파수 응답특성, 발열량1. 서 론
현재 화석 연료사용으로 인한 지구 온난화로 인해 신재생 에너지에 속하는 리튬이온 배터리가 주목받고 있다. 리튬이온 배터리는 높은 에너지 밀도와 출력을 특징으로 하며 가벼운 특성이 있어 여러 산업에서 사용되고 있다. 또한, 소형기기뿐만 아니라 리튬이온 배터리를 모듈 또는 팩 단위로 확장하여 EV와 같은 대형기기에도 많이 적용되고 있다.1)
EV에 적용되는 리튬이온 배터리의 경우 현재 주행거리 범위를 넓히려는 연구들이 활발하게 진행되고 있으며 그에 따라 리튬이온 배터리에 양극 활물질 소재로 NMC 혹은 NCA 등의 사용이 증가하고 있다.2-4) 하지만, 이 중에서도 니켈 함량이 높은 고용량 리튬이온 배터리는 안정성의 문제가 많고 고출력 리튬이온 배터리 대비 높은 저항 특성을 가지므로 온도상승이 쉽게 된다는 단점이 있다.5)
리튬이온 배터리는 사용 시 내부 화학 반응으로 인해 전기에너지를 생성하는데 이 과정에서 리튬 이온이동으로 인한 저항이 생기고 자체적인 발열이 발생한다. 리튬이온 배터리의 지속적인 발열은 내부 온도상승을 일으키고 전극을 보호하는 필름을 분해한다. 이에 따라 잔존 하는 리튬이온은 분해된 필름을 재구성하고 이 과정에서 배터리의 수명과 연관된 용량을 감소시키며 배터리 성능이 저하한다. 또한, 지속적인 온도상승은 과열로 이어지며 이는 기계적 결함을 발생시키고 전극 붕괴 혹은 분리막 손상으로 인한 단락을 발생시켜 열 폭주 현상, 배터리 고장 등을 불러일으킨다.6-8) 따라서 리튬이온 배터리를 효율적으로 사용할 수 있도록 온도관리가 이루어져야 하며 배터리 열관리 시스템을 효율적으로 운용하기 위해 배터리 SOC 상태에 따른 온도를 추정할 수 있어야 한다.
리튬이온 배터리의 온도 추정을 위해 현재 전기화학적-열 해석, 전기적-열 해석 등 다양한 방법으로 열 해석 연구가 진행되고 있다. 전기화학적-열 해석 방법을 이용하여 배터리 열 해석을 진행할 시 리튬이온 배터리의 내부 화학 반응에 대한 메커니즘을 상세하게 다루기 때문에 온도 추정 정확도가 높다는 장점이 있다. 하지만, 고려해야 할 내부 화학적 변수들이 많으므로 계산에 대한 복잡성이 높아진다. 따라서 높은 사양의 하드웨어가 요구되고 그에 따른 비용이 발생하게 된다. 반면에 전기적-열 해석 방법을 통해 열 해석을 진행할 경우 낮은 연산 양으로도 온도 추정이 가능하다. 하지만, 전기적-열 해석은 리튬이온 배터리 내부의 화학 반응에 대한 메커니즘을 전기적인 소자로 모사하여 열 해석 하는 방법이므로 온도 추정을 진행할 경우 추정값이 다소 정확하지 못하는 경우를 초래할 수 있다.9-11)
하지만, 배터리의 단위를 모듈 혹은 팩으로 확장할 시 배터리 온도 추정을 하기 위한 연산 양이 열 전도도를 고려한 Qcond와 배터리 셀 위치로 생기는 대류의 가변성으로 인해 복잡해진다. 이를 해결하기 위해 통상적으로는 전기적-열 해석 방법을 사용하여 배터리 셀 단위에서부터 낮은 연산 양의 온도 추정을 수행하는 단계적 개발을 진행한다.12)
발열량을 도출하기 위해서는 발열인자를 추출해야 하는데 배터리가 발열하는 원인으로는 내부저항이 가장 크다고 말할 수 있다. 따라서 배터리 발열량의 발열인자는 곧 배터리의 내부저항이라고 말할 수 있다. 전기적-열 해석에 사용되는 발열량을 도출하기 위해서는 배터리의 전기적 특성실험인 OCV 실험을 통해 SOC 100~0 % 중 5 % 구간마다 발열인자를 추출하고 이를 발열량 수식에 적용하여 온도 추정을 수행한다. 하지만, 본 논문에서는 전기적-열 해석에 사용되는 발열인자를 다른 방법을 통해 추출하고 온도 추정을 수행한다. 이는 배터리에 SOC 100~0 % 중 5 % 구간마다 정현파 형태의 전류를 인가하고 해당 주파수에 따른 발열인자를 추출하여 온도 추정 과정을 수행하는 방법이다. 배터리에 정현파의 전류를 인가하게 되면 내부 화학적인 특성을 반영한 발열인자를 추출할 수 있다.13-15) 이는 배터리 내부의 화학적 특성을 반영하지 못한 기존의 전기적-열 해석의 낮은 정확도에 대한 문제점을 해결한다. 또한, 배터리 온도 추정을 위해 열 해석 상용프로그램인 COMSOL을 사용하여 시뮬레이션을 진행하고 시뮬레이션 추정값을 검증하기 위해 실험 측정값과 비교 분석한다. 이를 통해 배터리 모듈 혹은 팩으로 단위를 확장했을 경우 전기적-열 해석의 장점인 낮은 연산 양과 주파수에 따른 배터리 응답특성을 반영한 발열인자 추출을 통해 낮은 연산 양으로 정확도 높은 온도 추정을 할 수 있는 배터리팩 열 해석 모델의 확장 가능성을 확보할 수 있다.
2. 주파수에 따른 배터리 응답특성
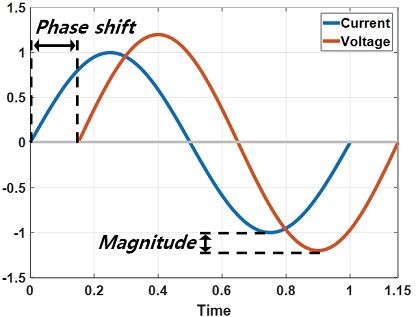
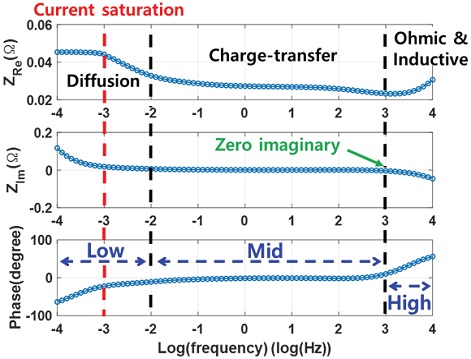
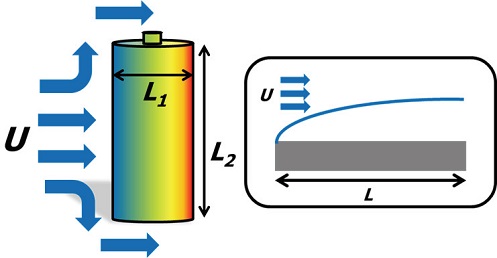
리튬이온 배터리의 대표적인 내부 화학적 반응으로는 전해질 내 이온의 이동, SEI층 형성, 전하전달 현상, 전극 내부와 전극 표면의 농도 차에 의한 이온 확산 등이 있다. 이러한 내부 화학적 반응들은 서로 다른 시정 수를 가지므로 Fig. 1과 같은 정현파 형태의 전류를 배터리에 인가할 경우 Fig. 2와 같이 인가된 주파수 영역에 따라 각각 다른 화학 반응들이 일어난다. 본 논문에서는 주파수 영역을 관측 가능한 내부 화학적 현상에 따라 고주파수, 중주파수, 저주파수로 분류한다. 고주파수 영역은 10 kHz~1 kHz로 구분되며 주로 전자의 이동과 관련된 임피던스 영역이다. 또한, 리튬이온의 이동이 불가능한 주파수 영역이며 ZIm가 0이 되는 부분에서는 전해질 저항 Re을 포함한다. 중주파수 영역인 1 kHz~1 Hz에서는 전극 계면에 리튬이온이 도달하여 삽입하고 탈리될 때 발생하는 저항 Rct를 분석할 수 있다. 저주파수 영역인 0.1 Hz~0.01 Hz에서는 주로 전극 내부와 외부의 농도 차로 인한 확산 저항 Rd를 분석할 수 있다. 또한, 주파수 영역이 0.01 Hz보다 더 낮은 저주파 영역으로 도달할 시 전류의 파형이 수렴하는 구간으로 더 이상의 정현파 형태의 실험 분석이라고 할 수 없는 구간이 되고 Fig. 2와 같이 ZRe의 임피던스값은 수렴한다.
3. 배터리 열 해석을 위한 발열량 도출
배터리 온도를 추정하기 위해서는 발열체로부터 발생하는 발열량을 도출해야 한다. 따라서 본 논문 3장에서는 열 해석에 필요한 발열량 도출방법을 소개한다. 기존에 배터리 전기적-열 해석을 진행할 시 도출하는 배터리 자체의 발열량 QCell은 식 (1)을 통해 도출할 수 있다.
| (1) |
- where QIrrev : irreversible heat generation rate (W/m3)
- Qrev : reversible heat generation rate (W/m3)
식 (1)에서의 QIrrev값은 리튬이온 배터리에 전류가 인가되고 충전과 방전이 진행될 때 발생하는 발열량으로 리튬이온들이 이동하는 과정에서 내부 전해질과 일어나는 저항으로 인해 발생하는 열을 포함한다고 말할 수 있다. 이는 인가되는 C-rate 크기에 따라 값이 크게 변동되며 식 (2)와 같이 도출할 수 있다.
| (2) |
QRev값은 가역적 발열량으로써 배터리 충전 시에는 흡열반응을 나타내고 방전 시에는 발열반응을 보이는 배터리 내부 화학적 에너지 변화로 인한 발열이다. 이는 통상 SOC 구간별 ETN 실험을 수행하여 엔트로피 계수 즉, ∆T당 ∆U인 값으로 계산하여 Table을 설계한다. 하지만, QCell에서의 QRev값은 초기 상태의 배터리일 경우와 배터리에 인가되는 C-rate가 0.7 C 이상으로 높아질 경우 영향력이 미소해지고 QIrrev을 지배적으로 사용하여 QCell값을 도출해낸다.16)
| (3) |
- where ΔU : open circuit voltage deviation (V)
전체적인 발열량 QTotal을 계산하기 위해서는 발열체인 배터리 자체의 발열량 계산뿐만 아니라 발열체 주변 환경의 조건으로 인한 열 소산량까지 고려되어야 한다. 배터리가 작동하는 환경이 진공상태가 아닐 경우 공기로 인해 대류 현상이 생기게 되는데 이로 인해 배터리표면에는 열 소산 현상이 일어난다. 이러한 대류 조건은 배터리를 냉각시키는 역할을 하고 배터리의 온도는 진공상태에서의 배터리 자체 온도보다 현저히 감소한다. 따라서 발열량 값을 도출할 때는 열 소산에 영향을 미치는 대류 조건을 고려해준다.
대류 조건으로 인한 열 소산은 식 (4)와 같이 뉴턴-냉각법칙을 사용하여 도출하고 총 발열량 QTotal을 식 (5)와 같이 도출한다.17)
| (4) |
| (5) |
- where QDiss : heat dissipation rate (W/m3)
- h : heat transfer coefficient (W/m2K)
- A : area (m2)
- Tamb : ambient temperature (K)
4. 실험방법에 따른 발열인자 추출
4.1 OCV 실험을 통한 발열인자 추출
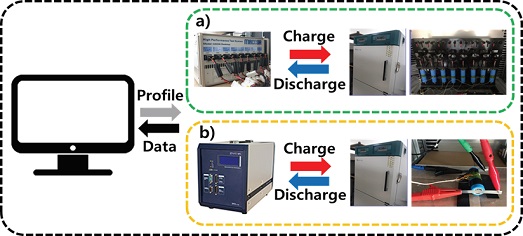
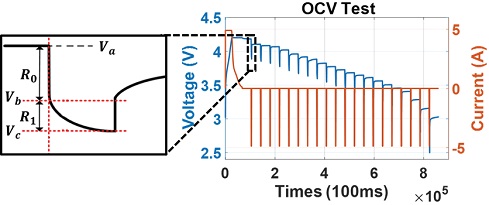
전기적 특성실험 중 배터리 충전 방전을 위해 MACCOR의 4300K 모델을 사용한다. 실험에 이용할 샘플은 Table 1과 같은 사양을 가지는 21700 50E 고용량 배터리를 이용하고, 항온 챔버 내부에서 실험을 진행한다. 챔버 내 온도는 상온인 25 oC에 맞추어 실험을 진행한다. 또한, 배터리 온도를 측정하기 위해 온도 센서를 배터리에 부착하여 동시 측정하고 이를 바탕으로 시뮬레이션으로 추정한 SOC 구간별 배터리의 온도 값과 비교 분석한다. OCV 실험은 Fig. 3(a)와 같이 진행한다.
본 장에서는 SOC 100~0 % 중 5 % 구간마다 발열량을 도출하기 위한 발열인자를 Fig. 4와 같은 방전 구간에서 전압 편차를 통해 식 (6)과 (7) 같이 추출하고 QIrrev에서의 R의 값으로 두 식에 대한 합을 적용한다.
| (6) |
| (7) |
4.2 주파수 응답특성을 반영한 발열인자 추출
본 논문에서 제안하는 배터리 주파수 응답특성을 반영한 열 해석을 수행하기 위해 Fig. 3(b)와 같이 WONATECH의 ZIVE SP5(5A용) 모델을 사용하여 실험을 진행한다. Fig. 2와 같이 고주파수에서 저주파수까지 영역별로 관측 가능한 배터리 내부 전기화학적 현상이 다르다. 그에 따라 임피던스값이 다르게 측정된다. 주파수 영역별로 도출하는 임피던스는 Fig. 2와 같이 영역을 3가지로 분류하였을 때 고주파수, 중주파수, 저주파수에 대한 함수식으로 정의할 수 있는데 고주파수와 중주파수에서의 함수식으로는 각각 식 (8)과 (9)와 같이 계산할 수 있다. 중주파수의 경우 양극과 음극에 대한 화학적 성분과 치수에 대한 차이 등 이온전도도에 영향을 미치는 요소들이 존재하는 영역이므로 2차 RC Ladder로 나뉘어 계산된다.
| (8) |
| (9) |
- where L : inductance (H)
- ω : angular frequency (rad/s)
저주파수에서는 식 (10)을 통해 해당 주파수 영역의 임피던스 값을 도출한다. S는 확산계수와 관련된 함수로써 식 (11)과 같이 나타내며 리튬이온이 전극에 도달한 후 농도 차로 발생하는 확산 현상을 고려하여 계산할 수 있다. 또한, 저주파수 영역에서 정현파 형태로 인가되는 전류가 수렴하게 되는 영역까지 도달하게 되면 임피던스값은 해당 주파수 영역에서의 ZRe축 임피던스값에 수렴하는 것을 고려한다. 따라서 식 (10)과 같이 저주파수 영역에서 임피던스를 도출하게 되면 고주파수와 중주파수 영역의 저항 성분이 포함되어 도출되는데 이를 통해 본 논문에서는 SOC 100~0 % 중 5 % 구간마다 저주파수에 해당하는 0.01 Hz의 정현파 전류를 배터리에 인가하고 SOC 별 ZRe축 임피던스값을 배터리 열 해석에 필요한 발열인자로 사용한다.18)
| (10) |
| (11) |
- where S : diffusion coefficient related function
- β : variation in electrode voltage concentration
- DDif : diffusion coefficient
- n : number of reaction electrons
- F : faraday constant
5. 배터리 온도 추정 시뮬레이션 및 결과 분석
5.1 열 해석 시뮬레이션 경계 조건 설정
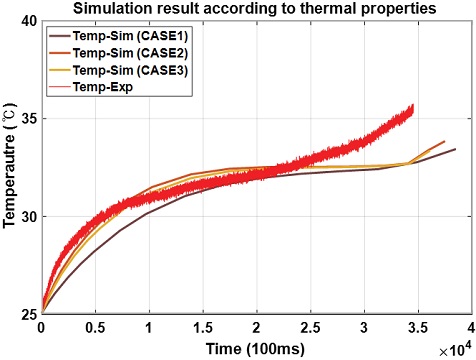
본 논문에서는 열 해석 상용프로그램 COMSOL을 이용하여 발열량을 도출하고 온도 추정 시뮬레이션을 진행한다. 배터리 열 유동 해석을 하기 위해서는 열 속성정보인 배터리 밀도와 열전도도 및 열용량 등이 필요하다. 이러한 열 속성정보는 과거부터 지금까지 다양하게 연구되었으며 본 논문에서는 배터리에 대한 다양한 열 속성정보를 통해 시뮬레이션으로 유추하고 정확도가 높은 CASE의 열 속성정보를 이용하여 배터리 C-rate 별 온도변화를 추정한다. 열 속성정보는 Table 2와 같은 3가지 CASE로 정리하고 이를 이용해 도출한 온도 추정값과 측정값을 비교하여 배터리 내부 열 속성정보를 유추해낸다.19-21) 각 CASE별 열 속성정보는 1C-rate에서의 온도 측정값과 비교분석하고 Fig. 5와 같은 결과를 통해 온도 측정값과 가장 유사한 CASE 2의 열 속성정보를 본 논문에서 사용한 배터리의 열 속성정보로 적용한다. 더불어, 배터리에 대한 SOC 별 온도 추정 시뮬레이션을 위해서 진행한 실험환경에 대해 경계 조건을 적용해야 한다. 실험은 챔버 내부에서 진행하므로 챔버 내부의 환경 조건을 고려한다. 챔버 내부에는 온도 조절을 위한 냉각 팬이 동작하는데 이는 챔버 내부에 공기 흐름을 만들고 배터리에 Fig. 6과 같은 강제대류 조건을 형성한다. 이로 인해 배터리 자체에서 방출되는 발열량은 챔버 내부 강제대류로 인해 일부 소산 되고 이를 열 해석 시뮬레이션에 적용하여 진행한다.
식 (4)에서의 대류 계수는 Nusselt 수를 통해 추출할 수 있는데 이는 물체 표면에서의 대류 열전달과 전도열전달의 비율을 나타낸다. 또한, Nusselt 수가 크면 클수록 물체의 표면에서 대류의 효과가 그만큼 큰 것을 의미한다.
| (12) |
| (13) |
- where Nu : nusselt number
- k : air thermal conductivity (W/mK)
- DDia : diameter of battery (m)
- CRey : correlation variables for Re calculation
- Re : reynolds number
- r : correlation variables for Re calculation
- Pr : prandtl number
대류 계수를 도출하는 과정 중에 필요한 Nusselt 수는 Prandtl 수와 Reynolds 수를 통해 도출하는데 이는 식 (14)와 식 (15)와 같이 계산된다. 또한, 이러한 수들은 Table 3과 같이 유체의 고유특성값을 통해 도출한다. Reynolds 수 같은 경우 층류와 난류에 대한 기준을 정하는 수로 식 (15)를 통해 값을 도출한 후 Table 4를 참고하여 Nusselt 수를 도출하는 함수식의 CRey와 r을 선정한다.22) 배터리에 적용되는 열 소산 값의 매 개체로는 공기로 인한 발열량 소산을 말할 수 있다. 챔버의 사양마다 바람의 세기는 다르다. 따라서 본 실험에서의 Ud에 대한 값은 사람이 거시적으로 바람을 느낄 수 있는 정도의 풍속인 2(m/s)로 설정하여 시뮬레이션을 진행한다.23)
| (14) |
| (15) |
- where v : kinematic viscosity (m2/s)
- a : air thermal diffusivity (m2/s)
- Ud : velocity(strong wind) (m/s)
5.2 시뮬레이션 결과 비교
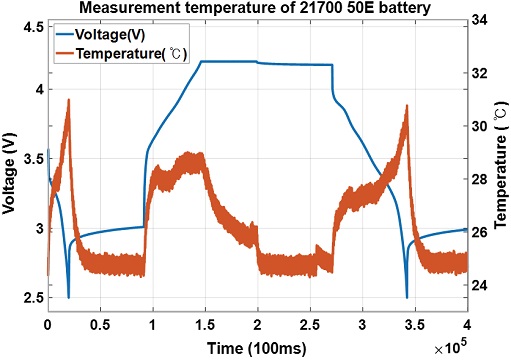
열 해석 상용프로그램인 COMSOL을 이용하여 온도 시뮬레이션을 진행할 시 연산 양을 최소한으로 줄이기 위해 충전, 방전 구간 중 한 구간에서의 온도 추정을 진행한다. 배터리 열 해석을 위한 온도 추정 구간 선정을 위해 충전 방전 실험을 진행한다. 그 결과, Fig. 7과 같이 충전 구간보다 방전 구간에서 온도가 높게 측정되는 것을 확인할 수 있었고 시뮬레이션 또한 방전 구간에서의 온도 추정만을 진행한다.
OCV 실험과 주파수 응답특성 실험을 통해 각 SOC 100~0 % 중 5 % 구간마다 추출한 발열인자는 Fig. 8과 같이 확인할 수 있었고 OCV 실험을 통해 추출하는 발열인자는 커패시터의 영향을 고려하지 않은 저항의 합으로만 계산되는 것을 알 수 있다. 반면에, 주파수 응답특성 실험의 경우 정현파의 전류를 인가하는 방법이므로 내부 임피던스 즉, 저항과 관련 있는 발열인자가 용량과 주파수에 반비례하여 결정되기 때문에 전체적인 발열인자 수치가 OCV 실험에 대한 발열인자보다 낮은 것을 알 수 있다.
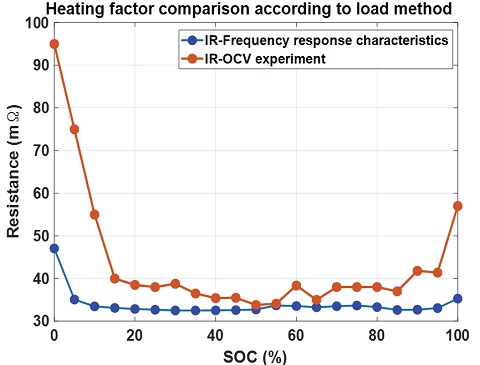
Comparison of heating factor by SOC according to current load method (Red: Internal resistance according to SOC derived through OCV experiment, Blue: Internal resistance according to SOC derived through frequency response characteristics)
본 논문에서는 열 해석 시뮬레이션의 경향성을 정확히 판단하기 위해 같은 환경 조건에서 0.5 C, 1 C, 2 C인 세 가지의 C-rate로 시뮬레이션을 진행하고 이를 통해 추정한 온도 값의 정확도를 판단하기 위해 21700 50E 고용량 배터리 방전 실험에서의 온도측정결과 값과 비교 분석한다.
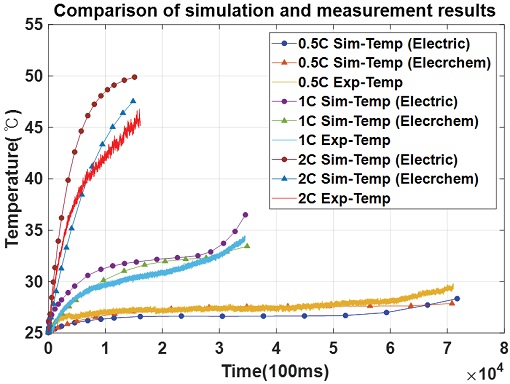
3D 모델링 된 21700 50E 고용량 배터리의 방전 구간 열 해석 시뮬레이션 결과는 Fig. 9와 같이 확인할 수 있다. 또한, Fig. 10과 같이 배터리 방전 구간에서의 온도측정 값과 OCV 실험 및 주파수 응답특성실험을 통해 추출된 발열인자 기반으로 시뮬레이션한 온도 추정값을 비교하는 그래프를 도출한다. 이 결과 최대 온도 편차는 각각 6 oC와 3 oC 이내로 주파수 특성실험을 통해 추출한 발열인자를 이용하여 시뮬레이션한 온도 추정값이 측정값과 더욱 유사한 것을 확인할 수 있다. 더불어, 0.5 C 구간에서 OCV 실험기반으로 추출한 발열인자를 통해 도출한 온도 추정값은 본 논문 3장에서 설명한 바와 같이 낮은 구간의 C-rate에서 발생하는 가역적 발열량의 영향을 제외하고 비가역적 발열량을 지배적으로 계산하여 QTotal을 도출했기 때문에 온도 수치가 전체적으로 낮게 추정된 것을 확인할 수 있다.
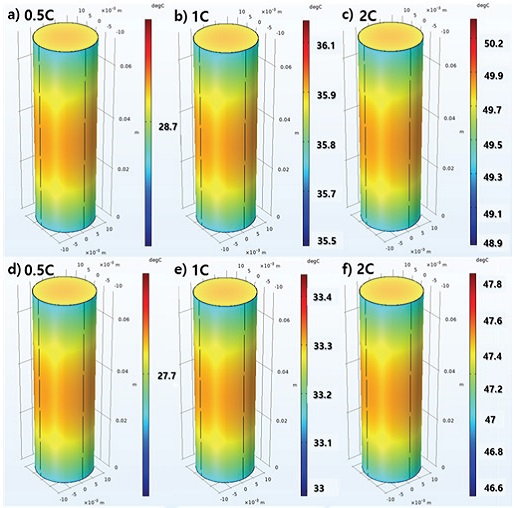
3D simulation results for each C-rate according to the heating factor extraction method (a~c: OCV experiment, d~f: Frequency response characteristics)
6. 결 론
EV에 적용되는 고용량 리튬이온 배터리의 성능변화 요인이 될 수 있는 환경 조건으로 온도변화를 말할 수 있으며 배터리의 효과적인 열관리를 위해서는 온도를 열관리의 지표로써 사용하여야 한다. 더불어, 온도 추정을 위해서는 발열량을 도출할 수 있어야 하는데 본 논문에서는 발열량 도출에 필요한 발열인자를 추출하는 방법으로 기존에 온도 추정을 위해 수행해왔던 OCV 실험을 통해 발열인자를 추출하는 방법과는 다른 방법을 적용한다. 두 가지 방법을 이용하여 추출한 발열인자 기반으로 발열량을 도출한 결과는 달랐으며 주파수 응답특성실험을 통해 추출한 발열인자를 통해 배터리 온도 추정을 진행한 시뮬레이션 결과가 최대 온도 편차 3 oC로 더 작은 것을 확인할 수 있었고 그에 따라 이번 연구내용에 관한 기여 내용은 다음과 같다.
- 1) 이러한 온도 추정 연구를 통해 Wireless 온도관측에 대한 가능성을 확보할 수 있다.
- 2) 배터리 내부의 화학적인 현상을 통해 관측할 수 있는 임피던스 정보를 추출한다. 이를 기반으로 온도 센서로 측정되는 배터리 표면 온도가 아닌 배터리 내부에 대한 온도 추정값을 통해 효율적인 냉각 시스템 동작이 가능할 수 있도록 열관리 지표로써 사용할 수 있다.
- 3) 배터리 셀 단계에서 배터리의 내부 화학적인 함수식을 이용하지 않더라도 정확도 높은 온도 추정을 수행할 수 있으므로 단위를 확장하여 팩 혹은 모듈 단위에서 또한, 정확성은 높고 연산 양이 낮은 온도 추정 모델을 개발할 수 있다는 신뢰성을 확보할 수 있다.
EV의 주행거리 범위를 넓히는 방법으로는 리튬이온 배터리의 특성변화를 최소화시켜 수명을 늘리거나 안전성을 최적화시키는 것에 있다. 따라서 본 연구에서 제안하는 온도 추정방법은 배터리의 특성변화에 영향을 미치는 열을 효율적으로 관리하고 배터리 활성화 환경을 최적으로 만들어주는 것에 대한 기초 연구에 기여한다.
Nomenclature
| NMC : | nickel manganese cobalt oxide |
| NCA : | nickel cobalt aluminum oxide |
| Q : | heat generation rate, W/m3 |
| OCV : | over circuit voltage, V |
| SOC : | state of charge |
| SEI : | solid electrolyte interphase |
| R : | resistance, Ω |
| Z : | impedance, Ω |
| C-rate : | current rate, C |
| ETN : | electrochemical thermodynamics measurement |
| C : | capacitance, F |
| ρ : | battery density, kg/m3 |
| k : | thermal conductivity, W/mK |
| C : | thermal capacity, J/kgK |
Subscripts
| cond : | conductivity |
| s, e, ct, d : | series, electrolyte, charge transfer, diffusion |
| Im : | imaginary |
| Re : | real |
| p, n : | positive, negative |
| th : | thermal |
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 산업기술평가관리원(KEIT) 연구과제(No. 20011626) 및 한국전력공사의 2019년 선정 기초연구개발 과제 연구비(R19XO01-45)의 지원을 받았습니다.
References
-
L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, “A Review on the Key Issues for Lithium-ion Battery Management in Electric Vehicles,” Journal of Power Sources, Vol.226, pp.272-288, 2013.
[https://doi.org/10.1016/j.jpowsour.2012.10.060]

- C. E. Park, S. W. Yoo, Y. H. Jeong and K. Kim, “Effect of Thermal Management of Lithium-Ion Battery on Driving Range of Electric Vehicle,” Journal of the Korea Academia-Industrial cooperation Society, Vol.18, No.5, pp.22-28, 2017.
-
U. H. Kim, J. H. Kim, J. Y. Hwang, H. H. Ryu, C. S. Yoon and Y. K. Sun, “Compositionally and Structurally Redesigned High-energy Ni-rich Layered Cathode for Next-generation Lithium Batteries,” Materials Today, Vol.23, pp.26-36, 2019.
[https://doi.org/10.1016/j.mattod.2018.12.004]

-
C. S. Yoon, K. J. Park, U. H. Kim, K. H. Kang, H. H. Ryu and Y. K. Sun, “High-energy Ni-rich Li[NixCoyMn1-x-y]O2 Cathodes via Compositional Partitioning for Next-generation Electric Vehicles,” Chemistry of Materials, Vol.29, No.24, pp.10436-10445, 2017.
[https://doi.org/10.1021/acs.chemmater.7b04047]

-
W. Yan, S. Yang, Y. Huang, Y. Yang and G. Yuan, “A Review on Doping/Coating of Nickel-rich Cathode Materials for Lithium-ion Batteries,” Journal of Alloys and Compounds, Vol.819, Paper No. 153048, 2020.
[https://doi.org/10.1016/j.jallcom.2019.153048]

-
Q. Wang, P. Ping, X. Zhao, G. Chu, J. Sun and C. Chen, “Thermal Runaway Caused Fire and Explosion of Lithium Ion Battery,” Journal of Power Sources, Vol.208, pp.210-224, 2012.
[https://doi.org/10.1016/j.jpowsour.2012.02.038]

-
B. J. Lee, G. J. Choi, S. H. Lee, Y. M. Jeong, Y. Park and D. U. Cho, “A Study on Explosion and Fire Risk of Lithium-Ion and Lithium-Polymer Battery,” The Journal of Korean Institute of Communications and Information Sciences, Vol.42, No.4, pp.855-863, 2017.
[https://doi.org/10.7840/kics.2017.42.4.855]

-
L. Yiding, W. Wenwei, L. Cheng, Y. Xiaoguang and Z. Fenghao, “A Safety Performance Estimation Model of Lithium-ion Batteries for Electric Vehicles under Dynamic Compression,” Energy, Vol.215, Paper No.119050, 2021.
[https://doi.org/10.1016/j.energy.2020.119050]

-
X. F. Lin, H. E. Perez, S. Mohan, J. B. Siegel, A. G. Stefanopoulou, Y. Ding and M. P. Castanier, “A Lumped-parameter Electro-thermal Model for Cylindrical Batteries,” Journal of Power Sources, Vol.257, pp.1-11, 2014.
[https://doi.org/10.1016/j.jpowsour.2014.01.097]

-
Y. Ma, Y. Cui, H. Mou, J. Gao and H. Chen, “Core Temperature Estimation of Lithium Ion Battery for EVs Using Kalman Filter,” Applied Thermal Engineering, Vol.168, Paper No.114816, 2020.
[https://doi.org/10.1016/j.applthermaleng.2019.114816]

-
W. B. Gu and C. Y. Wang, “Thermal-Electrochemical Modeling of Battery System,” Journal of The Electrochemical Society, Vol.147, No.8, pp.2910-2922, 2000.
[https://doi.org/10.1149/1.1393625]

-
T. W. Kang, S. Park, P. Y. Lee, I. H. Cho, K. Yoo and J. Kim, “Thermal Analysis of a Parallel-Configured Battery Pack(1S18P) Using 21700 Cells for a Battery-Powered Train,” Electronics, Vol.9, No.3, Paper No.447, 2020.
[https://doi.org/10.3390/electronics9030447]

-
M. Itagaki, N. Kobari, S. Yotsuda, K. Watanabe, S. Kinoshita and M. Ue, “In situ Electrochemical Impedance Spectroscopy to Investigate Negative Electrode of Lithium-ion Rechargeable Batteries,” Journal of Power Sources, Vol.135, Nos.1-2, pp.255-261, 2004.
[https://doi.org/10.1016/j.jpowsour.2004.04.004]

-
L. Ran, W. Junfeng, W. Haiying and L. Gechen, “Prediction of State Charge of Lithium-ion Rechargeable Battery with Electrochemical Impedance Spectroscopy Theory,” IEEE Conference on Industrial Electronics and Applications, pp.684-688, 2010.
[https://doi.org/10.1109/ICIEA.2010.5516984]

-
A. Guha, A. Patra and K. V. Vaisakh, “Remaining Useful Life Estimation of Lithium-ion Batteries Based on the Internal Resistance Growth Model,” IEEE Indian Control Conference, pp.33-38, 2017.
[https://doi.org/10.1109/INDIANCC.2017.7846448]

-
R. Zhao, J. Gu and J. Liu, “An Investigation on the Significance of Reversible Heat to the Thermal Behavior of Lithium Ion Battery through Simulations,” Journal of Power Sources, Vol.266, pp.422-432, 2014.
[https://doi.org/10.1016/j.jpowsour.2014.05.034]

-
M. I. Davidzon, “Newton’s Law of Cooling and Its Interpretation,” International Journal of Heat and Mass Transfer, Vol.55, Nos.21-22, pp.5397-5402, 2012.
[https://doi.org/10.1016/j.ijheatmasstransfer.2012.03.035]

-
J. K. Park, Principles and Applications of Lithium Secondary Batteries, Wiley-VCH, Weinheim, pp.239-248, 2012.
[https://doi.org/10.1002/9783527650408]

-
W. Tong, K. Somasundaram, E. Birgersson, A. S. Mujumdar and C. Yap, “Thermo-electrochemical Model for Forced Convection Air Cooling of a Lithium-ion Battery Module,” Applied Thermal Engineering, Vol.99, pp.672-682, 2016.
[https://doi.org/10.1016/j.applthermaleng.2016.01.050]

- S. M. H. Moghaddam, Designing Battery Thermal Management Systems (BTMS) for Cylindrical Lithium-ion Battery Modules Using CFD, M. S. Thesis, KTH School of Industrial Engineering and Management Energy Technology, Stockholm, 2019.
-
P. Peng and F. Jiang, “Thermal Behavior Analyses of Stacked Prismatic LiCoO2 Lithium-ion Batteries during Oven Tests,” International Journal of Heat and Mass Transfer, Vol.88, pp.411-423, 2015.
[https://doi.org/10.1016/j.ijheatmasstransfer.2015.04.101]

-
G. Jiang, L. Zhuang, Q. Hu, Z. Liu and J. Huang, “An Investigation of Heat Transfer and Capacity Fade in a Prismatic Li-ion Battery Based on an Electrochemical-thermal Coupling Model,” Applied Thermal Engineering, Vol.171, Paper No.115080, 2020.
[https://doi.org/10.1016/j.applthermaleng.2020.115080]

- Weather Forecast Office, “National Weather Service-estimating Wind Speed,” https://www.weather.gov/pqr/wind, , 2020.