재귀 최소 자승법을 이용하는 적분 슬라이딩 모드 및 MIT 규칙 기반 DC 모터의 적응형 속도 제어 알고리즘

1. 서 론

모터는 전기 에너지를 역학 에너지로 변화는 장치로써 자동차, 선박, 비행기와 같은 이동체와 제조 장비 등 다양한 산업 시스템에 적용되고 있다. 그중 DC 모터는 직류 전기를 활용하여 회전하며 DC 모터에 인가되는 전압과 모터의 회전 각속도는 상대적으로 비례하여 각도 및 속도 제어에 용이한 장점을 갖고 있다. DC 모터의 제어 성능을 확보하기 위해서는 파라미터를 정확하게 측정 후 제어기를 설계해야 한다. 하지만 DC 모터의 파라미터는 불확실성 및 노후화로 인해 정확한 값을 알기 어렵다는 한계점을 가지고 있다. 이러한 한계점을 극복하기 위한 DC 모터 제어 연구들이 진행되어왔다.

Dursun과 Durbu¹⁾는 슬라이딩 모드 제어기를 이용하여 DC 모터 속도 제어기를 개발하였으며 PID 제어기와 성능평가 결과를 비교하였다. 한창호와 정석권²⁾은 주기성 부하를 갖는 DC 모터 속도 제어 시스템의 슬라이딩 모드 제어기와 PI 제어의 강인성을 비교하였다. 1)~2)는 PI, PID 제어기와 슬라이딩 모드 제어기의 제어 성능을 비교함으로써 슬라이딩 모드 제어기의 강건함을 확인하였다.

윤영식 등³⁾은 터보차져 디젤엔진의 공기 순환계 모델링 및 모델기반 슬라이딩 모드 제어기를 개발하였다. 김정식⁴⁾은 타이어의 최적 노면 마찰력을 고려한 ABS 슬라이딩 모드 제어기를 개발하였다. 3)~4)는 슬라이딩 모드 제어기를 기반으로 강건한 제어를 수행할 수 있음을 보여주었다. Putra 등⁵⁾은 슬라이딩 모드 제어기의 슬라이딩 평면을 PID 형태로 설계하는 적응형 슬라이딩 모드 제어기를 개발하였다. Liu 등⁶⁾은 PI 제어입력에 적응형 슬라이딩 모드 제어 입력을 추가하여 PMSM의 토크 리플을 최소화하였다. Ren과 Zhou⁷⁾와 Ponce 등⁸⁾은 슬라이딩 모드 제어기와 Fuzzy logic을 접목시켜 슬라이딩 모드 제어기의 제어 입력 크기를 조절하고, DC 모터의 추종 제어 시나리오를 적용하였다. Nigam 등⁹⁾은 Fuzzy 슬라이딩 모드 제어기를 활용하여 Brushless DC 모터의 속도 제어기를 설계하였다. 7)~9)는 슬라이딩 모드 제어기와 Fuzzy logic을 접목시켜 슬라이딩 모드 제어기의 적응된 제어 입력을 인가함으로써 강인한 제어를 수행할 수 있음을 보여주었다.

Hafez 등¹⁰⁾은 기존 7)~9)에서 설계되었던 Fuzzy 슬라이딩 모드 제어기를 적응시키는 방법을 제안하였고, BLDC 모터의 속도 제어 시나리오를 기반으로 평가하였다. Murali와 Rao¹¹⁾는 슬라이딩 평면을 적응시키는 슬라이딩 모드 제어기를 개발하였다. Ren 등¹²⁾은 제어 대상의 불확실성을 추정하는 적응형 슬라이딩 모드 제어기를 개발하였고, Zheng 등¹³⁾은 지상 무인 차량에 활용되는 BLDC 모터를 제어하기 위해 적응 이산 시간 슬라이딩 모드 제어기를 개발하였다. 개발된 제어기는 기존 슬라이딩 모드 제어기의 Chattering 현상을 완화 시킬 수 있었다. Andrade¹⁴⁾는 재귀 최소 자승법과 슬라이딩 모드 제어기를 활용하여 ESR 추정을 통한 전해 커패시터의 상태 모니터링을 수행하였다. 김진성 등¹⁶⁾은 자율 주행 차량의 자동 차선 변경 시스템을 위해 슬라이딩 모드 제어기를 설계하였다. 김학주 등¹⁷⁾은 순환 최소 자승법 기반 Eta-reachability 조건을 이용하여 적응형 슬라이딩 모드 제어 알고리즘을 제안하였다. 기존 연구 조사를 통해 슬라이딩 모드 제어기의 강건한 제어 성능을 확인할 수 있었으며 슬라이딩 모드 제어기의 한계점을 극복하기 위해 PID 제어기, Fuzzy logic, 재귀 최소 자승법 기반 적응 규칙 기반 연구들이 진행되어왔다.

비적응형 제어의 경우 시스템 노후화로 인한 성능 저하 및 외란으로 인해 높아진 불확실성으로 인하여 합리적 제어 성능을 확보하기 어려운 한계점을 가지고 있다. 그러므로 시스템의 상태에 따른 적절한 파라미터 튜닝이 주기적으로 수행되어야 하는 과업이 발생 된다. 이러한 한계점을 극복하기 위해 변수 추정 적응 제어, 학습 기반 적응 제어 등 다양한 방법론이 적용되고 있다. 본 논문에서 제안하는 적응형 속도 제어기는 오차 동역학 모델 파라미터의 수학적 추정 기반 모델 자유 적응 제어 방법론을 제안한다. 제어 알고리즘은 시스템의 정확한 파라미터를 알지 못하여도 추정된 파라미터를 이용하여 합리적인 제어 성능을 확보할 수 있는 장점이 있다. 이를 위해 적분 슬라이딩 모드 평면을 설계하였고, 오차 동역학 모델의 집중화된 파라미터들을 재귀 최소 자승법으로 추정하였다. Lyapunonv 방법 기반 설계된 비용함수를 이용하여 안정성 조건을 만족하는 제어 입력을 도출하였다. 구체적으로 키르히호프 전압 법칙 기반 도출된 DC 모터의 전압 방정식과 회전 운동 방정식을 이용해 전압을 입력으로 하는 동적 방정식을 도출하였다. 도출된 동적 방정식과 정의된 속도 오차 상태량을 기반으로 오차 동역학 모델을 도출하였다. 도출된 오차 동역학 모델에서 정확히 알 수 없는 불확실성이 큰 파라미터들을 다중 망각 인자를 이용하는 재귀 최소 자승법을 기반으로 추정하였다. 오차의 비례 항과 적분 항을 이용해 슬라이딩 평면을 설계하였으며 적분 항의 적분 이득 값은 과도 응답성 향상을 위해 추정된 민감도와 MIT 규칙 기반 적응되었다. 성능평가를 위해 실 DC 모터 시스템(Quanser사의 DC 모터, QUBE-Servo 2)이 사용되었고, 사용된 DC 모터는 로터리 타입 엔코더 기반 회전 각도 신호를 출력할 수 있도록 시스템이 구성되어있다. 잡음의 영향을 최소화하고 계측값의 신뢰성을 높이기 위해 칼만 필터를 이용하여 DC 모터의 속도를 추정하였다. 실 DC 모터 시스템은 Matlab/ Simulink와 연동되어 평가가 수행되었고, 다양한 케이스에서 합리적인 제어 성능을 확인하였다.

본 논문은 다음과 같이 구성되었다. 2장에서는 적응형 속도 제어 알고리즘을 구성하는 2.1절 재귀 최소 자승법을 이용한 파라미터 추정과 2.2절 Lyapunov 기반 속도 제어 알고리즘을 기술한다. 3장에서는 시나리오 기반 성능평가 결과를 기술한다, 4장에서는 본 연구의 결론 및 한계점 분석에 따른 향후 계획을 기술한다.

2. 적응형 속도 제어 알고리즘

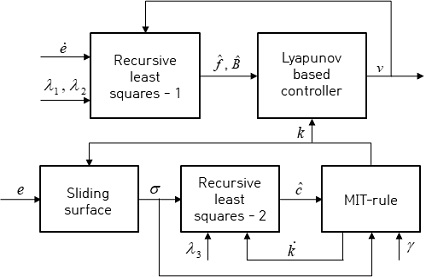
Fig. 1은 본 논문에서 제안하는 적응형 속도 제어기의 모델 개략도이다. DC 모터의 수학적 모델과 정의된 오차 상태량을 기반으로 오차 동역학 모델이 도출되었다. 도출된 오차 동역학 모델의 집중화된 파라미터들은 다중 망각 인자를 가지는 재귀 최소 자승법으로 추정되었다. 오차의 비례 항과 적분 항으로 슬라이딩 평면이 설계되었으며, 적분 항의 적응형 이득은 슬라이딩 평면과 적분 이득 변화율 간의 비례상수 및 MIT 규칙을 기반으로 결정되었다. 적응된 적분 이득 값과 추정된 오차 동역학 모델의 파라미터들은 Lyapunov 방법을 기반으로 설계된 비용함수에 반영됨으로써 제어 안정성 조건을 만족하는 제어 입력이 도출되었다.

Fig. 1

Model schematics for adaptive controller

2.1 재귀 최소 자승법을 이용한 파라미터 추정

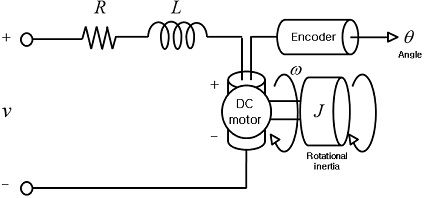
Fig. 2는 본 논문에서 제안하는 제어기의 성능평가를 위해 사용된 DC 모터의 전반적 시스템을 나타낸다.

Fig. 2

Overall DC motor system

Fig. 2에서 확인할 수 있듯 DC 모터 시스템은 전자기 회로와 기계 시스템으로 구분될 수 있다. 일반적인 DC 모터의 전압 및 운동 방정식은 키르히호프 전압 법칙 기반 전압 방정식과 동적 거동을 나타낼 수 있는 운동 방정식으로 표현되며 도출된 식 (1)과 (2)와 같다.

$\[ \frac{di}{dt}=\frac{v}{L}-\frac{R}{L}i-\frac{k_e}{L}\omega \]$

(1)

$\[ \frac{d\omega }{dt}=\frac{k_t}{J}i-\frac{b}{J}\omega \]$

(2)

식 (1)을 식 (2)에 대입하여 각속도의 변화율에 대해 정리하면 식 (3)과 같이 전개된다.

$\[ \dot{\omega }=\frac{k_t}{JR}v-\left(\frac{k_t{k}_e}{JR}+\frac{b}{J}\right)\omega -\frac{k_{t}L}{JR}\frac{di}{dt} \]$

(3)

오차는 식 (4)와 같이 요구 각속도와 DC 모터의 각속도의 차이로 정의하였으며 오차 동역학 모델은 앞서 도출된 식 (3)을 이용하여 식 (5)와 같이 도출되었다.

$\[ e={\omega }_d-\omega \]$

(4)

$\[ \dot{e}=-\frac{k_t}{JR}v+{\dot{\omega }}_d+\left(\frac{k_t{k}_e}{JR}+\frac{b}{J}\right)\omega +\frac{k_{t}L}{JR}\frac{di}{dt} \]$

(5)

식 (5)에서의 $$ -\frac{k_t}{JR}$$와 $$ {\dot{\omega }}_d+\left(\frac{k_t{k}_e}{JR}+\frac{b}{J}\right)\omega +\frac{k_{t}L}{JR}\frac{di}{dt}$$를 각각 입력 값 B_eq와 외란 값 F_eq로 정의하면 식 (5)는 아래와 같이 다시 정리될 수 있다.

$\[ \dot{e}=B_{eq}v+F_{eq} \]$

(6)

식 (6)에서 정의된 B_eq, F_eq를 추정하기 위해 다중 망각 인자를 가진 재귀 최소 자승법을 적용하였고 식 (6)을 식 (7)과 같이 선형 조합으로 표현하였다. 이때 출력, 회귀 인자, 추정값은 식 (8)~(10)에 해당된다.

$\[ y={\varphi }^T\theta \]$

(7)

$\[ y=\dot{e} \]$

(8)

$\[ \varphi ={\left[1 v\right]}^T \]$

(9)

$\[ \theta ={\left[{\widehat{F}}_{eq} {\widehat{B}}_{eq}\right]}^T \]$

(10)

추정을 위한 망각 인자 λ (0<λ≤1)는 설계 파라미터로써 정의되었으며 망각 인자의 크기는 1에 가까울수록 과거 데이터들을 상대적으로 많이 기억하며 추정한다. 본 연구에서는 정의된 입력과 외란의 변화 경향을 고려한 제어 입력 도출을 위해 λ를 1에 가까운 값으로 정의하였다. 다중 망각 인자(λ₁,λ₂)를 가진 재귀 최소 자승법의 목적함수는 아래와 같이 정의되었다.

$\[ \begin{array}{c}V\left({\widehat{\theta }}_1\left(k\right),{\widehat{\theta }}_2\left(k\right),k\right)\hfill \\ =\frac{1}{2}\sum _{i=1}^k{\lambda }_1^{k-i}{\left(y\left(i\right)-{\varphi }_1\left(i\right){\widehat{\theta }}_1\left(k\right)-{\varphi }_2\left(i\right){\theta }_2\left(i\right)\right)}^2\hfill \\ +\frac{1}{2}\sum _{i=1}^k{\lambda }_2^{k-i}{\left(y\left(i\right)-{\varphi }_1\left(i\right){\theta }_1\left(i\right)-{\varphi }_2\left(i\right){\widehat{\theta }}_2\left(k\right)\right)}^2\hfill \end{array} \]$

(11)

식 (11)에서 ϕ₁, ϕ₂는 각각 식 (9)에서 1과 v에 해당된다. 정의된 재귀 최소 자승법의 목적함수를 최소화하는 추정값은 아래와 같이 도출될 수 있다.

$\[ \begin{array}{c}\left[\begin{array}{c}{\widehat{\theta }}_1\left(k\right)\\ {\widehat{\theta }}_2\left(k\right)\end{array}\right]={\left[\begin{array}{cc}1& L_1\left(k\right){\varphi }_2\left(k\right)\\ L_2\left(k\right){\varphi }_1\left(k\right)& 1\end{array}\right]}^{-1}\times \hfill \\ \left[\begin{array}{c}{\widehat{\theta }}_1\left(k-1\right)+L_1\left(k\right)\left(y\left(k\right)-{\varphi }_1\left(k\right){\widehat{\theta }}_1\left(k-1\right)\right)\\ {\widehat{\theta }}_2\left(k-1\right)+L_2\left(k\right)\left(y\left(k\right)-{\varphi }_2\left(k\right){\widehat{\theta }}_2\left(k-1\right)\right)\end{array}\right]\hfill \end{array} \]$

(12)

L은 추정을 위한 이득 값으로 공분산 P와 같이 매 단계마다 갱신되며 추정을 위한 이득 값과 공분산의 계산식은 식 (13)과 식 (14)와 같다.

$\[ \left[\begin{array}{c}{L}_1\left(k\right)\\ L_2\left(k\right)\end{array}\right]=\left[\begin{array}{c}{P}_1\left(k-1\right){\varphi }_1\left(k\right)/\left({\lambda }_1+{\varphi }_1^T{P}_1\left(k-1\right){\varphi }_1\left(k\right)\right)\\ P_2\left(k-1\right){\varphi }_2\left(k\right)/\left({\lambda }_2+{\varphi }_2^T{P}_2\left(k-1\right){\varphi }_2\left(k\right)\right)\end{array}\right] \]$

(13)

$\[ \left[\begin{array}{c}{P}_1\left(k\right)\\ P_2\left(k\right)\end{array}\right]=\left[\begin{array}{c}\left(1-L_1\left(k\right){\varphi }_1^T\left(k\right)\right)P_1\left(k-1\right)/{\lambda }_1\\ \left(1-L_2\left(k\right){\varphi }_2^T\left(k\right)\right)P_2\left(k-1\right)/{\lambda }_2\end{array}\right] \]$

(14)

본 연구에서 다뤄진 다중 망각 인자를 가진 재귀 최소 자승법은 기존 연구¹⁵⁾를 참고하여 정의되었다. 다음 절에는 Lyapunov 방법의 안정성 조건을 만족하는 제어 입력 도출 과정을 기술한다.

3. 성능 평가

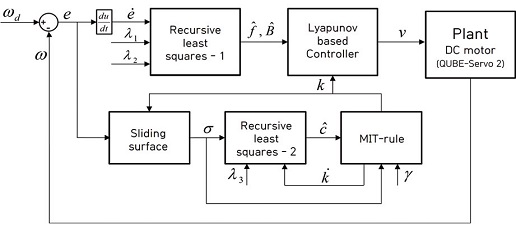
Fig. 3은 성능평가를 위한 본 연구에서 제안된 적응형 속도 제어기의 구체적 모델 개략도를 보여준다.

Fig. 3

Model schematics for performance evaluation

Fig. 4는 성능평가에 적용된 Quanser사의 DC 모터(QUBE-Servo 2)이고, 실 DC 모터의 물성치들을 Table 1에 정리하였다. 실 DC 모터 시스템의 회전각 정보는 Matlab/Simulink와 연동되어 시리얼 통신 기반 획득되었다. 측정된 회전각 정보를 이용해 칼만 필터 기반 모터의 각속도가 추정되었다. 추정된 각속도는 Matlab/Simulink 환경에서 설계된 적응형 속도 제어 알고리즘에 이용되어 성능평가가 진행되었다.

Fig. 4

DC motor platform for test (QUBE-Servo2)

Table 1

Parameters for DC motor(QUBE-Servo2)

성능평가를 위한 시나리오는 요구 각속도를 Step 형태로 인가한 경우를 Case [1], Sine wave 형태로 인가한 경우를 Case [2], Ramp 형태로 인가한 경우를 Case [3]로 분류하였다. 각 케이스는 세부적으로 부하의 부착 유/무와 적응형 적분 이득의 적용 유/무로 구분되었다. 적용된 케이스들은 아래 Table 2에서 확인할 수 있으며 성능 비교평가를 위해 적용된 고정 적분 이득 값(Constant k)의 경우 오차의 초기 수렴 성능 확보를 위한 케이스 별 서로 다른 값이 적용되었다.

Table 2

Simulation scenario for performance evaluation

3.1 Case [1]: Step input

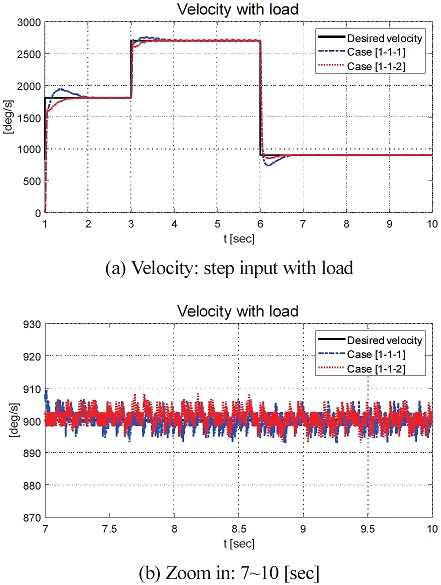
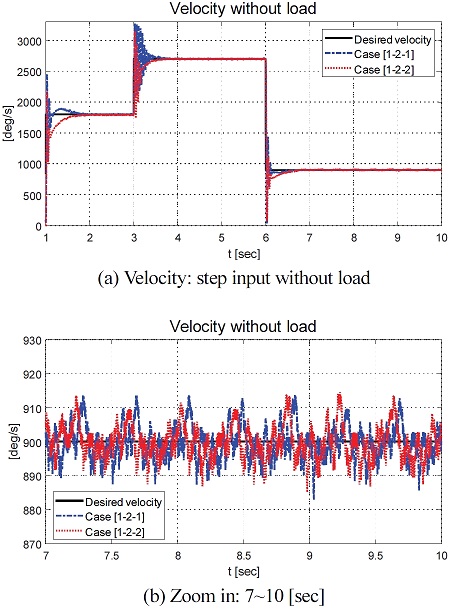
Fig. 5는 Case [1-1-1] (파란 단선)과 Case [1-1-2] (빨간 점선)의 각속도 및 Case [1]의 Step 형태의 요구 각속도(검은 실선)을 보여준다. Fig. 6은 요구 각속도 (검은 실선)과 Case [1-2-1] (파란 단선)과 Case [1-2-2] (빨간 점선)의 각속도를 보여준다. Fig. 5 및 6에서 확인할 수 있듯이 3 sec와 6 sec 구간에서 과도 응답 및 Chattering 현상이 발생함을 확인할 수 있었다. 그중 부하가 부착된 시나리오인 Case [1-1-1]과 [1-1-2]는 Case [1-2-1]과 [1-2-2]에 비해 비교적 작은 오차가 나타난 것을 확인할 수 있었다.

Fig. 5

Test results: velocity with load [Case 1]

Fig. 6

Test results: velocity without load [Case 1]

Fig. 5(b)와 Fig. 6(b)는 DC 모터의 속도 그래프의 확대된 일부를 보여준다. Case [1-1-1]과 Case [1-1-2]의 오차 범위는 약 10 deg/s 이내인 것을 확인할 수 있었으며 Case [1-2-1], Case [1-2-2]의 오차 범위는 약 20 deg/s 이내인 것을 확인할 수 있었다. Case 별 부하의 부착 유/무와 적응형 적분 이득 값의 적용 유/무로 구분된 성능평가 결과에서 확인할 수 있듯이 부하의 부착 유/무에 따라 과도 응답 특성이 달라지는 것을 Fig. 5(a)와 6(a)에서 확인할 수 있다. 부하가 부착되지 않은 경우 부하가 부착된 경우 대비 과도 구간에서 상대적 높은 진동 특성을 보였고 정상 상태 구간에서 상대적 큰 Chattering 현상을 확인할 수 있다. 적응형 적분 이득 값이 적용된 경우 고정 적분 이득 값이 적용된 경우 대비 과도 구간에서 상대적으로 수렴 시간이 짧아졌고, 최대 오버슛(Overshoot) 값이 작아졌음을 확인하였다.

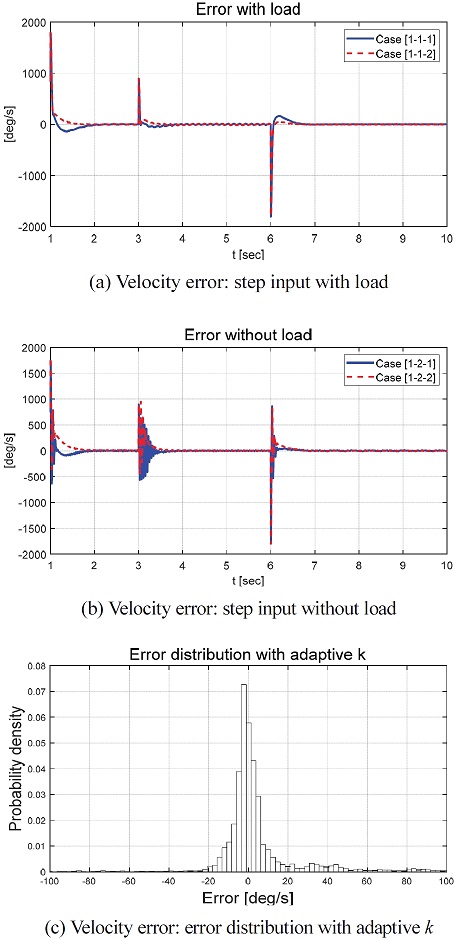
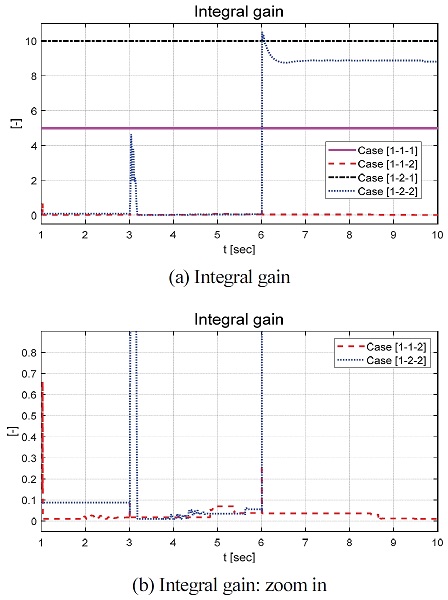
Fig. 7은 요구 각속도와 모터의 각속도 차이 값을 보여준다. Fig. 7(c)는 적응형 적분 이득 값이 반영된 Case [1-1-2]와 [1-2-2]의 오차 확률 밀도 그래프이다. 확률 밀도 그래프에서 볼 수 있듯이 오차 값이 0에 밀집하고 있으며, 약 크기 20 deg/s 외의 오차들은 상대적으로 양의 영역에 많이 분포하고 있음을 확인할 수 있었다. Fig. 8은 슬라이딩 평면 내 적분 이득 값의 그래프이다. Case [1-1]의 적분 이득 값은 Case [1-2]의 적분 이득 값보다 상대적으로 작은 값으로 적응 및 결정되었다. 그중 Case [1-1-2]의 경우, 적응형 적분 이득 값의 크기는 0에 가까운 값을 갖는 것을 확인할 수 있었다. Table 3은 성능평가를 위해 설정된 파라미터 값들을 보여준다. Table 3에서 Case [1-2-1]과 [1-2-2]의 파라미터들은 Case [1-1-1]과 [1-1-2]의 파라미터보다 큰 값으로 결정되었다. 비용함수의 감쇠율을 나타내는 α의 경우 적응형 적분 이득의 적용 유/무에 대해서 과도 구간 및 정상 상태 구간에서의 합리적 제어 성능 비교를 위하여 Case [1]에서는 Case [2], [3]과 달리 케이스 별 다른 값이 적용되었다.

Fig. 7

Test results: velocity error [Case 1]

Fig. 8

Test results: integral gain [Case 1]

Table 3

Control parameter for Case 1 [step]

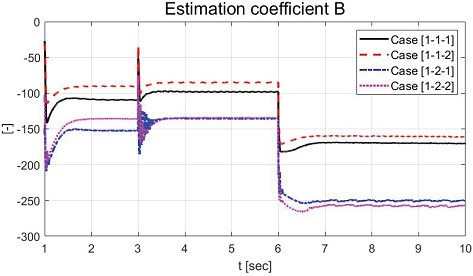
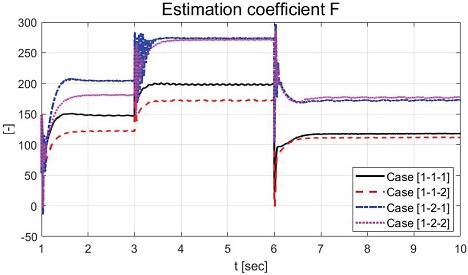
Fig. 9와 Fig. 10은 식 (6)의 $$ {\widehat{B}}_{eq}$$, $$ {\widehat{F}}_{eq}$$ 값을 다중 망각 인자 기반 재귀 최소 자승법으로 추정한 결과들을 보여준다. 추정된 입력 값 $$ {\widehat{B}}_{eq}$$는 식 (6)에서 정의되었듯이 음수 값으로 추정되는 것을 확인하였으며 $$ {\widehat{B}}_{eq}$$, $$ {\widehat{F}}_{eq}$$ 모두 부하가 부착된 경우가 부착되지 않은 경우보다 추정된 값들의 크기가 작은 것을 확인할 수 있었다.

Fig. 9

Test results: estimated coefficient B [Case 1]

Fig. 10

Test results: estimated coefficient F [Case 1]

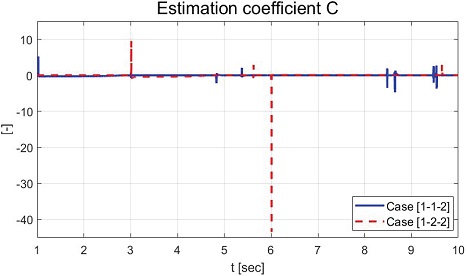
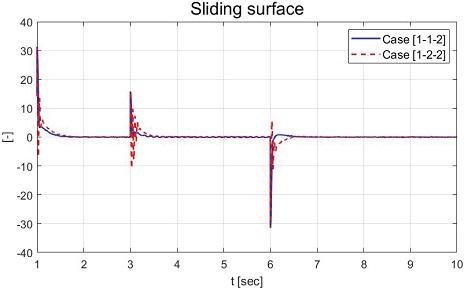
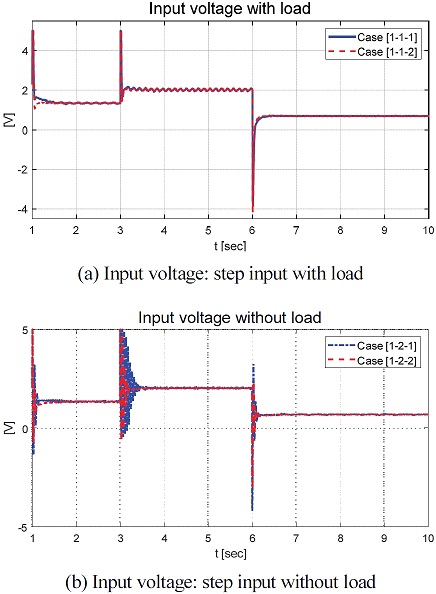
Fig. 11은 MIT 규칙 적용을 위해 필요한 민감도인 비례상수 $$ \widehat{C}$$의 추정 결과를 보여준다. Fig. 12는 정의된 슬라이딩 평면을 보여준다. Fig. 13은 도출된 입력 전압을 보여준다. 입력 전압의 경우 DC 모터의 제원을 반영하기 위해 –5~5 [v] 제한 값이 적용되었다.

Fig. 11

Test results: estimated coefficient C [Case 1]

Fig. 12

Test results: sliding surface [Case 1]

Fig. 13

Test results: input voltage [Case 1]

3.2 Case [2]: Sine input

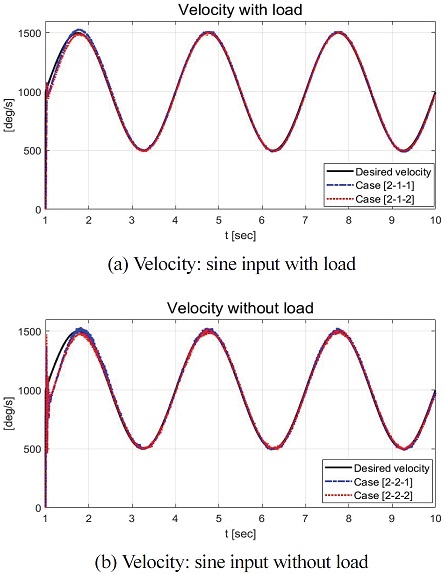
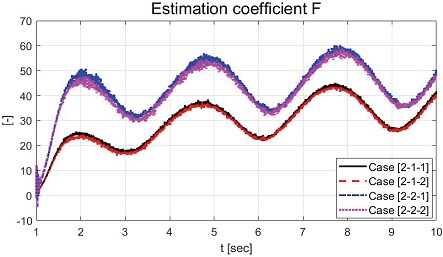
Case [2]에서 Fig. 14(a)는 Sine 형태의 요구 각속도(검은 실선)와 Case [2-1-1] (파란 단선), Case [2-1-2] (빨간 점선)의 각속도를 보여준다. Fig. 14(b)도 Case [2-2-1] (파란 단선), Case [2-2-2] (빨간 점선)의 각속도가 Sine 형태의 각속도를 합리적으로 추종함을 보여준다. Case [2-1-1]과 [2-1-2]는 부하가 부착된 시나리오로 Case [2-2-1], Case [2-2-2]와 비교되어 상대적 작은 과도 응답 현상을 확인할 수 있었다.

Fig. 14

Test results: velocity [Case 2]

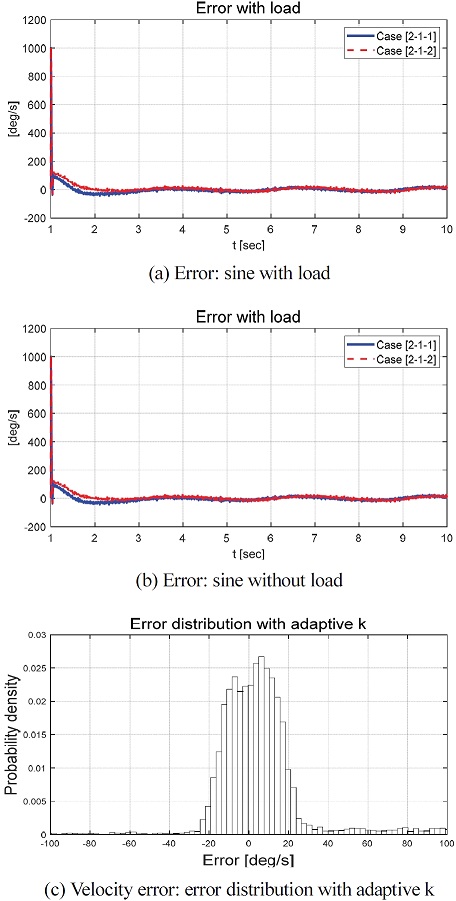
Case [2-2-1]과 [2-2-2]는 부하가 부착되지 않은 시나리오로 큰 값의 상태 변화량이 과도 응답 구간에서 확인되었다. 이는 정상 상태까지 도달하기까지의 시간 지연 현상의 원인임을 확인할 수 있었다. 시간 지연 현상은 오차 그래프 Fig. 15(b)의 약 1~2 sec 구간에서 확인할 수 있었다. 1~2 sec 구간에서의 오차는 약 200 deg/s 정도의 크기였으며 약 2 sec 이후 정상 상태에 도달하였음을 확인할 수 있었다. Fig. 15(c)는 Case [2-1-2]와 [2-2-2]의 오차 확률 밀도 그래프로써 오차가 다수 –20~20 deg/s에 분포함을 보여준다. 이는 제안하는 적응형 속도 제어 알고리즘이 Sine 형태의 요구 각속도를 기술된 오차 구간 내에서 합리적으로 추종함을 보여주는 결과이다.

Fig. 15

Test results: error [Case 2]

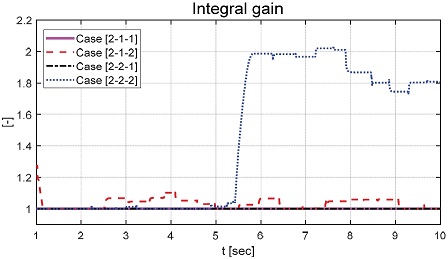
Fig. 16은 적분 이득 값을 보여주는 그래프이다. Case [2-1-1]과 [2-2-1]은 고정 적분 이득 값이 적용되었으며 Case [2-1-2]와 [2-2-2]는 MIT 규칙 기반 적응된 적분 이득 값이 적용되었다. Case [1]의 경우 적응된 적분 이득 값은 고정 적분 이득 값보다 상대적 작은 값을 가졌다. 반면 Case [2]의 경우 적응된 적분 이득 값은 고정 적분 이득 값보다 상대적 큰 값을 가진 것을 확인할 수 있었다. Table 4는 성능평가를 위한 파라미터들의 값을 보여준다.

Fig. 16

Test results: integral gain [Case 2]

Table 4

Control parameter for Case 2 [Sine]

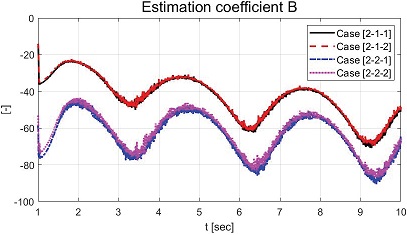
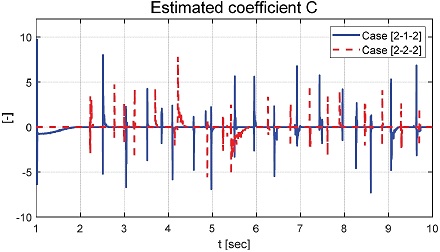
Fig. 17, 18은 각각 추정된 $$ {\widehat{B}}_{eq}$$, $$ {\widehat{F}}_{eq}$$ 값들을 보여주는 그래프이다. Fig. 19는 추정된 비례상수 $$ \widehat{C}$$의 값을 보여준다. Case [2-2-2]의 적응형 적분 이득 값의 경우 약 5 sec 이후 상대적 큰 변화가 발생 되었으며 이로 인해 Fig. 20의 슬라이딩 평면이 5~6 sec 구간에서 음의 값으로 작아진 것을 확인할 수 있었다. 이는 부하가 부착되지 않은 경우 상대적 큰 Chattering 현상에 의해 오차 변화율 값이 커질 수 있고, 추정되는 비례상수 값에 영향을 주어 적분 이득 값의 변화가 상대적으로 크게 발생한 것으로 볼 수 있다. Fig. 19에서 볼 수 있는 추정된 비례상수가 약 2 sec 내에서는 상대적으로 작은 변화율을 갖는 것을 확인할 수 있다. 이러한 결과는 Fig. 14에서 볼 수 있는 초기 약 2 sec 구간에서 시간 지연 현상과 연관됨을 확인할 수 있다.

Fig. 17

Test results: estimated coefficient B [Case 2]

Fig. 18

Test results: estimated coefficient F [Case 2]

Fig. 19

Test results: estimated coefficient C [Case 2]

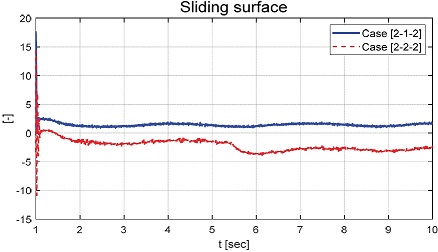
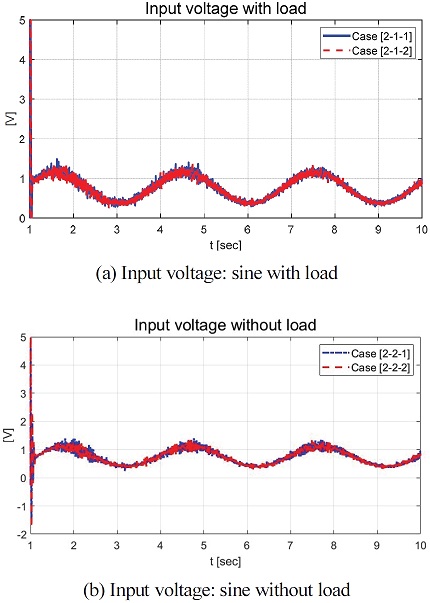
Fig. 20은 정의된 슬라이딩 평면을 보여준다. 본 연구에서 제안하는 제어기는 식 (16)과 식 (17)에 따라 슬라이딩 평면의 안정성을 확보할 수 있는 제어 입력을 도출할 수 있었다. Case [1]과 Case [3]의 슬라이딩 평면을 보여주는 Fig. 12와 Fig. 28과 달리 Case [2]의 Fig. 20에서 볼 수 있듯이 슬라이딩 평면이 안정성이 확보되지 못하는 것을 확인할 수 있었다. 부하가 부착된 시나리오인 Case [2-1-2]의 슬라이딩 평면은 양의 값을 나타내었으며, 부하가 부착되지 않은 Case [2-2-2]의 슬라이딩 평면은 음의 값을 나타내었다. 이는 부하가 부착됨으로 가중된 관성으로 과도 응답 현상이 커져 양의 값을 나타낼 수 있었으며, 부하가 부착되지 않은 경우 상대적으로 작은 관성으로 인하여 음의 값을 나타내었다. Fig. 20에서 볼 수 있듯이 제안하는 제어기는 인가되는 요구 각속도가 Sine 형태와 같이 지속적인 변화량이 주어지는 경우 추종 오차가 발생하는 한계점을 확인할 수 있었다. Fig. 21은 입력 전압을 나타내는 그래프로 Fig. 17, 18의 그래프 개형과 유사한 것을 확인하였다.

Fig. 20

Test results: sliding surface [Case 2]

Fig. 21

Test results: input voltage [Case 2]

3.3 Case [3]: Ramp input

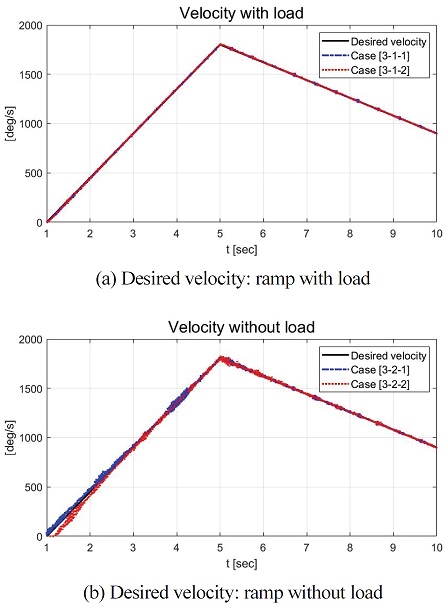
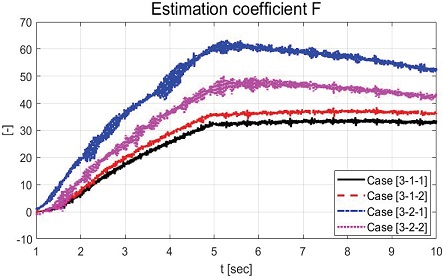
Fig. 22는 요구 각속도를 Ramp 형태로 인가하였을 때의 성능평가 결과이며 부하의 부착 유/무와 적응형 적분 이득의 적용 유/무에 따라 Case [3-1-1], Case [3-1-2], Case [3-2-1], Case [3-2-2]로 구분되었다. Fig. 22(a)와 (b)에서 볼 수 있듯이 부하가 부착되지 않은 시나리오인 Case [3-2-1], Case [3-2-2]에서 부하가 부착된 시나리오인 Case [3-1-1], Case [3-1-2]보다 상대적으로 Chattering 현상이 큰 것을 확인할 수 있었다. Fig. 22(b)에서 볼 수 있듯이 Case [3-2-2]는 Case [3-2-1]보다 상대적으로 작은 Chattering 현상을 확인할 수 있었다. 하지만 1~3 sec 구간에서 요구 각속도를 추종할 때 시간 지연이 발생하는 한계점을 확인할 수 있었다.

Fig. 22

Test results: Angular velocity [Case 3]

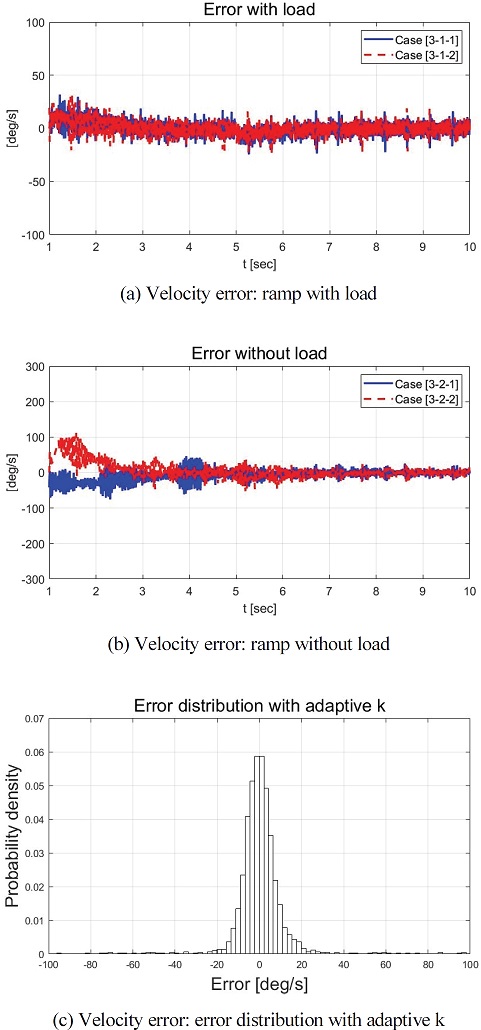
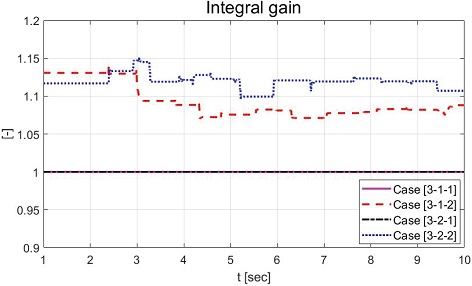
Fig. 23은 오차의 상태량을 보여준다. Fig. 23(c)는 Case [3-1-2], Case [3-2-2]의 오차를 확률 밀도 함수의 그래프이다. 그래프에서 볼 수 있듯이 시간 지연 현상에서 발생하는 큰 값의 오차를 제외하고 약 –20~20 deg/s 정도로 오차가 분포함을 확인할 수 있었다. Fig. 24는 모든 Case [3]의 모든 케이스에 적용된 적분 이득 값을 보여주는 그래프이다. Case [3]에 적용된 적분 이득 값은 Case [2]와 같이 추정된 민감도 기반 MIT 규칙으로 적응된 적분 이득 값이 고정 적분 이득 값보다 상대적으로 큰 것을 확인할 수 있었다. 성능평가를 위해 설계된 파라미터들을 Table 5에 정리되었다.

Fig. 23

Test results: Velocity error [Case 3]

Fig. 24

Test results: Integral gain [Case 3]

Table 5

Control parameter for Case 3 [Ramp]

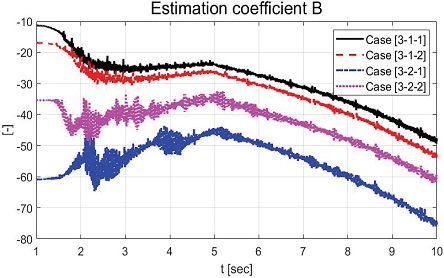
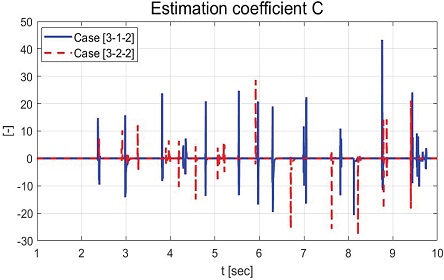
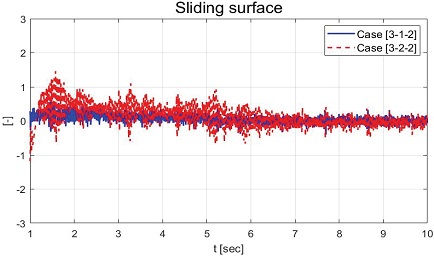
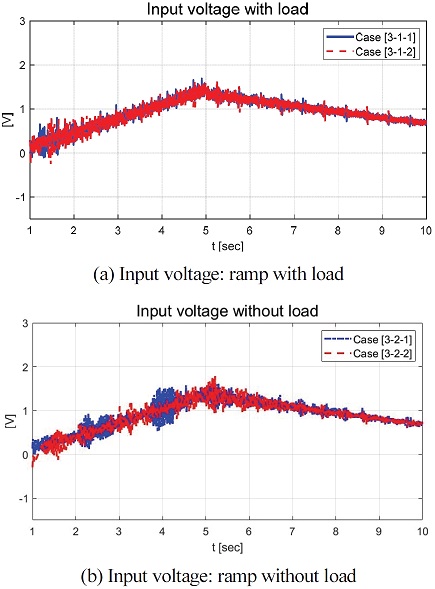
Fig. 25, 26은 각각 $$ {\widehat{B}}_{eq}$$, $$ {\widehat{F}}_{eq}$$,추정한 결과를 보여주는 그래프이다. Fig. 27은 $$ \widehat{C}$$의 추정 결과를 보여주는 그래프이다. Fig. 27에서 볼 수 있듯이 약 2 sec까지 추정된 비례상수의 변화가 상대적으로 작은 것은 Fig. 22의 약 2 sec까지의 시간 지연 현상에 영향을 주는 것을 확인할 수 있다. Fig. 28, Fig. 29는 각각 정의된 슬라이딩 평면과 입력 전압 그래프를 보여준다.

Fig. 25

Test results: estimated coefficient B [Case 3]

Fig. 26

Test results: estimated coefficient F [Case 3]

Fig. 27

Test results: estimated coefficient C [Case 3]

Fig. 28

Test results: sliding surface [Case 3]

Fig. 29

Test results: Input voltage [Case 3]

평가 결과를 확인하였을 때 요구 속도의 형태로 구분 된 케이스 별 초기 오차 수렴 성능은 서로 다른 것을 확인할 수 있었다. 각 케이스 별 요구 각속도를 추종하는 과정에서 발생하는 오차와 오차의 변화율은 서로 다른 값을 나타내고 오차와 오차의 변화율은 슬라이딩 평면 값 및 비례상수 추정에 영향을 주는 것을 확인할 수 있었다. 결과적으로 적응형 적분 이득 값의 결정에 영향을 미치며 제어 성능의 과도 응답 특성을 다르게 도출하는 결과를 확인할 수 있었다.

Figs. 9, 10, 17, 18, 25, 26에서 확인할 수 있듯이 추정된 파라미터들은 인가된 요구 각속도 형태에 따라 서로 다른 값으로 도출되었다. 이는 본 연구에서 적용된 모델 자유 적응 제어의 기법 중 재귀 최소 자승 기법은 시스템의 파라미터를 정확하게 추정하는 것이 아닌 설계된 수학적 형태를 이용하여 파라미터들을 추정하였다. 그럼에도 불구하고 제안하는 적응형 제어 방법에 의해 모든 케이스 별 합리적 제어 성능 확보가 가능함을 확인하였다.

4. 결 론

본 논문은 다중 망각인자 기반 재귀 최소 자승법을 이용하는 적분 슬라이딩 모드 및 MIT 규칙 기반 적응형 속도 제어 알고리즘을 제안하였다. 제안된 알고리즘은 대상 시스템의 정확한 파라미터를 알지 못하여도 시스템의 오차 동역학 모델 내 파라미터들의 추정 값들을 이용하여 시스템의 불확실성, 외란 및 부하의 변화에 강건한 제어를 수행할 수 있었다. 속도 제어를 위해 DC 모터의 전압 방정식과 운동 방정식으로 오차 동역학 모델을 도출하였다. 도출된 오차 동역학 모델에서 파라미터들은 다중 망각 인자를 가진 재귀 최소 자승법으로 추정되었다. 추정된 오차 동역학 모델의 파라미터들은 Lyapunov 방법을 기반으로 설계된 비용함수와 조건들에 반영되어 안정성 조건을 만족하는 제어 입력이 도출되었다. 제안된 적응형 제어 알고리즘의 성능평가를 위해 다양한 DC 모터 속도 제어 시나리오가 적용되었다. 성능평가 시나리오는 세 가지 요구 각속도(step, sine, ramp)와 부하의 부착 유/무, 적응형 적분 이득 값의 적용 유/무로 적용되었다. 적응형 적분 이득 값의 적용 유/무 시나리오를 비교함으로 본 논문에서 제안하는 제어기의 합리적 과도 응답 성능을 확인할 수 있었다. 성능평가 결과로 Case [1]에서 요구 각속도가 Step 형태로 인가될 때 과도 응답이 상대적으로 크게 발생하는 한계점을 확인하였으며 Case [2]와 Case [3]에서 추종 지연 시간이 존재하는 한계점을 확인할 수 있었다. 이러한 한계점에도 불구하고 과도 구간 이후 모든 케이스에서 제안하는 적응형 제어 알고리즘에 의한 모터의 합리적 속도 추종 성능을 확인할 수 있었다. 그리고 성능평가 과정에서 Case 별 적용된 요구 각속도의 형태와 부하 부착 유/무에 따라 망각 인자 및 비용함수의 감쇠율을 나타내는 α의 값을 일부 다르게 적용하여 평가하는 과정이 필요하였다. 따라서 향후 오차의 수렴 성능과 부하의 관계 분석을 통한 파라미터 온라인 튜닝 알고리즘 기반 제어 알고리즘 고도화 계획하고 있다. 또한 적용된 고정 망각 인자들이 시스템의 상태량에 따라 가변하기 위해 적응 및 학습 알고리즘의 개발을 통해 파라미터 조정이 필요 없는 모델 자유 적응 제어 알고리즘 고도화를 계획하고 있다. 추후 본 연구에서 개발된 적응 제어 알고리즘은 시스템의 정보 없이 다양한 DC 모터의 제어 및 미지 시스템의 제어 방법론으로 적용되고, 시스템 노후화에 따른 성능 저하에도 합리적 제어 성능을 확보할 수 있는 방법론으로써 적용 가능할 것을 기대한다.

Acknowledgments

A part of this paper was presented at the KSAE 2020 Fall Conference and Exhibition

References

• E. H. Dursun and A. Durbu, “Speed Control of a DC Motor with Variable Load Using Sliding Mode Control,” International Journal of Computer and Electrical Engineering, Vol.8, No.3, pp.219-226, 2016. [https://doi.org/10.17706/IJCEE.2016.8.3.219-226]
• C. H. Han and S. K. Jeong, “Comparison of Robustness of Sliding Mode and PI Control in DC Motor Speed Control System with Periodic Loads,” Journal of the Korean Society for Power System Engineering, Vol.22, No.3, pp.23-31, 2018. [https://doi.org/10.9726/kspse.2018.22.3.023]
• Y. S. Yoon, S. B. Choi, M. S. Ko and J. H. Lim, “Simplified Turbocharged Diesel Engine Air Path Modeling and Control Using Sliding Mode Controllers,” KSAE Annual Conference Proceedings, pp.548-558, 2010.
• J. S. Kim, “ABS Sliding Mode Control Considering Optimum Road Friction Force of Tyre,” Transactions of KSAE, Vol.21, No.1, pp.78-85, 2013. [https://doi.org/10.7467/KSAE.2013.21.1.078]
• E. H. Putra, Z. Has and M. Effendy, “Robust Adaptive Sliding Mode Control Design with Genetic Algorithm for Brushless DC Motor,” 2018 5th International Conference on Electrical Engineering Computer Science and Informatics, pp.330-335, 2018. [https://doi.org/10.1109/EECSI.2018.8752768]
• J. Liu, H. Liu and Y. Deng, “Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control,” IEEE Transactions on Power Electronics, Vol.33, No.4, pp.3655-3671, 2018. [https://doi.org/10.1109/TPEL.2017.2711098]
• H. P. Ren and R. Zhou, “Fuzzy Sliding Mode Tracking Control for DC Motor Servo System without Uncertainty Information,” 2017 12th IEEE Conference on Industrial Electronics and Applications, pp.1511-1515, 2017.
• P. Ponce, J. A. Rosales, A. Molina, H. Ponce and B. MacCleery, “Designing a Robust Controller Using SMC and Fuzzy Artificial Organic Networks for Brushed DC Motors,” Energies, Vol.13, No.12, pp.1-16, 2020. [https://doi.org/10.3390/en13123091]
• V. Nigam, S. Hussain and S. N. Agarwal, “A Hybrid Fuzzy Sliding Mode Controller for a BLDC Motor Drive,” 2016 IEEE 1st IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems, pp.1-4, 2016. [https://doi.org/10.1109/ICPEICES.2016.7853249]
• A. T. Hafez, A. A. Sarhan and S. Givigi, “Brushless DC Motor Speed Control Based on Advanced Sliding Mode Control (SMC) Techniques,” 2019 IEEE International Systems Conference, 2019. [https://doi.org/10.1109/SYSCON.2019.8836754]
• S. B. Murali and M. Rao, “Adaptive Sliding Mode Control of BLDC motor using Cuckoo Search algorithm,” 2nd International Conference on Inventive Systems and Control, pp.989-993, 2018. [https://doi.org/10.1109/ICISC.2018.8398950]
• H. P. Ren, R. Zhou and J. Li, “Adaptive Backstepping Sliding Mode Tracking Control for DC Motor Servo System,” 2017 Chinese Automation Congress, pp.5090-5095, 2017.
• Z. Zheng, N. Wang and H. Zhao, “Adaptive Discrete-Time Sliding Mode Control of Brushless DC Motor Servo System for Unmanned Surface Vehicles,” The International Conference on Cyber Security Intelligence and Analytics, pp.496-504, 2019. [https://doi.org/10.1007/978-3-030-15235-2_72]
• J. M. Andrade, “Condition Monitoring of Electrolytic Capacitors via ESR Estimation with Recursive Least Squares and Sliding Mode Techniques,” Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics, Vol.1, pp.474-481, 2018. [https://doi.org/10.5220/0006887704840491]
• A. Vahidi, A. Stefanopoulou and H. Peng, “Recursive Least Squares with Forgetting for Online Estimation of Vehicle Mass and Road Grade: Theory and Experiments,” Vehicle System Dynamics, Vol.43, No.1, pp.31-55, 2005. [https://doi.org/10.1080/00423110412331290446]
• J. S. Kim, S. H. Lee and C. C. Chung, “Design of Automated Lane Change System Using Sliding Mode Control,” KSAE Fall Conference Proceedings, pp.533-536, 2020.
• H. J. Kim and K. S. Oh, “Development of a Recursive Least Squares based Adaptive Sliding Mode Control Algorithm using Self-Tunning Eta-Reachability Condition,” KSAE Fall Conference Proceedings, pp.451-452, 2020.