[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 29, No. 6, pp.569-588

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jun 2021

Received 08 Feb 2021 Revised 05 Mar 2021 Accepted 09 Mar 2021

DOI: https://doi.org/10.7467/KSAE.2021.29.6.569

횡풍 안정성에 따른 샤시 설계변수의 민감도 분석

박재용¹⁾^{, 3)}

; 고영일²⁾

; 나성수¹⁾

; 이경수^*^{, 2)}

1)고려대학교 기계공학과
2)서울대학교 기계공학과
3)현대자동차 샤시통합컨셉시험팀

Analysis of Sensitivity for Chassis Design Parameters on X-wind Stability

Jaeyong Park¹⁾^{, 3)}

; Youngil Koh²⁾

; Sungsoo Na¹⁾

; Kyongsu Yi^*^{, 2)}

1)Department of Mechanical Engineering, Korea University, Seoul 02841, Korea
2)Department of Mechanical Engineering, Seoul National University, Seoul 08826, Korea
3)Total Chassis Concept Test Team, Hyundai Motor Company, 150 Hyundaiyeonguso-ro, Namyang-eup, Hwaseong-si, Gyeonggi 18280, Korea

Correspondence to: ^*E-mail: kyi@snu.ac.kr

Copyright Ⓒ 2021 KSAE / 187-09
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

The X-wind sensitivity of a vehicle becomes more important from the perspective of driving safety, since the driving speed in highway is climbing these days. The sensitivity of a vehicle to X-wind depends on many factors, including the design of the suspension and aerodynamics of the body, among others. What is known about this phenomenon, however, remains limited and must be improved in order to develop a vehicle with optimum characteristics for X-wind stability. In this research, the physics behind the sensitivity of a vehicle is discussed in detail through various kinds of virtual tests using a computer aided engineering(CAE) simulation scheme for investigating the moving stability of a vehicle under strong X-wind based on numerical analyses and driving simulator experiments. A reliable simulation model for vehicle, driver, wind generator and interactions is built. This integrated simulation environment for X-wind stability is verified by correlating with test results of real vehicles such as K&C(SPMD), Flat-Trac®, Wind Tunnel and Proving Ground Test. Subsequently, the sensitivity analyses on the whole design parameters are carried out to find the most dominant design parameters. Finally, the response surfaces are generated from the results of sensitivity analysis on vehicle design parameters. These are useful for vehicle developers to have insights on X-wind stability. Furthermore, these are utilized in various disciplines of vehicle development such as chassis/tyre, body structure and aerodynamics.

Keywords:

X-wind, Chassis design parameter, Sensitivity analysis, Driver’s model, Driving stability, Path’s error, Vehicle state variables

키워드:

횡풍, 샤시 설계 인자, 민감도 해석, 운전자 모델, 주행 안정성, 경로 오차, 차량 상태 변수

1. 서 론

최근에는 차량에 적용된 능동형 전자제어 기술 발전으로 인하여 불안정한 조건에서도 차량의 구동, 제동, 선회 등을 복합적으로 제어하는 기술이 보편화되고 있는 상황이다. 주행 중에 실제로 발생할 수 있는 어떠한 악조건 속에서도 운전자의 안전을 보장하기 위해서는 차량의 운동에 대한 다각적인 이해를 필요로 한다. 이는 차량을 구성하는 현가장치, 조향장치, 구동장치, 브레이크 시스템과 같은 기본 구성 요소와 더불어 운전자의 차량 조작 특성까지도 포함할 수 있어야 한다. 이 중에서 차량의 차선 유지 및 횡방향 운동 제어를 위하여 횡풍이 주행 중 차량에 미치는 영향에 대한 관심이 증가하고 있다. 실제로 도로를 주행하는 차량이 횡풍의 영향으로 인하여 경로를 벗어나 추돌사고를 일으킬 수 있으며, 보다 높은 풍속에서는 차량이 전도하면서 대형사고를 유발할 수도 있다. 이는 주행하는 동안 횡풍이 발생하게 되면 차체에 강력한 횡방향 외력의 발생으로 차량의 직진성이 저하되고 차량의 자세에 영향을 미치기 때문이다. 이와 관련하여 독일 FKFS에서 난류 유동에 대한 차량 모델의 불안정성 반응에 대한 연구가 있었다. 차량 후미 외형에 있어서 노치백과 해치백 타입에 대해서 20 % 축소 모델을 통해서 일반 도로에서 발생가능한 형태의 돌풍(Gust)을 발생시켜서 그에 따른 차량의 6자유도 공력 크기를 분석하는 내용이다.¹⁾ 그 밖으로는 드라이빙 시뮬레이터를 활용하여 강한 횡풍 외란을 주행중인 차량에 인가했을 때 운전자가 수정 조타하는 반응을 분석하여 목표 주행 궤적에서 벗어나는 정도를 예측하는 연구가 진행되었다.²⁾ 본 연구에서는 횡방향 부하로 인하여 발생하는 차량의 거동 변화를 이해하고자 차량의 현가계, 조향계 등을 구성하는 각각의 인자가 횡풍에 대한 차량의 거동에 어떠한 영향을 미치는지 제시하고자 한다. 드라이빙 시뮬레이터를 통한 횡풍 반응 운전자 모델을 정교화하고, 이를 다물체 동역학 정밀 차량 모델(ADAMS/CAR)에 MATLAB/Simulink 방식으로 연계시켜서, 횡풍 안정성에 대한 시뮬레이션을 진행하고 실제 횡풍안정성 평가 시험로에서 실측값과의 비교를 통해서 횡풍 예측 모델의 타당성을 검증하고자 한다.

2. 횡풍 안정성 시뮬레이션 모델

2.1 차량 모델

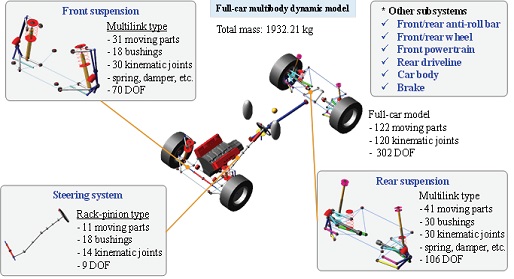
차량 모델은 종류에 따라 Bicycle 모델과 같은 단순한 저자유도 선형 모델(Linear model), 파라미터 모델(Parametric model), 함수형 현가장치 모델(Functional suspension model) 및 다물체 동역학 모델(Multibody dynamic model) 등으로 구분할 수 있다. 이들 방법에는 각각의 장단점이 존재하며, 해석의 목적 및 취득할 수 있는 데이터에 따라 다양한 방법을 채택할 수 있다. 저자유도 모델의 경우 모델이 매우 단순하여 빠른 해석결과를 도출할 수 있다는 장점을 가지고 있지만, 거동에 대한 직관적 이해를 제공하지만 상세 거동에 대한 특성을 비교, 분석할 수 없는 단점을 가지고 있다. 따라서, 이 모델은 주로 주요 인자에 대한 경향성 분석이나 제어 등과 연계된 실시간 모듈 개발을 위하여 주로 활용된다. 본 연구에서는 횡풍 안정성 해석을 위하여 다양한 해석 기법 중 가장 모델링 자유도가 높은 다물체 동역학 해석 기법을 채택하여 적용하였으며, 이를 위하여 상용 동역학 해석 소프트웨어인 ADAMS/Car를 이용하여 생성된 차량 모델을 활용하였다. 타이어 모델은 HMC가 보유한 MTS Flat-Trac^®에서 계측된 타이어 동적 특성을 기반으로 MF-Tool을 통해서 MF-Tyre 모델을 생성하여 차량 모델에 적용하였다(Fig. 1).

Fig. 1

Multibody dynamic model for full-car simulation

2.2 운전자 모델

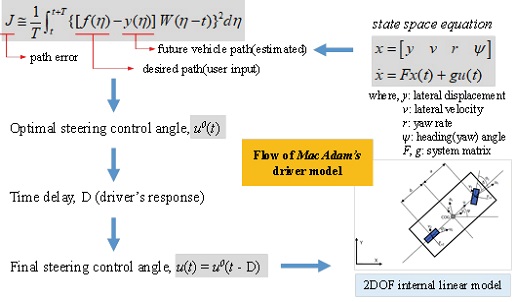
운전자의 조향 입력을 실제와 유사하게 모사하기 위하여 다양한 방법이 연구되어 왔다. 그 중 주행상태에 대한 운전자의 주관적인 인자들을 운전자 매개변수들과 차량의 특성을 이용하여 하나의 전달함수 형태로 표현하는 방법은 운전자가 차량에 미치는 영향을 해석적으로 고찰할 수 있지만, 운전자의 조향 특성이 모두 다르기 때문에 일반적인 다양한 경우에 대하여 고려하기 어렵다. 반면에 운전자가 원하는 경로를 따라서 차량이 주행하도록 동역학 모델을 활용하여 지속적으로 핸들의 조향각을 추정하는 방법은 현재 많은 연구에서 적용하는 방법으로 요구경로와 예측경로 사이의 횡방향 오차를 매개변수로 하여 운전자의 조향각을 결정한다. 횡방향 오차를 제어하는 방법으로는 일반적인 비례 미적분 제어기(PID controller), Fuzzy 제어기에서부터 전달함수를 이용하거나 최적화 모델을 이용하는 방법 등이 있다. 본 연구에서는 운전자 모델 중 최적 예측 제어(Optimal preview control) 방식이 적용된 MacAdam 모델을 운전자 모델로 사용하였다. MacAdam 모델은 전달함수 방식 등 타 방식에 비하여 경로 추적 및 성능이 우수하다고 알려져 있어 많은 연구에서 사용되고 있는 대표적인 운전자 모델이다.

2.2.1 MacAdam 운전자 모델

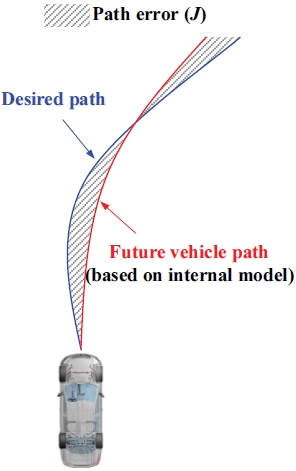
MacAdam 모델은 기본적으로 차량과 운전자 모델을 선형 시스템의 최적 예측 제어 문제로 간주하여 접근한다.³⁾ 즉, 예측 제어를 통해 차량의 요구 경로(Desired path)와 미래 차량 경로(Future vehicle path)간의 차이를 최소화하기 위한 조향각을 계산하는 것을 목적으로 한다. 요구 경로와 미래의 차량 경로 간의 오차에 대한 개념은 Fig. 2에 나타나 있다.

Fig. 2

MacAdam’s driver model control strategy

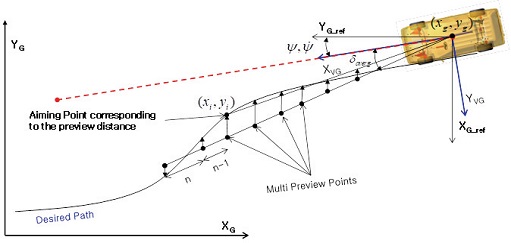
Fig. 2에서 빗금 친 영역의 면적이 횡방향 오차로 정의될 수 있다. 이 면적을 실제 동역학 해석 모델상에서 얻기 위하여 다중 예측 점(Multi preview points)들을 이용하여 근사할 수 있다. 이는 전역 좌표계서 Ground에 180도 변환한 Reference 좌표를 이용하여 표현할 수 있으며, Fig. 3에서 보듯이 각각의 예측점에서의 요구경로와 미래의 차량 경로의 오차를 통해 전체 시간 구간에서의 오차를 구할 수 있다.

Fig. 3

Vehicle-road geometry for multi preview points control

최소화 대상인 횡방향 오차(J)는 현재의 예측 구간 [t, t + T]에 대하여 아래와 같이 정의할 수 있다.

J ≅ 1 T ∫ t t + T f η - y η W η - t 2 d η

(1)

여기서, W는 현재 구간에 대한 임의의 가중치 함수이며, f는 지정된 입력이다. 위 식에서 y(η)는 차량의 미래 경로를 의미하며 이는 선형 차량 모델 운동방정식의 현재 상태와 관련되어 있다. 선형 시스템 이론에 근거하여 요구 경로와 미래의 차량 경로 간의 오차를 최소화하는 이상적인 최적화 결과 u⁰(t)는 아래 식과 같이 정의할 수 있다.

u 0 t = u t + ∫ t t + T ε η A η W η - t d η ∫ t t + T A 2 η W η - t d η

(2)

A η ≅ η - t m T I + ∑ n = 1 ∞ F n η - t n n + 1! g ε η ≅ f η - m T ϕ η, t x t - u t A η ϕ η, t ≅ I + ∑ n = 1 ∞ F n η - t n n!

(3)

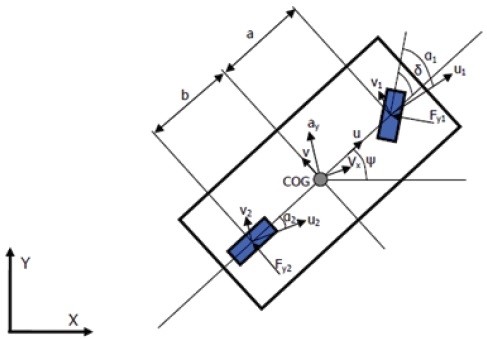
횡방향 경로 오차를 최소화하는 최적의 조향각을 구하기 위하여 사용되는 미래의 차량 경로는 현재 차량의 상태에서 예측되어야 하기 때문에 실제 차량의 동역학 모델로부터 얻어지는 것은 아니며, 2자유도 내부 선형 차량 동역학 모델(Internal linear vehicle dynamic model)을 통해 구해진다. Fig. 4는 내부 선형 모델을 보여준다.

Fig. 4

Internal linear vehicle dynamic model for lateral and yaw motions

운동방정식은 차량의 횡방향 거동과 요 거동을 고려할 수 있는 모델로 가정하여 아래와 같이 정의할 수 있다.⁴⁾

y ˙ = ν + U Ψ ν ˙ = - 2 C α f + C α r / m U ν + 2 b C α r - a C α f / m U - U r + 2 C α f / m δ F W r ˙ = 2 b C α r - a C α f / I U ν + - 2 a 2 C α r + a 2 C α r / I U r + 2 a C α r / I δ F W Ψ ˙ = r

(4)

위 수식을 상태공간 방정식으로 변환하기 위해 아래와 같이 행렬 형태로 표현할 수 있다.

x ˙ = F x + g δ F W

(5)

x = y v r Ψ, F = 010 U 0 A 1 B 1 0 0 A 2 B 2 0 0010, g = 0 C 1 C 2 0

(6)

A 1 = - 2 C α f + C α r / m U A 2 = 2 b C α r - a C α f / I U B 1 = 2 b C α r - a C α f / m U - U B 2 = - 2 a 2 C α f + b 2 C α r / I U C 1 = 2 C α f / m C 2 = 2 a C α f / I

(7)

한편, 횡방향 오차를 최소화하는 조향 입력 u⁰(t)는 이상적인 상태에서의 조향각이다. 하지만 실제 운전자는 신경학적으로 장애물, 횡풍과 같은 외부로부터의 방해를 인지하고 그에 따른 조향을 하기까지 일정 시간 지연이 되며 또한, 개개인의 운동신경, 운전 숙달 정도에 따라 모두 다른 반응을 갖는다. 따라서 이러한 효과에 대한 반영은 반드시 필요하다. 운전자가 상황을 인지하고 핸들을 조작하기까지의 시간 지연 D를 고려한 운전자 모델에서 출력되는 최종 조향 입력은 아래와 같이 정의할 수 있다.

u t = u 0 t - D

(8)

위에서 언급한 MacAdam 운전자 모델의 전체 흐름은 경로 오차를 최소화하기 위해 내부 선형 차량 모델을 이용하는 폐루프 형태이며 최종적으로 Fig. 5와 같이 정리할 수 있다.

Fig. 5

Flow of MacAdam’s driver model

2.2.2 주요 모델 파라메타 정의

MacAdam 운전자 모델에는 요구된 경로를 추종하기 위하여 내부 선형 차량 동역학 모델을 이용하여 미래의 경로를 예측하도록 구성되어 있다. 따라서 선형 모델의 주요 파라미터를 실제 차량 모델과 유사하게 정의하여야 올바르게 운전자의 조향을 모사할 수 있다. Table 1은 내부 선형 차량 모델에 필요한 주요 파라미터와 그 값들을 보여주고 있다.

Table 1

Parameters of internal linear vehicle model

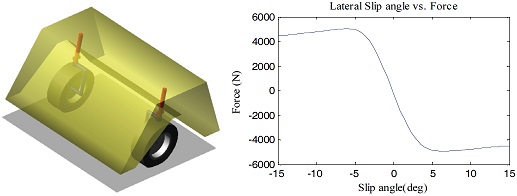
Table 1에 제시된 파라미터 중 전, 후륜 타이어의 코너링 강성(Cornering stiffness)은 타이어 모델과 타이어 테스트 리그를 이용하여 얻을 수 있다. 일정 수직력을 받는 타이어에 회전을 준 후, 횡방향 슬립각을 인가하고 그 때 타이어에서 발생하는 횡력과의 관계를 이용하여 추출하였다. 횡방향 슬립각 1~3 deg의 선형구간에서의 기울기는 53,490.33 N/rad으로 이 값을 선형 모델 파라미터로 사용하였다. Fig. 6은 각각 타이어 테스트 리그 모델의 모습 및 타이어의 횡방향 슬립과 횡력과의 관계이다.

Fig. 6

Tire virtual test rig and lateral slip angle vs. force

위의 파라미터 외에도 MacAdam 운전자 모델에는 운전자의 모델 특성을 고려할 수 있는 Preview time(T_p)과 Delay time(T_d)이 고려된다. Preview time은 내부 차량 모델을 이용하여 예측하는 거리 범위와 관련이 있으며 운전의 숙달 정도를 반영할 수 있는 파라미터이다. 즉, Preview time이 길수록 상대적으로 먼 지점까지의 횡방향 경로를 예측할 수 있으며, 이로 인하여 보다 정확하게 요구 경로를 추종할 수 있다. 반면, Delay time은 운전자가 핸들 조작의 필요성을 인지하고 실제로 반응하기까지의 속도와 관련된 파라미터로 짧을수록 빠르게 반응한다는 의미가 된다. Table 2는 실험을 통해 획득한 다양한 운전자 특성에 따른 파라미터를 보여준다. 본 연구에서 ‘Rough’, ‘Smooth’, ‘Over-reacting’, ‘Precise’로 분류된 총 4가지 특성 중 운전자의 특성을 ‘Precise’로 채택하고 적용하였다.

Table 2

Parameters of driver’s characteristics

2.3 공력 시뮬레이션 모델

2.3.1 공기 역학적 힘 및 모멘트 정의

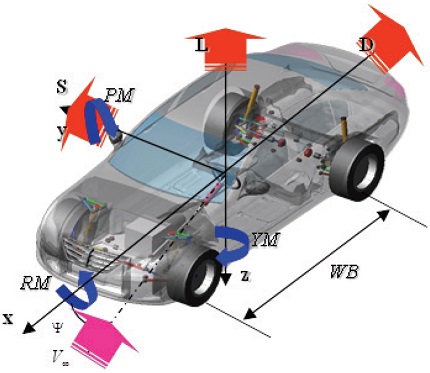
주행 중 차량에 전달되는 공기 역학적인 힘은 대표적으로 이동방향으로 발생하는 주행 저항, 측면에서 불어오는 횡풍으로 압축할 수 있다. 이와 같은 공기 역학적인 힘은 매우 불규칙하며 차량의 형상, 면적 변화, 차량의 속도, 횡풍의 속도, 횡풍 방향 등에 따라 다양하게 변화하며 차량 거동에 영향을 미치게 된다. 과도상태의 횡력을 해석 모델 상에서 고려하기 위하여 순간의 힘을 정상상태의 횡력으로 가정할 수 있으며, 차량에 대한 유동해석이 목적이 아닌 이상 이와 같은 방법이 적용되고 있다. 3차원 공간상에서 차량에 작용하는 정상상태 공력은 차량내에 위치한 임의의 압력 중심에 대하여 작용하는 3개의 직교하는 힘과 모멘트로 나눌 수 있다. Fig. 7은 SAE(Society of Automobile Engineering)에서 제시한 차량의 Reference frame에 대한 정의를 보여준다.

Fig. 7

The SAE vehicle reference frame

위 그림에서 3개의 직교하는 힘은 전후 방향(x), 좌우 방향(y), 수직 방향(z)에 대하여 각각 공기저항(Drag force), 횡력(Side force), 양력(Lift force)이라 하며, x, y, z축에 대한 모멘트는 롤링 모멘트(Rolling moment), 피칭 모멘트(Pitching moment), 요잉 모멘트(Yawing moment)라 한다. 공기저항은 주행을 저해하는 것으로 고속에서의 가속성능이나 연비, 최고속에 영향을 미친다. 횡력은 차를 옆으로 미는 힘으로 횡풍과 관련이 있으며 차량의 직진성, 주행 안정성과 연관이 있다. 횡력이 작용점 즉, 공력 중심과 차량의 무게중심과 다를 시 요잉 모멘트가 동시에 발생하게 된다. 양력은 차를 들어 올리려고 하는 힘으로, 양력이 발생하면 타이어의 접지 하중이 작아지고 접지력(Grip force)이 저하된다. 피칭 모멘트는 양력 중심이 차량의 무게중심과 다를 때 발생하며 역시 차량의 조종 안정성과 연관된다. 공력으로 인하여 발생하는 힘과 모멘트는 아래와 같이 정의할 수 있다.⁵⁾

D A = 12 ρ V ∞ 2 C D A

(9)

S A = 12 ρ V ∞ 2 C S A

(10)

L A = 12 ρ V ∞ 2 C L A

(11)

R M = 12 ρ V ∞ 2 C R M A L

(12)

P M = 12 ρ V ∞ 2 C P M A L

(13)

Y M = 12 ρ V ∞ 2 C Y M A L

(14)

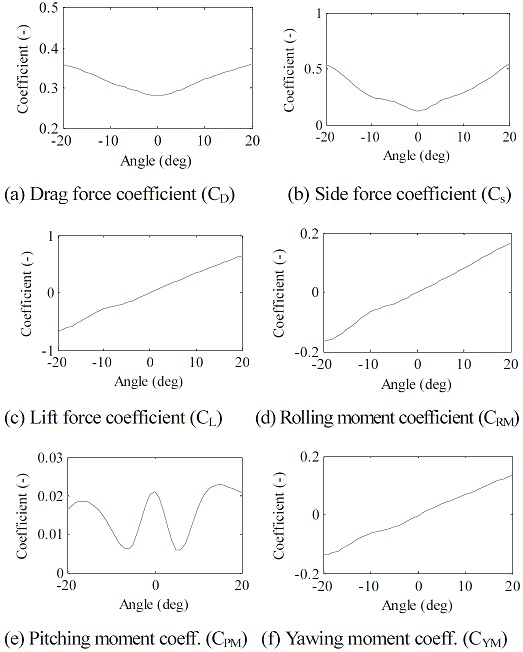
식 (9)부터 식 (14)까지는 각각 공기저항, 횡력, 양력, 롤링 모멘트, 피칭 모멘트, 요잉 모멘트를 의미한다. 또한 ρ는 공기밀도, V_∞는 상대 공기 흐름 속도(Relative air flow velocity), A는 차량의 전면 면적 그리고 L은 축거(Wheel base)를 의미하며. C_d, C_s, C_L, C_R_M, C_P_M, C_Y_M은 각각 6방향의 힘과 모멘트에 대한 무차원 계수이다. 이 무차원 계수는 실제 차량의 차량의 풍동 시험을 통해 얻을 수 있으며 횡풍의 입사각도에 대한 힘이다.⁶⁾ Fig. 8은 본 연구에서 적용된 대상차량의 공력계수이다.⁷⁾

Fig. 8

Aerodynamic coefficient of test car

2.3.2 상대 공기 흐름 속도 정의

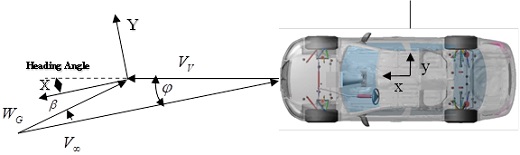
식 (15)에서 상대 공기 흐름 속도 혹은 최종 공기 흐름 속도(V_∞)는 차량을 기준으로 외부에서 인가되는 모든 공력의 합에 대한 공기 흐름 속도를 의미한다. 차량이 주행 중에 횡풍의 영향을 받을 때, 이 상대 공기 흐름 속도는 차량의 속도 벡터와 β의 입사각으로 차량에 작용하는 횡풍의 합 벡터로 Fig. 9와 같이 정의할 수 있으며, 전역 기준 좌표계(Global reference coordinates)를 기준으로 다음과 같은 수식으로 나타낼 수 있다.

V ∞ = - V V + W G

(15)

Fig. 9

Wind velocity in ground reference frame

여기서, V_v와 W_G는 각각 차량의 속도벡터와 횡풍의 속도 벡터를 나타낸다. 차량의 진행방향 축 즉, x축에 대한 총 외력의 입사각(Resultant air flow angle) ϕ는 최종 공기 흐름 속도(Resultant air flow velocity)의 x방향 성분과 y방향 성분을 이용하여 아래와 같이 구할 수 있다.

φ = t a n - 1 V ∞ y V ∞ x

(16)

위 식에서 V_{∞_y}와 V_{∞_x}는 각각 최종 공기 흐름 속도의 x성분과 y성분을 의미한다. 한편, 3차원 공간상에서 전역 좌표계를 기준으로 기술된 횡풍의 속도 벡터와 차량의 기준 좌표를 기준으로 기술된 차량 속도 벡터의 합을 얻기 위해 횡풍의 속도 벡터를 차량의 기준 좌표에 대한 표현으로 변환해주어야 한다. 횡풍의 속도 벡터는 전역 좌표계를 기준으로 각 방향 성분의 합으로 표현할 수 있다.

W G = W G X I + W G X J + W G X K

(17)

여기서, I, J 그리고 K는 각각 전역 기준 좌표계 X, Y, Z 축에 대한 단위 벡터이며, WGX, WGY, WGZ는 각 방향 성분이다. 전역 기준 좌표계로부터 차량 기준 좌표계(x, y, z)로의 변환행렬을 도입하면 속도 벡터의 각 방향 성분을 차량 기준 좌표계에 대한 표현으로 변환할 수 있다.

W G x W G y W G z = T W G X W G Y W G Z

(18)

여기서

W_Gi = i component of the wind velocity in vehicle reference frame
T = transformation matrix

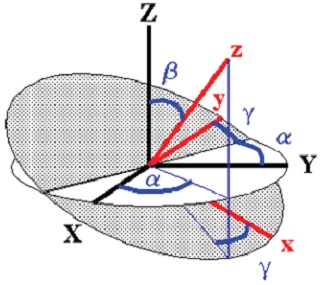
Fig. 10에 제시된 오일러 각(Euler angle) γ, θ, ϕ를 이용하여 변환행렬을 다음과 같이 정의할 수 있다.

T = Φ Θ Γ

(19)

Γ = cos ⁡ γ sin ⁡ γ 0 - sin ⁡ γ cos ⁡ γ 0 001

(20)

Θ = 100 0 cos ⁡ θ sin ⁡ θ 0 - sin ⁡ θ cos ⁡ θ

(21)

Φ = cos ⁡ ϕ sin ⁡ ϕ 0 - sin ⁡ ϕ cos ⁡ ϕ 0 001

(22)

Fig. 10

Euler angle roation

위 변환 행렬을 이용하여 횡풍 속도 성분을 차량 기준 좌표계에 대한 표현으로 정리하면 아래와 같이 쓸 수 있다.

W G = W G x i + W G y j + W G z k

(23)

여기서,

W_Gx = W_GX (cosγ cosϕ - sinϕ cosθ)
+W_GY(sinγ cosϕ - cosθ cosγ sinϕ) + W_GZ(sinϕ cosθ)
W_Gy = W_GX (-sinϕ cosγ - sinγ cosθ cosϕ)
+W_GY(-sinϕ sinγ + cosθ cosγ cosϕ) + W_GZ(cosϕ sinθ)
W_Gz = W_GX(sinθ sinγ) + W_GY(-sinθ cosγ + W_GZ(cosθ)

오일러 각 θ는 일반적인 주행 조건에서는 매우 작다. 또한 (γ +ϕ)는 Ground를 기준으로 차량의 진행 방향 각도와 유사하다. 식 (24)은 차량 좌표계를 기준으로 한 각 방향 성분의 합으로 표현할 수 있다.

V ∞ = - V V x + W G x i + - V V y + W G y j + - V V z + W G z k V ∞ = V ∞ x i + V ∞ y j + V ∞ z k

(24)

i, j, k는 차량 기준 좌표계의 x, y, z축에 대한 단위 행렬이다. 최종적으로 Resultant air velocity 의 크기는 아래와 같이 계산할 수 있다.

V ∞ = V ∞ x 2 + V ∞ y 2 + V ∞ z 2

(25)

본 연구에서는 위에서 설명한 횡풍 해석 모델을 ADAMS/Car에 외부 Sub-routine으로 적용하였으며, 횡풍 조건과 차량의 자세 변화, 그리고 측정한 6방향 공력계수에 따라 차량에 인가되는 횡력을 계산하고 다양한 조건과 차량 설계 변경에 따른 횡풍 안정성 변화를 해석 및 평가한다.

2.4 횡풍 안정성 통합 시뮬레이션 모델 개요

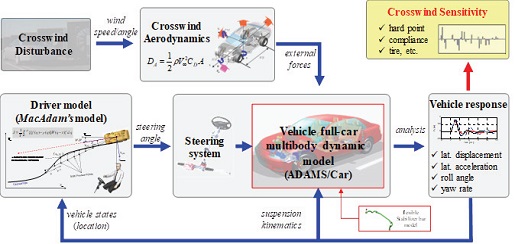
Fig. 11은 앞 절에서 언급한 다물체 동역학 차량 모델, MacAdam 운전자 모델, 횡풍 해석 모델을 통합한 횡풍 안정성 해석 모델의 개요를 보여준다. 횡풍 재현기에서는 사전에 정의된 횡풍의 속도 및 입사각을 기준으로 차량으로 특정 함수 형태의 횡풍을 인가하게 된다. 횡풍 해석 모델에서는 이 횡풍을 차량의 자세와 속도, 그에 따른 공력 계수 등을 고려하여 차량 기준 좌표계에 대한 6축 횡력으로 변환하여 차량 모델의 공력의 작용점(CP, Center of Pressure)에 인가해준다. 해석이 진행되는 매 스텝마다 이를 실시간으로 계산하여 적용한다. 운전자 모델에서는 내부 선형 차량 동역학 모델과 다중 Preview point를 이용하여 산출한 차량의 미래 횡방향 경로가 사전에 정의된 요구 경로와 일치하는 지 여부 즉, 오차를 판단하여 요구 경로를 적절하게 추종할 수 있는 조향각을 최적 예견 제어 이론에 근거하여 계산하고 이를 차량 모델의 조향각으로 출력해주게 된다. 이때, 운전자의 특성에 따라 달라지는 반응 시간 등이 조향각 생성 시 적용된다. 차량 모델에서는 운전자 모델로부터 실시간으로 전달되는 조향각과 횡풍 모델로부터 전달되는 횡력을 고려하여 차량의 주행 거동을 시간적분을 통해 산출하게 된다. 차량은 다물체 동역학 해석 기법을 기반으로 모델링 되어 실제 차량에 존재하는 각종 부품들을 세부적으로 고려할 수 있는 장점을 가지고 있다. 이와 같은 차량, 공력, 운전자 모델이 통합된 횡풍 안정성 해석 폐루프 모델을 이용하여 현가계, 타이어, 스프링, 댐퍼, 부싱 등과 같은 차량 주요 인자의 설계 변화가 주행 중 발생하는 차량의 거동에 어떤 영향을 미치는지 해석 결과를 통해 확인하고, 민감도 분석을 통해 횡풍에 대하여 강건한 설계 인자를 도출한다. 횡풍 시뮬레이션에 대한 해석 환경 구성은 Yang⁸⁾의 연구를 참고하였다.

Fig. 11

Overall flow of X-wind closed-loop response analysis model

3. 횡풍 실차 평가 및 시뮬레이션 모델

3.1 횡풍 안정성 평가 방법

시험차를 대상으로 차량의 횡풍 안정성을 평가하는 방법은 일반적으로 두 가지 평가 방법이 적용되고 있다. 첫 번째는 횡풍 재현기(X-Wind Generator)를 이용하는 방법이다. 이 방법은 횡풍을 임의적으로 생성하는 장비를 활용하기 때문에 재현성과 반복성이 뛰어나다는 점과 외부의 대기 조건의 영향을 상대적으로 적게 받는다는 점, 이로 인하여 데이터 분석이 용이하다는 장점을 가지고 있다. 하지만 이 방법은 임의적으로 횡풍을 생성하기 때문에 실제 주행 중에 운전자가 느끼는 횡풍과 괴리가 있다는 점, 반복 평가 시 학습 효과가 생긴다는 단점을 가지고 있다. 두 번째 방법으로는 실도로 주행을 통하여 횡풍 안정성을 평가하는 방법이 있다. 이 방법은 횡풍이 많이 발생하는 구간을 직접 주행하면서 차량거동과 풍향/풍속을 측정한 후, 차량 모델 및 운전자 모델을 이용하여 데이터를 분리해내고 상관성 분석을 하여 차량의 횡풍 안정성을 판단하는 방법이다. 실도로 대기 횡풍 평가법의 장점으로 실주행 시 운전자가 느끼는 상황과 평가 환경이 유사다는 점과 운전자의 학습효과가 상대적으로 적다는 점이 있으나, 예측이 불가능한 대기 환경의 영향을 많이 받는다는 단점이 있다. 두 가지 평가 방법 중 횡풍 재현기를 이용하는 방법은 운전자의 핸들 작동 여부, 핸들의 고정 여부에 따라 Table 3과 같이 3가지 종류로 분류할 수 있다.

Table 3

Evaluation method for X-wind stability

3.2 시험 결과와의 비교 검증

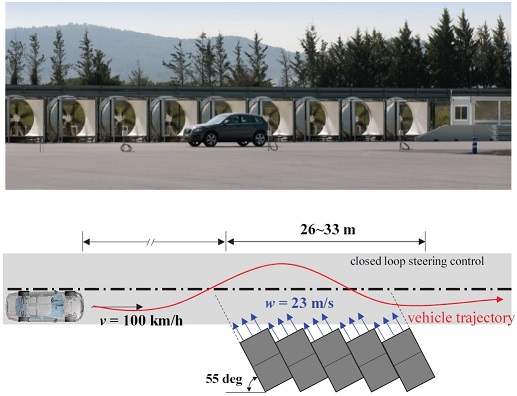
본 연구에서는 앞장에서 언급한 횡풍 안정성 해석 모델을 타당성을 확인하기 위하여 유사한 조건에서의 실제 시험 결과를 이용하여 비교, 검증하였다. 횡풍 안정성 시험은 스페인 IDIADA社에서 수행하였다. 횡풍 안정성 시험은 앞 절에서 언급한 시험 방법들 중 ‘X-wind open-loop fixed steering’과 ‘X-wind closed-loop’이 채택되어 수행되었으며, 해석 조건 역시 시험 조건과 유사하기 설정하고 해석을 수행하였다. Fig. 12는 본 연구에서 적용한 폐루프 평가에 대한 시험 및 해석 시나리오이다.

Fig. 12

Analysis scenario of X-wind closed-loop test

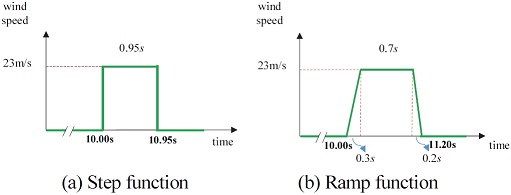
차량의 주행속도는 100 km/h이며, 횡풍 구간의 길이는 26~33 m, 횡풍 재현기에서 생성되는 바람의 속도는 약 23 m/s, 횡풍이 인가되는 입사각은 55도이다. 횡풍발생기의 배치 및 설치 설정값은 구현하고자 하는 시나리오에 맞춰서 시험자가 설계할 수 있으나,¹⁴⁾ 미국 및 스페인 주행시험장에 있는 횡풍시험로 기본 규격을 사용하였다. 앞서 언급 하였듯이 본 해석 조건은 스페인 IDIADA社에서 수행한 시험 환경과 유사한 환경이다. 본 평가 시나리오를 바탕으로 해석 조건을 생성하였다. 앞장에서 언급한 ADAMS/Car에 사용자 서브루틴으로 적용된 횡풍 재현기 모듈은 횡풍 재현기의 효과를 스텝 함수(Step function) 혹은 램프 함수(Ramp function) 형태의 횡풍 함수로 입력하도록 되어 있다. 차량 다물체 동역학 모델 상에서 횡풍은 차량 내부에 압력 중심(CP, Center of Pressure) 즉, 한 점에 6축 방향의 횡력의 효과가 인가되도록 되어 있지만, 실제로는 차체의 전두부부터 후미부까지 연속적으로 횡풍이 차량에 영향을 미친다. 따라서 횡풍의 효과를 스텝 함수로 인가할 시, 횡풍 구간의 시작 부분과 종료 부분에서 실제와는 다른 불연속적인 거동이 나타난다. 이러한 효과를 완화하고 자 램프 함수 형태의 횡풍 함수도 동시에 적용하여 거동을 비교하였다. 이 역시도 실제 환경과 같이 연속적인 효과를 정확히 반영하는 것은 아니지만 반력 빌드업 구간을 설정하여 간접적으로 유사한 효과를 내도록 설정하였다.⁹⁾ 하지만 본 연구에서는 차량 설계 인자 변경에 따른 횡풍 거동 변화를 분석하는 것이 목적이기 때문에 횡풍이 차량에 인가되는 순간의 효과를 정확하게 고려할 필요는 없으며, 이와 같은 간접적으로 고려하는 방법만으로도 민감도를 분석하는 것에는 충분한 조건이다. Table 4는 앞서 언급한 두 가지 형태의 횡풍 함수에 대한 해석 조건이며, Fig. 13은 각 횡풍 모사 함수의 형태를 보여준다. 두 횡풍 모사 함수의 형태는 상이하지만 인가되는 바람의 총 량 즉, 그래프 상에서의 면적은 동일하다.

Table 4

Definition of analysis condition

Fig. 13

Step and ramp wind function

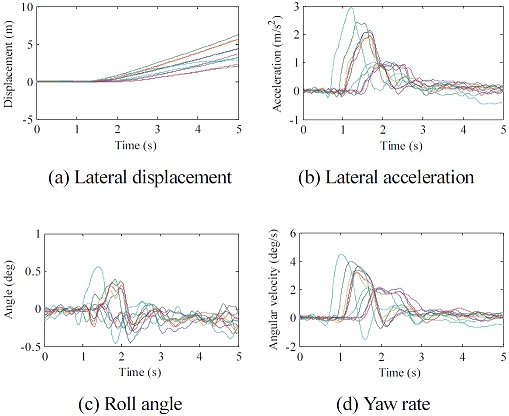
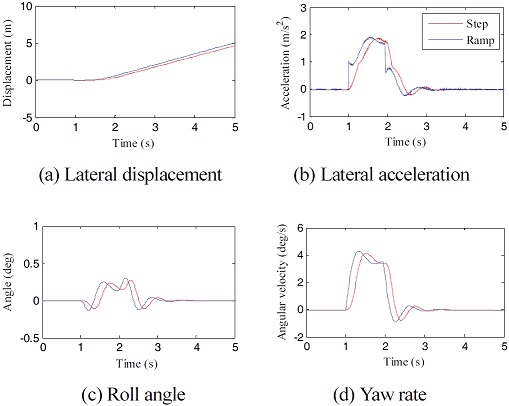
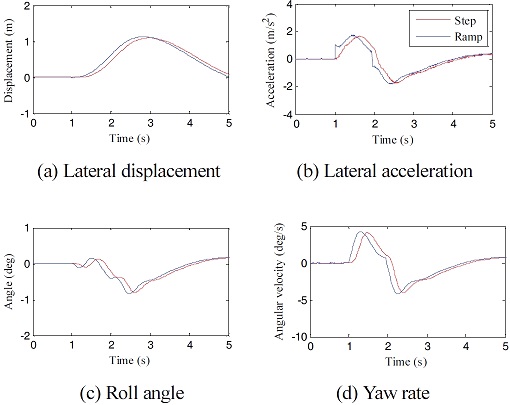
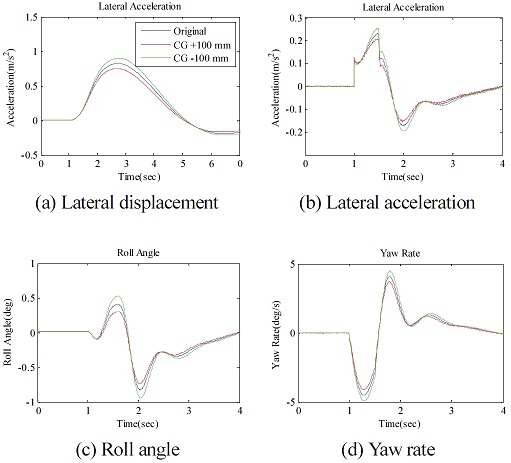
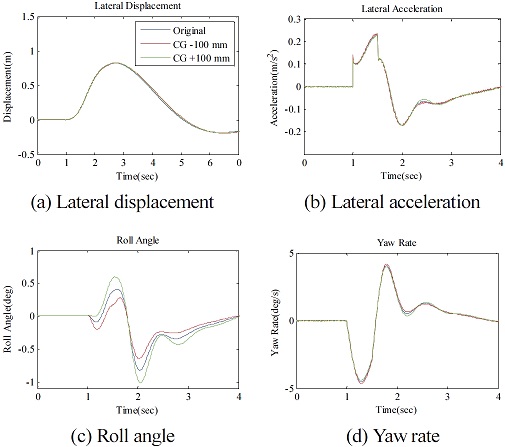
해석은 앞서 언급하였듯이 두 가지 방법 즉 조향각을 0도로 고정한 개루프 시험의 해석과 운전자 모델이 추가되어 요구 경로를 추종하게 하는 폐루프 시험의 해석을 수행하였다. 아래에서 제시하는 시험 평가 항목으로는 차량의 횡방향 안정성 평가 시, 대표적으로 취급되는 횡 변위(Lateral displacement), 횡 가속도(Lateral acceleration), 롤 각도(Roll angle), 요 각속도(Yaw angular velocity)를 채택하였다. 주행 중에 생성되는 다수의 결과 값들 중 최대값(Peak value)을 평가에 대표 인자로 선정하였으며, 시험 결과의 경우 다수의 시험이 수행되었기 때문에 그 결과들의 평균값을 사용하여 비교하였다. Fig. 14와 Fig. 15은 각각 개루프 횡풍 해석에 대한 시험 결과 및 해석 결과이며, Fig. 16과 Fig. 17은 각각 폐루프 횡풍 평가에 대한 시험 결과 및 해석 결과이다.¹⁰⁾ 해석결과에서 횡풍 입력은 1 s 시점에서 시작한 것으로 설정하였다.

Fig. 14

Open-loop test results

Fig. 15

Open-loop simulation results

Fig. 16

Closed-loop test results

Fig. 17

Closed-loop simulation results

개루프 및 폐루프 시험 결과를 보면, 각각 11개, 15개의 시험 데이터가 비교되었는데, 횡 변위, 횡 가속도, 롤 각도, 요 각속도 4개의 평가 인자에 대하여 시간에 따른 전체적인 거동은 유사하지만 각 시험마다 편차가 큰 것을 볼 수 있다.¹¹⁾ 이는 시험 계측과정에서 발생하는 오차, 횡풍 재현기에서 생성하는 바람의 불규칙성, 외부 바람의 영향으로 인한 결과로 판단되며, 폐루프 횡풍 안정성 시험의 경우 실제 시험 운전자의 조향 입력이 작용하기 때문에 더욱 편차가 커진 것으로 판단된다. 따라서 전체 시험 데이터의 경향성을 파악하기 위해서 각 시험 데이터 최대값의 평균을 대표값으로 선정하고 비교하였다. 두 시험 결과에서 횡 변위의 경우 개루프 시험에서는 조향각이 초기 조향각으로 고정되기 때문에 횡풍 재현기를 통과할 때, 차량의 Heading 방향이 바뀌게 되고 그대로 주행하게 되며, 폐루프 시험에서는 횡풍 재현기를 통과할 때 차량이 기존 경로에서 이탈되다가 운전자의 조향에 의해 다시 본래의 경로로 돌아오는 것을 볼 수 있다. 횡 가속도, 롤 각, 요 각속도에 대해서도 이와 같은 거동차이로 인하여 계형이 상이하게 나타나는 것을 볼 수 있다. 개루프와 폐루프 해석 결과를 보면, 횡풍 모사 함수를 스텝 형태로 인가하였을 때와 램프 형태로 인가하였을 때를 비교하면, 스텝 함수의 경우 횡풍 재현기 구간을 진입할 때와 이탈할 때 그래프의 계형에 불연속적인 지점이 발생한다.¹²⁾ 반면에 램프 함수를 적용하였을 경우 연속적인 형태로 산출되는 것을 확인할 수 있다. 결과를 통해 알 수 있듯이 횡풍 함수로 스텝 함수를 적용했을 때보다 램프 함수를 적용하였을 때, 다소 최대값이 줄어든 것을 볼 수 있으나 큰 차이는 없을 것 또한 확인할 수 있다.

4. 횡풍 안정성 민감도 및 상관관계 분석 절차

4.1 시뮬레이션 조건 정의 및 결과

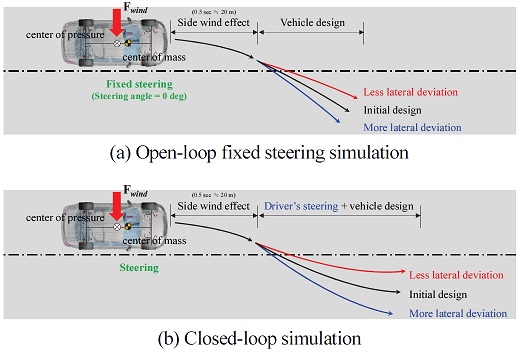
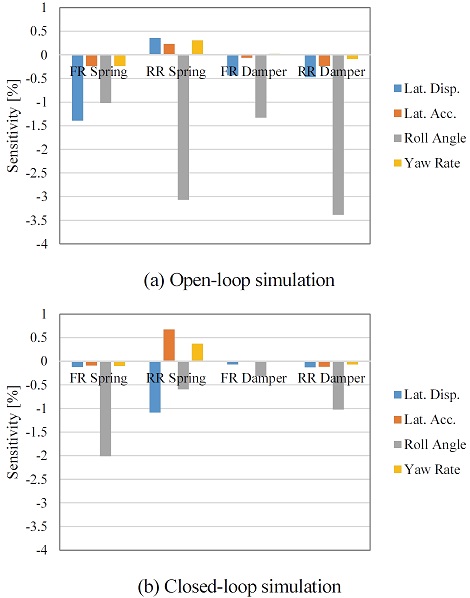
본 절에서는 민감도 분석을 위한 횡풍 안정성 해석 조건을 정의하고 초기 설계안에 대한 해석 결과를 제시한다. 횡풍 안정성 해석 조건은 앞장에서 언급한 국제 규정 ISO에 근거한 개루프 방법(‘Open-loop fixed steering’)과 운전자의 조향 효과를 고려한 폐루프 방법(‘Closed-loop simulation’)을 적용하였다. Fig. 18(a)와 (b)는 각각 두 가지 조건의 해석에 대한 개요도를 보여준다. 차량의 속도 및 기타 조건은 고속 주행 시의 거동을 기준으로 판단하기 위하여 주행속도는 140 km/h, 횡풍의 속도는 20 m/s, 횡풍의 입사각은 55 deg, 그리고 횡풍 인가 시간은 0.5 sec, 횡풍 인가 형태는 스텝 함수로 설정하였다. 해당 차량 속도에 대해서 횡풍 인가 시간을 고려하면 횡풍 구간의 길이는 약 20 m 정도로 간주할 수 있다.

Fig. 18

Overview of open and closed-loop simulation

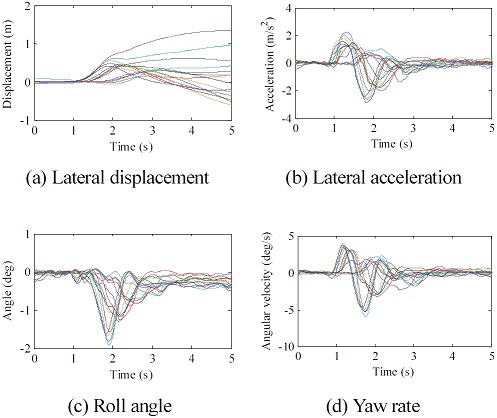
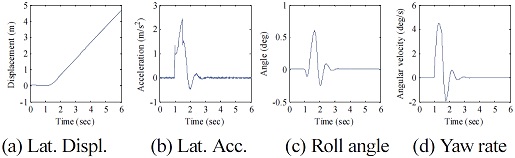
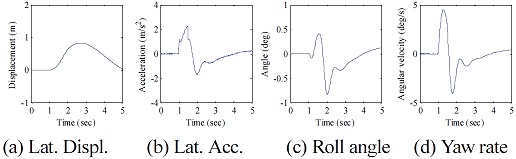
Fig. 19와 Fig. 20은 각각 개루프 해석과 폐루프 해석에 대한 초기 차량 설계안의 횡풍에 대한 주행 거동이다. 여기서 초기 차량 설계안이란, 민감도 분석 등을 위해 설계 변경을 하지 않은 최초의 차량 설계안을 의미한다. 본 해석 결과는 앞서 제시한 결과와 유사하므로 간략하게 제시한다.¹³⁾

Fig. 19

Results of open-loop simulation for sensitivity analysis

Fig. 20

Results of closed-loop simulation for sensitivity analysis

각 그래프에서 1초부터 0.5초 동안 횡풍의 영향을 받는데, 횡 가속도와 요 각속도는 차량이 횡력을 인가 받는 구간에서 최대값을 갖는다는 것이다. 반대로 횡 이탈량 및 롤 각도는 횡풍 구간을 벗어난 지점에서 최대치가 발생한다. 이러한 점이 각 평가 인자 혹은 설계인자 변화와 상관성을 가질 것으로 판단된다.

4.2 K&C 성능 관련 인자 선정

본 연구에서는 전, 후륜 현가장치의 하드포인트와 부싱 설계 변화에 따른 민감도 파악 후, 이들이 현가계의 기구학(Kinematics) 및 컴플라이언스(Compliance) 특성 변화와 어떠한 관계가 있는지 파악하기 위해 횡방향 주행거동과 관련된 몇 가지 K&C 인자를 선정하고 설계 변화와의 상관관계를 도출하였다. 실제 차량의 SPMD(Suspension Parameter Measuring Device)를 통해 추출할 수 있는 총 10개의 시험 모드의 약 75개의 인자들 중에서 3개의 시험 모드 9개의 K&C 인자를 선정하였다. 3개의 시험 모드는 공차 중량에서의 수직 모드, 롤 모드, 횡 모드이며, 수직 모드(Vertical mode)에서는 범프 시, 휠 레이트(Wheel rate), 토우 변화량(Toe change), 휠 베이스 변화량(Wheel base change)을, 롤 모드(Roll mode)에서는 롤 강성 배분(Suspension roll stiffness distribution), 롤 게인(Roll gain), 롤 축 구배(Roll axis gradient)를, 횡 모드(Lateral mode)에서는 강체 타이어 패치에서의 횡 강성(Lateral stiffness-rigid tire patch), 횡 컴플라이언스 조향 계수(Lateral compliance steer coefficient), 횡 컴플라이언스 캠버 계수(Lateral compliance camber coefficient)가 채택되었다.

4.3 시뮬레이션 연구 진행 흐름 및 절차

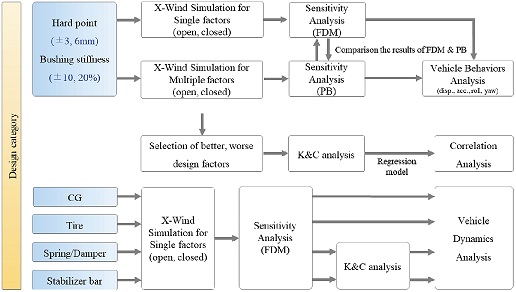
주요 설계인자들이 횡풍 안정성에 미치는 영향을 알아보기 위하여 각 인자들에 대한 민감도 분석을 수행하였다. 설계 변수는 전/후륜 현가계의 하드포인트, 전/후륜 현가계 부싱 강성, 차량 무게중심 위치, 타이어 주요 인자, 전/후륜 현가계 스프링 강성 및 댐퍼 감쇠계수, 스테빌라이져 바 특성으로 설정하였다. 여기서 하드포인트의 경우 한 개의 하드포인트 당 3차원 공간상에 x, y, z 방향 3개의 설계변수를 고려하였으며, 부싱 강성의 경우에 6개의 설계변수를 고려하였다. 설계 범위는 하드포인트의 경우에는 ±3 mm로 부싱 강성의 경우 강성의 Scale factor를 조정하여 ±10 %로 설정하였지만 설계범위가 미소한 편이기 때문에 ±6 mm, ±20 %에 대하여도 민감도 분석을 수행하였다. 전/후륜 현가계의 하드포인트와 부싱 강성에 대하여 기본적으로 유한차분법(FDM)을 적용하여 단일인자의 효과를 분석하였지만, 현가계가 다양한 링크들과 힘 요소들이 복잡하게 연계되어 있는 시스템이기 때문에 다중인자 설계 변경을 통한 민감도 분석 방법도 적용하여 이들 결과를 비교, 분석하였다. 다중인자 설계 변경을 적용한 경우 단일인자만을 변경하였을 시 나타나지 않는 효과가 나타날 수도 있기 때문에 이와 같은 방법의 적용이 민감도를 보다 합리적으로 파악할 수 있게 해준다고 판단된다. 다중인자 설계 변경은 앞서 언급한 실험적 방법 중 Plackett-Burman 방법(PB)을 이용하여 고려하였다. 이 방법은 각 실험에 대한 설계는 모두 직교하기 때문에 불필요한 실험이 발생하지 않으며, 이 방법이 다수의 설계변수를 최소한의 실험 수로 고려할 수 있다는 장점이 있어 본 연구에서 적용하기에 적합한 방법이다. 현가계의 경우 서로 다른 두 가지 방법으로 민감도 분석을 하고 결과를 비교하고, 각 실험에서의 거동들이 어떠한 경향성을 보이는지 분석한다. 또한 다중인자 설계 변경 시 사용되었던 직교 설계안들 중 횡풍 안정성 평가 인자가 개선 혹은 악화된 일부 케이스를 추출하여 이들에 대하여 K&C 해석을 수행하고 이러한 설계안들이 어떤 공통점을 갖는지 회귀 모형을 이용하여 분석하였다. 현가계 관련 인자 외의 타 인자들은 각 인자들간의 연관관계 보다는 개별적인 인자의 민감도가 관심 대상이기 때문에 단일인자 설계변경 해석 만을 수행하고 유한차분법을 적용한 민감도 분석을 수행하였다. 자세한 내용은 Fig. 21로 대체한다.

Fig. 21

Overview of sensitivity analysis for X-Wind

본 연구는 설계 변수의 범위 및 개수가 상대적으로 많은 편이기 때문에 이들을 자동적으로 처리할 수 있는 별도의 처리기가 필요한데 이는 Matlab을 이용하여 자체적으로 개발하였다. 개발된 코드는 ADAMS/Car와 In-house 결과 후처리 프로그램과 연결되어 민감도 분석 해석 케이스에 대하여 자동 해석을 수행하여 주고 결과 파일들을 불러들어 민감도를 산출하여 주는 기능을 한다. 또한 각 시험 모드에 대한 K&C 해석 및 상관관계 도출도 개발된 코드를 이용하여 수행되었다.

4.4 횡풍 안정성 민감도 및 상관관계 분석

본 장에서는 앞 장에서 설명한 해석 모델, 민감도 분석 방법 및 절차, 설계 변수 및 목적 함수를 대상으로 한 민감도 분석 결과를 제시한다. 설계 변수의 개수가 많고 모든 변수가 차량 거동과 서로간에 연계되어 관련된 것이 아니기 때문에 연계된 것들끼리 분류하여 민감도 분석을 수행하였다. 목적함수는 횡 변위, 횡 가속도, 롤 각도, 요 각속도로 이들을 통합하여 고려하거나 각자 고려하였다.

4.4.1 현가계 하드포인트 위치 및 부싱 강성

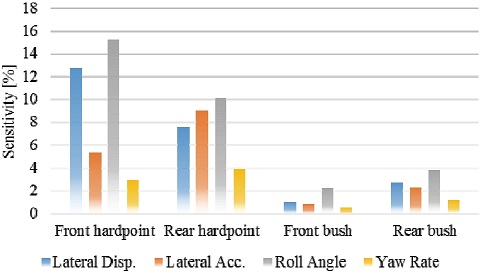
Fig. 22는 개별 현가계 설계인자의 민감도 분석 결과를 종합하여 각 차량 구성 요소가 횡풍 안정성 변화에 미치는 영향도를 나타낸 그림이다. 아래 결과는 하드포인트 설계 범위 ±3 mm, 부싱 강성 설계 범위 ±10 % 적용 시에 대한 결과로 두 설계 범위가 서로 동일한 정도라고 할 수는 없으나 본 연구에서 설정한 범위인 만큼 해당 범위를 적용하여 비교해 보았다. 산출 근거는 전체 민감도 분석 결과 즉, 개루프, 폐루프 해석과 FDM, PB를 이용한 민감도 분석 결과의 전체 평가 인자별 평균이다. 그림을 통해 알 수 있듯이 횡풍에 대한 차량 거동 중에서 롤 각 및 횡 변위의 개선 폭이 타 인자에 비해서 상대적으로 큰 것을 알 수 있다. 또한 하드포인트의 변화 즉, Kinematic steer가 부싱 강성의 변화 즉, Compliance steer 보다 횡풍 안정성에 대한 영향도가 크다는 것도 알 수 있다. 이는 비단 횡풍 안정성에만 해당하는 것은 아니며, 차량의 성능 개선을 위해서는 현가계의 기구학적 특성을 최적화할 필요가 있다는 사실을 확인시킨다.

Fig. 22

Effect of design changes in front and rear hardpoint and bushing

4.4.2 K&C 해석 결과와의 상관관계 분석

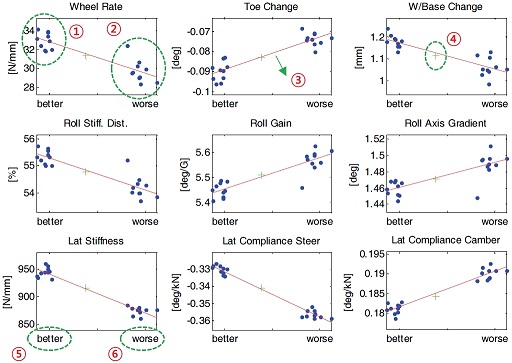
본 절에서는 해석결과와 K&C 분석 결과와의 상관관계 분석을 통해 어떠한 기구학, 컴플라이언스 특성을 갖는 차량이 횡풍에 보다 안정적인지 고찰해보도록 한다. 흔히 차량의 성능을 예측할 때, K&C 특성 변화를 통해 분석한다. 이 이유는 사실상 실질적인 설계 변경에서 성능과 연관된 의미를 도출할 수 없기 때문이며, 각각의 K&C 인자들은 조종 안정성, 횡풍 안정성 등과 같은 성능에 대하여 의미를 가지고 있기 때문이다. 현가계의 설계 변경은 매우 종속적이며 각 성능들이 상충적이기 때문에 하나의 인자에 대한 효과를 분석하는 것은 매우 힘들다. 가령, 임의의 하드포인트를 이동하게 되면 거의 대부분의 K&C 인자가 변화한다. 해석 모델 상에서도 함수형 현가장치 모델처럼 개별적인 K&C 인자가 고려되는 경우 개별 특성 변화에 따른 성능변화를 파악할 수 있으나 다물체 동역학 모델이나 실제 차량을 보더라도 개별 K&C 인자만의 효과를 파악하는 것은 불가능하다. 따라서, 본 연구에서는 이러한 실질적인 설계 조건에서 경향성 및 의미를 추출하기 위하여 다음과 같은 방법을 통해 상관성을 분석한다. 민감도 분석 중 다중인자 설계 변경 시, 사용되었던 직교 설계안에 대한 해석 결과 중 기존 설계안 대비 성능이 향상 혹은 악화된 평가인자 별 상, 하위 10개씩, 총 20개의 설계를 채택하여 앞서 추출된 3개의 모드에 대한 K&C 해석을 수행한 후, 이들의 공통적이 경향성을 분석하는 방법이다. 여기서 직교 설계안을 사용한 이유는 단일 인자 설계 변경에 대한 효과는 매우 미비하여 특성을 추출하기 힘들기 때문이다. 또한 상, 하위 성능을 갖는 20개의 설계안 만을 고려한 이유도 보다 뚜렷한 경향성을 추출하기 위함이다. Fig. 23은 본 방법에 대한 예로 요 각속도를 기준으로 한 전륜 부싱 강성 변화에 대한 K&C해석 결과 및 회귀 모형이다.

위 그림에서 각 부분에 대한 설명은 아래와 같다.

① 최대값이 기존 설계안 대비 작게 산출된 10개의 설계안에 대한 K&C 해석 결과
② 최대값이 기존 설계안 대비 크게 산출된 10개의 설계안에 대한 K&C 해석 결과
③ 전체 결과에 대한 선형 회귀 모델
④ 기존 설계안의 K&C 해석 결과
⑤ Better: 기존 설계안 대비 안정성 향상을 의미(최대값 감소)
⑥ Worst: 기존 설계안 대비 안정성 감소를 의미(최대값 증가)

Fig. 23

Relation between performance and K&C factor (FR compliance, yaw rate)

위 그림을 보면 Wheel rate, toe change, w/base change, roll stiffness distribution, roll gain, roll axis gradient, lateral stiffness, lateral compliance steer, lateral compliance camber 총 9개의 K&C 인자에 대하여 요 각속도의 최대치가 감소한 설계안과 그렇지 않은 설계안의 경향성이 어느정도 뚜렷하게 나타난다. 이를 통해 횡풍 안정성과 연관된 특정인자의 설계 개선을 위하여 확보해야 하는 K&C 성능을 파악할 수 있다. 이와 같은 방법으로 경향성 분석을 수행하되, 방대한 양의 결과를 보다 함축적이고 정량적 제시하기 위해 통계적인 방법을 추가적으로 적용하였다. Fig. 23에서 Wheel rate의 결과는 대략적인 경향성은 보이나 Lateral compliance steer와 비교하였을 때, 경향성의 뚜렷한 정도가 다르다. 이러한 점을 정량화하기 위하여 선형 회귀 모델을 추출하였고, R-square(결정계수)를 도입하여 이를 정량화 하였다. R-square란 추세의 강도를 나타내는 지표로써, 다른 추세지표 특히 선형회귀곡선이나 표준오차의 보조지표로서 많이 활용된다. R-square의 산출 근거를 아래와 같다.

R 2 = 1 - S S r e s S S t o t = 1 - ∑ i y i - f i 2 ∑ i y i - y ¯ 2 0 ≤ R 2 ≤ 1

(26)

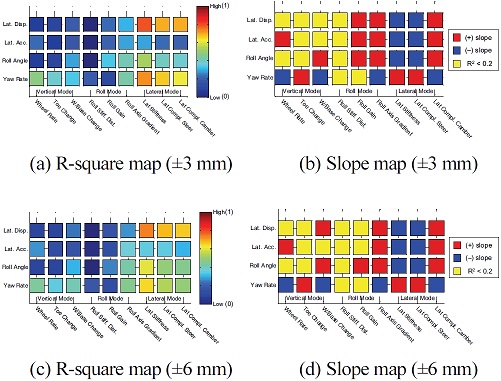
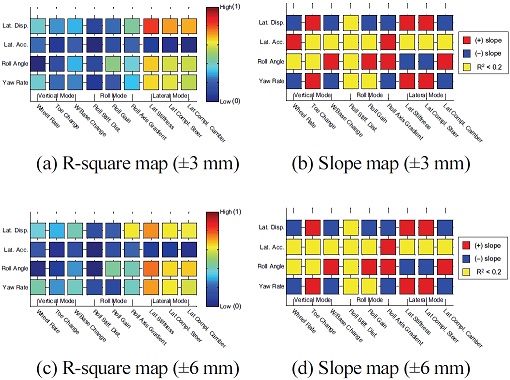
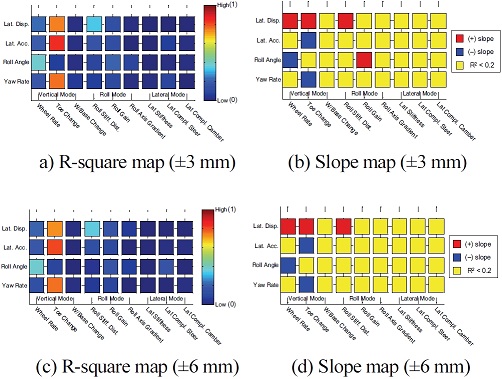
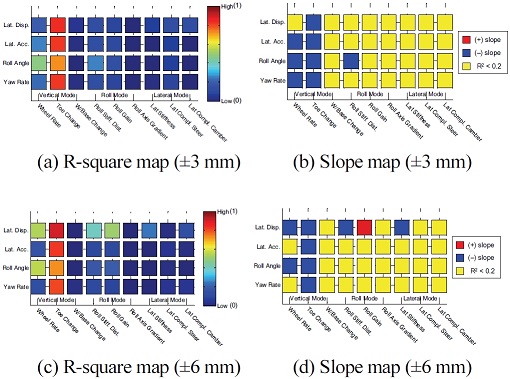
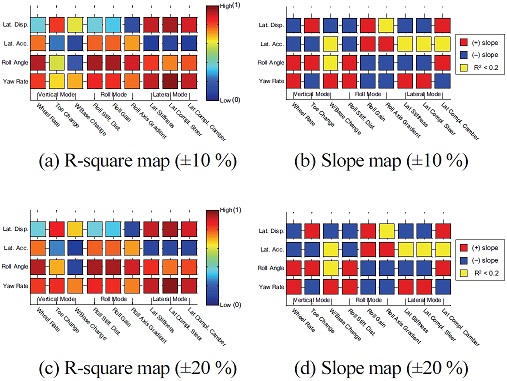
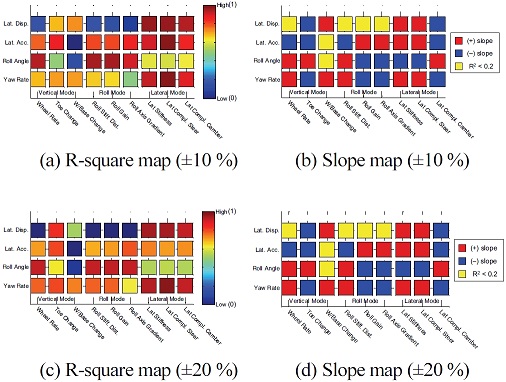
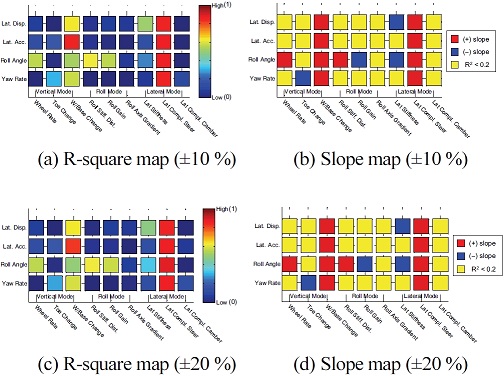
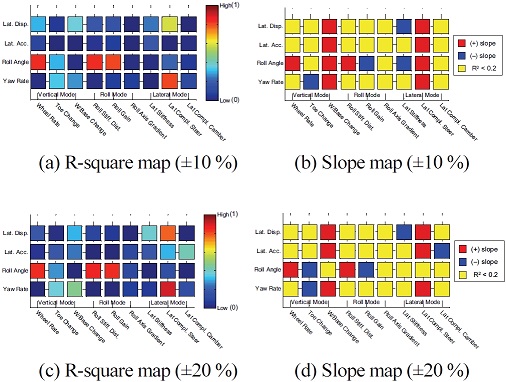
여기서, SS_t_o_t는 총 제곱합(Total sum of squares), SS_r_e_s는 잔차 제곱합(Regression sum of squares)이며, i는 데이터의 개수, y_i는 각 데이터의 값, $y ¯$ 는 데이터의 평균, f_i는 선형회귀 곡선에서의 값을 의미한다. 아래 제시되는 Fig. 24부터 Fig. 31은 전/후륜 서스펜션 하드포인트, 부싱 강성을 대상으로 개루프 해석, 폐루프 해석시 결과에 대한 성능인자와 K&C 해석 결과간에 상관관계를 보여준다. 설계 범위는 보다 다양한 범위에 대하여 결과를 검토하기 위하여 하드포인트의 경우 ±3, 6 mm, 부싱 강성의 경우는 ±10, 20 %를 고려하였다. 추가적으로 R-square map에서는 데이터들이 얼마나 회귀곡선과 일치하는지 여부만 판단가능하고, 경향성의 방향은 판단이 불가하기 때문에 이와 더불어 Slope map을 도입하여 이를 나타내었다. Slope map에서 붉은색으로 표시된 영역은 ‘+’ 기울기로 설계인자의 값이 클수록 최대치가 감소한다는 의미이고 반대로 파란색으로 표시된 영역, ‘–’ 기울기로 전자와 반대의 의미이다. 또한, 노란색으로 표시된 영역은 R-square가 0.2 이하로 매우 작기 때문에 상관성이 부족하다고 판단한 부분이다.

Fig. 24

Results of correlation analysis (Front hardpoint, Open-loop)

Fig. 25

Results of correlation analysis (Front hardpoint, Closed-loop)

Fig. 26

Results of correlation analysis (Rear hardpoint, Open-loop)

Fig. 27

Results of correlation analysis (Rear hardpoint, Closed-loop)

Fig. 28

Results of correlation analysis (Front compliance, Open-loop)

Fig. 29

Results of correlation analysis (Front compliance, Closed-loop)

Fig. 30

Results of correlation analysis (Rear compliance, Open-loop)

Fig. 31

Results of correlation analysis (Rear compliance, Closed-loop)

결과에서 전체 K&C가 예측되는 이론상의 경향성(서스펜션의 키네매틱 특성이 컴플라이언스 특성보다 차량 반응에 더 민감하다.)과 정확하게 일치하는 것은 아니지만 어느정도 일치하는 것을 볼 수 있으며, 특히 횡 방향 모드의 결과는 앞에서 언급한 경향성과 운전자 모델 고려여부까지 포함하여 일치하는 것을 볼 수 있다. 또한 전륜에 비해 후륜의 상관관계가 낮은 것은 후륜 현가장치의 특성이 교호작용이 많아 일관된 경향성을 추출하기가 어려운 것으로 판단된다. 본 결과는 단순 상관관계와 경향성을 제시할 뿐 설계인자가 성능에 얼마나 큰 영향을 미치는지에 대해서는 나타내고 있지 않으며, 상관관계가 부족하다고 해서 그 인자의 중요성이 낮다는 의미는 아니기 때문에 본 결과는 이러한 점을 고려하여 참고해야 할 것이다.

4.4.3 차량 무게중심(CG) 위치

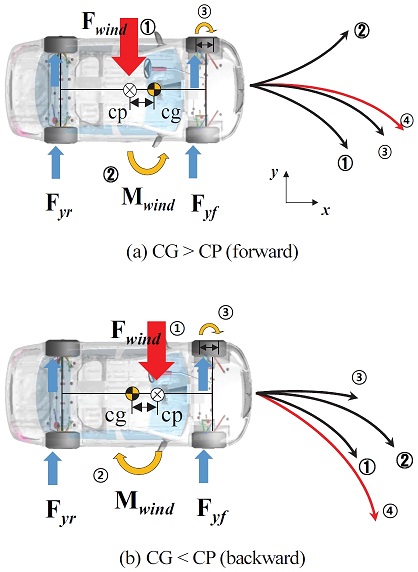
전/후륜 현가계의 하드포인트, 부싱 강성에 이어 차량 무게중심 위치 변화에 따른 횡풍 안정성을 파악하였다. 현재 차량 모델 상에서 횡풍은 공력의 작용점(CP)에 인가되도록 정의되어 있으며, 공력의 작용점은 무게중심(CG)과 일치하지 않는다. 따라서 횡풍으로 인한 횡력이 작용하게 되면 주행 방향 즉 전역 x축 방향에 대하여 차량 무게중심과의 거리로 인하여 모멘트가 발생하게 되는데 이 때, 작용점과 무게중심의 위치관계에 따라 모멘트의 방향이 다르게 정의될 수 있다. 만약, 공력 작용점이 무게중심 보다 전방에 위치할 경우 무게중심 지점에서 발생하는 횡풍에 대한 모멘트의 반력이 상승하게 되고 이는 곧 총 합력의 상쇄를 야기하게 되어 횡풍 안정성 향상에 도움을 주게 된다. Fig. 32에 두 가지 경우에 대한 역학 관계를 도시하였다. 아래 그림에서 ①은 횡력에 의한 선회력, ②는 횡력 인가 위치에 따른 모멘트, ③은 캐스터 트레일(Caster trail)에 의한 조향 모멘트, ④는 ①~③이 합해진 최종 합력을 의미한다.

Fig. 32

Dynamics according to the change in position of CG (x-direction)

무게중심 위치 변화와 같이 선회 반대 방향 모멘트 생성으로 인한 총 합력의 상쇄는 현가장치 설계 변경과는 조건이 다르다고 할 수 있다. Fig. 33은 초기 설계안과 무게중심의 종 방향 위치를 ±100 mm 이동 시켰을 때의 폐루프 해석에 대한 결과를 보여준다. 그림을 통해 알 수 있듯이 차량의 무게중심이 앞으로 이동하였을 때, 전체 평가인자에 대한 최대값이 감소하였다. 따라서 무게중심 위치의 변동은 횡풍 안정성 측면에서 유용한 개선책이 될 수 있다.

Fig. 33

Analysis results for CG x position (Closed-loop)

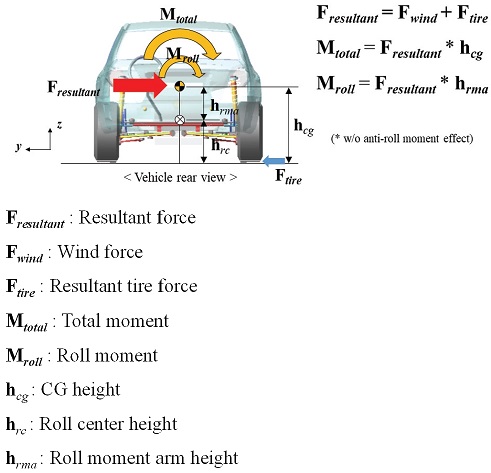
Fig. 34는 차량을 후면에서 본 그림으로 차량 무게중심의 수직방향 위치 변경에 따른 역학관계를 보여준다. 횡풍에 의한 횡력의 합력이 차량의 무게중심에 인가된다고 가정할 때, 그에 따라 차량의 롤 센터를 중심으로 롤 모멘트(M_r_o_l_l)가 발생하게 되며, 차량 전체의 총 롤 모멘트(M_t_o_t_a_l)는 지면에서부터 무게중심까지의 높이에 비례하여 발생한다. 따라서 무게중심의 위치가 높아질 수록 차량이 받는 롤 모멘트가 커지게 되고 롤 성능이 악화된다.¹⁵⁾

Fig. 34

Dynamics according to the change in position of CG (z-direction)

Fig. 35를 통해 알 수 있듯이 무게중심의 수직방향 위치가 낮아질수록 최대치가 감소하는 것을 볼 수 있으며 특히 롤 각에 지배적인 경향을 보이는 것을 볼 수 있다. 횡 변위, 횡 가속도, 요 각속도는 롤 각 증가에 따라 범프 시 선회 외측의 수직하중이 증가하고 그로 인하여 선회 특성이 변화하는 것으로 인해 거동의 차이를 보이지만 그 차이가 크지 않다.

Fig. 35

Analysis results for CG z position (Closed-loop)

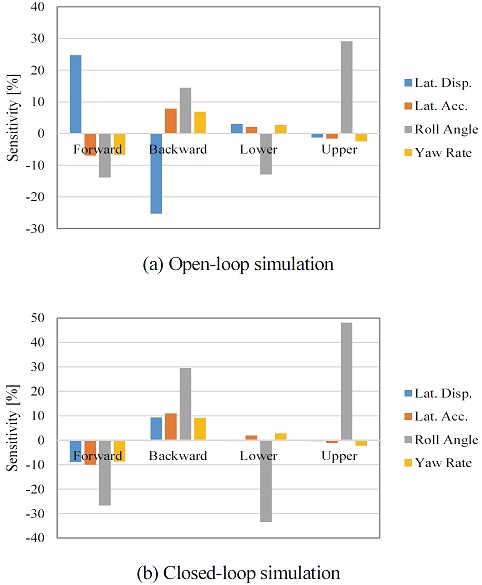
Fig. 36(a), (b)는 각각 개루프와 폐루프 횡풍 해석에 대하여 차량 무게중심의 위치를 초기 설계안 대비 전/후 방향, 상/하 방향으로 이동시켜 민감도를 분석한 결과이다. 무게중심 전,후 방향에 대한 결과를 보면 운전자 모델 고려 여부와는 상관없이 무게중심이 전방으로 이동하였을 때, 4개의 평가 인자에 대하여 최대치가 감소하는 것을 볼 수 있다. 4개의 평가인자에 대하여 모두 개선되는 이유는 선회 방향 모멘트가 상쇄되기 때문에 차량에 인가되는 최종 모멘트의 크기가 감소하기 때문이다. 무게중심의 수직방향 위치 변화에 대하여는 롤 각에 상당히 지배적이고 무게중심의 위치가 낮아질수록 롤 각의 최대치가 감소하는 것을 볼 수 있다.

Fig. 36

Results of sensitivity analysis (CG position)

4.4.4 타이어 주요 인자

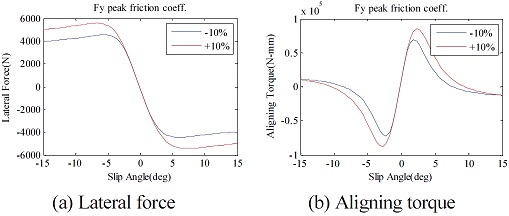
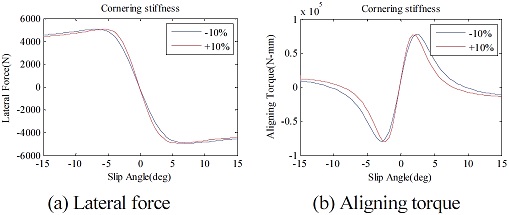
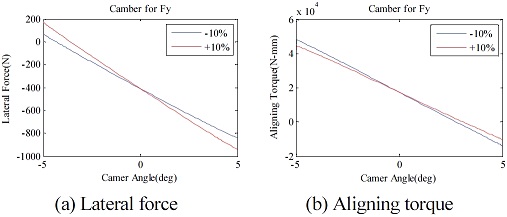
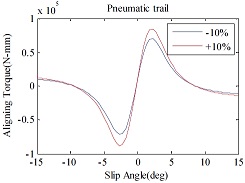
본 연구에서 타이어는 ADAMS/Car에서 제공하는 실험 기반의 타이어 모델인 MF-tire을 이용하였으며, 타이어에 대한 특성 파라미터는 주관기관으로부터 제공받았다. 선정된 인자는 횡 방향의 최대 마찰 계수, 코너링 강성, 횡력에 대한 캠버 변화, 최대 뉴메틱 트레일, 이완 길이이며 해당 타이어 정보에서 Scale factor를 조정하여 성능을 변화시켰다. 주요 인자 변화에 따른 횡풍 거동 변화 해석을 하기에 앞서 타이어 물성 파일의 인자 조절 시, 타이어 특성이 올바르게 변화하는 지 확인하였다. 해당 특성 변화 확인은 타이어만 별도로 해석할 수 있는 Tire test-rig를 이용하여 수행하였다. 타이어에 -15 deg부터 +15 deg까지 횡방향 슬립 각(Slip angle)을 인가하였을 때, 발생하는 횡력 및 정렬토크(Aligning torque)를 파악하였으며, 해당 특성치를 ±10 % 변화시켜가며 거동을 비교하였다. 캠버 변화에 대한 타이어 특성은 횡방향 슬립각은 유지한 채로 타이어에 캠버 각을 -5 deg부터 +5 deg까지 변화시켜가며 거동을 비교하였다.

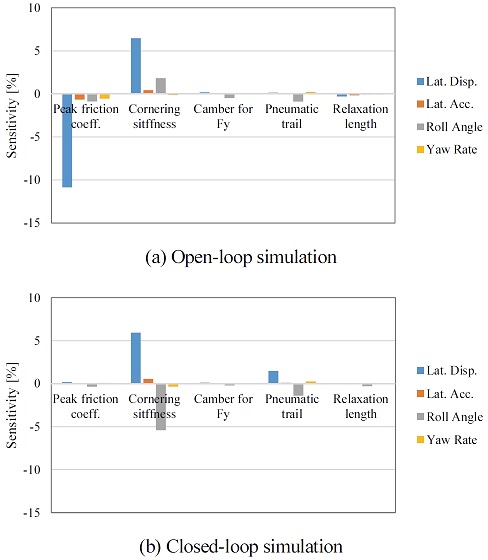
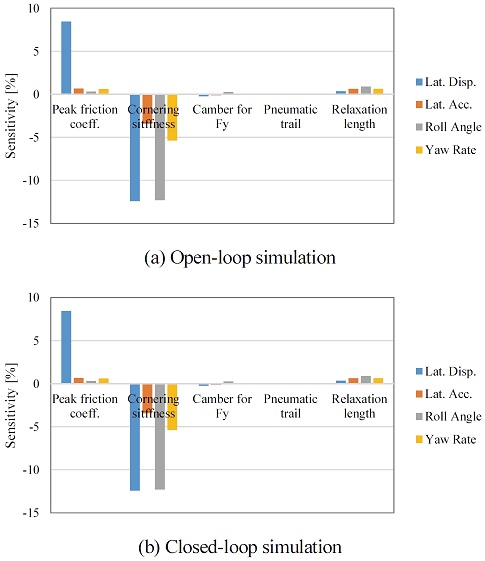
Fig. 37에 나타난 횡 방향 최대 마찰력 변화에 따른 타이어 특성을 보면 횡력과 정렬토크에 대하여 슬립 각 변화에 따라 최대치가 증가한 것을 볼 수 있다. 하지만 실제 횡풍에 영향을 받을 때는 발생하는 타이어의 슬립각 범위는 ±2 deg 미만이며, 그 영역에서는 횡력과 정렬토크의 변화가 미소한 것을 볼 수 있다. Fig. 38은 타이어의 코너링 강성 변화에 대한 결과이며, 코너링 강성 변화 시, 횡력과 정렬토크의 선형구간의 기울기가 변화하는 것을 볼 수 있다. 동일한 슬립 각에 대하여 발생하는 횡력과 토크의 차이가 발생하는 것을 볼 수 있으며 이는 차량의 선회거동에 밀접한 영향을 미칠 것으로 예상된다. Fig. 39의 캠버각 변화에 대한 거동을 살펴보면 예상되는 것과 같이 동일한 슬립 각에서 캠버각에 따라 횡력과 정렬토크가 변화한다. Fig. 40의 뉴메틱 트레일이란 타이어의 접촉점으로부터 횡력의 합력 발생 지점까지의 거리를 의미하는데, 정렬토크는 횡력과 이 뉴메틱트레일에 의해서 결정된다. 그림을 통해 알 있듯이 최대 뉴메틱트레일이 증가할수록 정렬 토크의 최대값이 증가하는 것을 볼 수 있다. 하지만 정렬 토크 강성 변화는 미비한 것 또한 확인할 수 있다. 또한 최대 뉴메틱 트레일 변경 시 횡력 특성은 변하지 않는다. 마지막으로 이완 길이는 슬립 각 발생 후 코너링 힘이 정상상태가 될 때까지의 회전거리를 의미하는데, 이 인자에 대한 결과 제시는 생략한다. Fig. 41과 Fig. 42는 전, 후륜 타이어 5개 인자에 대한 개루프, 폐루프 해석 시 민감도 분석 결과를 보여준다.

Fig. 37

Effect of Fy peak friction coefficient

Fig. 38

Effect of cornering stiffness

Fig. 39

Effect of camber for Fy

Fig. 40

Effect of peak pneumatic trail

Fig. 41

Results of sensitivity analysis (Front tire)

Fig. 42

Results of sensitivity analysis (Rear tire)

위의 민감도 분석 결과를 보면, 전체 해석결과에서 코너링 강성이 가장 민감한 영향을 미치는 인자임을 확인할 수 있으며, 전륜의 경우 개루프 해석에서는 코너링 강성이 클수록 횡 변위와 롤 각도의 최대치가 커지는 것을 볼 수 있으며, 운전자의 조향 효과가 고려될 시, 롤 각도의 경향이 반대로 산출되는 것을 볼 수 있다. 후륜 코너링 강성의 경우 운전자 모델의 고려와 상관없이 강성이 클수록 4개의 평가 인자의 최대치가 감소하는 것을 볼 수 있다. 따라서 후륜의 코너링 강성이 횡풍 안정성을 향상 시키기 위한 민감한 인자임을 확인하였다. 또한 개루프 해석 시 전, 후륜의 횡 방향 최대 마찰 계수의 크기가 횡 변위와 밀접한 관련이 있음을 확인할 수 있다. 일부 조건에 대하여 최대 뉴메틱 트레일 및 이완 길이가 거동에 영향을 미치지만 상대적으로 미소한 편이다. 본 타이어 주요 인자 변경에 대한 민감도는 추가적인 역학관계 분석을 통해 보다 명확히 이해되어야 할 것이다.

4.4.5 스테빌라이져 바

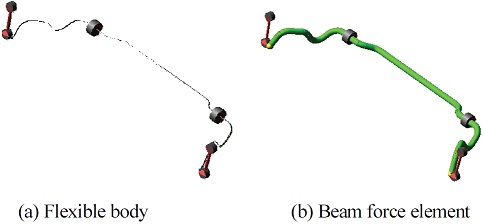
스테빌라이져 바(Stabilizer bar)는 안티-롤 바(Anti-roll bar)로도 불리우며 현가장치에서 롤 특성만을 독립적으로 제어하기 위한 수단으로 사용된다. 따라서, 전, 후륜 스테빌라이져의 직경 및 강성 증가 시, 롤 특성이 개선된다는 점은 자명하다. 본 연구에서는 단순하게 바의 직경 증가에 대한 민감도 분석 대신 차량이 동일한 롤 게인을 갖을 때, 전, 후 롤 강성 배분에 따른 성능 변화를 파악하였다. 롤 게인은 앞서 언급하였듯이 차량이 단위 횡가속도를 받을 때 발생하는 롤 각으로 정의되며, 전, 후륜의 롤 강성과 차량의 기하학적 배치에 따라 결정되게 된다. 따라서 롤 게인을 동일하게 유지시키기 위해서는 전륜의 롤 강성을 증가할 시, 후륜은 감소하고 반대로 후륜의 강성이 증가할 시 전륜은 감소시켜야 한다. ADMAS/Car 다물체 동역학 모델에서 일반적으로 스테빌라이져 바는 모달 기반의 유연체 요소로 모델링되는데, 본 연구에서는 유연체 요소 대신에 다수의 빔 포스 요소가 조합되어 있는 형태의 스테빌라이져 바 모델을 이용하였다. 본 모델은 별도의 툴킷을 이용하여 생성가능하며 입력된 바의 직경 및 특성치에 따라 적절한 빔 요소 기반 스테빌라이져 바 모델을 생성하여 준다. 본 연구에서 사용한 빔 요소 기반 스테빌라이져 바 모델은 바를 200개의 파트 및 199개의 힘 요소를 사용하여 근사하는 방법으로 모델링되었다. Fig. 43(a), (b)는 각각 기존 모달 기반의 유연체 스테빌라이져 바 모델 및 선형 빔 요소 기반 스테빌라이져 바의 모습을 보여준다.

Fig. 43

Stabilizer bar model

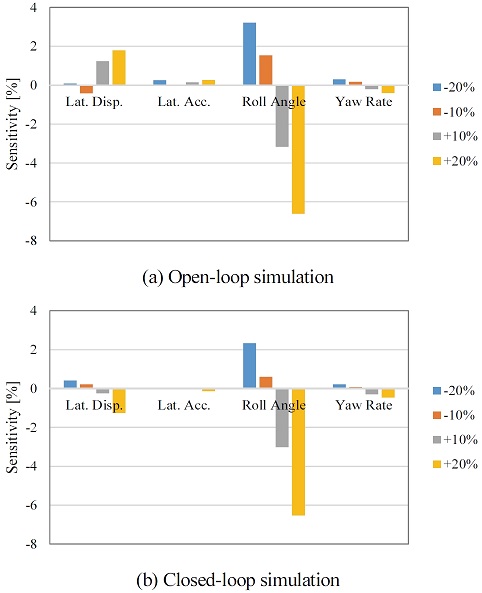
전, 후륜 롤 강성 배분은 각각 ±10, 20 %씩 증감하였으며, 본 설계안을 얻기 위하여 빔 요소 기반 스테빌라이져 바 템플릿 전용 생성 툴킷을 이용하여 직경을 임의로 변화시킨 템플릿 모델을 생성하고, 서브시스템 모델, 어셈블리 모델 개발 후 차량에 장착하여 K&C 해석을 수행하고 원하는 범위의 롤 강성 배분이 산출될 때까지 시행착오적 방법을 사용하였다.

설계 범위는 롤 강성 배분 ±10, 20 % 증감이며, Fig. 44의 민감도 분석 결과를 보면, 우선 전륜 롤 강성 배분이 증가할수록 운전자 모델 고려 여부와 관계없이 롤 각의 최대치는 감소하는 것을 볼 수 있으며, 롤 각도에 대한 민감도가 상대적으로 큰 것을 보아 개선에 효과가 있을 것으로 판단된다.

Fig. 44

Results of sensitivity analysis (Stabilizer bar)

4.4.6 스프링, 댐퍼 등 강체요소

전, 후륜 스프링의 강성 계수와 댐퍼의 감쇠 계수를 각각 ±10 % 증감하며 횡풍에 대한 민감도를 분석하였다.

Fig. 45의 결과를 보면 전륜 스프링 강성 증가 시, 4개의 평가 인자에 대하 최대치가 모두 감소하여 전체적인 횡풍안정성이 향상 된 것을 볼 수 있다. 하지만 후륜 스프링 강성의 횡 가속도 및 요 각속도의 최대값이 증가하는 경향을 보이며, 횡 변위는 운전자 모델 고려 여부에 따라서 상이한 결과를 보이는 것을 볼 수 있다. 또한 전, 후륜 댐퍼 감쇠 계수 증가 시에는 운전자 모델 고려 여부와 관계없이 전체적인 최대값이 감소하는 것을 확인할 수 있다. 마지막으로 전체 평가 인자 중 롤 각과 횡 변위에 대한 민감도가 상대적으로 큰 것을 볼 수 있다.

Fig. 45

Results of sensitivity analysis (Stabilizer bar)

5. 결 론

위 연구 내용을 토대로 한 결론은 다음과 같다.

1) 평가 인자(횡 변위, 횡 가속도, 롤 각, 요 각속도)에 따라 설계 방향이 상충되는 경향을 보인다. 이는 운전자의 주관적인 느낌 및 차량 거동을 반영하는 대표 인자 선정 필요성을 알 수 있었다.
2) 하드포인트, 부싱 강성 설계 변화 경향성은 요 각속도 / 횡 변위, 횡 가속도 / 롤 각 순으로 상관성을 보였다.
3) 운전자 모델의 조향 입력이 횡 변위 결과의 차이를 야기, 해석 시 Open/closed-loop 설계 방향성 차이 발생시킨다. 이는 운전자 모델 타당성, 실제 운전자 반응과의 연계성 판단 및 다양한 운전자 모델 적용 검토 필요성을 확인시켰다.
4) K&C 상관관계 분석 시, Lateral mode에 대한 상관성 및 경향성이 분명하다.
5) CG가 CP보다 전륜 쪽에 위치할수록, 아래에 위치할수록 Resultant force의 감소로 횡풍 안정성이 향상된다.
6) 전륜 롤 강성 배분 증가는 개루프 해석 시, 롤 각 최대치는 감소하지만 횡풍에 대한 반력 감소로 횡 변위는 증가시키고, 폐루프 해석 시 롤 각 및 횡 변위 최대치 모두 감소시키며, 나머지 인자의 영향은 미미하다.
7) 타이어 특성은 후륜 코너링 강성의 증가가 횡풍 안정성 향상에 기여한다는 것을 알 수 있다.
8) 전륜 스프링, 전/후륜 댐퍼 계수 증가가 횡풍 안정성 향상에 기여한다.
9) 하드 포인트의 변화(Kinematic)가 차량 거동 변화(횡풍 안정성)에 큰 비중을 차지한다.
10) 롤 각, 횡 변위에 대한 민감도 및 변화량이 상대적으로 크다.

본 연구의 결론을 요약하자면, 횡풍에 대하여 운전자 모델 고려 여부에 따라 상이한 해석 결과가 나오며 개루프 해석 조건에서는 언더스티어 경향을 보이는 차량이 즉, 둔감한 차량이 횡풍에 안정적이며, 폐루프 해석 조건에서는 운전자의 반응이 중요하기 때문에 조종성이 우수한 차량이 결과적으로 안정적인 거동을 보인다는 것이다. HMC에서 2010년도 초기에 양산한 후륜 구동 고급 세단 차량부터 현재는 대부분의 양산 차종에 본 연구에서 도출된 결과를 설계에 적용하고 있다.

Nomenclature


y :	internal lateral displacement of the vehicle mass center
v :	lateral velocity in the vehicle body axis system
r :	yaw rate about the vertical body axis
ψ :	vehicle heading(yaw) angle
δ_FW :	front tire steer angle, control variable
U :	forward vehicle velocity
C_af, C_ar :	front and rear tire cornering stiffness
a, b :	forward and rearward locations of tires from the vehicle mass center
m, I :	vehicle mas and yaw inertia

Acknowledgments

본 연구는 정밀기계설계공동연구소(SNU-IAMD)의 지원 및 미래창조과학부 재원으로 한국연구재단(NRF-2016R1E1A1A01943543)의 지원을 받아 수행된 연구임.

References

D. Stoll, C. Schoenleber, F. Wittmeier, T. Kuthada and J. Wiedemann, “Investigation of Aerodynamic Drag in Turbulent Flow Conditions,” SAE 2016-01-1605, 2016.
Y. Maruyama and F. Yamazaki, “Driving Simulator Experiment on the Moving Stability of an Automobile Under Strong X-wind,” Journal of Wind Engineering and Industrial Aerodynamics, Vol.94, No.4, pp.191- 205, 2006. [https://doi.org/10.1016/j.jweia.2005.12.006]
C. C. Macadam, “Understanding and Modeling the Human Driver,” Vehicle System Dynamics, Vol.40, Nos.1-3, pp.101-134, 2003. [https://doi.org/10.1076/vesd.40.1.101.15875]
R. N. Jazar, Vehicle Dynamics: Theory and Applications, Springer International Publishing, Melbourne, Ch.10 Vehicle Planar Dynamics, pp.609-620, 2008. [https://doi.org/10.1007/978-0-387-74244-1_10]
W. A. H. Oraby and D. A. Crolla, “Passenger Car Stability Under Random Wind Excitation,” SAE 2001-01-0133, 2001. [https://doi.org/10.4271/2001-01-0133]
D. B. Sims-Williams, “Cross Winds and Transients: Reality, Simulation and Effects,” SAE 2011-01-0172, 2011.
J. Howell and G. Le Good, “The Influence of Aerodynamic Lift on High Speed Stability,” SAE 1999-01-0651, 1999. [https://doi.org/10.4271/1999-01-0651]
H. H. Yang, Driver Models to Emulate Human Anomalous Behaviors Leading to Vehicle Lateral and Longitudinal Accidents, Ph. D. Dissertation, The University of Michigan, Ann Arbor, Michigan, 2010.
P. Gilliéron and C. Noger, “Contribution to the Analysis of Transient Aerodynamic Effects Acting on Vehicles,” SAE 2004-01-1311, 2004. [https://doi.org/10.4271/2004-01-1311]
M. Gajendra Singh, Q. H. Nagpurwala, N. Abdul and S. R. Shankapal, “Numerical Investigations on X-wind Aerodynamics and Its Effect on the Stability of a Passenger Car,” SAE 2009-26-0059, 2009. [https://doi.org/10.4271/2009-26-0059]
J. Mayer, M. Schrefl and R. Demuth, “On Various Aspects of the Unsteady Aerodynamic Effects on Cars Under X-wind Conditions,” SAE 2007-01-1548, 2007. [https://doi.org/10.4271/2007-01-1548]
N. Kobayashi and M. Yamada, “Stability of a One Box Type Vehicle in a Cross-Wind-An Analysis of Transient Aerodynamic Forces and Moments,” SAE 881878, 1988. [https://doi.org/10.4271/881878]
C. Britcher, W. Mokhtar and S. Way, “Simulation Considerations for Commercial Vehicles in Strong X-wind Conditions,” SAE 2014-01-2452, 2014. [https://doi.org/10.4271/2014-01-2452]
J. A. Sedarous, A. Soliman and M. Dunlop, “Modeling and Calibration of an Aerodynamic Cross-Wind Gust Test Facility,” SAE 2007-01-1550, 2007. [https://doi.org/10.4271/2007-01-1550]
G. Zhengqi, and H. Guichun, “Research on the Transient State Steering Stability in Side Winds for a High-speed Vehicle Using ADAMS^Ⓡ,” SAE 2005-01-0982, 2005. [https://doi.org/10.4271/2005-01-0982]

Notation	Description	Unit	Value
a	forward location of tire from the vehicle mass center	m	1.4869
b	rearward location of tire from the vehicle mass center	m	1.5219
m	vehicle mass	kg	1,932.21
I	rotational inertia	kg-m²	7,780.03
C_af	front tire cornering stiffness	N/rad	53,490.3
C_ar	rear tire cornering stiffness	N/rad	53,490.3
-	Steering gear overall ratio	-	16.1

Test mode	Standard	Test procedures
X-wind open loop free steering	-	Pass through X-wind section with releasing steering wheel (SWT = 0)
X-wind open loop fixed steering	ISO 12021-1	Pass through X-wind section with fixing steering wheel (SWA = 0)
X-wind closed loop	ISO 12021-2	Pass through X-wind section with correcting steering wheel for keeping target lane

	Notation	Rough	Smooth	Over-reacting	Precise
Preview time	T_p(sec)	1.1	1.3	1.1	1.5
Delay time	T_d(sec)	0.2	0.4	0.2	0.2
Yaw rate weight	-	50	100	100	200

	Unit	Step function	Ramp function
Vehicle speed	km/h	100
Wind speed	m/s	23
Wind angle	Deg	55
Duration time	Sec	0.95	0.7
Rising time		0	0.3
Fall time		0	0.2