4륜 독립 구동 전기 자동차의 제동력 분배 방법에 대한 연구

1. 서 론

최근 EU의 CO₂ 규제와 테슬라라는 혁신적 선도 기업의 출현으로 전기 자동차 시장이 확대되고 있다. 블룸버그 뉴에너지 파이낸스(BNEF)에서 발간한 Electricity Vehicle Outlook 2017에서는 2025년에서 2030년 사이에 전기 자동차의 판매량이 급증할 것이고 2040년에는 전기 자동차가 신차 판매량의 54 %를 전 세계 자동차의 33 %를 점유할 것으로 전망하고 있다.¹⁾ 이러한 흐름에 따라 다양한 구동 형태의 전기차가 시장에 나타나고 있으며 특히 4륜 독립 구동 모터를 탑재한 고성능 전기차가 개발되고 있다. 이러한 4륜 독립 구동 전기차에서는 동력의 분배 방법이 매우 중요하며 에너지 효율과 차량 안정성이 동시에 고려가 되어야한다. 특히, 제동 시 제동력의 적절한 분배는 승객의 안전에 매우 중요한 시스템으로 무엇보다도 우선하여 안정성이 확보되어야 한다.

전기 모터를 동력원으로 사용하는 전기 자동차는 제동을 위해 유압식 브레이크의 마찰제동력뿐만 아니라 모터의 회생제동력을 이용할 수 있다. 이는 제동을 위해 두 시스템을 모두 이용할 수 있기 때문에 제어의 자유도가 높아진다는 장점이 있지만, 두 시스템의 동특성 차이로 인해 동시 작동 시 이질감 문제를 일으킬 수 있다. 따라서 이러한 회생 제동 장치와 유압 제동 장치의 블렌딩(Blending)에 대한 다양한 연구들이 수행되어 왔다. 회생 제동 장치와 유압 제동 장치를 통합할 경우 두 시스템간 천이 구간에서 발생하는 승차감 및 안정성 손실 문제를 개선하기위한 연구,^2,3) 그리고 제동력 손실 최소화 및 주행 안정성을 확보하기 위해 퍼지 제어(Fuzzy control)를 사용하여 하중 특성에 맞게 전/후 제동비를 결정하는 연구가 수행되었다.⁴⁾ 또한, 수동 변속기를 장착한 전/후륜 독립 모터 방식의 4WD HEV 차량에 대하여 운전자 제동 의지와 차량의 주행 상태에 따라 회생제동 에너지를 최대로 회수 할 수 있는 전/후륜 회생 제동 제어 로직이 개발되었고,^5,6) 타이어의 여유 힘(Margin), 요레이트 에러, 그리고 슬립률이 고려된 제/구동 분배 로직에 대한 연구도 소개되고 있다.^7-10) 모터 2개를 이용한 구동 방식이 전기 자동차의 가장 일반적인 형태이기 때문에 대부분의 연구들은 전/후륜 독립 모터를 대상시스템으로 선정하여 전/후륜의 제동력을 결정하고있다.

본 연구에서는 4륜 독립 모터 전기 자동차의 제동 분배 방법에 대한 연구를 수행하였다. 주요 연구 범위는 일정 이상의 제동이 요구되어 안정성에 대한 고려가 필요한 상황으로 기존 EBD 제어시스템의 동작이 필요한 상황으로 정하였다. 4륜 독립 모터는 각 4휠의 제동력/구동력을 독립적으로 제어할 수 있는 장점이 있기 때문에 보다 다양하고, 극한 주행상황에서 차량의 안정성을 확보할 수 있다. 4륜 독립 모터의 회생 제동과 기존 유압 마찰 제동을 통합하여 제동 상황, 제동 중 선회 상황에서의 차량 안정성을 향상시키기 위한 제어 로직을 개발하였다. 그리고 해당 로직은 탑승자나 트렁크 짐에 따라 하중 변화가 빈번히 발생하는 상황에 강건하도록 설계하였다. 마지막으로 모터 회생 제동과 유압 마찰 제동 간의 새로운 분배 방식을 개발하였다. 이 두 시스템에 제동력을 분배하는 전략은 크게 2개로 나눌 수 있다. 첫 번째가 회생 제동을 최대한 사용하여 에너지 회수량을 최대화하기 위한 분배이고, 두 번째가 차량 제동 및 선회 상황에서의 안정성을 우선적으로 확보하기 위한 분배이다. 본 연구에서는 이 두 전략을 모두 포함한 분배 방법을 개발하였다. 분배 전략 간 천이는 튜닝 변수 하나로 간단히 천이 시킬 수 있다. 이렇게 개발 된 제어 로직은 Carsim, Matlab/Simulink로 그 성능을 검증 하였다.

2. 전자 제동 분배(EBD) 로직 설계

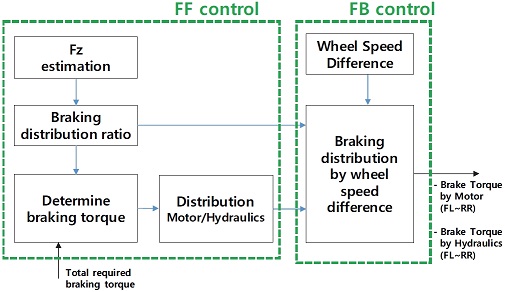
Fig. 1은 제동력을 분배하는 전자 제동 분배 로직의 기능 아키텍처를 나타내고 있다. 해당 로직은 크게 FF(FeedForward) 제어와 FB(FeedBack) 제어로 구성되어 있다. FF 제어는 제동 그리고 제동-선회 상황에서의 안정성을 확보하기 위해 차량의 기본(Nominal) 제원의 정보를 이용하여 각 휠의 수직 항력에 비례하도록 제동력을 결정하는 모듈이고, FB 제어는 차량의 무게가 변했을 경우 수직 항력 추정 오차로 발생하는 FF 제어의 오차, 혹은 각 휠의 노면 마찰계수가 다를 경우의 휠속차를 보상하기 위한 모듈이다. 차량의 무게 변화를 실시간으로 정확히 추정하는 것을 불가능하기 때문에 FB제어에서는 4륜의 휠 속 차이를 보상하는 제어기를 설계함으로써 무게 변화 및 노면 마찰계수 차이에 강건성을 확보하였다. 추정 오차가 존재하는 타이어 수직 항력 정보만을 이용한 FF 제어는 때로는 각 휠에 제동 불균형이 발생시키고, 이는 각 휠의 속도 차이를 발생시키게 된다. 따라서 본 논문에서는 이러한 휠속차 되먹임을 통해 무게 변화에 대응할 수 있다고 판단하였다. 지금부터 각 모듈들에 대해 상세히 기술하도록 한다.

Fig. 1

Functional architecture of electronic brake distribution logic

2.1 FF(FeedForward) control

FF 제어는 Fz estimation(수직 항력 추정), Braking distribution ratio(제동 분배 비), Determine braking torque(제동 토크 결정), 그리고 Distribution Motor/Hydraulics(모터/유압 제동 토크 분배) 이렇게 4가지 모듈로 구성되어 있다. 이중 수직 항력 추정은 차량의 기본(Nominal) 제원과 차량의 종/횡 가속도 신호를 이용한 추정 방법으로 기존 문헌에 많이 다뤄진 내용으로 본 논문에서는 기술하지 않는다.¹¹⁾

2.1.1 제동 분배 비 & 제동 토크 결정

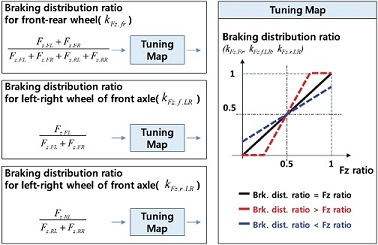
각 휠의 제동 토크는 제동 토크 결정 모듈에서 운전자 제동 페달로 결정된 총 제동 토크에 전/후 그리고 좌/우 제동 분배 비를 곱하여 식 (1)과 같이 결정된다.

$\[ \begin{array}{c}{T}_{b.FL,Fz}=k_{Fz.fr}\cdot k_{Fz.f.LR}\cdot T_{b.Total}\hfill \\ T_{b.FR,Fz}=k_{Fz.fr}\cdot \left({1-k}_{Fz.f.LR}\right)\cdot T_{b.Total}\hfill \\ T_{b.RL,Fz}=\left(1-k_{Fz.fr}\right)\cdot k_{Fz.r.LR}\cdot T_{b.Total}\hfill \\ T_{b.RR,Fz}=\left(1-k_{Fz.fr}\right)\cdot \left(1-k_{Fz.r.LR}\right)\cdot T_{b.Total}\hfill \end{array} \]$

(1)

여기에서, T_b.i.Fz (i=FL, FR, RL, RR)은 각 휠의 요구 제동 토크, k_Fz.fr은 제동 토크 전/후 분배 비, k_Fz.f.LR은 전륜 제동 토크의 좌/우 분배 비, k_Fz.r.LR은 후륜 제동 토크의 좌/우 분배 비, 그리고 T_b.Total은 총 요구 제동 토크를 의미한다. 분배 비를 전/후, 전륜 좌/우, 후륜 좌/우로 나눈 이유는 실차 성능 개발 시 튜닝의 용이성을 확보하기 위함이다. 수직 항력의 비율대로 제동 비를 결정하는 것이 안정성 측면에서는 가장 이상적인 제동 분배이나, 실제 적용에 있어서 전/후 분배 비율과 좌/우 분배 비율에 차이를 두는 것이 감성적으로 더 좋은 평가를 받을 수도 있기 때문이다. 그리고 제동 분배 비인 k_Fz.fr, k_Fz.f.LR, k_Fz.r.LR은 추정된 각 휠의 수직 항력을 이용하여 제동 분배 비 모듈에서 결정된다. Fig. 2는 추정된 수직 항력을 이용하여 제동 분배 비 결정 방법을 나타내고 있다. 보는 바와 같이 수직 항력의 비를 연산하고, 이 값을 튜닝 Map에 적용하여 최종 제동 분배 비를 결정한다. 이 또한 실차 성능 개발 상황에서의 튜닝 용이성 확보 차원으로, 실제로 실차 시험을 했을 때 무게 비율대로 제동 분배를 하는 것 보다 다르게 제동 분배가 이루어질 때 제동 성능뿐만 아니라 피치 거동이나 휠 안정성 여유 등 종합적인 차량의 거동이 더 좋은 경우를 대비하기 위함이다.

Fig. 2

Method to determine the braking distribution ratio

2.1.2 모터-유압 제동 토크 분배

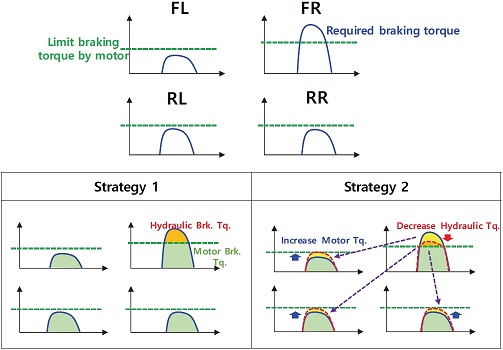
모터-유압 제동 토크 분배에서는 제동 토크 결정 모듈에서 연산 된 각 휠의 제동 토크를 발생시키기 위해 각 휠의 요구 모터 회생 제동 토크와 요구 유압 제동 토크를 결정하게 된다. 서론에서 언급했듯이, 이 두 시스템에 제동력을 분배하는 전략은 회생 제동 최대화를 통한 에너지 회수량 최대화 전략과 제동 및 선회 상황에서의 안정성을 확보하기위한 분배 전략으로 나눌 수 있다. 본 연구에서는 이 두 전략을 모두 포함한 분배 로직을 개발하였다. Fig. 3은 두 가지 분배 전략의 컨셉을 나타내고 있다. 파란색 선은 제동 토크 결정 모듈에서 연산 된 각 휠의 요구 제동 토크이고, 녹색 점선은 모터의 한계 토크이다. 각 휠의 요구 제동 토크는 수직 항력에 비례하기 때문에 모두 다른 제동 토크 량을 요구할 수 있다. 따라서 그림과 같이 요구 제동 토크가 모터의 한계 제동 토크를 초과하는 휠과 그렇지 않은 휠이 존재하게 된다. 이때 전략 1은 안정성 관점에서의 분배로 이전 모듈에서 요구하는 각 휠의 제동력을 유지하는 것이 목적이다. 요구 제동력이 모터 한계를 초과하지 않은 경우 모두 모터로 제동하고, 초과한 경우 초과된 제동 토크에 대해서는 유압으로 제동을 분배해주는 방식이다. 전략 2는 안정성을 일부 유지를 하며 에너지 회수량을 최대화하는 것이 목적이다. 요구 제동 토크가 모터 용량 한계를 초과한 경우 초과된 제동 토크에 대해 유압으로 제동을 우선 분배하지 않고 나머지 휠에 추가 모터 회생 제동 마진이 있으면 그 휠에 모터 제동 토크를 먼저 분배해주는 방식이다.

Fig. 3

Concept of braking distribution strategy

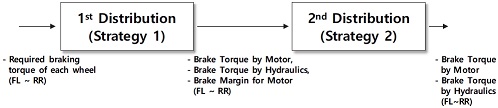
모터-유압 제동 토크 분배 로직은 전략 1 분배를 담당하는 1차 분배와 그 결과를 입력 받아 전략 2 분배를 담당하는 2차 분배 이렇게 2가지 모듈로 구성되어 있다. 즉, 전략 1의 분배 결과가 있어야 전략 2의 분배가 가능한 구조이다.

Fig. 4

Structure of braking distribution logic

1) 1차 분배(1^st Distribution)

1차 분배는 안정성 관점에서의 분배로 이전 모듈에서 요구하는 각 휠의 제동 토크를 유지하는 것을 목적으로 한다. 요구 제동 토크가 모터 한계를 초과하지 않은 경우 모두 모터로 회생 제동하고, 초과한 경우 초과된 제동 토크에 대해서는 유압으로 제동을 분배해주는 방식이다. 따라서 1차 분배의 결과는 아래 식 (2)와 같이 간단히 구현할 수 있다.

(2)

여기에서 T_b.Fz.i는 이전 모듈에서 요구하는 각 휠의 제동 토크, T_b.Lim.i는 각 모터의 한계 회생 제동 토크, T_b.M.i^1st는 1차 분배로 결정된 각 휠의 요구 모터 회생 제동 토크, T_b.H.i^1st는 1차 분배로 결정된 각 휠의 요구 유압 제동 토크, 그리고 T_b.M.Mar.i는 1차 분배 결정시 예측되는 각 휠의 모터 여유 회생 제동 토크이다.

2) 2차 분배(2^nd Distribution)

2차 분배는 안정성을 일부 유지를 하며 에너지 회수량을 최대화하는 것이 목적이다. 요구 제동 토크가 모터 한계를 초과한 경우 초과된 제동 토크에 대해 유압으로 제동을 우선 분배하지 않고 나머지 휠에 모터 회생 제동 마진이 있으면 그 휠에 모터 회생 제동 토크를 먼저 분배해주는 방식이다. 2차 분배 구현을 위해 우선 1차 분배의 출력 값들인 유압 제동 토크(T_b.H.i^1st)와 모터 여유 회생 제동 토크(T_b.M.Mar.i)를 이용한다. 유압 제동 토크를 줄이고 줄어든 토크만큼 모터 회생 제동 토크의 사용을 증가시켜야 하기 때문에, 이 두 값들을 이용해 각 휠에 추가해야 할 모터 회생 제동 토크를 아래 식 (3)과 같이 산출할 수 있다.

$\[ \begin{array}{cc}\text{Δ}{T}_{b.M.i}=\frac{WF\cdot T_{b.M.Mar.i}}{\sum T_{b.M.Mar.i}}\sum {T_{b.H.i}}^{1st}, & i=FL~RR\end{array} \]$

(3)

식 (3)을 통해 각 휠에 할당해야 할 추가 모터 회생 제동 토크는 1차 분배에서 결정된 전체 유압 제동 토크를 각 휠이 가지고 있는 모터 여유 회생 제동에 비례하게 분배함으로써 결정됨을 알 수 있다. 그리고 WF(Weighting Factor)는 분배 전략들을 천이시키기 위한 튜닝 변수이다. WF가 0이면 1차 분배에서 결정된 제어량들이 그대로 쓰이기 때문에 전략 1의 분배가 되는 것이고, WF가 1이면 전략 2의 분배가 된다고 할 수 있다. WF가 0에서 1사이의 값이면 전략1과 전략 2 사이의 분배가 된다. 해당 로직의 경우 4휠의 제동력이 모두 다르기 때문에 이로 인해 발생되는 요모멘트에대한 영향을 고려하여 WF를 설정할 필요가 있다. 식 (3)의 결과로부터 각 휠의 모터 회생 제동 토크를 아래 식 (4)와 같이 산출할 수 있다.

$\[ \begin{array}{cc}{T_{b.M.i}}^{pre}={T_{b.M.i}}^{1st}+\text{Δ}{T}_{b.M.i},& i=FL~RR\end{array} \]$

(4)

하지만 위 결과는 모터의 한계 제동 토크를 고려하지 않았기 때문에 식 (4)의 결과가 모터로 낼 수 있는 회생 제동 토크라 할 수 없다. 이를 해결하기 위해 식 (4)의 결과에 모터 한계 제동 토크를 고려하여 FF 제어의 최종 모터 회생 제동 토크(추가 모터 토크 포함)가 아래와 같이 산출되었다.

(5)

추가 모터 토크(ΔT_b.M.i)는 FF 제어의 최종 유압 제동 토크를 결정하는데 사용된다. 최종 유압 제동 토크를 구하기 위해 우선 총 필요 유압 토크를 결정해야한다. 총 필요 유압 토크는 1차 분배의 유압 제동 토크의 합과 식 (5)에서 계산된 ΔT_b.M.i를 이용하여 아래와 같이 구한다.

$\[ \begin{array}{cc}{T}_{b.H.total}=\sum {T_{b.H.i}}^{1st}-\sum \text{Δ}{T}_{b.M.i}& ,i=FL~RR\end{array} \]$

(6)

이렇게 계산된 총 필요 유압 토크를 1차 분배의 요구 유압 제동 토크의 비율대로 분배함으로써 각 휠의 최종 유압 제동 토크를 산출할 수 있다.

$\[ \begin{array}{cc}{T_{b.H.i}}^{FF}=\frac{{T_{b.H.i}}^{1st}}{\sum {T_{b.H.i}}^{1st}}{T}_{b.H.total}& ,i=FL~RR\end{array} \]$

(7)

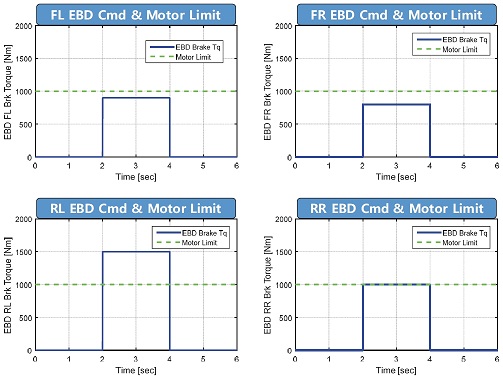
이렇게 개발된 모터-유압 제동 토크 분배 로직의 적합성을 판단하기 위해 단위 기능 검증을 수행하였다. Fig. 5는 단위 기능 검증을 위한 시나리오이다. 파란색 실선은 수직 항력 비로 요구되는 제동 토크이고, 초록색 점선은 모터 한계 제동을 의미한다. FL과 FR 휠은 모터 여유 회생 제동이 있고, RL 휠은 요구 제동 토크가 모터 한계를 초과하고, RR 휠은 요구 제동 토크가 모터 한계와 같은 상황의 시나리오이다.

Fig. 5

Scenario for verification of braking distribution logic

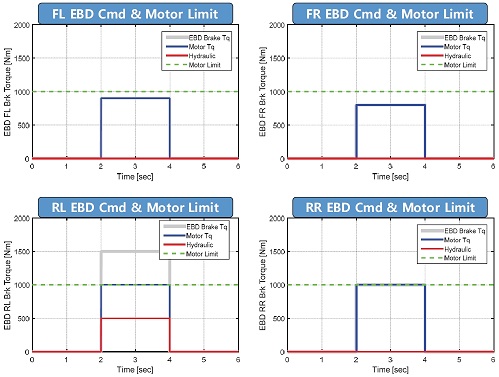
Fig. 6은 전략 1의 결과로 식 (3)에 WF를 0으로 설정하였을 때의 결과를 보여주고 있다. 회색 실선은 요구 제동 토크를, 파란색 실선은 모터 제동 토크를, 빨간색 실선은 유압 제동 토크를, 그리고 초록색 점선은 모터 한계 토크를 의미한다. 보는 바와 같이 각 휠의 요구 제동력을 만족시키기 위해 FL, FR, 그리고 RR 휠은 모터 회생 제동 만을 사용하고, RL 휠은 모터와 유압 제동을 동시에 사용함을 확인할 수 있다.

Fig. 6

Validation results for strategy 1 (WF=0)

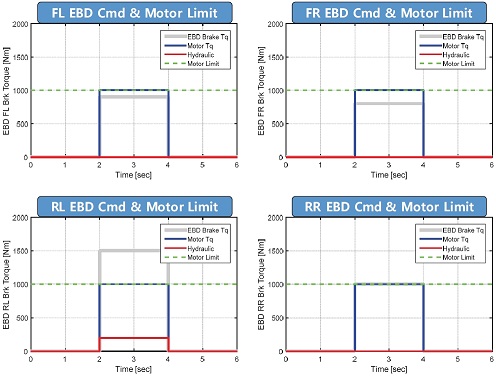
Fig. 7은 WF를 1로 설정한 전략 2의 결과이다. 보는 바와 같이 요구 제동 토크를 일부 만족시키지 못하는 대신 각 휠의 모터 사용이 최대화됨을 알 수 있다. 모터 사용이 증가된 만큼 유압 제동의 감소됨을 RL휠의 결과를 통해 확인할 수 있다.

Fig. 7

Validation results for strategy 2 (WF=1)

2.2 FB(FeedBack) control

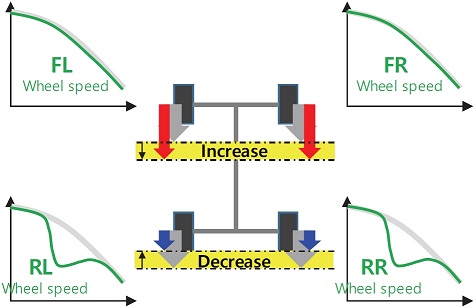
FB 제어는 Wheel speed difference(휠속 차이 계산)와 Braking distribution by wheel speed difference(휠속차 보상 제동 분배) 이렇게 2가지 모듈로 구성되어 있다. 앞서 언급했듯이 해당 모듈은 차량의 무게 변화및 노면 마찰계수 차이에 대한 제어의 강건성 확보를 목표로 각 휠의 속도 차이를 보상하는 모듈이다. Fig. 1의 아키텍처를 보면 FF 제어의 모터-유압 분배 이후에 FB 제어 모듈이 수행되고 있음을 알 수 있다. 휠속 차이가 발생한다는 것은 ABS(Anti-lock Braking System) 작동 영역에 가까운 위험한 상황이라 할 수 있다. 그렇기 때문에 FB 제어는 가장 우선권이 높아야 하고, 기능적으로 맨 마지막에 수행되어야 한다. 본 모듈에서는 이전 모듈(FF제어)에서 결정된 제동 토크(유압+모터)에 추가로 가/감해야 할 제동 토크를 계산하고 이를 다시 모터 제동과 유압 제동으로 재 분배를 하게 된다. Fig. 8은 본 모듈의 컨셉을 표현하고 있다. 제동 시 후륜 휠속이 전륜에 비해 상대적으로 감소하게 되면 후륜의 제동 토크를 감소시키고, 감소된 제동 토크만큼 전륜의 제동을 증가시키는 방식으로 모듈이 설계되었다.

Fig. 8

Concept of FB control

휠속 차이 보상 방법은 FF 제어의 수직 항력 비를 이용한 제동 분배 로직과 동일하다. 우선 전/후 휠속 차이를 보상하기 위한 전/후 전달 제동 토크를 결정하고, 이렇게 결정된 전/후 전달 제동 토크는 좌/우 휠속 차이에 의해 좌/우로 분배된다. 지금부터 휠속 차이 계산과 휠속차 보상 제동 분배 모듈에 대해 상세히 기술하도록 한다.

2.2.1 휠속 차이 계산

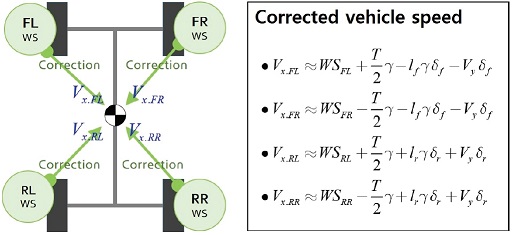
휠속 차를 보상하기 위해 휠속 차를 계산해야한다. 선회 상황에 따라 내/외륜 바퀴는 서로 다른 휠속을 가지기 때문에 정확한 휠속 차이 계산을 위해선 먼저 측정된 각 휠의 속도를 동일한 기준으로 보정해야한다. 본 연구에서는 각 바퀴의 휠속을 무게중심을 기준으로 보정했다. 아래 Fig. 9는 휠속 보정에 대한 내용을 나타내고 있다. 그림에서 WS_i(i=FL, FR, RL, RR)는 각 휠에서 측정된 휠속, V_y는 무게 중심에서의 횡 속도, γ는 차량의 요레이트, T는 차 폭, l_f는 무게중심에서 전륜 축까지의 거리, l_r은 무게중심에서 후륜 축까지의 거리, δ_f는 전륜 타이어 각도, 그리고 δ_r은 후륜 타이어 각도를 의미한다.

Fig. 9

Wheel speed compensation

보정된 휠속 정보를 이용하여 휠속 차이를 계산할 수 있다. 앞서 언급한 바와 같이 휠속 차이 보상은 전/후 휠속차 보상, 전륜의 좌/우 휠속차 보상, 후륜의 좌/우 휠속차 보상을 하기 때문에, 아래 식 (8)과 같이 3가지의 휠속 차이를 계산한다.

$\[ \begin{array}{c}∆V_{x.fr}=\min \left(V_{x.FL},V_{x.FR}\right)-\min \left(V_{x.RL},V_{x.RR}\right)\hfill \\ ∆V_{x.f.LR}=V_{x.FL}{-V}_{x.FR}\hfill \\ ∆V_{x.r.LR}=V_{x.RL}-V_{x.RR}\hfill \end{array} \]$

(8)

ΔV_x.fr 은 전/후 휠속 차이, ΔV_x.f.LR 은 전륜의 좌/우 휠속 차이, 그리고 ΔV_x.r.LR 은 후륜의 좌/우 휠속 차이를 의미한다. 전/후 휠속 차이 같은 경우 좌/우 휠속 중 작은 값을 기준으로 차이를 계산한다.

2.2.2 휠속차 보상 제동 분배

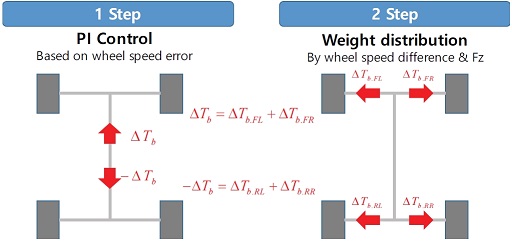
휠속차 보상 제동 분배 모듈에서는 앞 절에서 산출된 각 휠속 차이 정보를 이용하여 각 휠에 추가로 가/감 해줘야 할 제동 토크를 결정하고, 모터와 유압으로의 재 분배를 수행한다. Fig. 10은 휠속차 보상 제동 분배 방법에 대한 내용을 나타내고 있다. 보는 바와 같이 2 단계로 분배가 수행된다. 1 단계에서는 전/후 휠속 차이를 통해 전륜으로 추가해야 할 제동 토크를 결정한다. 결정 방법은 휠속 차이에 기반한 PI(비례적분, Proportional and Integral) 제어기를 사용하였다. 이렇게 결정된 제동 토크는 좌/우 수직 항력과 휠속 차이에 의한 가중치를 이용해 좌/우로 분배된다.

Fig. 10

Brake distribution method by wheel speed difference

전륜으로 추가해야 할 제동 토크를 구하기 위해 우선 식 (9)와 같이 전/후 휠속 차이에 기반한 PI 제어기를 설계한다.

$\[ ∆T_b=K_P∆V_{x.fr}+K_I\int ∆V_{x,fr} \]$

(9)

식 (9)의 결과를 이용하여 좌/우 추가 제동 토크를 다음과 같이 분배한다.

(10)

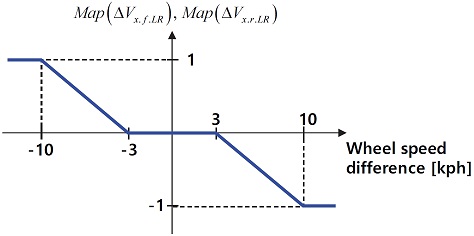
기본적으로 수직 항력의 비율로 분배하고, 좌/우 휠속차가 일정 값 이상 발생하게 되면 이를 보상하기 위해 분배 비율을 조절하는 구조이다. Fig. 11은 식 (10)에 사용된 휠속 보상 Map(Map(ΔV_x.f.LR), Map(ΔV_x.r.LR))을 나타내고 있다. 좌/우 휠속 차이가 3 kph 이하일 경우 휠속 보상 분배는 이루어지지 않고, 휠속 차이가 10 kph 이상이면 전/후륜에 분배된 제동 토크가 모두 한쪽 휠로 전달된다. 또한 위 결과는 FF 제어기의 제동 토크에 추가로 가/감해야 할 제동 토크로 전체 합은 0 이어야 한다.

Fig. 11

Wheel speed difference compensation map

식 (10)에서 산출된 추가 제동 토크 또한 모터 제동과 유압 제동으로 분배되어야 한다. 아래 식 (11)은 유압/제동 분배 방법을 나타내고 있다. 추가 제동 토크가 양수인 경우 모터의 추가 제동이 가능하다면 모터 회생 제동을 먼저 수행하고, 반대인 경우 현재 유압 제동이 있는 상황이면 유압 제동을 먼저 감압시켜 모터의 회생 제동을 최대한 활용하도록 분배하였다.

$\[ \begin{array}{c}if ∆T_{b.i}\ge 0\hfill \\ {{ ∆T}_{b.M.i}}^{FB}=\min \left[∆T_{b.i},\max \left[0,T_{b.LIm.i}-{{∆T}_{b.M.i}}^{FF}\right]\right]\hfill \\ {{ ∆T}_{b.H.i}}^{FB}=∆T_{b.i}-{∆T_{b.M.i}}^{FB}\hfill \\ \hfill \\ else\hfill \\ {{ ∆T}_{b.H.i}}^{FB}=\max \left[∆T_{b.i}-{T_{b.H.i}}^{FF}\right]\hfill \\ {{ ∆T}_{b.M.i}}^{FB}=∆T_{b.i}-{∆T_{b.H.i}}^{FB}\hfill \\ \left(i=FL,FR,RL,RR\right)\hfill \end{array} \]$

(11)

식 (5), (7), 그리고 (11)을 통해 최종 회생 제동 토크및 유압 제동 토크 제어량을 다음과 같이 결정할 수 있다.

$\[ \begin{array}{c}{T}_{b.M.i}={T_{b.M.i}}^{FF}+{{∆T}_{b.M.i}}^{FB}\hfill \\ T_{b.H.i}={T_{b.H.i}}^{FF}+{{∆T}_{b.H.i}}^{FB}\hfill \end{array} \]$

(12)

위 식 (12)에서 보는 바와 같이 FB 제어는 FF 제어에 Overlay 형태로 반영되기 때문에, 휠속 차이가 발생하지 않는 경우 최종 제어량은 FF 제어의 전략과 모터/유압 분배비를 유지함을 알 수 있다.

3. 시뮬레이션 기능 검증

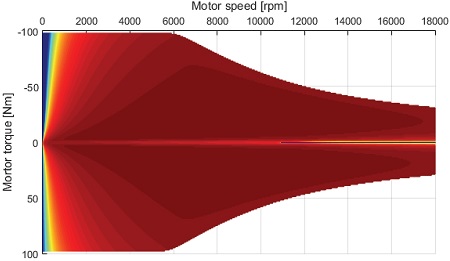
앞 절에서 개발된 전자 제동 분배 로직을 평가하기 위해 시뮬레이션 해석을 Carsim, Matlab/Simulink를 이용하여 실시하였다. FF 제어와 FB 제어에 대한 효과를 검증하기 위해 하중 변화가 없는 경우와 있는 경우 이렇게 2 가지 케이스로 시뮬레이션을 수행하였다. 제안된 로직의 타당성을 검증하기 위해 Carsim에서 기본적으로 제공되는 제동 분배 모델(EBD OFF)과 그 성능을 비교하였다. Carsim에서 제공되는 제동 분배 모델의 경우 급 제동 시 전/후륜 제동 분배가 가능한 모델로 제안된 로직과의 성능 비교가 타당하다고 판단하였다. 시뮬레이션에 사용된 모터 출력은 75 kW로 아래 Fig. 12와 같은 특성을 보이고, Table 1은 제어 대상 차량의 제원을 나타내고 있다.

Fig. 12

Motor characteristics

Table 1

Vehicle specification

3.1 시뮬레이션 검증 w/o 하중 변화

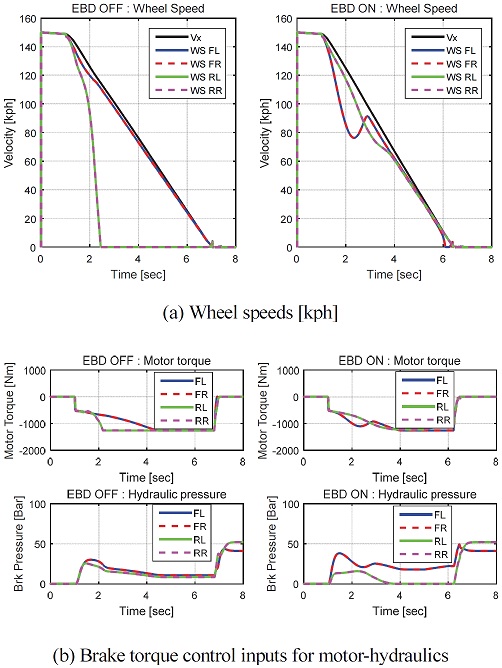
본 절에서는 FF 제어의 효과를 검증하기 위해, 차량의 하중 변화가 없는 경우 직진-제동 그리고 제동-선회 상황에서 차량의 안정성이 확보됨을 보이기 위한 시뮬레이션이 수행되었다. 직진-제동은 고마찰 노면이고 초기 속도가 150 kph 인 상황에서 직진을 유지하며 휠 Lock이 발생할 때까지 제동압을 5 bar씩 증가시켜가며 시뮬레이션을 수행하였다. 그 결과 EBD OFF의 경우 50 bar까지 휠 Lock 발생 없이 제동이 가능하였고, EBD ON인경우 55 bar까지 제동이 가능함을 확인하였다. Fig. 13은 직진-제동 상황에서 55 bar의 제동을 인가했을 때의 시뮬레이션 결과이다. Fig. 13(a)는 EBD OFF/ON에 대한 휠속을 나타내고 있다. 결과를 보면, EBD OFF의 경우 후륜 휠에 Lock이 발생하였고, EBD ON의 경우에는 휠 Lock 발생 없이 감속됨을 확인할 수 있다. 이는 후륜의 제동력을 감소시키고 감소된 제동력을 전륜 제동력의 증가로 보상했기 때문이다. 따라서 EBD ON의 경우 전륜의 휠속이 줄어듬을 보이고 있다. 이 결과를 통해 전륜 휠의 안정성에 대한 이슈 사항이 있을 수 있다. 하지만 본 로직은 각 휠의 제동력을 최적으로 분배하여 제동 성능 개선뿐만 아니라 ABS의 작동을 최소화 하는 것을 목적으로 하고 있기 때문에 해당 결과로도 충분히 개선되었다고 할 수 있다. 그리고 (b)는 각 휠의 모터/유압 제동 토크를 나타내고 있다. 분배 전략 1에 대한 결과로, 각 4휠의 요구 제동 토크가 모두 모터 한계 제동을 초과하여 모든 휠이 모터 제동을 한계까지 쓰고 있음을 보이고 있다.

Fig. 13

Simulation results for straight & braking scenario

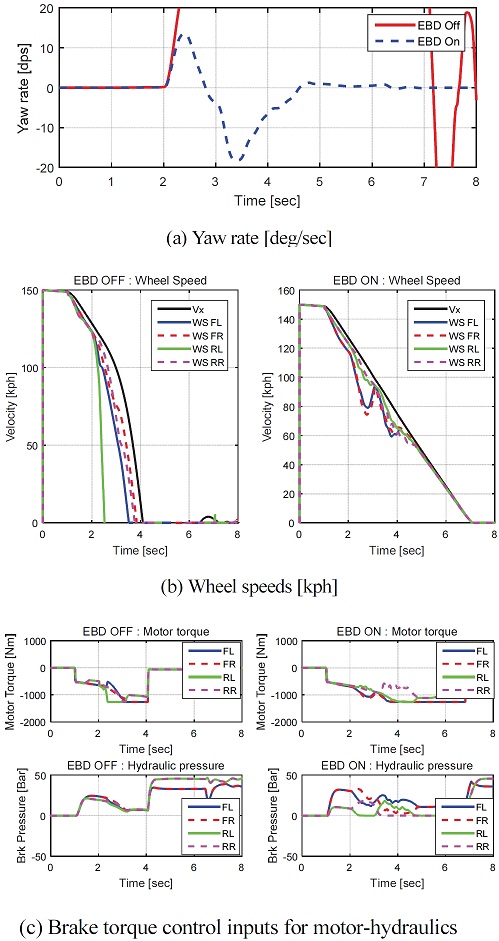
제동-선회 상황은 직진-제동의 결과에 기반하여 시뮬레이션이 수행되었다. 직진-제동 결과 EBD OFF/ON 모두 휠 Lock이 발생하지 않는 최대 제동압(50 bar)을 인가시킨 상태에서 Open-loop single sine 조향이 수행 되었다. 직진-제동과 동일하게 휠 Lock이 발생할 때까지 조향각의 크기를 5 deg 씩 증가시켰고 그 결과 EBD OFF의 경우 조향각 5 deg까지 휠 Lock 발생없이 제동-선회가 가능하였고, EBD ON의 경우 80 deg까지 제동-선회가 가능함을 보였다. Fig. 14는 제동(50 bar)-선회(80 deg)에 대한 결과를 보이고 있다. Fig. 14(a)는 Single sine 조향에 의해 발생되는 요레이트이고, (b)는 휠속을, 그리고 (c)는 각 휠의 모터/유압 제동을 나타내고 있다. 보는 바와 같이 EBD ON인 경우 조향에 대한 요레이트의 반응 그리고 휠 안정성 적인 측면에서 OFF 대비 우세함을 알 수 있다.

Fig. 14

Simulation results for braking & turning scenario

3.2 시뮬레이션 검증 w 하중 변화

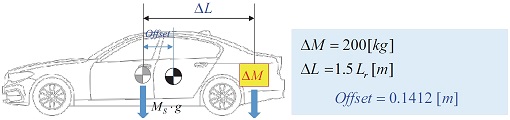
FB 제어의 효과를 검증하기 위해, 차량의 무게 변화를 주어 시뮬레이션을 수행하였다. 무게 변화를 주기 위해 Fig. 15와 같이 트렁크에 200 kg의 짐을 실었을 경우를 가정하였다. 시뮬레이션 시나리오는 초기 속도 130 kph에서 직진을 유지하며 55 bar의 제동을 인가한 경우이다.

Fig. 15

Schematic for load change

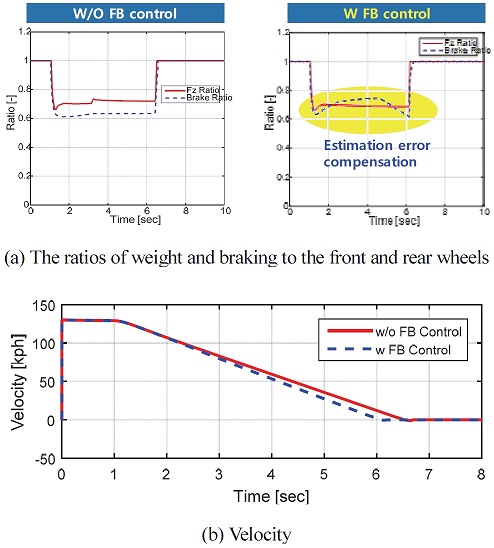
Fig. 16은 시뮬레이션 결과이다. Fig. 16(a)에서 빨간색 실선은 실제 수직 항력의 비(후륜 하중/전륜 하중)를, 그리고 파란색 점선은 제어기의 제동 토크 비(후륜 제동/전륜 제동)를 나타내고 있다. FB 제어를 실시하지 않은 경우 수직 항력 추정 오차로 인해 실제 수직 항력의 비와 제동 토크 비에 오차가 발생함을 보이고 있지만, FB 제어를 통해 수직 항력 추정 오차에 대한 부분이 보상됨을 보이고 있다. 이로 인해 FB 제어를 한 경우 제동 성능이 향상됨을 Fig. 16(b)를 통해 확인할 수 있다.

Fig. 16

Simulation results for load change

위 시뮬레이션 이외에 휠속 결과 그리고 제동-선회에 대한 결과 모두 앞 절의 결과와 동등한 성능을 보이기 때문에 생략하도록 한다.

4. 결 론

본 연구에서는 4륜 독립 구동 전기 자동차의 제동 분배 방법에 대한 연구를 수행하였다. 해당 로직은 차량의 제동 안정성 확보를 위해 수직 항력에 기반한 FF제어와 하중 변화에 강건성 확보를 위한 FB 제어로 구성하였다. FF 제어에서는 기본적으로 제동 안정성을 위해 모터-유압 제동 토크 분배가 이루어지지만 필요에 따라 에너지 회수량을 최대화하기 위한 분배 전략이 적용 가능하도록 모터-유압 분배 로직을 새롭게 설계하였다. 제안한 분배 로직은 단위 기능 검증을 통해 안정성 최대화와 회생 제동 최대화가 가능함을 보였고, 전체적인 전자 제동 분배 로직(EBD)은 Carsim 시뮬레이션을 통해 직진-제동과 제동-선회 상황에서의 안정성과 하중 변화에 대한 보상 효과를 확인하였다. 향후에는 개발된 로직을 실차 환경에서 검증하고, 신뢰성 확보를 위해 Fail-safe 로직을 개발할 예정이다.

Acknowledgments

이 논문은 2020학년도 한국기술교육대학교 신임교수 연구과제 연구비 지원에 의하여 연구되었음.

References

• Science & Technology Global Policy Service, https://now.k2base.re.kr/portal/trend/mainTrend/view.do?poliTrndId=TRND0000000000031785&menuNo=200004&searchSubj=03&pageIndex=8, , 2017.
• B. Cho, H. Kim, J. Park and S. Hwang, “A Study on the Characteristics for Electronic Brake Distribution Algorithm of Electric Vehicle,” KSAE Spring Conference Proceedings, pp.125-131, 2010.
• M. W. Kim, J. Lee, H. K. Yang, J. H. Choe and J. W. Park, “Inverter Sliding Mode Control Method for Maintaining Braking Force in Braking Force Distribution Transient of Electric Vehicle,” KIEE Summer Conference Proceedings, pp.226-227, 2020.
• S. Kim and H. Kim, “A Study on a Fuzzy Controller for the Electronic Braking Force Distribution System,” Transactions of KSAE, Vol.8, No.6, pp.220-229, 2000.
• D. Kim and H. Kim, “Vehicle Stability Control for a 4WD HEV using Regenerative Braking and Electronic Brake Force Distribution,” Transactions of KSAE, Vol.13, No.1, pp.166-173, 2005.
• H. Yeo, D. Kim, T. Kim, C. Kim, S. Hwang and H. Kim, “Development of Regenerative Braking Control Algorithm for a 4WD Hybrid Electric Vehicle,” Transactions of KSAE, Vol.13, No.6, pp.38-47, 2005.
• S. T. H. Jansen, J. J. P. Boekel, S. S. Iersel, I. J. M. Besselink and H. Nijmeijer, “Vehicle State Estimator Based Regenerative Braking Implementation on an Electric Vehicle to Improve Lateral Vehicle Stability,” World Electric Vehicle Symposium and Exhibition (EVS27), 2013. [https://doi.org/10.1109/EVS.2013.6915034]
• N. Mutoh and Y. Takahashi, “Front-and-Rear-Wheel-Independent-Drive Type Electric Vehicle (FRID EV) with the Outstanding Driving Performance Suitable for Next-generation Adavanced EVs,” IEEE Vehicle Power and Propulsion Conference, pp.1064-1070, 2009. [https://doi.org/10.1109/VPPC.2009.5289731]
• N. Mutoh, Y. Hayano, H. Yahagi and K. Takita, “Electric Braking Control Methods for Electric Vehicles with Independently Driven Front and Rear Wheels,” IEEE Transactions on Industrial Electronics, Vol.54, No.2, pp.1168-1176, 2007. [https://doi.org/10.1109/TIE.2007.892731]
• N. Mutoh, Y. Takahashi and Y. Tomita, “Failsafe Drive Performance of FRID Electric Vehicles With the Structure Driven by the Front and Rear Wheels Independently,” IEEE Transactions on Industrial Electronics, Vol.55, No.6, pp.2306-2315, 2008. [https://doi.org/10.1109/TIE.2008.918405]
• W. Cho, J. Yoon, S. Yim, B. Koo and K. Yi, “Estimation of Tire Forces for Application to Vehicle Stability Control,” IEEE Transactions on Vehicular Technology, Vol.59, No.2, pp.638-649, 2010. [https://doi.org/10.1109/TVT.2009.2034268]