3자유도 등가 캐빈 현가장치 모델을 이용한 상용차 승차감 성능 최적설계 프로세스 개발

1. 서 론

상용차는 승용차와는 사용목적이 뚜렷하게 나뉨에 따라 다양한 차이가 존재한다. 그 중 특히 운전자의 입장에서 직업적 특성에 의한 장시간 주행이 많으며, 실내 캐빈에서의 탑승시간 비율은 일반 승용차와 비교했을 때 매우 높은 편에 속한다. 또한, 비포장도로 및 공사장 등의 거친 도로 환경에서 발생하는 노면 입력에 따라 일반 승용차 운전자에 비하여 더욱 많은 피로감을 느끼게 된다.

따라서 소비자들의 승차감 성능에 대한 요구가 크며 상용차 생산 업계에서는 승차감에 지대한 영향을 미치는 캐빈 현가장치 해석 모델 구축 및 설계에 대한 연구개발을 진행하고 있다.

일반적으로 캐빈 및 차량의 거동 해석을 위해 3자유도 1/4 차량 수학적 모델¹⁾ 혹은 다자유도 전체 차량 수학적 모델²⁾을 사용한다. 이 경우 캐빈 시스템의 해석 정확도가 낮고 구조적 커플링(Coupling)에 의한 특성의 반영이 어렵다. 이러한 단점을 보완하기 위해 보다 정확한 캐빈의 거동 예측이 필요한 경우 유한요소 모델³⁾이나 다물체 동역학 모델⁴⁾을 구성하여 이용하거나, 목적에 따라 일부 부품의 상세 모델이 포함된 모델을 사용한다.⁵⁾ 하지만 이러한 상세 모델의 경우 정확도는 높지만 부품의 형상 및 힘요소 특성이 결정되어야 모델링이 가능하다는 한계를 가진다. 따라서, 하드포인트 및 힘요소 특성이 결정되지 않은 설계 초기단계에서는 사용이 불가능하다.

본 논문에서는 설계 초기단계에 사용 가능하며 다물체 동역학 캐빈 현가장치 모델이 갖는 수준의 정확도를 만족하는 3자유도 등가 캐빈 현가장치 모델을 개발하고 개발한 등가 모델을 이용한 효율적인 설계 프로세스를 제시하고자 한다.

2장에서는 3자유도 등가 캐빈 현가장치 모델과 차량모델을 개발한다. 3장에서는 캐빈 현가장치 설계 프로세스에 대해 설명하고, 설계 시 기준점이 되는 차량 성능 평가방법 및 성능 지수에 대하여 설명한다. 4장에서는 앞서 개발한 3자유도 등가 캐빈 현가장치 모델을 이용한 설계프로세스의 적용 결과를 설명한다.

2. 3자유도 등가 캐빈 현가장치 및 차량 모델 개발

실제 캐빈 현가장치는 소형, 중형, 대형 차량에 적용되는 종류가 다양하다. 또한 수많은 부품으로 구성되어있으며 매우 복잡한 구조로 설계되어 있다. 따라서 다물체 동역학 기반의 캐빈 현가장치는 많은 설계 변수를 가지게 됨에 따라 차량 레벨에서의 최적화에 많은 시간이 소요된다. 이러한 문제점 해결을 위해 3자유도 등가 캐빈 현가장치 모델을 개발하였다. 또한 설계 적용시 사용할 차량모델을 개발하였다

2.1 3자유도 등가 캐빈 현가장치 모델 개발

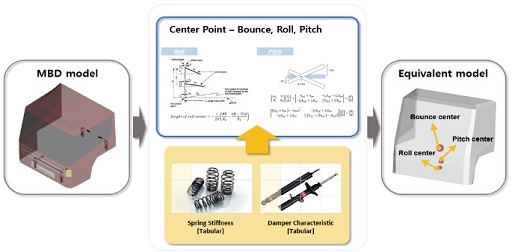
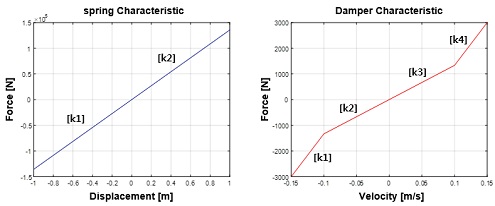
3자유도 등가 캐빈 현가장치 모델은 Fig. 1과 같이 기존 다물체 동역학 기반의 캐빈 현가장치 모델의 움직임을 3자유도(Bounce, Roll, Pitch)로 정의하고, 각 자유도의 중심점은 이론적인 내용을 토대로 도출하였다. 상하운동모드(Bounce mode)의 중심점이 되는 상하운동중심(Bounce center)과 피치모드(Pitch mode)의 중심점이 되는 피치중심(Pitch center)은 질량중심(Center of mass)을 기준으로 서로 반대편에 위치하며 전⋅후 차축 외부에 위치하고 있는 질점이 상하운동중심에 해당하고 전⋅후 차축 내부에 위치하고 있는 질점이 피치중심에 해당한다. 롤모드(Roll mode)의 경우 전⋅후 차축 각각에 위치한 롤중심(Roll center)을 연결한 가상의 선으로 정의되는 롤 축을 중심으로 차체가 회전하게 된다.

Fig. 1

Development of 3-DOF equivalent cabin suspension model

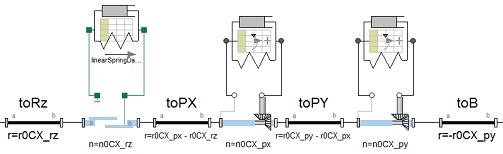
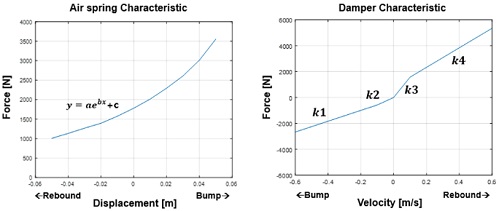
스프링 모델은 초기하중(Pre-Load)과 하중-변위 선도를 2개의 1차식 조합으로 표현하고 모델링하였다. 댐퍼 모델은 하중-속도 선도를 3개의 1차식 조합으로 표현하고 모델링하였다. 상기의 방법을 통해 개발한 3자유도 등가 캐빈 현가장치 모델은 Fig. 2와 같다.

Fig. 2

3-DOF equivalent cabin suspension model

2.2 캐빈 현가장치 평가 방법

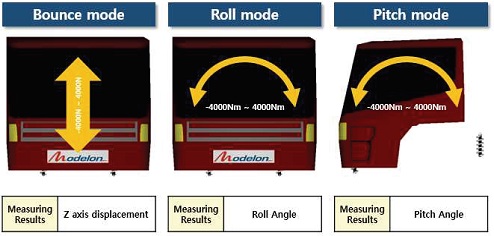
캐빈 현가장치는 각 자유도에 대한 움직임을 바운스, 롤, 피치 모션으로 구분한다. 실제 차량의 거동은 3가지 모션이 연성되어 발생하지만, 각 특성을 파악하기 위해 Fig. 3과 같이 3가지 모드에 대한 해석을 독립적으로 수행한다. 각 모드에 대하여 정적(Static) 해석과 동적(Dynamic) 해석을 통해 실제 캐빈 현가장치의 거동을 모사할 수 있는 3자유도 등가 캐빈 현가장치를 설계 할 수 있다.

Fig. 3

Cabin susp. bounce, roll, pitch mode analysis

2.3 캐빈 현가장치 모델 비교 및 검증

다물체 동역학 기반의 모델과 3자유도 등가 모델에 대하여 각각 위에서 제시한 평가방법에 따라 시험을 진행하였고 두 모델의 해석 결과 비교를 통하여 새로 개발한 3자유도 등가 캐빈 현가장치 모델의 정합성을 검증하였다.

2.3.1 정적시험(Static Test)

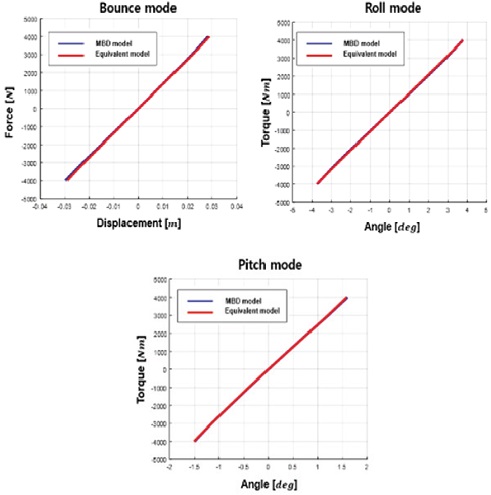
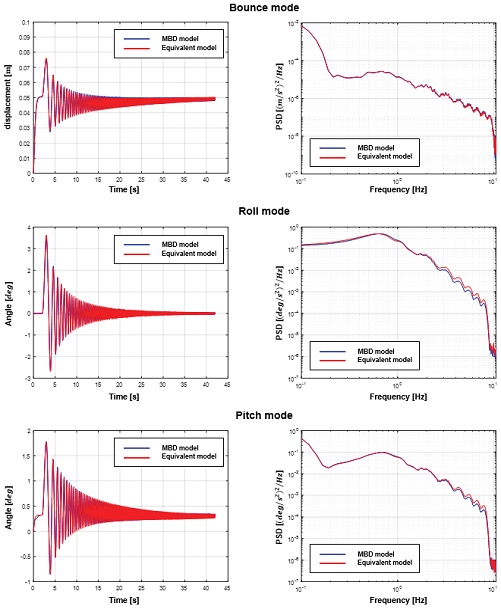
시험 방법은 Table 1과 같으며, 결과는 Fig. 4와 Table 2에 나타내었다. 결과 분석을 통해 두 모델간의 오차가 1 % 미만임을 확인하였다.

Table 1

Cabin susp. static test maneuver

Fig. 4

Cabin susp. static test result graph

Table 2

Cabin susp. static test result analysis

2.3.2 동적 시험(Dynamic Test)

시험 방법은 Table 3과 같으며, 결과는 Fig. 5와 Table 4에 나타내었다.

Table 3

Cabin susp. dynamic test maneuver

Fig. 5

Cabin susp. dynamic test result graph

Table 4

Cabin susp. dynamic test result analysis

검증 결과 Fig. 5에 나타난 시간영역 그래프와 주파수영역에서의 PSD(Power Spectrum Density) 선도를 통해 시험 주파수 범위에서 정합성을 확인할 수 있으며, Fig. 7의 제곱평균제곱근(RMS : Root Mean Square)값의 비교 결과 2 % 이내의 오차를 확인하였다. 또한 MBD 모델의 해석시간은 101초, 등가 모델의 해석시간은 13.7초로 7배 가량 줄어듦을 확인할 수 있다.

3. 캐빈 현가장치 설계 프로세스 개발

3.1 캐빈 현가장치 설계 방법론

본 절에서는 앞서 개발한 3자유도 등가 캐빈 현가장치 모델을 사용한 캐빈 현가장치 설계 방법론에 대해 설명하고자 한다.

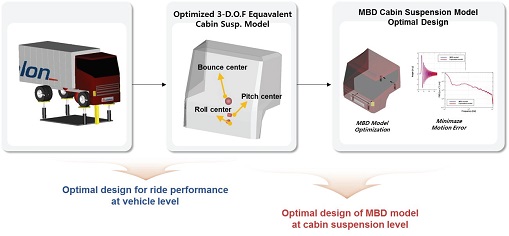
이 방법론은 Fig. 6과 같이 차량 레벨에서의 승차감을 성능 지수로 선정하여 3자유도 등가 모델의 최적 설계안을 개발하고, 최종적으로 등가 모델의 거동을 구현하는 다물체 동역학 모델의 최적설계를 진행한다.

Fig. 6

Cabin suspension design process

3.2 캐빈 현가장치 설계 플랫폼

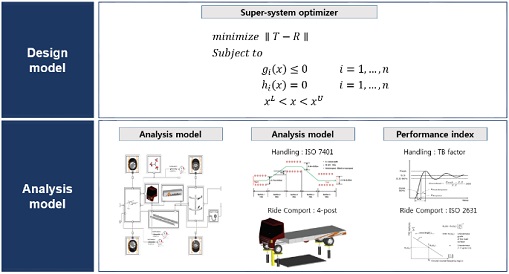
해석 모델은 Fig. 7과 같이 전 차량 모델, 시험 환경 모델, 시험 조건 및 성능 평가 방법의 카테고리로 분류 되어있다. 설계 모델의 경우 설계 변수와 최적설계문제 정식화를 통해 목표를 만족하는 모델을 도출할 수 있도록 구성된다.

Fig. 7

Cabin suspension design model & vehicle analysis model

4. 등가 캐빈 현가장치 최적설계

본 장에서는 앞서 개발한 3자유도 등가모델을 적용한 설계목표전이기법 기반의 캐빈 현가장치 설계 프로세스의 유효성 및 효율성을 검증하고자 차량레벨에서 최적 설계를 진행 후, 최적 해에 부합하는 하드포인트, 힘 요소 특성을 설계하였다.

4.1 해석 모델

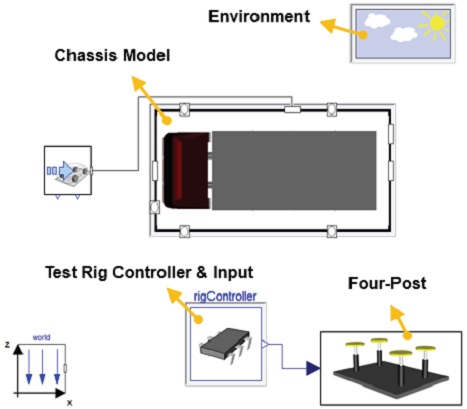
차량 레벨의 최적설계를 위해 앞서 개발한 차량모델을 이용하여 승차감 평가를 위한 Four-Post 시험 환경을 구성하였으며, Fig. 8과 같다. 모델을 구성하는 각 요소는 샤시 모델과 노면 입력을 위한 컨트롤러 및 리그로 구성되어있다. 시험 입력 신호는 ISO 도로 노면 거칠기 분류 중 C등급에 해당하는 노면을 사용하였다. 성능지수는 시트 바닥면에서의 수직 가속도, 롤 각가속도, 피치 각가속도의 가중화된 RMS값을 사용하였다.

Fig. 8

Four-post test environment

4.1.1 차량 레벨 설계 변수

최적설계 진행을 위해 설계 변수로 힘요소 특성(스프링, 댐퍼)을 선정하였다. 선정된 힘 요소의 특성은 Fig. 9와 같이 설계 변수화 하였다. 스프링 특성의 경우 인장⋅압축시 기울기를, 댐퍼 특성은 인장⋅압축시 각각 0.1 m/s의 속도를 기준으로 나누어 총 4개의 기울기를 설계 변수로 선정하였다. 최종적으로 18개의 설계 변수로 선정하였고 Table 5와 같이 각각 설계 변수에 대한 설계 범위를 선정하였다.

Fig. 9

Selected vehicle level design variables description of spring & damper characteristics

Table 5

Selected vehicle level design variables & range

4.1.2 차량 레벨 최적 설계 문제 정식화

최적 설계 진행을 위해 목적함수와 제약조건을 정의하고 수학적 정식화 과정을 통해 설계 문제를 정의한다. 우선, 첫째로 ISCD-II(Incomplete Small Composite Design–II) 실험계획법을 통해 메타모델을 생성하였다. 메타 모델 생성은 방사 기저 함수(Radial basis function)의 Gaussian을 적용하였다. 다음으로, 최적설계 문제를 정의하였다. 목적함수는 승차감 성능을 판단하는 성능지수로 4∼8 Hz 영역의 캐빈 수직 가속도 RMS값의 최소화로 선정하였으며, 제약조건은 캐빈의 롤⋅피치 각가속도의 RMS값을 유지 혹은 감소와 설계변수 힘 요소 특성 ±20 %로 설계 문제를 정식화 하였고 아래의 식 (2)와 같다.

$\[ \begin{array}{c} Object\hfill \\ \begin{array}{cc}& Minimize CabinRM{S}_{Vetical Acc.}\end{array}\\ Subject to\hfill \\ \begin{array}{cc}& \begin{array}{c}CabinRM{S}_{Roll Angular Acc.}\le Base\\ CabinRM{S}_{Pitch Angular Acc.}\le Base\end{array}\end{array}\\ \\ \begin{array}{c}base•0.8\le Force elements characteristics\\ \le base•1.2\end{array}\end{array} \]$

(2)

4.1.3 차량 레벨 최적 설계 결과

본 단계에서는 Ride 목표성능을 만족하도록 앞서 선정한 설계 변수들의 최적 해를 찾기 위한 최적 설계를 진행한다. 최적설계는 메타모델 기반의 근사 최적화 기법을 사용하여 수행하였으며, 여타 최적기법에 비해해석 시간 및 비용의 단축이 용이하고 전역 최적해를 도출할 수 있다는 장점을 가진다.

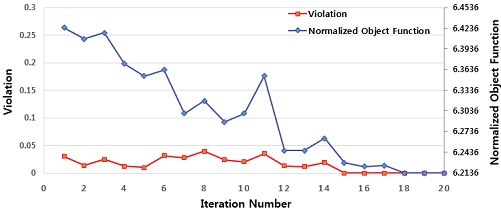
최적화를 수행을 통해 설계 문제 정식화를 만족하는 최적 설계안을 도출하였으며, 초기 실험점을 통해 생성된 메타모델은 Iteration 20번 만에 수렴하였다. Fig. 10에 Convergence history를 나타내었다.

Fig. 10

Vehicle level convergence history of optimization process

Violation은 메타모델의 정확도를 나타내는 지표로 실제 모델과의 오차를 나타낸다. Normalized object function은 설계 문제 정식화를 통해 설정한 목적함수에 대한 수렴 정도를 뜻한다.

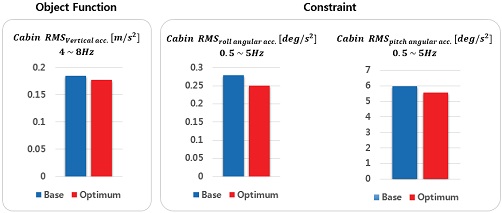
Fig. 11은 설계문제 정식화를 통해 목적함수와 제약조건으로 정의한 성능지수들의 초기모델과 최적 설계치 간의 해석 결과 값을 비교한 것이다.

Fig. 11

Comparison of vehicle level optimal design performance index between base model & optimal model

결과적으로 목적함수인 캐빈의 수직방향 가속도의 RMS값은 4 % 감소하였으며, 제약 조건인 롤⋅피치 각가속도의 경우도 각각 10 %, 7 % 감소하였다. 따라서 기존의 캐빈 현가장치 성능 대비 승차감 성능이 향상된 설계안을 도출하였다.

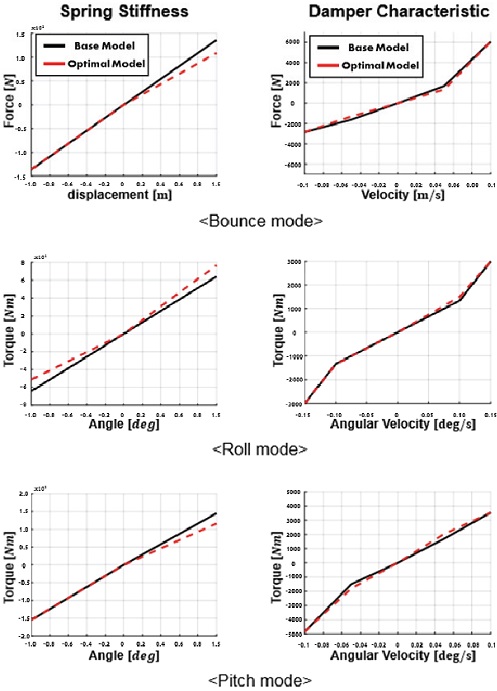
설계 변수인 힘요소 특성의 경우 Bounce의 스프링 특성은 Soft, 댐퍼 특성은 Hard한 방향으로 설계되었다. Roll의 스프링 특성은 구간 별로 Soft, Hard 두 가지 방향으로 진행되었고, 댐퍼 특성은 Hard한 방향으로 설계되었다. Pitch의 스프링특성은 Soft, 댐퍼 특성은 Hard하게 설계되었다. 최적설계 결과로 얻은 힘요소 특성은 Fig. 12에 나타내었다.

Fig. 12

Comparison of vehicle level optimal design force element characteristics between base model & optimal model

4.2 캐빈 현가장치 레벨 다물체 동역학 모델 최적설계

캐빈 현가장치 레벨의 최적 설계 문제는 앞선 차량 레벨에서 도출한 등가모델을 전이시켜 다물체 동역학 기반의 캐빈 현가장치 모델의 설계 목표로 하는 설계문제이다. 본 절에서는 캐빈 현가장치 레벨에서의 최적설계를 위해 설계 변수 정의 및 설계 문제 정식화를 통해 최적 설계를 진행하였으며 다음 4.2.1∼3을 통해 일련의 과정을 설명한다.

4.2.1 캐빈 현가장치 레벨 설계 변수

다물체 동역학 기반의 캐빈 서스펜션 최적설계를 위해 사용한 설계 변수는 크게 하드포인트와 힘요소 특성으로 나뉜다. 하드포인트의 경우 Front⋅Rear air spring의 상단 마운트 위치로 선정하였고, 힘요소 특성은 Air spring stiffness, Damper characteristic으로 선정하였다. 선정된 힘요소 특성 설계 변수는 Fig. 13과 같이 함수화 하여 사용하였다. 또한 Table 6에 총 16개의 설계 변수에 대한 설계 변경 범위를 표기하였다.

Fig. 13

Selected cabin susp. level design variables description of air spring & damper

Table 6

Selected cabin susp. level design variables & range

4.2.2 캐빈 현가장치 레벨 최적 설계 문제 정식화

앞서 4.1.3의 과정을 캐빈 현가장치 레벨에서 진행하였으며, 목적함수는 등가모델과 다물체 동역학 모델간의 캐빈 바운스 수직 가속도 및 롤⋅피치 각가속도 RMS값 간의 오차 최소화로 선정하였으며, 제약조건은 하드포인트 설계 변수 ±30 mm, 힘 요소 특성 설계 변수 ±20 %로 설계 문제 정식화 하였고 아래의 식 (3)과 같다.

$\[ \begin{array}{c} Object\hfill \\ Minimize Error of RM{S}_{Vertical Acc.,Roll\cdot Pitch Angular Acc }\hfill \\ Subject to\hfill \\ base-30mm\le Hardpoints\le base+30mm\\ \begin{array}{c}base•0.8\le Force elements characteristics\\ \le base•1.2\end{array}\end{array} \]$

(3)

4.2.3 캐빈 현가장치 레벨 최적 설계 결과

최적설계 결과, 차량 레벨에서 최적화된 3자유도 등가 모델과 같은 거동을 나타낼 수 있는 다물체 동역학 모델의 파라미터를 도출하였다. Fig. 14에 각 모드별 가속도 및 각가속도의 PSD선도를 나타내었고, Table 7에 나타낸 목적함수 값을 통해 두 모델간의 오차가 1 % 내외로 매우 적음을 확인하였다.

Fig. 14

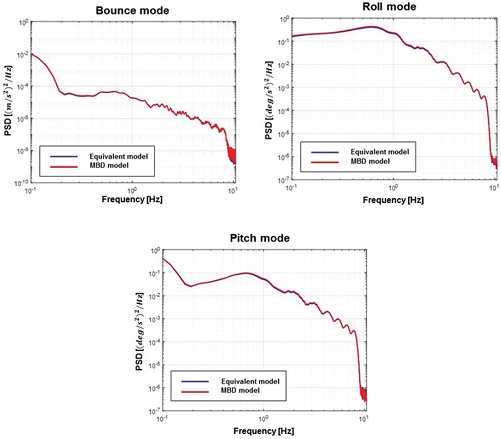
Comparison of cabin susp. level bounceㆍrollㆍpitch mode acceleration PSD between MBD model & Equivalent model

Table 7

Comparison of cabin susp. level performance index between MBD model & Equivalent model

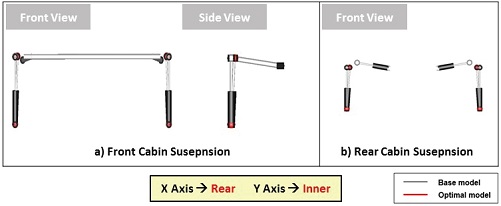
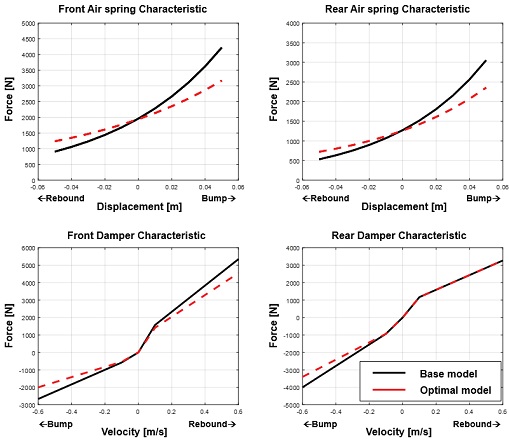
Fig. 15와 Fig. 16에 최적설계안을 나타내었다. 하드 포인트의 경우 Front 에어 스프링의 X는 Rear방향, Y는 Inner방향, Z는 Lower방향으로 설계 변경되었고, Rear 에어 스프링의 X는 기존의 값과 같고 Y, Z는 Front와 동일한 경향으로 설계 변경 되었다. 힘 요소의 경우 Front air spring과 Rear air spring, Front damper, Rear damper 특성이 모두 Soft하게 설계되었다.

Fig. 15

Comparison of cabin susp. hardpoints between base model & optimal model

Fig. 16

Comparison of cabin susp. force element characteristics between base model & optimal model

4.3 최적 설계안 검증

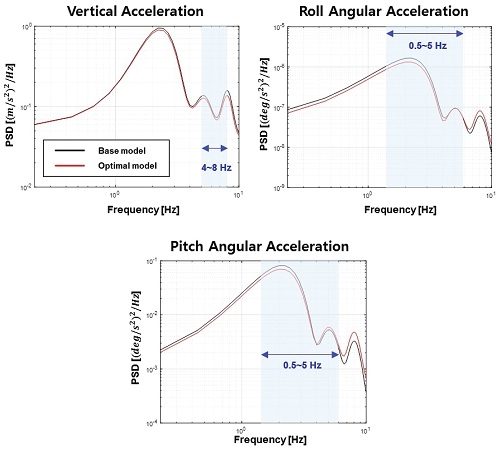
앞서 도출한 최적 설계안과 기존 모델간의 성능 비교를 통해 최적 설계안의 타당성을 검증한다. 각 모델에 대해 ISO 노면 거칠기 C에 해당하는 입력 신호를 사용한 Four-Post 시험 진행하였다. Fig. 17에 수직 가속도 및 롤⋅피치 각가속도의 주파수 영역 PSD선도를 표시하였다. 전체적인 P에너지량이 감소함을 확인하였으며 특히 각 모드 별 인체 민감 주파수 영역에서의 뚜렸한 에너지량의 감소를 확인하였다.

Fig. 17

Comparison of ride comfort index between base model & optimal model

5. 결 론

본 논문에서는 상용차량 캐빈 현가장치 설계의 효율성을 높이기 위한 3자유도 기반 등가 캐빈 현가장치 모델을 이용한 설계 프로세스를 제시했다.

먼저, 기존의 다물체 동역학 기반 모델과 동일한 거동을 나타내는 3자유도 기반 등가 캐빈 현가장치 모델을 포함한 차량 모델을 개발하였다. 이후, 개발된 차량 모델을 이용한 캐빈 현가장치 설계 프로세스를 개발하였다.

끝으로 본 논문에서 제안하는 설계 프로세스 적용을 통해 차량 레벨에서 기존 모델대비 수직가속도 RMS값은 4 %, 롤⋅피치 각가속도의 RMS도 각각 10 %, 7 % 감소된 등가 캐빈 현가장치 모델을 개발하였으며, 캐빈 현가장치 레벨에서 개발된 등가 모델과 2 % 이내의 오차를 갖는 다물체 동역학 기반의 캐빈 현가장치를 개발하였다.

본 논문에서는 개발 설계 프로세스 적용 시 캐빈 현가장치의 주 기능에 해당하는 승차감 성능에 대해서만 최적설계를 진행하였다. 향 후 제시한 설계 프로세스 적용 시 핸들링 성능을 고려한 다분야 최적 설계에 대한 연구가 이루어져야 할 것이다.

Acknowledgments

이 논문은 2021년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(NO. 5199990814084).

References

• K. H. Sim, H. Y. Lee and S. H. Hwang, “Development of Control Algorithm for Semi-active Suspension of Utility Vehicle,” The Korea Fluid Power Systems Society Conference Proceedings, pp.140-144, 2015.
• S. K. Sharma, V. Pare, M. Chouksey and B. R. Rawal, “Numerical Studies Using Full Car Model for Combined Primary and Cabin Suspension,” Procedia Technology, Vol.23, pp.171-178, 2016. [https://doi.org/10.1016/j.protcy.2016.03.014]
• P. Sathish Kumar, M. Manikandan and N. Mahendra, “Virtual Durability Analysis of Heavy Commercial Truck Cabin for Proving Ground Inputs,” SAE 2013-01-2788, 2013. [https://doi.org/10.4271/2013-01-2788]
• K. H. Lee and H. S. Jeong, “Hydropneumatic Modeling and Dynamic Characteristic Analysis of a Heavy Truck Semi-active Cabin Air Suspension System,” Transactions of KSAE, Vol.19, No.2, pp.57-65, 2011.
• J. H. Song, D. C. Lee, H. D. Kim and C. Y. Oh, “Development of a Finite Element Model for Crashworthiness Analysis of a Small-Size Bus,” KSAE Fall Conference Proceedings, pp.982-987, 2000.