다중 제약조건을 고려하는 4륜 독립 조향 차량의 요 변화율 추종을 위한 적분 제어 기반 모델 예측 고장 허용 제어

1. 서 론

최근 전자식 주행 안정화 제어(ESC) 및 토크 벡터링(Torque vectoring)과 같은 차량의 핸들링 성능 및 선회 안정성 확보를 위한 다양한 섀시 기술이 연구개발되고 있으며 후륜 조향(Rear Wheel Steering, RWS), 4륜 독립 조향(4-Wheel Independent Steering, 4WIS) 등 다양한 조향 시스템을 이용한 제어 연구가 수행되고 있다. 특히 4륜 독립 조향 시스템은 시스템이 갖는 제어 자유도 향상 및 대각 주행과 제자리 선회 등의 기능적 장점으로 인해 관련 기술 개발 및 연구가 가속화되고 있다. 기존 전륜 조향 시스템을 이용하는 차량의 경우 선회 시 언더스티어(Under-Steer)의 특성을 보이기 때문에 운전자 의도 대비 핸들링 성능이 낮을 수 있으며 상대적 제어 자유도가 낮은 특성 때문에 불안정한 주행 상황에서 주행 안정성 확보가 어려울 수 있다. 이러한 기존 전륜 조향 시스템의 한계점 극복을 위해 4륜 독립 조향 제어를 위한 다양한 제어 기법들이 기능적 조향 모드와 함께 연구 개발되고 있다.

기존 연구 중 차량의 핸들링 성능 향상을 위한 연구들은 다음과 같다. Chen과 Zhang¹⁾은 4륜 독립 조향 차량의 통합 섀시 제어를 위해 모델 예측 제어기를 이용한 제어 입력 분배 방법을 제시하였다. Tan 등²⁾은 4륜 조향 시스템의 핸들링 및 안정성 향상을 위해 슬라이딩 모드 제어기를 이용한 조향 제어 알고리즘을 제안하였다. Hang 등³⁾은 4륜 독립 조향 전기 차량의 경로 추종을 위해 모델 예측 제어기를 이용한 조향 제어 알고리즘을 제안하였다. Jin 등⁴⁾은 인휠 모터를 이용한 4륜 독립 구동 전기 차량 구동 제어를 위해 강건한 H∞ 퍼지(Fuzzy) 제어 알고리즘을 제안하였다. Wang과 Yang⁵⁾은 직접 요 모멘트 제어 시스템 및 능동형 전륜 조향 시스템의 횡방향 안정성 및 핸들링 성능 향상을 위해 퍼지 이론 기반 H∞ 제어 전략을 개발하였다. Coskun과 Langari⁶⁾는 능동형 전륜 조향 차량의 핸들링 및 안정성 향상을 위해 전륜 조향 시스템, 능동형 제동 및 서스펜션 서브 시스템들을 이용한 통합 제어 알고리즘을 개발하였다. Setiawan 등⁷⁾은 4륜 독립 조향 자율 안내 차량을 개발하였으며, 비상시 차량의 핸들링 성능 및 경로 추종 성능 향상을 위해 비선형성을 고려한 능동형 조향 및 모멘트 제어 방법을 제안하였다. 차량 주행 중 발생 가능 고장에 대한 안전을 위해 기업들과 연구소 및 대학에서는 다양한 방법으로 주행 안정성 확보를 위한 연구들을 진행하고 있다. Zong 등⁸⁾은 4WID/4WIS 전기차의 구동기 고장을 방지하기 위해 고장 감지 모듈을 이용한 재구성 가능한 제어 할당(Reconfigurable control allocator) 체계를 기반으로 FTC(Fault Tolerant Control)를 제안하였다. Zhang 등⁹⁾은 4륜 독립 조향 차량의 안정성 향상을 위한 재구성 제어 할당 분배 기법을 이용한 고장 탐지 및 허용 제어 알고리즘을 제안하였다. 이기범과 이민영¹⁰⁾은 4륜 구동 차량의 안정성 향상을 위해 고장 허용 전기적 안정성 제어(Fault tolerant electronic stability control, FT-ESC) 알고리즘을 제안하였다. Li 등¹¹⁾은 4WIS/4WID 전기 자동차의 고장 대응을 위해 슬라이딩 모드 제어기를 이용하는 고장 허용 제어 알고리즘을 제안하였다. Guo와 Chen¹²⁾은 4륜 독립 구동 시스템의 구동기 고장 허용 제어를 위해 적응형 고속 슬라이딩 모드 허용 제어 알고리즘을 제안하였다. Guo 등¹³⁾은 4륜 독립 조향의 자율주행 차량 횡방향 고장 안전을 위해 강건한 H∞ 고장 허용 제어 알고리즘을 제안하였으며 Chen 등¹⁴⁾은 능동 조향 시스템의 고장 허용 제어를 위해 타카기-수게노 퍼지(Takagi-Sugeno Fuzzy) 모델을 이용한 H∞ 제어 알고리즘을 제안하였다. 오세찬 등¹⁵⁾은 4륜 독립 조향 시스템의 고장 안전을 위해 모델 예측 제어 및 적분 제어를 이용한 고장 허용 제어 알고리즘을 제안하였다. Schaeffler group은 모빌리티 서비스를 제공하는 자율주행 배터리 전기차로 Schaeffler mover를 개발하였으며, 개발된 차량은 인휠 모터가 내장되어 다양한 기능적 조향이 가능하다.¹⁶⁾ Toyota는 자율주행 모빌리티로 e-Palette를 개발하였으며, e-Palette는 4륜 독립 조향이 가능한 차량으로 제자리 회전, 대각 조향 등의 기능 조향이 가능한 차량이다.¹⁷⁾ 기존 연구들을 살펴보면 핸들링 및 안정성 향상을 위한 4륜 독립 조향 시스템 기반 다양한 제어 연구 및 자율주행 기반 모빌리티 서비스 제공을 위한 차량 시스템 개발이 진행되고 있음을 확인할 수 있었다. 하지만 제안된 제어 방법들은 고장 상태를 고려한 최적 제어 입력 분배 문제와 불확실성에 의한 모델 기반 제어 기법의 한계점을 동시에 고려하지 않는 것을 확인할 수 있었다.

본 연구에서는 4륜 독립 조향 시스템의 요 변화율 추종을 위한 최적 조향 제어 할당을 위해 모델 예측 제어 알고리즘을 설계하였다. 수학적 모델이 갖는 불확실성에 의한 제어 성능 저하를 극복하기 위해 적분 제어 입력이 추가 적용되었다. 또한 조향 시스템 고장 발생 시 제약조건을 이용한 고장 허용 제어 알고리즘을 제안하였다. 목표 물리량은 차량의 주행 안정성 확보를 위한 1계 전달함수 기반 시간 지연된 차량의 요 변화율이 적용되었다. 도출된 모델 예측 제어 입력과 적분 제어 입력은 운전자 입력과 더해져 최종 조향각이 결정되도록 제어 알고리즘이 설계되었다. 모델 예측 제어 알고리즘의 다중 제약조건으로 조향각 및 변화율 제약조건 반영을 위한 경계 및 부등호 제약조건이 반영되었으며 고장 허용 제어를 위해 등가 제약조건이 적용되었다. 본 연구에서 제안하는 4륜 독립 조향을 위한 고장 안전 시스템은 고장 탐지 및 허용 제어를 위한 대응이 가능하다고 가정하였다. 제안된 알고리즘은 Matlab/Simulink 환경에서 제어 알고리즘과 제약조건 그리고 허용 제어 방법을 포함하는 전체 시스템이 설계되었다. 제약조건은 고장 발생 이전에는 물리적 제약조건만 적용되었으며, 고장 발생 후에는 허용 제어를 위한 등가 제약조건이 추가적용 되도록 알고리즘이 설계되었다. 설계된 알고리즘의 성능평가 및 분석을 위해 상용 소프트웨어인 CarMaker에서 제공되는 차량을 기반으로 성능평가를 수행하였다. CarMaker는 차량 시뮬레이션 소프트웨어로 차량, 제어 알고리즘, 주행 환경 및 요소들을 개발 및 구성하여 다양한 평가가 가능한 소프트웨어이며 Nalic 등은 자율주행 차량을 가상에서 현실적 평가를 위해 교통 흐름을 구성하는 소프트웨어 PTV Vissim과 차량 시뮬레이션 소프트웨어인 CarMaker를 연동하여 자율주행 시스템의 교통 체증 평가 방법을 제안하였다.¹⁸⁾

본 논문의 나머지 부분은 다음과 같다. 2장에서는 4륜 독립 조향 시스템의 발생 가능 고장에 대한 분석 및 고장-안전 구조를 제안하고, 3장에서는 적분 제어 기반 모델 예측 제어 알고리즘에 대해 기술한다. 4장에서는 성능평가 결과를 보여준다. 5장에서는 결론 및 한계점 분석과 함께 향후 계획에 대해 기술한다.

2. 4륜 독립 조향 시스템의 고장 분석 및 고장-안전 구조

Table 1은 4륜 독립 조향 시스템 구성에 필요한 요소들과 각 요소들의 발생 가능 고장을 보여준다.

Table 1

Components and fault classification of 4WIS

Table 1에서 4륜 독립 조향 시스템의 발생 가능 고장을 센서, 구동기, 전원, 통신으로 분류하였고 분류된 각 고장 발생에 따른 조향 시스템 안전을 확보하기 위해서는 고장 안전 시스템이 필요하다. 송태준 등은 자율 주행 자동차의 기능 안전을 위한 고장 단계 판단 알고리즘을 제안하였으며, 제안된 고장 안전 시스템의 기능적 인지, 판단, 제어 관점에서의 체계를 Table 2에서 보여준다.¹⁹⁾

Table 2

Overall frame for fail-safe system

Table 2에서 볼 수 있듯이 고장 안전 체계 내 인지 단계에서는 고장을 탐지하고 대응 가능한 제어 방법을 판단하기 위해 고장을 분류하거나 재건한다. 판단 단계에서는 고장 레벨이 판단되며 고장의 레벨에 따라 성능 유지 또는 안전 확보를 위한 제어 전략이 결정된다. 제어 단계에서는 경고, 허용 및 비상 제어 등의 전략을 통해 고장에 대한 성능 유지 또는 안전을 확보한다. 본 연구에서는 고장 안전 시스템 내 인지 및 판단 단계에서의 조향 시스템 고장 탐지 및 고장 레벨 판단이 가능하다고 가정하였다. 그리고 조향 시스템 고장 발생 시 허용 제어를 위한 휠 고정 대응과 함께 안전 제어 성능 유지를 위한 허용 제어 알고리즘을 설계하였다. 다음 장에서는 제안하는 모델 예측 제어 알고리즘에 대해 기술한다.

3. 적분 제어 기반 모델 예측 제어 알고리즘

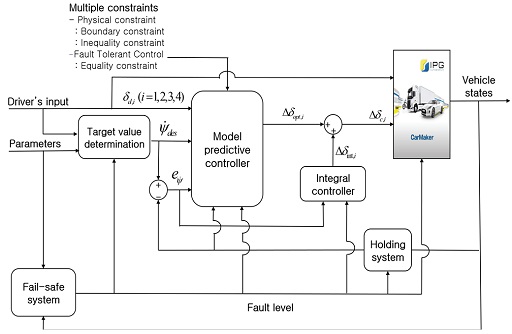
본 논문에서는 요 변화율 추종을 위한 독립 조향 제어 입력 도출을 위해 모델 예측 제어기와 적분 제어기가 동시에 사용되었다. 모델 예측 제어기는 다중 입력 다중 출력(Multi-Input Multi-Output, MIMO) 시스템의 최적 제어 입력 도출이 가능하고, 상태량 및 입력의 제약조건 적용이 가능하기 때문에 대상 시스템의 최적 제어 할당 및 물리적 제약조건을 반영할 수 있다. 하지만 사용되는 모델의 불확실성 정도에 따라 제어 성능 확보의 한계점이 존재할 수 있고, 이를 극복하기 위한 적분 제어 입력이 개별 조향 입력에 추가되었다. Fig. 1은 4륜 독립 조향 차량을 위한 적분 제어 기반 모델 예측 고장 허용 제어 알고리즘의 모델 개략도이다.

Fig. 1

Model schematics for integral action based model predictive control algorithm

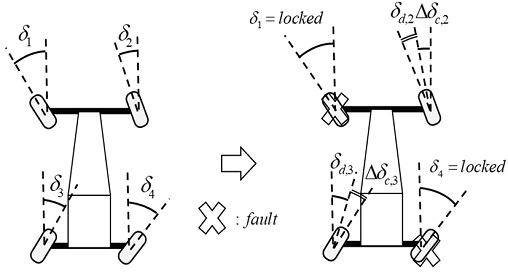
본 연구에서는 고장 허용 제어 알고리즘 적용을 위해 고장 발생 시 고장이 탐지된 시점으로부터 특정 시간 이후 휠이 기계적으로 고정되고, Fig. 1의 Holding system에 의해 각도 신호 또한 고정되어 출력된다는 가정이 적용되었다. MPC 블록에서는 고장이 탐지된 시점으로부터 잠긴 휠의 제어 입력이 0이 되는 등가 제약조건과 조향 시스템의 물리적 제약조건을 이용하여 Target value determination 블록에서 출력되는 목표 요 변화율을 추종하기 위한 최적 조향 입력을 도출한다. Fig. 2는 본 연구에서 제안하는 적분 제어 입력 기반 모델 예측 허용 제어 알고리즘의 개념을 나타낸다.

Fig. 2

Concept of fault tolerant control

Fig. 2에서 좌측 그림은 정상 독립 조향 상태를 나타내며 우측 그림은 1, 4번 휠에 고장이 발생한 후 고장 탐지 후 휠을 고정하고 2, 3번 휠은 목표 물리량을 추종하도록 고장 허용 제어를 수행하는 것을 나타낸다. 본 연구에서 설계된 고장 허용 제어를 위한 목표 물리량은 차량의 자세 제어를 위한 차량 요 변화율의 시간 지연 값으로 설계하였고, 설계된 목표 물리량은 다음과 같다.

식 (1)에서 τ_delay는 지연된 요 변화율 도출을 위한 시정수, s는 라플라스 변수, ψ_vehicle은 차량의 요 변화율을 나타낸다. 다음 절에서는 설계된 목표 요 변화율을 추종하기 위한 제약조건 기반 모델 예측 조향 제어 알고리즘에 대해 설명한다.

3.1 모델 예측 제어 알고리즘

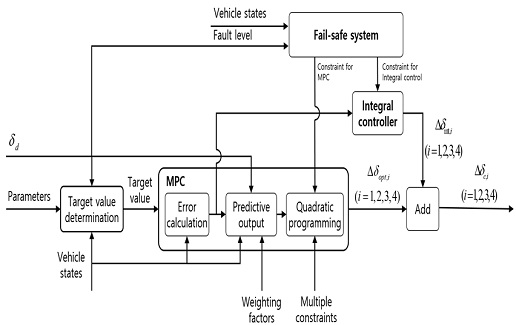
Fig. 3은 세부적인 적분 제어 기반 모델 예측 제어기의 모델 개략도이다.

Fig. 3

Detailed model schematics of integral action based model predictive control algorithm

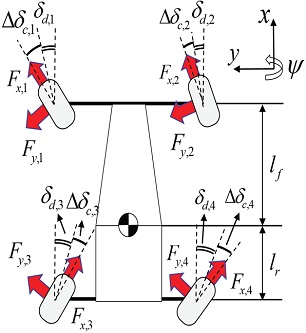
Fig. 3에서 모델 예측 제어기는 MPC 블록과 같으며 Error calculation 블록에서 오차 역학은 비선형 4륜 독립 조향 모델로부터 도출하고 Predictive output 블록에서는 예측된 출력을 계산한다. 결과적으로 MPC는 예측된 출력을 목적 함수에 대입하고 2차 계획법(Quadratic programming)을 이용하여 다중 제약조건을 고려한 최적 입력을 도출한다. Fig. 4는 모델 예측 제어 알고리즘 설계를 위해 사용된 차량 평면 모델의 자유 물체도를 나타낸다. 차량 평면 모델의 수학적 모델 도출을 위해 차량의 종방향 속도는 일정하며 타이어 횡력은 휠 슬립각에 비례한다고 가정하였다.

Fig. 4

Free body diagram of planar vehicle model

Fig. 4에서 δ_d,i는 운전자 입력, ∆δ_c,i는 제어 입력을 나타낸다. 두 조향 입력을 더하여 전체 제어 입력 δ_i로 정의하였으며 아래의 수식들은 차량 평면 모델 기반 횡방향 및 요 동역학 모델을 보여준다.

$\[ \begin{array}{c}m\left(\dot{v_y}+v_x\dot{\psi }\right)=F_{x,1}\text{sin}{\delta }_1+F_{x,2}\text{sin}{\delta }_2+F_{x,3}\text{sin}{\delta }_3+F_{x,4}\text{sin}{\delta }_4\\ +F_{y,1}\text{cos}{\delta }_1+F_{y,2}\text{cos}{\delta }_2+F_{y,3}\text{cos}{\delta }_3+F_{y,4}\text{cos}{\delta }_4\end{array} \]$

(2)

$\[ \begin{array}{c}{I}_2\ddot{\psi }=l_f\left[F_{y,1}\text{cos}{\delta }_1+F_{x,1}\text{sin}{\delta }_1+F_{y,2}\text{cos}{\delta }_2+F_{x,2}\text{sin}{\delta }_2\right]\\ +\frac{t_w}{2}\left[F_{y,1}\text{sin}{\delta }_1+F_{x,1}\text{cos}{\delta }_1+F_{y,3}\text{sin}{\delta }_3-F_{x,3}\text{cos}{\delta }_3\right]\\ -l_r\left[F_{y,3}\text{cos}{\delta }_3+F_{x,3}\text{sin}{\delta }_3+F_{y,4}\text{cos}{\delta }_4+F_{y,4}\text{sin}{\delta }_4\right]\\ +\frac{t_w}{2}\left[F_{x,2}\text{cos}{\delta }_2-F_{y,2}\text{sin}{\delta }_2+F_{x,4}\text{cos}{\delta }_4-F_{y,4}\text{sin}{\delta }_4\right]\end{array} \]$

(3)

비선형 차량 평면 모델의 선형화를 위해 상태 벡터 $$ {\left[v_y,\dot{\psi }\right]}^T$$와 조향 입력 벡터 [∆δ₁∆δ₂∆δ₃∆δ₄]^T에 관한 자코비안 행렬을 도출하였다. 선형화된 차량 동역학 모델을 상태 공간 방정식과 이를 구성하는 행렬식들은 다음과 같다.

$\[ \dot{X}=AX+Bu \]$

(4)

$\[ X={\left[v_y,\dot{\psi }\right]}^T, u={\left[\text{Δ}{\delta }_1\text{Δ}{\delta }_2\text{Δ}{\delta }_3\text{Δ}{\delta }_4\right]}^T \]$

(5)

$\[ A=\left[\begin{array}{cc}\begin{array}{c}\frac{\partial f_{v_y}}{\partial v_y}\\ \frac{\partial f_{\dot{\psi }}}{\partial v_y}\end{array}& \begin{array}{c}\frac{\partial f_{v_y}}{\partial \dot{\psi }}\\ \frac{\partial f_{\dot{\psi }}}{\partial \dot{\psi }}\end{array}\end{array}\right], B=\left[\begin{array}{c}\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\frac{\partial f_{v_y}}{\partial \text{Δ}{\delta }_1}\\ \frac{\partial f_{\dot{\psi }}}{\partial \text{Δ}{\delta }_1}\end{array}& \begin{array}{c}\frac{\partial f_{v_y}}{\partial \text{Δ}{\delta }_2}\\ \frac{\partial f_{\dot{\psi }}}{\partial \text{Δ}{\delta }_2}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\frac{\partial f_{v_y}}{\partial \text{Δ}{\delta }_3}\\ \frac{\partial f_{\dot{\psi }}}{\partial \text{Δ}{\delta }_3}\end{array}& \begin{array}{c}\frac{\partial f_{v_y}}{\partial \text{Δ}{\delta }_4}\\ \frac{\partial f_{\dot{\psi }}}{\partial \text{Δ}{\delta }_4}\end{array}\end{array}\end{array}\end{array}\right] \]$

(6)

고장 허용 제어를 위한 모델 예측 제어 알고리즘의 목표 물리량은 식 (1)에 정의하였으며 이를 이용한 목표 물리량 모델은 다음식과 같다.

$\[ \dot{X_d}=A_d{X}_d+B_d{u}_d \]$

(7)

$\[ X_d={\left[v_{y,des} {\dot{\psi }}_{des}\right]}^T, u_d={\left[v_{y,target} {\dot{\psi }}_{delay}\right]}^T \]$

(8)

$\[ A=\left[\begin{array}{cc}\begin{array}{c}-\frac{1}{{\tau }_{des}}\\ 0\end{array}& \begin{array}{c}0\\ -\frac{1}{{\tau }_{des}}\end{array}\end{array}\right], B=\left[\begin{array}{cc}\begin{array}{c}\frac{1}{{\tau }_{des}}\\ 0\end{array}& \begin{array}{c}0\\ \frac{1}{{\tau }_{des}}\end{array}\end{array}\right] \]$

(9)

행렬 X_d의 v_y,des과 $$ {\dot{\psi }}_{des}$$는 각각 시간 지연이 반영된 목표 횡방향 속도와 요 변화율을 의미하고, τ_des는 목표 물리량의 시간 지연을 위한 시정수를 의미한다. 식 (7)은 시간 지연된 횡방향 속도 및 요 변화율을 도출하기 위한 상태 공간 방정식이며 u_d는 목표 물리량으로 정의된다. 본 연구에서는 추종을 위한 목표 물리량으로 요 변화율만을 고려하였고, 식 (4)와 식 (7) 기반 알고리즘 설계를 위한 오차 동역학 모델은 다음과 같다.

$\[ \dot{e}=A_{e}e+B_{e}u+F_{e}w \]$

(10)

$\[ e=X_d-X \]$

(11)

$\[ A_e=A, B_e=-B, F_e=\left(A_d-A\right)X_d+B_d{u}_d, w=1 \]$

(12)

오차에 대한 가중치가 적용된 출력 y와 이산화된 오차 동역학 모델은 다음과 같은 수식으로 표현된다.

$\[ y=C_{e,d}e\left(k\right) \]$

(13)

$\[ e\left(k+1\right)=A_{e,d}e\left(k\right)+B_{e,d}u\left(k\right)+F_{e,d}w\left(k\right) \]$

(14)

식 (13)에 C_e,d는 오차에 대한 상대적 가중치 행렬을 나타내며, 식 (14)에서 행렬 A_e,d, B_e,d와 F_e,d는 각각 상태 행렬, 입력 행렬 및 외란 행렬을 나타낸다. 오차 동역학 기반 예측된 출력 오차 벡터 Y는 다음과 같다.

$\[ Y=Ge\left(k\right)+HU+Lu\left(k\right)+MW+Kw\left(k\right) \]$

(15)

$\[ G={\left[C_d{A}_d{C}_d{A}_d^2\cdots C_d{A}_d^{N_p}\right]}^T \]$

(16)

$\[ H=\left[\begin{array}{cccc}0& 0& \cdots & 0\\ C_d{B}_d& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_d{A}_d^{N_p-2}{B}_d& C_d{A}_d^{N_p-3}{B}_d& \cdots & 0\end{array}\right] \]$

(17)

$\[ U={\left[u\left(k+1\right)u\left(k+2\right)\cdots u\left(k+N_p\right)\right]}^T \]$

(18)

$\[ L={\left[\begin{array}{cccc}{CB}_{e,d}& {CA}_{e,d}{B}_{e,d}& \cdots & {CA}_{e,d}^{N_p-1}{B}_{e,d}\end{array}\right]}^T \]$

(19)

$\[ M=\left[\begin{array}{cccc}0& 0& \cdots & 0\\ C_d{F}_d& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_d{A}_d^{N_p-2}{F}_{e,d}& C_d{A}_d^{N_p-3}{F}_{e,d}& \cdots & 0\end{array}\right] \]$

(20)

$\[ W={\left[w\left(k+1\right)w\left(k+2\right)\cdots w\left(k+N_p\right)\right]}^T \]$

(21)

$\[ K={\left[C_d{F}_{e,d} C_d{A}_d{F}_{e,d}\cdots {C_{d}A}_d^{N_p-1}{F}_{e,d}\right]}^T \]$

(22)

식 (15)부터 (22)에서 C_d는 오차에 대한 가중치 행렬이며, N_p는 MPC의 예측 횟수이다. 최적 제어 입력 도출을 위해 설계된 목적 함수 J는 다음과 같다.

$\[ J=Y^{T}Y+r{U}^T{D}^{T}DU \]$

(23)

식 (23)에서 r과 D는 각각 목적 함수 내 입력에 대한 가중치와 차이 행렬을 나타낸다. 식 (23)에서 정의된 비용함수를 2차 형태로 나타내면 다음과 같다.

$\[ J=\frac{1}{2}{U}^{T}QU+f^{T}U \]$

(24)

$\[ Q=r{D}^{T}D+H^{T}H \]$

(25)

$\[ f=H^T\left(Ge\left(k\right)+Lu\left(k\right)+MW+Kw\left(k\right)\right) \]$

(26)

최적 제어 입력 벡터 U는 Matlab에서 제공하는 Quadprog 함수를 사용하여 도출되었으며 설계된 목표 요 변화율을 추종하기 위한 최적 조향 입력으로 사용되었다. 계산된 최적 조향 제어 입력 내 4륜 독립 조향 제어 입력은 다음과 같이 정의되었다.

$\[ u_{opt}={\left[U\left(1\right) U\left(2\right) U\left(3\right) U\left(4\right)\right]}^T \]$

(27)

$\[ u_{con}=u_{opt}+k_i{\int }_0^t{e}_{\dot{\psi }}dt \]$

(28)

식 (27)의 u_opt은 최적 제어 입력 값을 나타내며 식 (28)의 u_con는 최적 제어 입력과 적분 제어 입력의 합을 나타낸다. 식 (28)의 적분 제어 입력은 모델 불확실성에 의한 제어 성능 한계를 극복하기 위해 적용된 것이며 적분 제어 이득 k_i와 요 변화율 오차 $$ e_{\dot{\psi }}$$를 이용해 계산된다. 다음 절에서는 모델 예측 고장 허용 제어를 위해 적용된 제약조건들에 대해 기술한다.

4. 성능평가

제안하는 알고리즘의 성능평가를 위해 Fig. 1에 나타내는 알고리즘을 Matlab/Simulink 환경에서 구성하였으며 상용 소프트웨어인 CarMaker와 연동하여 성능평가를 수행하였다. CarMaker에서 제공하는 전륜 조향 및 후륜 구동 시스템 기반 차량이 성능평가에 이용되었다. 정상 원선회(Case-1) 및 직진 주행(Case-2) 시 고장 발생 시나리오가 적용되었으며 Table 3은 성능평가를 위해 적용된 파라미터와 값을 보여준다.

Table 3

The used parameters and values

Table 4는 성능평가를 위해 사용된 카메이커 제공 차량의 기본 물성치들을 보여준다.

Table 4

Vehicle parameters used for performance evaluation

Table 5는 합리적 성능평가를 위해 적용된 시나리오와 각 시나리오에서의 평가 조건들을 보여준다.

Table 5

Driving conditions for performance evaluation

Table 5에서 볼 수 있듯이 운전자가 정상 원 선회 중 후륜의 우측 휠에 고장이 적용된 시나리오와 직진 주행 중 후륜의 두 개 휠에 고장이 발생하는 시나리오를 기반으로 성능평가가 수행되었다. 성능평가를 위해 적용된 고장 상황의 경우 고장 발생 시 조향 휠이 특정 방향으로 급격히 회전하여 큰 조향각을 갖는 고장 상황이 적용되었다. 현 연구 단계에서는 극한의 고장 상황이 적용되어 성능평가가 진행되었지만 추후 다양한 고장 상황에서의 성능평가를 계획하고 있다. 운전자 입력의 경우 성능평가를 위해 사용된 상용 소프트웨어에서 제공되는 운전자 모델이 사용되었다. 다음 절부터는 Case-1과 Case-2에서의 고장 허용 제어 결과가 분석되었다.

4.1 Case–1 : 1-wheel fault(rear-right)

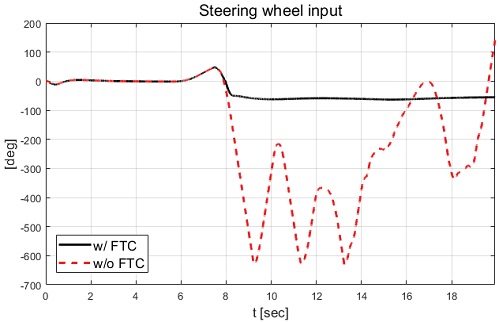
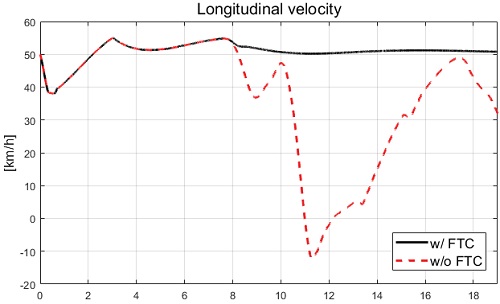
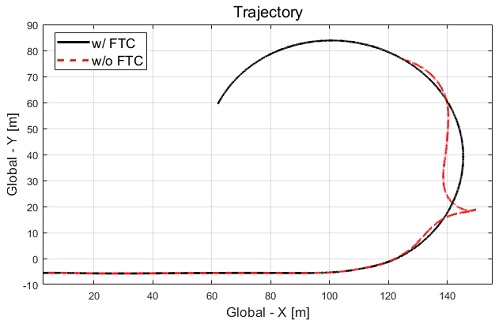
Case-1은 종방향 속도 55 kph에서 정상 원 선회 중 고장이 발생하는 시나리오이며 고장은 7.5 sec부터 후륜의 우측 휠에 발생하도록 적용되었다. 성능평가 결과로 운전자 조향 입력은 Fig. 5에서 확인할 수 있으며 종방향 주행 속도 및 차량의 거동은 Fig. 6 및 Fig. 7과 같다.

Fig. 5

Driver input: steering wheel input

Fig. 6

Result: longitudinal velocity

Fig. 7

Result: trajectory

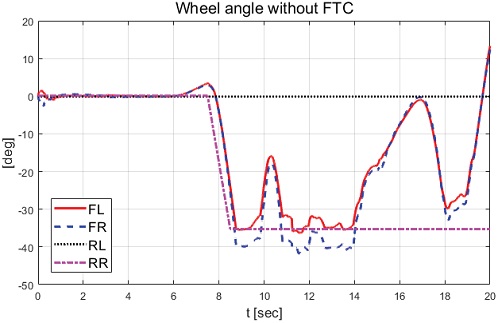
Fig. 6에서 차량은 고장 허용 제어가 적용 및 미적용된 모든 경우 고장 주입 시간인 7.5 sec 이전까지는 종방향 속도가 55 kph를 유지하는 것을 확인할 수 있으며 고장 허용 제어 미적용의 경우 고장 적용 시간 이후 스핀 아웃 현상에 의해 종방향 속도가 급격히 줄어드는 것을 확인할 수 있다. Fig. 9에서 확인할 수 있듯이 후륜 우측 휠은 적용된 고장으로 인하여 조향각이 -35 deg 값을 갖으며, 후륜 좌측 휠은 평가에 이용된 차량이 전륜 조향 차량이기 때문에 0 deg의 값을 유지하는 것을 확인할 수 있다. 고장 허용 제어 미적용 경우 Fig. 7에서 스핀 아웃 현상이 발생하여 차량의 불안정한 궤적을 보여준다. 반면 고장 허용 제어가 적용된 경우 안정적으로 정상 원선회 궤적을 보여주었다. 고장 허용 제어가 적용된 휠 각도 및 제어 입력들을 각각 Fig. 10, Fig. 11 및 Fig. 12에서 보여준다.

Fig. 8

Result: fault level (0 - no fault, 1 - fault)

Fig. 9

Result: wheel angles without FTC

Fig. 10

Result: wheel angle with FTC

Fig. 11

Result: MPC steering input

Fig. 12

Result: integral steering input

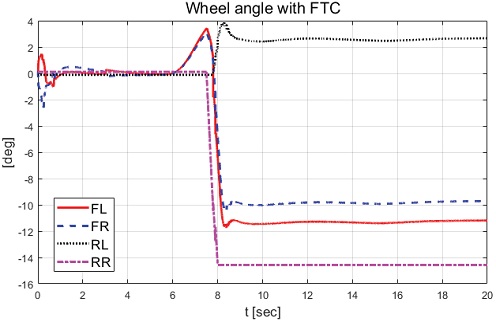
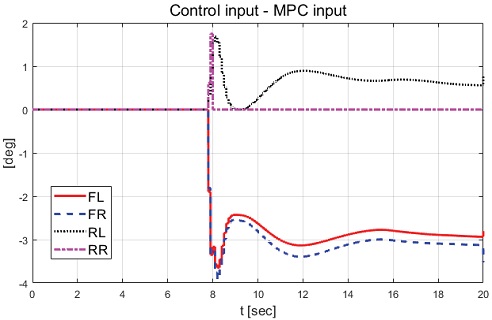
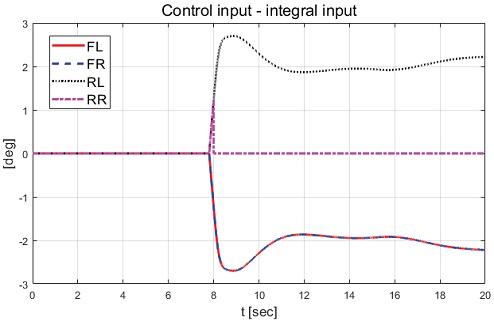
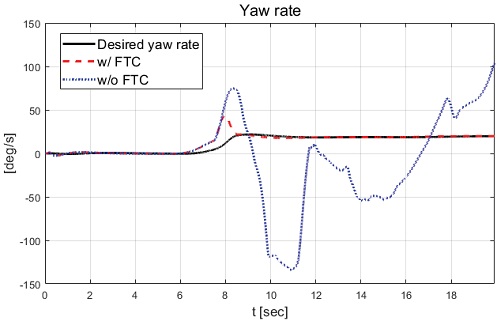
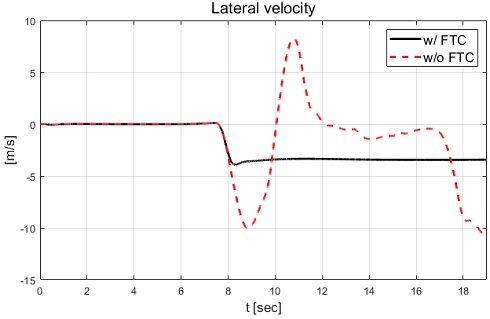
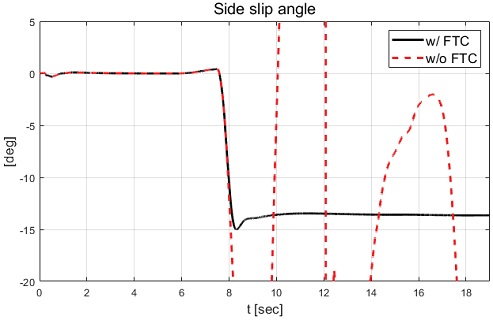
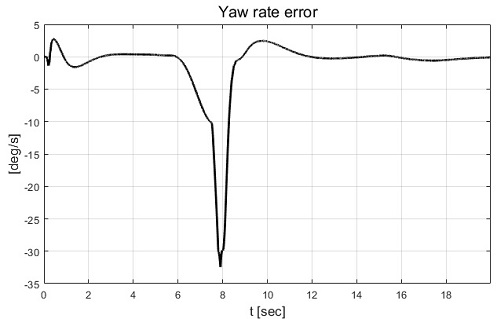
Fig. 10에서 볼 수 있듯이 고장을 탐지하고 고장이 탐지된 휠을 약 -14 deg로 고정한 것을 확인할 수 있다. 그리고 Fig. 9와 Fig. 10에서 휠 조향각이 일정 구간 양의 값을 갖는 것은 적용된 고장으로 차량의 도로 이탈을 막기 위해 운전자 모델에 의한 입력이 차량 거동의 반대 방향으로 인가되고 있기 때문이다. Fig. 11과 Fig. 12에서 후륜 우측 휠의 제어 입력은 고장을 탐지하고 일정 시간 이후 등가 제약조건 및 적분 제어 제약조건에 의해 제어 입력이 0 값을 보이는 것을 확인할 수 있다. Fig. 13부터 Fig. 16은 요 변화율, 횡방향 속도, 슬립각 및 요 변화율 오차이다.

Fig. 13

Result: yaw rate

Fig. 14

Result: lateral velocity

Fig. 15

Result: side slip angle

Fig. 16

Result: yaw rate error

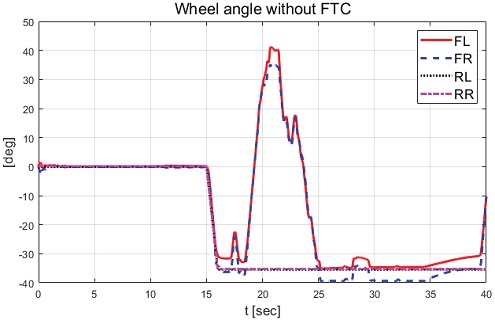
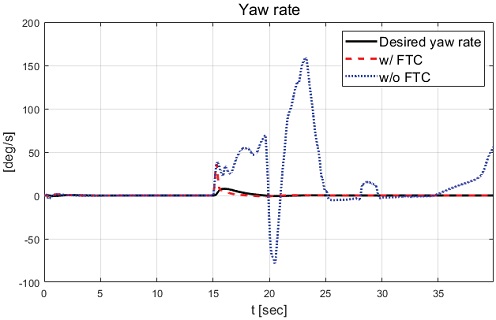
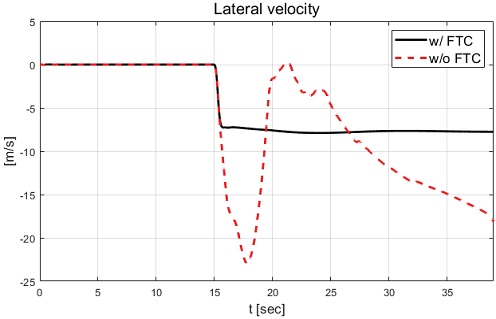
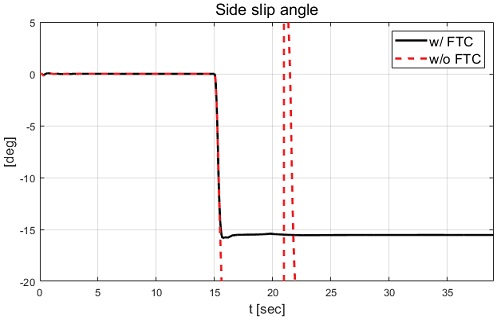
Figs. 13∼15에서 고장 허용 제어를 적용하지 않은 경우 고장에 의한 스핀 아웃 현상이 발생하는 것을 확인할 수 있었고, 이로 인해 차량의 불안정한 요 변화율, 횡방향 속도 및 슬립각이 발생한 것을 확인할 수 있었다. 고장 허용 제어가 적용된 경우 논문에서 제안된 목표 요 변화율인 시간 지연된 요 변화율을 합리적으로 추종하면서 약 12 sec 이후 정상 상태에 진입하여 요 변화율 오차가 0으로 수렴하는 결과를 Fig. 16에서 확인할 수 있다. Fig. 14와 Fig. 15에서는 고장 허용 제어 적용 결과 8.5 sec 이후 후륜과 전륜이 동위상을 이루어 횡방향 속도는 약 -4 m/s와 횡방향 슬립각을 약 -15 deg의 값을 보여준다. 다음 절에서는 직진 주행 시 두 개의 후륜 휠에 고장 발생 경우에 대한 성능평가 결과를 기술하고 분석한다.

4.2 Case–2 : 2-wheel fault(rear-left/right)

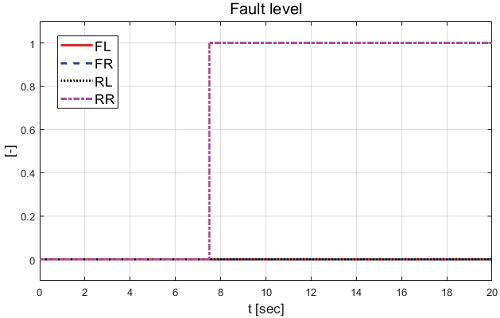
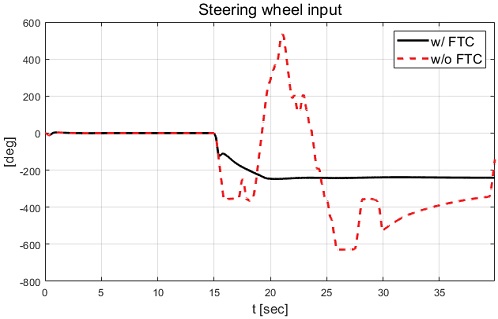
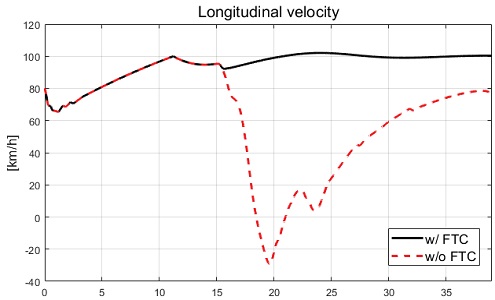
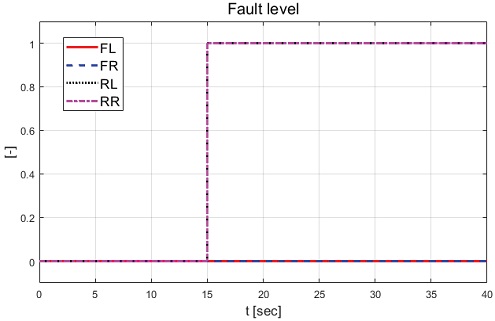
Case-2는 종방향 속도 100 kph로 직진 주행 중 고장이 발생하는 시나리오가 적용되었다. 고장은 후륜 좌측 및 우측 휠에 적용하며 고장이 적용된 경우를 1, 고장이 적용되지 않은 경우를 0으로 표현한 고장 레벨은 Fig. 20과 같다. Case-1과 동일하게 CarMaker에서 제공되는 운전자 모델을 이용한 종방향 속도 유지 및 조향 입력이 인가되었다. 운전자 입력, 종방향 속도 및 차량 거동을 각각 Fig. 17, Fig. 18, Fig. 19에서 보여주며 고장 허용 제어가 미적용된 경우의 조향각은 Fig. 21과 같다.

Fig. 17

Result: steering wheel input

Fig. 18

Result: longitudinal velocity

Fig. 19

Result: trajectory

Fig. 20

Result: fault level (0 - no fault, 1 - fault)

Fig. 21

Result: wheel angle without FTC

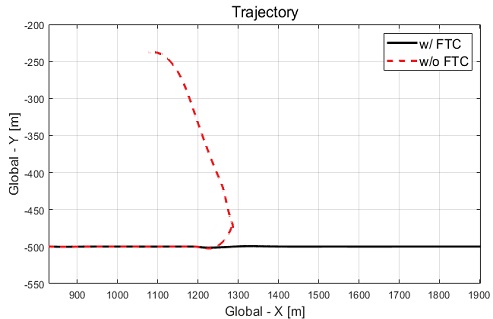
Fig. 18에서 차량은 고장 허용 제어가 적용 및 미적용된 모든 경우는 종방향 속도가 100 kph에 도달한 것을 보여준다. Fig. 19에서는 고장 허용 제어가 미적용된 경우 스핀 아웃 현상이 발생하여 직진 주행 성능을 확보하지 못하는 차량 궤적을 확인할 수 있다. Fig. 21은 발생한 스핀 아웃으로 운전자 입력과 함께 발생한 휠 조향각을 보여준다. 반면 고장 허용 제어가 적용된 경우 직진 주행 성능을 확보하는 거동을 확인할 수 있었다. 고장 허용 제어를 적용한 경우의 휠 조향각과 제어 입력들은 Fig. 22부터 Fig. 24에서 확인할 수 있다.

Fig. 22

Result: wheel angle with FTC

Fig. 23

Result: MPC steering input

Fig. 24

Result: integral steering input

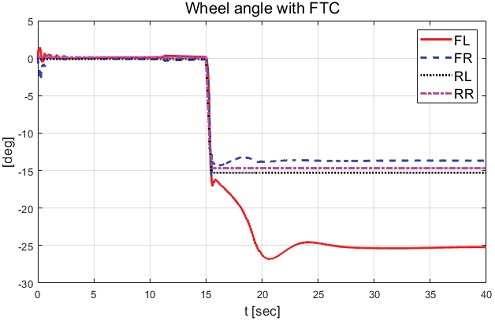
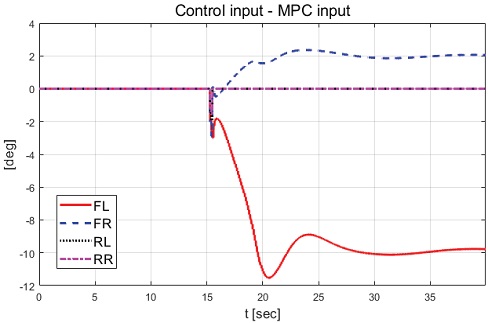
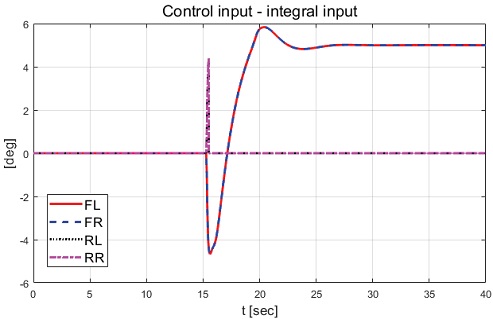
Fig. 22에서 후륜의 좌측 및 우측 휠의 고장을 탐지하여 고장이 탐지된 휠들이 최대 조향각을 갖기 이전에 고정되는 결과를 보여준다. 고정된 조향각은 약 -15 deg의 값을 갖는 결과를 확인할 수 있다. Fig. 23과 Fig. 24에서 모델 예측 제어기의 불확실성으로 Case-1과 달리 모델 예측 제어 입력은 적분 제어 입력과 상반되는 입력 형태를 보이는 한계점을 확인할 수 있었다. 그럼에도 불구하고 적용된 적분 제어 입력에 의해 안정적인 직진 주행 결과를 확인할 수 있었다. 횡방향 거동 분석을 위한 고장 허용 제어 적용 및 미적용 경우의 요 변화율, 횡방향 속도, 횡방향 슬립각 및 요 변화율 오차 결과들을 Fig. 25부터 Fig. 28에서 보여준다.

Fig. 25

Result: yaw rate

Fig. 26

Result: lateral velocity

Fig. 27

Result: side slip angle

Fig. 28

Result: yaw rate error

Fig. 24에서 고장 허용 제어 미적용의 경우 고장 주입 후 불안정한 요 변화율을 보이며 최대 약 160 deg/s 의 값을 보이는 것을 확인할 수 있다. Fig. 25에서 볼 수 있듯이 고장 발생 휠이 갖는 특정 조향각과 적용된 시나리오의 운전자 모델에 의한 조향 입력이 전륜에 인가되면서 차량의 요 변화율은 0 deg/s이 아닌 값을 갖는 것을 확인할 수 있다. 이로 인해 시간 지연 요 변화율인 요구 요 변화율 또한 0 deg/s이 아닌 값을 갖는 것을 확인할 수 있다. Fig. 28에서 확인할 수 있듯이 고장 허용 제어가 적용된 경우 목표 요 변화율을 추종하면서 약 20 sec 이후 0 deg/s로 수렴하는 결과를 확인할 수 있다. Fig. 22에서 고장 허용 제어의 적용 결과 고장 발생 이후 고장 상태를 고려한 직진 궤적 주행을 위해 동위상 조향각이 형성되는 결과를 확인할 수 있었다. 이로 인해 Fig. 26에서는 차량의 횡방향 속도는 음의 값을 갖는 결과를 보이며 Fig. 27에서는 슬립각이 일정하게 유지되는 결과를 확인할 수 있다. Case-1과 Case-2에서 확인할 수 있듯이 고장 허용 제어를 적용한 결과 고장 발생 시점 직후에는 요 변화율 오차가 상대적으로 크게 발생하였으나 허용 제어에 의해 요 변화율 오차가 0 deg/s에 근사한 값으로 수렴하는 것을 확인하였다. 그러나 제안하는 알고리즘은 고장 종류와 파라미터에 따라 모델 예측 제어 가중치와 적분 제어 이득 값의 지속적 갱신이 필요한 한계점이 존재하였다. 다음 장에서는 본 논문에서 제안하는 알고리즘 및 성능평가 결과와 향후 계획을 포함한 결론을 기술한다.

5. 결 론

본 논문은 다중 제약조건이 존재하는 4륜 독립 조향 차량을 위한 적분 제어 기반 모델 예측 고장 허용 제어 알고리즘을 제안하였다. 제어기 설계를 위해 자코비안 행렬을 이용하여 비선형 동역학 모델을 선형화하였으며 고장 허용 제어를 위한 목표 물리량을 시간 지연된 요 변화율로 적용하였다. 모델 예측 제어기는 목표하는 값을 추종하기 위해 차량의 물리적 제약조건이 반영된 최적 제어 입력을 도출하며 적분 제어 입력과 운전자 입력을 더하여 최종 조향 입력이 적용되도록 알고리즘을 설계하였다. 성능평가는 각각 정상 원 선회 중 후륜 한 개 휠에 고장이 발생하는 시나리오와 직진 주행 중 후륜 두 개 휠에 고장이 발생하는 시나리오를 이용하여 수행되었다. 고장 허용 제어 적용 및 미적용 결과를 함께 비교하였으며 고장 허용 제어 미적용 경우 두 시나리오 모두 스핀 아웃 현상이 발생함을 확인할 수 있었다. 직진 주행 시나리오에서는 최대 약 160 deg/s 불안정한 요 변화율 값을 확인할 수 있었으나 고장 허용 제어가 적용된 경우 고장을 탐지하고 일정 시간 이후 허용 제어 입력에 의해 요 변화율 오차가 고장 발생 이후 최대 약 5 sec 이내에 0 deg/s에 근사하게 수렴하는 추종 제어 결과를 확인하였다. 향후 적응형 모델 예측 제어기 개발에 따른 가중치 및 적분 이득 값의 자가 동조와 고장 허용 제어를 위한 요구 요 변화율 설계 및 다양한 고장 상황에 따른 고장 허용 제어 평가를 계획하고 있으며 다양한 고장 주입 상황에 대한 평가 결과 분석에 따른 고장 허용 제어 알고리즘의 고도화를 계획하고 있다. 본 연구에서 제안하는 모델 예측 고장 허용 제어 알고리즘은 4륜 독립 조향 시스템의 주행 안전 확보를 위한 고장 안전 기술로써 적용될 수 있을 것으로 기대한다.

Acknowledgments

A part of this paper was presented at the KSAE 2020 Fall Conference and Exhibition

본 연구는 2020 현대자동차 연구과제의 지원을 받아 수행된 연구임.

References

• G. Chen and D. Zhang, “Research on Integrated Chassis Control Strategy for Four-Wheel Independent Control Electric Vehicle,” SAE 2014-01-2290, 2014. [https://doi.org/10.4271/2014-01-2290]
• L. Tan, S. Yu, Y. Guo and H. Chen, “Sliding Mode Control of Four Wheel Steering Systems,” 2017 IEEE International Conference on Mechatronics and Autonomation, pp.1250-1255, 2017. [https://doi.org/10.1109/ICMA.2017.8015996]
• P. Hang, F. Luo, S. Fang and X. Chen, “Path Tracking Control of a Four-Wheel-Independent-Steering Electric Vehicle based on Model Predictive Control,” IEEE 36th Chinese Control Conference, pp.9360-9366, 2017. [https://doi.org/10.23919/ChiCC.2017.8028849]
• X. Jin, Z. Yu, G. Yin and J. Wang, “Improving Vehicle Handling Stability Based on Combined AFS and DYC System via Robust Takagi-Sugeno Fuzzy Control,” IEEE Transactions on Intelligent Transportation Systems, Vol.19, No.8, pp.2696-2707, 2017. [https://doi.org/10.1109/TITS.2017.2754140]
• Y. Y. Wang and F. N. Yang, “Integrated Control to Improve Vehicle Handling and Stability Based on the Control Authority of Chassis Key Electronic Controller,” IEEE International Conference on Circuits, Devices and Systems, pp.209-216, 2017. [https://doi.org/10.1109/ICCDS.2017.8120480]
• S. Coskun and R. Langari, “Enhanced Vehicle Handling Performance for an Emergency Lane Changing Controller in Highway Driving,” IEEE Intelligent Vehicles Symposium, pp.334-340, 2017. [https://doi.org/10.1109/IVS.2017.7995741]
• Y. D. Setiawan, T. H. Nguyen, P. S. Pratama, H. K. Kim and S. B. Kim, “Path Tracking Controller Design of Four Wheel Independent Steering Automatic Guided Vehicle,” Springer International Journal of Control, Automation and System, Vol.14, No.6, pp.1550-1560, 2016. [https://doi.org/10.1007/s12555-015-0216-7]
• C. Zong, C. Liu, C. Zheng and J. Liu, “Fault Tolerant Control Against Actuator Failures of 4WID/4WIS Electric Vehicles,” SAE 2013-01-0405, 2013. [https://doi.org/10.4271/2013-01-0405]
• Y. Zhang, H. Zheng, J. Zhang and C. Cheng, “A Fault Tolerant Control Method for 4WIS/4WID Electric Vehicles based on Reconfiurable Control Allocation,” SAE 2018-01-0560, 2018. [https://doi.org/10.4271/2018-01-0560]
• K. Lee and M. Lee, “Fault Tolerant Stability Control for Independent Four Wheel Drive Electric Vehicle Under Actuator Fault Conditions,” IEEE Access, Vol.8, No.5, pp.91368-91378, 2020. [https://doi.org/10.1109/ACCESS.2020.2994530]
• B. Li, H. Du and W. Li, “Fault-Tolerant Control of Electric Vehicles with In Wheel Motors using Actuator Grouping Sliding Mode Controllers,” Mechanical Systems and Signal Processing, Vols.72-73, No.5, pp.462-485, 2015. [https://doi.org/10.1016/j.ymssp.2015.11.020]
• B. Guo and Y. Chen, “Robust Adaptive Fault Tolerant Control of Four Wheel Indpendently Actuated Electric Vehicles,” IEEE Transactions on Industrial Informatics, Vol.16, No.5, pp.308-316, 2016. [https://doi.org/10.1109/TII.2018.2889292]
• J. Guo, Y. Luo and K. Li, “Robust H∞ Fault Tolerant Lateral Control of Four Wheel Steering Autonomous Vehicles,” Int. J. Automoive Technology, Vol.21, No.4, pp.993-1000, 2020. [https://doi.org/10.1007/s12239-020-0094-8]
• L. Chen, X. Li, W. Xiao, P. Li and Q. Zhou, “Fault-Tolerant Control for Uncertain Vehicle Active Steering Systems with Time-Delay and Actuator Fault,” International Journal of Control, Automation and Systems, Vol.17, No.9, pp.2234-2241, 2019. [https://doi.org/10.1007/s12555-019-0003-y]
• S. Oh, M. Kim, B. Lee and K. Oh, “Development of a Model Predictive and Fault-Tolerant Control Algorithm of 4-Wheel Independent Steering System for Improving Vehicle Handling Performance,” KSAE Fall Conference Proceedings, pp.440-441, 2020.
• Schaeffler Mover, http://schaeffler-events.com/symposium/lecture/c1/index.html, .
• e-Palette, https://www.toyota-europe.com/startyourimpossible/e-palette, .
• D. Nalic, H. Li, A. Eichberger, C. Wellershaus, A. Pandurevic and B. Rogic, “Stress Testing Method for Scenario-based Testing of Automated Driving Systems,” IEEE Access, Vol.8, pp.224974-224984, 2020. [https://doi.org/10.1109/ACCESS.2020.3044024]
• T. Song, H. Lee, K. Oh, S. Park and K. Yi, “A Fault Level Decision Algorithm for Functional Safety of Autonomous Vehicles and Longitudinal Fault Detection Based Performance Evaluation,” Transaction Korean Society of Mechanical Engineering A, Vol.43, No.2, pp.119-128, 2019. [https://doi.org/10.3795/KSME-A.2019.43.2.119]