준정적해석을 통한 승용차용 등속조인트 부품의 접촉력 및 소성변형 분석
Copyright Ⓒ 2021 KSAE / 186-010
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In evaluating the strength and behavior of a constant velocity joint for a compact drive shaft considering a quasi-static state, the analysis has been carried out with the plastic deformation behavior of a cage where the fracture is mainly reported. The analysis was conducted according to the actual experimental conditions by simultaneously imposing low rotational speed and torque that are in a quasi-static state. The elasto-plastic material properties were set to the cage. The cage rotates while making contact with balls, an outer race and an inner race. It was found that the effective plastic strain at each location of the cage increased in the form of a step, and the increased location was determined according to the phase angle. The plastic deformation position in the cage could be verified through the analysis of the contact force between the parts according to the phase angle representing the cylindrical coordinate system.
Keywords:
Constant velocity joint, Ball cage, Equivalent plastic strain, Phase angle, Quasi-static analysis, Contact force키워드:
등속조인트, 볼 케이지, 등가소성변형률, 위상각, 준정적해석, 접촉력1. 서 론
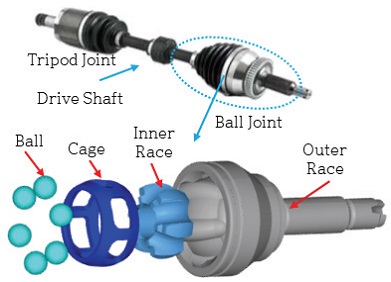
등속조인트(CVJ, Constant Velocity Joint)는 차량 엔진⋅변속기 등 구동부에서 나온 구동력을 바퀴로 전달하는 핵심 부품으로 변속기 측은 TJ(Tripod Joint), 휠 측은 BJ(Ball Joint)가 많이 사용된다. Fig. 1은 드라이브 샤프트와 등속조인트의 부품을 나타내고 있다. 최근 친환경, 고성능 차량, 대형 SUV 차량 등 소비자의 다양한 니즈에 따라 등속조인트는 경량, 대형, 고성능 특성의 요구가 급격히 증가되었다. 이러한 고성능, 프리미엄, 전기차는 일반 차량 대비 최대 토크가 3배 이상 높아 조인트 부품 파손이 우려된다. 특히 전기차는 초반부터 최대 토크를 발휘할 수 있어 파손의 우려가 높다. 등속조인트의 부품 파손은 저속의 고회전각에서는 케이지의 파손이 보고되고 있으며, 정적인 상태에서는 축의 파손이 보고된다.1,2)
최근의 짧아진 차량 개발 기간으로 신뢰성 시험만으로 대응이 어려워 해석기술의 정립 및 이것의 적극 활용이 필요하다. 특히, 파손에 대한 원인 규명 등 기술 축적 필요한 상황이다. 등속조인트의 부품 파손에 대한 연구는 해석기술의 발달과 함께 진행되었는데, 주로 동역학적 접근1,3-5)으로 부품 간 접촉력 분석을 많이 진행했으며, 유한요소해석을 통한 케이지의 변형을 분석한 연구6-8)도 진행되었다. 연구들 중에서는 파손이 빈번히 일어나는 케이지에 대한 연구1-3,6-8)가 많다. 유창범 등3)은 다물체 동역학과 실험의 비교를 통하여 볼과 케이지의 접촉력을 분석하였고, Ryu와 Lim8)은 정적, 준정적 해석을 통하여 케이지 기둥부에서의 파손을 연구하고 두 경우에 파단 토크의 차이를 비교하였다. 송명의 등7)은 연성동역학 해석으로 케이지 창의 접촉자세 분석을 수행하고, 트랙 형상변경을 통하여 기둥(Web)의 강도개선을 제안하였다.
본 연구에서도 준정적 상태에서 파손이 일어나는 케이지에 대한 역학적 원인 규명을 위하여 승용차용 소형 등속조인트에 대하여 외연적 방법을 이용한 준정적 해석을 수행하고 부품 간 접촉력 분석, 소성변형률의 분석을 수행하였다. 특히 실린더 좌표계를 이용하여 회전 위상각에 대한 그래프 출력을 통하여 케이지의 소성변형률이 발생하는 구간을 분석하였다.
2. 해석모델 및 조건
등속조인트는 부품 제작 후 침탄공정과 같은 열처리를 통하여 부품의 표면경도를 높인다. 해석을 위한 등속조인트 부품의 인장 물성을 취득하는 것이 어렵다. 일단 각 부품의 최대인장강도를 파악하기 위하여 등속조인트 완제품에서 인장이 가능한 시편을 추출하여 시험을 수행하였다. 시험결과는 Fig. 2에 도시되어있으며, 볼은 너무 작아 인장시편 제작이 어려워 일자형 시편으로 제작했지만 그립에서 슬립이 일어나 파단강도를 측정할 수 없었으며, 외륜은 1371.5 MPa, 내륜은 1145.8 MPa, 케이지는 979.8 MPa로 나타났다.
앞선 문헌이나 자체 시험에 의하면 주로 케이지에서 파손이 나타나기 때문에, 본 해석에서는 타 부품은 탄성으로 가정하고, 케이지만 탄소성으로 모델링하였다.
외연적 유한요소 준정적해석은 ABAQUS/Explicit를 사용하여 진행하였고, 해석에 사용된 요소는 Fig. 3에 도시된 것처럼 8절점 6면체 요소인 C3D8R로 모델링하였다. 총 15만 여개의 절점과 13만 여개의 요소로 구성되어 해석시간이 상당히 소요되었다.
해석의 경계조건은 강체로 모델링 된 드라이브 샤프트의 끝점을 43.5도 절각하고 2.5 RPM의 속도로 회전을 시키면서 휠 쪽의 외륜부의 외면을 MPC(Multi Point Constraints)로 잡아 90 N⋅m/rev의 증분으로 드라이브 샤프트와 반대방향으로 토크를 부과하였다. 절각은 0.725초 동안 수행하였고, 초기 볼과 케이지가 위치를 잡을 수 있도록 24초 동안 1회전을 부하가 걸리지 않은 상태에서 진행하였다. 이후 토크가 부과된 준정적 해석은 총 600초 동안 진행하여 총 25회전을 부과하였다.
접촉면에서의 접촉 수직하중, 전단하중 등의 접촉 데이터를 얻기 위해서 접촉경계조건은 접촉면이 자동으로 설정되는 “General contact”옵션이 아니라, 면을 직접 지정하는 방식을 사용하였다. 각각의 볼과 케이지 윈도우, 각각의 볼과 외륜 그루브 및 내륜 그루브, 케이지의 외면과 외륜의 내면, 케이지의 내면과 내륜의 외면을 지정하였다.
3. 준정적 해석결과
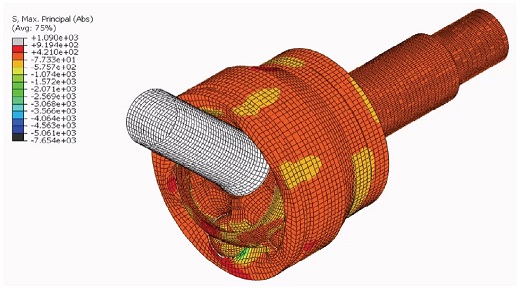
준정적 시험조건인 25회전 동안 선형으로 증가된 토크 2250 N⋅m를 부과하였을 때 등속조인트 전체의 최대주응력분포를 Fig. 4에 도시하였다. 인장 주응력은 최대 1,090 MPa이 걸리고, 압축 주응력은 더 크게 나타난다. 등속조인트 부품은 열처리를 통하여 표면의 경도가 Hv. 700이상으로 경화되고, 주로 취성의 성질을 갖게 되어 von Mises 응력 보다는 인장 주응력을 보고 파단 지점을 판단해야 한다.
Fig. 5에는 주로 파괴가 일어나는 케이지에서 최대주응력 분포를 도시하였다. 실험을 통하여 파단이 일어난 케이지는 기둥 하단부와 윈도우 상단부에서 파괴된 것으로 나타나고, 이러한 위치는 회색으로 도시된 인장영역과 일치하는 것을 확인할 수 있다.
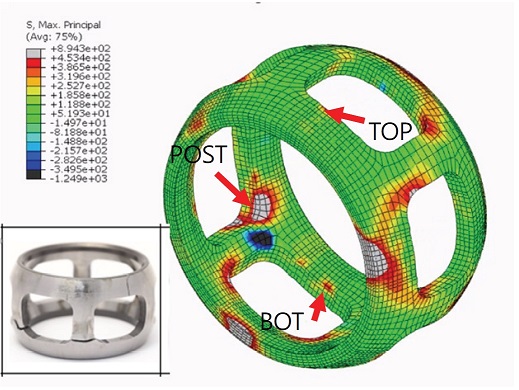
Distribution of the maximum principal stress of cage at the final torque applied and a typical fracture of cage
케이지에서 나타나는 파단을 분석하기 위하여 소성변형이 일어나는 부위에 대한 접촉면압을 분석하였다. 케이지에서 유효소성변형률이 발생하는 부위는 Fig. 5에 도시된 기둥(POST), 케이지 윈도우의 상단면(TOP), 하단면(BOT)에서 나타나기 때문에, 이 부위에 부과되는 접촉면압을 1번 볼의 회전 위치인 위상각에 따라 도시하면 Fig. 69)과 같다. Fig. 6에서 각각의 부위의 접촉면압은 특정 위상에서만 증가하고 있으며, 이는 케이지의 소성변형이 특정 위치를 통과하면서 발생한다는 것을 유추할 수 있다.
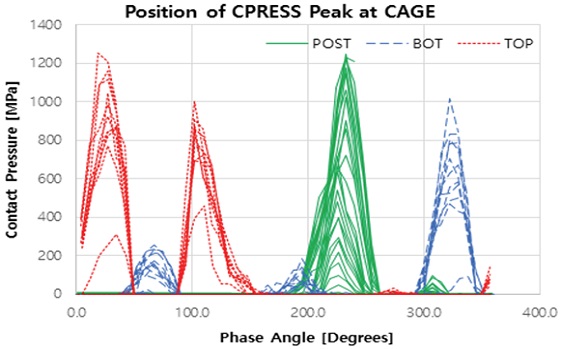
Distribution of the contact pressure(CPRESS) of cage with respect to positions according to the phase angle
케이지의 상단면은 볼이 약 20도, 100도의 위상각 위치를 지날 때, 즉 볼이 외륜의 바깥에서 내측으로 들어가기 시작하는 지점과 드라이브 샤프트가 최대로 꺾여 들어간 지점에서 바깥으로 나오기 시작할 때 나타난다. 이는 볼의 움직임으로 보면 타당한 결과로 생각되며 자세한 분석은 부품간의 접촉력 분석을 통하여 진행하였다.
3. 1 부품간 접촉력 분석
등속조인트 부품 간의 접촉력을 분석하기 위하여 ABAQUS 해석결과로 얻을 수 있는 부품 간의 접촉면에서 얻을 수 있는 수직 접촉력(CNORMF)와 접선 접촉력(CSHEAR)를 통하여 총 접촉력을 구하고, 이 접촉력을 케이지 또는 외륜의 회전 수직면에 맞추어 실린더 좌표계로 변환하여 반경방향 하중(F-Radial), 접선방향 하중(F-Tangential), 해당 부품의 축방향(F-Axial) 하중으로 계산하였다. 이렇게 변환된 결과를 위상각에 따라 직교좌표 그래프나 극좌표 그래프로 도시하면 부품간의 하중 이력을 더 잘 파악할 수 있다. 해석 상 최종 회전에서의 결과를 이용하여 선도를 도시하였다.
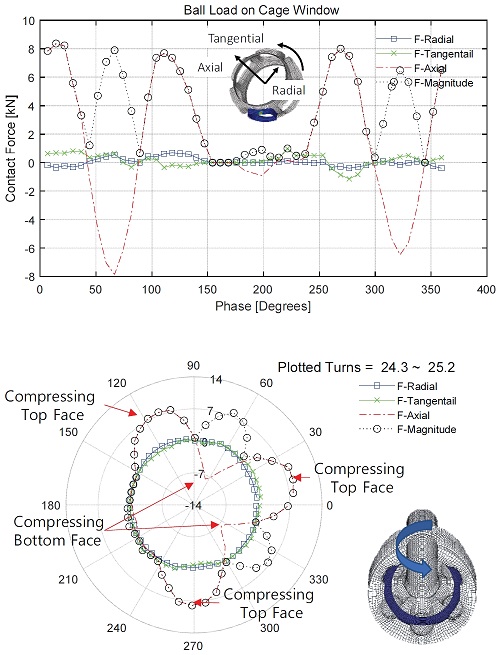
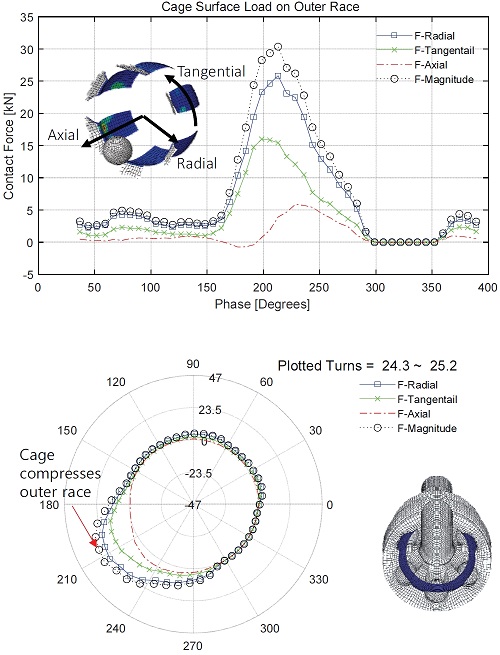
볼과 케이지의 접촉력을 구하기 위하여 6개의 볼 중 1번 볼의 결과를 이용하였다. Fig. 7에 도시된 볼과 케이지의 접촉하중은 여러 번의 교번하중 형태로 나타나며, 각 회전수에 따라 일정한 위치에서 값들이 나타난다. F-Radial과 F-Tangential은 거의 나타나지 않으며, 케이지를 밖으로 밀어내거나 안으로 누르는 F-Axial 방향의 하중이 주로 나타난다. 양의 값은 3번 나타나며, 음의 값이 2회 나타나며, 양의 값은 케이지를 밖으로 빼내는 하중이고, 음의 값은 외륜 안으로 넣는 하중으로 볼 수 있다.
위상에 따라 외륜의 형상에 맞추어 실린더 좌표계로 변환하면, Fig. 7의 아래와 같이 극좌표 형태로 도시할 수 있다. 케이지가 외륜의 내측으로 들어가는 약 15도 정도에서 볼이 케이지를 누르는 형태 즉 TOP 부분이 압축되는 형태가 나타나며, 가장 내측에서 다시 올라오는 약 120도 근처에서도 TOP 부분이 압축되는 즉 볼이 케이지를 끌어당기고 있는 것을 알 수 있다. 케이지가 최고 바깥쪽으로 위치한 270도에서도 볼이 케이지를 휠 방향으로 끌어당기고 있다. 이 결과는 Fig. 6에서 나타난 접촉압력의 이력과도 일치한다.
BOT가 압축되는 것은 케이지가 내측으로 이동하면서, 거의 최저점에서 발생하는데, 이러한 형태는 토크를 받으면서 회전할 동안, 등속조인트의 케이지는 중심위치에 있는 것이 아니라 토크에 의하여 한쪽으로 틀어져 변형하고 있다는 것을 의미한다.
볼과 외륜의 접촉은 6개의 볼이 계속 닿으면서 진행이 되지만, 해석에서는 계속 회전하면서 토크만 달라지며 동일한 상태로 진행되기 때문에, 1번 볼의 결과를 이용하여 접촉력 선도를 작성하고 분석하도록 하였다.
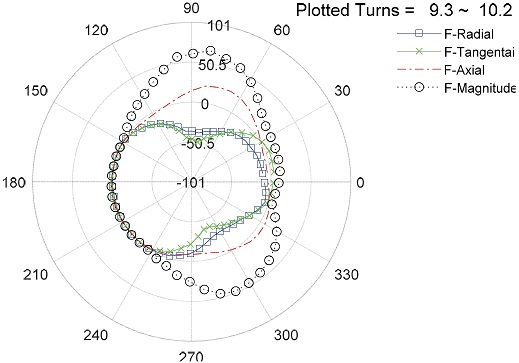
1번 볼의 외측면에서의 외륜 그루브와의 접촉반력을 Fig. 8에 도시하였고, 위상각을 x축으로 접촉 하중을 y축으로 놓은 상단 그림에서 F-Axial 하중은 거의 음의 값을 가지고 있어 볼이 외륜을 누르는 방향으로 하중이 가해지고 있는 것을 알 수 있다. F-Radial 하중은 거의 모든 영역에서 양의 값을 가지며 이것은 볼이 외륜 방향으로 밀고 나가는 하중이 걸려있는 것을 의미한다. F-Tangential 방향의 하중도 같은 위치에서 같이 나타나고 있는데, 이는 볼이 외륜을 돌리면서 밖으로 밀어내는 하중도 작용하는 것을 알 수 있다.
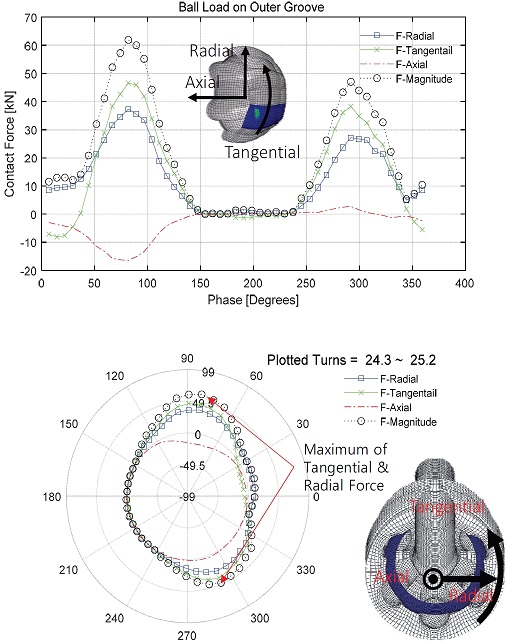
Variation of the contact force between the ball and the outer race groove according to the phase angle
하중을 극 좌표계로 옮긴 Fig. 8의 하단 그림을 보면, 볼이 외륜을 반경방향과 접선방향으로 누르게 되는 영역은 약 80도 정도와 약 300도 근처에서 나타나며, 이것은 볼이 외륜의 외부로 노출되다가 다시 내려가기 시작하는 위치와 가장 아래쪽으로 내려가기 직전의 위치에서 나타나고 있는 것을 알 수 있다. 이 역시 볼이 토크를 받으면 볼이 외부로 나오는 쪽보다는 내측으로 밀고 들어가는 쪽으로 편심되어 하중을 받는 다는 것을 알 수 있다. 드라이브 샤프트에서 바라볼 때, 1사분면과 4사분면에서 반경방향 및 접선방향으로 하중을 주며, 특히 1사분면에서는 Axial 방향으로 음의 하중이 걸리는 것을 볼 수 있는데, 이것은 볼이 외륜의 그루브를 타고 나오려는 것으로 생각해볼 수 있다.
Fig. 9에는 볼과 내륜 그루브에 걸리는 접촉하중을 도시하였다. Fig. 8의 볼과 외륜 그루브에 걸리는 접촉하중과의 형태를 비교해 보면 하중의 방향이 반대인 것을 알 수 있고, 하중 벡터의 크기는 동일한 양상을 나타내는 것을 확인할 수 있다. 이것은 외륜에 볼이 주는 하중과 내륜에 볼이 주는 하중이 작용-반작용력으로 작용하기 때문이다.
외륜의 그루브와 그루브 사이의 오목한 산 부위에서 케이지와의 접촉이 발생한다. 케이지는 볼을 자리에 위치시키는 역할을 하지만 하중에 의해서 외륜과도 접촉이 일어난다. Fig. 10의 상단의 그림과 같이 외륜에서 접촉하중이 특정부위에서 나타나고 있는 것을 알 수 있다. 약 210도 근처에서 반경방향, 접선방향 하중이 크게 나타나며, Axial 방향은 200도 근처에서 교번하고 있는 것을 알 수 있다. 이것을 통해 200도 근처에서 케이지가 약간 회전하는 형태를 보이는 것이라 생각할 수 있다.
하단의 위상에 따른 극 좌표로 나타낸 하중선도에서는 약 210도 부근인 3사분면에서 접촉력이 발행하여 케이지가 외륜을 누르는 것으로 되어있는데, 이는 앞서 볼과 외륜과의 접촉은 1사분면(80도)과 4사분면(300도)에서 일어나는 것에 비해 약 120도 정도의 간격으로 힘이 작용하는 것을 알 수 있다. 내륜과 볼, 외륜은 1, 4사분면에서 가장 크게 힘을 받고 있을 때, 내륜-케이지-외륜은 두 지점의 합성력 방향으로 힘을 받는 것을 알 수 있다.
앞서 볼과 외륜, 내륜과의 접촉힘 관계처럼, 케이지와 외륜 사이의 하중은 케이지와 내륜 사이의 하중과 부호만 다른 관계를 가지며, 이는 작용-반작용으로 생각할 수 있다.
3. 2 케이지 부품의 소성변형 분석
케이지에서의 파단 양상을 소성변형을 통하여 분석하기 위하여 케이지에서 소성변형이 발생하는 부위를 지정하여 유효소성변형률 이력을 파악하였다.
우선 각각의 볼이 위치한 케이지 윈도우의 상단부에 있는 요소에서 유효소성변형률을 시간에 따라 출력하고, 이를 토크의 증가와 관련하여 도시하면 Fig. 11과 같이 토크에 따라 계단형태로 유효소성변형률이 증가하는 것으로 나타난다. 이는 Ryu와 Lim8)의 참고문헌의 결과와 동일한 형태를 보인다. 이러한 계단형태의 증가는 특정 위치에서 하중이 부과되어 소성변형 상태가 되고, 나머지 위치에서는 하중이 낮아져 다시 탄성 복원상태에 있다고 생각할 수 있다.
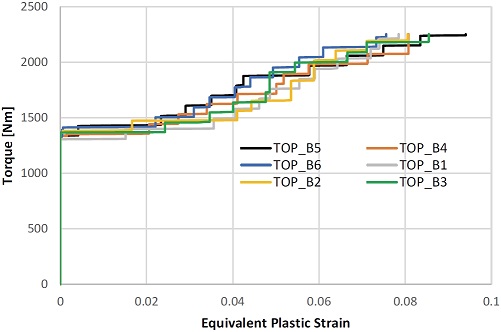
Variation of the torque with respect to the equivalent plastic strain according to the top position of cage windows where each ball is located
6개의 볼이 닿는 TOP 부위의 유효소성변형률 전체를 앞 절의 접촉력 분석과 마찬가지로 위상각에 맞추어 선도를 다시 그리면 Fig. 12와 같다. 볼이 닿은 모든 TOP 부위의 유효소성변형률이 약 100도 정도의 위상각 위치에서 증가되는 것을 알 수 있고, 이것을 통해 특정 위상 위치에서 소성변형을 일으킨다는 것을 확인할 수 있다. 유효소성변형률의 시간에 따른 증분을 위상에 맞추어 극좌표계로 작성하면 Fig. 12의 하단 우측과 같은 선도를 얻을 수 있다. 유효소성변형률의 증분은 115도 정도에서 나타나고 있는 것을 확인할 수 있다.
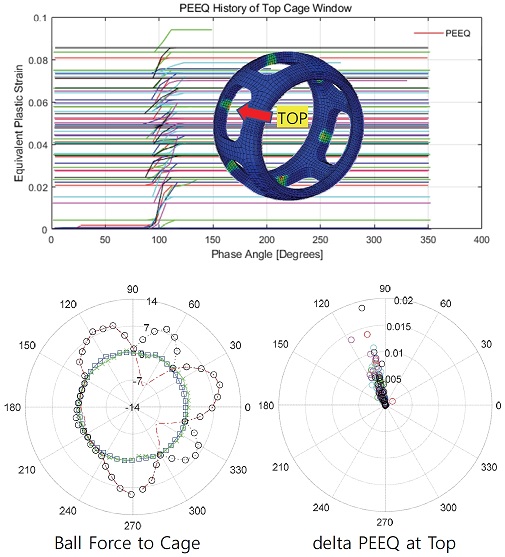
The PEEQ history of the top cage window and the ball force curve against the cage according to the phase angle
케이지 윈도우의 상단의 변형은 볼과 케이지의 접촉에서 발생하기 때문에 볼과 케이지 윈도우와의 접촉력을 비교할 필요가 있다. 앞선 Fig. 7의 선도를 Fig. 12의 하단 우측에 다시 도시하여 비교하였다. 약 115도에서 120도의 위상각의 위치에서 Axial 방향으로 양의 하중이 발생하여 TOP 부위를 누르게 되고 이 위치에서 유효소성변형률이 발생할 것을 확인할 수 있다. 볼과 케이지의 하중선도를 보면 상대적으로 15도와 270도의 위치에서도 접촉력은 크게 나타나지만 이 데이터는 동일 토크에서의 데이터가 아니라 토크가 점점 증가하고 있는 상태의 데이터이다. 상세분석 결과 동일 토크 상태에서 볼이 105도와 120도 사이에 있을 때에는 다른 위치보다 이 위치에서 접촉력이 가장 높게 나타났다.
케이지 하단부의 소성변형률의 이력을 위상으로 변환하면 Fig. 13과 같은 선도를 얻을 수 있다. TOP 부위의 결과인 Fig. 12와 같이 특정 위상에서 유효소성변형률이 발생한다는 것을 알 수 있으며, 그 위상각은 Fig. 12의 상단부와는 다르게 약 70도 정도에서 나타난다. 이를 극 좌표계로 변환하고, 유효소성변형률의 증분만 표시하면 우측 하단과 같은 그래프를 얻을 수 있다.
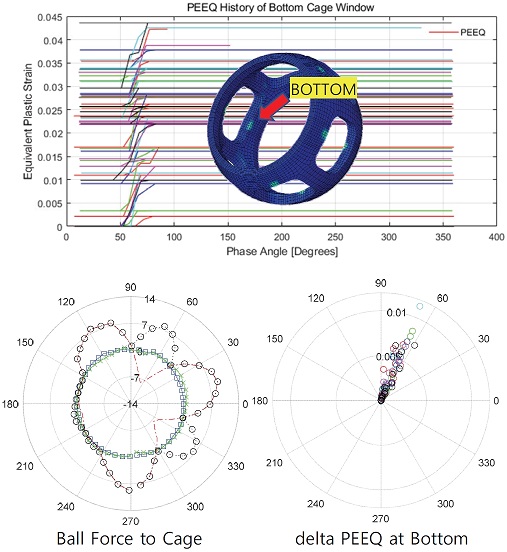
The PEEQ history of the bottom cage window and the ball force curve against the cage according to the phase angle
케이지의 윈도우 하단의 변형은 볼에 의하여 발생되기 때문에, 좌측 하단에 있는 그래프와 같이 볼과 케이지의 접촉 하중선도를 도시하면, 드라이브 샤프트 쪽으로 누르는 하중은 약 70도에서 가장 크게 나타나기 때문에 이와 동일한 위치에서 유효소성변형률이 지속적으로 발생하는 것을 예측할 수 있다.
Fig. 14에는 케이지의 기둥 코너부에서의 유효소성변형률의 분포를 위상각을 중심으로 도시하였다. 케이지 코너부에서는 하단과 상단보다는 낮은 소성변형률이 발생하였고, 우측 하단의 위상으로 표현한 그래프에서 약 230도 정도에서 유효소성변형률이 증가하고 있는 것을 확인할 수 있다. 이 위치는 앞선 상단부와 하단부와는 다르게 볼과 케이지와의 접촉력과 일치성을 찾을 수는 없으며, 케이지와 외륜과의 접촉력 선도인 Fig. 10과의 연관성이 있음을 알 수 있다. 이 선도를 Fig. 14의 좌측 하단에 다시 표시하면 약 220도 근처의 하중 증가에 의하여 발생하는 것으로 판단할 수 있다.
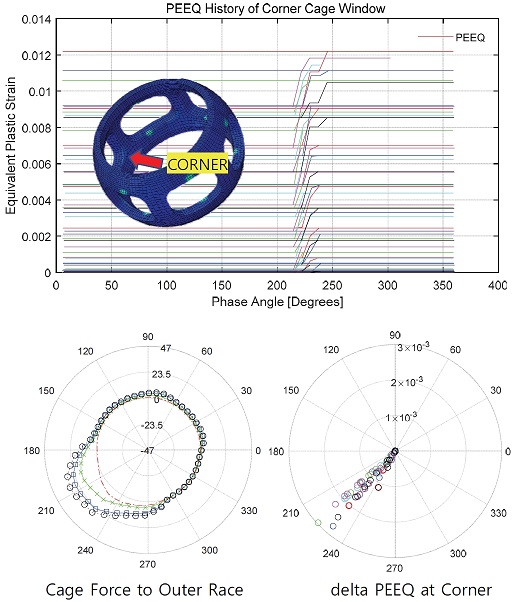
The PEEQ history of the post corner of cage window and the ball force curve against the cage according to the phase angle
마지막으로 케이지 기둥의 측면 부위에서 유효소성변형률의 이력을 위상으로 표현하여 Fig. 15에 도시하였다. Fig. 15의 그림에서 보면 위상각 약 240도 근처에서 소성변형률이 증가하는 것으로 보인다. 하지만 다른 위치와는 달리 소성변형률이 발생하는 위치가 조금 넓게 분포해있으며, 약 200도 정도와 약 250도 정도로 두 영역에서 발생하는 것으로 판단되기도 한다. 그 위치는 코너부와 유사하게 외륜과 케이지의 접촉력 분포에서 하중이 높은 위상 위치와 유사하다.
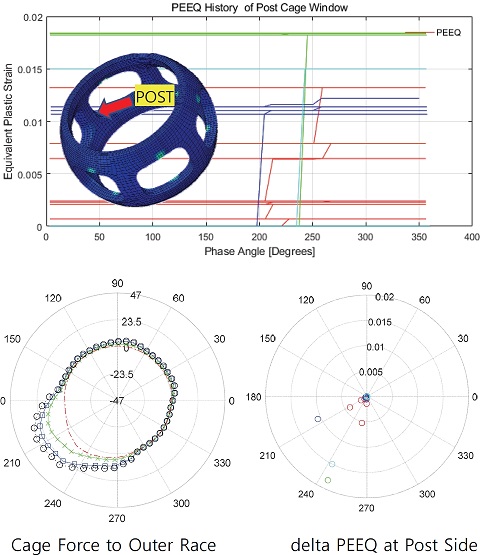
The PEEQ history of the post side of cage window and the ball force curve against the cage according to the phase angle
Fig. 15의 좌측 하단에 도시된 케이지와 외륜의 접촉력은 약 200도에서 240도에서 파란색의 반경방향의 하중도 가해지지만 녹색의 접선방향의 하중 역시 크게 나타나고 있다. 따라서 케이지 기둥은 압축과 함께 전단력도 받고 있는 것을 알 수 있다. 코너부와 함께 포스트에서는 주로 인장응력이 걸러 하단부와 상단부와 같이 압축상태에서 소성변형을 받는 것보다는 파손에 더 영향을 줄 수 있다.
4. 결 론
본 연구에서는 승용차용 소형 등속조인트에 대하여 외연적 유한요소 준정적해석을 수행하고 주로 파손이 발생하는 케이지의 소성변형을 중심으로 등속조인트 부품 간의 접촉력, 파단 발생 위상 등을 분석하였다. 접촉력은 케이지나 외륜을 중심으로 실린더 좌표계로 변환하여 분석하였다. 분석된 내용을 정리하면 아래와 같다.
- 1) 볼과 케이지의 접촉력은 약 70도 간격으로 케이지 윈도우의 상단면과 하단면을 번갈아 압축한다. 또한 준정적 해석에 따라 볼은 외륜와 내륜의 중심에 위치하는 것이 아니라 토크에 의해서 편심된다.
- 2) 볼과 외륜의 접촉은 약 85도와 300도 근처의 위상각에서 최대값이 나타나며, 내륜과의 접촉은 작용-반작용으로 나타난다.
- 3) 케이지와 외륜의 접촉은 약 210도 근처의 위상에서 최대가 되며, 반경방향의 접촉이외에도 전단방향의 접촉력도 크게 나타난다.
- 4) 케이지의 소성변형의 원인은 부품간의 접촉력을 분석하였을 때, 두 가지로 볼 수 있다. 첫째, 윈도우의 상단부와 하단부는 볼과의 접촉이 원인으로 상단부는 100도의 위상각, 하단부는 약 70도의 위상각에서 소성변형이 일정하게 일어난다. 둘째, 기둥의 코너부와 측면은 내륜과 외륜 사이에서의 접촉이 원인으로 둘 다 위상각 약 230도 근처에서 발생한다. 기둥의 측면부는 상대적으로 좀 더 넓은 위상 범위를 가지고 있다.
본 연구에서는 케이지의 각 부위에서 소성변형률이 발생하는 위상각을 도출하였다. 이 각도는 향후 최적설계 등 해석량이 많은 연구에서 시간이 많이 걸리는 준정적 해석을 사용하기 힘들다고 판단되어 단순한 정적 해석을 활용하고자 할 때 해석 경계조건 설정에 사용할 수 있을 것이다.
Nomenclature
| PEEQ : | equivalent plastic strain |
| CF : | contact force, N |
| S : | stress, MPa |
| TOP : | top position in cage window |
| BOT : | bottom position in cage window |
| POST : | posts of the cage |
| B : | ball |
Acknowledgments
A part of this paper was presented at the KSAE 2020 Fall Conference and Exhibition
본 연구는 2020년도 한국교통대학교 LINC+ 사업 산학공동기술개발과제의 지원을 받아 수행하였습니다.
References
- C. Yu, S. Kim and B. Oh, “Study on Optimization of Contact Forces on a Cage of Ball type CV Joint,” KSAE Annual Conference Proceedings, pp.759-764, 2012.
- J. Choe, D. Kim and B. Jo, “A Development of the High Durable Cage for Constant Velocity Joint,” KSAE Spring Conference Proceedings, pp.1166-1167, 2018.
- C. Yu, J. Park and B. Oh, “Multibody Dynamic Analysis of Internal Forces for Birfield Joint(BJ),” KSAE Annual Conference Proceedings, pp.1339-1344, 2010.
-
J. Mao, Y. Luo and J. Liu, “Dynamics Performance and Abrasive Wear of the Automotive Drive Shaft,” Advances in Mechanical Engineering, Vol.6, 2014.
[https://doi.org/10.1155/2014/713824]

- K. Kim, S. Moon and J. Lee, “A Study on Sensitivity Analysis and Optimization of Design Factor for CVJ Bending Resistance Reduction,” KSAE Fall Conference Proceedings, pp.556-560, 2019.
- B. Oh, “Strength Analysis of Cross Groove Type Constant Velocity Joint Cage for Propeller Shaft,” Transactions of KSAE, Vol.16, No.2, pp.74-79, 2008.
- M. Song, Y. Lim, S. An, I. Lee and J. Kim, “A Study of Dynamic Influence Factor on Cage Strength of Ball type CVJ,” KSAE Annual Conference Proceedings, pp.1242-1247, 2010.
-
I. Ryu and Y. Lim, “Finite-element Analysis of Quasistatic Fracture in CV Joints under Full-turn and Full-throttle Conditions,” Int. J. Automotive Technology, Vol.12, No.2, pp.199-205, 2011.
[https://doi.org/10.1007/s12239-011-0024-x]

- H. Lee, J. Y. Jeong, H. Cho and B. Oh, “Analysis of Plastic Deformation of Cage in Compact C.V. Joint for Passenger Car using Quasi-static Analysis,” KSAE Fall Conference Proceedings, pp.402-403, 2020.