이산 푸리에 변환 기반의 엔진 실화 진단
Copyright Ⓒ 2021 KSAE / 186-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper deals with the methodology for detecting misfired cycles by using the discrete Fourier transform-based frequency analysis. This methodology discriminates single or dual cylinder misfires at first, and then it identifies misfired cylinders for misfired cycles. In general, the highest amplitude of DFT exists at lower harmonic modes than the number of cylinders during misfires. However, because it is located at the same harmonic mode with the number of cylinders at high speed conditions even though misfires take place, origin shift should be introduced in order to identify the misfired cycles even at a high speed operating condition. New origin can be located at the averaged real and imaginary values of the transformed engine rpm on the complex plane during normal combustion cycles. Based on this new origin of the complex plane, the circle of threshold can be derived as a boundary for detecting misfires at each harmonic mode. Single cylinder misfires can be detected when transformed engine rpms are located outside this circle of threshold at both the first and second harmonic modes. In case of opposing dual cylinder misfires, misfires can be detected when transformed engine rpms are located outside this circle of threshold at the first harmonic mode and inside it at the second harmonic mode. On the contrary, the transformed engine rpms of the non-opposing dual cylinder misfires are inside it at the first harmonic mode and outside it at the second harmonic mode. In other words, the misfire detection criteria of a non-opposing dual cylinder misfire are vice versa of the opposing dual cylinder misfire. The misfired cylinders of single cylinder and opposing dual cylinder misfires can be identified by their phases at the first harmonic mode, and those of the non-opposing dual cylinder misfire can be done by them at the second harmonic mode.
Keywords:
Misfire detection, Discrete fourier transform, Origin shifting, Circle of threshold, Amplitude, Phase키워드:
실화진단, 이산 푸리에 변환, 원점 이동, 임계원, 강도, 위상1. 서 론
실화는 엔진으로 분사된 연료가 정상적으로 연소되지 않고, 미연소한 연료가 그대로 대기로 배출되는 비정상적 연소 현상이다. 실화는 규제 범위를 초과하는 차량 배기가스를 대기로 배출하므로, 대기 환경에 악영향을 미치게 된다. 또한, 엔진에서 연소되지 않는 연료가 촉매 인근에서 연소하면, 고가의 촉매에 치명적인 손상을 입히게 된다. 이에, ‘90년대에 엔진 실화 진단이 California Air Resource Board(CARB)에 의해 법제화되면서,1) 이를 전후로 해서 최근에 이르기 까지 엔진 실화 진단 방법에 대한 연구가 꾸준히 진행되어 왔다. 보쉬가 Engine roughness를 도입하여 실화 진단의 양산 개발에 성공하면서, 1990년대 말에는 Engine roughness방식이 차량의 실화진단 로직에 적용되기 시작했다.2,3) 같은 Crankshaft Position Sensor(CKPS) 신호를 이용하되, Segment time을 이용하는 Engine roughness방식과는 달리, Tooth time을 이용하여 실화를 진단하는 연구가 진행되기도 하였다.4) 아울러, Ionic current와 Combustion pressure를 직접 계측하여 실화를 진단하는 방법이 개발되었으나, Engine roughness 방식에 비해 부품 비용 증가와 엔진 설계상의 공간 제약 등 여러 요인으로 인해 양산 차량에는 제한적으로 적용되었다.5,6) 또한, 기존의 Exhaust gas pressure sensor와 Oxygen sensor에서 계측된 신호를 이용한 실화진단 연구가 수행되기도 하였다.7,8) 한편, 주파수 분석 방식의 엔진 실화 진단 방법에 관한 연구도 상당히 진행되었다. Engine roughness방식처럼 CKPS신호를 이용하되, 1차원의 시계열 데이터인 엔진속도를 2차원의 복소평면으로 맵핑하는 주파수 분석을 적용하여, 실화를 진단하는 연구가 진행되었다. 현대차에서는 삼각함수 대신 보다 단순한 형태의 Walsh 함수를 Discrete Fourier Transform(DFT)에 적용한 연구가 진행되었으나, 1차 Harmonic 함수 만을 이용하여 Top Dead Center(TDC) 간격의 Moving window 방식을 사용함으로써, 다양한 조합의 복수 실화까지 진단하는 것이 어려웠다.9) 델파이에서는 DFT의 실수항과 허수항에 대해 정규화 기법을 적용하고, Amplitude와 Phase를 이용하여 실화 발생 여부와 실화 실린더를 진단하는 연구 결과에 근거하여 특허를 출원하였다.10) 또한, Phase를 이용하여, Target wheel의 같은 반원에 위치한 복수 실린더에서 실화가 발생하는 경우와 서로 다른 반원에 위치한 복수 실린더에서 실화가 발생하는 경우의 실화 진단 방법이 제시되기도 하였다.11)
주파수 분석 방식은 진단 로직이 복잡하여 연산량이 많고 메모리 사용량은 커서, 낮은 사양의 Engine Control Unit(ECU)에는 탑재할 수 없었다. 하지만, 주파수 분석 방식은 같은 CKPS 신호를 사용하는 Engine roughness대비 실화 진단 성능이 우수하며, 진단 가능 영역이 확장 가능하다는 장점이 있다.11) 한편, 최근에는 차량용 반도체의 고성능화로 인해, 현재의 ECU사양에서도 주파수 분석 방식이 탑재 가능하게 되었다. 이에, 본 연구에서는 DFT 기반의 엔진 실화 진단에 대한 방법론을 새로이 제안하고자 한다. 우선, 정상 연소 사이클의 Amplitude와 Phase를 기준으로 모든 사이클의 DFT 결과를 보정한 후 실화 진단용 임계값을 정의하고, 사이클 단위로 단수 및 여러 조합의 복수 실린더 실화를 진단하는 방법을 도출하기로 한다. 이어서, 실화가 발생한 것으로 진단된 사이클에 대해서는 보정된 Phase를 이용하여 실화 발생 실린더를 식별하는 방법을 제시하기로 한다.
2. 본 론
2. 1 Misfire test
시험에 사용된 차량은 기아 자동차의 유럽 수출형 모닝이었다. Table 1에는 시험 차량의 주요 제원을 나타내었다.
Specifications of the target vehicle
또한, Fig. 1은 실화 시험을 위해 테스트 벤치에 장착된 시험차량을 보여주고 있다.
Test vehicle in the test facility
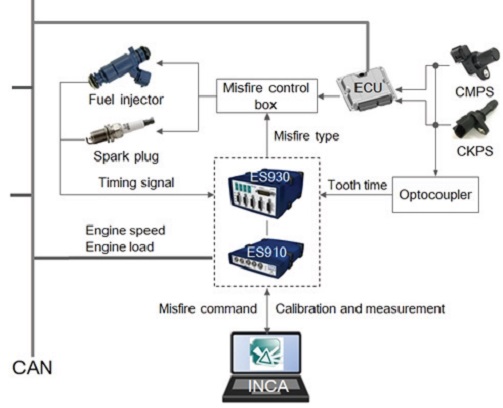
시험에 사용된 시험장치는 Fig. 2에 나타내었다. 실화 발생기는 점화를 시키지 않거나 또는 연료를 분사하지 않는 조건중에서 하나를 선택하여 실화를 발생시키도록 하였다. 실제 운전 상의 실화는 연료가 분사된 상태에서 점화플러그에서 점화가 일어나지 않거나 불완전한 연소 반응이 일어난 경우이나, 본 연구에서는 시험장 내의 환경을 고려하여, 연료를 분사시키지 않는 조건으로 실화 현상을 구현하였다. 캠축과 크랭크축 위치센서에서 측정된 신호는 Optocoupler와 ETAS 장비를 통해서 데이터 수집 노트북에 전송되었다. 또한, 엔진속도, 부하 및 기타 필요한 데이터 신호는 On Board Diagnosis(OBD) Controller Area Network(CAN) 및 ETAS 장비를 사용하여 데이터 수집 노트북에 저장되도록 하였다.
Misfire test apparatus
실화시험은 Idle과 1,500 rpm, 3,000~6,000 rpm 구간에서는 매 1,000 rpm마다, 중립 및 15~75 %의 여러 부하 조건에서 실시되었다. Table 2에는 엔진속도와 부하에 대한 시험조건을 나타내었다. 우선적으로, 본 연구에서는 3,000 rpm 및 50 % load와 4,500 rpm 및 30 % load 조건에서 주파수 분석 방식의 실화 진단 이론을 유도하고자 한다. 이후, 이번 실화시험에서 획득한 데이터를 이용하여, 주파수 분석 방식의 실화 진단 이론을 전 시험 영역으로 확대 적용하여, 본 연구 결과를 일반화할 예정이다.
Misfire test conditions for engine speed and load
2. 2 Misfire Generation
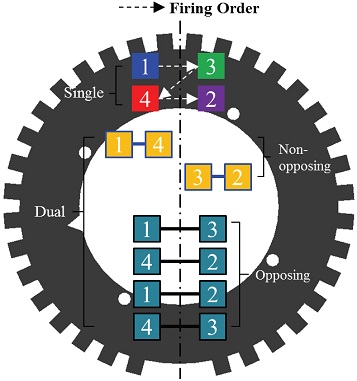
본 연구에서는 사이클 단위로 단수와 여러 개의 복수 실린더 조합에서 실화를 발생시켰다. 실린더 수에 해당하는 단수 실린더 실화 조건과 4C2=6개의 복수 실린더 실화 조합이 사용되었다. 한편, 시험 대상 차량의 엔진 점화 순서는 1-3-4-2이었다. 따라서, 단수 및 복수 실린더 실화는 Fig. 3에서 보는 바와 같이, 1~4의 단수 실린더 실화, Target wheel의 같은 반원에 위치하하는 Non-opposing 조건에 해당하는 1-4와 3-2 복수 실린더 실화 및 Target wheel의 서로 다른 반원에 위치함으로써 Opposing 조건에 해당하는 1-3과 4-2, 1-2와 3-4 복수 실린더 실화 조건으로 세분화될 수 있다. 한편, 본 연구에서는 3개 이상의 복수 실린더 실화 조건은 고려하지 않았다.
Combination for misfired cylinders including opposing and non-opposing dual cylinders
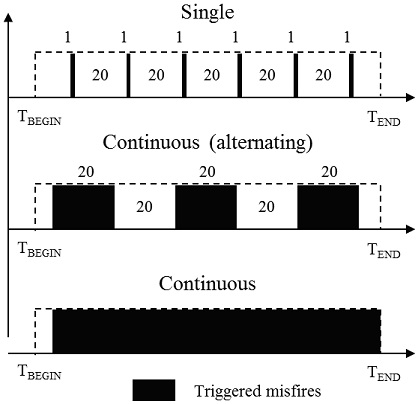
한편, 본 연구에서는 단수 및 복수 실린더 실화를 단일 또는 연속 조건으로 발생시켰다. 본 연구에서 사용된 단일 및 연속 실화의 발생 패턴은 Fig. 4와 같다. 단일 실화 시험에서는 단일 실화 사이클 사이에 20개의 정상 연소 사이클을 배치하였다. 연속 실화로는 20개의 실화 사이클 후에 20개의 정상 연소 사이클이 뒤따르는 경우(Alternating)와 실화를 발생시킨 후에 실화 사이클로 시험을 끝내는 경우(Continuous), 2가지 패턴을 사용하였다. 여기서, Alternating 조건을 사용한 이유는 연속 실화가 주기적으로 반복될 때에도 실화가 잘 검출되는지를 확인하기 위함이었다.
Patterns for generating misfires
2. 3 Frequency Analysis
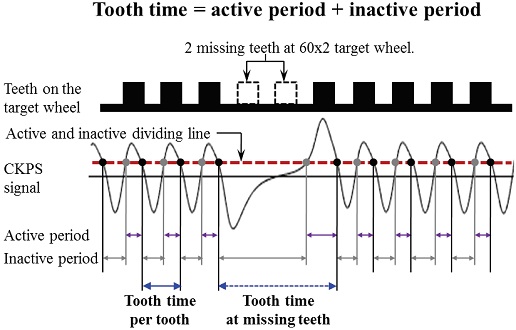
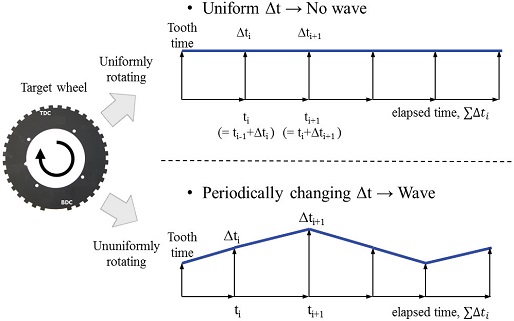
자동차의 엔진속도는 Inductive 또는 Hall형 CKPS로 계측되는데, 본 연구의 시험차량는 Hall형을 사용하였다. CKPS내 영구자석이나 코일에 흐르는 전류에 의해 자기장이 형성되고, Target wheel이 회전하는 동안 Tooth의 프로파일이 자기장을 교란하여 발생시킨 유도전압으로 Tooth time을 측정한다. 본 연구에서는 Fig. 5와 같이, Tooth time을 정량화하기 위해 특정 CKPS신호값 이상인 구간에서는 1(Active), 이하인 구간은 0(Inactive)으로 하고, Tooth마다 계측된 Active와 Inactive 시간을 합하여 Tooth time을 계산하였다.
Tooth time measurement using CKPS
Tooth time이 측정되는 Target wheel에는 원주방향으로 60-2개의 Teeth가 일정한 가격으로 배열되어 있다. 각 실린더마다 4행정을 거치면서 각 Teeth의 Tooth time은 Fig. 6과 같이 주기적으로 증감을 반복하게 되며, 엔진 속도는 Tooth time의 역수에 해당하므로, Target wheel의 원주 속도는 일정한 파형을 형성한다. 이에, 일정한 파형을 형성하는 엔진속도에 DFT를 적용하여 주파수 분석을 수행할 수 있게 된다.
Wave of tooth time caused by its periodical change
DFT는 1차원의 시계열 데이터를 2차원의 복소평면 상으로 맵핑을 하는 과정이다. 식 (1)의 hk는 엔진속도의 k차 Harmonic항으로 식 (2)와 같이 실수 항과 허수 항을 갖는 복소수이다. 여기서, N은 한 사이클에 포함된 Tooth갯수로, 본 연구에서는 60-2 Teeth target wheel을 사용하므로 N = 60/rev*2 rev = 120이다.
| (1) |
| (2) |
복소평면의 원점에서 hk항까지의 거리와 각도는 각각 Amplitude와 Phase로 정의되며, 식 (3)과 같다.
| (3) |
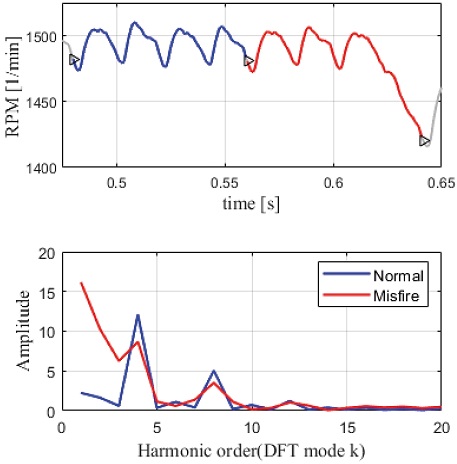
정상연소 중인 다기통 엔진에서는 한 사이클마다 실린더 수 만큼의 점화가 일어나므로, 정상적으로 연소하는 사이클의 엔진 속도에는 실린더 수에 해당하는 파형이 존재하게 된다. 본 연구에서는 4기통 엔진을 대상으로 하므로, Fig. 7 및 Fig. 8과 같이 정상연소 중인 사이클에서는 4개의 유사한 파형(Blue line)이 나타나는 것을 확인할 수 있다. 또한, 실화가 발생한 실린더에서는 엔진속도가 감소하면서 엔진 파형에 변화가 발생하는 것도 볼 수 있다(Red line).
Engine rpm(upper) and DFT amplitude(lower) for the misfire of cylinder 2 at 1,500 rpm & 25 % load
Engine rpm(upper) and DFT amplitude(lower) for the misfire of cylinder 2 at 5,000 rpm & 3 7 % load
4기통 엔진의 정상연소 사이클에 이산 푸리에 변환을 적용하면, 식 (1)의 DFT 4차 Harmonic 모드에서 구해진 Amplitude가 최대가 된다. 만약 실화가 발생하게 되면, 실화 실린더의 위치에서 엔진속도가 감소하면서, Fig. 7(Lower)처럼 정상 연소 사이클 보다 낮은 저주파 신호가 나타나게 된다. 따라서, 실화 사이클에 이산 푸리에 변환을 적용하면, Fig. 7(Lower)와 같이 4차 Harmonic값이 아닌, 1차 또는 2차 Harmonic값이 최대 Amplitude가 된다. 단수 실린더 실화 또는 Opposing 복수 실린더 실화의 경우에는 1차 Harmonic 모드에서 최대 Amplitude가 나타나는데, 2개의 실린더에서 연속으로 실화가 발생하는 Opposing 복수 실린더 실화에서 엔진 속도의 감소량이 더 크므로 단수 실린더 실화 보다는 Amplitude가 커진다. 한편, Non-opposing 복수 실린더 실화에서는 연속하지 않는 2개의 실린더에서 실화가 발생함에 따라, 하나의 사이클 내에서 2번의 엔진속도 감소 파형이 나타나므로, 2차 Harmonic 모드에서 최대 Amplitude가 나타나게 된다. 이에, 한 사이클 단위로 이산 푸리에 변환을 한 후에 최대 Amplitude가 4차 보다 낮은 차수의 Harmonic값에서 나타난 경우를 실화로 진단할 수 있게 된다.
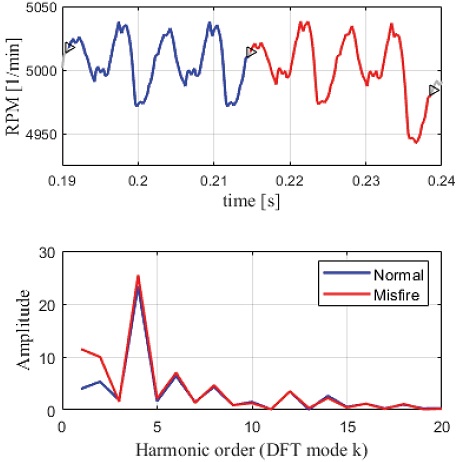
그런데, 고속 운전 조건에서는 Crankshaft system의 관성모멘트가 커져서, Fig. 8(Upper)에서 보는 바와 같이 실화가 발생하더라도 엔진속도가 평행 이동을 하듯이 감소함에 따라, Fig. 8(Lower)처럼 정상연소와 실화 모두 최대 Amplitude가 4차 Harmonic값에서 나타났다. 따라서, 낮은 운전속도 조건과는 달리, 고속에서는 정규화되지 않은 DFT 결과만으로 정상연소와 실화를 구분할 수 없으므로, 이에 대한 해결 방안이 요구되고 있다.
3. 결과 및 분석
3. 1 Origin Shifting
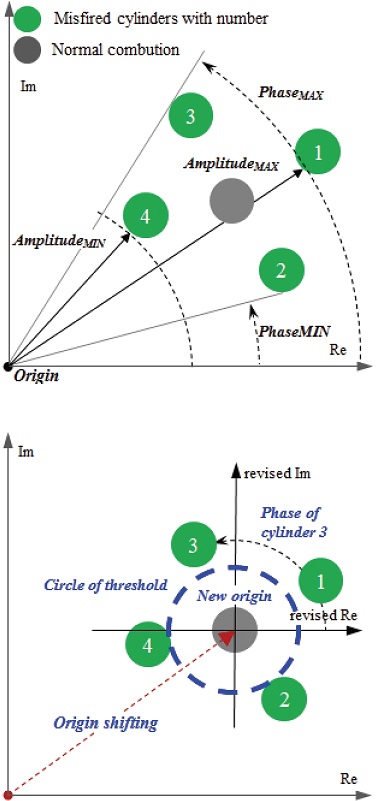
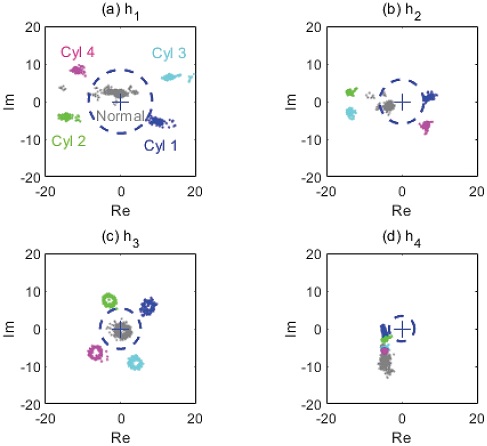
고속 조건에서 복소평면 상의 DFT 결과는 Fig. 9(a)에서 보는 바와 같이 정상연소와 실화 모두 에서 특정한 방향으로 치우쳐서 위치하는 경우가 발생할 수 있다(특히, 기통수에 해당하는 Harmonic 모드에서). 그래서, 정상연소의 DFT amplitude와 Phase가 각각 실화의 최소~최대 범위 내에 위치함에 따라, Fig. 8(Lower)와 같은 형태로 4차 Harmonic mode에서 최대 Amplitude가 도출되므로, 실화 진단이 불가능해 진다. 그런데, Fig. 9(b)와 같이 원점이동을 해 주고 나면, 복소평면 상에서 새로운 좌표축을 기준으로, 임계값(즉, 임계원)을 구할 수 있게 되고, 이 임계값과 보정된 Amplitude를 비교함으로써, 실화 진단이 가능해진다.
Schematics for origin shifting, upper) before origin shifting and lower) after origin shifting
3. 2 DFT Compensation
Cut-off frequency를 고려하여, Fig. 10에는 3,000 rpm과 50 % load 조건의 시험 결과에 대해 1~4차 Harmonic 모드의 정규화하지 않은 DFT의 결과를 복소평면 상에 나타내었다. DFT를 수행하기 전에, Tooth time데이터에 Detrend와 1차 저주파 통과 필터를 적용하고 나서, Tooth time을 엔진속도로 변환을 하였다. 여기서, Detrend는 시계열 데이터의 선형 경향성을 제거하는 과정이다. 엔진속도의 감가속시 나타날 수 있는 엔진속도의 선형 경향성을 Detrend를 거쳐 필터링함으로써, DFT 직전의 엔진속도 그래프에서는 실화에 의한 엔진속도의 감속 영향만이 남게 된다. 이때 엔진속도의 선형경향성은 선형회귀법으로 구하였다.
| (4) |
Complex plane of DFT 1st to 4th harmonic modes for sporadic single misfire at 3,000 rpm & 50 % load
본 연구에서 사용한 1차 저주파 통과 필터를 식 (4)에 나타내었는데, a=0.25로 설정하여 입력항과 관성항의 가중치는 각각 0.25와0.75가 됨으로써, 6차 Harmonic이하의 신호만이 필터를 통과하도록 하였다. 이에, Fig. 10과 Fig. 11에서 보듯이, 4차 Harmonic 이하의 모드만을 대상으로 하여, 실화 진단을 검토하게 되었다.
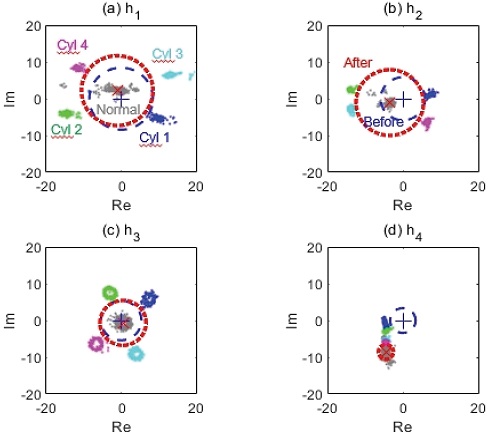
Origin shifting applied to DFT 1st to 4th harmonic modes of Fig. 10. Red and blue circles are circles of threshold after- and before-origin shifting, respectively
Fig. 10에서 보면, DFT 1~3차 Harmonic 모드에서 정상연소 데이터는 원점에서 조금씩 벗어나 있으나, 대체로 원점 인근에 위치하고 있다. 정상연소 데이터의 평균 위치가 원점에서 벗어나 DFT 모드 별로 조금씩 이동하는 현상을 Normal variability라 하며,10,11) 이것은 Target wheel의 투스 가공공차나, 실린더별 연소반응 에너지의 차이 또는 크랭크축의 비틀림 진동 등에 의해 샘플링 시간이 균일하지 않기 때문에 발생하는 현상이다.
복소평면의 원점을 중심으로 정상 연소와 실화의 경계를 나타내는 원(Circle of threshold)을 그려보면, DFT 모드 별로 Circle of threshold의 크기 차이가 있지만, Circle of threshold을 기준으로 정상연소와 실화를 구분할 수 있다. 이에, Circle of threshold는 DFT-based 엔진 실화 진단에서 실화 사이클을 식별하는 임계값이 된다. 한편, Fig. 10(d)의 DFT 4차 Harmonic 모드에서는 3차에 비해 Circle of threshold의 크기가 증가하였지만, 정상연소와 실화가 모두 Circle of threshold외부에 위치함으로써, 정상연소와 실화를 구분하는 것이 불가능하였다. 그런데, Normal variability가 증가하게 되면, Fig. 10(b)의 2차 Harmonic모드와 같이 복소평면 상에서 정상연소의 위치가 원점에서 크게 벗어나게 되므로, 실화 진단의 정확성이 낮아질 수밖에 없다. 이에, 식 (5)와 같이 Circle of threshold의 원점을 복소평면 원점에서 정상연소 데이터의 평균점으로 이동시켜 주면, Fig. 10은 Fig. 11과 같이 변하고, DFT 1~3차 Harmonic 모드의 Circle of threshold의 크기가 커지면서 실화를 기존보다 명확하게 구분할 수 있게 된다. 또한, DFT 4차 Harmonic 모드의 경우에서도 정상연소와 실화 구분이 가능하게 되었다. 이때, 식 (5)에서 P는 정상연소 데이터의 시료 수이며, 하첨자 Amp와 NC는 각각 Amplitude와 Normal combustion의 약어이다.
| (5) |
이로써, 1~4차 Harmonic 모드 전체에서 원점 이동 이후, 새로운 원점을 기준으로 실화가 발생한 실린더들의 Amplitude와 Circle of threshold의 반지름을 비교하여 실화가 발생한 사이클을 진단할 수 있게 되었다. 각 Harmonic 차수에서 Amplitude가 Circle of threshold의 반지름 보다 크면(즉, DFT된 Engine rpm이 Circle of threshold 외부에 위치하면), 실화가 발생한 것으로 진단된다. 또한, Fig. 11을 살펴보면, 3차 및 4차 DFT 모드에 비해 1차와 2차 DFT 모드에서 Circle of threshold의 크기가 컸다. 이로써, Fig. 1에서 보듯이 실화가 발생할 경우, 1차 또는 2차 Harmonic 모드에서 DFT amplitude가 가장 크게 나타나는 현상을 설명할 수 있게 되었다.
3. 3 Misfire Detection for Dual Cylinders
Fig. 11은 단수 실린더 실화에 대한 진단 방법을 설명하고 있으며, 복수 실린더 실화에서도 이 방법이 유효한지를 확인할 필요가 있다. Fig. 12에는 단수 실린더 실화 결과)를 기반으로 구한 Circle of threshold을 기준으로, 단수 실린더 실화(Black point) 및 Non-opposing 1-4 복수 실린더 실화(Blue point)와 Opposing 1-3 복수 실린더 실화(Red point)의 DFT 결과를 복소평면 상에 함께 나타내었다.
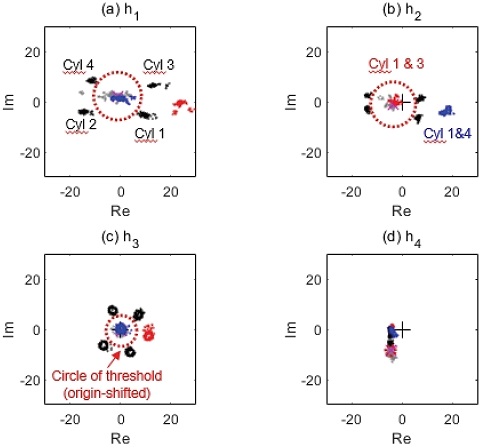
Circle of threshold on the complex plane of the 1st to the 4th harmonic modes after origin shifting. Red circles are origin-shifted circle of threshold
Fig. 12에서 보는 바와 같이, 단수 실린더 실화에서는 DFT 1~4차 모드 모두에서 실화 신호가 Circle of threshold 외부에 위치하였다. 반면, 복수 실린더 실화의 DFT결과에서는 1차 및 3차 Harmonic모드에서 Non-opposing 복수 실린더 1-4의 실화 신호는 Circle of threshold 내부에, Opposing 복수 실린더 1-3의 실화 신호는 Circle of threshold 외부에 위치하였다. 한편, DFT 2차 Harmonic모드는 DFT 1차 및 3차 Harmonic모드와는 정반대의 결과를 보여주었으며, DFT 4차 모드에서는 단수 실린더 실화와 같이 Non-opposing과 Opposing 모두 Circle of threshold 외부에 위치하는 결과를 보여주고 있다.
Fig. 13(a)에서 보면, Non-opposing 복수 실린더 실화의 경우에는 1차 Harmonic 모드에서 실수항과 허수항이 모두 0이 된다. 이에 Non-opposing 복수 실린더 실화의 1차 Harmonic 모드의 DFT값은 이상적인 경우에는 Origin-shifted원점에 위치하며, 3차 Harmonic 모드에서도 동일한 결과가 나타나야 한다. Fig. 12(a)에서 보듯이, Non-opposing 복수 실린더 실화의 1차 Harmonic 모드에서 실수항과 허수항이 0은 아니지만, Circle of threshold 내부에서 복소평면상의 새로운 원점인 정상연소의 DFT 결과 부근에 위치하는 것은 이와 같은 이유 때문이다. 반면에, Fig. 13(b)에서 보면, Opposing복수 실린더 실화의 경우에는 2차 Harmonic 모드에서 실수항과 허수항이 모두 0이 된다. 따라서, Fig. 12(b)와 같이, Opposing 복수 실린더 실화의 2차 Harmonic 모드에서 DFT 결과가 Circle of threshold 내부에서 정상연소 데이터 부근(즉, 원점이동 후의 새로운 원점)에 위치하게 된다. 단수 실린더 실화와 복수 실린더 실화에 대해서 Circle of threshold을 살펴보면, 다른 차수에 비해 DFT 1차 및 2차 모드에서 Circle of threshold의 크기가 크고, 실화 신호도 실린더 마다 특정 위치에 집중적으로 분포하는 형태를 보여주고 있다. 이로써, 실화 실린더의 조합에 따른 DFT 결과의 분포 위치를 분석하면, 단수 및 복수 실린더 실화는 1차 및 2차 Harmonic 모드의 DFT 결과를 사용하여 실화발생 여부를 진단할 수 있게 된다.
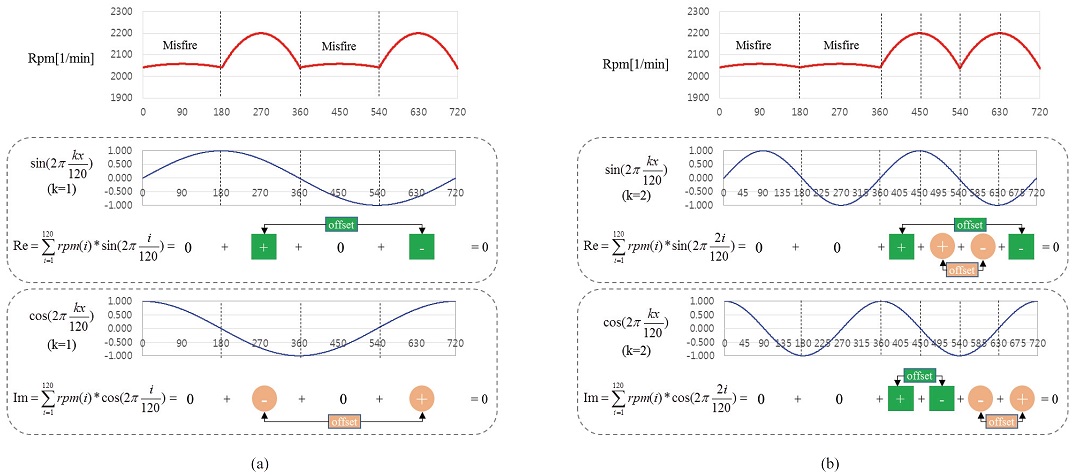
DFT result of (a) non-opposing dual misfire at the 1st mode and (b) opposing dual misfire at the 2nd mode
그리고, 1차 Harmonic 모드에서 Non-opposing 복수 실린더 실화와 2차 Harmonic 모드에서 Opposing 복수 실린더 실화의 DFT 결과가 Origin-shifted원점에서 정확하게 일치하지 않는 것은 기계가공 공차와 엔진속도에 의해 모든 Tooth에서의 Tooth time이 균일하지 않기 때문에, 실제 운전 환경하에서의 Normal variability 가 발생하기 때문이다. 실화가 발생할 때에는, Normal variability가 증가하는 것이 일반적이므로, 그 차이는 좀 더 증가하게 된다. 따라서, Fig. 12(a)와 (b)에서 처럼, Circle of threshold 내부에는 위치하되, 정상연소와 실화간 DFT 결과의 분포 위치가 다르게 나타나는 것이다.
한편, Fig. 12(a)의 1차 Harmonic 모드와 Fig. 12(b)의 2차 Harmonic 모드의 복소평면을 보면, 단수 및 복수 실린더 실화 간의 DFT 결과의 차이만 확인될 뿐, 특정의 실화 실린더 조합의 DFT 결과가 일정한 위상 부근에서 집중적으로 분포하는 것으로 보아, 단일 및 연속 실화간의 차이는 크지 않는 것으로 판단된다. 한편, 1차 및 2차 Harmonic 모드와는 달리, 3차 Harmonic 조건에서는 정상연소나 실화 모두에서 DFT 결과가 상대적으로 폭넓게 분포하고 있다. 이것은 단일과 연속 실화간 차이의 영향으로도 판단된다. 하지만, 실화 진단에 1차와 2차 Harmonic 모드에서의 DFT 결과만을 사용한다면, 실화 진단에 있어서 단일 및 연속 실화간 차이의 영향은 거의 없을 것으로 예상할 수 있다.
3. 4 Identification of Misfired Cylinders
고속 고부하 조건에서는 Target wheel을 포함한 크랭크축 시스템의 관성모멘트가 증가하여, 실화에 의한 엔진속도의 변화는 크지 않다. 이런 경우에는 복소평면 상에서 원점이동된 Engine rpm은 실화가 발생하였을 때와 발생하지 않았을 때의 위치가 특정한 범위 내에서 혼재함에 따라, Amplitude와 Phase를 이용하여 정상연소와 실화를 구분하는 것이 불가능해 질 수 있다. Fig. 14에는 DFT 결과에 원점이동을 적용한 이후의 복소평면을 도식화 하였는데, 원점이동 이후에는 새로운 원점을 중심으로 실화가 발생한 실린더의 위치가 원주방향으로 확연하게 구분될 수 있음을 보여주고 있다.
Discrimination of misfired cylinders
원점 이동을 적용한 이후에는 정상연소의 데이터는 점화 순서에 무관하게, 새로운 원점 부근에 집중적으로 분포하는데 반해, 실화가 발생하면 새로운 원점에서 벗어나되, 원주 방향으로 점화 순서에 따라 실린더 마다 분포 위치가 다르게 나타나게 된다. 이에, Fig. 14에서 보면, 각 실화 실린더의 원점이동된 Phase의 분포 영역간 적정 위치에서 실화 실린더를 구분하는 임계선을 선정할 수 있다. 따라서, 원점이동된 Phase 임계선을 기준으로 실화가 발생한 실린더를 식별할 수 있게 된다. 이와 같은 실화 실린더 진단 방법에 따라, 4,500 rpm과 30 % load 조건의 실화 시험 데이터를 Fig. 15의 복소평면 상에 나타내었다.
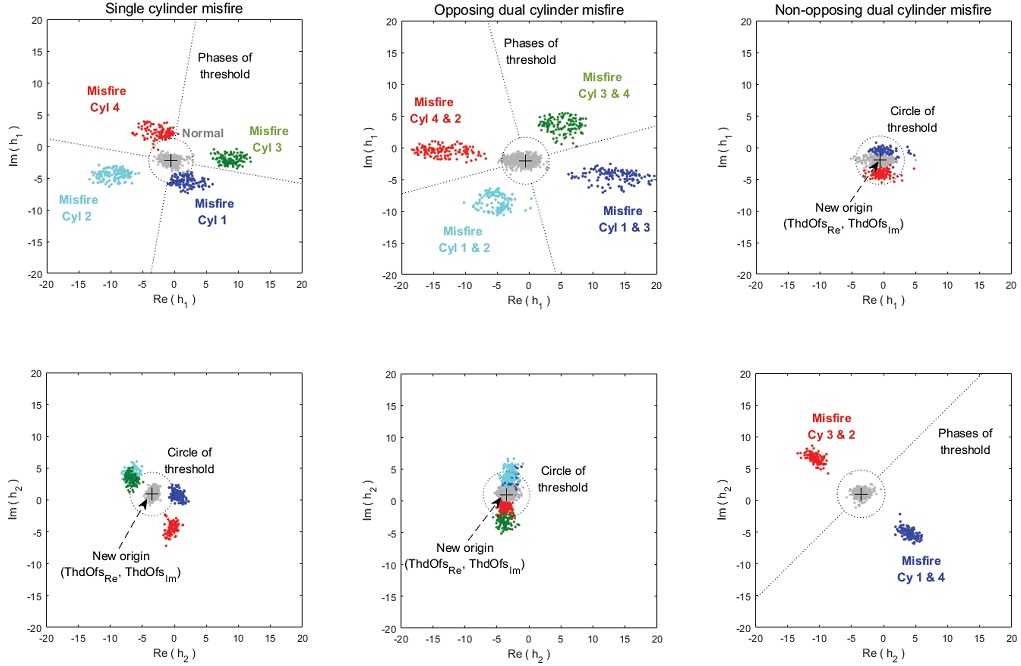
Thresholds of amplitude and phase at 1st and 2nd harmonics to detect continuously-misfired cycles and cylinders. left) single cylinder misfire, mid) opposing dual cylinder misfire, right) non-opposing dual cylinder misfire at the operation condition of 4,500 rpm and 30 % load
Fig. 15에는 4가지의 단수 실린더와 6가지 경우의 복수 실린더 조합에 대한 실화 데이터를 모두 포함하고 있다. Fig. 15 left)는 단수 실린더 실화에 대해 1차와 2차 Harmonic 모드의 복소평면을 보여주고 있다. DFT 1차 Harmonic모드에서는 각 실린더를 4개의 Phase 임계선으로 영역을 구분하여, 각 실린더 별로 DFT 결과가 위치하는 영역을 지정함으로써, Fig. 14에서 설명하였듯이 Phase를 이용하여 실화 실린더를 식별할 수 있다. 한편, 2차 Harmonic모드에서는 일부 실린더들의 DFT 결과가 중첩되어 나타남에 따라, 2차 Harmonic 모드는 실화 실린더 진단에 사용할 수 없음을 알게 되었다. Fig. 15 mid)의 Opposing복수 실린더 경우에서도 DFT 1차 Harmonic모드에서 복소평면을 4개의 Phase 선을 정의하여, 4개의 실린더 조합별로 DFT 결과가 위치하는 Phase영역을 지정함으로써, 실화 실린더 조합을 찾아낼 수 있다. 한편, 2차 Harmonic모드에서는 DFT 결과로서 실수항과 허수항이 새로운 원점 인근에 위치함에 따라, 4개 실린더 조합 모두에서 Circle of threshold 내부에 위치함을 확인할 수 있었다. Fig. 15 right)의 Non-opposing복수 실린더 조합에서는 DFT 2차 모드의 복소평면을 2개의 Phase 선으로 등분하여 실화 실린더를 식별할 수 있음을 알아냈다. Opposing 경우와 유사하게, 1차 Harmonic 모드에서는 2개 실린더 조합이 모두 Circle of threshold 내부에 위치하였기 때문에, Opposing 복수 실린더처럼 1차 Harmonic 모드를 사용할 수 없었다.
한편, Fig. 15 mid)의 2차 Harmonic 모드에서 보면, Opposing 복수 실린더 조합 중에서 1-2와 3-4 조합에서 일부 데이터가 Circle of threshold의 내부가 아니라 외부에 위치하고 있는 것을 볼 수 있다. 마찬가지로 Fig. 15 right)의 1차 Harmonic 모드에서도 일부 데이터가 Circle of threshold의 외부에 위치하고 있다. 이것은 복수 실린더 실화를 단수 실린더 실화로 오진할 수 있는 가능성을 의미하므로, 이에 대해서는 추가적인 연구가 필요하다.
Table 3에는 DFT 1차와 2차 Harmonic모드의 Amplitude와 Phase를 이용하여 실화를 진단하는 로직을 정리하였다. 실화 진단을 위해서는 우선 사이클의 실화 발생 여부를 진단한다. 이어, 사이클에서 실화가 진단되면 실화 실린더를 식별하는 2개 단계로 구성하였다. 이에, 제 1단계에서는 1차 및 2차 Harmonic 모드에서 Amplitude를 각각의 Circle of threshold와 비교하여 사이클의 실화 여부를 진단한다. 이때 사용되는 Circle of threshold는 1차 및 2차 Harmonic 모드별로 1개씩 정의되어야 한다. 제 2단계에서는 실린더 마다 1차 및 2차 Harmonic 모드의 Phase를 실화 실린더의 조합에 해당하는 Threshold와 비교하여 실화 실린더를 구분하도록 하였다. 1차 Harmonic 모드에서는 4개의 실린더 조합 별로 각각 1개씩, 2차 Harmonic 모드에서는 2개의 실린더 조합별로 2개의 Phase Threshold lines 이 정의되어 있어야 한다.
Misfire detection logic
4. 결 론
본 연구를 통해서 DFT 기반의 엔진 실화 진단에 관한 실험 및 해석적 연구를 수행하는 과정에서 Origin shifting 개념을 도입함으로써, 실화 진단의 정확성을 향상시켜주고, 관성모멘트의 영향이 크게 나타나는 고속 조건에서도 실화 진단을 가능하게 하는 방안을 새로이 제안하였다. 아울러, 단수 및 복수 실린더 실화와 실화 실린더를 식별하는 방안을 연구하여, 다음과 같은 결론을 구할 수 있었다.
- 1) DFT-based 주파수 분석으로 구한 최대 Amplitude가 나타나는 Harmonic 차수가 기통수에 해당하는 차수보다 작으면 실화로 발생한 것으로 진단 할 수 있다. 하지만, Normal variability현상으로 실화 진단의 정확성이 낮아질 수 있으며, 고속 조건에서는 크랭크축 계의 관성 모멘트가 증가하면서 엔진속도 그래프 상에 저주파에 해당하는 파형이 나타나지 않았기 때문에 실화 진단도 불가능해 짐을 실험적으로 확인하였다.
- 2) 각 Harmonic 모드 별로 정상연소 사이클에서 DFT된 Engine rpm의 평균점을 새로운 원점으로 사용하여, 실화 진단의 임계값으로 사용 가능한 Circle of threshold를 새로이 정의하였다. 이로써, 사이클 마다 DFT된 Engine rpm의 Amplitude와 Circle of threshold의 반지름간의 크기를 비교함으로써, 사이클 단위로 실화 진단을 할 수 있었다. 즉, DFT의 1차 및 2차 Harmonic모드에서 Amplitude와 Circle of threshold의 반지름과의 크기를 비교하여, 단수 및 복수 실린더 실화를 진단하는데, 단수 실린더 실화는 1차 및 2차 Harmonic 모드에서 Amplitude가 Circle of threshold의 반지름보다 크며, Opposing 복수 실린더 실화는 1차 Harmonic 모드에선 Amplitude가 Circle of threshold의 반지름보다 크지만, 2차 Harmonic 모드에선 작았다. 또한, Non-opposing 복수 실린더 실화의 경우에서는 Opposing 복수 실린더 실화와 정반대였다.
- 3) 원점이동된 복소평면 상에서 Phase를 이용하여 실화 실린더의 조합을 진단하였다. 단수 실린더와 Opposing 복수 실린더 실화에서는 1차 Harmonic 모드의 복소평면에서 인근의 실화 실린더 조합과의 Phase와의 크기 비교를 통해 실화가 발생된 실린더를 구분하였다. Non-opposing 복수 실린더의 경우에는 2차 Harmonic 모드의 복소평면에서 역시 인접하는 실화 실린더 조합과의 크기를 비교하여 실화를 진단할 수 있다.
Nomenclature
| Amp : | amplitude |
| CARB : | califonia air resource board |
| CAN : | controller area network |
| CKPS : | crankshaft position sensor |
| Cyl : | cylinder |
| DFT : | discrete Fourier transformation |
| ECU : | engine control unit |
| Im : | imaginary |
| N : | the number of teeth in one cycle |
| NC : | normal combustion |
| OBD : | on-board diagnosis |
| P : | the number of normal combustion cycles |
| Re : | real |
| RPM : | revolution per minute |
| TDC : | top dead center |
References
- Amend section 1968.2 of Title 13, California Code of Regulation(CCR), OBD II Regulatory Documents, 2015.
-
M. Klenk, W. Moser, W. Mueller and W. Wimmer, “Misfire Detection by Evaluating Crankshaft Speed-A Means to Comply with OBD II,” SAE Transactions, Vol.102, Section 3, pp.598-607, 1993.
[https://doi.org/10.4271/930399]
-
J. Förster, A. Lohmann, M. Mezger and K. Ries-Müller, “Advanced Engine Misfire Detection for SI-Engines,” SAE 970855, 1997.
[https://doi.org/10.4271/970855]
-
P. G. Han, “A Study on Misfire Detection Index Not Affected by Post Oscillation of Engine Speed,” Transactions of KSAE, Vol.28, No.2, pp.143-150, 2020.
[https://doi.org/10.7467/KSAE.2020.28.2.143]
-
S. Chatterjee and A. Sivasubrahmaniyan, “Comparison of Misfire Detection Technologies in Spark-ignition Engines for Meeting On-Board Diagnostic Regulation,” SAE 2013-01-2884, 2013.
[https://doi.org/10.4271/2013-01-2884]
-
L. Peron, A. Charlet, P. Higelin, B. Moreau and J. F. Burq, “Limitations of Ionization Current Sensors and Comparison with Cylinder Pressure Sensors,” SAE 2000-01-2830, 2000.
[https://doi.org/10.4271/2000-01-2830]
-
M. Willimowski and R. Isermann, “A Time Domain Based Diagnostic System for Misfire Detection in Spark-Ignition Engines by Exhaust-Gas Pressure Analysis,” SAE 2000-01-0366, 2000.
[https://doi.org/10.4271/2000-01-0366]
-
Y. K. Chung, C. S. Bae, S. M. Choi and K. J. Yoon, “Application of a Wide Range Oxygen Sensor for the Misfire Detection,” SAE 1999-01-1485, 1999.
[https://doi.org/10.4271/1999-01-1485]
- J. B. Kim, T. P. Lee, J. S. Eo and K. H. Yim, “Detection of Misfire in Car Engines using Walsh Discrete Fourier Transform,” The Institute of Electronics Engineers of Korea-T, Vol.35, No.1, pp.67-74, 1998.
- US Patent, Fourier-based Misfire Detection Strategy, US 7,530,261 B2, 2009.
-
G. W. Malaczynski and R. Van der Poel, “Phase Diagrams of Different Modes of Misfire Calculated from the Digital Fourier Transformation of Angular Crankshaft Velocity,” SAE 2010-01-0167, 2010.
[https://doi.org/10.4271/2010-01-0167]